Using Window Regression to Gap-Fill Landsat ETM+ Post SLC-Off Data
Abstract
1. Introduction
2. Materials and Methods
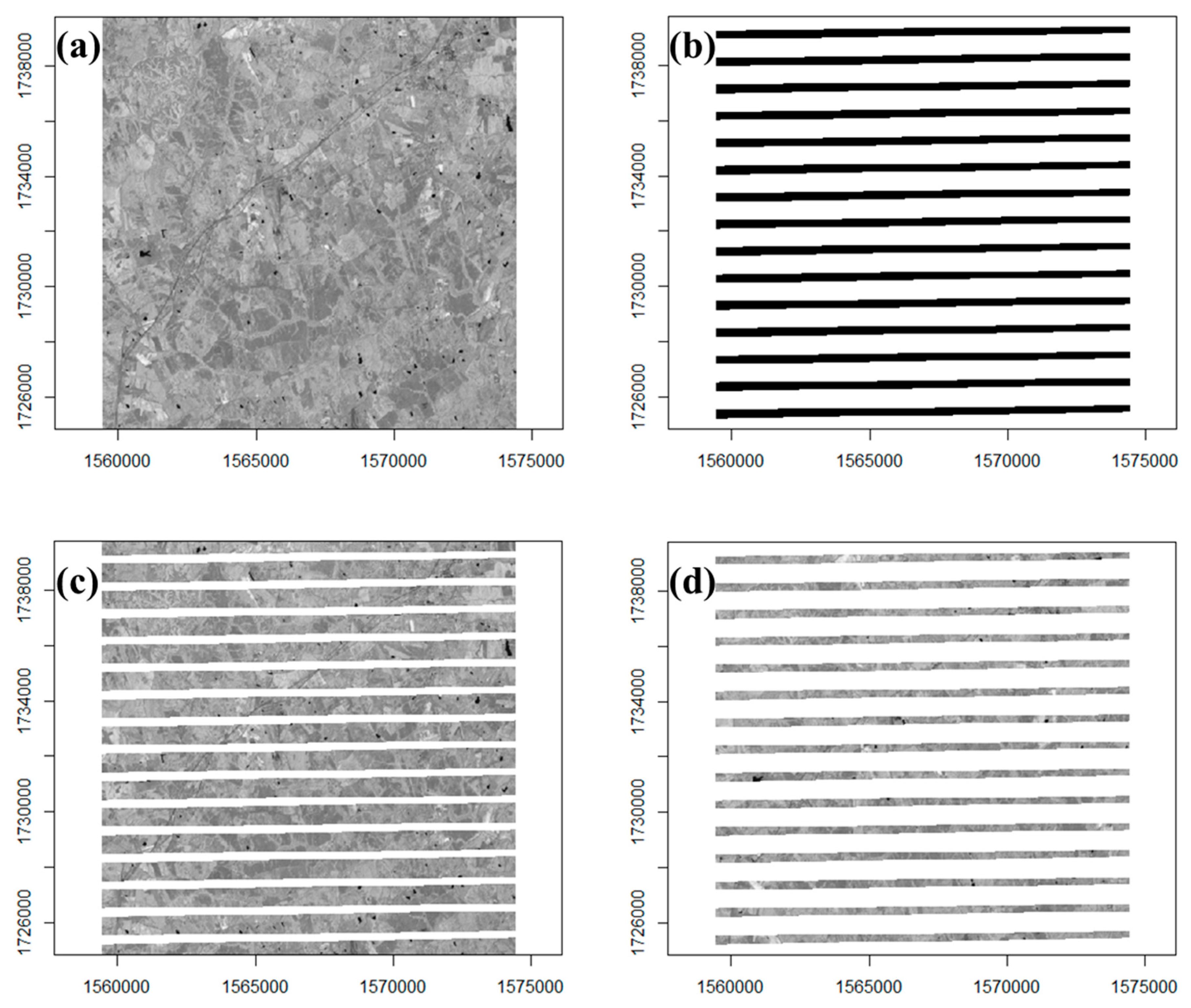
2.1. Study Area
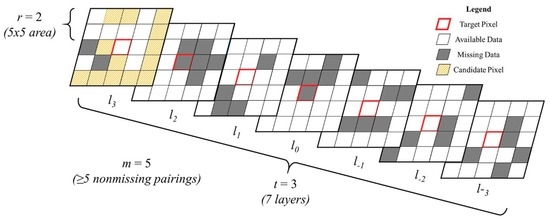
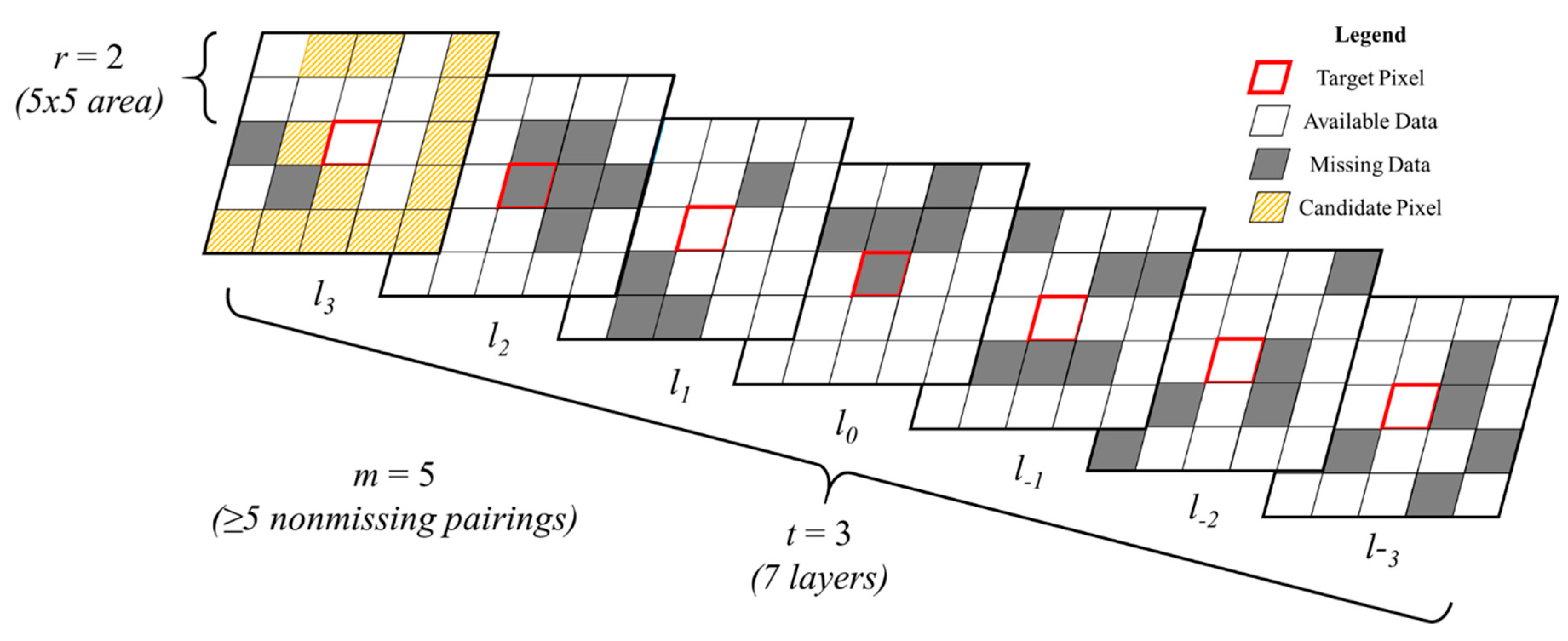
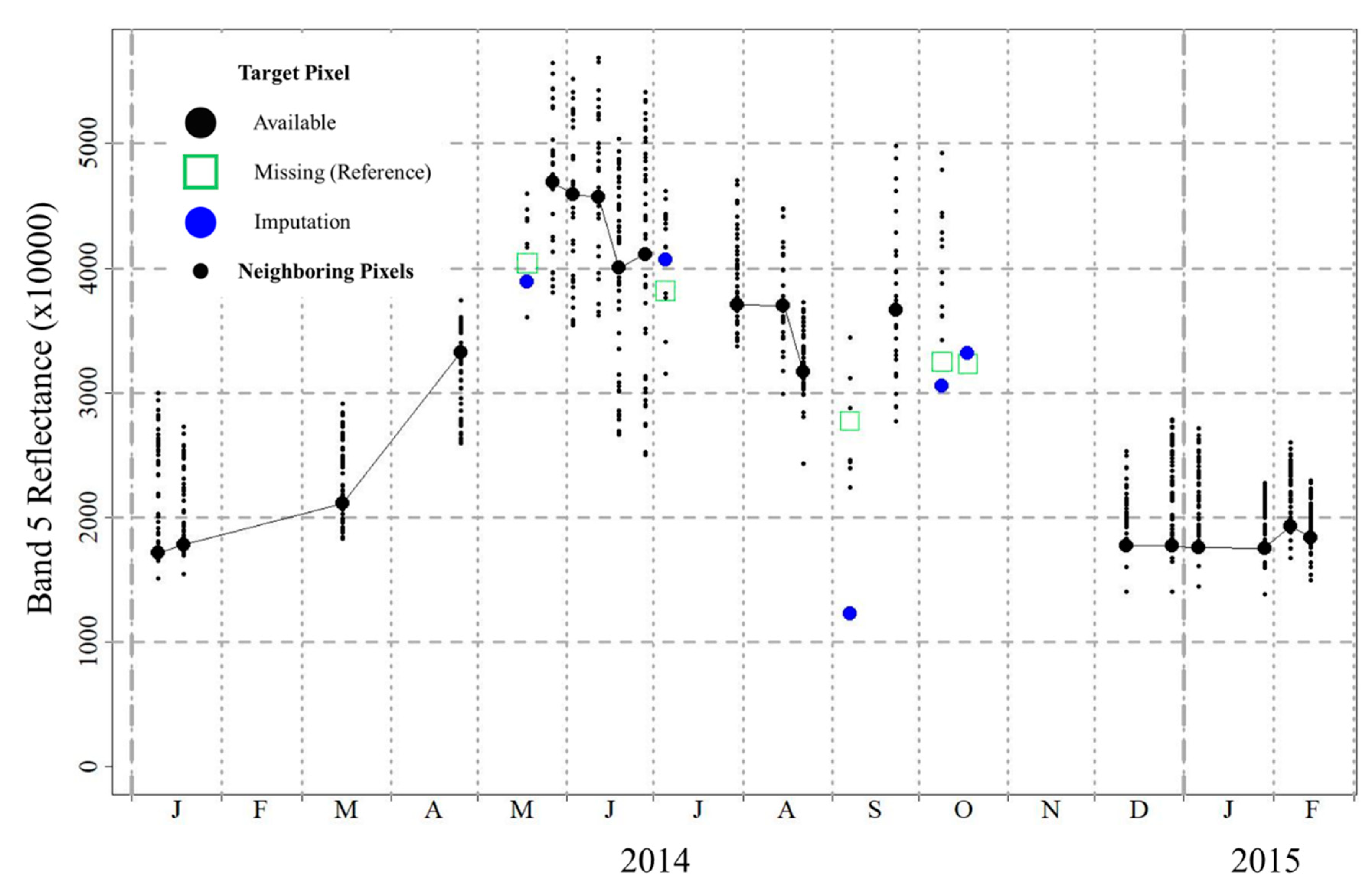
2.2. Window Regression
2.3. Parameter Space Exploration
2.4. Analysis
3. Results
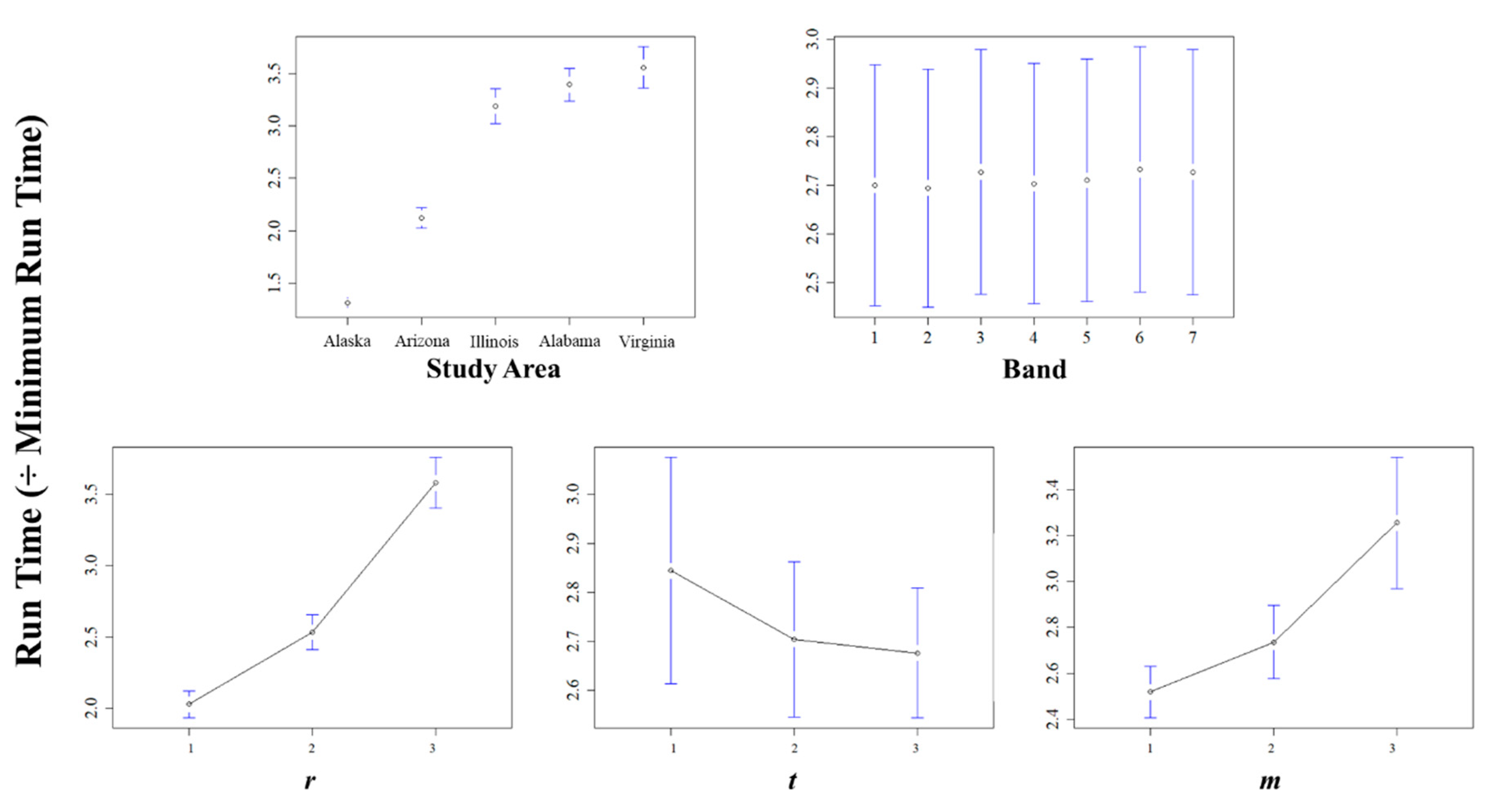
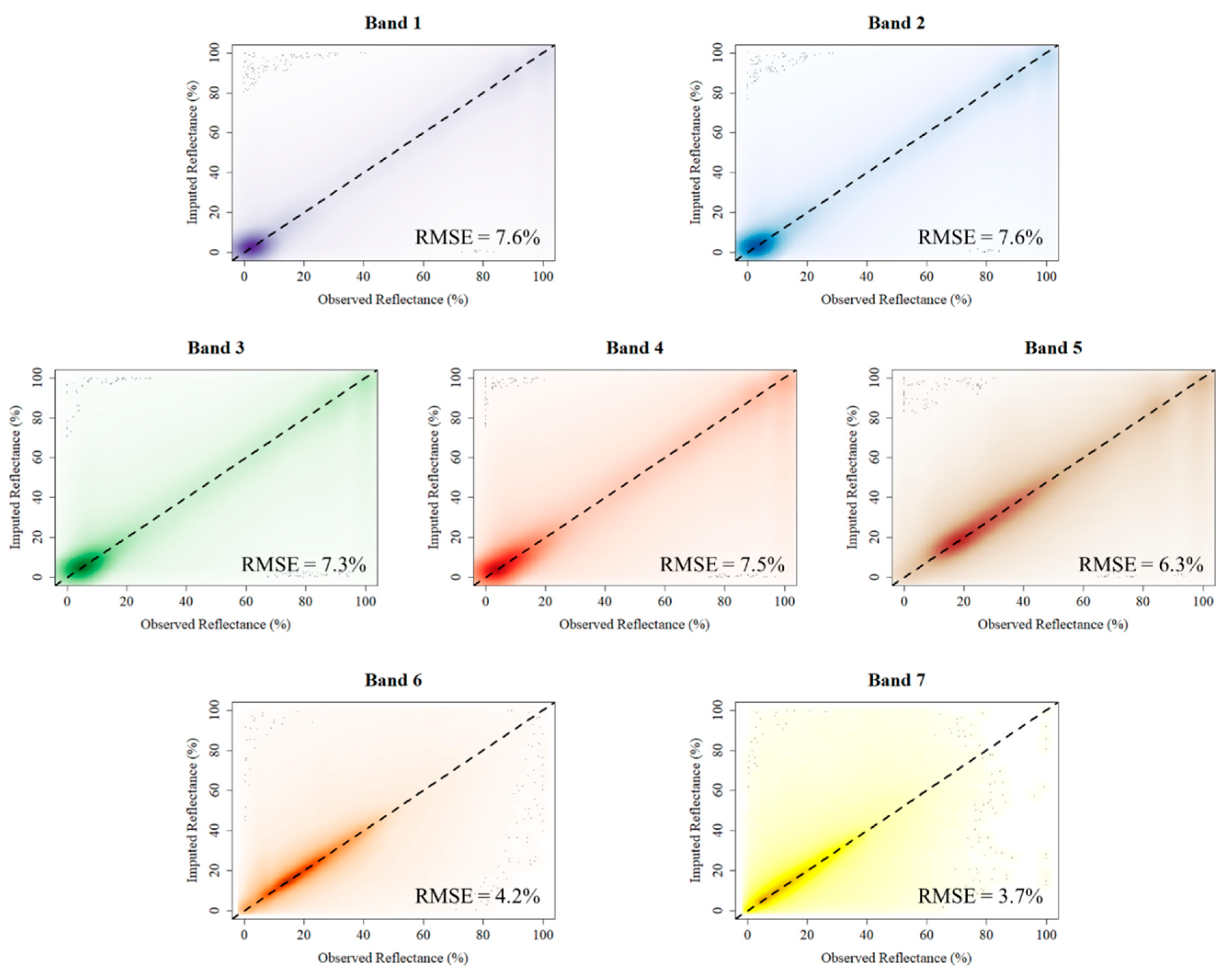
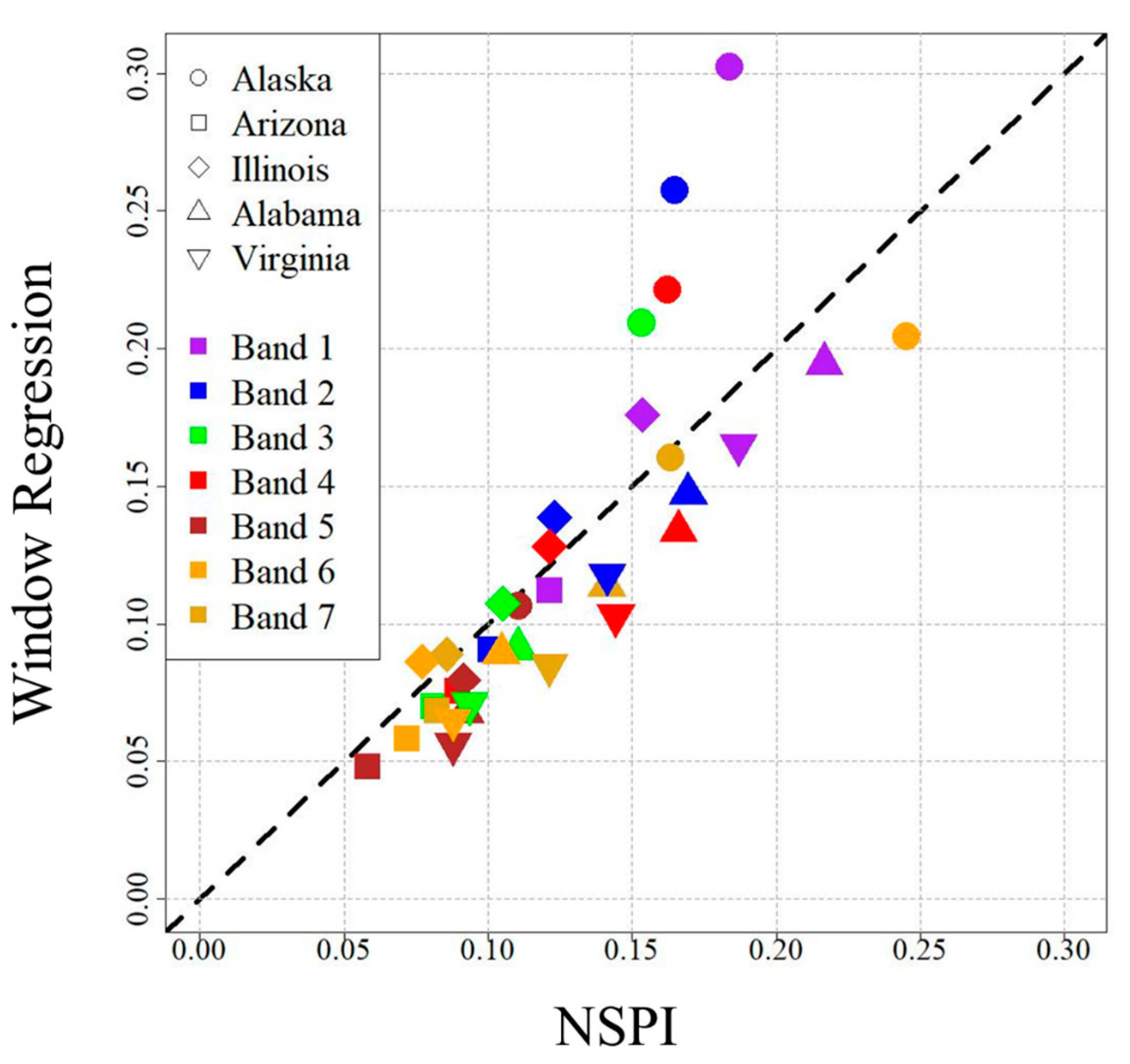
3.1. Overall Results
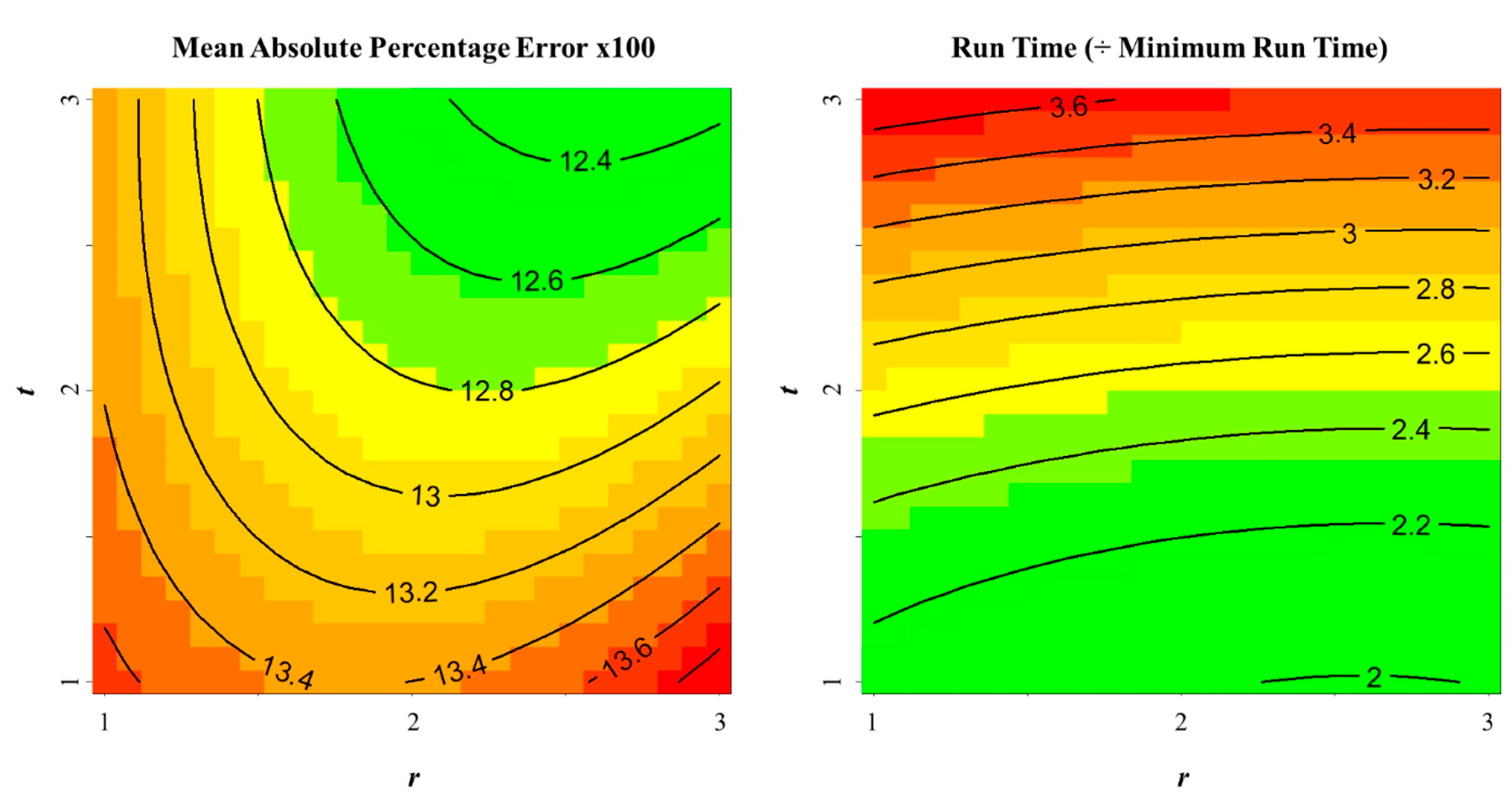
3.2. Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Study Area | ARD Tile | Acquisition Year | Acquisition Date |
|---|---|---|---|
| Western Alaska | AK h3v5 | 2014 | 2/21, 3/9, 3/16, 3/25, 4/1, 4/10, 4/26, 5/19, 8/23, 9/8, 9/24, 10/3 |
| 2015 | 3/12, 3/19, 4/4, 4/20, 4/29, 5/6, 5/31, 6/16, 6/23 | ||
| 2016 | 3/5, 3/21, 3/30 | ||
| Central Arizona | CU h7v12 | 2014 | 1/12, 3/17, 5/4, 5/20, 6/5, 6/21, 7/23, 8/8, 10/11, 10/27, 11/12, 11/28, 12/14, 12/30 |
| 2015 | 1/15, 2/16, 3/4, 3/20, 4/5, 4/21, 5/7, 6/8, 6/24, 7/10 | ||
| East Central Illinois | CU h21v9 | 2014 | 1/19, 2/11, 2/27, 3/15, 4/9, 4/16, 4/25, 5/11, 5/18, 6/3, 7/21, 7/30, 10/25, 11/3 |
| 2015 | 1/13, 2/7, 2/23, 3/11, 4/28, 5/5, 8/2, 8/25, 9/3, 10/21 | ||
| West Central Alabama | CU h22v14 | 2014 | 1/12, 2/13, 3/10, 3/26, 5/4, 5/20, 7/7, 7/16, 8/8, 8/24, 9/25, 10/4, 10/27, 11/21, 11/28, 12/7 |
| 2015 | 1/8, 1/31, 4/21, 4/30, 5/7, 5/23, 6/17, 7/10 | ||
| Central Virginia | CU h27v10 | 2014 | 1/9, 1/18, 3/14, 4/24, 5/17, 5/26, 6/2, 6/11, 6/18, 6/27, 7/4, 7/29, 8/14, 8/21, 9/6, 9/22, 10/8, 10/17, 12/11, 12/27 |
| 2015 | 1/5, 1/28, 2/6, 2/13 |
References
- Loveland, T.R.; Dwyer, J.L. Landsat: building a strong future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Markham, B.L.; Helder, D.L. Forty-year calibrated record of earth-reflected radiance from Landsat: A review. Remote Sens. Environ. 2012, 122, 30–40. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Loveland, T.R.; Woodcock, C.E.; Belward, A.S.; Cohen, W.B.; Fosnight, E.A.; Shaw, J.; Masek, J.G.; Roy, D.P. The global Landsat archive: status, consolidation, and direction. Remote Sens. Environ. 2016, 185, 271–283. [Google Scholar] [CrossRef]
- Zhu, Z. Change detection using landsat time series: A review of frequencies, preprocessing, algorithms, and applications. ISPRS J. Photogramm. 2017, 130, 370–384. [Google Scholar] [CrossRef]
- Yin, G.; Mariethoz, G.; Sun, Y.; McCabe, M.F. A comparison of gap-filling approaches for Landsat-7 satellite data. Int. J. Remote Sens. 2017, 38, 6653–6679. [Google Scholar] [CrossRef]
- Zhang, C.; Li, W.; Travis, D. Gaps-fill of SLC-off Landsat ETM+ satellite image using a geostatistical approach. Int. J. Remote Sens. 2007, 28, 5103–5122. [Google Scholar] [CrossRef]
- Scaramuzza, P.; Micijevic, E.; Chander, G. SLC Gap-Filled Products Phase One Methodology. Available online: https://on.doi.gov/2QEVyGy (accessed on 18 September 2018).
- Maxwell, S. Filling Landsat ETM+ SLC-off gaps using a segmentation model approach. Photogramm. Eng. Remote Sens. 2004, 70, 1109–1112. [Google Scholar]
- Maxwell, S.; Schmidt, G.; Storey, J. A multi-scale segmentation approach to filling gaps in Landsat ETM+ SLC-off images. Int. J. Remote Sens. 2007, 28, 5339–5356. [Google Scholar] [CrossRef]
- Zheng, B.; Campbell, J.B.; Shao, Y.; Wynne, R.H. Broad-scale monitoring of tillage practices using sequential Landsat imagery. Soil Sci. Soc. Am. J. 2013, 77, 1755–1764. [Google Scholar] [CrossRef]
- Pringle, M.; Schmidt, M.; Muir, J. Geostatistical interpolation of SLC-off Landsat ETM+ images. ISPRS J. Photogramm 2009, 64, 654–664. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, D.; Chen, J. A new geostatistical approach for filling gaps in Landsat ETM+ SLC-off images. Remote Sens. Environ. 2012, 124, 49–60. [Google Scholar] [CrossRef]
- Malambo, L.; Heatwole, C.D. A multitemporal profile-based interpolation method for gap filling nonstationary data. IEEE Trans. Geosci. Remote 2016, 54, 252–261. [Google Scholar] [CrossRef]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ. 2008, 112, 3112–3130. [Google Scholar] [CrossRef]
- Wijedasa, L.S.; Sloan, S.; Michelakis, D.G.; Clements, G.R. Overcoming limitations with Landsat imagery for mapping of peat swamp forests in Sundaland. Remote Sens. 2012, 4, 2595–2618. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Brooks, E.B.; Coulston, J.W.; Wynne, R.H.; Thomas, V.A. Improving the precision of dynamic forest parameter estimates using Landsat. Remote Sens. Environ. 2016, 179, 162–169. [Google Scholar] [CrossRef]
- Cohen, W.; Healey, S.; Yang, Z.; Stehman, S.; Brewer, C.; Brooks, E.; Gorelick, N.; Huang, C.; Hughes, M.; Kennedy, R.; et al. How similar are forest disturbance maps derived from different Landsat time series algorithms? Forests 2017, 8. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.; Kenneth Brewer, C.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.; Joseph Hughes, M.; Kennedy, R.E.; et al. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Brooks, E.B.; Thomas, V.A.; Wynne, R.H.; Coulston, J.W. Fitting the multitemporal curve: A Fourier series approach to the missing data problem in remote sensing analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3340–3353. [Google Scholar] [CrossRef]
- Wilson, B.; Knight, J.; McRoberts, R. Harmonic regression of Landsat time series for modeling attributes from national forest inventory data. ISPRS J. Photogramm. 2018, 137, 29–46. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of forest disturbance using all available Landsat imagery. Remote Sens. Environ. 2012, 122, 75–91. [Google Scholar] [CrossRef]
- Brooks, E.B.; Wynne, R.H.; Thomas, V.A.; Blinn, C.E.; Coulston, J.W. On-the-fly massively multitemporal change detection using statistical quality control charts and Landsat data. Trans. Geosci. Remote Sens. 2014, 52, 3316–3332. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- de Oliveira, J.C.; Epiphanio, J.C.N.; Rennó, C.D. Window regression: A spatial-temporal analysis to estimate pixels classified as low-quality in MODIS NDVI time series. Remote Sens. 2014, 6, 3123–3142. [Google Scholar] [CrossRef]
- EarthExplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 19 September 2018).
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 18 September 2018).
- Hijmans, R.J.; van Etten, J. Raster: Geographic Data Analysis and Modeling. Available online: https://bit.ly/2xi9I8C (accessed on 18 September 2018).
- Greenberg, J. Spatial Tools: R FUNctions for Working with Spatial Data. Available online: https://bit.ly/2peW5T0 (accessed on 18 September 2018).
- Lenth, R.V. Response-surface methods in R, using rsm. J. Stat. Softw. 2009, 32, 1–17. [Google Scholar] [CrossRef]
- Zhu, X.; Gao, F.; Liu, D.; Chen, J. A modified neighborhood similar pixel interpolator approach for removing thick clouds in Landsat images. IEEE Geosci. Remote Sens. 2012, 9, 521–525. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Chen, J.; Liu, D. An Automatic System for Reconstructing High-Quality Seasonal Landsat Time Series. Available online: https://bit.ly/2D8FgTH (accessed on 18 September 2018).
- Open Source Code—Remote Sensing & Spatial Analysis Lab. Available online: https://xiaolinzhu.weebly.com/open-source-code.html (accessed on 19 September 2018).
- Snyder, G.I. The 3D Elevation Program: Summary of Program Direction. Available online: https://pubs.usgs.gov/fs/2012/3089/ (accessed on 18 September 2018).




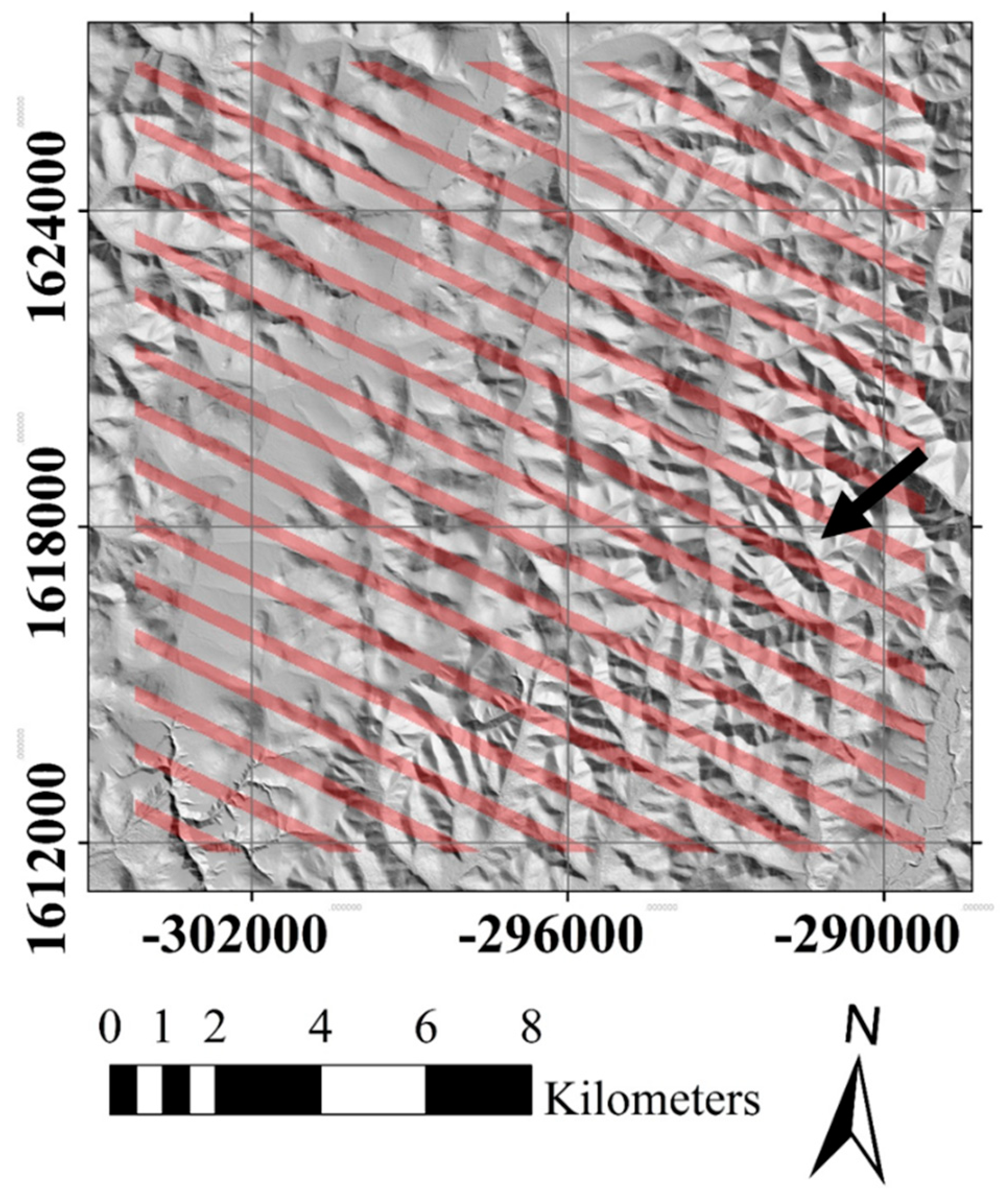
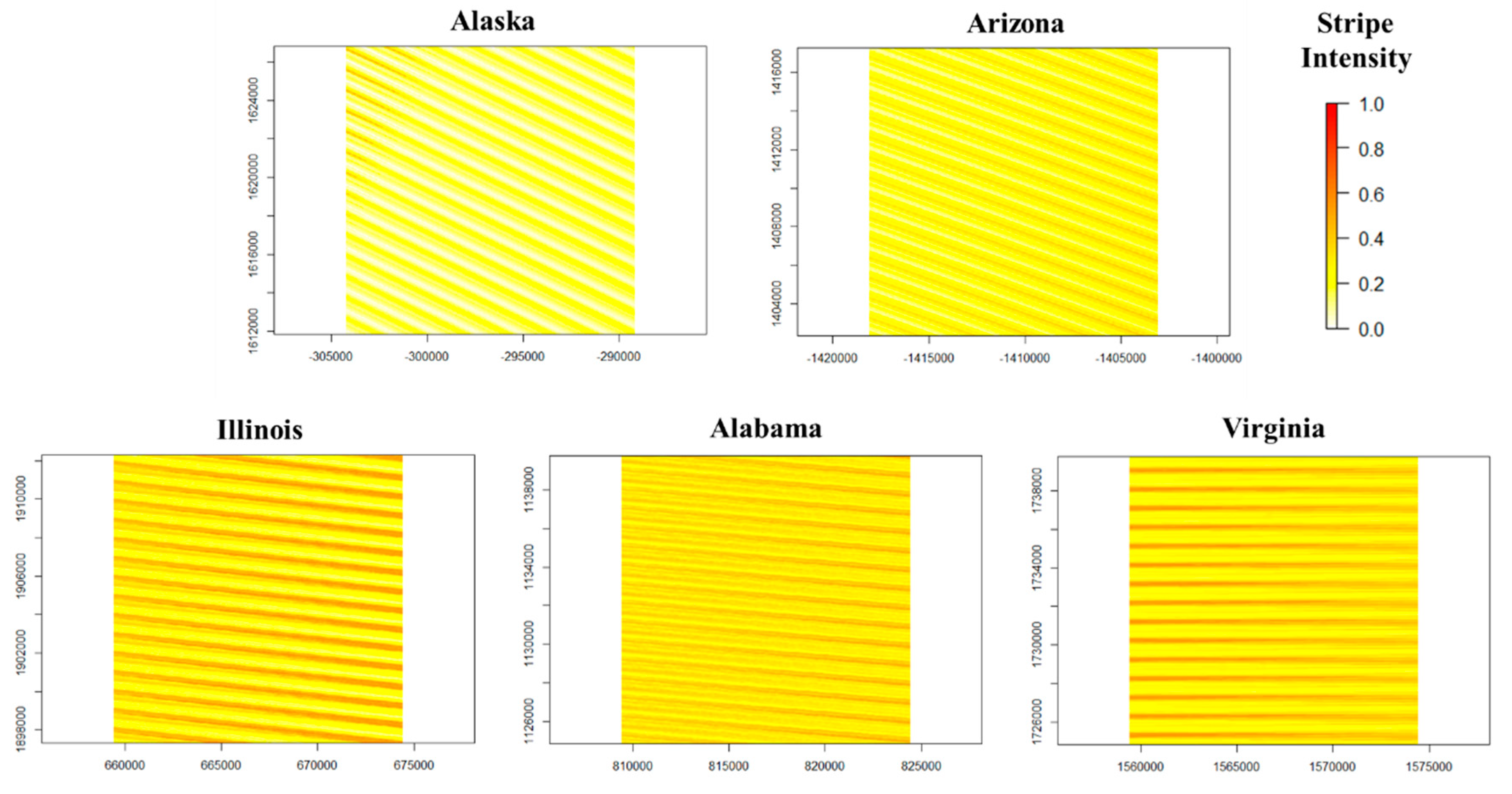
| Study Area | Subregion | ARD Tile | Example WRS2 Path/Row | Nearby City/Town | Features |
|---|---|---|---|---|---|
| Alaska | Western Alaska | AK h3v5 | 77/15 | Shaktoolik | Snowy mountains |
| Arizona | Central Arizona | CU h7v12 | 37/36 | Sedona | Arid land |
| Illinois | East Central Illinois | CU h21v9 | 23/32 | Villa Grove | Agricultural land |
| Alabama | West Central Alabama | CU h22v14 | 21/37 | Centreville | Loblolly pine plantations |
| Virginia | Central Virginia | CU h27v10 | 16/34 | Amelia Court House | Deciduous forest |
| Spatial Radius, (Window Size = | Temporal Radius, (Window Depth = | Minimum Pairings, |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 3, 5 | |
| 3 | 3, 5, 7 | |
| 2 | 1 | 3 |
| 2 | 3, 5 | |
| 3 | 3, 5, 7 | |
| 3 | 1 | 3 |
| 2 | 3, 5 | |
| 3 | 3, 5, 7 |
| Parameter | Description | Value |
|---|---|---|
| min_similar | The minimum sample size of similar pixels | 30 |
| num_class | The number of classes | 4 |
| num_band | The number of spectral bands in each image stack | 1 |
| DN_min | The minimum allowed spectral value | 0 |
| DN_max | The maximum allowed spectral value | 10,000 |
| patch_long | The size of the block in pixels (for processing) | 500 |
| Factor | MAPE | Run Time |
|---|---|---|
| Study Area | X | X * |
| Band | X | |
| r | X | X |
| t | X | |
| m | X | |
| r × Study Area | X | X * |
| r × Band | ||
| r × t | X | |
| r × m | X | |
| t × m |
| Band | Alaska | Arizona | Illinois | Alabama | Virginia |
|---|---|---|---|---|---|
| 1 | X | X | X | ||
| 2 | X | X | X | ||
| 3 | X | X | X | ||
| 4 | X | X | X | ||
| 5 | X | X | X | X | X |
| 6 | X | X | X | X | |
| 7 | X | X | X | X |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brooks, E.B.; Wynne, R.H.; Thomas, V.A. Using Window Regression to Gap-Fill Landsat ETM+ Post SLC-Off Data. Remote Sens. 2018, 10, 1502. https://doi.org/10.3390/rs10101502
Brooks EB, Wynne RH, Thomas VA. Using Window Regression to Gap-Fill Landsat ETM+ Post SLC-Off Data. Remote Sensing. 2018; 10(10):1502. https://doi.org/10.3390/rs10101502
Chicago/Turabian StyleBrooks, Evan B., Randolph H. Wynne, and Valerie A. Thomas. 2018. "Using Window Regression to Gap-Fill Landsat ETM+ Post SLC-Off Data" Remote Sensing 10, no. 10: 1502. https://doi.org/10.3390/rs10101502
APA StyleBrooks, E. B., Wynne, R. H., & Thomas, V. A. (2018). Using Window Regression to Gap-Fill Landsat ETM+ Post SLC-Off Data. Remote Sensing, 10(10), 1502. https://doi.org/10.3390/rs10101502