Analysis of the Spatial Variability of Land Surface Variables for ET Estimation: Case Study in HiWATER Campaign
Abstract
:1. Introduction
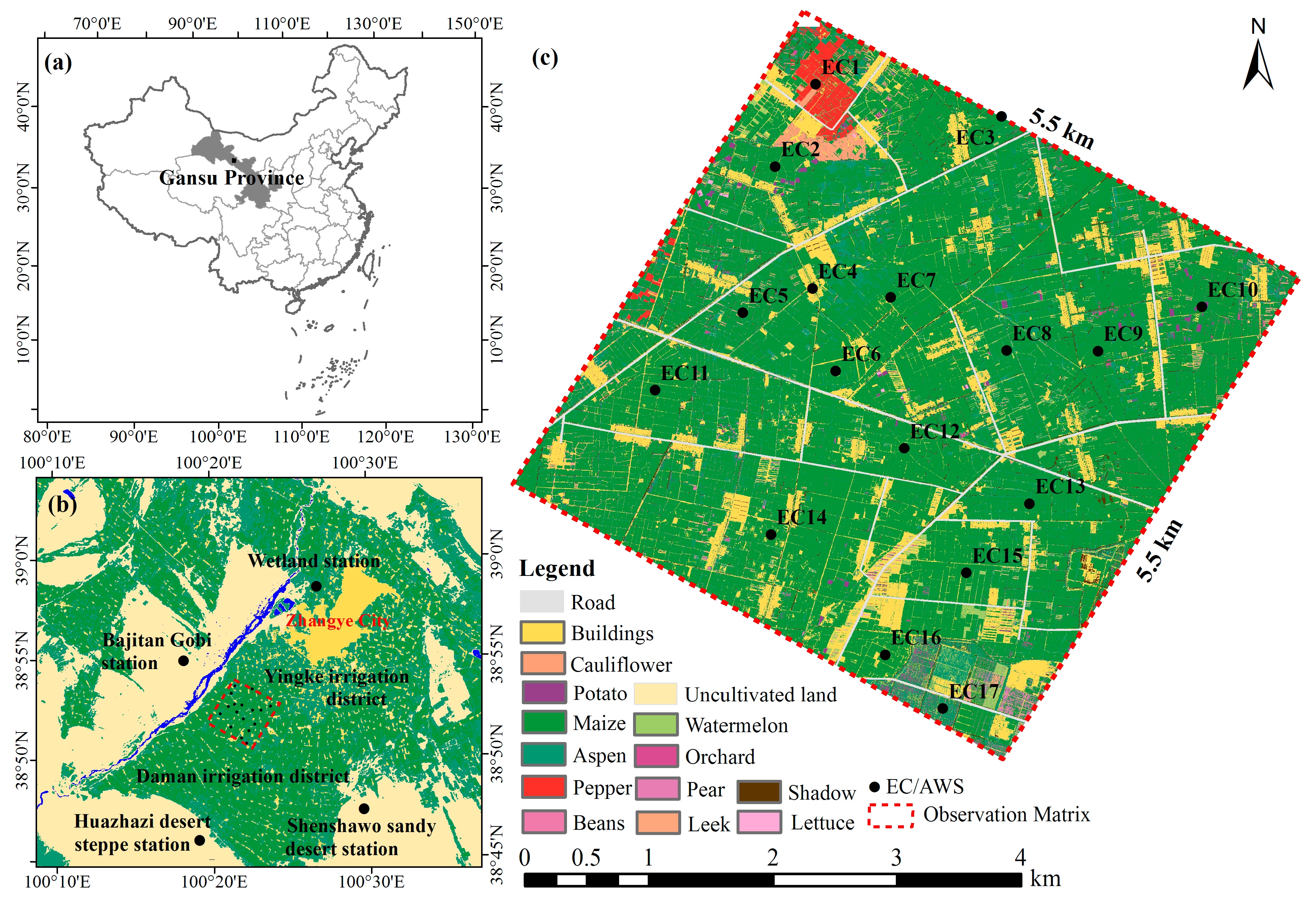
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
2.2.1. Ground Observation Data
2.2.2. Airborne Data
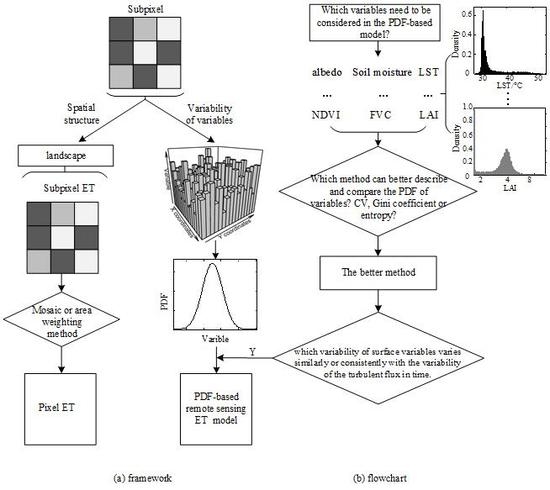
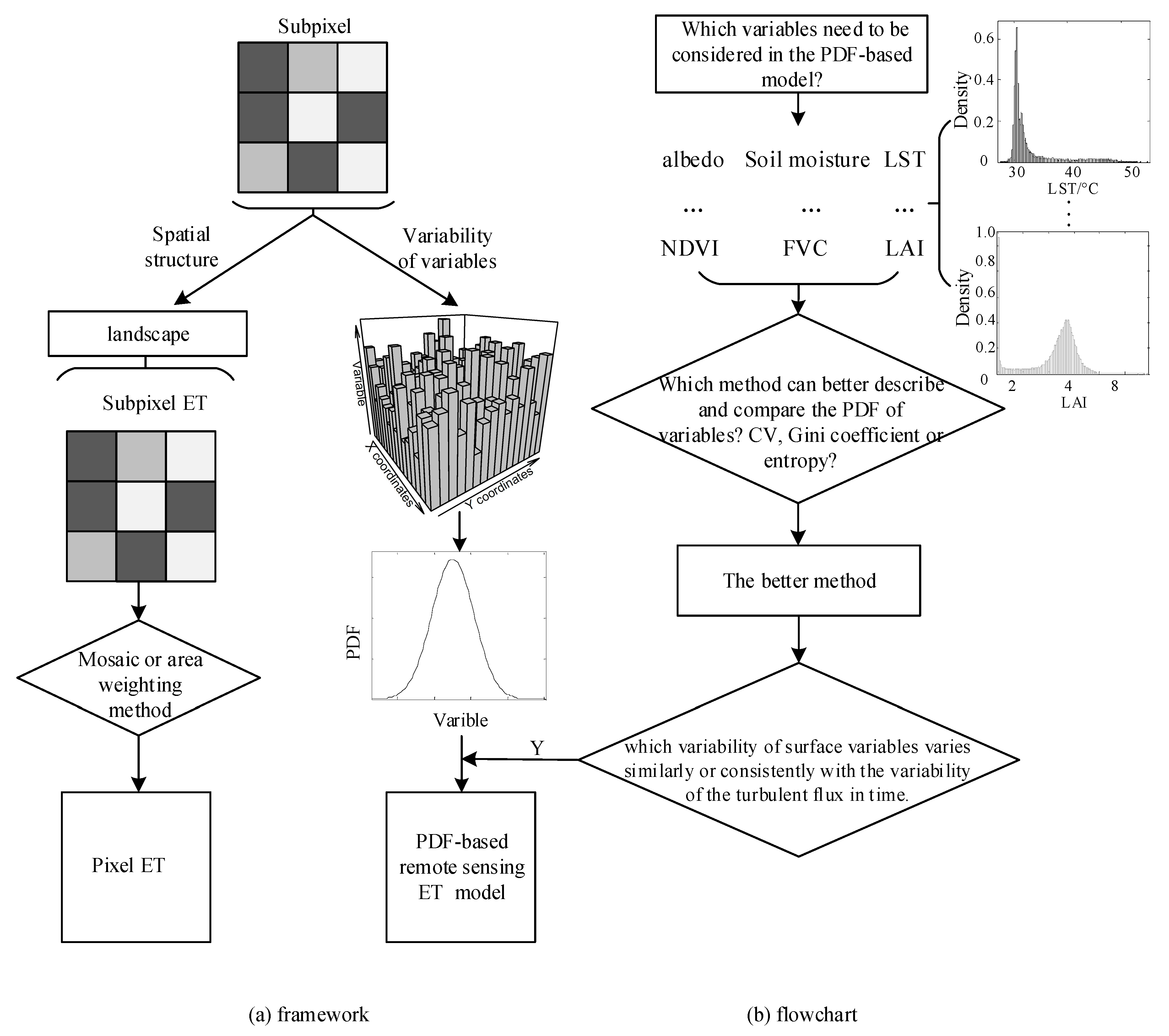
3. Methodology
4. Results and Analysis
4.1. Analysis Based on Simulation Data
4.2. Analysis Based on Field Experimental Data
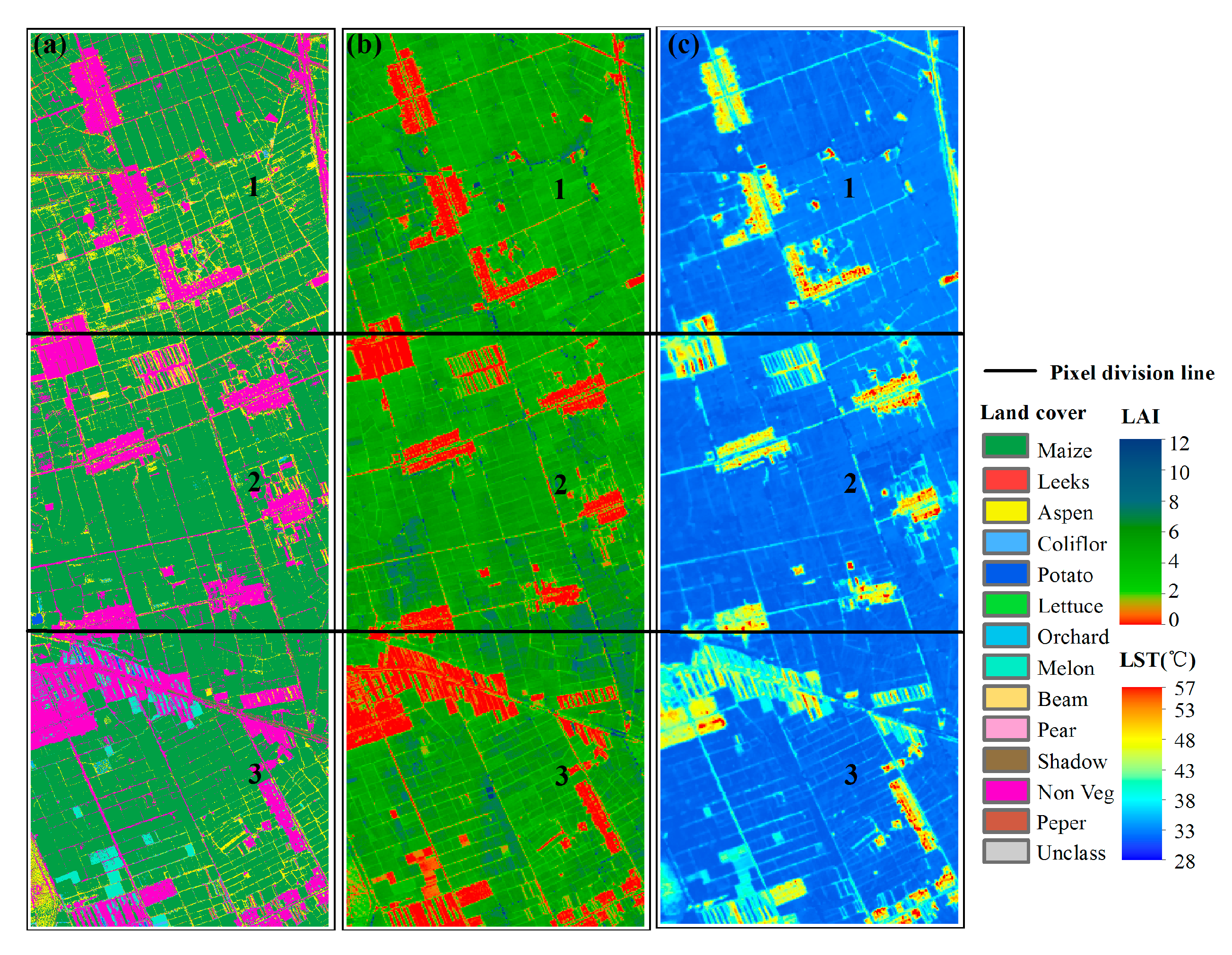
4.2.1. Analysis Based on Airborne Data
- (1)
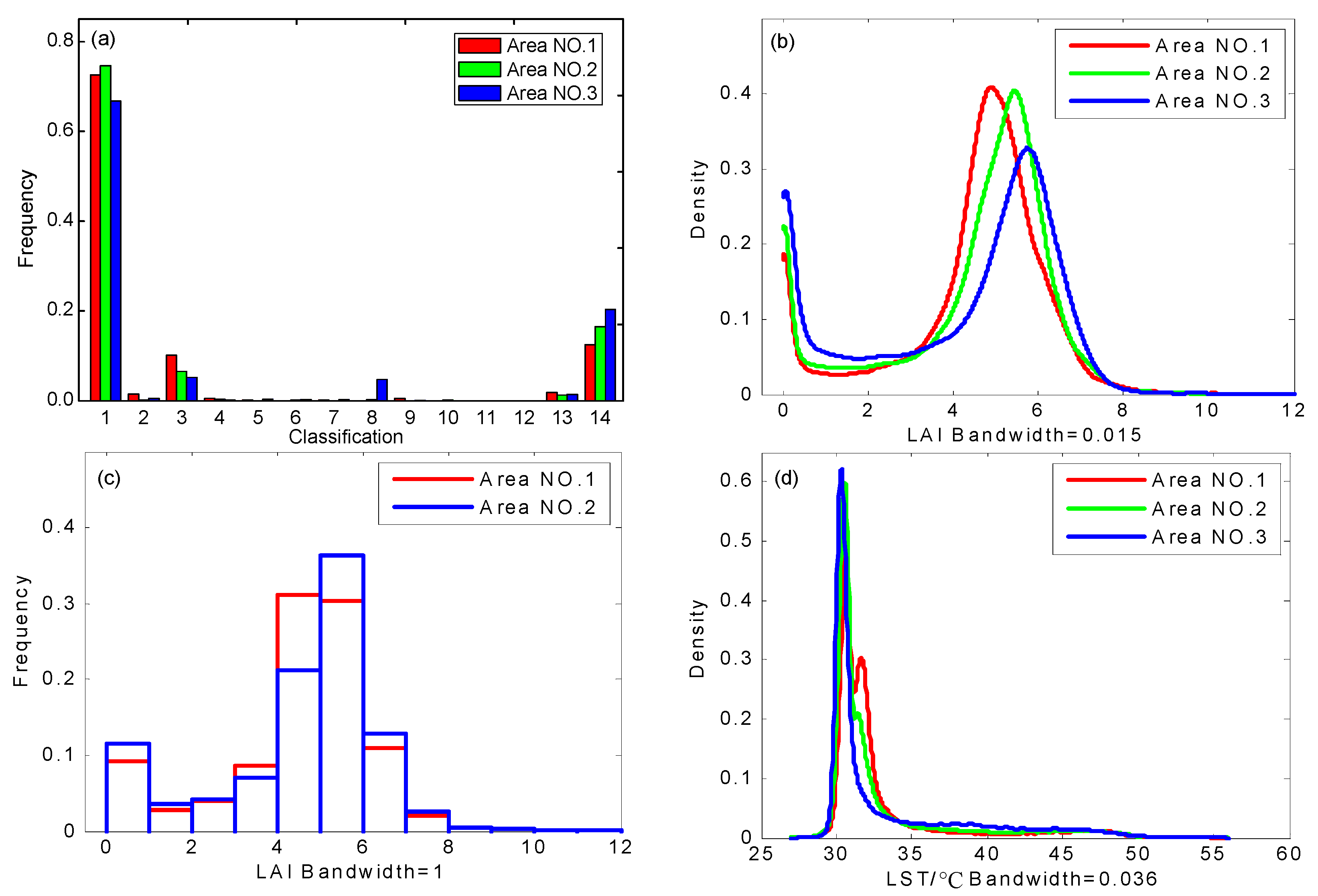
- Figure 6b shows that the LAI values of the three study areas are mainly distributed near 0 and high value (between 4.0 and 7.0), thus showing a bimodal distribution. For the LAI, the CV and Gini coefficient calculation results show that Area NO. 2 has more variation than Area NO. 1, although the entropy results show that Area NO. 1 is more variable. A comparison of the frequency distribution histograms (bandwidth = 1) of LAI in the two study areas (Figure 6c) shows that the LAI peak width of Area NO. 2 is narrower, meaning that the probability distribution of LAI in Area NO. 2 is more concentrated; therefore, the entropy of Area NO. 2 is smaller than that of Area NO. 1. Moreover, the proportion of non-vegetated area (LAI = 0) in Area NO. 2 is larger, which results in a widened standard deviation and a lower mean. Therefore, the calculated CV and Gini coefficient results are relatively large. However, the spatial variability of LAI in Area NO. 1 is greater overall than that in Area NO. 2.
- (2)
- The LST range of Area NO. 1~Area NO. 3 is nearly 30 °C, and the distribution of the values is mainly between 30~35 °C (Figure 6d). For the LST, the entropy, CV and Gini coefficient calculation results are consistent and all are incremental; thus, the LST variability of the three study areas is as follows: Area NO. 3 > Area NO. 2 > Area NO. 1.
- (3)
- For the variability of variables, LAI > LST. Although the value range of LST is larger than that of LAI, the variability of LAI is larger than that of LST, which can be directly obtained via calculations using the three methods.
- (4)
- The variability of LST seems to have a certain relationship with the variability of LAI, in this paper, the LST-LAI variability is negative. Because of the complex relationship between vegetation information and LST (e.g., NDVI-LST) [48], the correlation between the two variabilities needs to be further studied.
4.2.2. Analysis Based on Ground Observation Data
5. Discussion
- Entropy is more consistent with PDF when describing spatial variability, and in some extreme distributions, entropy can express spatial variability more accurately, while CV and Gini coefficients cannot.
- In this paper, the unit of entropy is nats, which can be used directly to compare the spatial variability of variables. While the CV and Gini coefficients cannot, they are affected by the specific value (i.e., the average) of the variable.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Peng, Z.Q.; Xin, X.Z.; Jiao, J.J.; Zhou, T.; Liu, Q.H. Remote sensing algorithm for surface evapotranspiration considering landscape and statistical effects on mixed pixels. Hydrol. Earth Syst. Sci. 2016, 20, 4409–4438. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Xiong, Y.J.; Qiu, G.Y.; Zhang, Q.T. Is scale really a challenge in evapotranspiration estimation? A multi-scale study in the Heihe oasis using thermal remote sensing and the three-temperature model. Agric. For. Meteorol. 2016, 230–231, 128–141. [Google Scholar] [CrossRef]
- Li, X.J.; Xin, X.Z.; Jiao, J.J.; Peng, Z.Q.; Zhang, H.L.; Shao, S.S.; Liu, Q.H. Estimating subpixel surface heat fluxes through applying temperature-sharpening methods to MODIS data. Remote Sens. 2017, 9, 836. [Google Scholar] [CrossRef]
- Jacob, F.; Weiss, M. Mapping biophysical variables from solar and thermal infrared remote sensing: Focus on agricultural landscapes with spatial heterogeneity. IEEE Geosci. Remote Sens. Lett. 2016, 11, 1844–1848. [Google Scholar] [CrossRef]
- Kustas, W.; Li, F.; Jackson, T.; Prueger, J.; MacPherson, J.; Wolde, M. Effects of remote sensing pixel resolution on modeled energy flux variability of croplands in Iowa. Remote Sens. Environ. 2004, 92, 535–547. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluating the effects of subpixel heterogeneity on pixel average fluxes. Remote Sens. Environ. 2000, 74, 327–342. [Google Scholar] [CrossRef]
- Arain, A.M.; Michaud, J.; Shuttleworth, W.J.; Dolman, A.J. Testing of vegetation parameter aggregation rules applicable to the Biosphere Atmosphere Transfer Scheme (BATS) and the FIFE site. J. Hydrol. 1996, 177, 1–22. [Google Scholar] [CrossRef]
- Chehbouni, A.; Njoku, E.; Lhomme, J.; Kerr, Y. Approach for averaging surface parameters and fluxes over heterogeneous terrain. J. Clim. 1995, 8, 1386–1393. [Google Scholar] [CrossRef]
- Koster, R.D.; Suarez, M.J. A comparative analysis of two land surface heterogeneity representations. J. Clim. 1992, 5, 1379–1390. [Google Scholar] [CrossRef]
- Li, B.; Avissar, R. The impact of spatial variability of land-surface characteristics on land-surface heat fluxes. J. Clim. 1994, 7, 527–537. [Google Scholar] [CrossRef]
- Blyth, E.M.; Harding, R.J. Application of aggregation models to surface heat flux from the Sahelian tiger bush. Agric. For. Meteorol. 1995, 72, 213–235. [Google Scholar] [CrossRef]
- Avissar, R. Conceptual aspects of a statistical-dynamical approach to represent landscape subgrid-scale heterogeneities in atmospheric models. J. Geophys. Res. Atmos. 1992, 97, 2729–2742. [Google Scholar] [CrossRef]
- Maayar, M.E.; Chen, J.M. Spatial scaling of evapotranspiration as affected by heterogeneities in vegetation, topography, and soil texture. Remote Sens. Environ. 2006, 102, 33–51. [Google Scholar] [CrossRef]
- Tittebrand, A.; Berger, F. Spatial heterogeneity of satellite derived land surface parameters and energy flux densities for LITFASS-area. Atmos. Chem. Phys. 2009, 9, 16219–16254. [Google Scholar] [CrossRef]
- Mölders, N.; Raabe, A. Numerical investigations on the influence of subgrid-scale surface heterogeneity on evapotranspiration and cloud processes. J. Appl. Meteorol. 1996, 35, 782–795. [Google Scholar] [CrossRef]
- Norman, J.M.; Anderson, M.C.; Kustas, W.P.; French, A.N.; Mecikalski, J.; Torn, R.; Diak, G.R.; Schmugge, T.J.; Tanner, B.C.W. Remote sensing of surface energy fluxes at 101-m pixel resolutions. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Bayala, M.I.; Rivas, R.E. Enhanced sharpening procedures on edge difference and water stress index basis over heterogeneous landscape of sub-humid region. Egypt. J. Remote Sens. Space Sci. 2014, 17, 17–27. [Google Scholar] [CrossRef]
- Mukherjee, S.; Joshi, P.K.; Garg, R.D. A comparison of different regression models for downscaling Landsat and MODIS land surface temperature images over heterogeneous landscape. Adv. Space Res. 2014, 54, 655–669. [Google Scholar] [CrossRef]
- Wu, H.; Tang, B.H.; Li, Z.L. Impact of nonlinearity and discontinuity on the spatial scaling effects of the leaf area index retrieved from remotely sensed data. Int. J. Remote Sens. 2013, 34, 3503–3519. [Google Scholar] [CrossRef]
- Zeng, X.M.; Zhao, M.; Su, B.K.; Tang, J.P.; Zheng, Y.Q.; Zhang, Y.J.; Chen, J. Effects of the land-surface heterogeneities in temperature and moisture from the “combined approach” on regional climate: A sensitivity study. Glob. Planet. Chang. 2003, 37, 247–263. [Google Scholar] [CrossRef]
- Giorgi, F. An approach for the representation of surface heterogeneity in land surface models. Part II: Validation and sensitivity experiments. Mon. Weather Rev. 1997, 125, 1900–1919. [Google Scholar] [CrossRef]
- Yeh, P.J.F.; Eltahir, E.A.B. Representation of water table dynamics in a land surface scheme. Part I: Model development. J. Clim. 2005, 18, 1861–1880. [Google Scholar] [CrossRef]
- Giorgi, F. An approach for the representation of surface heterogeneity in land surface models. Part I: Theoretical framework. Mon. Weather Rev. 1997, 125, 1885–1899. [Google Scholar] [CrossRef]
- Wang, Q.; Ni, J.; Tenhunen, J. Application of a geographically-weighted regression analysis to estimate net primary production of Chinese forest ecosystems. Glob. Ecol. Biogeogr. 2010, 14, 379–393. [Google Scholar] [CrossRef]
- Odongo, V.; Hamm, N.; Milton, E. Spatio-temporal assessment of Tuz Gölü, Turkey as a potential radiometric vicarious calibration site. Remote Sens. 2014, 6, 2494–2513. [Google Scholar] [CrossRef]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Quantifying spatial heterogeneity at the landscape scale using variogram models. Remote Sens. Environ. 2006, 103, 81–96. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Rahman, A.F.; Gamon, J.A.; Sims, D.A.; Schmidts, M. Optimum pixel size for hyperspectral studies of ecosystem function in southern California chaparral and grassland. Remote Sens. Environ. 2003, 84, 192–207. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.S. Combined spectral and spatial processing of ERTS imagery data. Remote Sens. Environ. 1974, 3, 3–13. [Google Scholar] [CrossRef]
- Csillag, F.; Kabos, S. Wavelets, boundaries, and the spatial analysis of landscape pattern. Écoscience 2002, 9, 177–190. [Google Scholar] [CrossRef]
- Qiu, B.W.; Zeng, C.Y.; Cheng, C.C.; Tang, Z.H.; Gao, J.Y.; Sui, Y.P. Characterizing landscape spatial heterogeneity in multisensor images with variogram models. Chin. Geogr. Sci. 2014, 24, 317–327. [Google Scholar] [CrossRef]
- Cosh, M.H.; Brutsaert, W. Microscale structural aspects of vegetation density variability. J. Hydrol. 2003, 276, 128–136. [Google Scholar] [CrossRef]
- Zhang, L.J.; Ma, Z.H.; Luo, G. An evaluation of spatial autocorrelation and heterogeneity in the residuals of six regression models. For. Sci. 2009, 55, 533–548. [Google Scholar]
- Hintz, M.; Lennartz-Sassinek, S.; Liu, S.F.; Shao, Y.P. Quantification of land-surface heterogeneity via entropy spectrum method. J. Geophys. Res. Atmos. 2014, 119, 8764–8777. [Google Scholar] [CrossRef]
- Brunsell, N.A.; Ham, J.M.; Owensby, C.E. Assessing the multi-resolution information content of remotely sensed variables and elevation for evapotranspiration in a tall-grass prairie environment. Remote Sens. Environ. 2008, 112, 2977–2987. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index–radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Wang, D.; Wang, G.; Anagnostou, E.N. Use of satellite-based precipitation observation in improving the parameterization of canopy hydrological processes in land surface models. J. Hydrometeorol. 2005, 6, 745–763. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Song, L.S.; Zhao, Q.Y.; Ge, Y.; Xu, T.R.; Ma, Y.F.; Zhu, Z.L.; Jia, Z.Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230, 97–113. [Google Scholar] [CrossRef]
- Xu, Z.W.; Liu, S.M.; Li, X.; Shi, S.J.; Wang, J.M.; Zhu, Z.L.; Xu, T.R.; Wang, W.Z.; Ma, M.G. Intercomparison of surface energy flux measurement systems used during the HiWATER-MUSOEXE. J. Geophys. Res. Atmos. 2013, 118, 13140–13157. [Google Scholar] [CrossRef]
- Ran, Y.H.; Li, X.; Sun, R.; Kljun, N.; Zhang, L.; Wang, X.F.; Zhu, G.F. Spatial representativeness and uncertainty of eddy covariance carbon flux measurements for upscaling net ecosystem productivity to the grid scale. Agric. For. Meteorol. 2016, 230–231, 114–124. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Huang, N.; Wang, C.; Gao, S.; Wu, C. Airborne LiDAR technique for estimating biomass components of maize: A case study in Zhangye City, Northwest China. Ecol. Indic. 2015, 57, 486–496. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, C.Y.; Xiao, Q.; Yan, G.J.; Fang, L. Separating vegetation and soil temperature using airborne multiangular remote sensing image data. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 66–75. [Google Scholar] [CrossRef]
- Valbuena, R.; Maltamo, M.; Mehtätalo, L.; Packalen, P. Key structural features of boreal forests may be detected directly using L-moments from airborne lidar data. Remote Sens. Environ. 2017, 194, 437–446. [Google Scholar] [CrossRef]
- Journel, A.G.; Deutsch, C.V. Entropy and spatial disorder. Math. Geol. 1993, 25, 329–355. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Silverman, B.W. Density estimation in the exploration and presentation of data. In Density Estimation for Statistics and Data Analysis, 1st ed.; CRC Press: Boca Raton, FL, USA, 1986; pp. 2–4. [Google Scholar]
- Raynolds, M.K.; Comiso, J.C.; Walker, D.A.; Verbyla, D. Relationship between satellite-derived land surface temperatures, arctic vegetation types, and NDVI. Remote Sens. Environ. 2008, 112, 1884–1894. [Google Scholar] [CrossRef]
- Jin, R.; Li, X.; Yan, B.; Li, X.; Luo, W.; Ma, M.; Guo, J.; Kang, J.; Zhu, Z.; Zhao, S. A nested ecohydrological wireless sensor network for capturing the surface heterogeneity in the midstream areas of the Heihe River Basin, China. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2015–2019. [Google Scholar] [CrossRef]
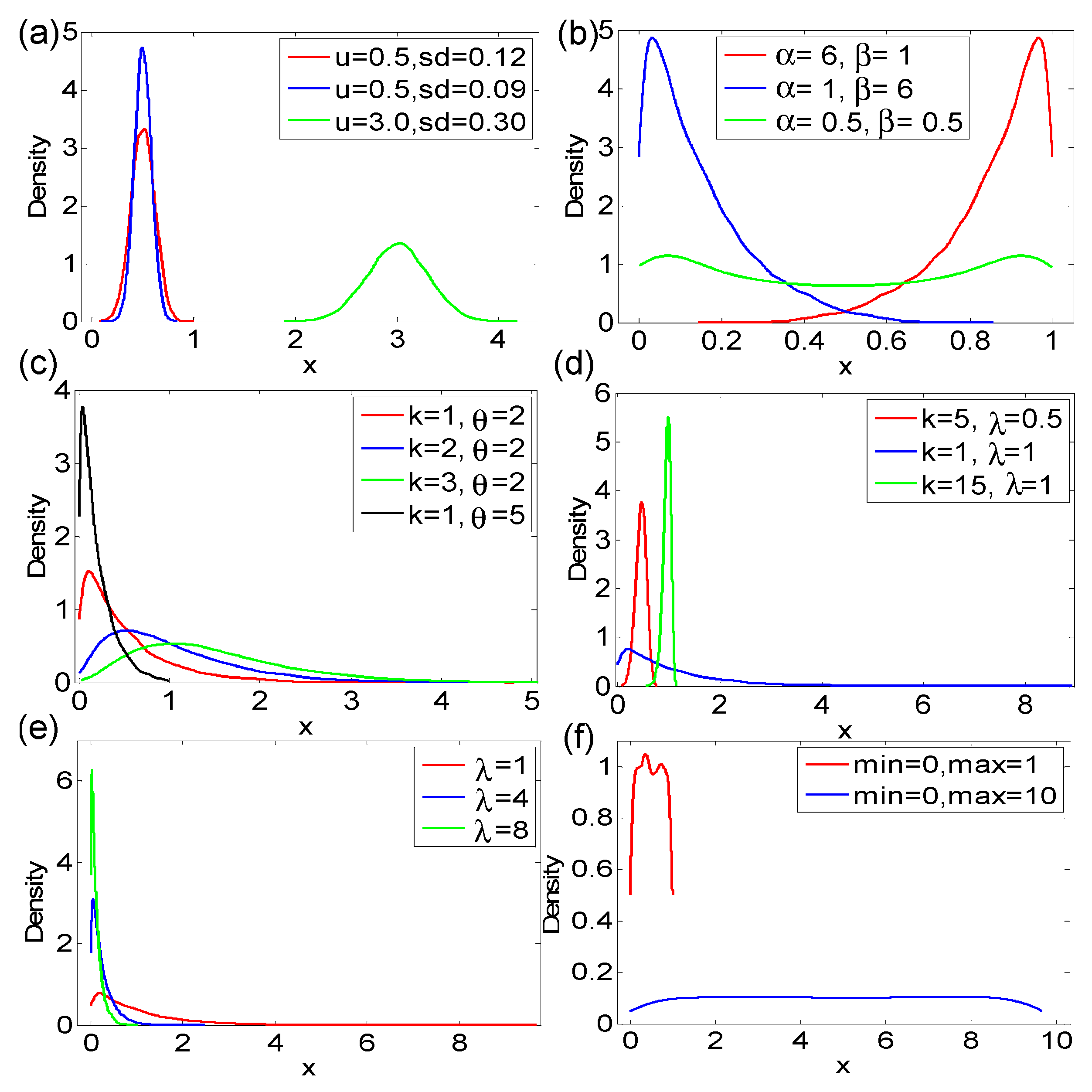
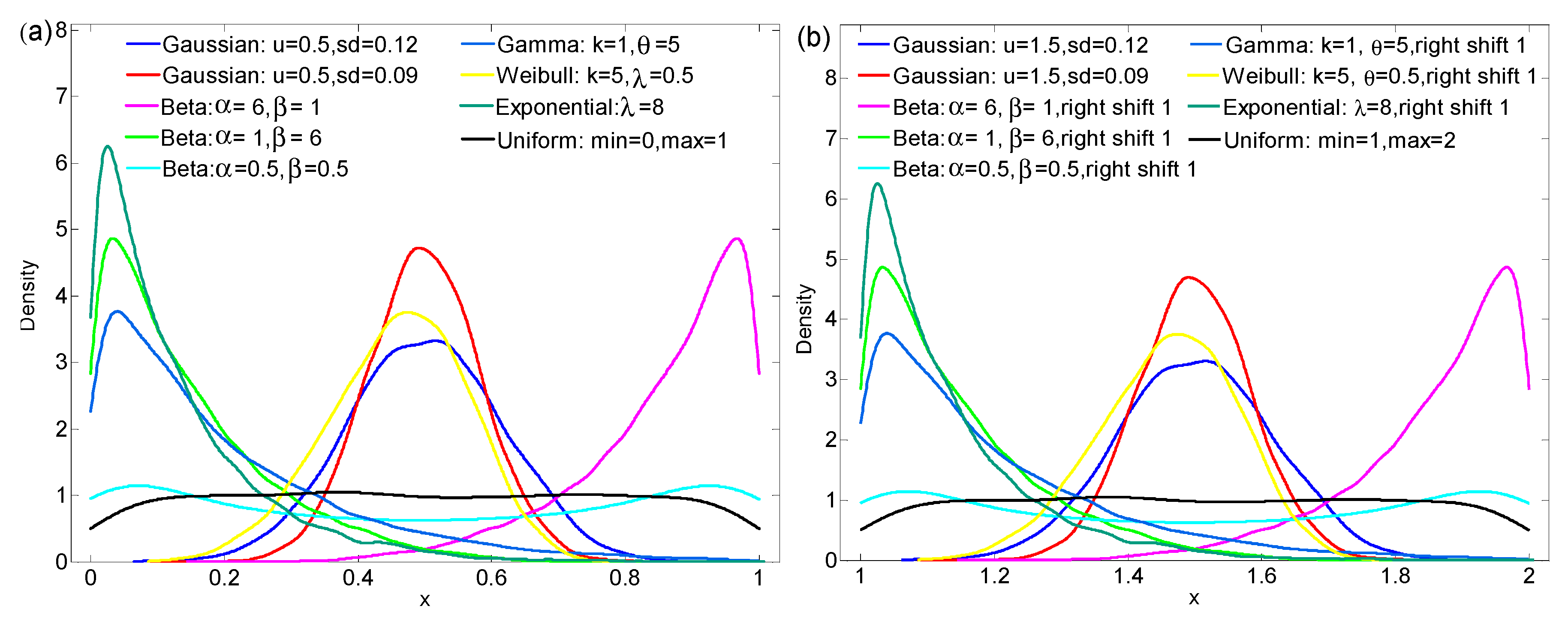


| Distribution Type | Specific Parameters | S | CV | Gini |
|---|---|---|---|---|
| Normal | N(1) u = 0.5, sd = 0.12 | 3.8596 | 0.2311 | 0.1305 |
| N(2) u = 0.5, sd = 0.09 | 3.5437 | 0.1685 | 0.0950 | |
| N(3) u = 3, sd = 0.30 | 4.7925 | 0.0986 | 0.0557 | |
| Beta | B(1) α = 6, β = 1 | 5.0479 | 0.1445 | 0.0771 |
| B(2) α = 1, β = 6 | 5.0478 | 0.8697 | 0.4638 | |
| B(3) α = 0.5, β = 0.5 | 5.7996 | 0.7081 | 0.4057 | |
| Gamma | G(1) k = 1, θ = 2 | 4.3049 | 0.9901 | 0.4965 |
| G(2) k = 2, θ = 2 | 4.8676 | 0.7066 | 0.3756 | |
| G(3) k = 3, θ = 2 | 5.1169 | 0.5777 | 0.3126 | |
| G(4) k = 1, θ = 5 | 3.3721 | 0.9291 | 0.4848 | |
| Weibull | W(1) k = 5, λ = 0.5 | 2.9733 | 0.2262 | 0.1278 |
| W(2) k = 1, λ = 1 | 4.8165 | 0.9824 | 0.4947 | |
| W(3) k = 15, λ = 1 | 2.6494 | 0.0807 | 0.0446 | |
| Exponential | E(1) λ = 1 | 4.7244 | 1.0090 | 0.5011 |
| E(2) λ = 4 | 3.3821 | 0.9968 | 0.4975 | |
| E(3) λ = 8 | 2.7327 | 0.9941 | 0.5005 | |
| Uniform | U(1) min = 0, max = 1 | 3.7550 | 0.5779 | 0.3336 |
| U(2) min = 0, max = 10 | 5.9966 | 0.5734 | 0.3310 |
| Distribution Type | Specific Parameters | S | CV | Gini |
|---|---|---|---|---|
| Normal | (a) u = 0.5, sd = 0.12 | 5.2604 | 0.2311 | 0.1305 |
| (b) u = 0.5, sd = 0.09 | 4.9459 | 0.1685 | 0.0950 | |
| Beta | (c) α = 6, β = 1 | 5.0479 | 0.1445 | 0.0771 |
| (d) α = 1, β = 6 | 5.0478 | 0.8697 | 0.4638 | |
| (e) α = 0.5, β = 0.5 | 5.8003 | 0.7081 | 0.4057 | |
| Gamma | (f) k = 1, θ = 5 | 5.3579 | 0.9291 | 0.4848 |
| Weibull | (g) k = 5, λ = 0.5 | 5.1505 | 0.2262 | 0.1278 |
| Exponential | (h) λ = 8 | 4.9230 | 0.9941 | 0.5005 |
| Uniform | (i) min = 0, max = 1 | 5.9984 | 0.5779 | 0.3336 |
| Distribution Type | Specific Parameters | S | CV | Gini |
|---|---|---|---|---|
| Normal | (a) u = 1.5, sd = 0.12 | 5.2604 | 0.0771 | 0.0435 |
| (b) u = 1.5, sd = 0.09 | 4.9459 | 0.0561 | 0.0316 | |
| Beta | (c) α = 6, β = 1 | 5.0479 | 0.0667 | 0.0356 |
| (d) α = 1, β = 6 | 5.0478 | 0.1085 | 0.0578 | |
| (e) α = 0.5, β = 0.5 | 5.8003 | 0.2361 | 0.1353 | |
| Gamma | (f) k = 1, θ = 5 | 5.3579 | 0.1516 | 0.0791 |
| Weibull | (g) k = 5, λ = 0.5 | 5.1505 | 0.0713 | 0.0403 |
| Exponential | (h) λ = 8 | 4.9230 | 0.1103 | 0.0556 |
| Uniform | (i) min = 1, max = 2 | 5.9984 | 0.1924 | 0.1111 |
| Track NO. | Area NO. | S | CV | Gini | Track NO. | Area NO. | S | CV | Gini | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LAI | LST | LAI | LST | LAI | LST | LAI | LST | LAI | LST | LAI | LST | ||||
| track 5-1 | 1 | 5.3350 | 4.4594 | 0.4050 | 0.1303 | 0.2114 | 0.0545 | track 10-1 | 10 | 5.3660 | 4.2306 | 0.4715 | 0.1329 | 0.2478 | 0.0574 |
| 2 | 5.3209 | 4.5029 | 0.4427 | 0.1389 | 0.2334 | 0.0604 | 11 | 5.3818 | 4.0387 | 0.4022 | 0.1023 | 0.2093 | 0.0401 | ||
| 3 | 5.3494 | 4.6007 | 0.5692 | 0.1494 | 0.3128 | 0.0708 | 12 | 5.5580 | 4.3174 | 0.4653 | 0.1106 | 0.2528 | 0.0473 | ||
| track 5-2 | 4 | 5.3034 | 4.5020 | 0.4014 | 0.1288 | 0.2080 | 0.0543 | track 11-1 | 13 | 5.5324 | 4.3848 | 0.5158 | 0.1292 | 0.2814 | 0.0571 |
| 5 | 5.3407 | 4.5748 | 0.4309 | 0.1347 | 0.2268 | 0.0591 | 14 | 5.5262 | 3.9989 | 0.3937 | 0.0968 | 0.2065 | 0.0383 | ||
| 6 | 5.3939 | 4.5033 | 0.5083 | 0.1410 | 0.2750 | 0.0632 | 15 | 5.5739 | 4.1628 | 0.4020 | 0.0997 | 0.2120 | 0.0402 | ||
| track 7-2 | 7 | 5.3480 | 4.1616 | 0.3737 | 0.1140 | 0.1925 | 0.0434 | track 12-1 | 16 | 4.8339 | 4.4876 | 0.7941 | 0.1176 | 0.4462 | 0.0523 |
| 8 | 5.3573 | 4.3790 | 0.4258 | 0.1196 | 0.2240 | 0.0508 | 17 | 4.7221 | 4.1904 | 0.7181 | 0.0868 | 0.3955 | 0.0362 | ||
| 9 | 5.4848 | 4.5773 | 0.5030 | 0.1357 | 0.2751 | 0.0667 | 18 | 4.8323 | 4.3546 | 0.6973 | 0.1084 | 0.3830 | 0.0480 | ||
| Variable | Number of Observation | Variable | Number of Observation | Variable | Number of Observation |
|---|---|---|---|---|---|
| H | 17 | RH_5m | 17 | albedo | 16 |
| LE | 17 | Ta_5m | 17 | Rn | 16 |
| Ustar | 17 | Ms_2cm | 17 | Ts_0cm | 17 |
| Variable | MIN | MAX | MEAN | STD |
|---|---|---|---|---|
| H | 0.649 | 1.000 | 0.913 | 0.061 |
| LE | 0.747 | 1.000 | 0.929 | 0.048 |
| Ustar | 0.798 | 1.000 | 0.946 | 0.036 |
| RH_5m | 0.748 | 1.000 | 0.923 | 0.041 |
| Ta_5m | 0.693 | 1.000 | 0.875 | 0.050 |
| Ms_2cm | 0.863 | 1.000 | 0.982 | 0.024 |
| albedo | 0.670 | 1.000 | 0.919 | 0.049 |
| Rn | 0.423 | 1.000 | 0.918 | 0.056 |
| Ts_0cm | 0.769 | 1.000 | 0.932 | 0.048 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Xin, X.; Peng, Z.; Zhang, H.; Yi, C.; Li, B. Analysis of the Spatial Variability of Land Surface Variables for ET Estimation: Case Study in HiWATER Campaign. Remote Sens. 2018, 10, 91. https://doi.org/10.3390/rs10010091
Li X, Xin X, Peng Z, Zhang H, Yi C, Li B. Analysis of the Spatial Variability of Land Surface Variables for ET Estimation: Case Study in HiWATER Campaign. Remote Sensing. 2018; 10(1):91. https://doi.org/10.3390/rs10010091
Chicago/Turabian StyleLi, Xiaojun, Xiaozhou Xin, Zhiqing Peng, Hailong Zhang, Chuanxiang Yi, and Bin Li. 2018. "Analysis of the Spatial Variability of Land Surface Variables for ET Estimation: Case Study in HiWATER Campaign" Remote Sensing 10, no. 1: 91. https://doi.org/10.3390/rs10010091
APA StyleLi, X., Xin, X., Peng, Z., Zhang, H., Yi, C., & Li, B. (2018). Analysis of the Spatial Variability of Land Surface Variables for ET Estimation: Case Study in HiWATER Campaign. Remote Sensing, 10(1), 91. https://doi.org/10.3390/rs10010091