Comparative Analysis of Chinese HJ-1 CCD, GF-1 WFV and ZY-3 MUX Sensor Data for Leaf Area Index Estimations for Maize
Abstract
1. Introduction
2. Materials and Methods
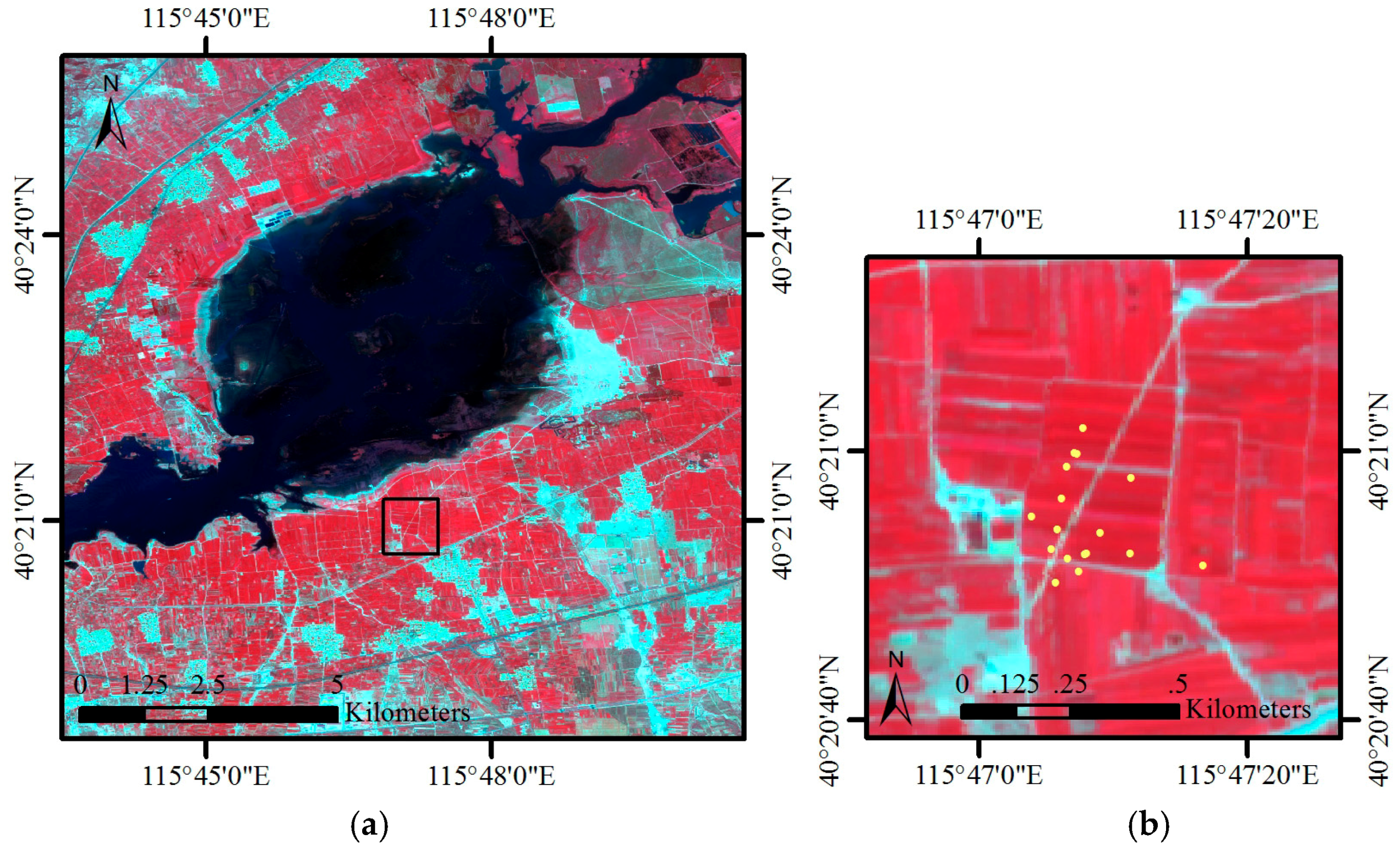
2.1. Study Area and Field Measurements
2.2. Remote Sensing Data and Preprocessing
2.2.1. Remote Sensing Data Acquisition
2.2.2. Remote Sensing Data Preprocessing
2.3. Generating the Forward Simulations
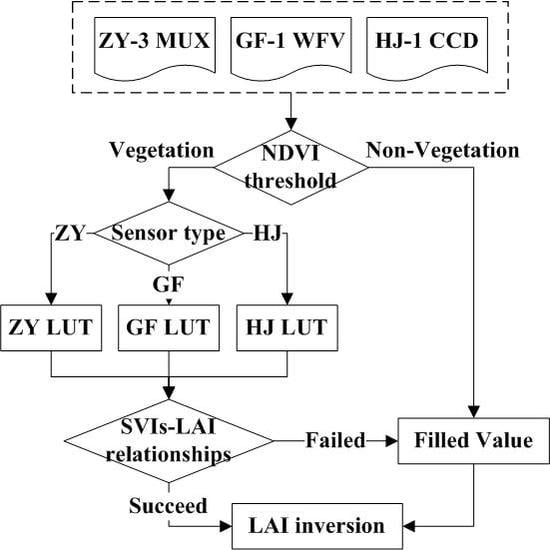
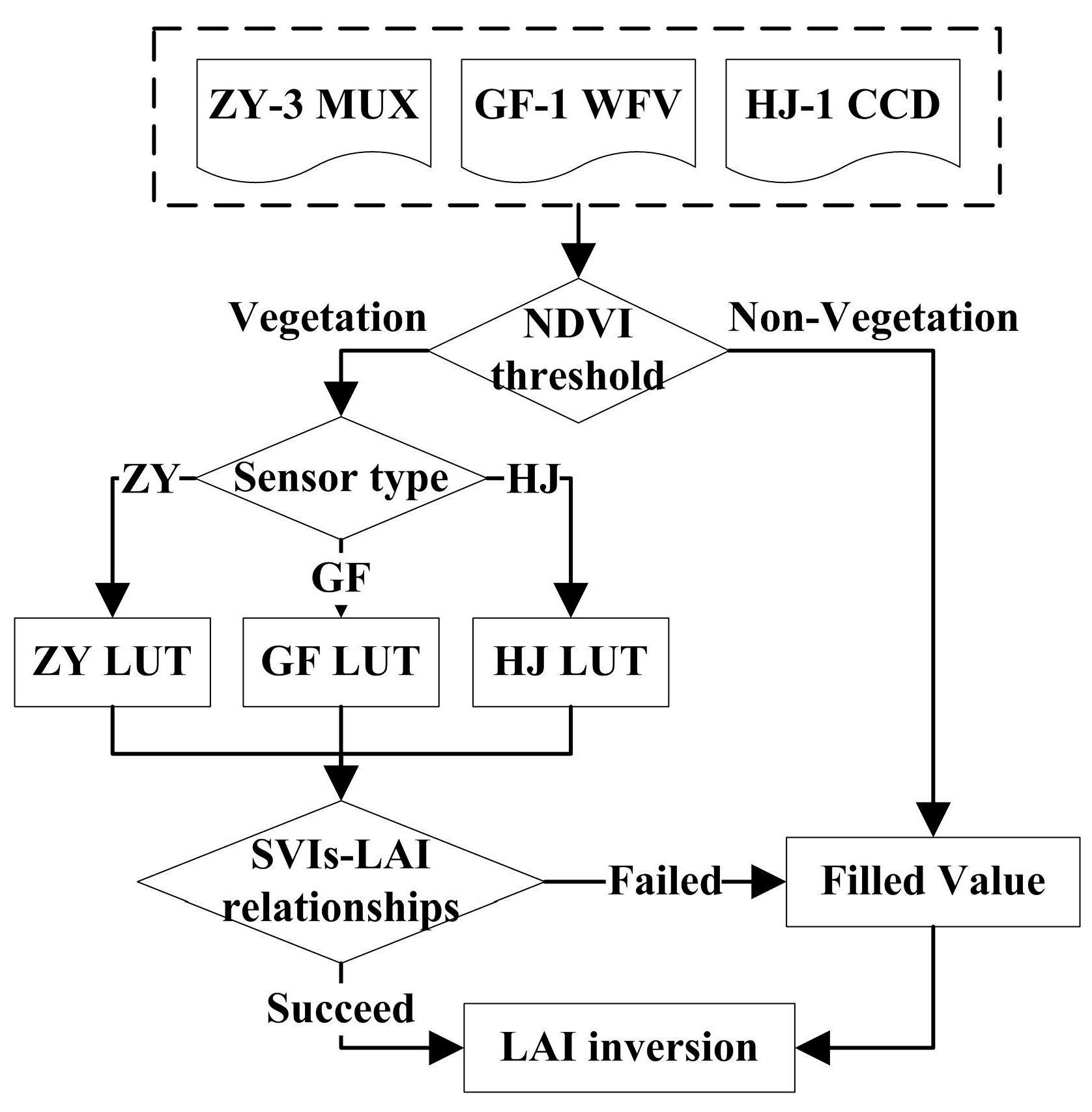
2.4. LAI Inversion Procedures
2.5. Assessment of LAI Inversions for a Heterogeneous Surface
3. Results and Analysis
3.1. LAI Validation for ZY-3 MUX, GF-1 WFV and HJ-1 CCD
3.2. Influence of Spatial Resolution on LAI Inversion
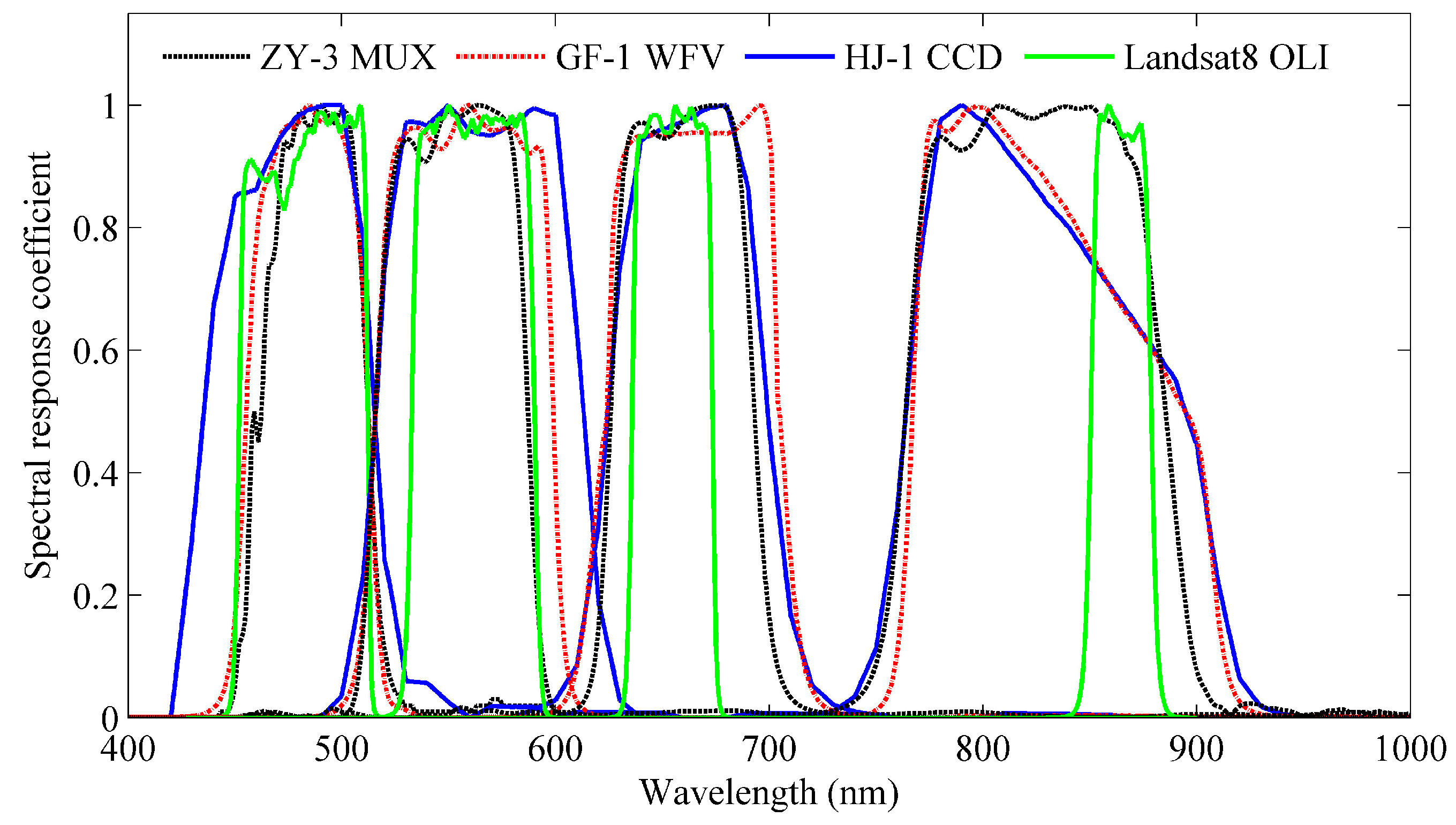
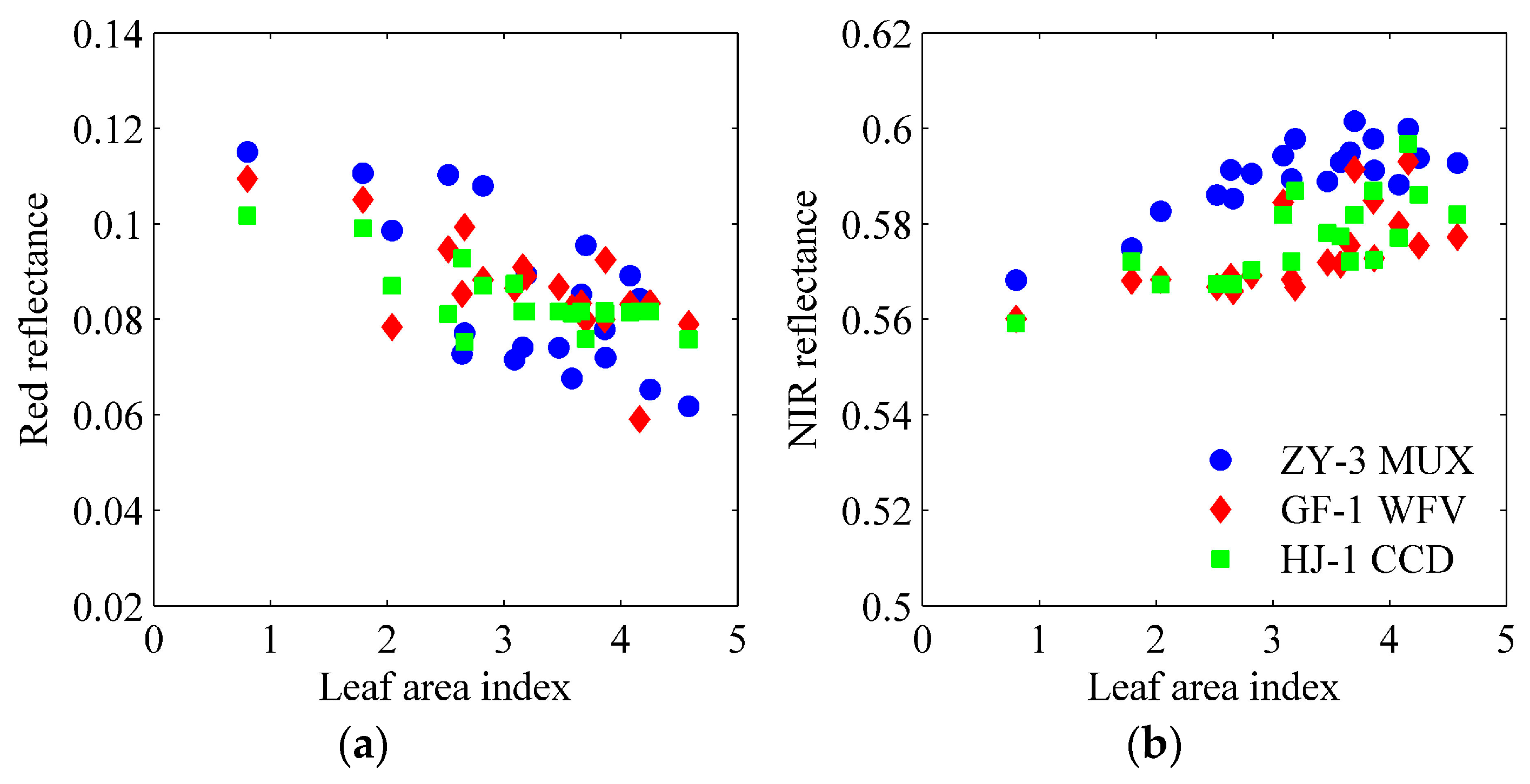
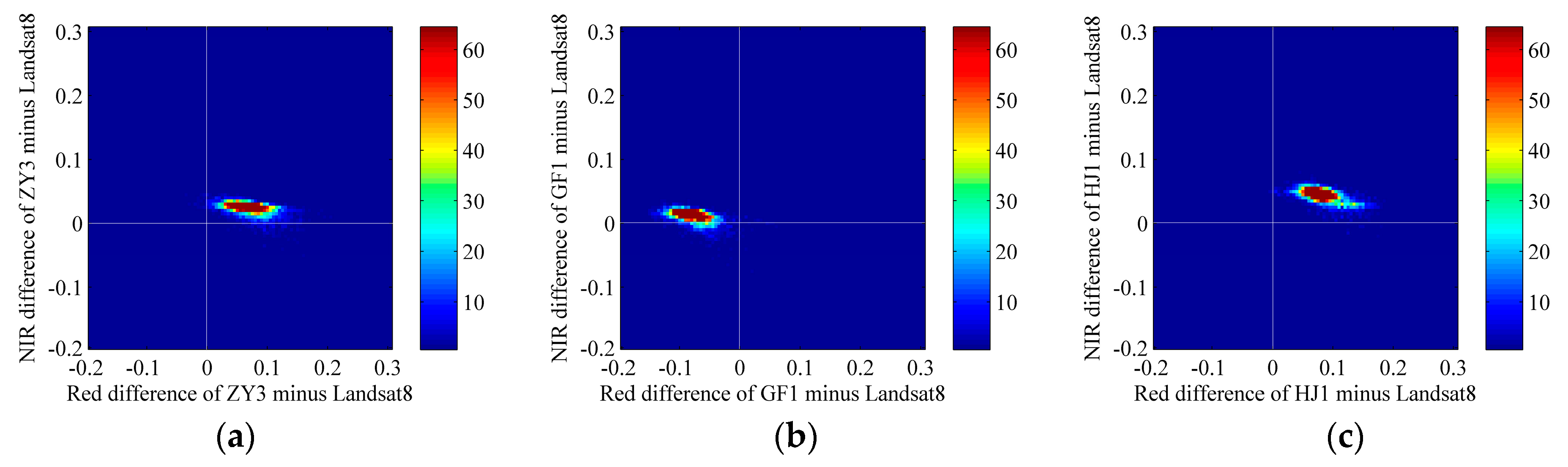
3.3. Comparison of Reflectance among Different Sensors
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Duveiller, G.; Weiss, M.; Baret, F.; Defourny, P. Retrieving wheat green area index during the growing season from optical time series measurements based on neural network radiative transfer inversion. Remote Sens. Environ. 2011, 115, 887–896. [Google Scholar] [CrossRef]
- Kobayashi, H.; Suzuki, R.; Kobayashi, S. Reflectance seasonality and its relation to the canopy leaf area index in an eastern siberian larch forest: Multi-satellite data and radiative transfer analyses. Remote Sens. Environ. 2007, 106, 238–252. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. Geov1: LAI and FAPAR essential climate variables and fcover global time series capitalizing over existing products. Part1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Peng, J.; Dan, L.; Dong, W. Estimate of extended long-term LAI data set derived from AVHRR and MODIS based on the correlations between LAI and key variables of the climate system from 1982 to 2009. Int. J. Remote Sens. 2013, 34, 7761–7778. [Google Scholar] [CrossRef]
- Clark, D.B.; Olivas, P.C.; Oberbauer, S.F.; Clark, D.A.; Ryan, M.G. First direct landscape-scale measurement of tropical rain forest leaf area index, a key driver of global primary productivity. Ecol. Lett. 2008, 11, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Coyne, P.I.; Aiken, R.M.; Maas, S.J.; Lamm, F.R. Evaluating yieldtracker forecasts for maize in western kansas. Agron. J. 2009, 101, 671–680. [Google Scholar] [CrossRef]
- Sharma, L.K.; Bali, S.K.; Dwyer, J.D.; Plant, A.B.; Bhowmik, A. A case study of improving yield prediction and sulfur deficiency detection using optical sensors and relationship of historical potato yield with weather data in maine. Sensors 2017, 17, 1095. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Scurlock, J.M.O.; Hicke, J.A. Global synthesis of leaf area index observations: Implications for ecological and remote sensing studies. Glob. Ecol. Biogeogr. 2003, 12, 191–205. [Google Scholar] [CrossRef]
- Li, Z.; Tang, H.; Xin, X.; Zhang, B.; Wang, D. Assessment of the MODIS LAI product using ground measurement data and HJ-1A/1B imagery in the meadow steppe of hulunber, China. Remote Sens. 2014, 6, 6242–6265. [Google Scholar] [CrossRef]
- Tian, Y.; Woodcock, C.E.; Wang, Y.; Privette, J.L.; Shabanov, N.V.; Zhou, L.; Zhang, Y.; Buermann, W.; Dong, J.; Veikkanen, B.; et al. Multiscale analysis and validation of the MODIS LAI product : II. Sampling strategy. Remote Sens. Environ. 2002, 83, 431–441. [Google Scholar] [CrossRef]
- Yang, F.; Sun, J.; Zhang, B.; Yao, Z.; Wang, Z.; Wang, J.; Yue, X. Assessment of MODIS LAI product accuracy based on the PROSAIL model, TM and field measurements. Trans. Chin. Soc. Agric. Eng. 2010, 26, 192–197. [Google Scholar]
- Cohen, W.B.; Maiersperger, T.K.; Gower, S.T.; Turner, D.P. An improved strategy for regression of biophysical variables and Landsat ETM+ data. Remote Sens. Environ. 2003, 84, 561–571. [Google Scholar] [CrossRef]
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using landsat tm images. Remote Sens. Environ. 1996, 55, 153–162. [Google Scholar] [CrossRef]
- Colombo, R.; Bellingeri, D.; Fasolini, D.; Marino, C.M. Retrieval of leaf area index in different vegetation types using high resolution satellite data. Remote Sens. Environ. 2003, 86, 120–131. [Google Scholar] [CrossRef]
- Soudani, K.; François, C.; Maire, G.L.; Dantec, V.L.; Dufrêne, E. Comparative analysis of IKONOS, SPOT, and ETM+ data for leaf area index estimation in temperate coniferous and deciduous forest stands. Remote Sens. Environ. 2006, 102, 161–175. [Google Scholar] [CrossRef]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ. 1999, 70, 52–68. [Google Scholar] [CrossRef]
- Heiskanen, J. Estimating aboveground tree biomass and leaf area index in a mountain birch forest using aster satellite data. Int. J. Remote Sens. 2006, 27, 1135–1158. [Google Scholar] [CrossRef]
- Korhonen, L.; Hadi; Packalen, P.; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the estimation of boreal forest canopy cover and leaf area index. Remote Sens. Environ. 2017, 195, 259–274. [Google Scholar] [CrossRef]
- Fassnacht, K.S.; Gower, S.T.; Mackenzie, M.D.; Nordheim, E.V.; Lillesand, T.M. Estimating the leaf area index of north central wisconsin forests using the landsat thematic mapper. Remote Sens. Environ. 1997, 61, 229–245. [Google Scholar] [CrossRef]
- He, L.I.; Chen, Z.X.; Jiang, Z.W.; Wen-Bin, W.U.; Ren, J.Q.; Liu, B.; Hasi, T. Comparative analysis of GF-1, HJ-1, and Landsat-8 data for estimating the leaf area index of winter wheat. J. Integr. Agric. 2017, 16, 266–285. [Google Scholar]
- Thomas, V.; Noland, T.; Treitz, P.; Mccaughey, J.H. Leaf area and clumping indices for a boreal mixed-wood forest: Lidar, hyperspectral, and landsat models. Int. J. Remote Sens. 2011, 32, 8271–8297. [Google Scholar] [CrossRef]
- Wu, M.; Wu, C.; Huang, W.; Niu, Z.; Wang, C. High-resolution leaf area index estimation from synthetic landsat data generated by a spatial and temporal data fusion model. Comput. Electron. Agric. 2015, 115, 1–11. [Google Scholar] [CrossRef]
- Ilangakoon, N.T.; Gorsevski, P.V.; Milas, A.S. Estimating leaf area index by bayesian linear regression using terrestrial Lidar, LAI-2200 plant canopy analyzer, and landsat tm spectral indices. Can. J. Remote Sens. 2015, 41, 315–333. [Google Scholar] [CrossRef]
- Pu, R. Mapping leaf area index over a mixed natural forest area in the flooding season using ground-based measurements and landsat tm imagery. Int. J. Remote Sens. 2012, 33, 6600–6622. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.M.; Huang, B.; Song, H.; Li, Y. Reconstructing seasonal variation of landsat vegetation index related to leaf area index by fusing with modis data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 950–960. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.L.; Gitelson, A.A. Algorithms for estimating green leaf area index in C3 and C4 crops for MODIS, Landsat TM/ETM+, MERIS, Sentinel MSI/OLCI, and venµs sensors. Remote Sens. Lett. 2015, 6, 360–369. [Google Scholar] [CrossRef]
- Tang, S.; Chen, J.M.; Zhu, Q.; Li, X.; Chen, M.; Sun, R.; Zhou, Y.; Deng, F.; Xie, D. Lai inversion algorithm based on directional reflectance kernels. J. Environ. Manag. 2007, 85, 638–648. [Google Scholar] [CrossRef] [PubMed]
- Eklundh, L. Estimating leaf area index in coniferous and deciduous forests in sweden using landsat optical sensor data. Proc. SPIE 2003, 4879, 379–390. [Google Scholar]
- Qu, Y.; Zhang, Y.; Xue, H. Retrieval of 30-m-resolution leaf area index from china HJ-1 CCD data and MODIS products through a dynamic bayesian network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 222–228. [Google Scholar]
- Walthall, C.; Dulaney, W.; Anderson, M.; Norman, J.; Fang, H.; Liang, S. A comparison of empirical and neural network approaches for estimating corn and soybean leaf area index from landsat ETM+ imagery. Remote Sens. Environ. 2004, 92, 465–474. [Google Scholar] [CrossRef]
- González-Sanpedro, M.C.; Toan, T.L.; Moreno, J.; Kergoat, L.; Rubio, E. Seasonal variations of leaf area index of agricultural fields retrieved from landsat data. Remote Sens. Environ. 2008, 112, 810–824. [Google Scholar] [CrossRef]
- Chen, B.; Wu, Z.; Wang, J.; Dong, J.; Guan, L.; Chen, J.; Yang, K.; Xie, G. Spatio-temporal prediction of leaf area index of rubber plantation using HJ-1A/1B CCD images and recurrent neural network. ISPRS Photogramm. Remote Sens. 2015, 102, 148–160. [Google Scholar] [CrossRef]
- Chen, W.; Cao, C.X.; He, Q.S.; Guo, H.D.; Zhang, H.; Li, R.Q.; Sheng, Z.; Xu, M.; Gao, M.X.; Zhao, J.; et al. Quantitative estimation of the shrub canopy LAI from atmosphere-corrected HJ-1 CCD data in mu us sandland. Sci. China Earth Sci. 2010, 53, 26–33. [Google Scholar] [CrossRef]
- Fernandes, R.; Weiss, M.; Camacho, F.; Berthelot, B.; Baret, F.; Duca, R. Development and assessment of leaf area index algorithms for the sentinel-2 multispectral imager. In Proceedings of the Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3922–3925. [Google Scholar]
- Richter, K.; Hank, T.B.; Vuolo, F.; Mauser, W.; D’Urso, G. Optimal exploitation of the Sentinel-2 spectral capabilities for crop leaf area index mapping. Remote Sens. 2012, 4, 561–582. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F.; Muñoz-Marí, J.; Clevers, J.G.P.W.; Camps-Valls, G.; Moreno, J. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Houborg, R.; Mccabe, M.; Cescatti, A.; Gao, F.; Schull, M.; Gitelson, A. Joint leaf chlorophyll content and leaf area index retrieval from landsat data using a regularized model inversion system (regflec). Remote Sens. Environ. 2015, 159, 203–221. [Google Scholar] [CrossRef]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Methods for leaf area index determination. Part I: Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Price, E. Lai-2200c plant canopy analyzer. In Proceedings of the American Society for Horticultural Science Conference, Orlando, FL, USA, 28–31 July 2014. [Google Scholar]
- Leblanc, S.G.; Chen, J.M.; Kwong, M. Tracing radiation and architecture of canopies. Trac manual version 2.1.3. Gastroenterology 2002, 78, 722–727. [Google Scholar]
- Decagon Devices, I. Accupar Par/Lai Ceptometer Model Lp-80; Decagon Devices, Inc.: Pullman, WA, USA, 2015. [Google Scholar]
- Campos-Taberner, M.; García-Haro, F.J.; Moreno, Á.; Gilabert, M.A.; Sánchez-Ruiz, S.; Martínez, B.; Camps-Valls, G. Mapping leaf area index with a smartphone and gaussian processes. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2501–2505. [Google Scholar] [CrossRef]
- Confalonieri, R.; Foi, M.; Casa, R.; Aquaro, S.; Tona, E.; Peterle, M.; Boldini, A.; Carli, G.D.; Ferrari, A.; Finotto, G. Development of an app for estimating leaf area index using a smartphone. Trueness and precision determination and comparison with other indirect methods. Comput. Electron. Agric. 2013, 96, 67–74. [Google Scholar] [CrossRef]
- Francone, C.; Pagani, V.; Foi, M.; Cappelli, G.; Confalonieri, R. Comparison of leaf area index estimates by ceptometer and pocketlai smart app in canopies with different structures. Field Crop. Res. 2014, 155, 38–41. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Liu, Q.; Fan, W.; Zhong, B.; Wu, S.; Yang, L.; Zeng, Y.; Xu, B.; Yin, G. Leaf area index retrieval combining HJ1/CCD and Landsat 8/OLI data in the heihe river basin, China. Remote Sens. 2015, 7, 6862–6885. [Google Scholar] [CrossRef]
- Zhan, Y.; Menga, Q.; Wanga, C.; Li, J.; Zhouab, K.; Li, D. Fractional vegetation cover estimation over large regions using GF-1 satellite data. In Proceedings of the SPIE Asia-Pacific Remote Sensing, Beijing, China, 27–31 October 2014. [Google Scholar]
- Jia, K.; Liang, S.; Gu, X.; Baret, F.; Wei, X.; Wang, X.; Yao, Y.; Yang, L.; Li, Y. Fractional vegetation cover estimation algorithm for chinese GF-1 wide field view data. Remote Sens. Environ. 2016, 177, 184–191. [Google Scholar] [CrossRef]
- Wang, L.; Niu, Z.; Wang, C.; Huang, W.; Chen, H.; Gao, S.; Li, D.; Muhammad, S. Combined use of airborne lidar and satellite GF-1 data to estimate leaf area index, height, and aboveground biomass of maize during peak growing season. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4489–4501. [Google Scholar]
- Wang, L.; Yang, R.; Tian, Q.; Yang, Y.; Zhou, Y.; Sun, Y.; Mi, X. Comparative analysis of GF-1 WFV, ZY-3 MUX, and HJ-1 CCD sensor data for grassland monitoring applications. Remote Sens. 2015, 7, 2089–2108. [Google Scholar] [CrossRef]
- Zeng, Y.; Li, J.; Liu, Q.; Li, L.; Xu, B.; Yin, G.; Peng, J. A sampling strategy for remotely sensed lai product validation over heterogeneous land surfaces. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3128–3142. [Google Scholar] [CrossRef]
- Satellite Surveying and Mapping Application Center (SASMAC) of National Administration of Surveying Mapping and Geo-Information of China (NASG). Available online: http://sjfw.sasmac.cn/en.html (accessed on 14 December 2017).
- Gaofen Satellite Data and Information Service System (GFDIS). Available online: http://210.72.27.32:8080/SNFFWeb/WebUI/Main/HomePage.jsp (accessed on 14 December 2017).
- China Centre for Resources Satellite Data and Application (CRESDA). Available online: http://www.cresda.com/CN/index.shtml (accessed on 14 December 2017).
- United States Geological Survey (USGS) Earthexplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 14 December 2017).
- Zhong, B.; Zhang, Y.; Du, T.; Yang, A.; Lv, W.; Liu, Q. Cross-calibration of hj-1/ccd over a desert site using landsat etm imagery and aster gdem product. IEEE Trans. Geosci. Remote Sens. 2014, 1–17. [Google Scholar]
- Zhang, Y.H. HJ1-CCD Cross Radiometric Calibration. Master’s Thesis, Shandong University of Science and Technology, Shandong, China, 2011. [Google Scholar]
- Zhong, B. Improved estimation of aerosol optical depth from Landsat TM/ETM+ imagery over land. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 3304–3307. [Google Scholar]
- Kuusk, A. The hot spot effect in plant canopy reflectance. In Photon-Vegetation Interactions: Applications in Optical Remote Sensing and Plant Ecology; Myneni, R., Ross, J., Eds.; Springer: New York, NY, USA, 1991; pp. 139–159. [Google Scholar]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The sail model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Zarco-Tejada, P.J.; Asner, G.P.; Francois, C.; Ustin, S.L. PROSPECT+SAIL: 15 years of use for land surface characterization. In Proceedings of the IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July–4 August 2006; pp. 1992–1995. [Google Scholar]
- Xiao, Y.; Zhao, W.; Zhou, D.; Gong, H. Sensitivity analysis of vegetation reflectance to biochemical and biophysical variables at leaf, canopy, and regional scales. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4014–4024. [Google Scholar] [CrossRef]
- Zeng, X.; Dickinson, R.E.; Walker, A.; Shaikh, M.; Defries, R.S.; Qi, J. Derivation and evaluation of global 1-km fractional vegetation cover data for land modeling. J. Appl. Meteorol. 2000, 39, 826–839. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J. Derivation of the green vegetation fraction of the whole china from 2000 to 2010 from modis data. Earth Interact. 2016, 20, 1–8. [Google Scholar] [CrossRef]
- Sharma, L.K.; Bu, H.; Franzen, D. Active Optical Sensor Algorithm for Corn Yield Prediction and Corn Side Dress Nitrogen Rate Aid; North Dakota State University: Fargo, ND, USA, 2014. [Google Scholar]
- Sharma, L.K.; Bu, H.; Denton, A.; Franzen, D.W. Active-optical sensors using red ndvi compared to red edge ndvi for prediction of corn grain yield in North Dakota, U.S.A. Sensors 2015, 15, 27832–27853. [Google Scholar] [CrossRef] [PubMed]
- Bu, H.; Sharma, L.K.; Denton, A.; Franzen, D.W. Comparison of satellite imagery and ground-based active optical sensors as yield predictors in sugar beet, spring wheat, corn, and sunflower. Agron. J. 2017, 109, 1–10. [Google Scholar] [CrossRef]
- Sharma, L.K.; Bu, H.; Franzen, D.W. Comparison of two ground-based active-optical sensors for in-season estimation of corn (Zea mays, L.) yield. J. Plant Nutr. 2016, 39, 957–966. [Google Scholar] [CrossRef]
- Sharma, L.K. Evaluation of Active Optical Ground-Based Sensors to Detect Early Nitrogen Deficiencies in Corn. Ph.D. Thesis, North Dakota State University of Agriculture and Applied Sciences, Fargo, ND, USA, April 2014. [Google Scholar]
- Franzen, D.W.; Sharma, L.K.; Bu, H.; Denton, A. Evidence for the ability of active-optical sensors to detect sulfur deficiency in corn. Agron. J. 2016, 108, 1–5. [Google Scholar] [CrossRef]
- Bu, H.; Sharma, L.K.; Denton, A.; Franzen, D.W. Sugar beet yield and quality prediction at multiple harvest dates using active-optical sensors. Agron. J. 2016, 108, 273–284. [Google Scholar] [CrossRef]
- Sharma, L.K.; Bu, H.; Franzen, D.W.; Denton, A. Use of corn height measured with an acoustic sensor improves yield estimation with ground based active optical sensors. Comput. Electron. Agric. 2016, 124, 254–262. [Google Scholar] [CrossRef]
- Sharma, L.K.; Franzen, D.W. Use of corn height to improve the relationship between active optical sensor readings and yield estimates. Precis. Agric. 2012, 15, 331–345. [Google Scholar] [CrossRef]
- Tian, Q.; Luo, Z.; Chen, J.M.; Chen, M.; Hui, F. Retrieving leaf area index for coniferous forest in xingguo county, China with Landsat ETM+ images. J. Environ. Manag. 2007, 85, 624–627. [Google Scholar] [CrossRef] [PubMed]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Li, J.; Liu, Q.; Huete, A.R.; Yu, Q.; Zeng, Y.; Yin, G.; Zhao, J.; Yang, L. Evaluating spatial representativeness of station observations for remotely sensed leaf area index products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3267–3282. [Google Scholar] [CrossRef]
- Zhu, X.; Feng, X.; Zhao, Y. Scale effect and error analysis of crop LAI inversion. J. Remote Sens. 2010, 14, 579–592. [Google Scholar]
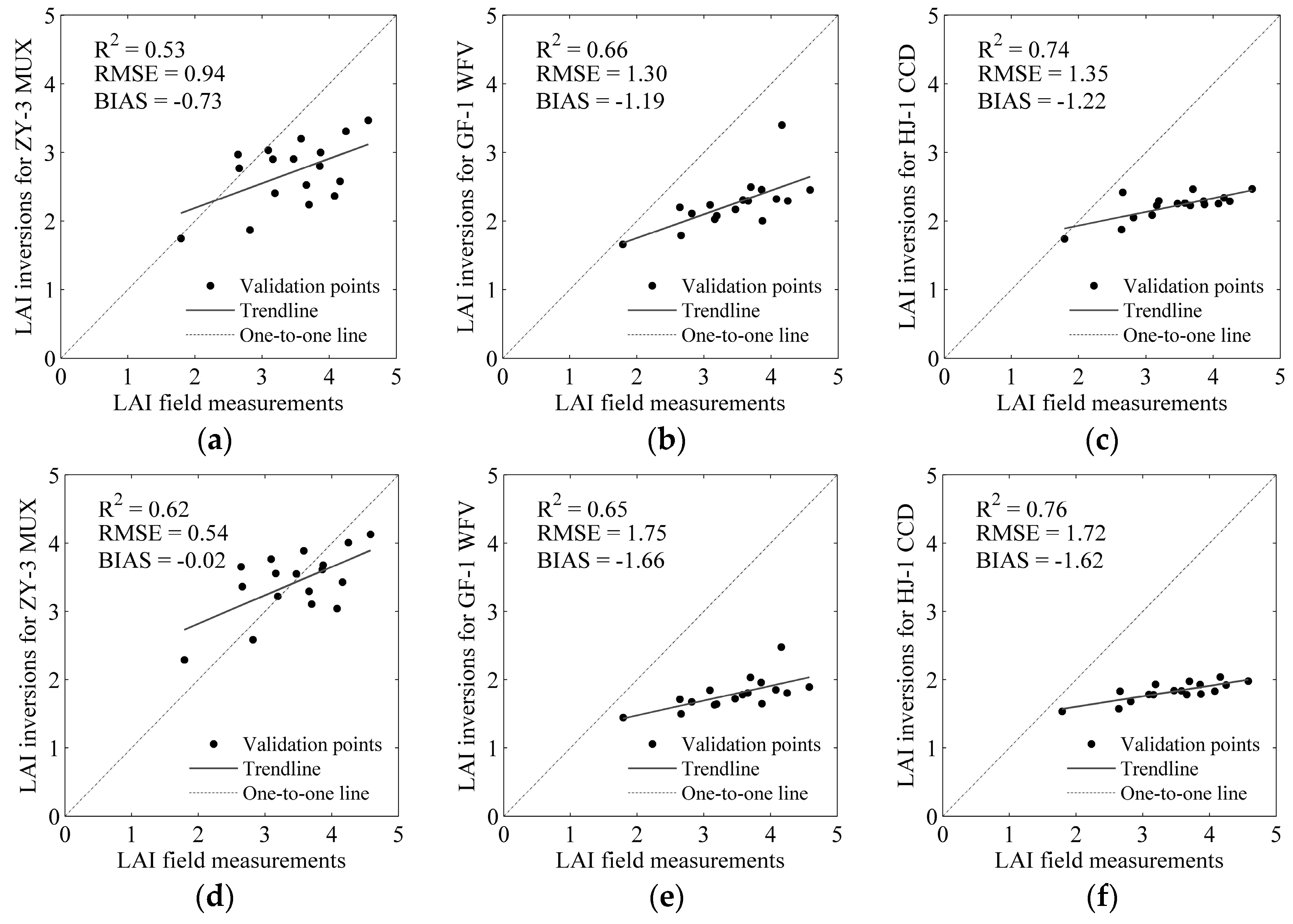
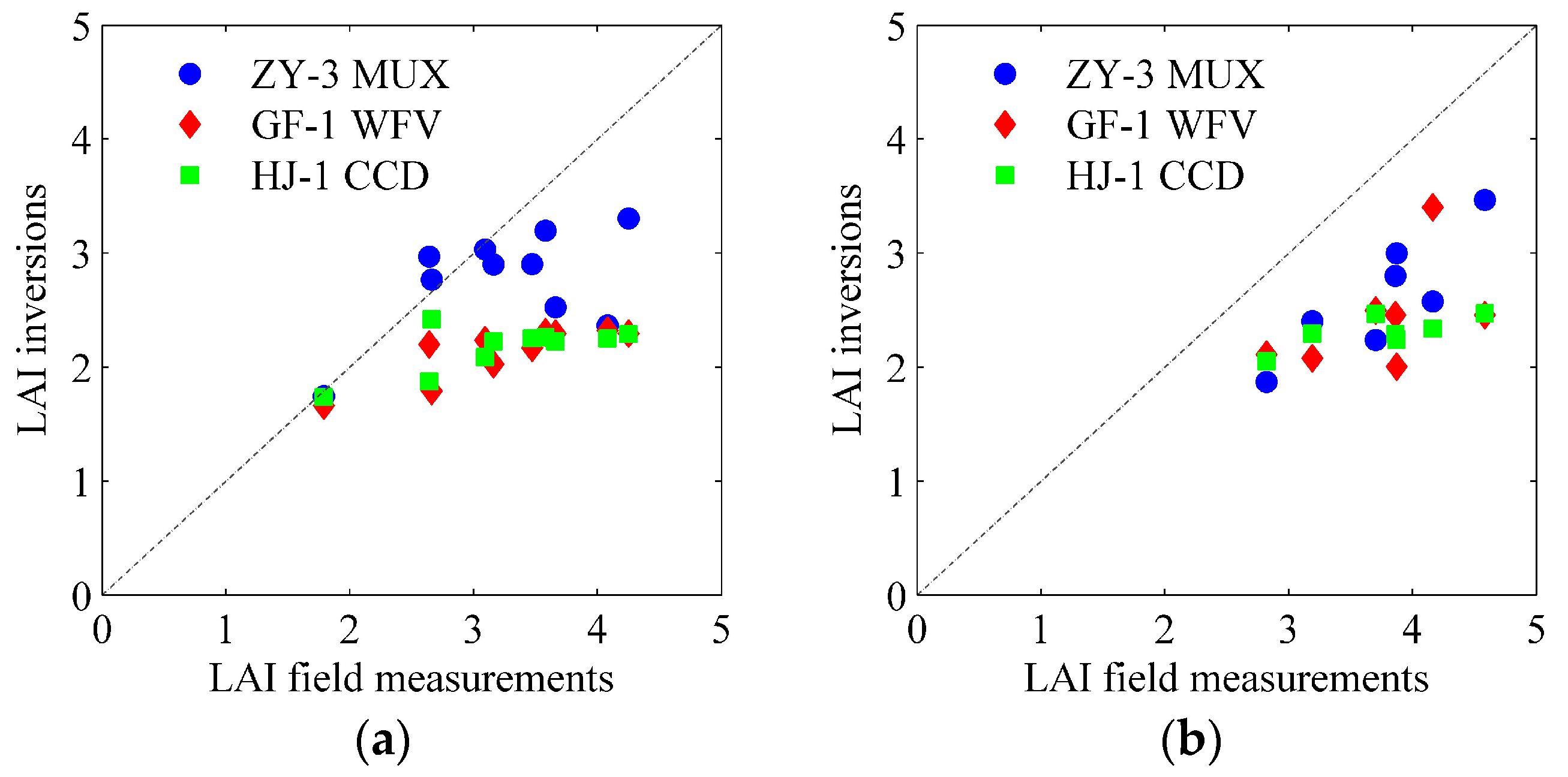

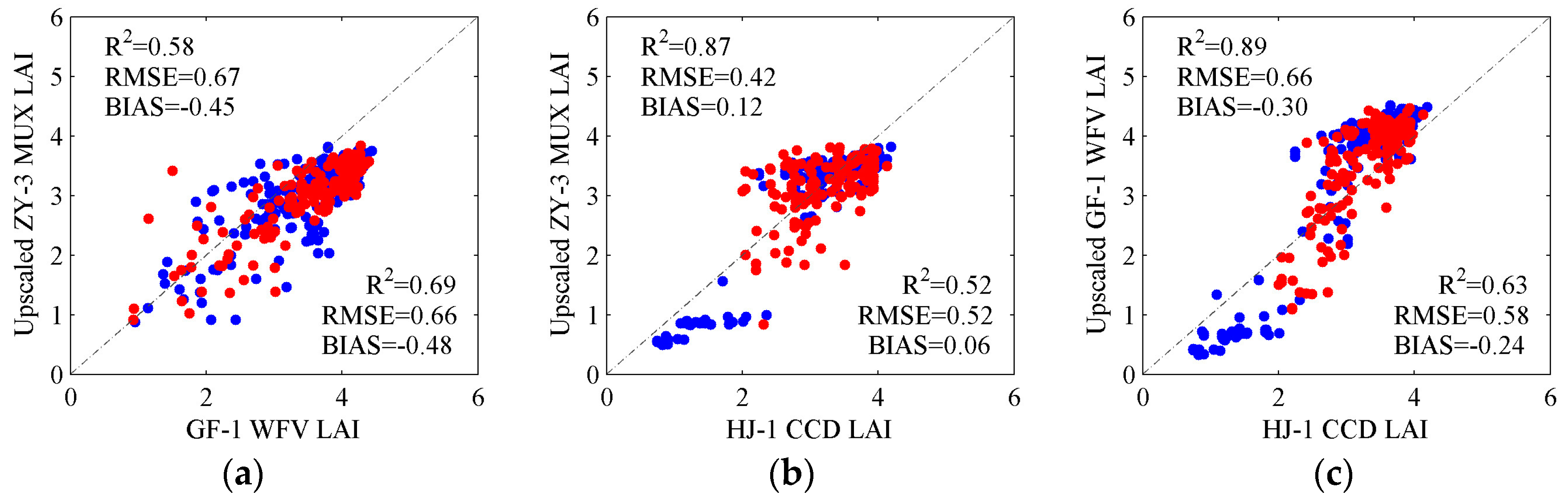

| Sensor | ZY-3 MUX | GF-1 WFV | HJ-1 CCD | |||
|---|---|---|---|---|---|---|
| Spectral characteristics | Bands | Wavelength (μm) | Bands | Wavelength (μm) | Bands | Wavelength (μm) |
| 1 | 0.45–0.52 | 1 | 0.45–0.52 | 1 | 0.43–0.52 | |
| 2 | 0.52–0.59 | 2 | 0.52–0.59 | 2 | 0.52–0.60 | |
| 3 | 0.63–0.69 | 3 | 0.63–0.69 | 3 | 0.63–0.69 | |
| 4 | 0.77–0.89 | 4 | 0.77–0.89 | 4 | 0.76–0.90 | |
| Spatial resolution (m) | 5.8 | 16 | 30 | |||
| Radiometric resolution (Bit) | 10 | 10 | 8 | |||
| Swath width (km) | 51 | 200 (single); 800 (4 cameras) | 360 (single); 700 (two) | |||
| Revisit time (days) | 5 | 4 | 4 | |||
| Sensor | Date | Local Time | Solar Zenith Angle | Solar Azimuth Angle | View Zenith Angle (Mean) | View Azimuth Angle (Mean) |
|---|---|---|---|---|---|---|
| ZY-3 MUX | 20140727 | 11:15:23 | 25.28° | 216.38° | 0° | 216.38° |
| GF-1 WFV | 20140727 | 11:50:19 | 22.08° | 201.62° | 29.97° | 74.57° |
| HJ-1 CCD | 20140728 | 10:00:09 | 34.97° | 295.49° | 25° | 53.59° |
| Landsat-8 OLI | 20140725 | 10:59:34 | 27.67° | 131.88° | 0° | 95.31° |
| Sensor | HJ-1 CCD | GF-1 WFV | ZY-3 MUX | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Gain | Offset | Gain | Offset | Gain | Offset | ||||
| Band 1 | 1.1451 | 4.6344 | 1929.81 | 0.1713 | 0.0000 | 1968.12 | 0.2509 | 0.0000 | 1958.30 |
| Band 2 | 1.1660 | 4.0982 | 1831.14 | 0.1600 | 0.0000 | 1841.69 | 0.2338 | 0.0000 | 1855.71 |
| Band 3 | 0.7647 | 3.7360 | 1549.82 | 0.1497 | 0.0000 | 1540.30 | 0.1885 | 0.0000 | 1548.72 |
| Band 4 | 0.7558 | 0.7385 | 1078.32 | 0.1435 | 0.0000 | 1069.53 | 0.2035 | 0.0000 | 1085.60 |
| Parameters | Abbreviations | Units | Value Range | Interval |
|---|---|---|---|---|
| Leaf mesophyll structure | N | - | 1.518 | - |
| Leaf chlorophyll-a and -b content | Cab | μg/cm | 40–60 | 10 |
| Leaf dry matter content | Cm | g/cm | 0.003662 | - |
| Leaf water content | Cw | cm | 0.0131 | - |
| Carotenoid content | Car | μg/cm | 10 | - |
| Brown pigment content | Cbrown | - | 0.05 | - |
| Average leaf inclination angle | ALA | ° | 40–70 | 10 |
| Hot-spot | Hot-spot | - | 0.1 | - |
| Leaf area index | LAI | m2/m2 | 0–8 | 0.1 |
| Solar zenith angle | SZA | ° | 0–85 | 1 |
| View zenith angle | VZA | ° | 0–35 | 1 |
| SVIs | NDVI-LAI Relationship | NIRv-LAI Relationship | ||
|---|---|---|---|---|
| Expression | R2 | Expression | R2 | |
| ZY-3 MUX | LAI = 0.0484 exp(5.2397 * NDVI) | 0.91 | LAI = 0.1725 exp(6.4087 * NIRv) | 0.98 |
| GF-1 WFV | LAI = 0.0385 exp(5.4728 * NDVI) | 0.92 | LAI = 0.1578 exp(5.6711 * NIRv) | 0.98 |
| HJ-1 CCD | LAI = 0.0380 exp(5.4241 * NDVI) | 0.91 | LAI = 0.1543 exp(5.6960 * NIRv) | 0.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Li, J.; Liu, Q.; Wang, H.; Chen, C.; Xu, B.; Wu, S. Comparative Analysis of Chinese HJ-1 CCD, GF-1 WFV and ZY-3 MUX Sensor Data for Leaf Area Index Estimations for Maize. Remote Sens. 2018, 10, 68. https://doi.org/10.3390/rs10010068
Zhao J, Li J, Liu Q, Wang H, Chen C, Xu B, Wu S. Comparative Analysis of Chinese HJ-1 CCD, GF-1 WFV and ZY-3 MUX Sensor Data for Leaf Area Index Estimations for Maize. Remote Sensing. 2018; 10(1):68. https://doi.org/10.3390/rs10010068
Chicago/Turabian StyleZhao, Jing, Jing Li, Qinhuo Liu, Hongyan Wang, Chen Chen, Baodong Xu, and Shanlong Wu. 2018. "Comparative Analysis of Chinese HJ-1 CCD, GF-1 WFV and ZY-3 MUX Sensor Data for Leaf Area Index Estimations for Maize" Remote Sensing 10, no. 1: 68. https://doi.org/10.3390/rs10010068
APA StyleZhao, J., Li, J., Liu, Q., Wang, H., Chen, C., Xu, B., & Wu, S. (2018). Comparative Analysis of Chinese HJ-1 CCD, GF-1 WFV and ZY-3 MUX Sensor Data for Leaf Area Index Estimations for Maize. Remote Sensing, 10(1), 68. https://doi.org/10.3390/rs10010068