Vertical Accuracy Simulation of Stereo Mapping Using a Small Matrix Charge-Coupled Device
Abstract
:1. Introduction
2. Method
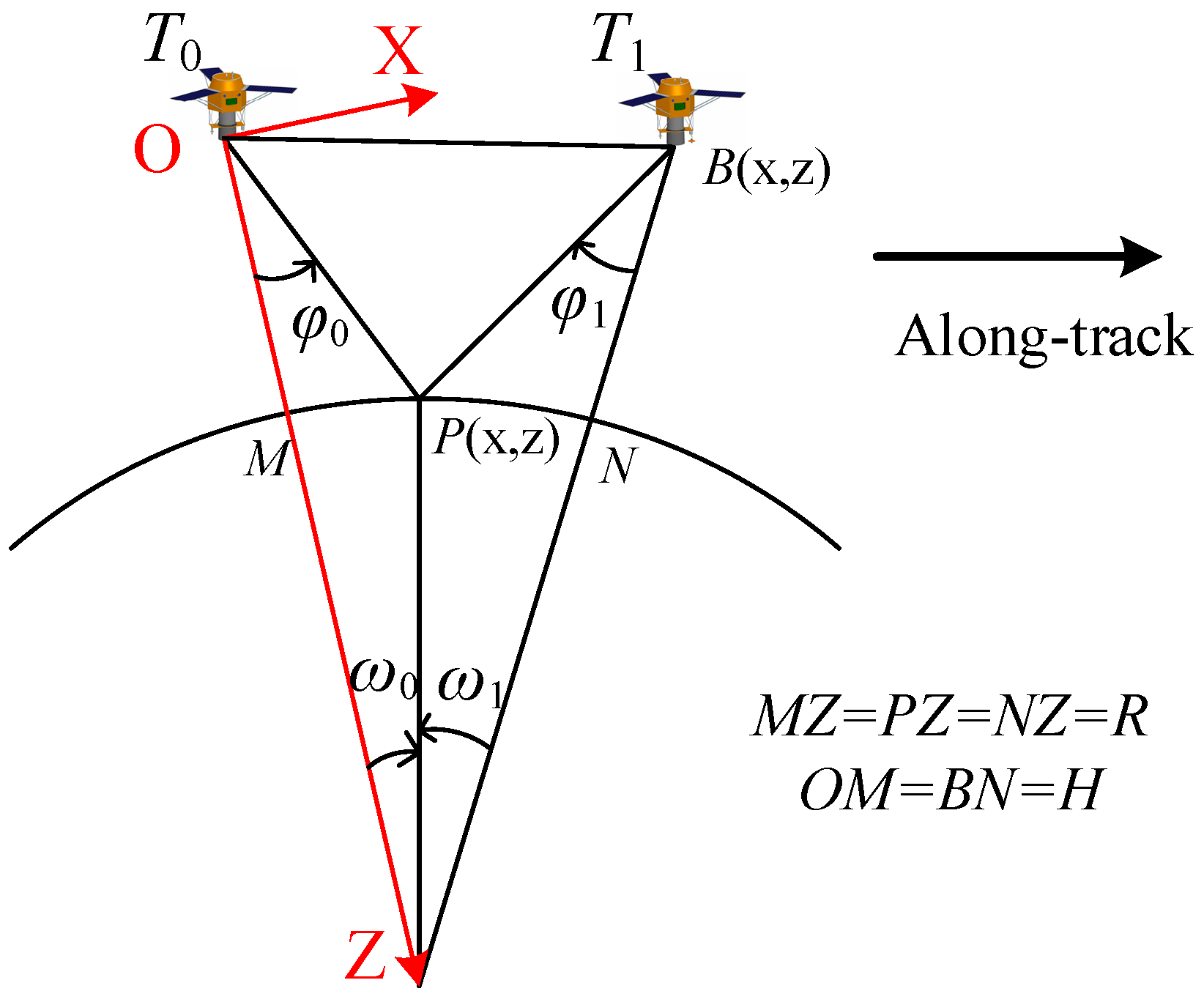
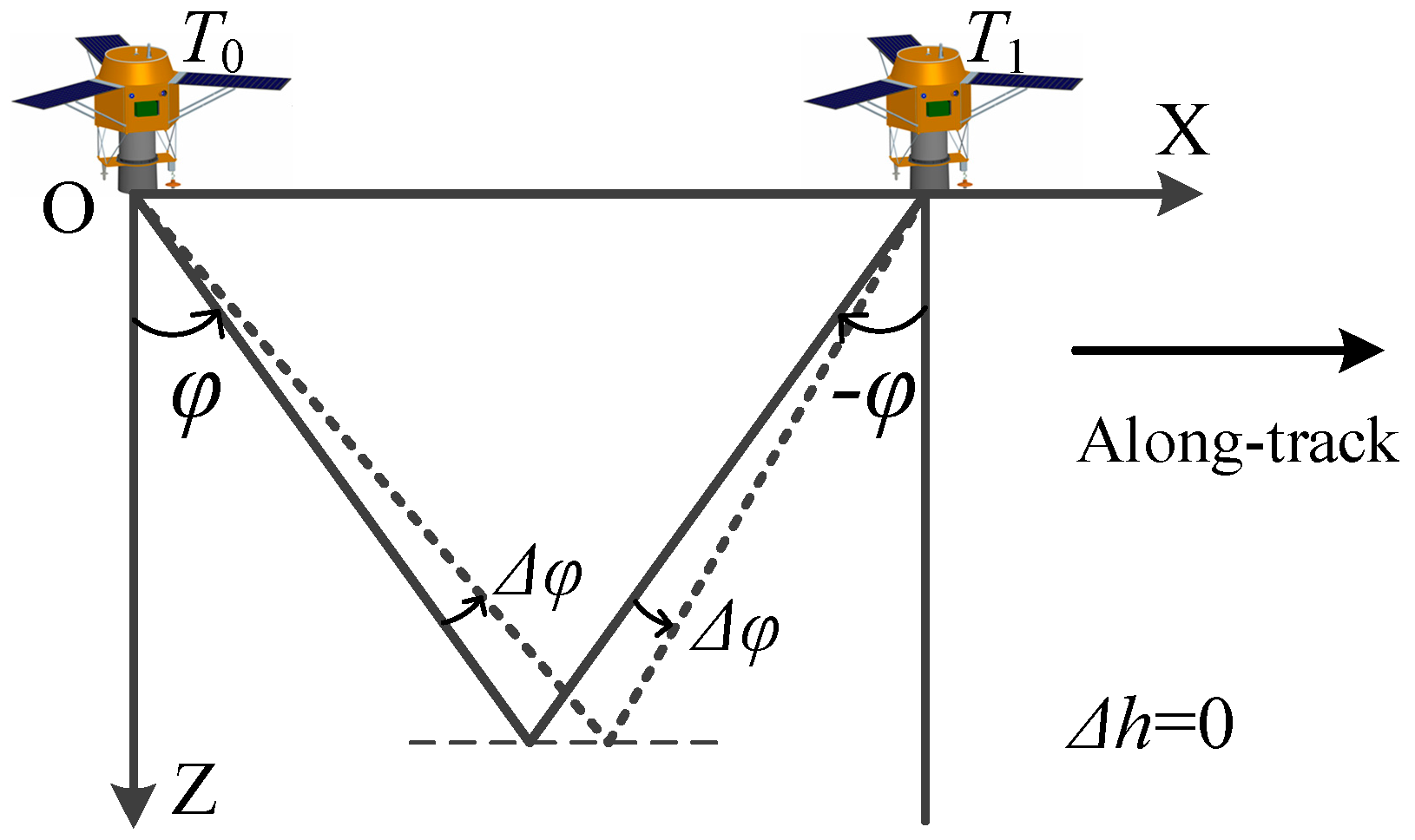
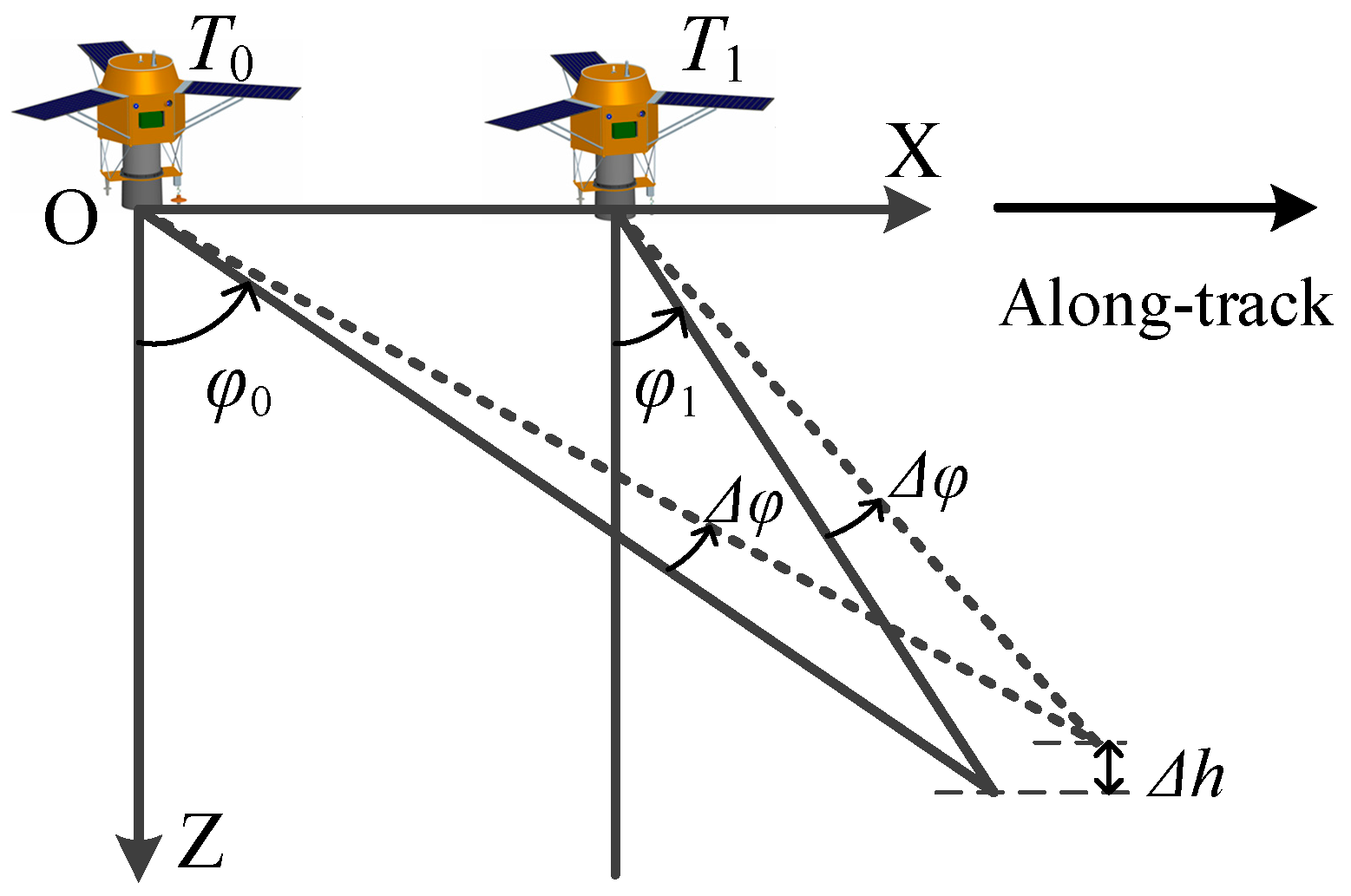
2.1. Accuracy Analysis of Symmetrical Stereo Mode
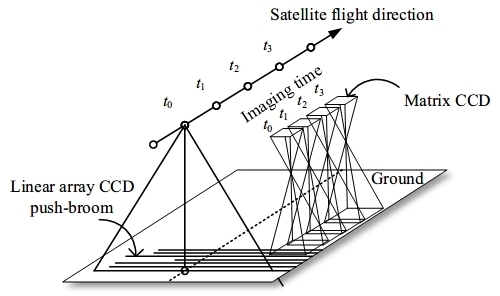
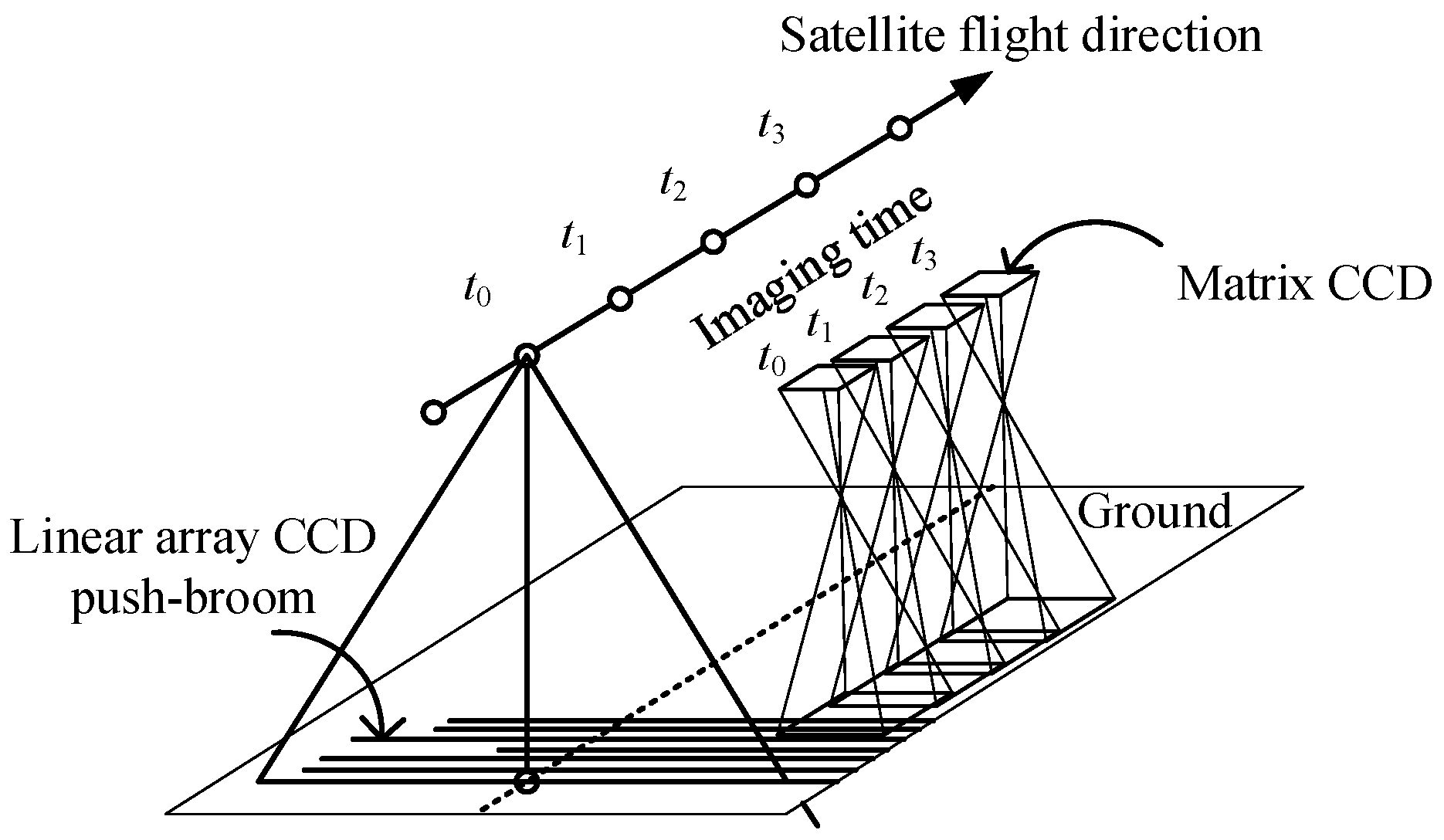
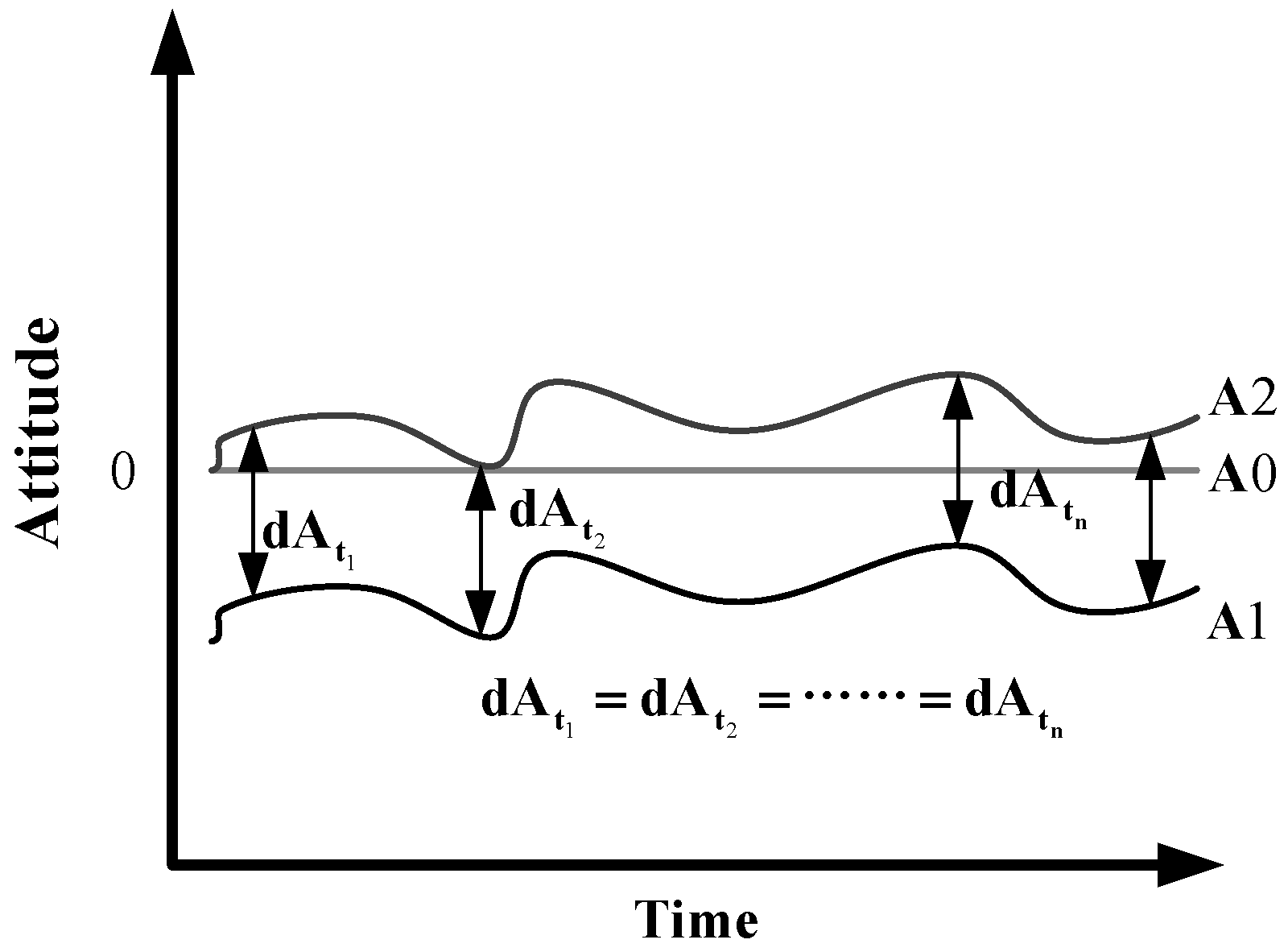
2.2. Vertical Accuracy Improvement Using Small Matrix CCD
3. Results and Discussion
3.1. Experimental Data Simulation
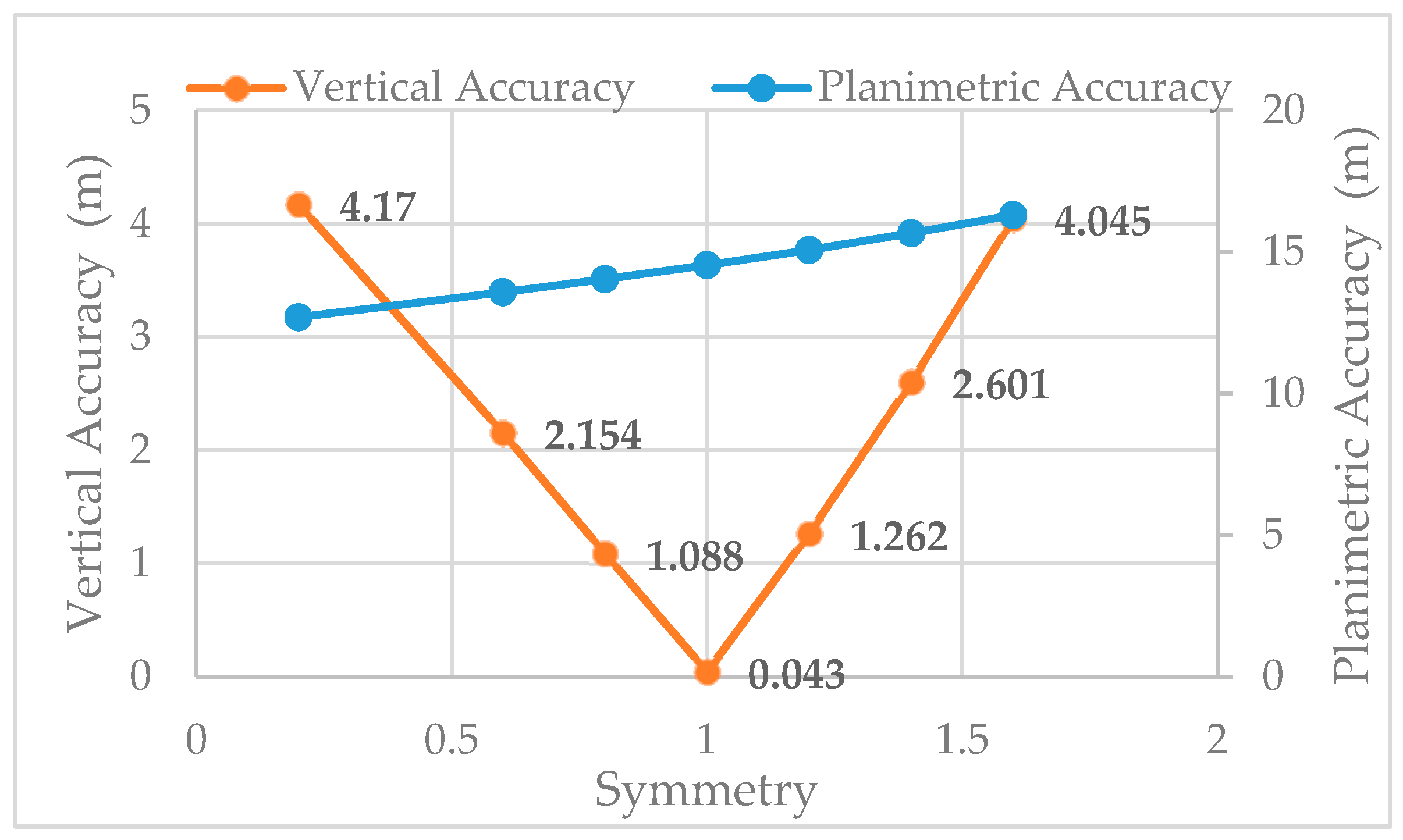
3.2. Symmetry and Vertical Accuracy
3.3. Promotion of Matrix CCD Images for Vertical Accuracy
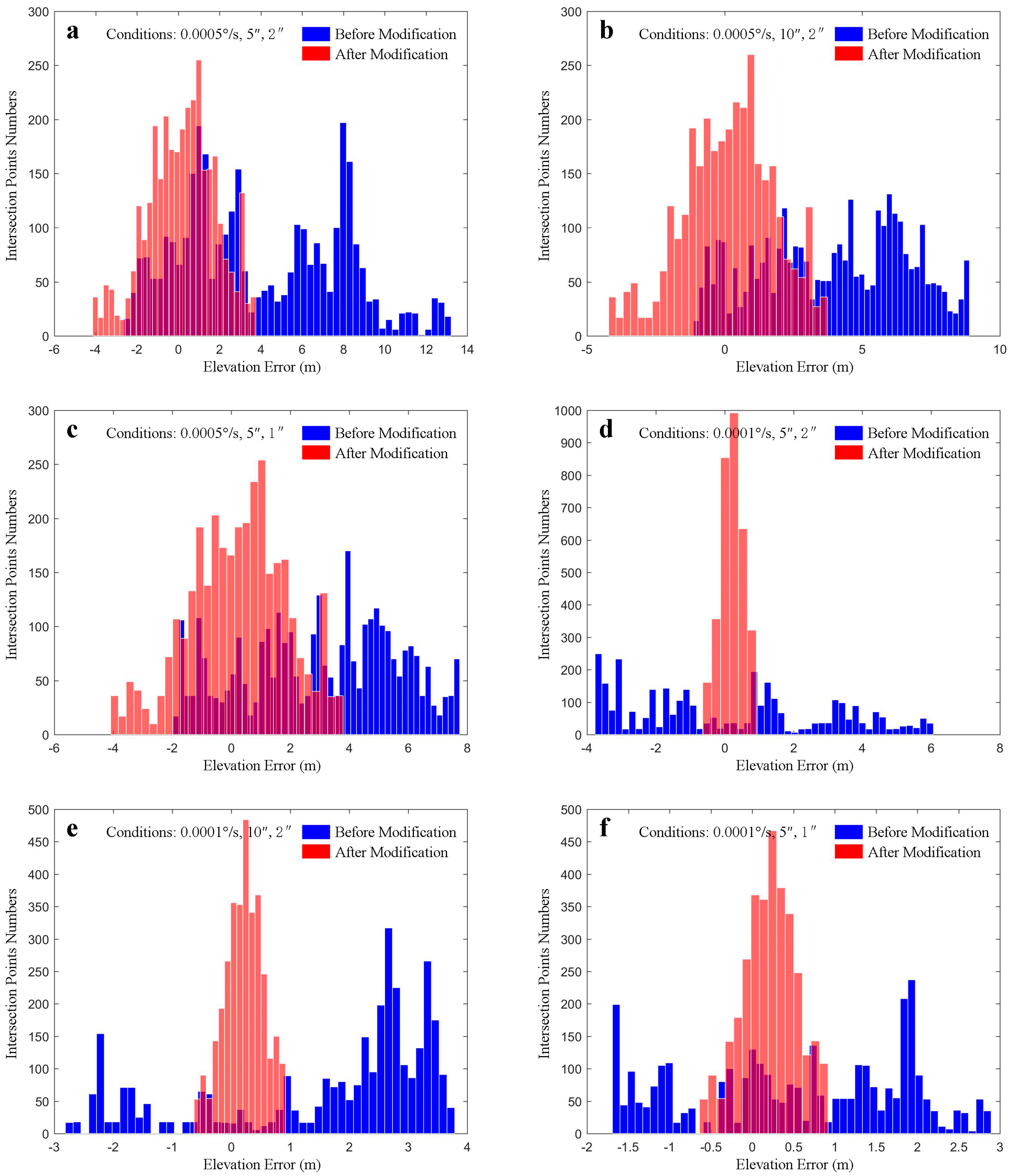
- For the original RMSE accuracy of (Figure 11a,b), the attitude stability was 0.0005°/s and attitude random error was 2″. When the systematic error increased from 5″ to 10″, the vertical accuracy only changed from 5.566 to 4.757 m, but the planimetric error increased from 17.978 to 37.393 m. When the systematic error doubled, the vertical accuracy was almost the same (Figure 11d,e). This confirms that under the symmetric stereo mode, attitude systematic error has little influence on vertical accuracy. However, the symmetric stereo mode cannot offset attitude systematic error for planimetric accuracy. After matrix CCD processing, the vertical accuracy increased from 5.566 to 1.662 m (Figure 11a), and from 2.826 to 0.395 m (Figure 11d), while the planimetric accuracy did not change significantly. These results confirm that, under the symmetric stereo condition, images from the small matrix CCD can effectively restore the relative accuracy of attitude, but are unable to improve the absolute accuracy of attitude. In summary, vertical accuracy can be increased greatly by using matrix CCD processing, but planimetric accuracy changes little.
- Compared with the original accuracy (Figure 1a,c), under attitude stability of 0.0005°/s and systematic error of 5″, and as attitude random error changed from 2″ to 1″, vertical accuracy rose from 5.566 to 3.952 m. After small matrix CCD image processing, vertical accuracy increased to 1.662 m. The same situation can be seen in Figure 11d,f, which verifies that under symmetric stereo conditions, vertical accuracy is affected by the random error of the measurement (including the attitude low-frequency drift that removed the systematic part). After matrix CCD processing, the relative accuracy of the attitude was increased, and the vertical accuracy was also improved.
- By comparing Figure 11a–c with Figure 11d–f, the relative accuracy of the attitude can be seen to have increased indirectly with increasing attitude stability, such that the vertical accuracy without GCPs improved under symmetric stereo conditions. When attitude stability is high, restraining the influence of random errors and low-frequency drift of attitude through matrix CCD can result in vertical accuracy of better than 0.4 m without GCPs, which is suitable for large-scale mapping.
4. Conclusions
- Under the symmetric stereo mode, attitude systematic errors can be canceled out, which guarantees a high vertical accuracy.
- Attitude stability and attitude random errors are the main error sources for vertical accuracy under the symmetric stereo mode. When these are decreased, the vertical accuracy increases.
- The relative accuracy of the attitude can be improved using matrix CCD image processing. By using the improved attitude in stereo image production, the vertical accuracy without GCPs can be significantly improved.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bouillon, A. SPOT5 HRG and HRS first in-flight geometric quality results. In Proceedings of the International Symposium on Remote Sensing, Crete, Greece, 22–27 September 2002; Volume 4881, pp. 212–223. [Google Scholar]
- Breton, E.; Bouillon, A.; Gachet, R.; Delussy, F. Pre-flight and in-flight geometric calibration of SPOT 5 HRG and HRS images. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2002, 34, 20–25. [Google Scholar]
- Tadono, T.; Shimada, M.; Watanabe, M.; Hashimoto, T.; Iwata, T. Calibration and validation of PRISM onboard ALOS. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2004, 35, 13–18. [Google Scholar]
- Tadono, T.; Shimada, M.; Murakami, H.; Takaku, J. Calibration of PRISM and AVNIR-2 onboard ALOS “daichi”. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4042–4050. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T. PRISM on-orbit geometric calibration and DSM performance. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4060–4073. [Google Scholar] [CrossRef]
- Muralikrishnan, S.; Pillai, A.; Narender, B.; Reddy, S.; Venkataraman, V.R.; Dadhwal, V.K. Validation of Indian national DEM from Cartosat-1 data. J. Indian Soc. Remote Sens. 2013, 41, 1–13. [Google Scholar] [CrossRef]
- Longbotham, N.W.; Pacifici, F.; Malitz, S.; Baugh, W.; Campsvalls, G. Measuring the Spatial and Spectral Performance of WorldView-3. In Proceedings of the Fourier Transform Spectroscopy and Hyperspectral Imaging and Sounding of the Environment, Lake Arrowhead, CA, USA, 1–4 March 2015. [Google Scholar]
- Li, G.Y.; Hu, F.; Zhang, C.Y. Introduction to Imaging Mode of WorldView-3 Satellite and Image Quality Preliminary Evaluation. Bull. Surv. Map. 2015, 2, 11–16. [Google Scholar]
- Hu, F.; Gao, X.M.; Li, G.Y.; Li, M. DEM extraction from Worldview-3 stereo-images and accuracy evaluation. Int. Arch. Photogram. Remote Sens. 2016, XLI-B1, 327–332. [Google Scholar] [CrossRef]
- Wang, T.Y.; Zhang, G.; Li, D.R.; Tang, X.M.; Jiang, Y.H.; Pan, H.B. Geometric accuracy validation for ZY-3 satellite imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1168–1171. [Google Scholar] [CrossRef]
- Tang, X.M.; Zhang, G.; Zhu, X.Y.; Pan, H.B.; Jiang, Y.H.; Zhou, P. Triple linear-array image geometry model of ziyuan-3 surveying satellite and its validation. Acta Geod. Cartogr. Sin. 2012, 4, 33–51. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Zhang, G.; Tang, X.M.; Zhu, X.Y.; Qin, Q.; Li, D.R. High accuracy geometric calibration of ZY-3 three-line image. Acta Geod. Cartogr. Sin. 2013, 42, 523–529. [Google Scholar]
- Pan, H.B.; Zhang, G.; Tang, X.M.; Wang, X.; Zhou, P.; Xu, M. Accuracy analysis and verification of ZY-3 products. Acta Geod. Cartogr. Sin. 2013, 42, 738–751. [Google Scholar]
- Wang, R.X.; Wang, J.R.; Hu, X. First Practice of LMCCD Camera Imagery Photogrammetry. Acta Geod. Cartogr. Sin. 2014, 43, 221–225. [Google Scholar]
- Wang, R.X.; Hu, X.; Wang, J.R. Photogrammetry of Mapping Satellite-1 without Ground Control Points. Acta Geod. Cartogr. Sin. 2013, 42, 1–5. [Google Scholar]
- Michaels, D. Ball aerospace star tracker achieves high tracking accuracy for a moving star field. In Proceedings of the 2005 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005; pp. 1–7. [Google Scholar]
- “WorldView-3”. Earth Observation Portal. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/v-w-x-y-z/worldview-3 (accessed on 30 October 2017).
- Wang, M.; Fan, C.; Yang, B.; Jin, S.; Pan, J. On-Ground Processing of Yaogan-24 Remote Sensing Satellite Attitude Data and Verification Using Geometric Field Calibration. Sensors 2016, 16, 1203. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Xie, J.; Wang, X.; Jiang, W. High-Precision Attitude Post-Processing and Initial Verification for the ZY-3 Satellite. Remote Sens. 2015, 7, 111–134. [Google Scholar] [CrossRef]
- Wang, R.X.; Hu, X.; Yang, J.F. Proposal to Use LMCCD Camera for Satellite Photogrammetry. Acta Geod. Cartogr. Sin. 2004, 33, 116–120. [Google Scholar]
- Wang, R.X.; Wang, J.R.; Yang, J.F. The Satellite Photogrammetric performance of LMCCD camera. Sci. Surv. Map. 2004, 29, 10–12. [Google Scholar]
- Tang, X.M.; Xie, J.F.; Fu, X.K.; Fan, M.O.; Li, S.N.; Dou, X. Zy3-02 laser altimeter on-orbit geometrical calibration and test. Acta Geod. Cartogr. Sin. 2017, 46, 714–723. [Google Scholar]
- Tang, X.M.; Li, G.Y.; Gao, X.M.; Chen, J. The rigorous geometric model of satellite laser altimeter and preliminarily accuracy validation. Acta Geod. Cartogr. Sin. 2016, 45, 1182–1191. [Google Scholar]
- Guo, J.; Zhao, Q.L.; Li, M.; Hu, Z.G. Centimeter level orbit determination for HY2A using GPS data. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 52–55. [Google Scholar]
- Jiang, Y.H.; Xu, K.; Zhang, G. A Method of Exterior Auto-Calibration for Linear CCD Array Pushbroom Optical Satellites. J. Tongji Univ. 2016, 44, 1266–1271. [Google Scholar]
- Wang, Z.Z. The Principle of Photogrammetry; China Surveying and Mapping: Beijing, China, 1979. [Google Scholar]
- Iwata, T. High-Bandwidth Attitude Determination Using Jitter Measurements and Optimal Filtering. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Chicago, IL, USA, 10–13 October 2009. [Google Scholar]
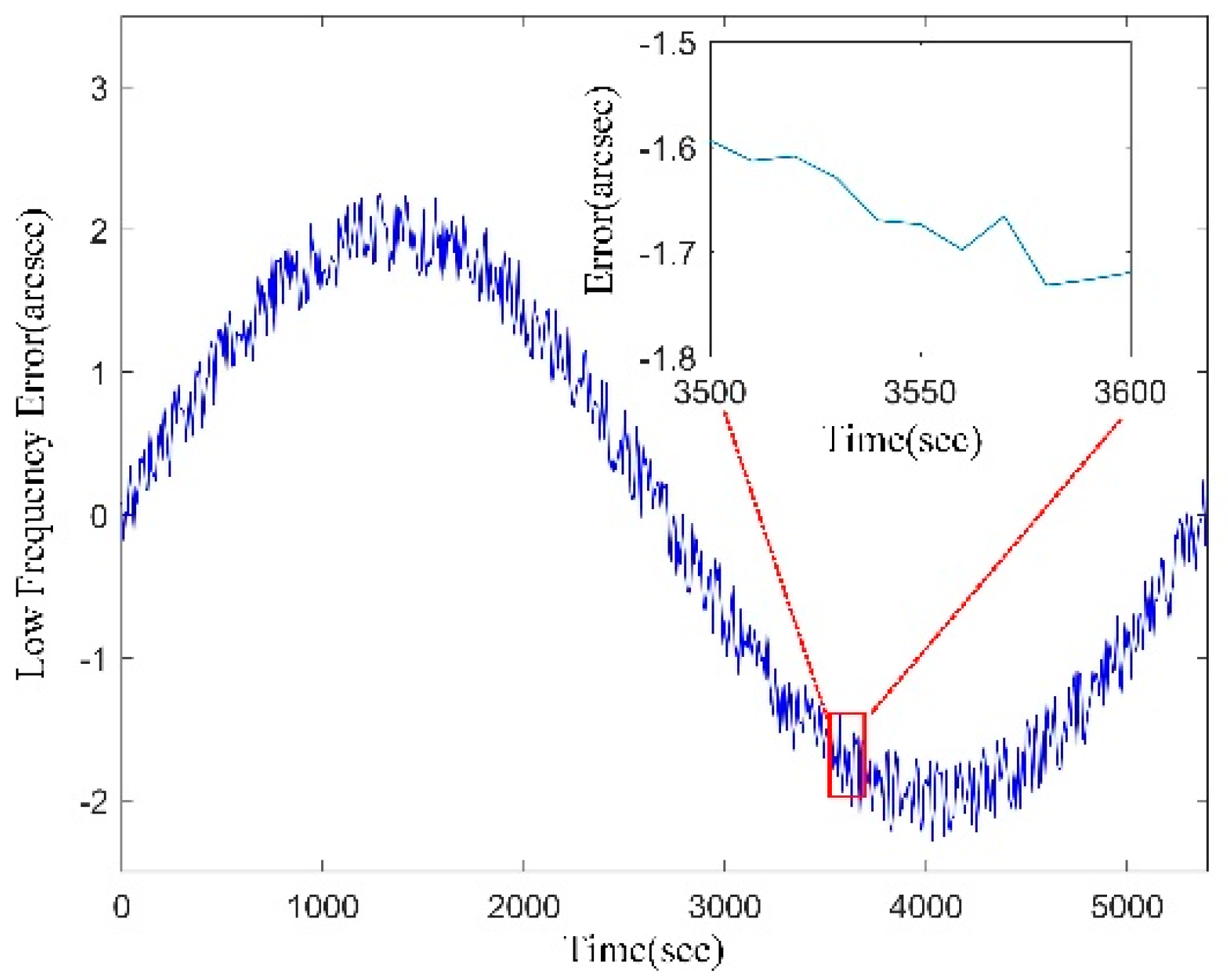
- Lu, X.; Wu, Y.P.; Zhong, H.J.; Li, C.Y.; Zheng, R. Low Frequency Error Analysis of Star Sensor. Aerosp. Control Appl. 2014, 40, 1–7. [Google Scholar]
- Xiong, K.; Zong, H.; Tang, L. On Star Sensor Low Frequency Error In-Orbit Calibration Method. Aerosp. Control Appl. 2014, 40, 8–13. [Google Scholar]
- Lai, Y.; Gu, D.; Liu, J.; Li, W.; Yi, D. Low-Frequency Error Extraction and Compensation for Attitude Measurements from STECE Star Tracker. Sensors 2016, 16, 1669. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.X.; Wang, J.R.; Hu, X. Low-frequency Errors Compensation of Attitude Determination System in Satellite Photogrammetry. Acta Geod. Cartogr. Sin. 2016, 45, 127–130. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Zhang, G.; Tang, X.M.; Li, D.R.; Huang, W.C.; Pan, H.B. Geometric Calibration and Accuracy Assessment of ZiYuan-3 Multispectral Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4161–4172. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Zhang, G.; Tang, X.M.; Li, D.R.; Huang, W.C. Detection and Correction of Relative Attitude Errors for ZY1-02C. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7674–7683. [Google Scholar] [CrossRef]
- Pan, H.B.; Zhang, G.; Tang, X.M.; Zhou, P.; Jiang, Y.H.; Zhu, X.Y. The Geometrical Model of Sensor Corrected Products for ZY-3 Satellite. Acta Geod. Cartogr. Sin. 2013, 42, 516–522. [Google Scholar]
- Riazanofi, S. SPOT Satellite Geometry Handbook; SPOT Image: Toulouse, France, 2002. [Google Scholar]
- Jiang, Y.H.; Zhang, G.; Chen, P.; Li, D.R.; Tang, X.M.; Huang, W.C. Systematic error compensation based on a rational function model for ziyuan1-02c. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3985–3995. [Google Scholar] [CrossRef]
- Jiang, Y.H.; Zhang, G.; Tang, X.; Li, D.R.; Wang, T.; Huang, W.C. Improvement and assessment of the geometric accuracy of chinese high-resolution optical satellites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 8, 4841–4852. [Google Scholar] [CrossRef]
- Li, D.R. China’s First Civilian Three-line-array Stereo Mapping Satellite: ZY-3. Acta Geod. Cartogr. Sin. 2012, 41, 317–322. [Google Scholar]


| Orbit Parameters | Attitude Parameters | ||
|---|---|---|---|
| Orbit height | 506 km | Initial attitude | 0° |
| Pointing longitude | 113.19° | Attitude stability | 5 × 10−4°/s |
| Pointing latitude | 34.42° | Attitude systematic error | |
| Simulation time | 100 s | Attitude random error | |
| Output frequency | 1 Hz | Output frequency | 4 Hz |
| Linear Array CCD | Small Matrix CCD | ||
|---|---|---|---|
| Focal length | 1.7 m | Focal length | 1.54 m |
| Pixel numbers | 2000 | Pixel numbers | 256 × 256 |
| Pixel size | 7 | Pixel size | 10 |
| Forward camera installing | Output frequency | 20 Hz | |
| Backward camera installing | |||
| Forward/Backward Camera Angle | Symmetry | Planimetric Accuracy/m | Vertical Accuracy/m |
|---|---|---|---|
| −35.2°/+22° | 1.6 | 16.298 | 4.045 |
| −30.8°/+22° | 1.4 | 15.661 | 2.601 |
| −26.4°/+22° | 1.2 | 15.073 | 1.262 |
| −22°/+22° | 1 | 14.539 | 0.043 |
| −17.6°/+22° | 0.8 | 14.043 | 1.088 |
| −13.2°/+22° | 0.6 | 13.576 | 2.154 |
| −4.4°/+22° | 0.2 | 12.694 | 4.17 |
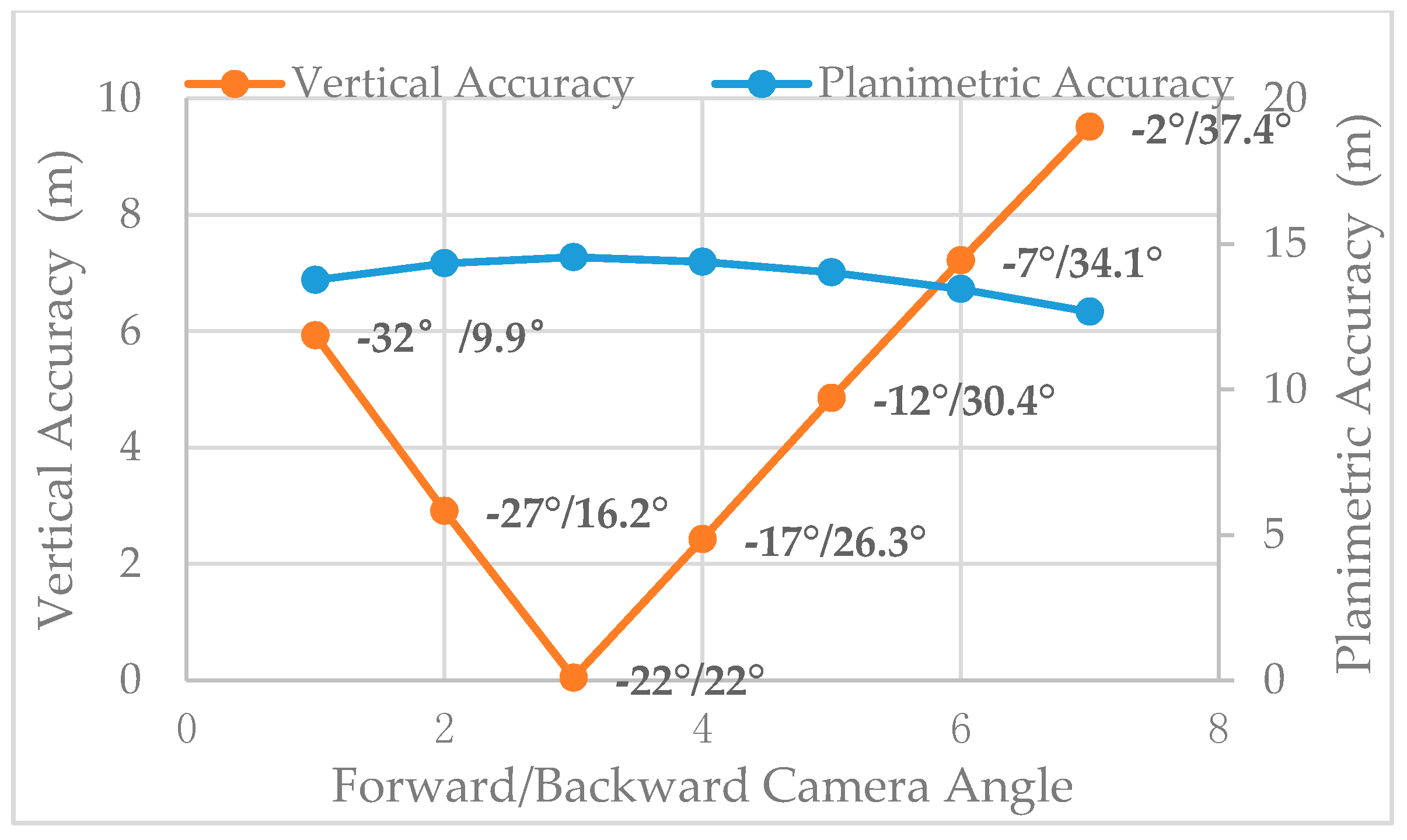
| Front/Back Camera Angle | Base:Height Ratio | Planimetric Accuracy/m | Vertical Accuracy/m |
|---|---|---|---|
| −32°/+9.9° | 0.8 | 13.761 | 5.931 |
| −27°/+16.2° | 0.8 | 14.33 | 2.911 |
| −22°/+22° | 0.8 | 14.539 | 0.043 |
| −17°/+26.3° | 0.8 | 14.38 | 2.424 |
| −12°/+30.4° | 0.8 | 14.018 | 4.852 |
| −7°/+34.1° | 0.8 | 13.448 | 7.215 |
| −2°/+37.4° | 0.8 | 12.665 | 9.514 |
| Figure No. | Stability, System Errors, Random Errors | Original RMSE Accuracy/m | Processed RMSE Accuracy/m | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Along-Track | Across-Track | Planimetry | Elevation | Along-Track | Across-Track | Planimetry | Elevation | ||
| 11a | 0.0005°/s, 5″, 2″ | 14.853 | 10.129 | 17.978 | 5.566 | 9.807 | 7.999 | 12.655 | 1.662 |
| 11b | 0.0005°/s, 10″, 2″ | 30.477 | 21.665 | 37.393 | 4.757 | 24.883 | 20.365 | 32.154 | 1.657 |
| 11c | 0.0005°/s, 5″, 1″ | 15.997 | 11.310 | 19.591 | 3.952 | 9.392 | 10.175 | 13.847 | 1.667 |
| 11d | 0.0001°/s, 5″, 2″ | 17.420 | 12.001 | 21.154 | 2.826 | 9.691 | 10.733 | 14.461 | 0.395 |
| 11e | 0.0001°/s, 10″, 2″ | 29.875 | 21.690 | 36.918 | 2.467 | 21.918 | 24.061 | 32.547 | 0.397 |
| 11f | 0.0001°/s, 5″, 1″ | 15.612 | 11.382 | 19.321 | 1.390 | 9.302 | 10.329 | 13.900 | 0.395 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Z.; Jiang, Y.; Zhang, G. Vertical Accuracy Simulation of Stereo Mapping Using a Small Matrix Charge-Coupled Device. Remote Sens. 2018, 10, 29. https://doi.org/10.3390/rs10010029
Guan Z, Jiang Y, Zhang G. Vertical Accuracy Simulation of Stereo Mapping Using a Small Matrix Charge-Coupled Device. Remote Sensing. 2018; 10(1):29. https://doi.org/10.3390/rs10010029
Chicago/Turabian StyleGuan, Zhichao, Yonghua Jiang, and Guo Zhang. 2018. "Vertical Accuracy Simulation of Stereo Mapping Using a Small Matrix Charge-Coupled Device" Remote Sensing 10, no. 1: 29. https://doi.org/10.3390/rs10010029
APA StyleGuan, Z., Jiang, Y., & Zhang, G. (2018). Vertical Accuracy Simulation of Stereo Mapping Using a Small Matrix Charge-Coupled Device. Remote Sensing, 10(1), 29. https://doi.org/10.3390/rs10010029