Application of Coupled-Wave Wentzel-Kramers-Brillouin Approximation to Ground Penetrating Radar
Abstract
:1. Introduction
2. Theoretical Method
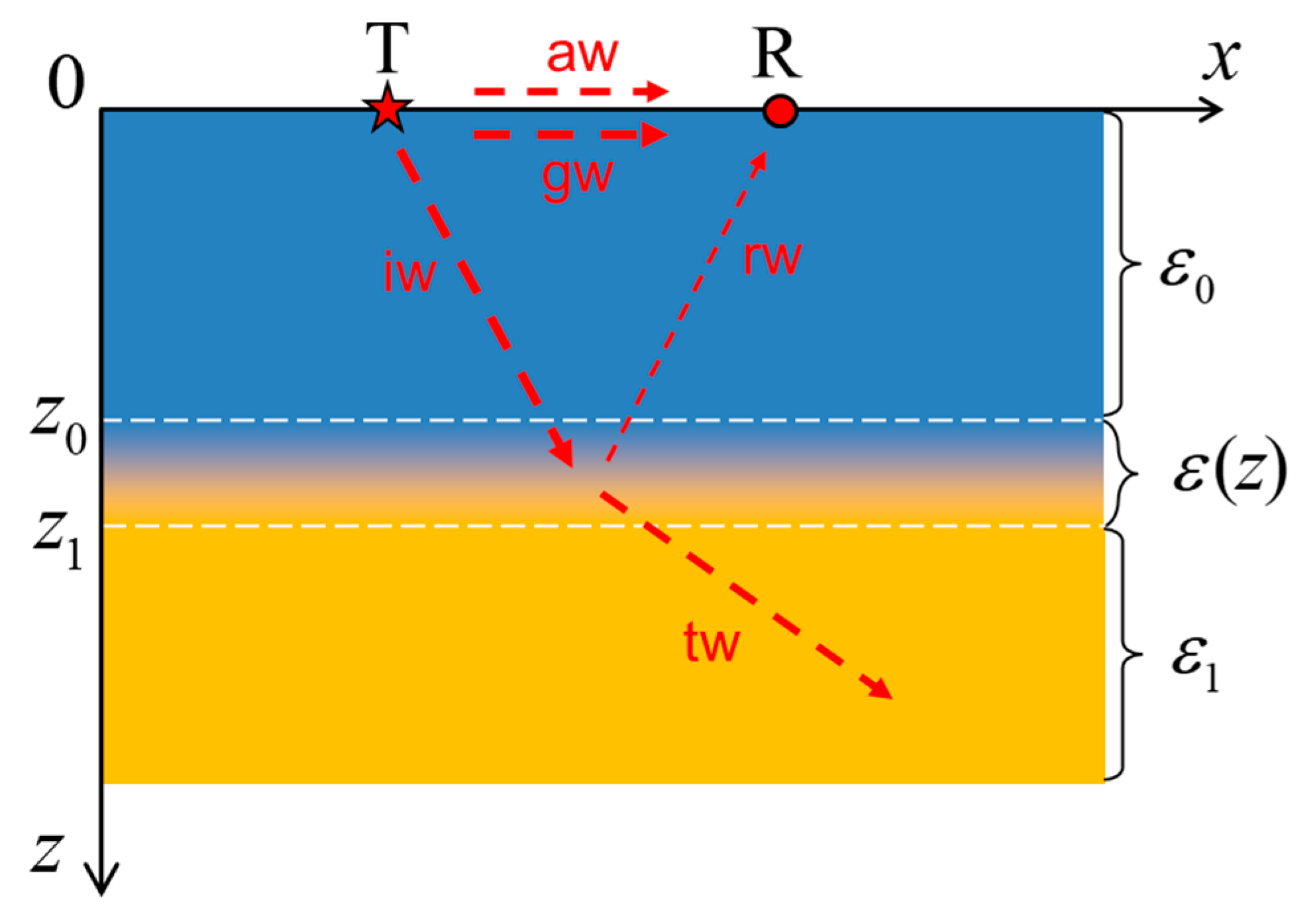
2.1. One-Dimensional Problem
2.2. 1.5-Dimensional Problem
2.3. Geometrical-Optics Interpretation
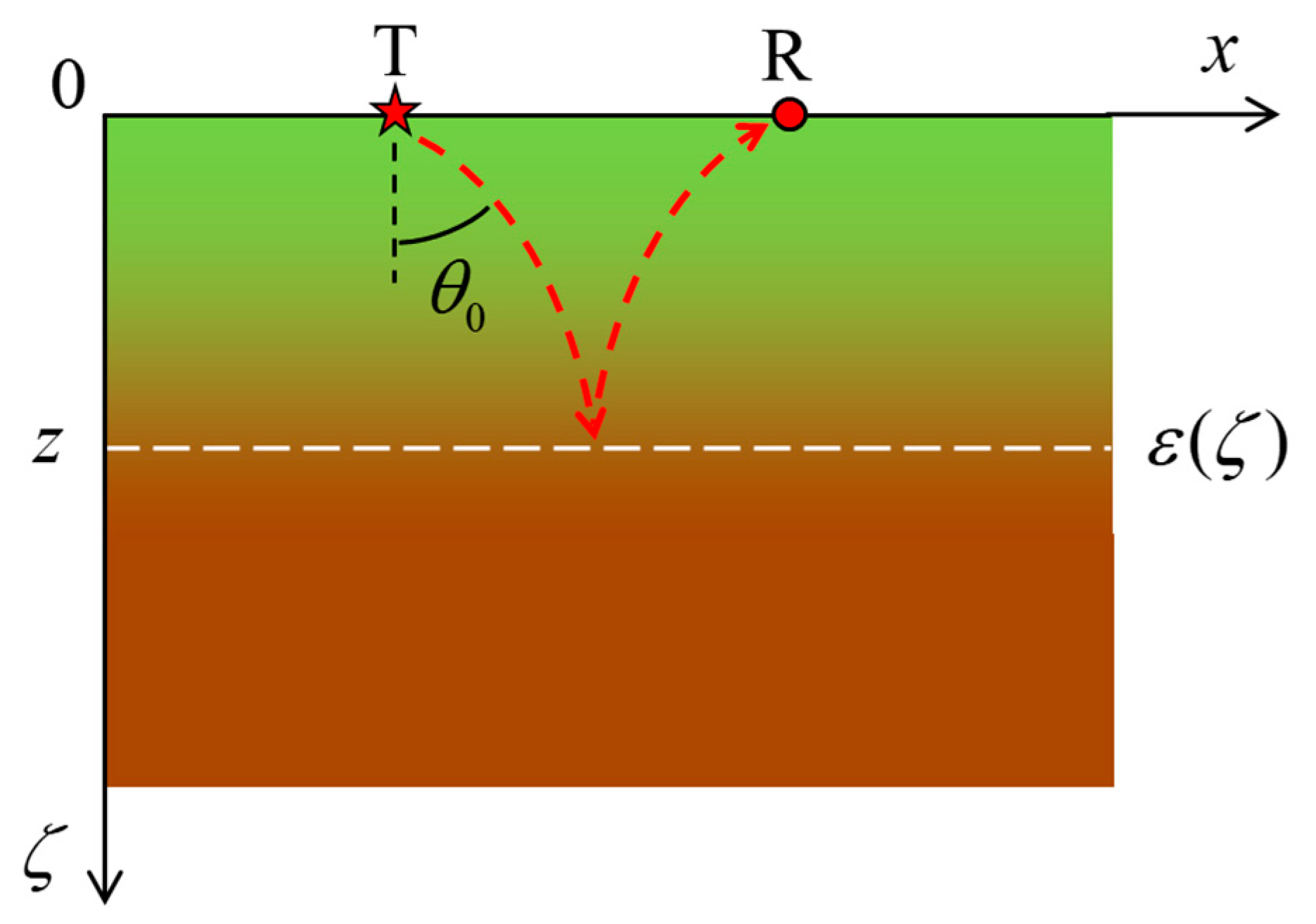
2.4. Quasi-Vertical Sounding
3. Numerical Integration
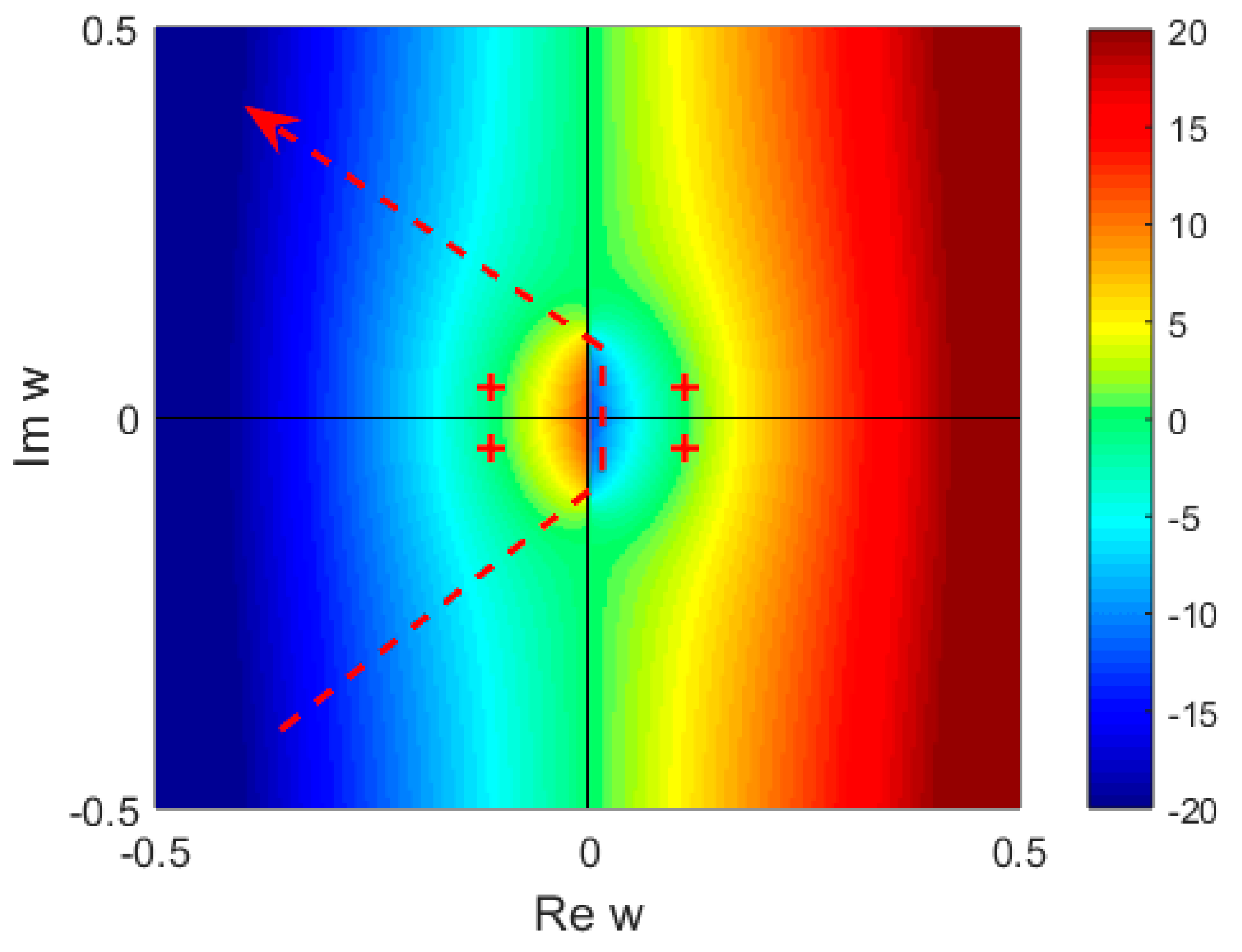
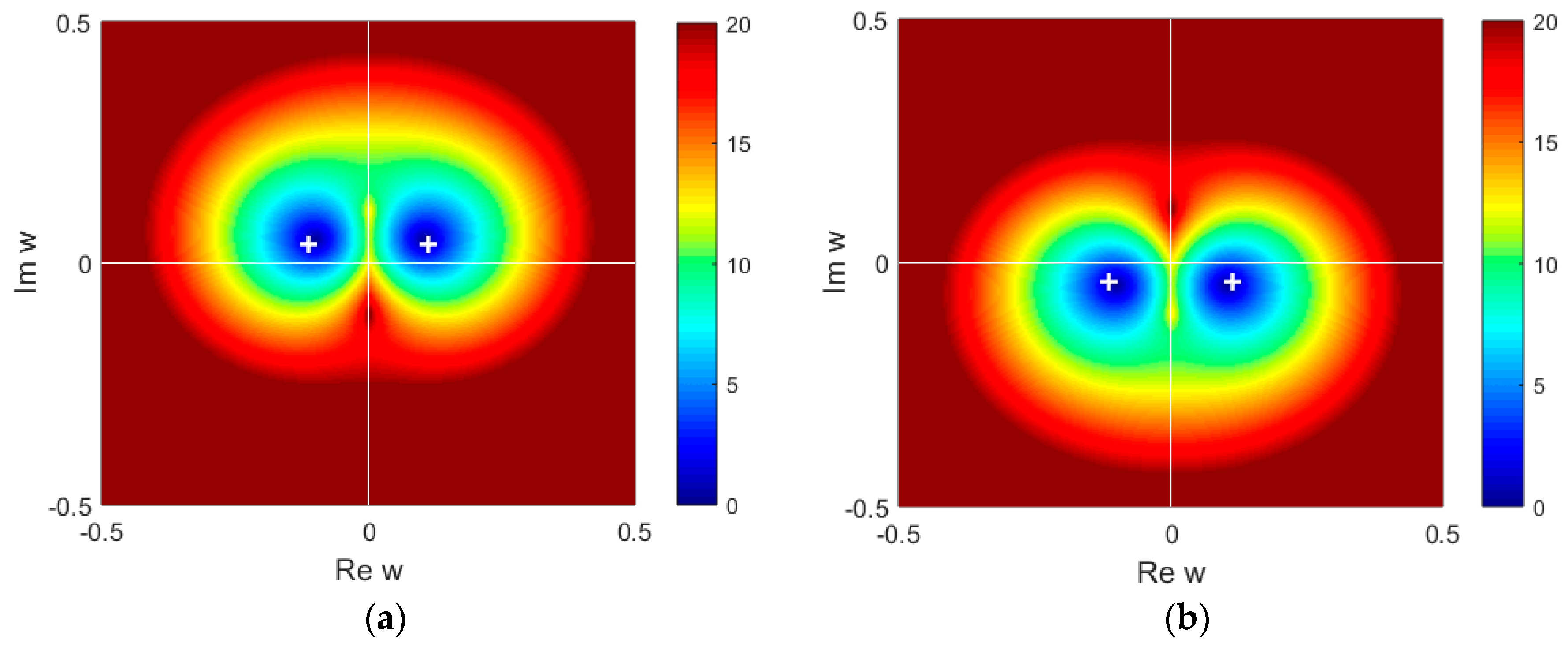
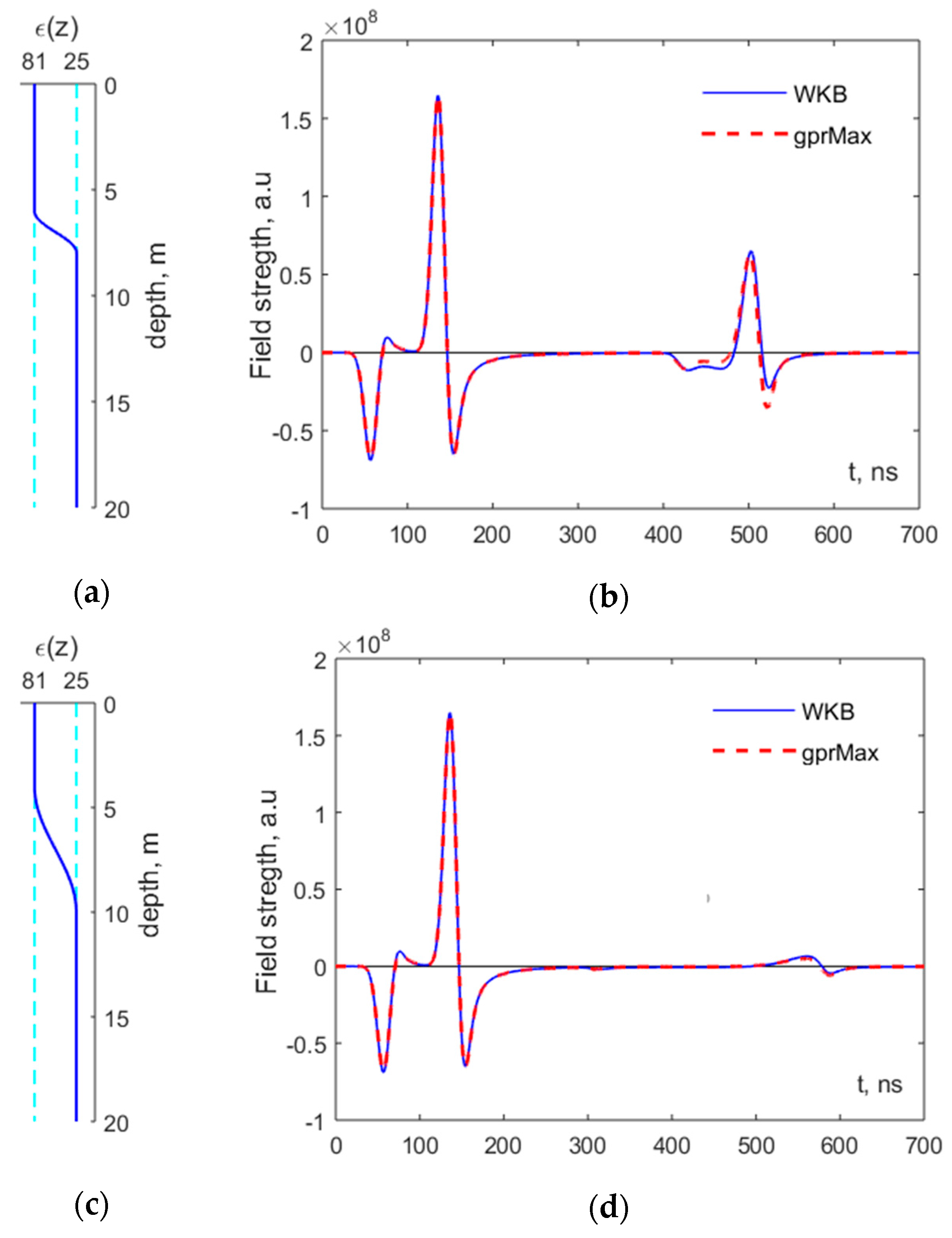
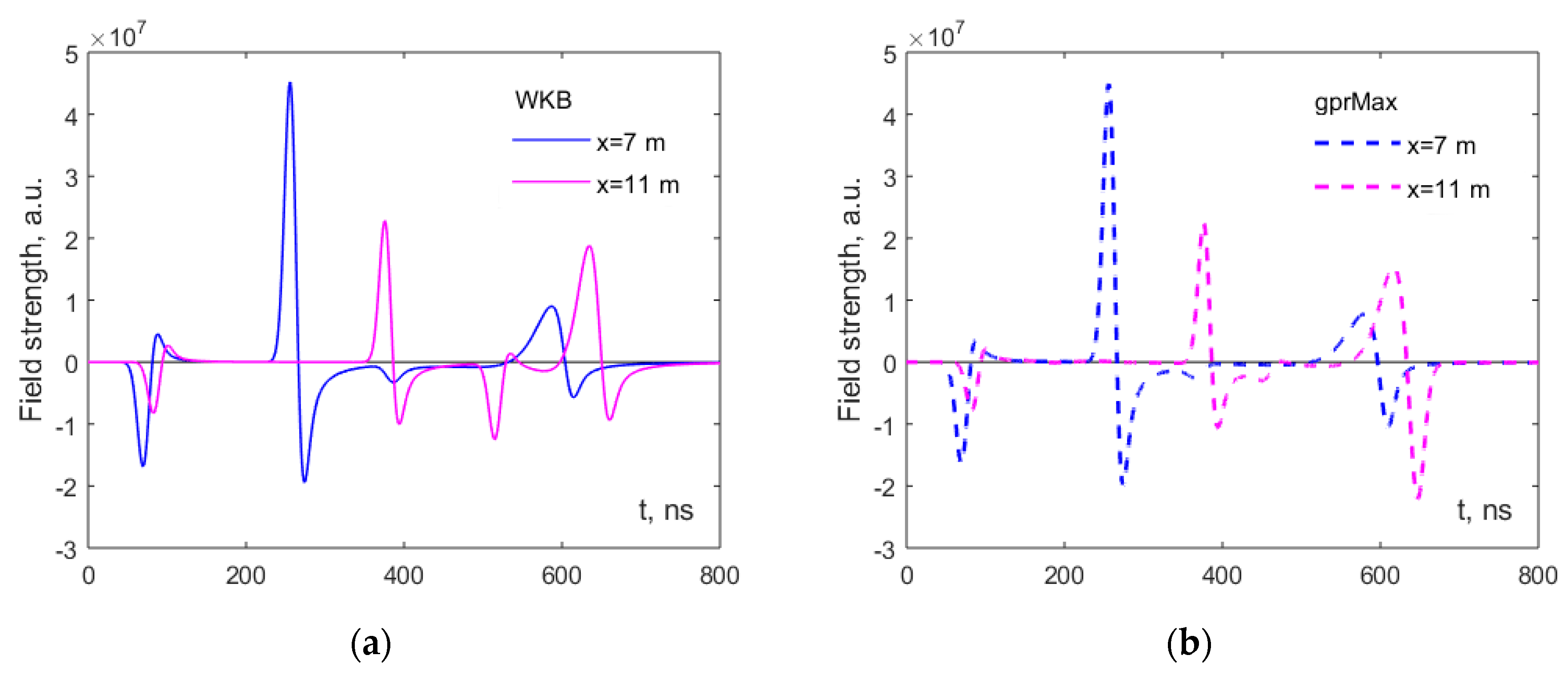
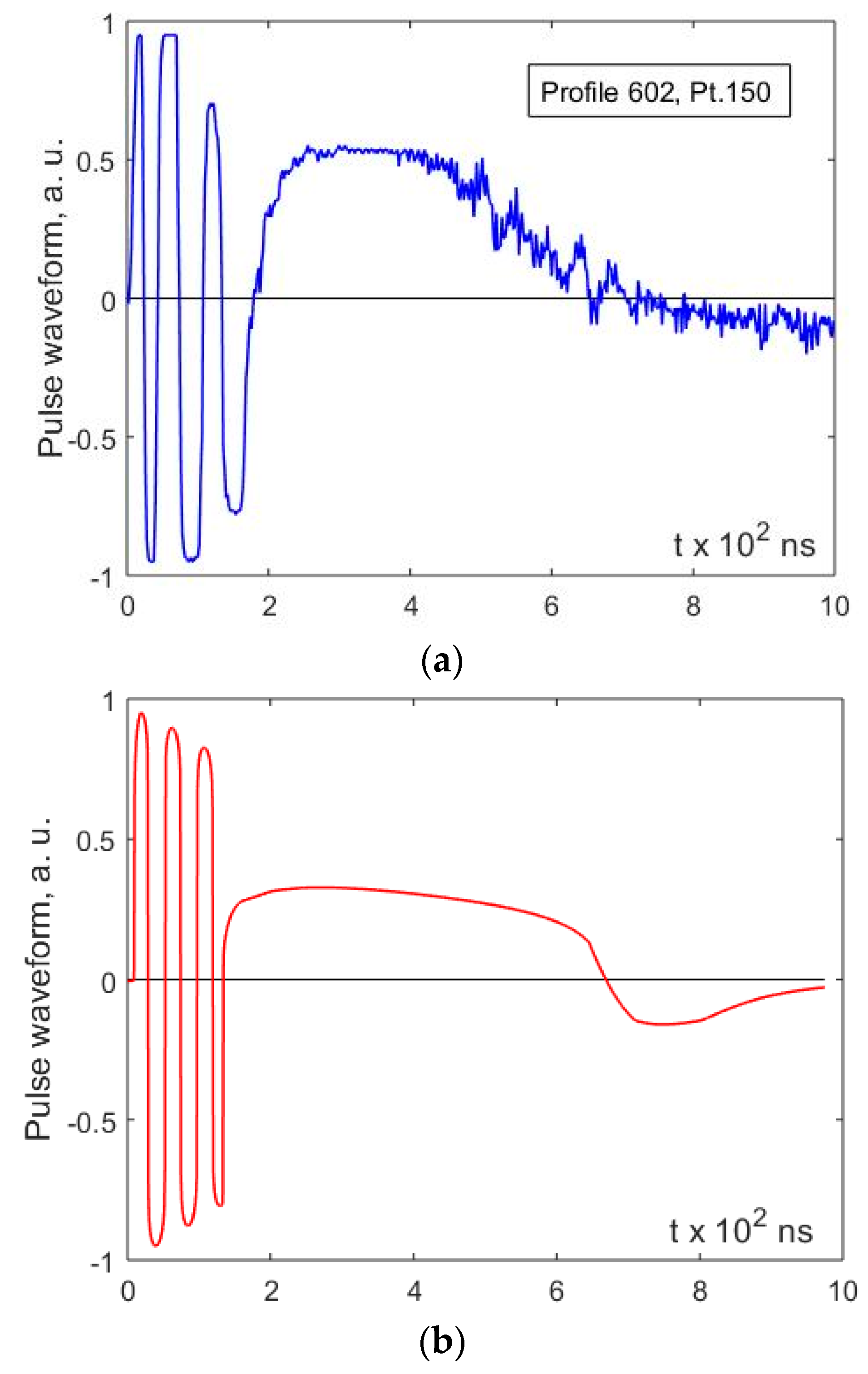
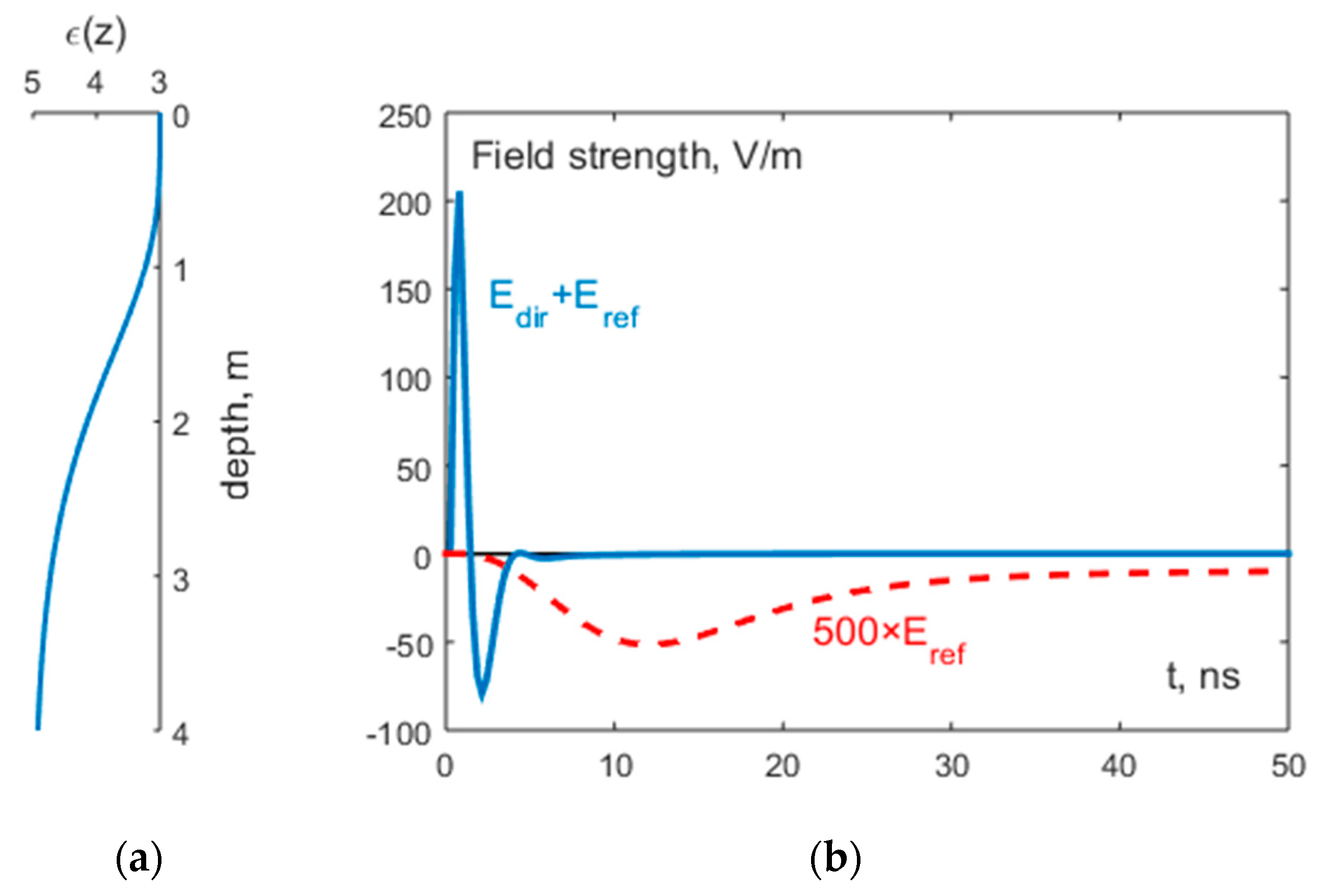
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Benedetto, A.; Pajewski, L. (Eds.) Civil Engineering Applications of Ground Penetrating Radar; Book Series: “Springer Transactions in Civil and Environmental Engineering”; Springer: New Delhi, India, 2015; p. 385. ISBN 978-3-319-04813-0. [Google Scholar] [CrossRef]
- Persico, R. Introduction to Ground Penetrating Radar: Inverse Scattering and Data Processing; Wiley-IEEE Press: New York, NY, USA, 2014; p. 392. ISBN 978-1-118-30500-3. [Google Scholar]
- Giannopoulos, A. Modelling ground penetrating radar by GprMax. Constr. Build. Mater. 2005, 19, 755–762. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. An advanced GPR modelling framework—The next generation of gprMax. In Proceedings of the 8th International Workshop on Advanced Ground Penetrating Radar (IWAGPR 2015), Florence, Italy, 7–10 July 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A. Experimental and Modeled Performance of a Ground Penetrating Radar Antenna in Lossy Dielectrics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 29–36. [Google Scholar] [CrossRef]
- Frezza, F.; Mangini, F.; Pajewski, L.; Schettini, G.; Tedeschi, N. Spectral domain method for the electromagnetic scattering by a buried sphere. J. Opt. Soc. Am. A 2013, 30, 783–790. [Google Scholar] [CrossRef] [PubMed]
- Frezza, F.; Pajewski, L.; Ponti, C.; Schettini, G.; Tedeschi, N. Cylindrical-Wave Approach for Electromagnetic Scattering by Subsurface Metallic Targets in a Lossy Medium. J. Appl. Geophys. 2013, 97, 55–59. [Google Scholar] [CrossRef]
- Frezza, F.; Pajewski, L.; Ponti, C.; Schettini, G.; Tedeschi, N. Electromagnetic Scattering by a Metallic Cylinder Buried in a Lossy Medium with the Cylindrical-Wave Approach. IEEE Geosci. Remote Sens. Lett. 2013, 10, 179–183. [Google Scholar] [CrossRef]
- Bourlier, C.; Le Bastard, C.; Pinel, N. Full wave PILE method for the electromagnetic scattering from random rough layers. In Proceedings of the 15th International Conference on Ground Penetrating Radar (GPR 2014), Brussels, Belgium, 30 June–4 July 2014; pp. 545–551. [Google Scholar] [CrossRef]
- Poljak, D.; Dorić, V. Transmitted field in the lossy ground from ground penetrating radar (GPR) dipole antenna. WIT Trans. Model. Simul. 2015, 59, 3–11. [Google Scholar] [CrossRef]
- Poljak, D.; Dorić, V.; Birkić, M.; El Khamlichi Drissi, K.; Lallechere, S.; Pajewski, L. A simple analysis of dipole antenna radiation above a multilayered medium. In Proceedings of the 9th International Workshop on Advanced Ground Penetrating Radar (IWAGPR 2017), Edinburgh, UK, 28–30 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Winton, S.C.; Kosmas, P.; Rappaport, C.M. FDTD simulation of TE and TM plane waves at nonzero incidence in arbitrary layered media. IEEE Trans. Antennas Propag. 2005, 53, 1721–1728. [Google Scholar] [CrossRef]
- Diamant, R.; Fernandez-Guasti, M. Light propagation in 1D inhomogeneous deterministic media: The effect of discontinuities. J. Opt. A Pure Appl. Opt. 2009, 11, 045712. [Google Scholar] [CrossRef]
- Zeng, Q.; Delisle, G.Y. Transient analysis of electromagnetic wave reflection from a stratified medium. In Proceedings of the 2010 Asia-Pacific International Symposium on Electromagnetic Compatibility, Beijing, China, 12–16 April 2010; pp. 881–884. [Google Scholar] [CrossRef]
- Kaganovsky, Y.; Heyman, E. Pulsed beam propagation in plane stratified media: Asymptotically exact solutions. In Proceedings of the 2010 URSI International Symposium on Electromagnetic Theory, Berlin, Germany, 16–19 August 2010; pp. 829–832. [Google Scholar] [CrossRef]
- Diamanti, N.; Annan, A.P.; Redman, J.D. Impact of Gradational Electrical Properties on GPR Detection of Interfaces. In Proceedings of the 15th International Conference on Ground Penetrating Radar (GPR 2014), Brussels, Belgium, 30 June–4 July 2014; pp. 529–534. [Google Scholar] [CrossRef]
- Connor, K.M.; Dowding, C.H. GeoMeasurements by Pulsing TDR Cables and Probes; CRC Press: Boca Raton, FL, USA, 1999; p. 424. ISBN 9780849305863. [Google Scholar]
- Schlaeger, S. Inversion of TDR Measurements to Reconstruct Spatially Distributed Geophysical Ground Parameter. Ph.D. Thesis, University of Karlsruhe, Karlsruhe, Germany, 2002. [Google Scholar]
- Epstein, P.S. Reflection of waves in an inhomogeneous absorbing medium. Proc. Natl. Acad. Sci. USA 1930, 16, 627–637. [Google Scholar] [CrossRef] [PubMed]
- Weiland, T. A discretization model for the solution of Maxwell’s equations for six-component fields. Archiv Elektronik Uebertragungstechnik 1977, 31, 116–120. [Google Scholar]
- Miller, E.K.; Poggio, A.J.; Burke, G.J. An integro-differential equation technique for the time-domain analysis of thin wire structures. I. the numerical method. J. Comput. Phys. 1973, 12, 24–48. [Google Scholar] [CrossRef]
- Krueger, R.J.; Ochs, R.L., Jr. A Green’s function approach to the determination of internal fields. Appl. Math. Sci. 1989, 11, 525–543. [Google Scholar] [CrossRef]
- Lambot, S.; Slob, E.; Vereecken, H. Fast evaluation of zero-offset Green’s function for layered media with application to ground-penetrating radar. Geophys. Res. Lett. 2007, 34, L21405. [Google Scholar] [CrossRef]
- Larruquert, J.I. Reflectance optimization of inhomogeneous coatings with continuous variation of the complex refractive index. J. Opt. Soc. Am. A 2006, 23, 99–107. [Google Scholar] [CrossRef]
- Grafstrom, S. Reflectivity of a stratified half-space: The limit of weak inhomogeneity and anisotropy. J. Opt. A Pure Appl. Opt. 2006, 8, 134–141. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Quantum Mechanics: Non-Relativistic Theory; Butterworth-Heinemann: Oxford, UK, 1977; p. 677. ISBN 0750635398. [Google Scholar]
- Brekhovskikh, L.M. Waves in Layered Media, 2nd ed.; Academic Press: New York, NY, USA, 1980; 520p, ISBN 9780323161626. [Google Scholar]
- Bremmer, H. Propagation of Electromagnetic Waves. In Handbuch der Physik/Encyclopedia of Physics; Flugge, S., Ed.; Springer: Berlin/Goettingen/Heidelberg, Germany, 1958; Volume 4/16, pp. 423–639. [Google Scholar]
- Jones, A.R. Light scattering for particle characterization. Prog. Energy Comb. Sci. 1999, 25, 1–53. [Google Scholar] [CrossRef]
- Vinogradov, V.A.; Kopeikin, V.V.; Popov, A.V. An approximate solution of 1D inverse problem. In Proceedings of the 10th International Conference on Ground Penetrating Radar (GPR 2004), Delft, The Netherlands, 21–24 June 2004; pp. 95–98. [Google Scholar]
- Kopeikin, V.V.; Kuznetsov, V.D.; Morozov, P.A.; Popov, A.V.; Berkut, A.I.; Merkulov, S.V.; Alexeev, V.A. Ground Penetrating Radar Investigation of the Supposed Fall Site of a Fragment of the Chelabinsk Meteorite in Lake Chebarkul. Geochem. Int. 2013, 51, 636–642. [Google Scholar] [CrossRef]
- Buzin, V.; Edemsky, D.; Gudoshnikov, S.; Kopeikin, V.; Morozov, P.; Popov, A.; Prokopovich, I.; Skomarovsky, V.; Melnik, N.; Berkut, A.; et al. Search for Chelyabinsk Meteorite Fragments in Chebarkul Lake Bottom (GPR and Magnetic Data). J. Telecommun. Inf. Technol. 2017, 2017, 69–78. [Google Scholar] [CrossRef]
- Olhoeft, G.R.; Strangway, D.W. Dielectric Properties of the First 100 Meters of the Moon. Earth Planet. Sci. Lett. 1975, 24, 394–404. [Google Scholar] [CrossRef]
- Fritz, J. Partial Differential Equations, 4th ed.; Springer: New York, NY, USA, 1982; p. 672. ISBN 978-0-387-90609-6. [Google Scholar]
- Claerbout, J.F. Fundamentals of Geophysical Data Processing; Pennwell Books: Tulsa, OK, USA, 1985; 274p, ISBN 0865423059. [Google Scholar]
- Berkut, A.I.; Edemsky, D.E.; Kopeikin, V.V.; Morozov, P.A.; Prokopovich, I.V.; Popov, A.V. Deep penetration subsurface radar: Hardware, results, interpretation. In Proceedings of the 9th International Workshop on Advanced Ground Penetrating Radar (IWAGPR 2017), Edinburgh, UK, 7–10 July 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Matveev, Y.I.; Kostenko, V.I. Problems of Moving Ultrasound Penetrative Devices in a Dispersion Medium during Drilling of the Moon’s Regolith. Acoust. Phys. 2016, 62, 633–641. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prokopovich, I.; Popov, A.; Pajewski, L.; Marciniak, M. Application of Coupled-Wave Wentzel-Kramers-Brillouin Approximation to Ground Penetrating Radar. Remote Sens. 2018, 10, 22. https://doi.org/10.3390/rs10010022
Prokopovich I, Popov A, Pajewski L, Marciniak M. Application of Coupled-Wave Wentzel-Kramers-Brillouin Approximation to Ground Penetrating Radar. Remote Sensing. 2018; 10(1):22. https://doi.org/10.3390/rs10010022
Chicago/Turabian StyleProkopovich, Igor, Alexei Popov, Lara Pajewski, and Marian Marciniak. 2018. "Application of Coupled-Wave Wentzel-Kramers-Brillouin Approximation to Ground Penetrating Radar" Remote Sensing 10, no. 1: 22. https://doi.org/10.3390/rs10010022
APA StyleProkopovich, I., Popov, A., Pajewski, L., & Marciniak, M. (2018). Application of Coupled-Wave Wentzel-Kramers-Brillouin Approximation to Ground Penetrating Radar. Remote Sensing, 10(1), 22. https://doi.org/10.3390/rs10010022






