Unsupervised Clustering Method for Complexity Reduction of Terrestrial Lidar Data in Marshes
Abstract
1. Introduction
2. Study Areas and Dataset
2.1. Study Site
2.2. Dataset
3. Method
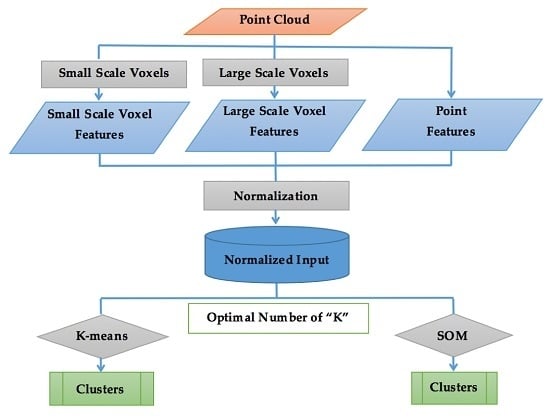
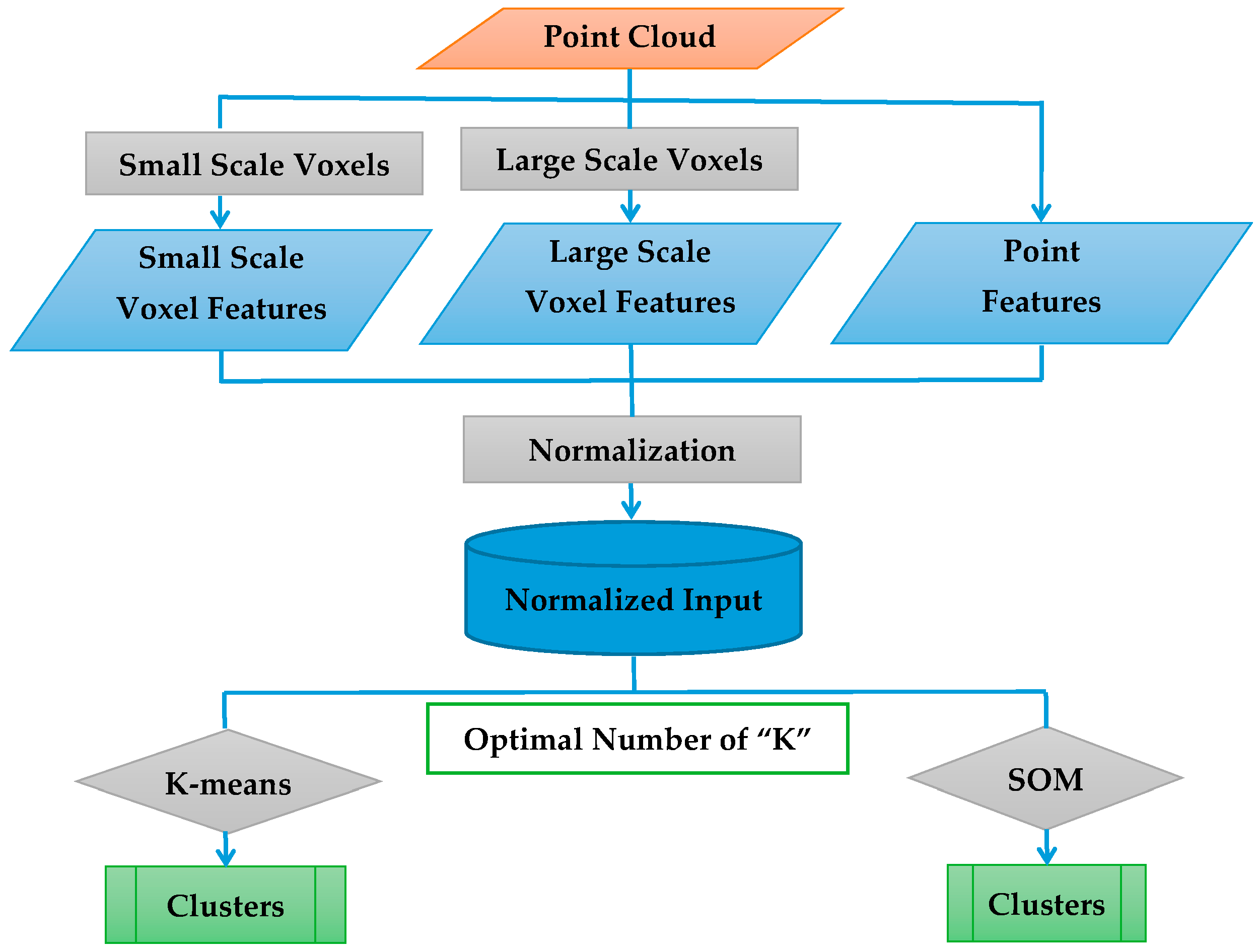
3.1. Overview
3.2. Feature Engineering
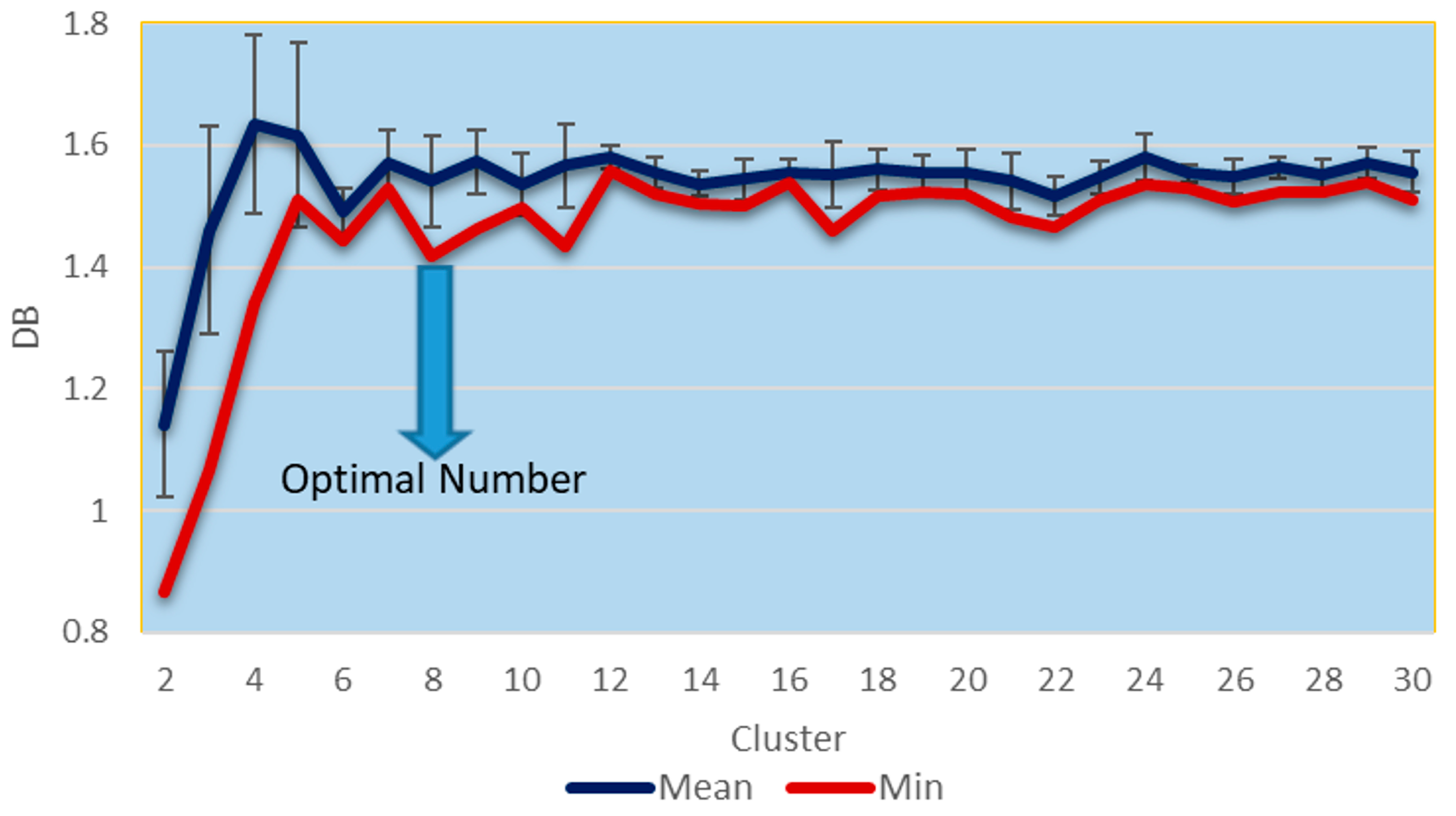
3.3. Determination of the Number of Clusters
3.4. K-Means
- Compute point-to-cluster-centroid distances for full data set and for each centroid.
- Apply a two-phase iterative algorithm to minimize the sum of point-to-centroid distances, summed over all k clusters.
- Batch updates: each iteration consists of reassigning points to their nearest cluster centroid, all at once, followed by recalculation of cluster centroids. This phase occasionally does not converge to a solution that is a local minimum. That is, a partition of the data where moving any single point to a different cluster increases the total sum of distances.
- Online updates: points are individually reassigned if doing so reduces the sum of distances, and cluster centroids are recomputed after each reassignment. Each iteration during this phase consists of one pass through all the points. This phase converges to a local minimum. Finding the global minimum is solved by an exhaustive choice of starting points by using variety of replicates with random starting points typically resulting in a solution.
- Compute the average values in each cluster to obtain k new centroid locations.
- Repeat steps 2 through 4 until cluster assignments no longer change, or the maximum number of iterations is reached.
3.5. SOM
- is the set of n training patterns ;
- is a grid of units where and are their coordinates on that grid;
- α is the learning rate, assuming values in , initialized to a given initial learning rate;
- r is the radius of the neighborhood function initialized to a given initial radius;
- Calculate for all with k = 1 to n.
- Select the unit that minimizes as the winner .
- Update each unit : .
- Decrease the value of α and r.
- Repeat steps 1–4 until α reaches 0.
4. Results and Discussion
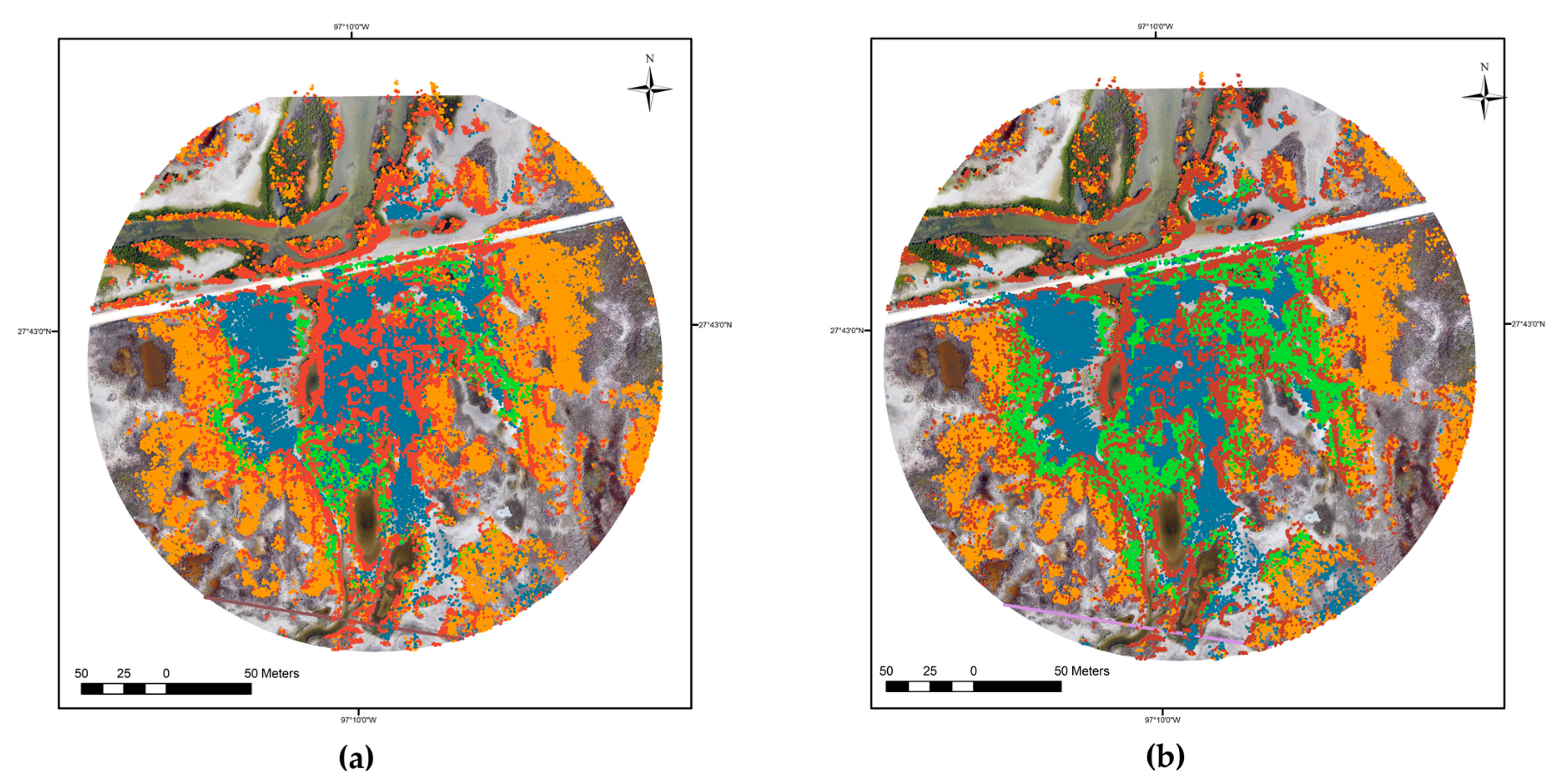
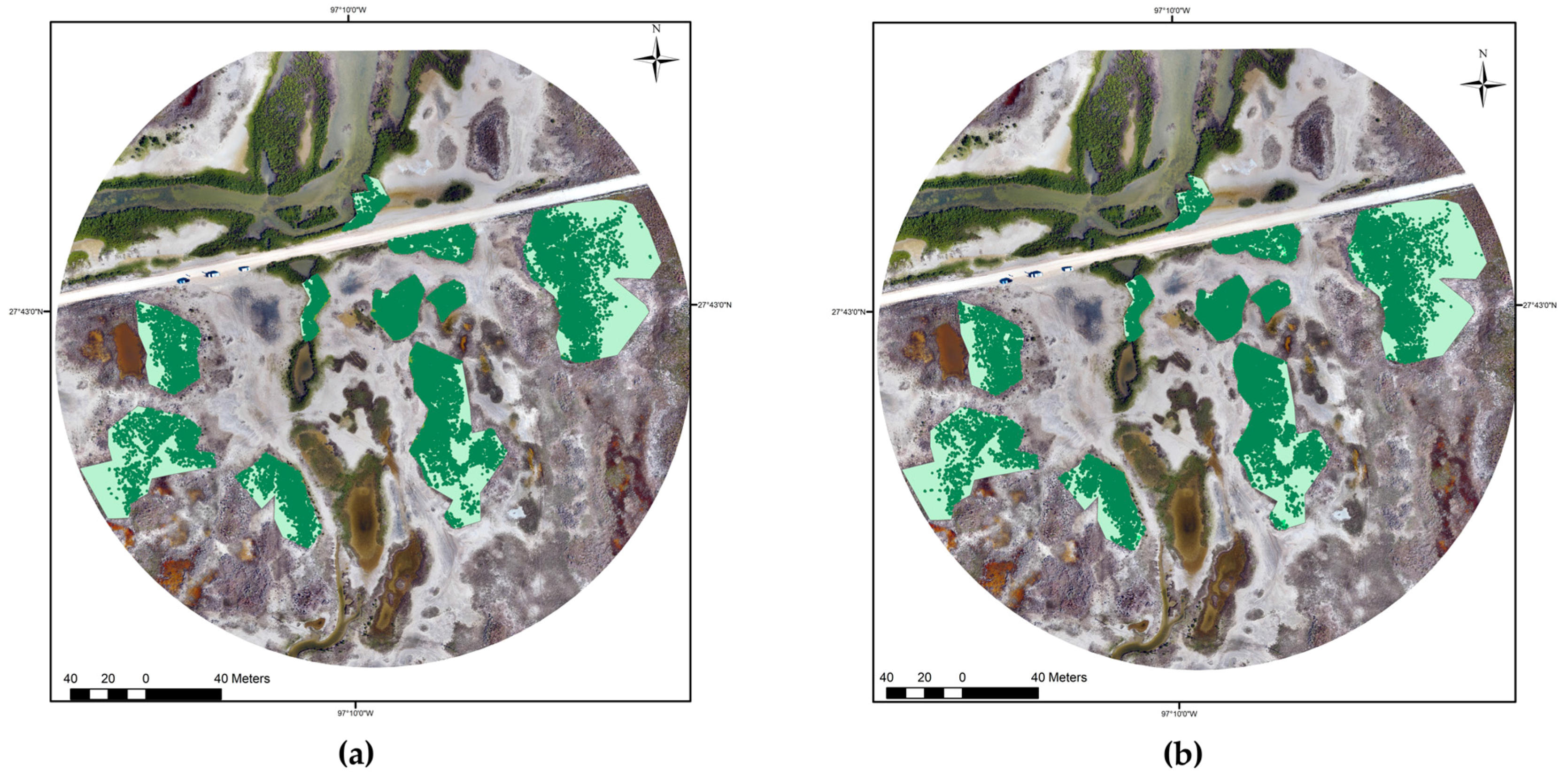
4.1. Clustering Results
4.2. Classification Accuracy
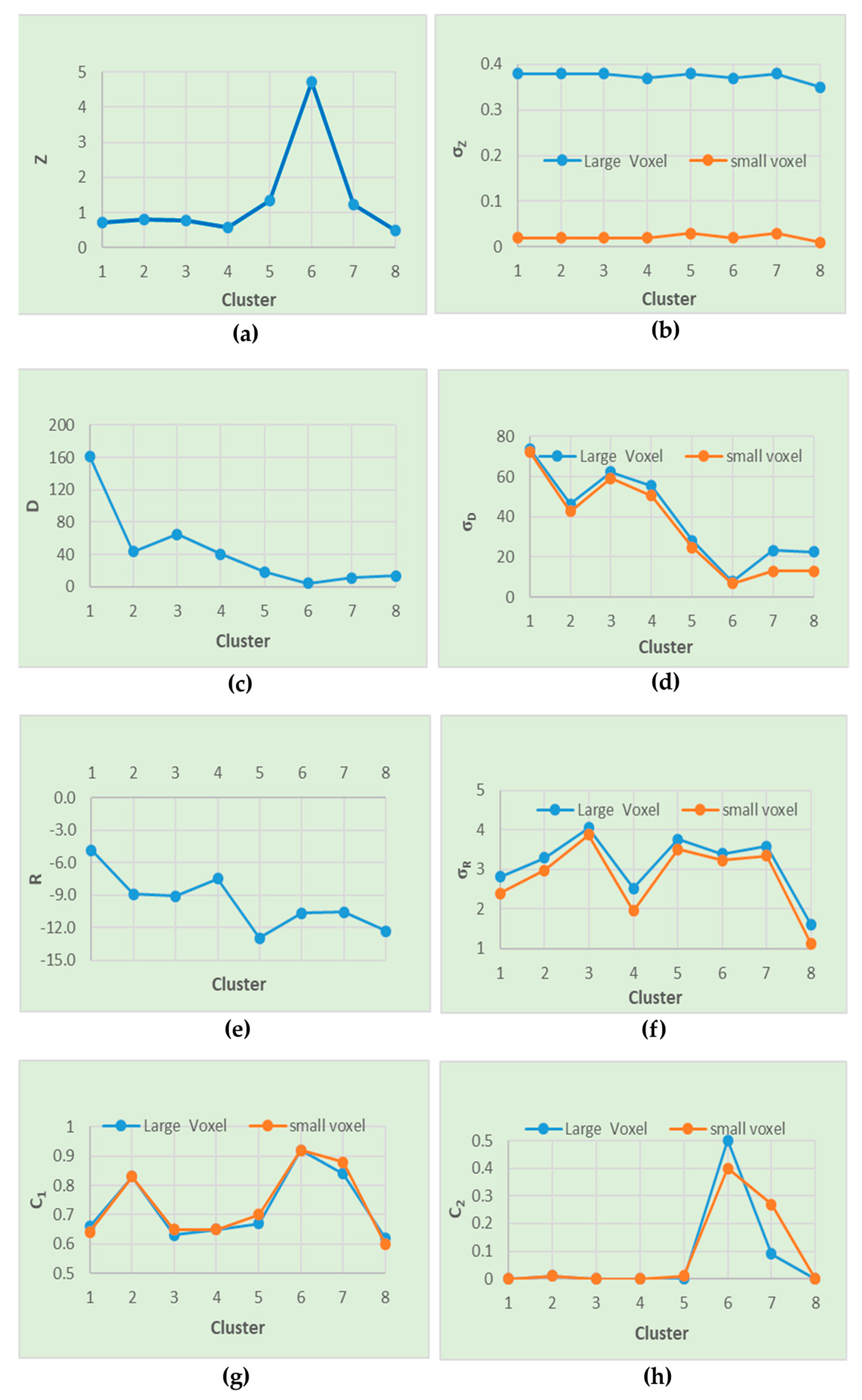
4.3. Feature Importance
4.4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barier, E.B.; Hacker, S.D.; Kennedy, C.; Koch, E.W.; Stier, A.C.; Silliman, B.R. The value of estuarine and coastal ecosystem services. Ecol. Monogr. 2011, 81, 169–193. [Google Scholar] [CrossRef]
- Boesh, D.F.; Turner, R.E. Dependence of fishery species on salt marshes: The role of food and refuge. Estuaries 1984, 7, 460–468. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Gosselink, J.G. The value of wetlands: Importance of scale and landscape setting. Ecol. Econ. 2000, 35, 25–33. [Google Scholar] [CrossRef]
- Moor, H.; Hylander, K.; Norberg, J. Predicting climate change effects on wetland ecosystem services using species distribution modeling and plant functional traits. AMBIO 2015, 44, 113–126. [Google Scholar] [CrossRef] [PubMed]
- Costanza, R.; Pérez-Maqueo, O.; Martinez, M.L.; Sutton, P.; Anderson, S.J.; Mulder, K. The Value of Coastal Wetlands for Hurricane Protection. AMBIO 2008, 37, 241–248. [Google Scholar] [CrossRef]
- Pennings, S.C.; Callaway, R.M. Salt Marsh Plant Zonation: The Relative Importance of Competition and Physical Factors. Ecology 1992, 73, 681–690. [Google Scholar] [CrossRef]
- Silvestri, S.; Defina, A.; Marani, M. Tidal regime, salinity and salt marsh plant zonation. Estuar. Coast. Shelf Sci. 2005, 62, 119–130. [Google Scholar] [CrossRef]
- Suchrow, S.; Jensen, K. Plant Species Responses to an Elevational Gradient in German North Sea Salt Marshes. Wetlands 2010, 30, 735–746. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33, 1944–8007. [Google Scholar] [CrossRef]
- NASA. Sea Level. Available online: https://climate.nasa.gov/vital-signs/sea-level/ (accessed on 9 September 2017).
- Warner, N.N.; Tissot, P.E. Storm flooding sensitivity to sea level rise for Galveston Bay, Texas. Ocean Eng. 2012, 44, 23–32. [Google Scholar] [CrossRef]
- Passeri, D.L.; Hagen, S.C.; Medeiros, S.C.; Bilskie, M.V.; Alizad, K.; Wang, D. The dynamic effects of sea level rise on low-gradient coastal landscapes: A review. Earths Future 2015, 3, 159–181. [Google Scholar] [CrossRef]
- Lemmens, M. Terrestrial Laser Scanning. In Geo-Information: Technologies, Applications and the Environment; Springer: Dordrecht, The Netherlands, 2011; pp. 101–121. [Google Scholar]
- Lichti, D.; Pfeifer, N.; Maas, H.-G. ISPRS Journal of Photogrammetry and Remote Sensing Theme Issue “Terrestrial Laser Scanning”; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Moorthy, I.; Miller, J.R.; Hu, B.; Chen, J.; Li, Q. Retrieving crown leaf area index from an individual tree using ground-based LiDAR data. Can. J. Remote Sens. 2008, 34, 320–332. [Google Scholar] [CrossRef]
- Straatsma, M.; Warmink, J.J.; Middelkoop, H. Two novel methods for field measurements of hydrodynamic density of floodplain vegetation using terrestrial laser scanning and digital parallel photography. Int. J. Remote Sens. 2008, 29, 1595–1617. [Google Scholar] [CrossRef]
- Buckley, S.J.; Howell, J.; Enge, H.; Kurz, T. Terrestrial laser scanning in geology: Data acquisition, processing and accuracy considerations. J. Geol. Soc. 2008, 165, 625–638. [Google Scholar] [CrossRef]
- Rosser, N.; Petley, D.; Lim, M.; Dunning, S.; Allison, R. Terrestrial laser scanning for monitoring the process of hard rock coastal cliff erosion. Q. J. Eng. Geol. Hydrogeol. 2005, 38, 363–375. [Google Scholar] [CrossRef]
- Starek, M.J.; Mitasova, H.; Hardin, E.; Weaver, K.; Overton, M.; Harmon, R.S. Modeling and analysis of landscape evolution using airborne, terrestrial, and laboratory laser scanning. Geosphere 2011, 7, 1340–1356. [Google Scholar] [CrossRef]
- Starek, M.J.; Mitásová, H.; Wegmann, K.; Lyons, N. Space-time cube representation of stream bank evolution mapped by terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1369–1373. [Google Scholar] [CrossRef]
- Heritage, G.; Hetherington, D. Towards a protocol for laser scanning in fluvial geomorphology. Earth Surf. Process. Landf. 2007, 32, 66–74. [Google Scholar] [CrossRef]
- Milan, D.J.; Heritage, G.L.; Hetherington, D. Application of a 3D laser scanner in the assessment of erosion and deposition volumes and channel change in a proglacial river. Earth Surf. Process. Landf. 2007, 32, 1657–1674. [Google Scholar] [CrossRef]
- Harman, C.J.; Lohse, K.A.; Troch, P.A.; Sivapalan, M. Spatial patterns of vegetation, soils, and microtopography from terrestrial laser scanning on two semiarid hillslopes of contrasting lithology. J. Geophys. Res. Biogeosci. 2014, 119, 163–180. [Google Scholar] [CrossRef]
- Feliciano, E.A.; Wdowinski, S.; Potts, M.D. Assessing mangrove above-ground biomass and structure using terrestrial laser scanning: A case study in the Everglades National Park. Wetlands 2014, 34, 955–968. [Google Scholar] [CrossRef]
- Guarnieri, A.; Vettore, A.; Pirotti, F.; Menenti, M.; Marani, M. Retrieval of small-relief marsh morphology from terrestrial laser scanner, optimal spatial filtering, and laser return intensity. Geomorphology 2009, 113, 12–20. [Google Scholar] [CrossRef]
- Hladik, C.; Alber, M. Accuracy assessment and correction of a LIDAR-derived salt marsh digital elevation model. Remote Sens. Environ. 2012, 121, 224–235. [Google Scholar] [CrossRef]
- Hladik, C.; Schalles, J.; Alber, M. Salt marsh elevation and habitat mapping using hyperspectral and lidar data. Remote Sens. Environ. 2013, 139, 318–330. [Google Scholar] [CrossRef]
- Bowen, Z.H.; Waltermire, R.G. Evaluation of light detection and ranging (lidar) for measuring river corridor topography. J. Am. Water Resour. Assoc. 2002, 38, 33–41. [Google Scholar] [CrossRef]
- Chasmer, L.; Hopkinson, C.; Treitz, P. Investigating laser pulse penetration through a conifer canopy by integrating airborne and terrestrial lidar. Can. J. Remote Sens. 2006, 32, 116–125. [Google Scholar] [CrossRef]
- Pirotti, F.; Guarnieri, A.; Vettore, A. Ground filtering and vegetation mapping using multi-return terrestrial laser scanning. J. Photogramm. Remote Sens. 2013, 76, 56–63. [Google Scholar] [CrossRef]
- Wang, M.; Tseng, Y.H. Incremental segmentation of LiDAR point clouds with an octree-structured voxel space. Photogramm. Rec. 2011, 26, 32–57. [Google Scholar] [CrossRef]
- Paine, J.G.; White, W.A.; Smyth, R.C.; Andrews, J.R.; Gibeaut, J.C. Mapping coastal environments with LiDAR and EM on Mustang Island, Texas, US. Lead. Edge 2004, 23, 894–898. [Google Scholar] [CrossRef]
- Raber, G.T.; Jensen, J.R.; Hodgson, M.E.; Tullis, J.A.; Davis, B.A.; Berglund, J. Impact of LiDAR nominal post-spacing on DEM accuracy and flood zone delineation. Photogramm. Eng. Remote Sens. 2007, 73, 793–804. [Google Scholar] [CrossRef]
- Perroy, R.L.; Bookhagen, B.; Asner, G.P.; Chadwick, O.A. Comparison of gully erosion estimates using airborne and ground-based LiDAR on Santa Cruz Island, California. Geomorphology 2010, 118, 288–300. [Google Scholar] [CrossRef]
- Douillard, B.; Underwood, J.; Kuntz, N.; Vlaskine, V.; Quadros, A.; Morton, P.; Frenkel, A. On the Segmentation of 3D LIDAR Point Clouds. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 2798–2805. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Brodu, N.; Lague, D. 3D terrestrial LiDAR data classification of complex natural scenes using a multi-scale dimensionality criterion: Applications in geomorphology. ISPRS J. Photogramm. Remote Sens. 2012, 68, 121–134. [Google Scholar] [CrossRef]
- Wakita, T.; Susaki, J. Multi-Scale-based Extraction of Vegetation from Terrestrial LiDAR Data for Assessing Local Landscape. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 263. [Google Scholar] [CrossRef]
- Pirotti, F.; Guarnieri, A.; Vettore, A. Vegetation filtering of waveform terrestrial laser scanner data for DTM production. Appl. Geomat. 2013, 5, 311–322. [Google Scholar] [CrossRef]
- Vandapel, N.; Huber, D.F.; Kapuria, A.; Hebert, M. Natural terrain classification using 3-D ladar data. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’04), New Orleans, LA, USA, 26 April–1 May 2004; pp. 5117–5122. [Google Scholar]
- Carlberg, M.; Gao, P.; Chen, G.; Zakhor, A. Classifying urban landscape in aerial LiDAR using 3D shape analysis. In Proceedings of the 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 1701–1704. [Google Scholar] [CrossRef]
- Visalakshi, N.K.; Thangavel, K. Impact of normalization in distributed K-means clustering. Int. J. Soft Comput. 2009, 4, 168–172. [Google Scholar]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 224–227. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007; pp. 1027–1035. [Google Scholar]
- Kohonen, T. Analysis of a simple self-organizing process. Biol. Cybern. 1982, 44, 135–140. [Google Scholar] [CrossRef]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef] [PubMed]
- Ray, S.; Turi, R.H. Determination of number of clusters in K-means clustering and application in colour image segmentation. In Proceedings of the 4th International Conference on Advances in Pattern Recognition and Digital Techniques, Calcutta, India, 28–31 December 1999; pp. 137–143. [Google Scholar]
- Montgomery, D.C.; Runger, G.C.; Hubele, N.F. Engineering Statistics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]



| Parameters | Specifications |
|---|---|
| Pulse repetition rate | Up to 300,000 kHz |
| Laser wavelength | 1550 nm |
| Beam divergence | 0.3 mrad |
| Spot size | 3 cm at 100 m distance |
| Range | 1.5 m (min), 600 m (max) * |
| Field of view | 100° vertical × 360° horizontal |
| Repeatability | 3 mm (1 sigma @ 100 m range) |
| Minimum stepping angle | 0.0024° |
| Marsh Environment | Cluster Numbers | Percentage (%) | ||
|---|---|---|---|---|
| K-Means | SOM | K-Means | SOM | |
| Tidal flats (high flats, low flats with sparing algal coverage, partially vegetated flats) | 1, 4, 8 | 1, 4, 8 | 61.2 | 50.3 |
| Black Mangrove vegetation | 2 | 2 | 10.8 | 9.3 |
| Low marsh to high marsh vegetation | 3 | 5, 7 | 17.2 | 30.7 |
| Upland vegetation | 5 | 6 | 10.4 | 9.5 |
| Power line | 6 | 3 | 0.1 | 0.2 |
| Mixed | 7 | 0.3 | ||
| Total | 100 | 100 | ||
| Marsh Environment | Cluster | Percentage | ||
|---|---|---|---|---|
| K-Means | SOM | K-Means | SOM | |
| Tidal flats (high flats, low flats with sparing algal coverage, partially vegetated flats) | 1, 4, 8 | 1, 4, 8 | 88.3 | 84.6 |
| Black Mangrove vegetation | 2 | 2 | 5.0 | 2.4 |
| Low marsh to high marsh vegetation | 3 | 5, 7 | 6.4 | 12.9 |
| Upland vegetation | 5 | 6 | 0.2 | 0.1 |
| Power line | 6 | 3 | 0.0 | 0.0 |
| Mixed | 7 | 0.1 | ||
| Total | 100 | 100 | ||
| K-Means | SOM | ||
|---|---|---|---|
| Features | F Statistic | Features | F Statistic |
| Curvature 2 of large voxel | 4,085,300 | Std of R of small voxel | 3,686,800 |
| Std of Z of small voxel | 3,334,000 | Std of Z of small voxel | 3,385,700 |
| Std of R of small voxel | 2,941,400 | Std of R of large voxel | 2,954,600 |
| Curvature 2 of small voxel | 2,919,800 | Std of D of small voxel | 2,638,000 |
| Std of D of small voxel | 2,576,100 | D | 2,549,300 |
| Std of R of large voxel | 2,409,500 | Std of D of large voxel | 2,348,400 |
| Z | 2,038,500 | Std of Z of large voxel | 2,000,600 |
| D | 1,886,100 | Curvature 2 of small voxel | 1,979,000 |
| Std of D of large voxel | 1,848,900 | Curvature 2 of large voxel | 1,858,700 |
| Std of Z of large voxel | 1,717,800 | Z | 1,693,500 |
| R | 1,079,300 | R | 1,306,200 |
| Curvature 1 of small voxel | 675,180 | Curvature 1 of large voxel | 662,320 |
| Curvature 1 of large voxel | 629,100 | Curvature 1 of small voxel | 561,240 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, C.; Starek, M.J.; Tissot, P.; Gibeaut, J. Unsupervised Clustering Method for Complexity Reduction of Terrestrial Lidar Data in Marshes. Remote Sens. 2018, 10, 133. https://doi.org/10.3390/rs10010133
Nguyen C, Starek MJ, Tissot P, Gibeaut J. Unsupervised Clustering Method for Complexity Reduction of Terrestrial Lidar Data in Marshes. Remote Sensing. 2018; 10(1):133. https://doi.org/10.3390/rs10010133
Chicago/Turabian StyleNguyen, Chuyen, Michael J. Starek, Philippe Tissot, and James Gibeaut. 2018. "Unsupervised Clustering Method for Complexity Reduction of Terrestrial Lidar Data in Marshes" Remote Sensing 10, no. 1: 133. https://doi.org/10.3390/rs10010133
APA StyleNguyen, C., Starek, M. J., Tissot, P., & Gibeaut, J. (2018). Unsupervised Clustering Method for Complexity Reduction of Terrestrial Lidar Data in Marshes. Remote Sensing, 10(1), 133. https://doi.org/10.3390/rs10010133