Incentive Model Based on Cooperative Relationship in Sustainable Construction Projects
Abstract
:1. Introduction
2. Stakeholders and Factors Surrounding Sustainable Construction
3. Model Description and Solution
3.1. Model Description
3.2. Model Solution
3.2.1. Solution under Non-Moral Hazard
3.2.2. Solution under Moral Hazard
4. Model Analysis and Simulations
4.1. Model Analysis
4.2. Model Simulations
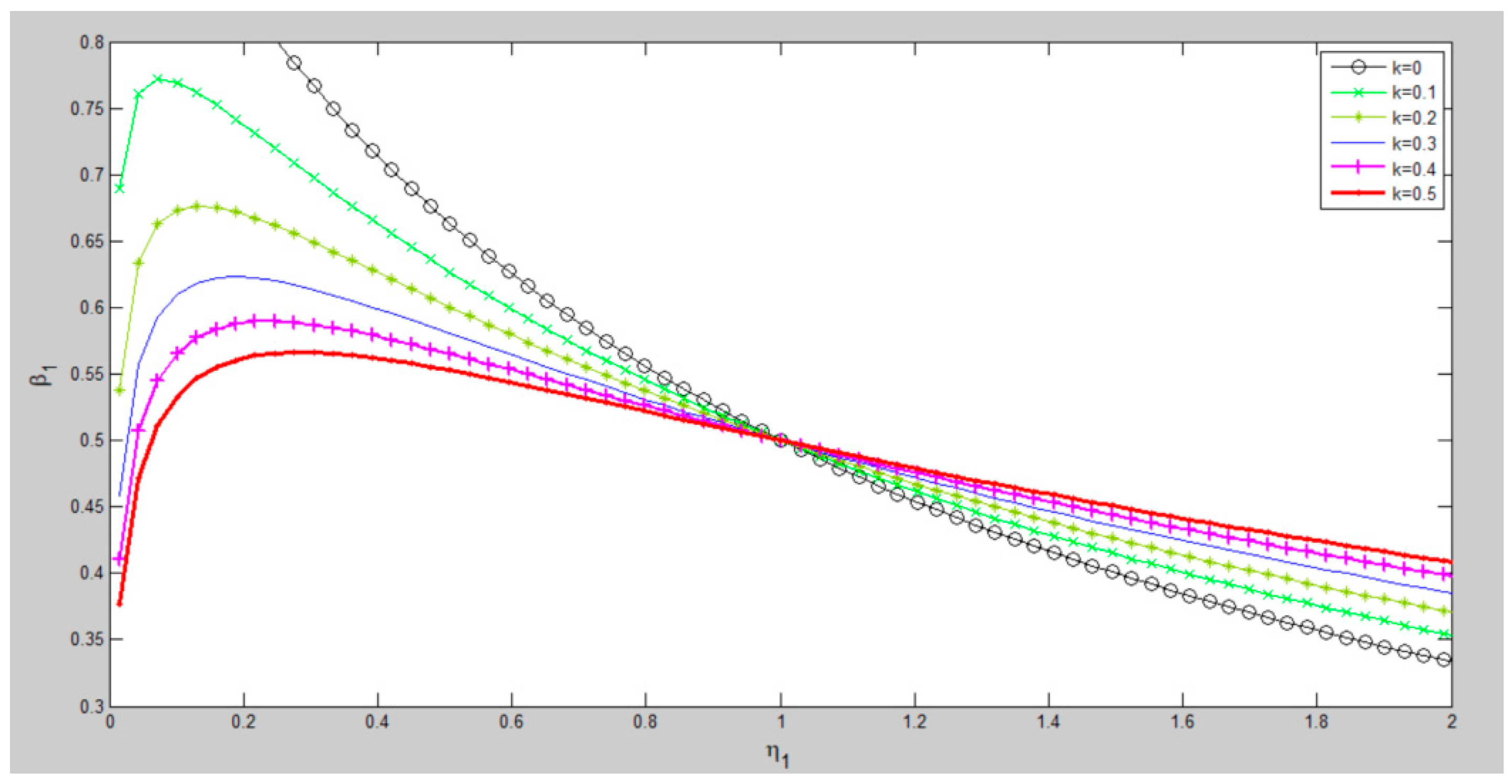
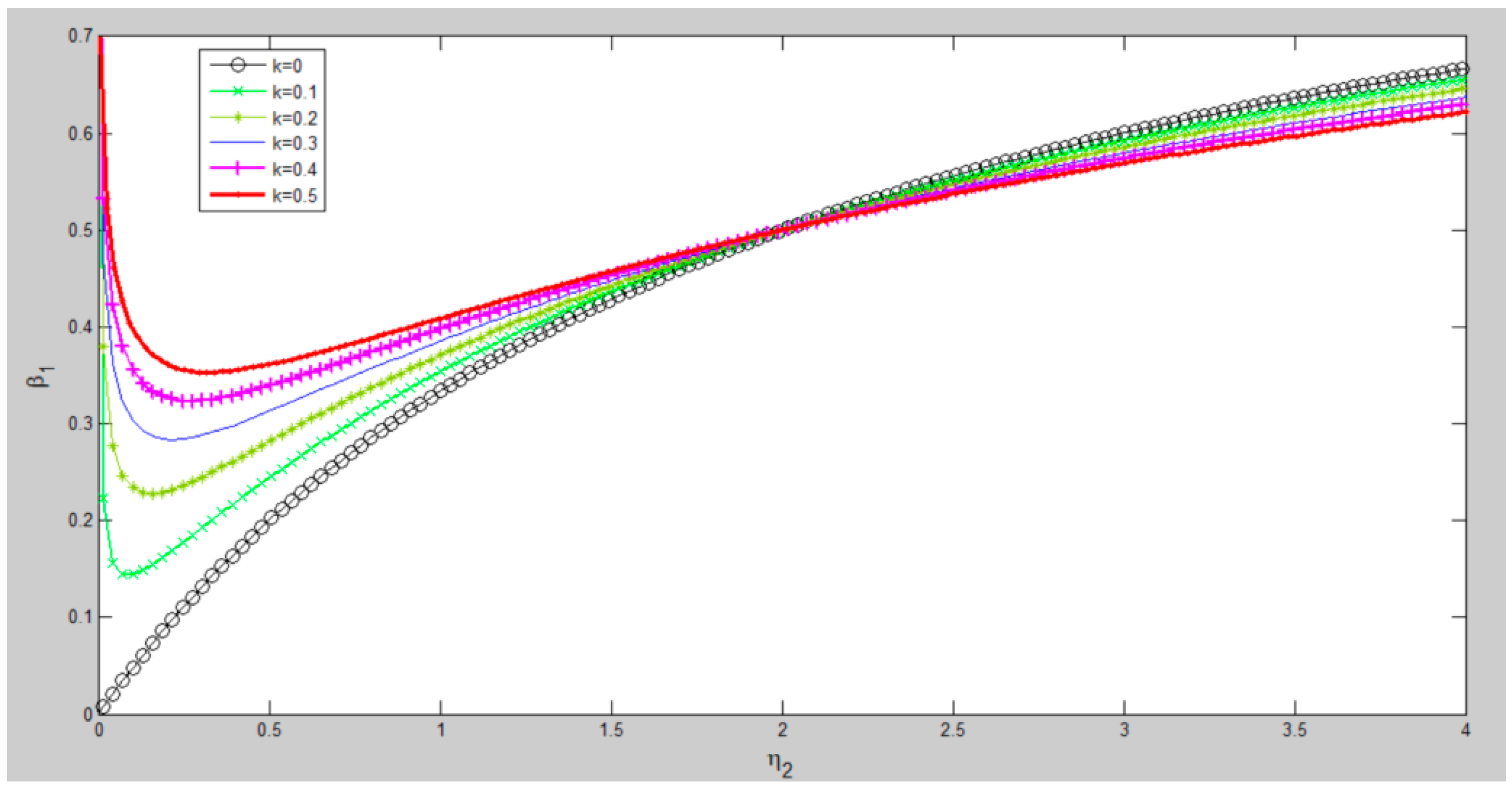
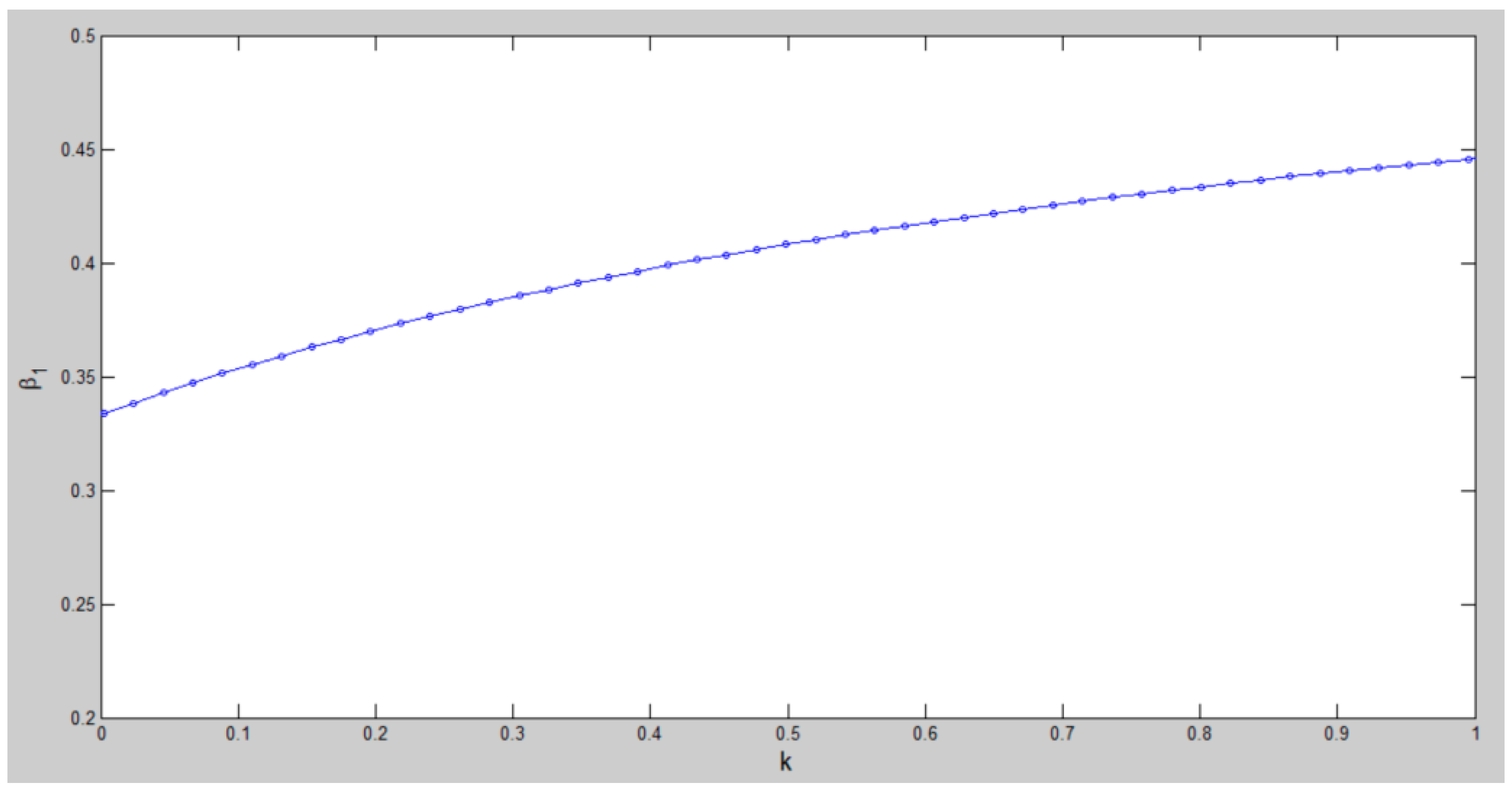
4.2.1. The Effects of Cooperative Relationship (k) on Benefit Allocation Coefficient (β1)
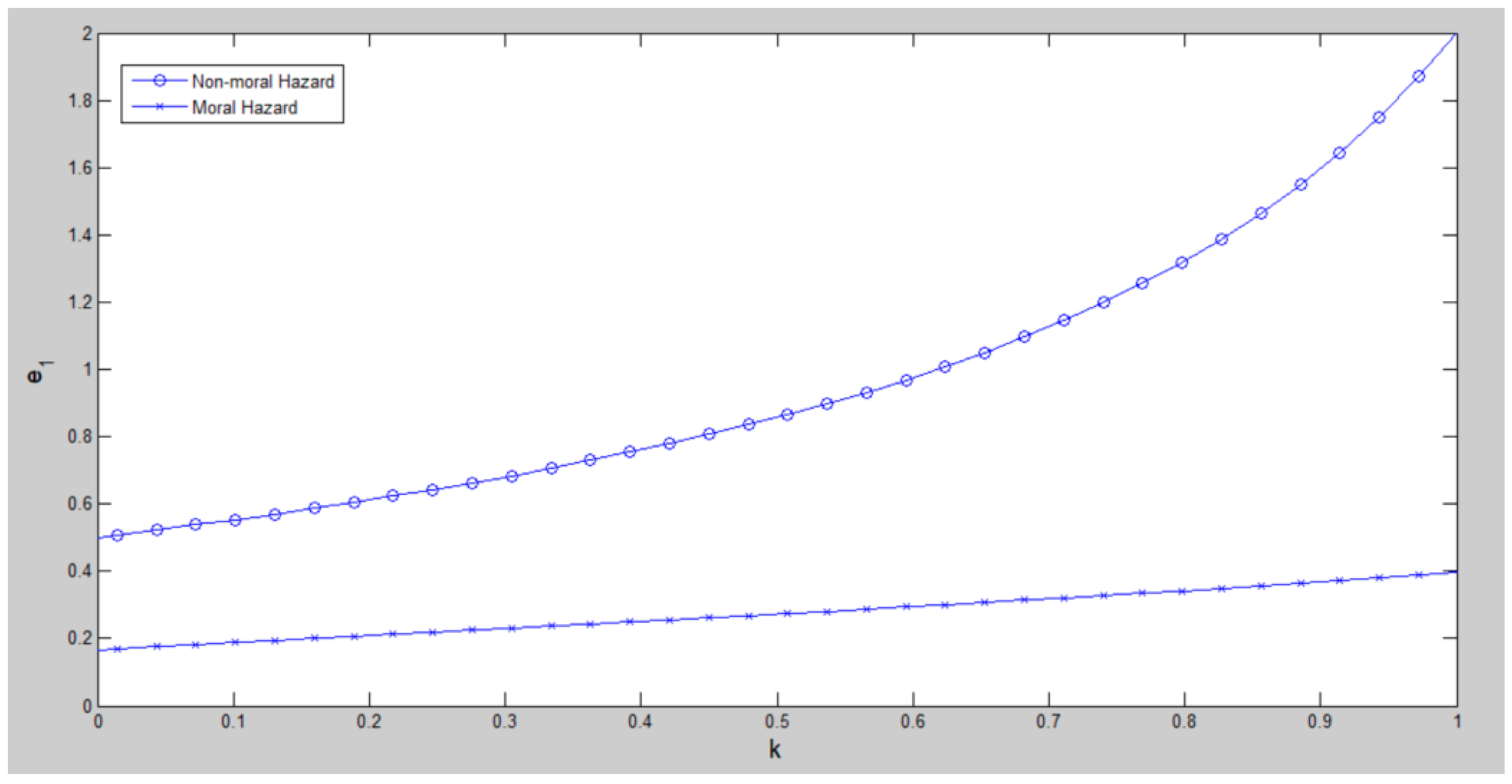
4.2.2. The Effects of Cooperative Relationship (k) on Effort Levels (e)
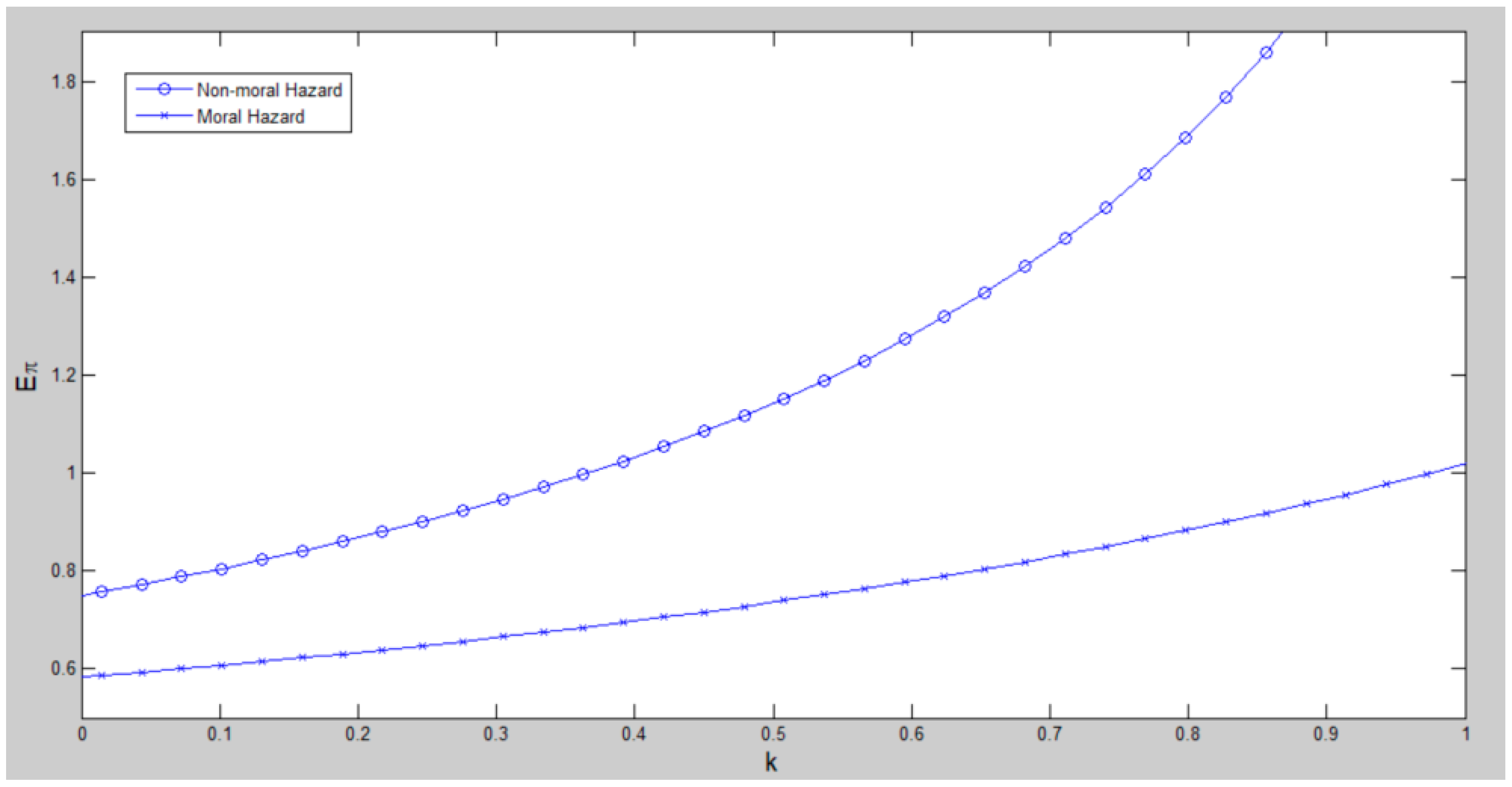
4.2.3. The Effects of Cooperative Relationship (k) on Project Benefit (Eπ)
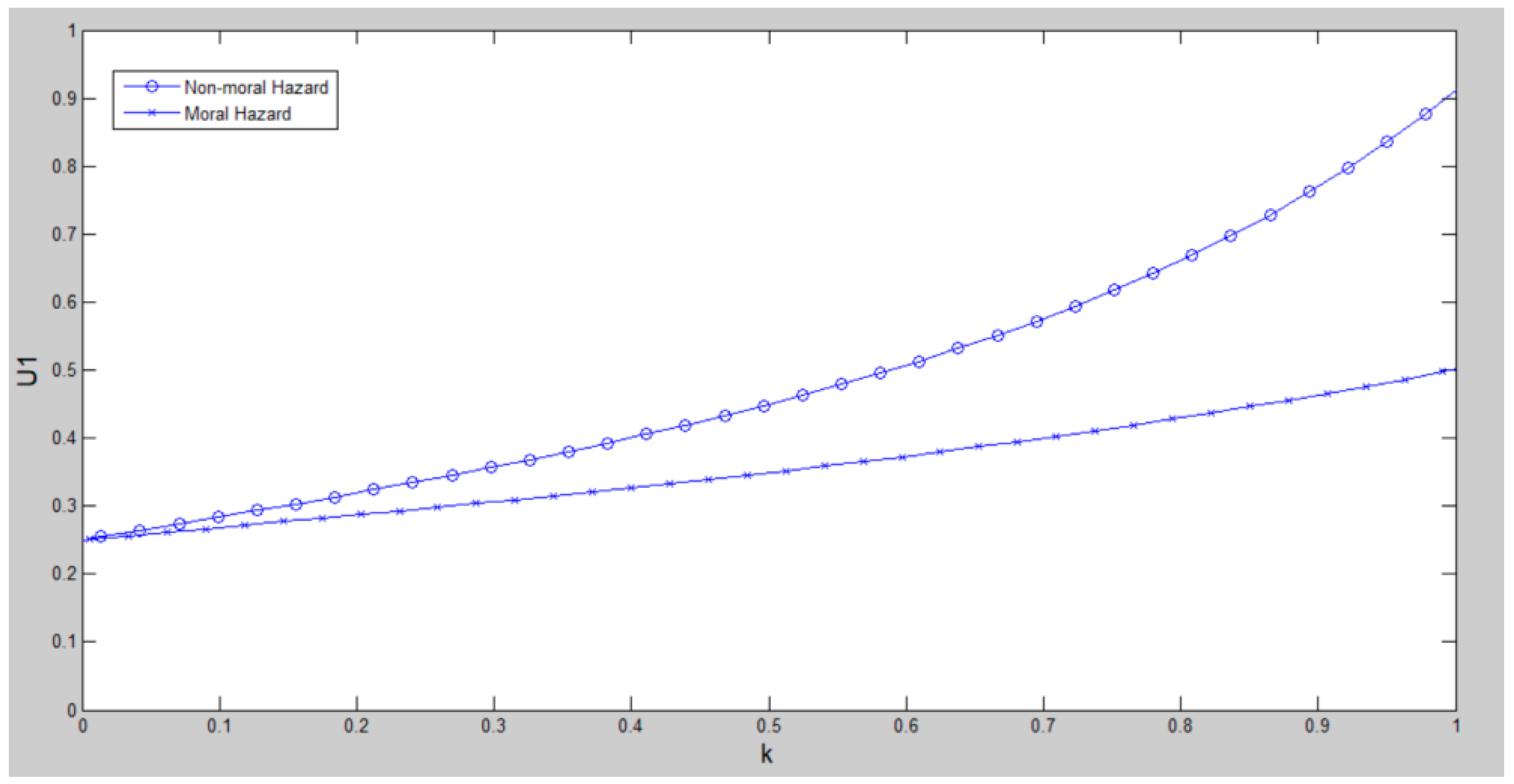
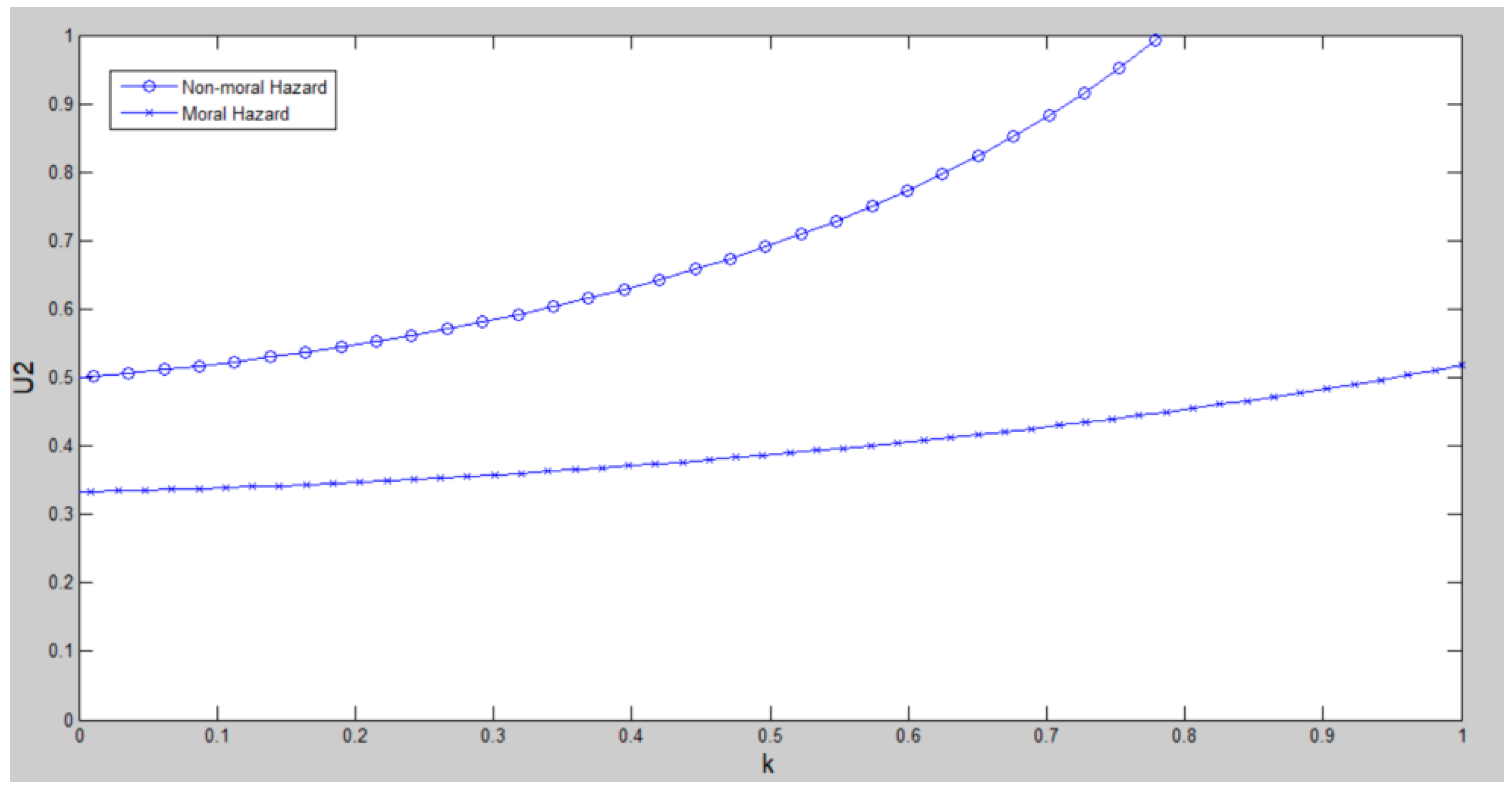
4.2.4. The Numerical Example of the Incentive Model
5. Conclusions and Implications
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Czarnecki, L.; Kaproń, M.; Van Gemert, D. Sustainable construction: Challenges, contribution of polymers, researches arena. Restor. Build. Monum. 2013, 19, 81–96. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Ng, S.T.; Skitmore, M. Quantifying stakeholder influence in decision/evaluations relating to sustainable construction in China—A Delphi approach. J. Clean. Prod. 2017. [Google Scholar] [CrossRef]
- Czarnecki, L.; Kaproń, M. Sustainable construction as a research area. Int. J. Soc. Mater. Eng. Resour. 2010, 17, 99–106. [Google Scholar] [CrossRef]
- Shi, L.; Ye, K.; Lu, W.; Hu, X. Improving the competence of construction management consultants to underpin sustainable construction in China. Habitat Int. 2014, 41, 236–242. [Google Scholar] [CrossRef]
- Manoliadis, O.; Tsolas, I.; Nakou, A. Sustainable construction and drivers of change in Greece: A Delphi study. Constr. Manag. Econ. 2006, 24, 113–120. [Google Scholar] [CrossRef]
- Gan, X.; Zuo, J.; Ye, K.; Skitmore, M.; Xiong, B. Why sustainable construction? Why not? An owner’s perspective. Habitat Int. 2015, 47, 61–68. [Google Scholar] [CrossRef]
- Karakhan, A.A.; Gambatese, J.A. Identification, quantification, and classification of potential safety risk for sustainable construction in the United States. J. Constr. Eng. Manag. 2017. [Google Scholar] [CrossRef]
- Glass, J. The state of sustainability reporting in the construction sector. Smart Sustain. Built Environ. 2012, 1, 87–104. [Google Scholar] [CrossRef]
- Sfakianaki, E. Resource-efficient construction: Rethinking construction towards sustainability. World J. Sci. Technol. Sustain. Dev. 2015, 12, 233–242. [Google Scholar] [CrossRef]
- Whang, S.W.; Kim, S. Balanced sustainable implementation in the construction industry: The perspective of Korean contractors. Energy Build. 2015, 96, 76–85. [Google Scholar] [CrossRef]
- Waring, T.M.; Goff, S.H.; McGuire, J.; Moore, Z.D.; Sullivan, A. Cooperation across organizational boundaries: Experimental evidence from a major sustainability science project. Sustainability 2014, 6, 1171–1190. [Google Scholar] [CrossRef]
- Presley, A.; Meade, L. Benchmarking for sustainability: An application to the sustainable construction industry. Benchmarking Int. J. 2010, 17, 435–451. [Google Scholar] [CrossRef]
- Karakhan, A.A. LEED-Certified projects: Green or sustainable? J. Manag. Eng. 2016. [Google Scholar] [CrossRef]
- Dave, B.; Koskela, L. Collaborative knowledge management—A construction case study. Autom. Constr. 2009, 18, 894–902. [Google Scholar] [CrossRef]
- Hanna, A.S.; Thomas, G.; Swanson, J.R. Construction risk identification and allocation: Cooperative approach. J. Constr. Eng. Manag. 2013, 139, 1098–1107. [Google Scholar] [CrossRef]
- Khanzadi, M.; Eshtehardian, E.; Chalekaee, A. A game theory approach for optimum strategy of the owner and contractor in delayed projects. J. Civ. Eng. Manag. 2016, 22, 1066–1077. [Google Scholar] [CrossRef]
- Schröpfer, V.L.M.; Tah, J.; Kurul, E. Mapping the knowledge flow in sustainable construction project teams using social network analysis. Eng. Constr. Archit. Manag. 2017, 24, 229–259. [Google Scholar] [CrossRef]
- Wen, Q.; Qiang, M.; An, N. Collaborating with construction management consultants in project execution: Responsibility delegation and capability integration. J. Constr. Eng. Manag. 2017. [Google Scholar] [CrossRef]
- Xue, X.; Shen, Q.; Ren, Z. Critical review of collaborative working in construction projects: Business environment and human behaviors. J. Manag. Eng. 2010, 26, 196–208. [Google Scholar] [CrossRef]
- Schieg, M. Strategies for avoiding asymmetric information in construction project management. J. Bus. Econ. Manag. 2008, 9, 47–51. [Google Scholar] [CrossRef]
- Dugar, S.; Shahriar, Q. Group identity and the moral hazard problem: Experimental evidence. J. Econ. Manag. Strateg. 2012, 21, 1061–1081. [Google Scholar] [CrossRef]
- Poblete, J.; Spulber, D. The form of incentive contracts: Agency with moral hazard, risk neutrality, and limited liability. RAND J. Econ. 2012, 43, 215–234. [Google Scholar] [CrossRef]
- Rowell, D.; Connelly, L.B. A history of the term “moral hazard”. J. Risk Insur. 2012, 79, 1051–1075. [Google Scholar] [CrossRef]
- Black, C.; Akintoye, A.; Fitzgerald, E. Analysis of success factors and benefits of partnering in construction. Int. J. Proj. Manag. 2000, 18, 423–434. [Google Scholar] [CrossRef]
- Asgari, S.; Afshar, A.; Madani, K. Cooperative game theoretic framework for joint resource management in construction. J. Constr. Eng. Manag. 2014. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, P. Game analysis on moral hazard of construction project managers in China. Int. J. Civ. Eng. 2014, 12, 429–438. [Google Scholar]
- Phua, F.T.T.; Rowlinson, S. How important is cooperation to construction project success? A grounded empirical quantification. Eng. Constr. Archit. Manag. 2004, 11, 45–54. [Google Scholar] [CrossRef]
- Hughes, D.; Williams, T.; Ren, Z. Differing perspectives on collaboration in construction. Constr. Innov. 2012, 12, 355–368. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Fu, Y.; Zhang, W. Do prior interactions breed cooperation in construction projects? The mediating role of contracts. Int. J. Proj. Manag. 2017, 35, 633–646. [Google Scholar] [CrossRef]
- Karunasena, G.; Rathnayake, R.M.N.U.; Senarathne, D. Integrating sustainability concepts and value planning for sustainable construction. Built Environ. Proj. Asset Manag. 2016, 6, 125–138. [Google Scholar] [CrossRef]
- Akintoye, A.; Main, J. Collaborative relationships in construction: The UK contractors’ perception. Eng. Constr. Archit. Manag. 2007, 14, 597–617. [Google Scholar] [CrossRef]
- Myerson, R. Game Theory: Analysis of Conflict; Harvard University: Cambridge, MA, USA, 1991. [Google Scholar]
- San Cristobal, J. The use of Game Theory to solve conflicts in the project management and construction industry. Int. J. Inf. Syst. Proj. Manag. 2015, 3, 43–58. [Google Scholar]
- Javed, A.A.; Lam, P.T.I.; Chan, A.P.C. Change negotiation in public-private partnership projects through output specifications: An experimental approach based on game theory. Constr. Manag. Econ. 2014, 32, 323–348. [Google Scholar] [CrossRef]
- He, W.; Tang, W.; Wei, Y.; Duffield, C.F.; Lei, Z. Evaluation of cooperation during project delivery: Empirical study on the hydropower industry in southwest China. J. Constr. Eng. Manag. 2016. [Google Scholar] [CrossRef]
- Chen, T.C.; Lin, Y.C.; Wang, L.C. The analysis of BOT strategies based on game theory—Case study on Taiwan’s high speed railway project. J. Civ. Eng. Manag. 2012, 18, 662–674. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Wang, Y. Using bargaining game theory for risk allocation of Public-Private Partnership projects. J. Constr. Eng. Manag. 2017. [Google Scholar] [CrossRef]
- Goh, C.S.; Rowlinson, S. Conceptual maturity model for sustainable construction. J. Leg. Aff. Disput. Resolut. Eng. Constr. 2013, 5, 191–195. [Google Scholar] [CrossRef]
- Abidin, N.Z. Investigating the awareness and application of sustainable construction concept by Malaysian developers. Habitat Int. 2010, 34, 421–426. [Google Scholar] [CrossRef]
- Eyian-Botwe, E.; Aigbavboa, C.; Thwala, W. Mega Construction Projects: Using stakeholder management for enhanced sustainable construction. Am. J. Eng. Res. 2016, 5, 80–86. [Google Scholar]
- Abidin, N.Z. Sustainable construction in Malaysia–Developers’awareness. World Acad. Sci. Eng. Technol. 2009, 5, 122–129. [Google Scholar]
- Fuerst, F.; Kontokosta, C.; McAllister, P. Determinants of green building adoption. Environ. Plan. B 2014, 41, 551–570. [Google Scholar] [CrossRef]
- Bal, M.; Bryde, D.; Fearon, D. A model of stakeholder management strategies for sustainable construction. In Proceedings of the 27th Annual ARCOM Conference, Bristol, UK, 5–7 Semptember 2011; pp. 1165–1174. [Google Scholar]
- Jamil, A.H.A.; Fathi, M.S. The integration of lean construction and sustainable construction: A stakeholder perspective in analyzing sustainable lean construction strategies in Malaysia. Procedia Comput. Sci. 2016, 100, 634–643. [Google Scholar] [CrossRef]
- Gan, X.; Li, S. The study of dynamic stakeholder management in sustainable construction project. Manag. Eng. 2012, 8, 156–159. [Google Scholar]
- Du Plessis, C. A strategic framework for sustainable construction in developing countries. Constr. Manag. Econ. 2007, 25, 67–76. [Google Scholar] [CrossRef]
- Wu, G. The Relationship between Project Team Dynamic Feature, Conflict Dimension and Project Success—An Empirical Research from Shanghai, China. Pak. J. Stat. 2013, 29, 935–952. [Google Scholar]
- Goh, C.S.; Rowlinson, S. Dimensions of sustainable construction: The perspectives of construction stakeholders. In Proceedings of the 4th World Construction Symposium, Colombo, Sri Lanka, 12–14 June 2015; pp. 224–230. [Google Scholar]
- Chong, W.K.; Kumar, S.; Haas, C.T.; Beheiry, S.M.; Coplen, L.; Oey, M. Understanding and interpreting baseline perceptions of sustainability in construction among civil engineers in the United States. J. Manag. Eng. 2009, 25, 143–154. [Google Scholar] [CrossRef]
- Ceric, A. Minimizing communication risk in construction: A Delphi study of the key role of project managers. J. Civ. Eng. Manag. 2014, 20, 829–838. [Google Scholar] [CrossRef]
- Son, J.; Rojas, E.M. Evolution of collaboration in temporary project teams: An agent-based modeling and simulation approach. J. Constr. Eng. Manag. 2011, 137, 619–628. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, Y.; Zhang, S.; Wang, W. Promoting cooperation in construction projects: An integrated approach of contractual incentive and trust. Constr. Manag. Econ. 2015, 33, 653–670. [Google Scholar] [CrossRef]
- Waroonkun, T.; Stewart, R.A. Pathways to enhanced value creation from the international technology transfer process in Thai construction projects. Constr. Innov. 2008, 8, 299–317. [Google Scholar] [CrossRef]
- Erdogan, B.; Anumba, C.J.; Bouchlaghem, D.; Nielsen, Y. Collaboration environments for construction: Management of organizational changes. J. Manag. Eng. 2014. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, S.; Gao, Y.; Ding, X. Contractual governance: Effects of risk allocation on contractors’ cooperative behavior in construction projects. J. Constr. Eng. Manag. 2016. [Google Scholar] [CrossRef]
- Dzeng, R.J.; Wang, P.R. C-negotiation game: An educational game model for construction procurement and negotiation. Autom. Constr. 2017, 75, 10–21. [Google Scholar] [CrossRef]
- Ahmed, M.O.; El-adaway, I.H.; Asce, M.; Coatney, K.T.; Eid, M.S. Construction bidding and the winner’s curse: Game theory approach. J. Constr. Eng. Manag. 2016. [Google Scholar] [CrossRef]
- Liu, J.; Gao, R.; Cheah, C.Y.J.; Luo, J. Evolutionary game of investors’ opportunistic behaviour during the operational period in PPP projects. Constr. Manag. Econ. 2017, 35, 137–153. [Google Scholar] [CrossRef]
- Ho, S.P. Model for financial renegotiations in Public-Private Partnership projects and its policy implications: A game theory approach. J. Constr. Eng. Manag. 2006, 132, 678–688. [Google Scholar] [CrossRef]
- Chiou, Y.C.; Lan, L.W.; Chang, K.L. Sustainable consumption, production and infrastructure construction for operating and planning intercity passenger transport systems. J. Clean. Prod. 2013, 40, 13–21. [Google Scholar] [CrossRef]
- Opoku, A.; Cruickshank, H.; Ahmed, V. Organizational leadership role in the delivery of sustainable construction projects in UK. Built Environ. Proj. Asset Manag. 2015, 5, 154–169. [Google Scholar] [CrossRef]
- Ujene, A.O.; Edike, U.E. Relationships among internal stakeholders in construction projects: A cognitive evaluation for sustainable team integration in Nigeria. Int. J. Constr. Manag. 2015, 15, 71–81. [Google Scholar] [CrossRef]
- Pena-Mora, F.; Tamaki, T. Effect of delivery systems on collaborative negotiations for large-scale infrastuctures projects. J. Manag. Eng. 2001, 17, 105–121. [Google Scholar] [CrossRef]
- Wu, G.D. Knowledge collaborative incentive based on inter-organizational cooperative innovation of project-based supply chain. J. Ind. Eng. Manag. 2013, 6, 1065–1081. [Google Scholar] [CrossRef]
- Tang, D.; Wu, G.; Shi, J. Behavioral coordination mechanism of inter-organizational knowledge innovation in real estate projects. J. Interdiscip. Math. 2016, 19, 395–412. [Google Scholar] [CrossRef]
- Wu, G. Project-based supply chain cross-organizational bidirectional incentives model based on cooperative innovation. Soft Sci. 2012, 26, 16–22. [Google Scholar]
- Meyer, A.D.; Loch, C.H.; Pich, M.T. Managing project uncertainty: From Cariation to Chaos. MIT Sloan Manag. Rev. 2002, 43, 60–67. [Google Scholar]
- Pich, M.T.; Loch, C.H.; Meyer, A. De On uncertainty, ambiguity, and complexity in project management. Manag. Sci. 2002, 48, 1008–1023. [Google Scholar] [CrossRef]
- Demirel, H.C.; Leendertse, W.; Volker, L.; Hertogh, M. Flexibility in PPP contracts–Dealing with potential change in the pre-contract phase of a construction project. Constr. Manag. Econ. 2016, 35, 196–206. [Google Scholar] [CrossRef]
- Zaghloul, R.; Hartman, F. Construction contracts: The cost of mistrust. Int. J. Proj. Manag. 2003, 21, 419–424. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers Definitions, Theorems, and Formulas for Reference and Review; Courier Corporation: North Chelmsford, MA, USA, 2000. [Google Scholar]

| K = 0 | K = 0.1 | K = 0.2 | K = 0.3 | K = 0.4 | |
|---|---|---|---|---|---|
| (0.333,0.333) | (0.189,0.659) | (0.210,0.656) | (0.231,0.657) | (0.252,0.663) | |
| (0.500, 1.000) | (0.553,1.055) | (0.612,1.122) | (0.681,1.204) | (0.761,1.304) | |
| (0.333, 0.667) | (0.354,0.646) | (0.371,0.629) | (0.385,0.615) | (0.398,0.602) | |
| (0.167,0.833) | (0.183,0.817) | (0.201,0.799) | (0.217,0.783) | (0.235,0.765) | |
| (U1*,U2*) | (0.333,0.167) | (0.268,0.339) | (0.287,0.347) | (0.306,0.358) | (0.327,0.371) |
| (U1**,U2**) | (0.125,0.625) | (0.147,0.657) | (0.174,0.693) | (0.204,0.738) | (0.243,0.790) |
| (Eπ*,Eπ**) | (0.500,0.750) | (0.607,0.804) | (0.634,0.867) | (0.664,0.942) | (0.698,1.033) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Zuo, J.; Zhao, X. Incentive Model Based on Cooperative Relationship in Sustainable Construction Projects. Sustainability 2017, 9, 1191. https://doi.org/10.3390/su9071191
Wu G, Zuo J, Zhao X. Incentive Model Based on Cooperative Relationship in Sustainable Construction Projects. Sustainability. 2017; 9(7):1191. https://doi.org/10.3390/su9071191
Chicago/Turabian StyleWu, Guangdong, Jian Zuo, and Xianbo Zhao. 2017. "Incentive Model Based on Cooperative Relationship in Sustainable Construction Projects" Sustainability 9, no. 7: 1191. https://doi.org/10.3390/su9071191
APA StyleWu, G., Zuo, J., & Zhao, X. (2017). Incentive Model Based on Cooperative Relationship in Sustainable Construction Projects. Sustainability, 9(7), 1191. https://doi.org/10.3390/su9071191







