A Hybrid Estimation of Distribution Algorithm for Multi-Objective Multi-Sourcing Intermodal Transportation Network Design Problem Considering Carbon Emissions
Abstract
:1. Introduction
2. Literature Review
3. Problem Description and Model Formulation
3.1. Formulation of Proposed Mathematical Model
| An infinite number; | |
| Amount of freight from sourcing place i, ; | |
| Set of available nodes of stage j, ; | |
| Available nodes of stage 0 and =N; | |
| Available node of stage M and =1; | |
| Set of available transportation modes of stage j, ; | |
| The handling capacity for the kth node of stage j, , , ; | |
| Carbon emission cost of freight i from the lth node in stage to the hth node in stage j under the transportation mode w, , , ; | |
| Transportation cost of freight i from the lth node in stage to the hth node in stage j under the transportation mode w, , , ; | |
| Transportation time of freight i from the lth node in stage to the hth node in stage j under the transportation mode w, , , , ; | |
| Switch cost of freight i from transportation mode w to v for the kth node of stage j, , , , ; | |
| Switch time of freight i from transportation mode w to v for the kth node of stage j, , , , ; and | |
| . | |
| ; |
| ; |
| the start time at the stage j for freight i; and |
| the leave time at the stage j for freight i. |
3.2. Modification of Established Model
4. HEDA for MO_MSITNDP
4.1. Solution Representation
4.2. Multi-Objective Handling Method
4.3. The Proposed Heterogeneous Probability Model and Update Mechanism
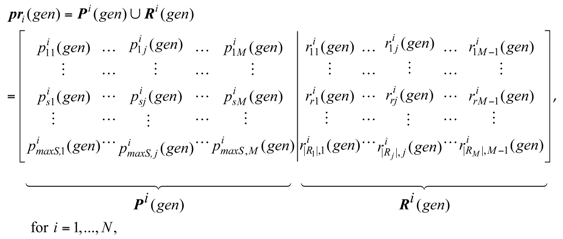
4.4. New Population Generation Method
4.5. Problem-Dependent Local Search
4.6. Procedure of HEDA
5. Computational Results and Comparisons
5.1. Experimental Setup
5.2. Performance Metrics
 is the union of non-dominated solutions with regard to , and then
is the union of non-dominated solutions with regard to , and then  is the number of non-dominated solutions in
is the number of non-dominated solutions in 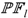 which are not dominated by solutions in
which are not dominated by solutions in 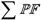 as shown in Equation (20). The larger the value of
as shown in Equation (20). The larger the value of  is, the better performance of Algorithm l.
is, the better performance of Algorithm l.
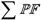 , shown as following Equation (21). The higher the value of
, shown as following Equation (21). The higher the value of 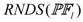 is, the better performance of Algorithm l.
is, the better performance of Algorithm l.
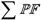 to
to 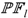 [40], then DIR can be defined in Equation (22). Obviously, a smaller
[40], then DIR can be defined in Equation (22). Obviously, a smaller 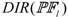 means a better convergence performance to
means a better convergence performance to 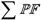 , as well as a better distribution of
, as well as a better distribution of 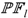 .
.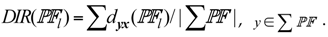
5.3. Comparisons Results
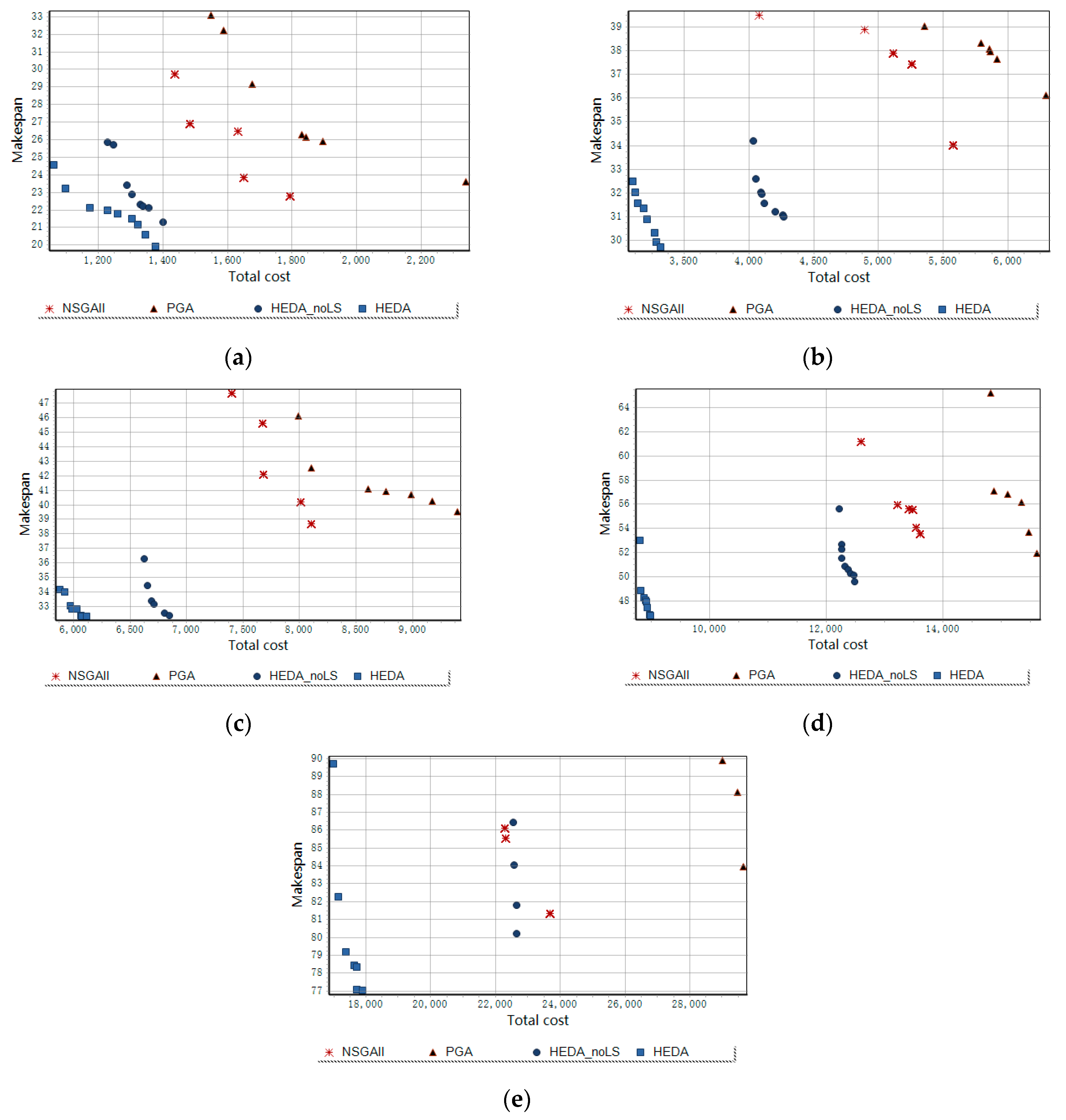
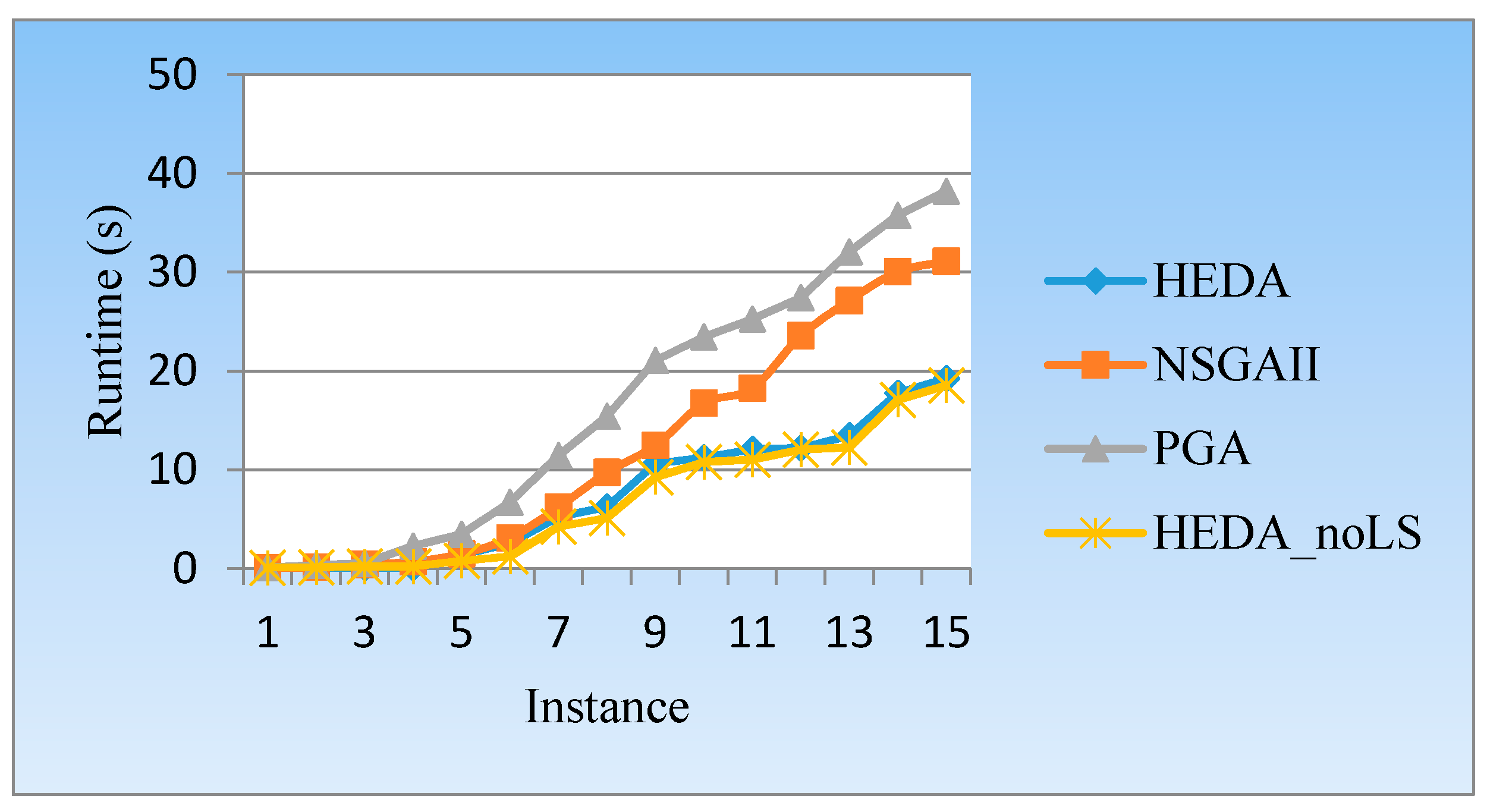
5.3.1. Comparison with Existing Algorithms
5.3.2. Comparison with Optimization Solver
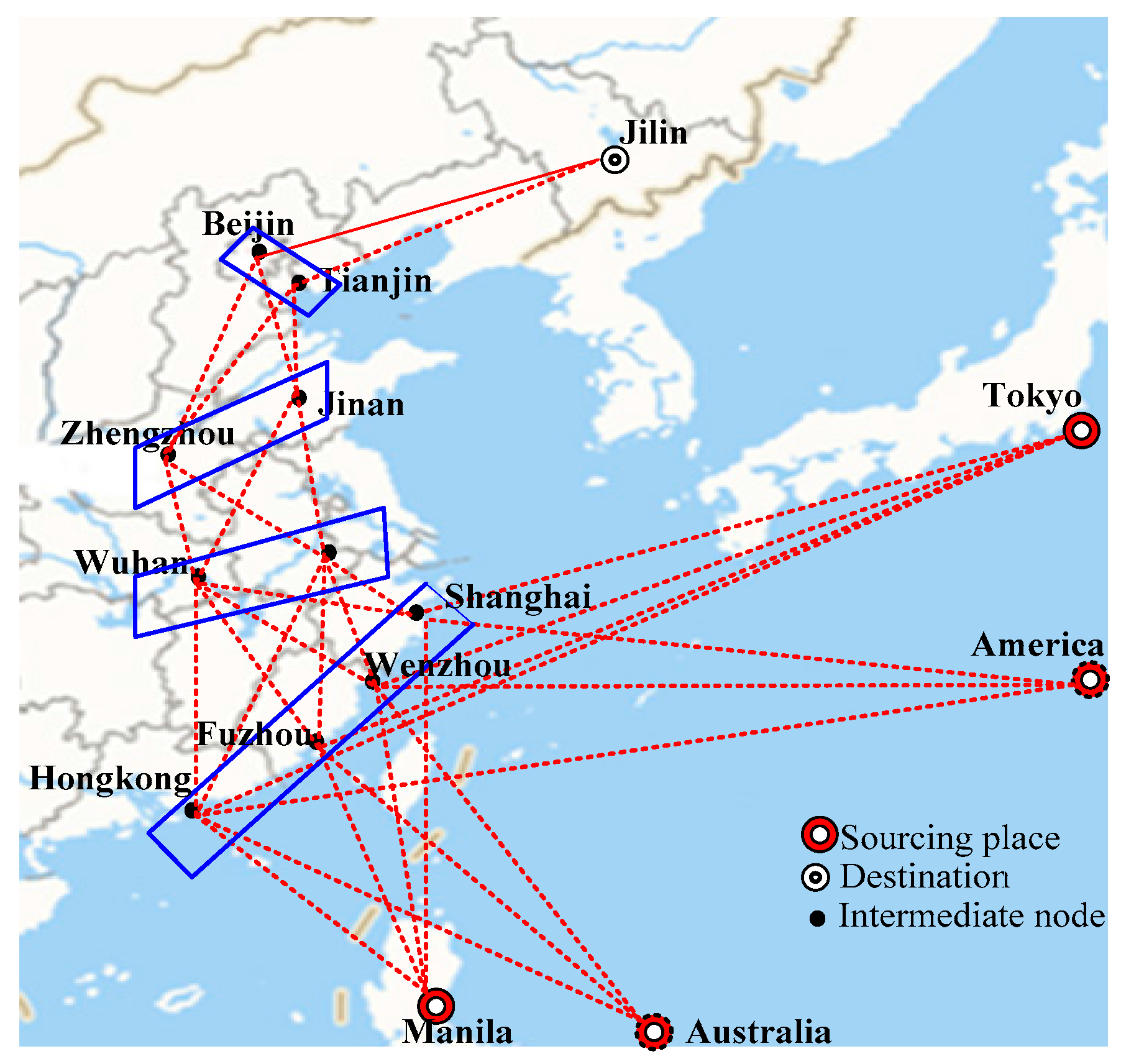
5.4. Case Study
5.5. Management Insights
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Duan, X.; Heragu, S. Carbon Emission Tax Policy in an Intermodal Transportation Network. In Proceedings of the IIE Annual Conference, Nashville, TN, USA, 30 May–2 June 2015. [Google Scholar]
- Zheng, H.Y.; Wang, L. Reduction of carbon emissions and project makespan by a Pareto-based estimation of distribution algorithm. Int. J. Prod. Econ. 2015, 164, 421–432. [Google Scholar] [CrossRef]
- Bouchery, Y.; Fransoo, J. Cost, carbon emissions and modal shift in intermodal network design decisions. Int. J. Prod. Econ. 2014, 164, 388–399. [Google Scholar] [CrossRef]
- Li, Y.; Bao, L.; Li, W.; Deng, H. Inventory and Policy Reduction Potential of Greenhouse Gas and Pollutant Emissions of Road Transportation Industry in China. Sustainability 2016, 8, 1218. [Google Scholar] [CrossRef]
- Piecyk, M.I.; Mckinnon, A.C. Forecasting the carbon footprint of road freight transport in 2020. Int. J. Prod. Econ. 2010, 128, 31–42. [Google Scholar] [CrossRef]
- Benjaafar, S.; Li, Y.; Daskin, M. Carbon footprint and the management of supply chains: Insights from simple models. IEEE Trans. Autom. Sci. Eng. 2013, 10, 99–116. [Google Scholar] [CrossRef]
- Lam, S.L.; Gu, Y. A market-oriented approach for intermodal network optimisation meeting cost, time and environmental requirements. Int. J. Prod. Econ. 2016, 171, 266–274. [Google Scholar] [CrossRef]
- Kim, N.S.; Wee, V.B. Toward a better methodology for assessing CO2 emissions for intermodal and truck-only freight systems: A European case study. Int. J. Sustain. Transp. 2014, 8, 177–201. [Google Scholar] [CrossRef]
- Zheng, Y.; Liao, H.; Yang, X. Stochastic Pricing and Order Model with Transportation Mode Selection for Low-Carbon Retailers. Sustainability 2016, 8, 48. [Google Scholar] [CrossRef]
- Craig, A.J.; Blanco, E.E.; Sheffi, Y. Estimating the CO2 intensity of intermodal freight transportation. Transp. Res. D Transp. Environ. 2013, 22, 49–53. [Google Scholar] [CrossRef]
- Kaur, H.; Singh, S.P. Flexible dynamic sustainable procurement model. Ann. Oper. Res. 2017. [Google Scholar] [CrossRef]
- Steadieseifi, M.; Dellaert, N.P.; Nuijten, W.; Woensel, T.V.; Raoufi, R. Multimodal freight transportation planning: A literature review. Eur. J. Oper. Res. 2014, 233, 1–15. [Google Scholar] [CrossRef]
- Meng, Q.; Wang, X. Intermodal hub-and-spoke network design: Incorporating multiple stakeholders and multi-type containers. Transp. Res. B Meth. 2011, 45, 724–742. [Google Scholar] [CrossRef]
- Limbourg, S.; Jourquin, B. Optimal rail-road container terminal locations on the European network. Transp. Res. E Log. 2009, 45, 551–563. [Google Scholar] [CrossRef]
- Vermam, M.; Verter, V.; Zufferey, N. A bi-objective model for planning and managing rail-truck intermodal transportation of hazardous materials. Transp. Res. E Log. 2012, 48, 132–149. [Google Scholar] [CrossRef]
- Francesco, M.D.; Lai, M.; Zuddas, P. Maritime repositioning of empty containers under uncertain port disruptions. Comput. Ind. Eng. 2013, 64, 827–837. [Google Scholar] [CrossRef]
- Bandeira, D.L.; Becker, J.L.; Borenstein, D.A. DSS for integrated distribution of empty and full containers. Decis. Support Syst. 2009, 47, 383–397. [Google Scholar] [CrossRef]
- Yang, X.; Low, J.M.W.; Tang, L.C. Analysis of intermodal freight from China to Indian Ocean: A goal programming approach. J. Transp. Geogr. 2011, 19, 515–527. [Google Scholar] [CrossRef]
- Resat, H.G.; Turkay, M. Design and operation of intermodal transportation network in the Marmara region of Turkey. Transp. Res. E Log. 2015, 83, 16–33. [Google Scholar] [CrossRef]
- Domuţa, C.; Radu, D.; Enache, M.; Aştilean, A. Application for Intermodal Transportation Routing using Bi-objective Time-dependent Modified Algorithm. Acta Electroteh. 2012, 53, 154–159. [Google Scholar]
- Namseok, K.; Janic, M.; Wee, B.V. Trade-off between carbon dioxide emissions and logistics costs based on multi-objective optimization. Transp. Res. Rec. J. Transp. Res. Board 2009, 2139, 107–116. [Google Scholar]
- Rudi, A.; Fröhling, M.; Zimmer, K.; Schultman, F. Freight transportation planning considering carbon emissions and in-transit holding costs: A capacitated multi-commodity network flow model. Eur. J. Transp. Log. 2016, 5, 123–160. [Google Scholar] [CrossRef]
- Demir, E.; Burgholzer, W.; Hrušovský, M.; Arıkan, E.; Jammernegg, W.; Woensel, T.V. A green intermodal service network design problem with travel time uncertainty. Transp. Res. B Meth. 2015, 42, 1439–1443. [Google Scholar] [CrossRef]
- Lee, C.T.; Hashim, H.; Ho, C.S.; Fan, Y.V.; Klemeš, J.J. Sustaining the low-carbon emission development in Asia and beyond: Sustainable energy, water, transportation and low-carbon emission technology. J. Clean. Prod. 2017, 146, 1–13. [Google Scholar] [CrossRef]
- KılıÇ, F.; Gök, M. A demand based route generation algorithm for public transit network design. Comput. Oper. Res. 2014, 51, 21–29. [Google Scholar] [CrossRef]
- Vermam, M.; Verter, V. A lead-time based approach for planning rail–truck intermodal transportation of dangerous goods. Eur. J. Oper. Res. 2010, 202, 696–706. [Google Scholar] [CrossRef]
- An, C.; Macharis, C.; Janssens, G.K. Corridor network design in hinterland transportation systems. Flex. Serv. Manuf. J. 2012, 2, 294–319. [Google Scholar]
- Braekers, K.; An, C.; Janssens, G.K. Optimal shipping routes and vessel size for intermodal barge transport with empty container repositioning. Comput. Ind. 2013, 64, 155–164. [Google Scholar] [CrossRef]
- Ishfaq, R.; Sox, C.R. Design of intermodal logistics networks with hub delays. Eur. J. Oper. Res. 2012, 220, 629–641. [Google Scholar] [CrossRef]
- Li, L.; Negenborn, R.R.; Schutter, B.D. Intermodal freight transport planning—A receding horizon control approach. Transp. Res. C Emerg. 2015, 60, 77–95. [Google Scholar] [CrossRef]
- Sterzik, S.; Kopfer, H.A. Tabu Search Heuristic for the Inland Container Transportation Problem. Comput. Oper. Res. 2013, 40, 953–962. [Google Scholar] [CrossRef]
- Nossack, J.; Pesch, E. A truck scheduling problem arising in intermodal container transportation. Eur. J. Oper. Res. 2013, 230, 666–680. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Q.; Zhang, L. A Study on the Paths Choice of Intermodal Transport Based on Reliability, 2014; Springer: Berlin, Germany, 2015; pp. 305–315. [Google Scholar]
- Wang, S.; Wang, L.; Xu, Y.; Liu, M. An effective estimation of distribution algorithm for the flexible job-shop scheduling problem with fuzzy processing time. Int. J. Prod. Res. 2013, 51, 3778–3793. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.; Zheng, X. A hybrid estimation of distribution algorithm for unrelated parallel machine scheduling with sequence-dependent setup times. IEEE. J. Autom. Sin. 2016, 3, 235–246. [Google Scholar]
- Salcedo-Sanz, S. A survey of repair methods used as constraint handling techniques in evolutionary algorithms. Comput. Sci. Rev. 2009, 3, 175–192. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Guo, G.; Zhou, Y.Q. Multiobjective optimization and hybrid evolutionary algorithm to solve constrained optimization problems. IEEE Trans. Syst. Man Cybern. B 2007, 37, 560–575. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evolut. Comput. 2009, 13, 284–302. [Google Scholar] [CrossRef]
- Nowicki, E.; Smutnicki, C. A fast tabu search algorithm for the permutation flow-shop problem. Eur. J. Oper. Res. 1996, 91, 160–175. [Google Scholar] [CrossRef]
- Qian, B.; Wang, L.; Huang, D.X.; Wang, X. Multi-objective no-wait flow-shop scheduling with a memetic algorithm based on differential evolution. Soft Comput. 2009, 13, 847–869. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Bérubé, J.F.; Gendreau, M.; Potvin, J.Y. An exact-constraint method for bi-objective combinatorial optimization problems: Application to the traveling salesman problem with profits. Eur. J. Oper. Res. 2009, 194, 39–50. [Google Scholar] [CrossRef]








| Instance | HEDA vs. NSGAII | HEDA vs. PGA | HEDA vs. HEDA_noLS | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSGAII | HEDA | PGA | HEDA | HEDA_noLS | HEDA | |||||||||||||
| MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | |
| 44 | 20.24 | 14.45 | 5 | 3.71 | 0.63 | 3 | 1.57 | 0.79 | 5 | 3.81 | 0.59 | 4 | 2.52 | 1.26 | 4 | 2.81 | 0.96 | |
| 53 | 6.29 | 13.99 | 8 | 5.48 | 1.65 | 2 | 0.10 | 0.43 | 6 | 4.57 | 1.22 | 8 | 2.76 | 2.04 | 8 | 3.81 | 2.38 | |
| 52 | 3.76 | 12.22 | 10 | 5.81 | 1.87 | 0 | 0.00 | 0.00 | 12 | 6.52 | 2.34 | 9 | 2.43 | 2.57 | 9 | 5.67 | 2.40 | |
| 36 | 6.81 | 12.55 | 9 | 4.86 | 2.05 | 1 | 0.14 | 0.35 | 9 | 4.62 | 2.08 | 6 | 2.00 | 1.90 | 6 | 3.43 | 1.47 | |
| 0 | 0.00 | 0.00 | 9 | 3.81 | 1.94 | 0 | 0.00 | 0.00 | 9 | 4.24 | 1.82 | 4 | 0.71 | 1.16 | 7 | 4.00 | 1.57 | |
| 0 | 0.00 | 0.00 | 8 | 3.67 | 1.98 | 0 | 0.00 | 0.00 | 9 | 3.86 | 1.61 | 2 | 0.52 | 0.73 | 7 | 3.95 | 1.43 | |
| 0 | 0.00 | 0.00 | 8 | 4.38 | 1.76 | 0 | 0.00 | 0.00 | 8 | 3.76 | 1.69 | 6 | 1.19 | 1.82 | 8 | 3.71 | 1.91 | |
| 0 | 0.00 | 0.00 | 10 | 4.48 | 1.99 | 0 | 0.00 | 0.00 | 8 | 3.48 | 1.94 | 3 | 0.29 | 0.70 | 7 | 3.76 | 1.74 | |
| 0 | 0.00 | 0.00 | 5 | 2.52 | 1.18 | 0 | 0.00 | 0.00 | 7 | 2.48 | 1.40 | 6 | 0.86 | 1.83 | 7 | 2.48 | 1.65 | |
| 0 | 0.00 | 0.00 | 7 | 2.38 | 1.40 | 0 | 0.00 | 0.00 | 5 | 2.48 | 1.33 | 3 | 0.67 | 0.99 | 4 | 2.00 | 1.07 | |
| 0 | 0.00 | 0.00 | 4 | 1.95 | 1.09 | 0 | 0.00 | 0.00 | 5 | 2.33 | 1.28 | 3 | 0.29 | 0.76 | 8 | 2.29 | 1.69 | |
| 0 | 0.00 | 0.00 | 4 | 2.00 | 1.07 | 0 | 0.00 | 0.00 | 6 | 2.10 | 1.38 | 3 | 0.29 | 0.76 | 3 | 1.67 | 0.64 | |
| 0 | 0.00 | 0.00 | 12 | 5.33 | 3.48 | 0 | 0.00 | 0.00 | 11 | 4.00 | 2.98 | 2 | 0.10 | 0.43 | 10 | 3.52 | 3.19 | |
| 0 | 0.00 | 0.00 | 6 | 2.33 | 1.32 | 0 | 0.00 | 0.00 | 6 | 3.14 | 1.39 | 1 | 0.10 | 0.29 | 5 | 1.86 | 1.04 | |
| 0 | 0.00 | 0.00 | 9 | 2.00 | 1.69 | 0 | 0.00 | 0.00 | 6 | 2.05 | 1.13 | 0 | 0.00 | 0.00 | 10 | 2.48 | 2.15 | |
| Average | 12.33 | 2.47 | 3.55 | 7.60 | 3.65 | 1.67 | 0.40 | 0.12 | 0.10 | 7.47 | 3.56 | 1.65 | 4.00 | 0.98 | 1.15 | 6.87 | 3.16 | 1.69 |
| Instance | HEDA vs. NSGAII | HEDA vs. PGA | HEDA vs. HEDA_noLS | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSGAII | HEDA | PGA | HEDA | HEDA_noLS | HEDA | |||||||||||||
| MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | MAX | AVG | SD | |
| 0.44 | 0.21 | 0.15 | 1.00 | 1.00 | 0.00 | 0.67 | 0.33 | 0.18 | 1.00 | 1.00 | 0.00 | 1.00 | 0.68 | 0.35 | 1.00 | 0.78 | 0.24 | |
| 0.53 | 0.07 | 0.14 | 1.00 | 1.00 | 0.00 | 0.25 | 0.01 | 0.05 | 1.00 | 1.00 | 0.00 | 1.00 | 0.55 | 0.38 | 1.00 | 0.69 | 0.34 | |
| 0.54 | 0.04 | 0.13 | 1.00 | 0.99 | 0.02 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.37 | 0.33 | 1.00 | 0.85 | 0.30 | |
| 0.36 | 0.07 | 0.13 | 1.00 | 1.00 | 0.00 | 0.25 | 0.04 | 0.09 | 1.00 | 1.00 | 0.00 | 1.00 | 0.43 | 0.38 | 1.00 | 0.99 | 0.05 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.75 | 0.17 | 0.26 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.50 | 0.13 | 0.19 | 1.00 | 0.99 | 0.03 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.20 | 0.30 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.50 | 0.06 | 0.13 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.86 | 0.13 | 0.27 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.17 | 0.26 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.75 | 0.07 | 0.19 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.12 | 0.30 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.05 | 0.21 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 1.00 | 0.07 | 0.23 | 1.00 | 1.00 | 0.00 | |
| 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 | 1.00 | 0.00 | |
| Average | 0.12 | 0.03 | 0.04 | 1.00 | 1.00 | 0.00 | 0.08 | 0.03 | 0.02 | 1.00 | 1.00 | 0.00 | 0.82 | 0.21 | 0.25 | 1.00 | 0.95 | 0.06 |
| Instance | HEDA vs. NSGAII | HEDA vs. PGA | HEDA vs. HEDA_noLS | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSGAII | HEDA | PGA | HEDA | HEDA_noLS | HEDA | |||||||||||||||
| MIN | AVG | SD | MIN | AVG | SD | MIN | AVG | SD | MIN | AVG | SD | MIN | AVG | SD | MIN | AVG | SD | |||
| 36.64 | 123.36 | 67.77 | 0.00 | 1107.72 | 1012.93 | 61.66 | 116.48 | 74.67 | 0.00 | 60.73 | 51.70 | 0.00 | 15.66 | 19.03 | 0.00 | 25.87 | 53.26 | |||
| 181.89 | 544.88 | 265.34 | 0.00 | 2286.86 | 5945.60 | 158.87 | 793.87 | 400.31 | 0.00 | 55.16 | 246.67 | 0.00 | 183.72 | 191.64 | 0.00 | 128.18 | 163.28 | |||
| 269.57 | 1225.25 | 758.57 | 0.00 | 1550.08 | 6811.30 | 647.41 | 1960.32 | 800.04 | 0.00 | 0.00 | 0.00 | 0.00 | 390.81 | 331.60 | 0.00 | 93.72 | 138.05 | |||
| 1598.90 | 3824.40 | 1870.46 | 0.00 | 9359.46 | 17,387.86 | 2038.44 | 4826.59 | 2376.99 | 0.00 | 203.33 | 504.80 | 32.09 | 829.86 | 593.75 | 0.00 | 652.71 | 968.25 | |||
| 1054.05 | 2843.73 | 1558.43 | 0.00 | 0.00 | 0.00 | 1954.42 | 4134.30 | 1889.59 | 0.00 | 0.00 | 0.00 | 157.67 | 1649.53 | 1260.86 | 0.00 | 233.46 | 401.39 | |||
| 1216.20 | 4652.32 | 3060.08 | 0.00 | 0.00 | 0.00 | 2946.40 | 6184.59 | 2407.24 | 0.00 | 0.00 | 0.00 | 1096.54 | 2973.23 | 1518.30 | 0.00 | 404.02 | 581.21 | |||
| 1650.11 | 5755.40 | 2848.66 | 0.00 | 0.00 | 0.00 | 1967.32 | 7092.64 | 3234.82 | 0.00 | 0.00 | 0.00 | 217.86 | 2257.73 | 1475.94 | 0.00 | 691.68 | 1160.49 | |||
| 1343.27 | 8610.60 | 3947.62 | 0.00 | 0.00 | 0.00 | 2449.42 | 10,036.65 | 6093.77 | 0.00 | 0.00 | 0.00 | 833.73 | 4881.32 | 2931.44 | 0.00 | 371.87 | 954.23 | |||
| 2254.08 | 6060.90 | 3079.91 | 0.00 | 0.00 | 0.00 | 2639.69 | 8937.82 | 5210.97 | 0.00 | 0.00 | 0.00 | 1347.68 | 4364.83 | 2613.23 | 0.00 | 1512.26 | 3231.31 | |||
| 1785.60 | 6760.44 | 4068.56 | 0.00 | 0.00 | 0.00 | 4635.60 | 11,795.78 | 6546.49 | 0.00 | 0.00 | 0.00 | 1730.08 | 4839.59 | 3264.24 | 0.00 | 1572.35 | 2319.77 | |||
| 3116.28 | 8257.92 | 4925.34 | 0.00 | 0.00 | 0.00 | 5636.08 | 15,186.47 | 8625.25 | 0.00 | 0.00 | 0.00 | 2451.58 | 8163.42 | 6419.59 | 0.00 | 1162.14 | 3194.25 | |||
| 3917.91 | 9219.88 | 5022.42 | 0.00 | 0.00 | 0.00 | 6149.95 | 15,340.45 | 10,717.45 | 0.00 | 0.00 | 0.00 | 2664.78 | 5933.61 | 2339.85 | 0.00 | 1003.98 | 2603.61 | |||
| 5795.40 | 19,982.45 | 10,818.12 | 0.00 | 0.00 | 0.00 | 9074.13 | 34,600.99 | 21,887.46 | 0.00 | 0.00 | 0.00 | 4809.12 | 15,213.67 | 10,688.43 | 0.00 | 525.18 | 2348.70 | |||
| 2128.72 | 7800.28 | 4562.72 | 0.00 | 0.00 | 0.00 | 6379.80 | 20,857.98 | 9415.57 | 0.00 | 0.00 | 0.00 | 3564.77 | 7778.40 | 5030.00 | 0.00 | 439.48 | 1358.51 | |||
| 4697.53 | 10,692.39 | 6753.19 | 0.00 | 0.00 | 0.00 | 10,426.97 | 22,517.95 | 12,695.50 | 0.00 | 0.00 | 0.00 | 5898.19 | 16,269.53 | 11,700.77 | 0.00 | 0.00 | 0.00 | |||
| Average | 2069.74 | 6423.61 | 3573.81 | 0.00 | 953.61 | 2077.18 | 3811.08 | 10,958.86 | 6158.41 | 0.00 | 21.28 | 53.54 | 1653.61 | 5049.66 | 3358.58 | 0.00 | 587.79 | 1298.42 | ||
| Instance | CPLEX | HEDA | ||||||
|---|---|---|---|---|---|---|---|---|
| ONSN | RNDS | DIR | Time | ONSN | RNDS | DIR | Time | |
| 47 * | 1.00 | 0.00 | <0.1 | 7 | 0.47 | 107.47 | <0.1 | |
| 55 * | 1.00 | 0.00 | 1.23 | 10 | 0.58 | 645.23 | <0.1 | |
| 61 * | 1.00 | 0.00 | 2.37 | 13 | 0.89 | 961.30 | <0.1 | |
| 38 * | 1.00 | 0.00 | 5.24 | 8 | 0.91 | 809.26 | <0.1 | |
| 8 | 0.88 | 879.01 | 8.78 | 10 | 0.98 | 2.54 | 1.38 | |
| 11 | 0.87 | 669.25 | 25.33 | 11 | 1.00 | 0.00 | 2.56 | |
| 9 | 0.74 | 420.21 | 38.36 | 10 | 1.00 | 0.00 | 5.25 | |
| 7 | 0.89 | 321.52 | 1 h limit | 9 | 1.00 | 0.00 | 6.24 | |
| 4 | 0.77 | 264.67 | 2 h limit | 7 | 1.00 | 0.00 | 10.62 | |
| 7 | 0.74 | 74.45 | 2 h limit | 6 | 1.00 | 0.00 | 11.23 | |
| 3 | 0.52 | 254.91 | 2 h limit | 5 | 1.00 | 0.00 | 12.08 | |
| 4 | 0.69 | 141.12 | 2 h limit | 6 | 1.00 | 0.00 | 12.21 | |
| 5 | 0.56 | 957.76 | 4 h limit | 11 | 1.00 | 0.00 | 13.45 | |
| - | - | - | - | 7 | 1.00 | 0.00 | 17.77 | |
| - | - | - | - | 10 | 1.00 | 0.00 | 19.25 | |
| Stage | Stage 1 | Stage 2 | Stage 3 | Stage 4 | Stage 5 |
|---|---|---|---|---|---|
| Nodes | Hong Kong (1) Fuzhou (2) Wenzhou (3) Shanghai (4) | Wuhan (1) Nanjing (2) | Zhengzhou (1) Jinan (2) | Beijing (1) Tianjin (2) | Jilin (1) |
| Sourcing Place | Tokyo | America | Australia | Manila |
|---|---|---|---|---|
| Supply/TEU | 80 | 50 | 50 | 120 |
| Mode | Waterway | Railway | Road | |
|---|---|---|---|---|
| Transportation cost ($/TEU-km) | 0.2 (Ship) | 0.18 (Barge) | 0.5 | 2 |
| Carbon emission cost ($/TEU-km) | 0.018 (Ship) | 0.015 (Barge) | 0.03 | 0.05 |
| Average speed (km/h) | 40 (Ship) | 30 (Barge) | 70 | 70 |
| Solution | Tokyo | America | Australia | Manilas | TTC/$ | MFT/h | CEC/$ | Feasibility (Yes/No) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1-4-2-1-1-1-2-2-2 | 1-1-3-2-1-1-1-1-3 | 1-1-2-2-1-2-3-2-2 | 1-1-2-2-1-2-2-1-2 | 110,799 | 601 | 2330 | Yes |
| 2 | 1-1-2-2-1-2-2-2-2 | 1-1-2-2-1-1-3-2-3 | 1-1-2-2-1-1-2-2-2 | 1-1-2-2-1-2-2-2-2 | 99,097 | 614 | 2041 | Yes |
| 3 | 1-1-2-1-1-2-2-2-2 | 1-1-2-2-1-2-3-1-3 | 1-1-2-2-1-2-2-1-2 | 1-1-2-1-1-2-2-1-2 | 92,188 | 617 | 1854 | Yes |
| 4 | 1-4-2-2-1-2-2-1-2 | 1-1-2-2-1-1-2-2-2 | 1-1-2-1-1-2-3-2-2 | 1-1-2-2-1-2-2-1-2 | 92,141 | 662 | 1850 | Yes |
| 5 | 1-1-2-2-1-2-3-2-2 | 1-1-2-2-1-1-3-1-3 | 1-1-2-1-1-2-2-1-2 | 1-1-2-2-1-2-2-1-2 | 103,661 | 610 | 2106 | Yes |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, S.-f.; Luo, R.-j. A Hybrid Estimation of Distribution Algorithm for Multi-Objective Multi-Sourcing Intermodal Transportation Network Design Problem Considering Carbon Emissions. Sustainability 2017, 9, 1133. https://doi.org/10.3390/su9071133
Ji S-f, Luo R-j. A Hybrid Estimation of Distribution Algorithm for Multi-Objective Multi-Sourcing Intermodal Transportation Network Design Problem Considering Carbon Emissions. Sustainability. 2017; 9(7):1133. https://doi.org/10.3390/su9071133
Chicago/Turabian StyleJi, Shou-feng, and Rong-juan Luo. 2017. "A Hybrid Estimation of Distribution Algorithm for Multi-Objective Multi-Sourcing Intermodal Transportation Network Design Problem Considering Carbon Emissions" Sustainability 9, no. 7: 1133. https://doi.org/10.3390/su9071133
APA StyleJi, S.-f., & Luo, R.-j. (2017). A Hybrid Estimation of Distribution Algorithm for Multi-Objective Multi-Sourcing Intermodal Transportation Network Design Problem Considering Carbon Emissions. Sustainability, 9(7), 1133. https://doi.org/10.3390/su9071133




