Sustainable Governance of Organic Food Production When Market Forecast Is Imprecise
Abstract
:1. Introduction
- Since forecast bias occurs often, how much of the OF producer’s profit is negatively affected?
- Because improving forecast precision is costly, a certain level of forecast bias is likely to be acceptable to OF producers. Is there a forecast bias threshold under which the OF producer can still make optimal (or near-optimal) decisions?
- It is common and reasonable for an OF producer to evaluate the risk of a decision regarding production quantity. Is it possible to analytically evaluate the OF producer’s maximum potential profit loss when he formulates production plans according to an imprecise demand forecast?
2. OF Producer’s Sustainable Production Decision Model
3. OF Producer’s Production Decision with Imprecise Demand Forecast
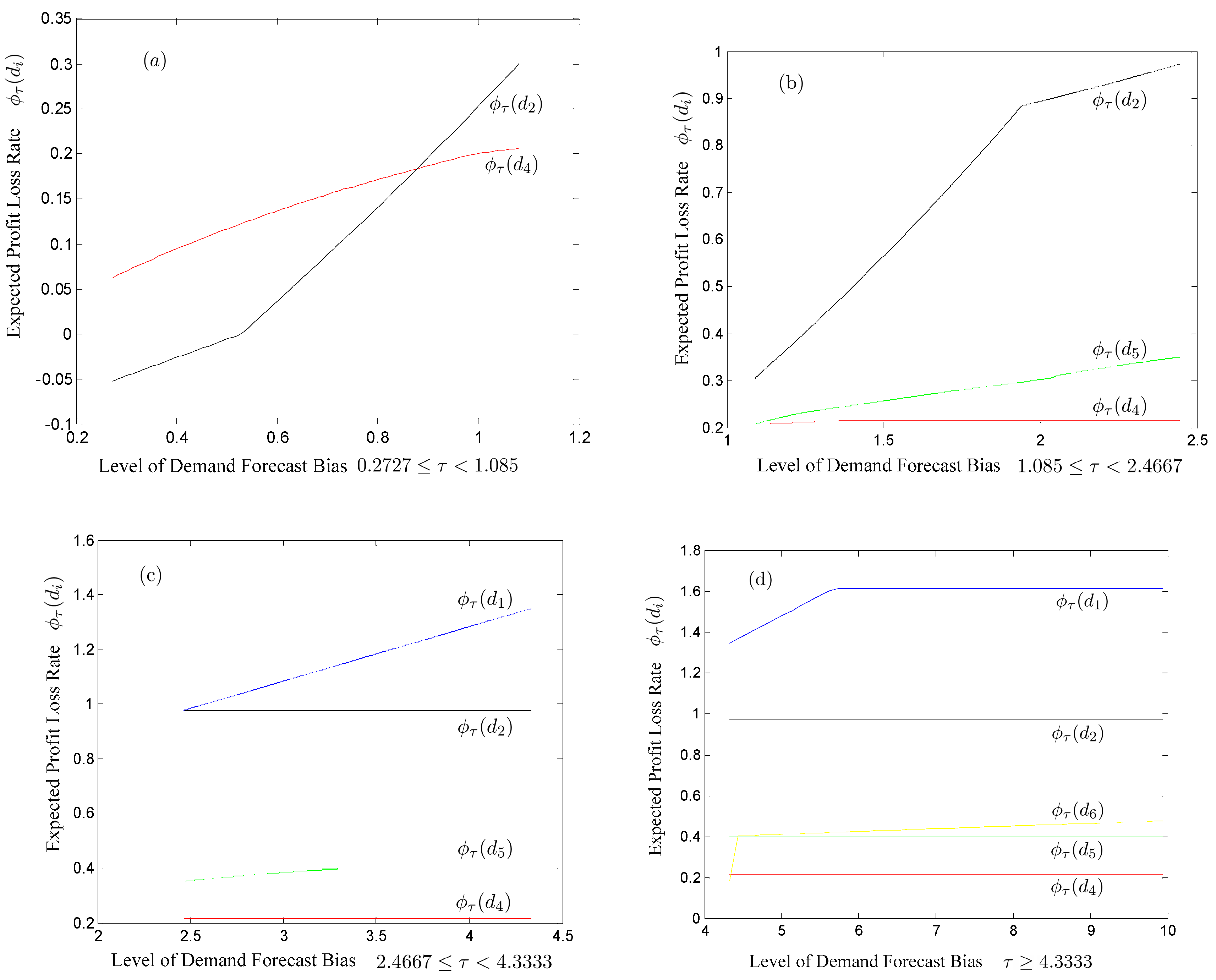
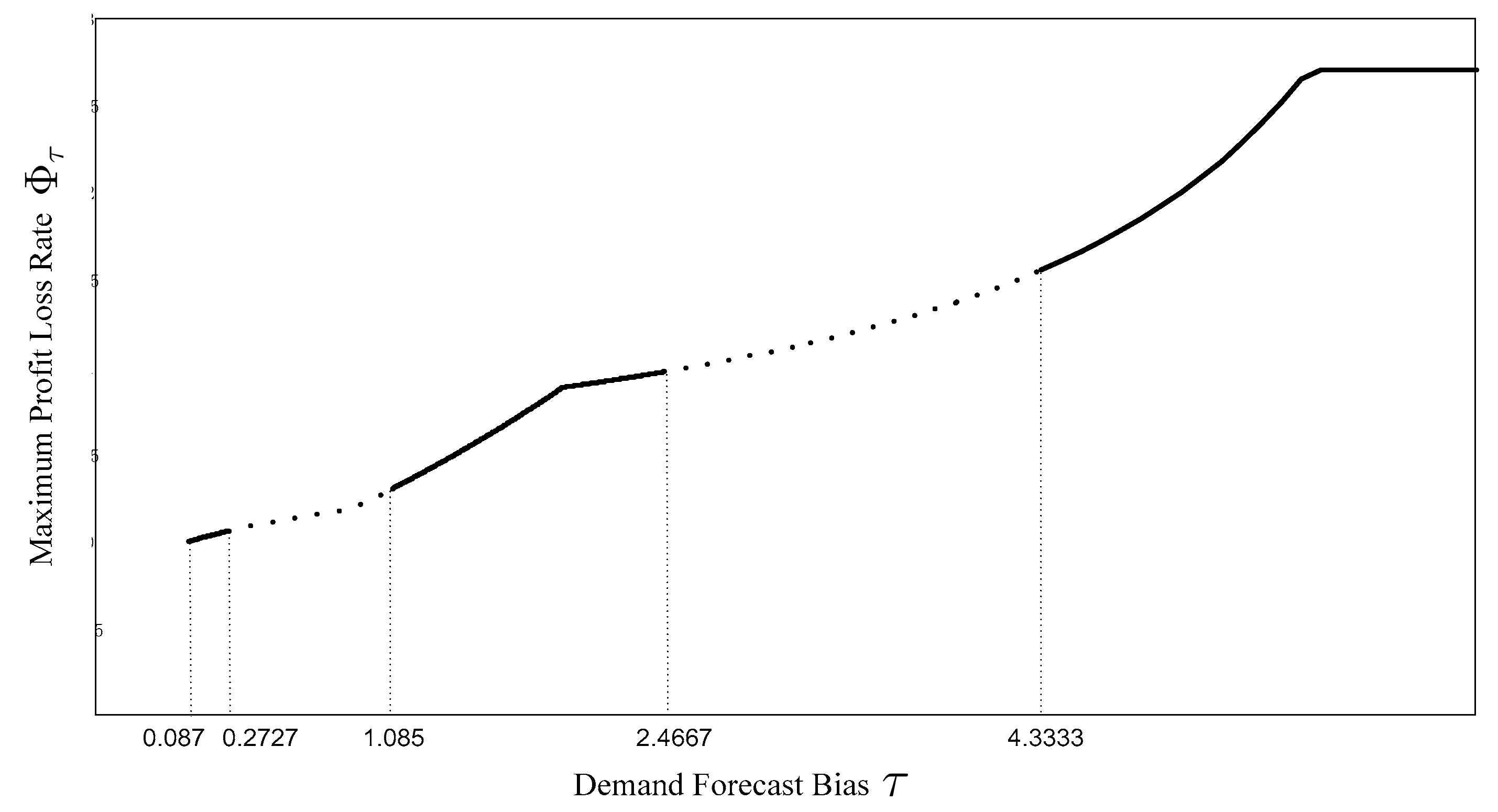
4. An Approach to Evaluating the OF Producer’s Maximum Profit Loss
5. Conclusions and Future Research Directions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CAGR | Compound Annual Growth Rate |
| USD | United States Dollar |
| OF | Organic Food |
Appendix A
References
- TechSci Research. Global Organic Food Market Forecast and Opportunities, 2020; TechSci Research: New York, NY, USA, 2015; Available online: https://www.techsciresearch.com/report/global-organic-food-market-forecast-and-opportunities-2020/450.html (accessed on 12 May 2017).
- Muhammad, S.; Fathelrahman, E.; Tasbih Ullah, R.U. Factors affecting consumers’ willingness to pay for certified organic food products in United Arab Emirates. J. Food Distrib. Res. 2015, 46, 37–45. [Google Scholar]
- Tregear, A.; Dent, J.B.; McGregor, M.J. The demand for organically grown produce. Br. Food J. 1994, 96, 21–25. [Google Scholar] [CrossRef]
- Chang, H.S.; Zepeda, L. Demand for Organic Food: Focus Group Discussions in Armidale, NSW; University of New England, Graduate School of Agricultural and Resource Economics & School of Economics: Armidale, Australia, 2004. [Google Scholar]
- Global Market Insights Inc. Industry Trends. 2015. Available online: https://www.gminsights.com/industry-analysis/biofertilizers-market (accessed on 18 May 2017).
- Statista. Statistics and Facts on the Organic Food Industry in the U.S. 2015. Available online: https://www.statista.com/topics/1047/organic-food-industry/ (accessed on 18 May 2017).
- Zhou, D.; Yu, X.; Herzfeld, T. Dynamic food demand in urban China. China Agric. Econ. Rev. 2015, 7, 27–44. [Google Scholar] [CrossRef]
- Himilä, E. Organic farming in Finland by 2020. Analysis and Review of Consumer Behaviour and Demand for Organic Food Products in Finland. Bachelor’s Thesis, University of Applied Science, Helsinki, Finland, 13 May 2016. [Google Scholar]
- Huang, K.S.; Lin, B.H. Estimation of Food Demand and Nutrient Elasticities from Household Survey Data; Technical Bulletin No. 1887; US Department of Agriculture, Economic Research Service: Washington, DC, USA, 2000. [Google Scholar]
- Zhi-Zhou, P. Demand for Food Quantity and Quality in China. Sci. Technol. Eng. 2009, 1, 46. [Google Scholar]
- Westenbrink, S.; Brunt, K.; van der Kamp, J.W. Dietary fibre: Challenges in production and use of food composition data. Food Chem. 2013, 140, 562–567. [Google Scholar] [CrossRef] [PubMed]
- Chang, H.S.; Zepeda, L. Consumer perceptions and demand for organic food in Australia: Focus group discussions. Renew. Agric. Food Syst. 2005, 20, 155–167. [Google Scholar] [CrossRef]
- Kleemann, L.; Abdulai, A.; Buss, M. Certification and access to export markets: Adoption and return on investment of organic-certified pineapple farming in Ghana. World Dev. 2014, 64, 79–92. [Google Scholar] [CrossRef]
- Garrone, P.; Melacini, M.; Perego, A. Opening the black box of food waste reduction. Food Policy 2014, 46, 129–139. [Google Scholar] [CrossRef]
- Bond, W.; Grundy, A.C. Non-chemical weed management in organic farming systems. Weed Res. 2001, 41, 383–405. [Google Scholar] [CrossRef]
- Grand View Research. Organic Food and Beverages Market to Grow at a CAGR of 15.7% from 2014 to 2020. 2015. Available online: http://www.grandviewresearch.com/press-release/global-organic-food-beverages-market (accessed on 12 June 2017).
- Betz, A.; Buchli, J.; Göbel, C.; Müller, C. Food waste in the Swiss food service industry—Magnitude and potential for reduction. Waste Manag. 2015, 35, 218–226. [Google Scholar] [CrossRef] [PubMed]
- Tse, T.S.M.; Poon, Y.T. Analyzing the use of an advance booking curve in forecasting hotel reservations. J. Travel Tour. Mark. 2015, 32, 852–869. [Google Scholar] [CrossRef]
- Weatherford, L.R.; Belobaba, P.P. Revenue impacts of fare input and demand forecast accuracy in airline yield management. J. Oper. Res. Soc. 2002, 53, 811–821. [Google Scholar] [CrossRef]
- Katajajuuri, J.; Silvennoinen, K.; Hartikainen, H.; Heikkilä, L.; Reinikainen, A. Food waste in the Finnish food chain. J. Clean. Prod. 2014, 73, 322–329. [Google Scholar] [CrossRef]
- Sonnino, R.; McWilliam, S. Food waste, catering practices and public procurement: A case study of hospital food systems in Wales. Food Policy 2011, 36, 823–829. [Google Scholar] [CrossRef]
- Strotmann, C.; Göbel, C.; Friedrich, S.; Kreyenschmidt, J.; Ritter, G.; Teitscheid, P. A participatory approach to minimizing food waste in the food industry—A manual for managers. Sustainability 2017, 9, 66. [Google Scholar] [CrossRef]
- Accorsi, R.; Cholette, S.; Manzini, R.; Pini, C.; Penazzi, S. The land-network problem: Ecosystem carbon balance in planning sustainable agro-food supply chains. J. Clean. Prod. 2016, 112, 158–171. [Google Scholar] [CrossRef]
- Manzini, R.; Accorsi, R. The new conceptual framework for food supply chain assessment. J. Food Eng. 2013, 115, 251–263. [Google Scholar] [CrossRef]
- Sgarbossa, F.; Russo, I. A proactive model in sustainable food supply chain: Insight from a case study. Int. J. Prod. Econ. 2016, 183, 596–606. [Google Scholar] [CrossRef]
- Beske, P.; Land, A.; Seuring, S. Sustainable supply chain management practices and dynamic capabilities in the food industry: A critical analysis of the literature. Int. J. Prod. Econ. 2014, 152, 131–143. [Google Scholar] [CrossRef]
- Dagevos, H. Beyond the marketing mix: Modern food marketing and the future of organic food consumption. In The Crisis of Food Brands: Sustaining Safe, Innovative and Competitive Food Supply; Gower Publishing, Ltd.: Farnham, UK, 2016; pp. 255–270. [Google Scholar]
- Vollmann, T.; Berry, W.; Whybark, C.; Jacobs, R. Manufacturing Planning and Control for Supply Chain Management; McGraw-Hill: New York, NY, USA, 2005. [Google Scholar]
- Goss, S. Making Local Governance Work: Networks, Relationships and the Management of Change; Palgrave MacMillan: Basingstoke, UK, 2001. [Google Scholar]
- Agrawal, N.; Smith, S.A. Estimating negative binomial demand for retail inventory management with unobservable lost sales. Nav. Res. Logist. 1996, 43, 839–861. [Google Scholar] [CrossRef]
- Hoppe, R.; Wodendorp, J.; Bandelow, N. Netherlands Report: Sustainable Governance Indicators; University of Twente: Enschede, The Netherlands, 2017. [Google Scholar]
- Morse, P.M.; Kimball, G.E.; Blackett, P.M.S. Methods of operations research. Phys. Today 1951, 4, 18–20. [Google Scholar] [CrossRef]
- Khouja, M. The single-period news-vendor problem: Literature review and suggestions for future research. Omega 1999, 27, 537–553. [Google Scholar] [CrossRef]
- Herrero, M.; Thornton, P.K.; Notenbaert, A.M.; Wood, S.; Msangi, S.; Freeman, H.A.; Lynam, J. Smart investments in sustainable food production: Revisiting mixed crop-livestock systems. Science 2010, 327, 822–825. [Google Scholar] [CrossRef] [PubMed]
- Scarf, H.; Arrow, K.J.; Karlin, S. A min-max solution of an inventory problem. In Studies in the Mathematical Theory of Inventory and Production; Stanford University Press: Redwood City, CA, USA, 1958. [Google Scholar]
- Yue, J.; Chen, B.; Wang, M.C. Expected value of distribution information for the newsvendor problem. Oper. Res. 2006, 54, 1128–1136. [Google Scholar]
- Perakis, G.; Roels, G. Regret in the newsvendor model with partial information. Oper. Res. 2008, 56, 188–203. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, J.; Ye, Y. Newsvendor Optimization with Limited Distribution Information; Working Paper; Stanford University: Stanford, CA, USA, 2006. [Google Scholar]
- Wang, Z.; Glynn, P.W.; Ye, Y. Likelihood robust optimization for data-driven newsvendor problems. Comput. Manag. Sci. 2009, 13, 241–261. [Google Scholar] [CrossRef]
- Goldman, A. Historical Demand and How to Remove Abnormalities. Available online: http://www.gaebler.com/Historical-Demand-and-How-to-Remove-Abnormalities.htm (accessed on 26 May 2017).
- O’Neil, S.; Zhao, X.; Sun, D.; Wei, J.C. Newsvendor problems with demand shocks and unknown demand distributions. Decis. Sci. 2016, 47, 125–156. [Google Scholar] [CrossRef]
- Andersson, J.; Jörnsten, K.; Nonås, S.L.; Sandal, L.; Ubøe, J. A maximum entropy approach to the newsvendor problem with partial information. Eur. J. Oper. Res. 2013, 228, 190–200. [Google Scholar] [CrossRef]
- Manzini, R.; Accorsi, R.; Ferrari, E.; Gamberi, M.; Giovannini, V.; Pham, H.; Persona, A.; Regattieri, A. Weibull vs. normal distribution of demand to determine the safety stock level when using the continuous-review (S, s) model without backlogs. Int. J. Logist. Syst. Manag. 2016, 24, 298–332. [Google Scholar]
- Oberlaender, M.; Dobhan, A. Behavioral analysis and adaptation of a negotiation based, quantitative planning approach for hybrid organizations. Int. J. Prod. Econ. 2014, 157, 31–38. [Google Scholar] [CrossRef]
- Johansen, S.G. Modified base-stock policies for continuous-review, lost-sales inventory models with poisson demand and a fixed lead time. Int. J. Prod. Econ. 2013, 143, 379–384. [Google Scholar] [CrossRef]
- Özer, Ö.; Zheng, Y.; Chen, K.Y. Trust in forecast information sharing. Manag. Sci. 2011, 57, 1111–1137. [Google Scholar] [CrossRef]
- Nevo, A. A Practitioner’s guide to estimation of random-coefficients logit models of demand. J. Econ. Manag. Strategy 2000, 9, 513–548. [Google Scholar] [CrossRef]
- Xia, W.; Zeng, Y. Consumer’s Willingness to Pay for Organic Food in the Perspective of Meta-Analysis. In Proceedings of the International conference on applied economics (ICOAE), Kastoria, Greece, 15–17 May 2008; pp. 933–943. [Google Scholar]
- Davies, A.; Titterington, A.J.; Cochrane, C. Who buys organic food? A profile of the purchasers of organic food in Northern Ireland. Br. Food J. 1995, 97, 17–23. [Google Scholar] [CrossRef]
- Sahota, A. The global market for organic food and drink. In The World of Organic Agriculture: Statistics and Emerging Trends; FIBL: Frick, Switzerland; IFOAM—Organics International: Bonn, Germany, 2009; pp. 59–64. [Google Scholar]
- Bradbury, K.E.; Balkwill, A.; Spencer, E.A.; Roddam, A.W.; Reeves, G.K.; Green, J.; Beral, V.; Pirie, K.; Banks, E.; Beral, V.; et al. Organic food consumption and the incidence of cancer in a large prospective study of women in the United Kingdom. Br. J. Cancer 2014, 110, 2321–2326. [Google Scholar] [CrossRef] [PubMed]
- OTA. Organic Market Analysis. 2017. Available online: https://www.ota.com/resources/market-analysis (accessed on 15 May 2017).
- SAC. The 2017 Organic Market Report. 2017. Available online: https://www.soilassociation.org/certification/food-drink/trade-news/2017/uk-organic-market-tops-2-billion/ (accessed on 15 May 2017).
- Lee, H.J.; Yun, Z.S. Consumers’ perceptions of organic food attributes and cognitive and affective attitudes as determinants of their purchase intentions toward organic food. Food Qual. Preference 2015, 39, 259–267. [Google Scholar] [CrossRef]
- Schaack, D.; Lernoud, J.; Schlatter, B.; Willer, H. The Organic Market in Europe 2012. In The World of Organic Agriculture: Statistics and Emerging Trends; FIBL: Frick, Switzerland; IFOAM—Organics International: Bonn, Germany, 2014; pp. 200–206. [Google Scholar]
- Bruno, C.C.; Campbell, B.L. Students’ willingness to pay for more local, organic, non-gmo and general food options. J. Food Distrib. Res. 2016, 47, 32–48. [Google Scholar]
- Statista. Statistics and Facts on the Organic Food Industry in the U.S. 2017. Available online: https://www.statista.com/topics/1047/organic-food-industry/ (accessed on 15 May 2017).
- Sustainable. What’s Next for NZ’s Growing Organic Food Market? 2017. Available online: http://sustainable.org.nz/sustainability-news/whats-next-for-nzs-growing-organic-food-market# (accessed on 15 May 2017).
- Dubé, J.P.; Fox, J.T.; Su, C.L. Improving the numerical performance of static and dynamic aggregate discrete choice random coefficients demand estimation. Econometrica 2012, 80, 2231–2267. [Google Scholar]
- Jörnsten, K.; Nonås, S.L.; Sandal, L.; Ubøe, J. Mixed contracts for the newsvendor problem with real options and discrete demand. Omega 2013, 41, 809–819. [Google Scholar] [CrossRef]
- Yu, C.; Ma, W.; Lo, H.K.; Yang, X. Optimization of mid-block pedestrian crossing network with discrete demands. Transp. Res. B Methodol. 2015, 73, 103–121. [Google Scholar] [CrossRef]
- Shin, H.; Tunca, T.I. Do firms invest in forecasting efficiently? The effect of competition on demand forecast investments and supply chain coordination. Oper. Res. 2010, 58, 1592–1610. [Google Scholar] [CrossRef]
- D-Lab. Newsvendor Inventory Problem. 2014. Available online: https://ocw.mit.edu/courses/sloan-school-of-management/15-772j-d-lab-supply-chains-fall-2014/calendar/MIT15_772JF14_Newsboy.pdf (accessed on 20 May 2017).
- Cao, J.; So, K.C. The value of demand forecast updates in managing component procurement for assembly systems. IIE Trans. 2016, 48, 1198–1216. [Google Scholar] [CrossRef]
- Foxnews. 10 Reasons Organic Food Is so Expensive. 2012. Available online: http://www.foxnews.com/food-drink/2012/03/11/10-reasons-organic-food-is-so-expensive.html (accessed on 27 May 2017).
- Chait, J. 10 U.S. Colleges That Offer Organic Agricultural Programs. 2016. Available online: https://www.thebalance.com/organic-agriculture-college-programs-2538094 (accessed on 27 May 2017).
- Gallego, G.; Moon, I. The distribution free newsboy problem: Review and extensions. J. Oper. Res. Soc. 1993, 44, 825–834. [Google Scholar] [CrossRef]


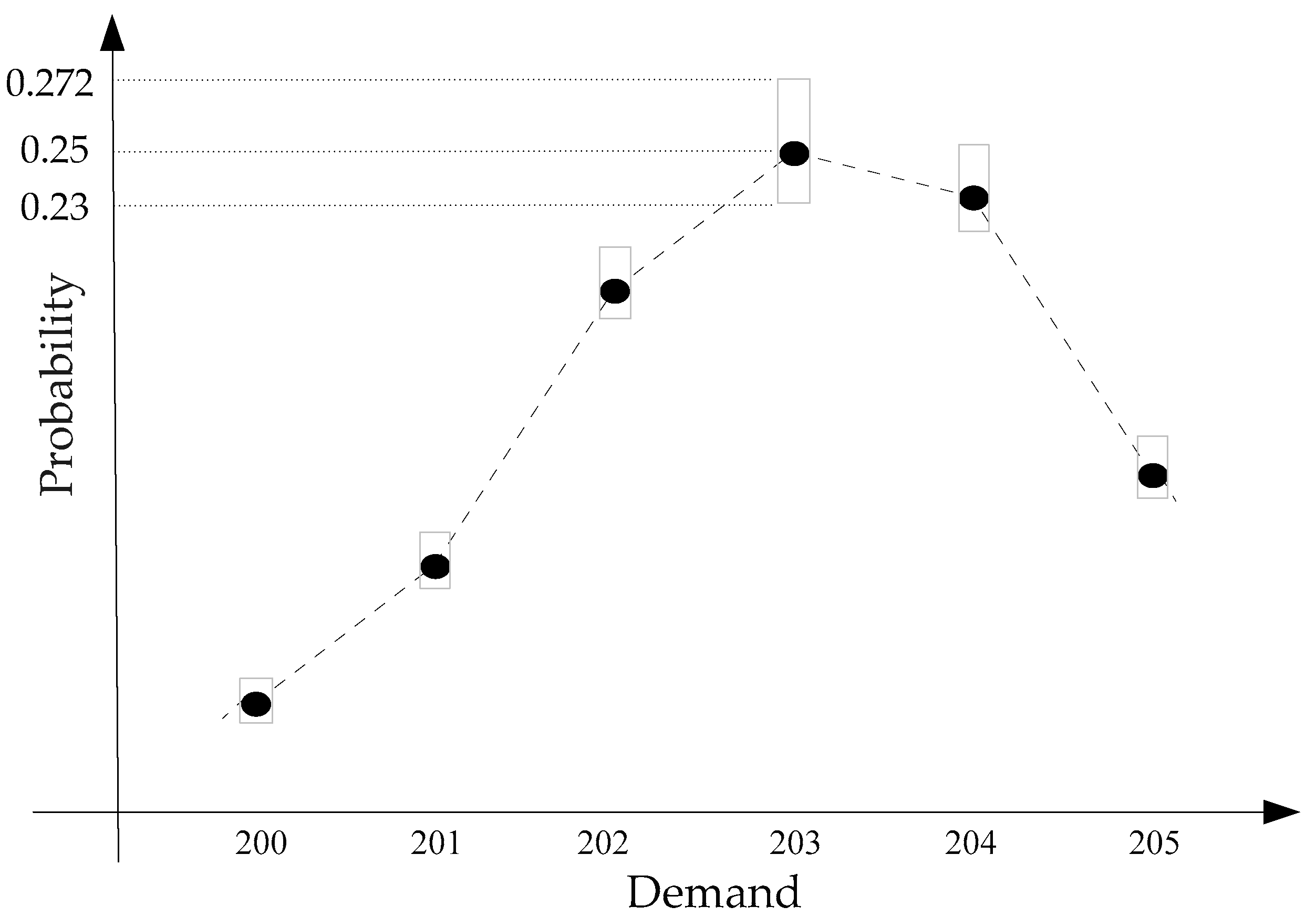

| Quantity of Demand (Units) | 200 | 201 | 202 | 203 | 204 | 205 |
| Probability Sector | 0.1 | 0.13 | 0.16 | 0.25 | 0.21 | 0.15 |
| Candidate Solution (Units) | 200 | 201 | 202 | 203 | 204 | 205 |
| Minimum Level of Forecast Bias | 2.4667 | 0.2727 | 0 | 0.087 | 1.085 | 4.3333 |
| Quantity of Demand (Units) | 200 | 201 | 202 | 203 | 204 | 205 |
| Probability Vector | 0.1 | 0.13 | 0.16 | 0.25 | 0.21 | 0.15 |
| Range of Real Probability Vector | (0.092, 0.1087) | (0.12, 0.141) | (0.147, 0.174) | (0.23, 0.272) | (0.193, 0.228) | (0.138, 0.163) |
| Forecast Bias | Candidate Solutions |
|---|---|
| [0, 0.087) | 202 units |
| [0.087, 0.2727) | 202 units, 203 units |
| [0.2727, 1.085) | 201 units, 202 units, 203 units |
| [1.085, 2.4667) | 201 units, 202 units, 203 units, 204 units |
| [2.4667, 4.3333) | 200 units, 201 units, 202 units, 203 units, 204 units |
| [4.3333, infinity) | 200 units, 201 units, 202 units, 203 units, 204 units, 205 units |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Pu, X.; Fan, B. Sustainable Governance of Organic Food Production When Market Forecast Is Imprecise. Sustainability 2017, 9, 1020. https://doi.org/10.3390/su9061020
Han G, Pu X, Fan B. Sustainable Governance of Organic Food Production When Market Forecast Is Imprecise. Sustainability. 2017; 9(6):1020. https://doi.org/10.3390/su9061020
Chicago/Turabian StyleHan, Guanghua, Xujin Pu, and Bo Fan. 2017. "Sustainable Governance of Organic Food Production When Market Forecast Is Imprecise" Sustainability 9, no. 6: 1020. https://doi.org/10.3390/su9061020
APA StyleHan, G., Pu, X., & Fan, B. (2017). Sustainable Governance of Organic Food Production When Market Forecast Is Imprecise. Sustainability, 9(6), 1020. https://doi.org/10.3390/su9061020






