1. Introduction
Carbon emission is a world-wide problem. To reduce carbon emission, many countries have applied various carbon emission regulations to motivate companies to curb carbon emission. For example, in 2009, Chinese government declared to curb its carbon emission per unit of GDP by 40–45% by 2020, comparing with its 2005 level [
1]. In China, provinces of Gansu, Hunan, and Jiangxi are assigned as experimental regions for the adoption of environmental tax regulations by the relevant ministries (the National Development and Reform Commission, the Ministry of Industry and Information Technology, the Ministry of Finance, Environmental Protection Agency, etc.) [
2]. Although carbon tax has not been implemented in China, some countries (Holland, Denmark, USA, Japan, etc.) have levied it. Jeff and Owen [
3] point out that, in some conditions, carbon tax policy is more effective than carbon trading regulation for economic growth and curbing emissions.
Environmentally friendly products benefit society as well as the environment. Based on a survey by the European Commission in 2014, 67% of Europeans are “ready” to buy environmentally friendly products [
4]. However, the manufacturers adopt abatement measure to produce more environment-friendly products compared to that of traditional products, which may not be beneficial because of higher cost. Meanwhile, the decision-maker of the supply chain needs to face the conflict and coordination problem among different supply chain members because of the double marginalization effect. Hence, by applying some contracts, the supply chain leader has incentive to stimulate the followers to actively implement the goal of emission reduction by coordinating the supply chain to maximize the supply chain members’ profit.
Extensive research on the wholesale price contract (WP) and cost-sharing contract (CS) exists. Bhaskaran and Krishnan [
5] analyzed a case of cost sharing, in which Alpha Labs (a little Labs company) can transfer part of the cost of diabetes drugs development to Mega (a large pharmaceutical company). Thus, both firms can achieve more profit. Ma et al. [
6] find that the quality of the product can be improved by adopting a cost sharing contract under the circumstance of symmetric information. Although these works emphasize the importance of channel coordination in WP and CS contracts, they do not consider how both firms can determine their optimal operation decisions (e.g., decisions of both retail price and emission reduction effort) under carbon tax. Thus, our research questions arise. According to the above background, we consider the coordination problem of a two-echelon supply chain, with decision including abatement effort level and retail price under carbon tax. Firstly, how does the unit carbon tax affect the abatement effort level and other operation decision variables under carbon tax? Secondly, can WP and CS contracts coordinate a supply chain under government’s carbon tax regulations? Finally, how can a new contract be designed if WP and CS contracts cannot coordinate the supply chain?
To answer these questions, this paper firstly describes the relationships between the unit carbon tax and other operation decision variables, and then studies the issue of channel coordination with carbon emission consideration for a two-echelon supply chain composed of a retailer and a manufacturer under carbon tax. The demand is affected by the retail price and emission reduction effort. To start, we determine the optimal level of retail price, optimal level of emission reduction and optimal supply chain profit in the wholesale price and cost-sharing contracts. Then, we investigate the issue of coordination for the supply chain in two contracts. Finally, we propose the TPT that integrates the optimal level of the emission reduction and optimal retail price and how to make all firms more profitable after supply chain coordination.
The rest of this paper is organized as follows.
Section 2 shows the relevant literature review.
Section 3 gives supply chain model description.
Section 4 introduces decision analysis.
Section 5 investigates both MW and MS contracts after the supply chain coordination. In
Section 6, we propose two-part tariff contract to implement the supply chain coordination and achieve a win–win outcome.
Section 7 presents numerical examples to illustrate the models and reports analytical results. Conclusions are made in
Section 8.
2. Literature Review
As carbon tax policy has received increasing attention, there is wide research on the appropriated operation decisions under carbon tax policy. Hao [
7] argues that carbon tax is one of critical regulation choices for curbing product carbon emissions, which can be levied by government for the dirty industry. Avi and Uhlmann [
8] maintain that carbon tax regulation is more applicable to abate carbon emissions than other carbon regulations. Focusing on the main research targets, the research related to this paper can be divided into two areas: the operation decisions under carbon tax and the supply chain coordination in abatement.
The research on the operation decisions under carbon tax can be classified in to three streams: the operation decision of firm, inventory management and the design of supply chain. In the operation decision of firm aspect, Yalabik and Fairchild [
9] study the initial carbon emission level and the effect of consumer to curb emissions under carbon tax policy based on the monopoly model. They find subsidies that support environmental innovation can be a better option to curb products carbon emission under certain conditions. In inventory management aspect, Absi et al. [
10] and Benjaafar et al. [
11] investigate the optimal retail price for single and multiple firms and inventory management problem under carbon tax and other systems based on simple and widely used models. They find that only adopting operational adjustments can curb product emissions requirements. He et al. [
12] analyze the influences of production and regulation parameters on the optimal production lot-size and carbon emissions based on economic order quantity (EOQ) model under carbon tax and other carbon regulations. In the design of supply chain aspect, Jin et al. [
13] investigate that how three carbon policies (e.g., carbon tax rate and carbon cap and trade) affect the major retailer to redesign its supply chain network. They find that, if using a high carbon tax, a high carbon price and a rigid carbon cap, the carbon emissions can be reduced effectively. The above literature focuses solely on the deterministic demand and does not consider the operation decisions with stochastic demand, which has important impact on carbon emission reduction under carbon tax, such as Song and Leng [
14], Rosič and Jammernegg [
15], Choi [
16] and Li et al. [
17]. Here, we do not look back on these studies at great length because this paper considers mainly the issue of the deterministic demand. There is little literature regarding the operation decisions of the supply chain under carbon tax. Penkuhn et al. [
18] investigate the issue of joint production planning in a nonlinear supply chain model under carbon tax. By implementing through process simulation system, the model is applied to a real world ammonia synthesis plant. Palak et al. [
19] study a supply chain with a single facility and its suppliers based on the EOQ model under carbon tax and other carbon regulation. They analyze how the carbon emission limitations affect the decision of inventory replenishment. Xu et al. [
20] study the joint production and pricing problem of a manufacturing firm with multiple products under carbon tax and carbon trade regulations, and compare the effects of the two regulations on the total carbon emissions. The above literature focuses solely on the operation decisions under carbon tax without any supply chain coordination. Under carbon tax, our work is motivated by the phenomenon that the supply chain members have incentive to cooperate with each other and share the abatement cost when adopting abatement measures.
Coordination in supply chain has attracted considerable attention in the past few years because it can increase the supply chain channel’s performance. Contracts with various coordination mechanisms have been widely used in supply chain coordination; for example, revenue-sharing contract [
21], two-part tariff contract [
22], buy back contract [
23], quantity discount contract [
24] and cost-sharing contract [
6]. The above studies do not consider the coordination mechanisms of supply chain after analyzing abatement decision behaviors. Swami and Shah [
25] study a two-stage supply chain model in which a manufacturer and a retailer put in their abatement effort for their operations. They find that a two-part tariff contract can coordinate the supply chain, which achieve a Pareto improvement. Zhang and Liu [
26] study a three-stage model in which a supplier, a manufacturer and a retailer consider the green degree of production to analyze the decision behaviors. They find that a revenue-sharing contract can coordinate the supply chain, which achieves a triple-win outcome. The above literature is studied without considering a carbon emission system. Xu et al. [
27] also study a two-stage supply chain that consists of a manufacturer and a retailer under cap and trade regulation. They assume that demand is the linear function of carbon emissions effort, analyze the optimal retail price and sustainability level under the centralized and decentralized supply chain, and show that revenue-sharing contract cannot coordinate the supply chain but a two-part tariff contract can. In contrast with Xu et al. [
27], we consider a two-echelon supply chain under carbon emissions tax and analyze the optimal retail price and abatement decisions. We find that this innovated contract that may combine a two-part tariff contract with the WP or CS contract can perfectly coordinate the supply chain, while the WP or CS contract cannot solely.
3. Supply Chain Model Description
We consider a two-echelon supply chain consisting of one manufacturer and one retailer. In this model, the manufacturer produces the eco-friendly product at a unit production cost , and sells it at a unit wholesale price to the retailer, who then sells the environment-friendly products to the eco-friendly consumers at a unit retail price . Without loss of generality, we assume the information is symmetrically known to the both the manufacturer and the retailer, who are rational and maximize their own profit. Hence, we adopt the term carbon emissions effort to denote manufacturer’s carbon emissions reduction effort.
In this model, to simplify our analysis, we only consider a kind of marginal cost intensive product (MIP), which means the carbon emission reduction cost is a marginal cost and linked to the carbon emission level; and assume the manufacturer can influence the demand by exerting abatement effort level
with cost of
, where
and
mean unit emission reduction cost (carbon emissions reduction cost coefficient) and the emission reduction effort level, respectively [
28].
According to Ma et al. [
6], we assume that market demand is a linear function of carbon emissions effort and retail price, i.e.,
where
is the base market size,
is the retail price, and
measures the influence of manufacturer’s abatement effort level
on demand. The market demand can be fulfilled in the selling period and are satisfied without stockout and inventory during this time.
In our model, we assume that the manufacturer is a Stackelberg leader and the retailer is a follower. That is, the manufacturer provides the carbon emission reduction effort at the level
and implements the wholesale price at
. Next, after observing the abatement effort level and the wholesale price, the retailer determines its retail price
.
Table 1 summarizes the major parameters and notations in the paper.
4. Decision Analysis
4.1. The Integrated Supply Chain: A Benchmark
In this section, we consider an integrated supply chain with a manufacturing sector and a retailing sector. The two sectors determine the optimal carbon emission effort and retail price jointly. The profit of the integrated supply chain can be express as
where
represents the emission of each product after investing in emission reduction and
stands for initial unit amount of carbon emissions from production process [
29]. All proofs are in the
Appendix A. Hence, we can obtain the following Proposition:
Proposition 1. In the integrated model, there exists a threshold of carbon tax (i.e., ) such that:
- (a)
If , we have , and .
- (b)
If , we have , and .
Proposition 1(a) indicates that, when carbon tax is lower than the threshold (), both the optimal abatement effort level and retail price increase (decrease) in carbon tax. This is because when carbon tax is below the threshold (), the integrated firm reduces the carbon emissions as a larger signifies a more expensive carbon tax cost, which would lower the integrated firm’s benefit from emission reduction, subsequently leading to a smaller product quantities and a higher retail price. Proposition 1(b) also suggests that, when carbon tax is above the threshold (), the profit of the integrated firm, the optimal emission reduction and retail price will keep constant as carbon tax increases. An intuitive explanation is that the integrated firm can make the unit product emission reduction level equal to zero under such circumstance because of the higher cost of carbon tax. Consequently, the government can levy a certain amount of carbon tax to stimulate the integrated firm to absolutely reduce carbon emission under such circumstance.
4.2. Decentralized Case with a Whole Price Contract (WP)
In the decentralized case, the two firms make decisions separately. When utilizing a wholesale price contract, both the retailer’s and the manufacturer’s profit can be expressed as follows:
Proposition 2. In the WP contract, the optimal operational decisions and profit are given by:
- (a)
If , , , , and .
- (b)
If , we have , , , and .
Proposition 2(a) indicates that, when carbon tax is lower than the threshold (), both the optimal emission reduction level and retail price increase (decrease) in carbon tax. This finding tells us that, as long as the carbon tax level charged by government is lower than the threshold (), the manufacturer can reduce the product carbon emissions levels, which result in a higher wholesale price. Consequently, the retailer’s price also increases with the wholesale price. Proposition 2(b) declares that, when carbon tax is higher than the threshold (), the profit of the manufacturer and the retailer, optimal emission reduction and retail price will keep unchanged as carbon tax increases. The reasons are similar to the integrated system. Consequently, the government can impose a certain amount of carbon tax to spur the manufacturer to completely curb product carbon emission under such circumstance.
We consider a special case in which the manufacturer selects to not curb product carbon emission (i.e.,
). We can obtain the demand function as
, where
and
denote the product quantities and retail price, respectively. We maximize the profits of both firms:
Form the analysis of Models (5) and (6), we can know that: , , and . Then, we have the following theorem.
Theorem 1. ; and .
Theorem 1 states that, in the WP contract, the manufacturer can participate in emission reduction to curb carbon emission, which brings more profit to both members comparing to the case without carbon emission reduction. Theorem 1 also affirms that the optimal retail price is greater with emission reduction than without. Hence, the Pareto improving outcome can be achieved for both firms if the manufacturer would voluntarily take part in emission reduction.
4.3. Decentralized Case with a Cost-Sharing Contract (CS)
In the CS model, the retailer shares the cost the manufacturer incurs in emission reduction effort. We design this contract as (
,
), where
is the wholesale price and
is the fraction of the emission reduction cost that the manufacturer bears, while the retailer undertakes the
percentage of the cost in emission reduction effort. The profits of the manufacturer and the retailer are as follows:
According to Equations (7) and (8), we can obtain the following proposition about the optimal emission reduction level, retail price and the profits of the manufacturer and the retailer with CS.
Proposition 3. In the CS contract, the optimal operational decisions and profit are given by:
- (a)
If , , , , and .
- (b)
If , , , , and .
By comparing Proposition 3 with Proposition 2, we find that both have the same properties. In other words, the optimal decisions are exactly the same as those under Proposition 2. In addition, the profits of the manufacturer and retailer are the same under WP and CS. However, the CS can encourage the supply chain members to share the costs of emission reduction effort, which leads the manufacturer to curb product carbon emission. Furthermore, the conclusion in Theorem 1 also supports Proposition 3. Namely, it is possible for the profit of both the manufacturer and the retailer to implement Pareto improvements with emission reduction effort as well as without the emission reduction effort.
Proposition 3 asserts that the manufacturer’s wholesale price increase is , although the retailer pays proportion of the emission reduction cost. For example, when , we find ; when , we find . The reason is the manufacturer can decrease the wholesale price to curbs the carbon emission as long as the retailer shares a larger percent of in emissions reduction cost with his manufacturer. That is to say, the manufacturer can sell a low-carbon product at the lower wholesale price. However, it is surprising that the manufacturer’s profit will decrease, while the retailer’s profit will increase. This is because consumers will order larger quantities and pay more for green product. In reality, it is difficult for the manufacturer to charge all the emission reduction cost when the abatement investment cost becomes more expensive. By comparing Proposition 3 with Proposition 2, we corroborate that both the optimal retail price and the profit of the Supply chain members are the same under CS and WP. Hence, the collaboration between the manufacturer and the retailer can curb the product carbon emissions, which does not influence on their profit.
Proposition 3 also illustrates that the optimal retail price and the firms’ profit do not depend on the value of . This finding is surprising. An intuitive explanation is that, as a leader of Stackelberg game, the manufacturer transfers part of the emission reduction cost by offering two suitable values of (, ). Namely, if the retailer shares the higher (lower) proportion of the emission reduction cost, then the manufacturer will decrease (increase) the wholesale price in response. This results that the increment (decrement) of the emission reduction cost offsets the decrement (increment) of the wholesale price. Hence, it is shown that the retail price and both firms’ profits are independent to the value of .
5. Coordination with Two Contract Mechanisms
In this section, we present two types of contracts (MW and MS) by combing WP or CS with TPT to coordinate the two-echelon supply chain system under carbon tax. By analyzing the conditions for win–win outcome, we compare these two sets of contracts and propose some management insights.
5.1. Coordination by MW Contract
From Propositions 1 and 3, we find that the optimal retail price in both the WP and CS is lower than that in the integrated model. To achieve the effective coordination, we propose the MW contract (, ) in which the manufacturer sets its wholesale price to encourage the retailer’s price to be the same as that in the integrated system. When the scheme is realized, we obtain the following Proposition.
Proposition 4. In the MW contract, the optimal operational decisions and profit are given by:
- (a)
If , we have , , , and .
- (b)
if , we have , , , and .
Proposition 4 indicates that MW contract offered by the manufacturer can coordinate the supply chain. However, in the decentralized model, the MW contract can coordinate the supply chain, bringing a win–win outcome. By comparing Proposition 4 with Proposition 2, we know that the manufacturer’s profit under MW is equal to zero after supply chain coordination. An intuitive explanation is that the manufacturer must transfer its all profit to the retailer to implement the supply chain coordination.
5.2. Coordination by MS Contract
In this subsection, we attempt to provide the MS model (, , ) to achieve the supply chain coordination. It can be described as follows: the manufacturer sets the wholesale price to tempt the retailer to determine its retail price as the same as that under the integrated supply chain. Thus, we obtain the following conclusion.
Proposition 5. In the MS contract, the optimal operational decisions and profit are given by:
- (a)
If , we have , , , , .
- (b)
if , we have , , , and .
Proposition 5 induces that the MS can also coordinate the supply chain and reduce the double marginalization. The conclusions of Proposition 5 are the same as that of Proposition 4. Thus, the MS cannot lead to perfect coordination, as the manufacturer’s profit under MS is less than that that in the traditional cost-sharing contract.
By comparing Proposition 5 with Propositon 4, we find that: (1) If , ; if , . This is because, to implement the supply chain coordination, the retailer shares a larger share of abatement cost with his manufacturer under MS, then the manufacturer can cut the wholesale price. (2) The profits of the manufacturer and the retailer remain the same under both contracts. A reasonable explanation is that, although the retailer pays () proportion of the cost of emission reduction, the manufacturer decreases only the wholesale price for supply chain coordination. As a result, the increase in emission reduction cost growth should be fully offset by the reduction in wholesale price decline. It shows that the MS can effectively curb the product carbon emissions.
Based on Propositions 4 and 5, we find that: (1) both the MW and the MS increase the retailer’s profit and improve the supply chain efficiency, but do not benefit the manufacturer; and (2) compared with the MS, the MW is simpler and more convenient, hence the MS contract is not a good candidate.
Next, we will discuss the implementation of the contracts (, ) and (, , ) with other complementary contracts between the manufacturer and the retailer that can achieve the supply chain coordination and get a win–win outcome for the manufacturer and the retailer.
6. Implementing the Contracts (, ) and (, , ) with TPT
TPT contract is a simple and effective contract that is extensively used to coordinate supply chain systems. Under TPT contract, the manufacturer charges a unit wholesale price
and a fixed fee
to the retailer [
3]. Now, we design two-part tariff agreement (
,
,
) and (
,
,
,
) for the supply chain. When a fixed fee
satisfies
and
, the retailer will accept the contracts (
,
) and (
,
,
), which brings
Proposition 6. Under either the MW or the MS contract, the supply chain can be coordinated when the retailer pays a fixed fee in the range (, ) to the manufacturer, which ensures a win–win outcome for both parties.
Proposition 6 shows that both the MW and the MS get a win–win outcome for both firms. The fixed fee is used to distribute the aggregate profit between the retailer and the manufacturer according to their bargaining power. Namely, if the bargaining power of the manufacturer is relatively large, the fixed payment transferred from the retailer to the manufacturer is large, i.e., the manufacturer can get significant profit form the bargaining. By comparing the wholesale price in Proposition 2 with that in Proposition 4 (Proposition 5), we demonstrate that (), which shows that the retailer can get higher profit in the traditional wholesale price contract than in the MW and MS. On the other hand, the manufacturer can increase some profits by adopting the two-part tariff agreement.
Proposition 6 declares that, if , then , and ; if , then . It implies that: (i) with the increase of carbon tax, and initially decrease then keep constant; and (ii) as the carbon tax increases, decreases more quickly than does, implying that the advantage of a coordinated supply chain is weakened and the manufacturer has less negotiation room on in the two-part tariff agreement.
7. Numerical Analysis
Numerical experiments are conducted in this section to obtain some managerial insights. Let , , , and .
7.1. Impact of on and under the WP Contract
With Proposition 2,
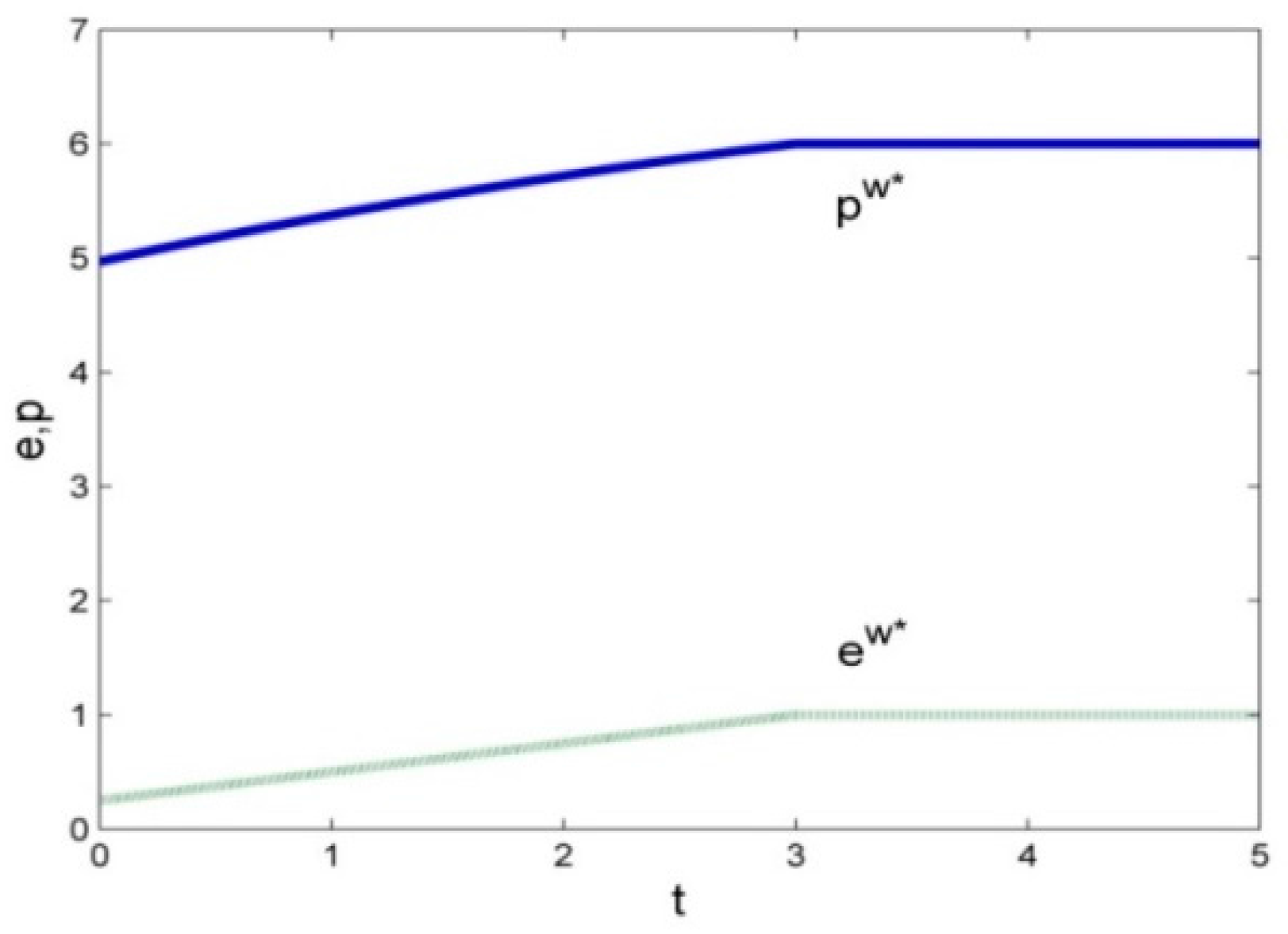
Figure 1 shows that both carbon emission and retail price initially become greater and then remain unchanged with the increase of carbon tax.
Figure 1 demonstrates that, if
, the optimal retail price is
and the optimal emission reduction level is
; if
, both the optimal retail price and the optimal carbon emission level increase with carbon tax. This happens when the carbon tax increases; the manufacturer’s cost also increases, which incentivizes it to curb product carbon emission and also indirectly results in the increase of retail price. On the other hand, if
, the optimal emission reduction level remains unchanged. One way to explain this is that, if carbon tax is high, then the manufacturer is more willing to increase product’s carbon emission reduction to the initial level of carbon emissions. Meanwhile, the optimal retail price is identified as an unchanged because both the manufacturer and the retailer can maximize their profit. At the same time, the results in Proposition 3 are similar to those in Proposition 1.
7.2. Impact of on under the MW and MS Contract
With Propositions 4 and 5, it can be known that, if
, the optimal wholesale price in the MS is less than that in the MW; and, if
, the optimal wholesale price in the MS and that in the MW are the same.
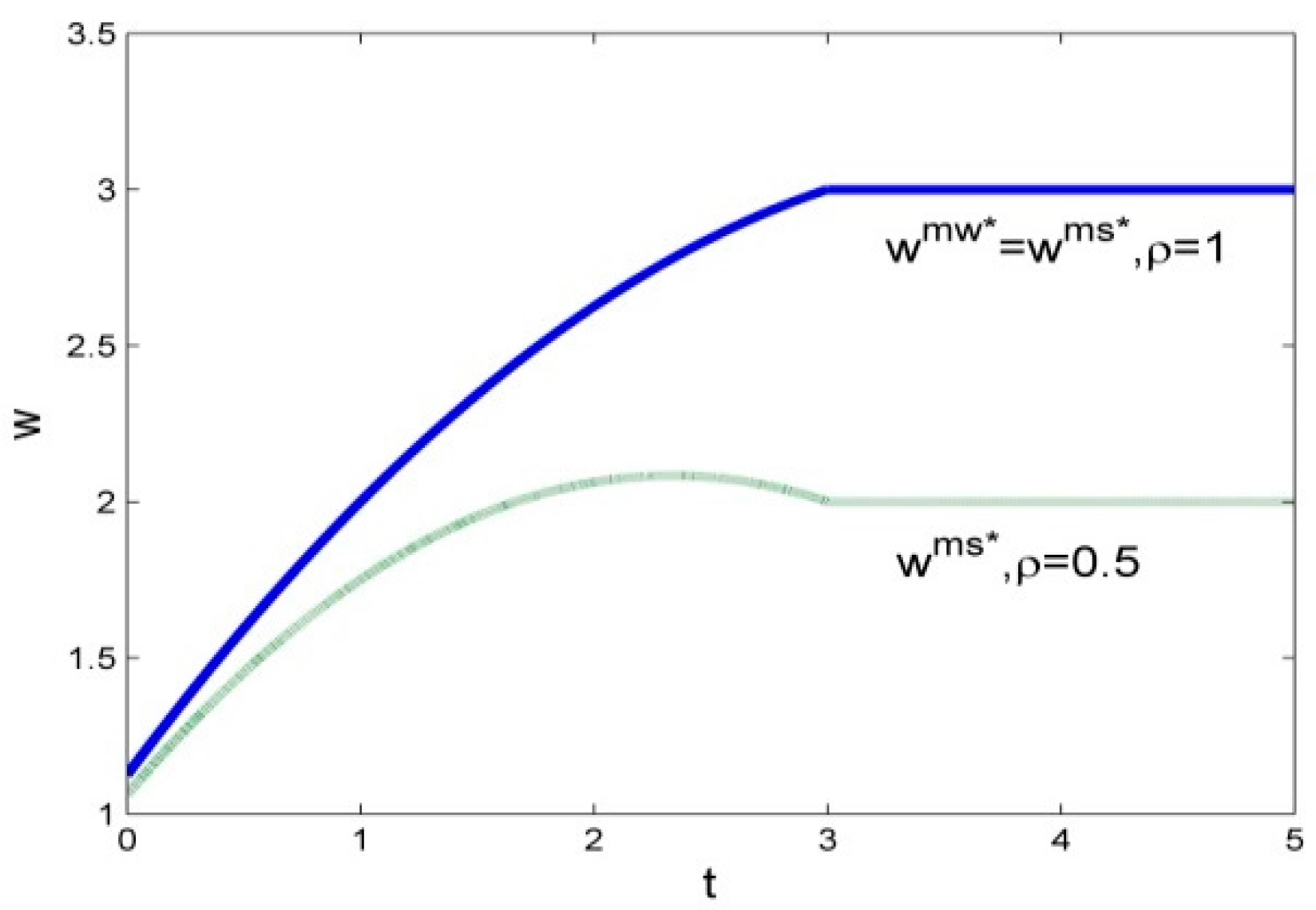
Figure 2 depicts the curves of optimal wholesale price in different model with respect to carbon tax in different proportion of emission reduction cost-sharing. Obviously, the optimal wholesale price has a much steeper climb in the MW contract than in the MS contract. It can be concluded that, if the emission reduction cost becomes cheap, the manufacturer can utilize the MS because this can decrease the manufacturer’s cost. If the emission reduction cost becomes expensive, the manufacturer can utilize the MW because the manufacturer can directly offset the emission reduction cost by increasing the wholesale price.
7.3. Win–Win Outcome with the TPT Contract
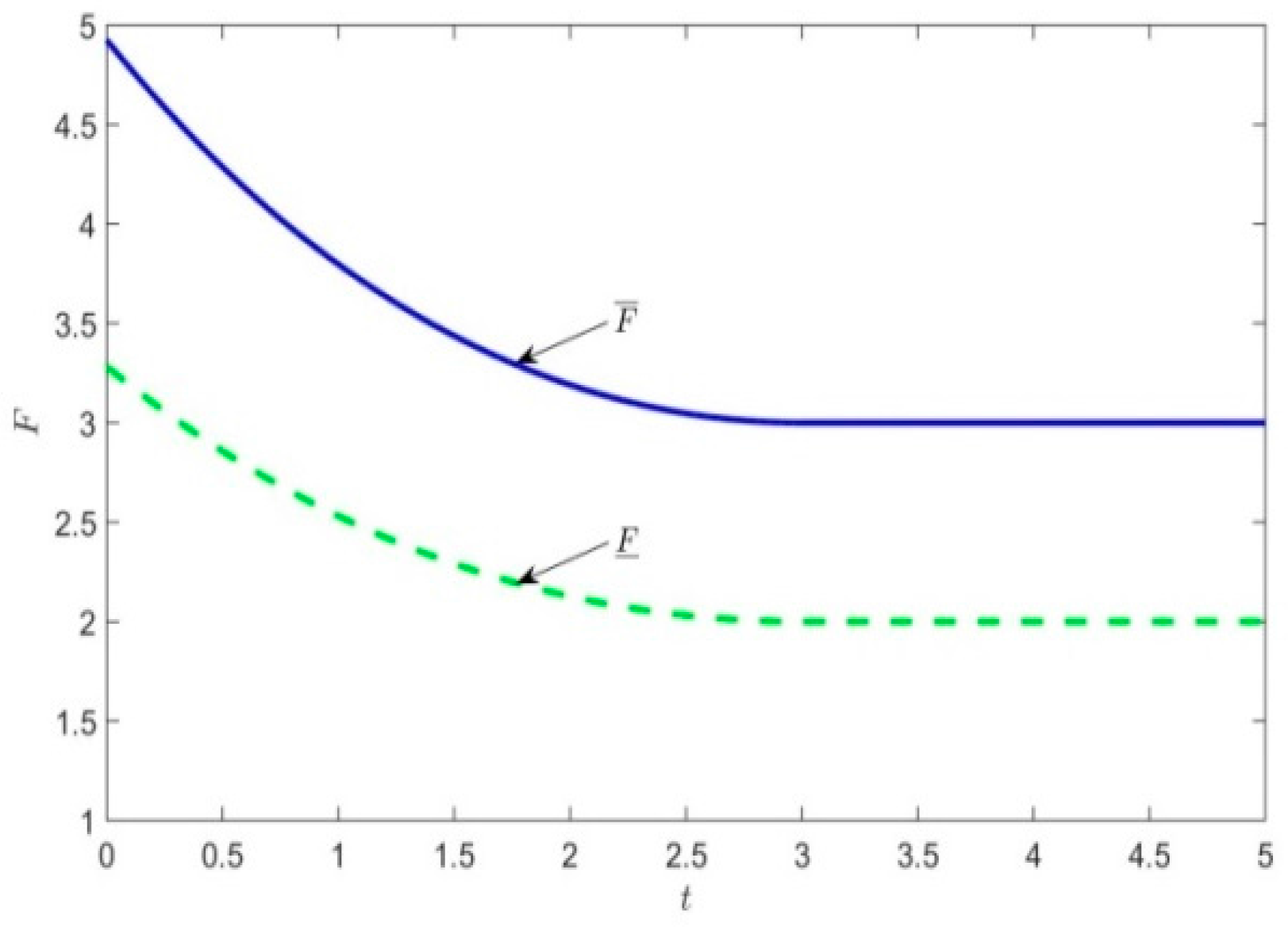
With Proposition 5,
Figure 3 illustrates how the upper bound (
) and lower bound (
) of the fixed fee change with the carbon tax for the contract (
,
,
).
Figure 3 shows that, as carbon tax increases,
decreases more slowly than
does, which indicates that the advantage of the coordinated channel is weakened, and the manufacturer has less negotiating room on
in two-part tariff agreement.
8. Conclusions
In this paper, we study how both MW and MS coordinate the two-echelon supply chain between a manufacturer and a retailer under carbon tax. We firstly derive the optimal operational decision variables (retail price and abatement level) and profit for the integrated and the decentralized supply chain under carbon tax, respectively. By analyzing the cooperation incentives of the manufacturer and the retailer, this paper develops MW and MS to coordinate the supply chain under certain conditions. Finally, we integrate the optimal retail price and abatement level under MW or MS with TPT, which achieves a win–win outcome for both firms.
Some conclusions are reached as follows. (1) With increase of carbon tax, the optimal retail price and emission reduction levels initially become greater and then remain unchanged. (2) The optimal operating decisions and firms’ profit are greater with abatement than without. (3) By integrating the firm’s optimal decisions under either MW or MS with TPT and finding the fixed fees, the retailer can pay to ensure a win–win outcome for the supply chain members.
Our results also reveal some managerial insights. (1) The manufacturer will set the same abatement level as long as government charges the same carbon tax level under the four contracts (WP, CS, MW and MS). (2) When compared to the case without abatement, four contracts will enhance manufacturer’s motivation for abatement, and it has higher motivation under MW and MS than under WP and CS. (3) Both MW and MS improve the supply chain performance but do not benefit the manufacturer after the supply chain coordination. (4) Using TPT contract, the manufacturer will invest in abatement to reduce the product emissions so long as the retailer can transfer a proper ratio of its profit to the manufacturer.
In future research, this paper might be extended in several aspects. First, we consider only a situation with a manufacturer and a retailer. In practice, it can be extended to the operational decisions of multiple manufacturers and retailers. Second, we only consider the single channel supply chain under carbon tax. Another worthy extension might be to examine the supply chain coordination in the dual-channel supply chain under carbon tax. Finally, our paper studies channel structures with a dominant manufacturer, yet interesting managerial insights might be gained from examination of the issue of the retailer-dominated or no single-agent dominance channel structure.