Electricity Consumption and Economic Growth: Evidence from 17 Taiwanese Industries
Abstract
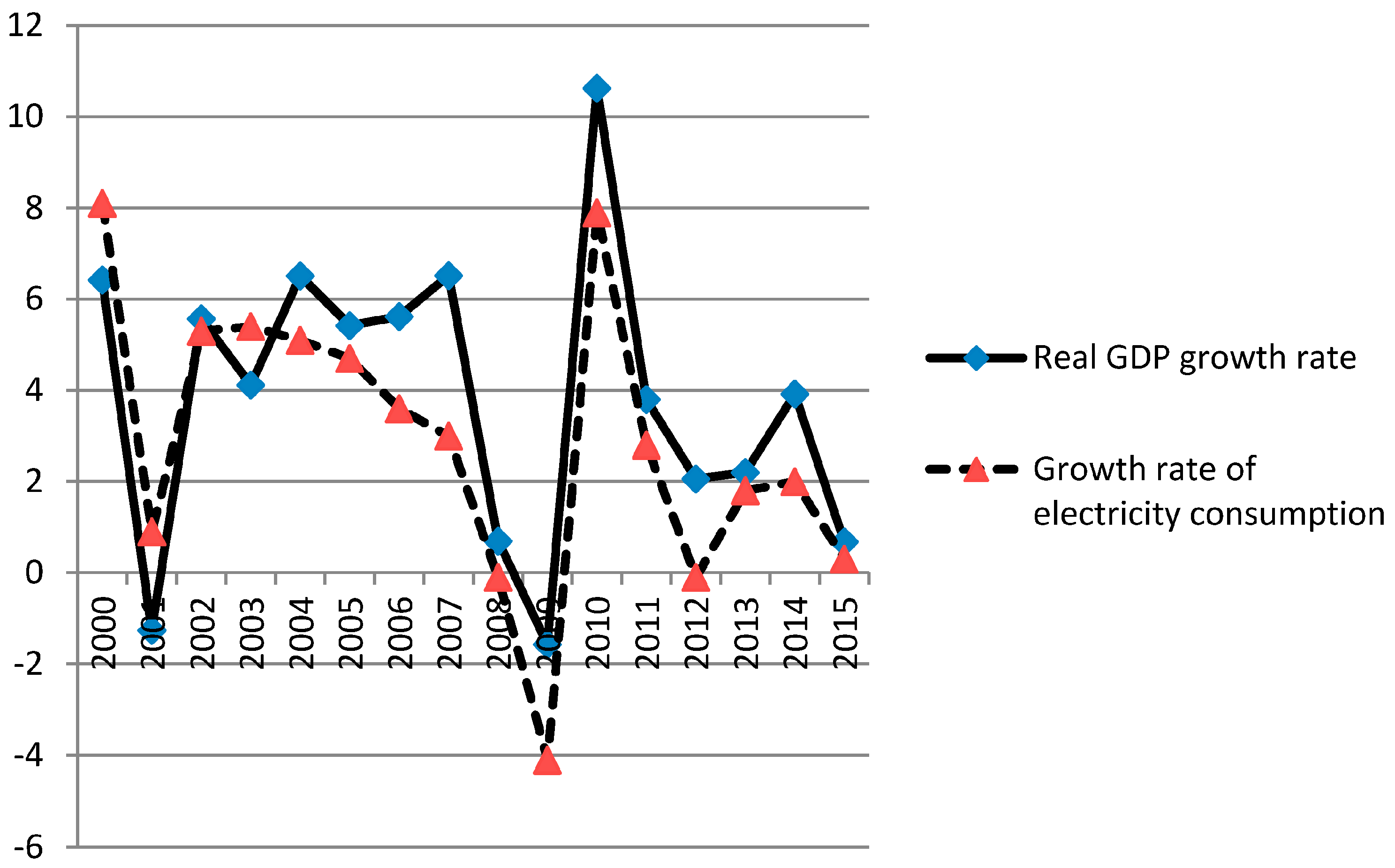
:1. Introduction
- (1)
- We find that electricity consumption and real industrial GDP are both integrated of order one. The findings of the Westerlund [22] cointegration test reveal that the two variables are cointegrated.
- (2)
- Applying the dynamic ordinary least squares method (hereafter, DOLS) to estimate the long-run equilibrium equation, we found that, in the mining and quarrying and wholesale trade industries, electricity consumption has a negative impact on GDP growth. Hence, the energy policy makers can safely adopt the energy (electricity) conservation policy without hindering the GDP growth. However, most of the panel DOLS test results in the current research indicate that electricity consumption has a positive impact on economic growth. A 1% increase in electricity consumption leads to a 1.72% increase in economic growth. The long-run relationship suggests the existence of a positive relationship between the two variables.
- (3)
- The short- and long-run Granger causality tests were examined and we discovered the existence of a bidirectional causal relationship between the real GDP growth and electricity consumption in the short- and long-run. The results imply that the reduction in energy or electricity consumption may adversely affect economic growth.
2. Literature Review
3. Econometric Analysis
3.1. Panel Unit Root Test
3.2. Panel Co-Integration Test
3.3. Panel Dynamic Ordinary Least Squares
3.4. Panel Granger Causality Tests
- (1)
- Short-run Granger causality:
- (2)
- Long-run Granger causality:
4. Data and Empirical Results
4.1. Data
4.2. The Unit Root Tests
4.3. Panel Cointegration Estimation
4.4. Cointegration Coefficient Results of DOLS
4.5. Panel Causality Analysis
5. Conclusions and Policy Implications
Acknowledgments
Conflicts of Interest
References
- Kraft, J.; Kraft, A. Relationship between energy and GNP. J. Energy Dev. 1978, 3, 401–403. [Google Scholar]
- Abdoli, G.; Farahani, Y.G.; Dastan, S. Electricity consumption and economic growth in OPEC countries: A cointegrated panel analysis. OPEC Energy Rev. 2015, 39, 1–16. [Google Scholar] [CrossRef]
- Aslan, A. Causality between electricity consumption and economic growth in Turkey: An ARDL bounds testing approach. Energy Source Part B 2014, 9, 25–31. [Google Scholar] [CrossRef]
- Bayar, Y. Electricity consumption and economic growth in energing economies. J. Knowl. Manag. Econom. Inf. Technol. 2014, 4, 1–18. [Google Scholar]
- Chang, C.C. A multivariate causality test of carbon dioxide emissions, energy consumption and economic growth in China. Appl. Energy 2010, 87, 3533–3537. [Google Scholar] [CrossRef]
- Chen, S.T.; Kuo, H.I.; Chen, C.C. The relationship between GDP and electricity consumption in 10 Asian countries. Energy Policy 2007, 35, 2611–2621. [Google Scholar] [CrossRef]
- Sadorsky, P. Renewable energy consumption, CO2 emissions and oil prices in the G7 countries. Energy Econ. 2009, 31, 456–462. [Google Scholar] [CrossRef]
- Nazlioglu, S.; Kayhan, S.; Adiguzel, U. Electricity consumption and economic growth in Turkey: Cointegration, linear and nonlinear Granger causality. Energy Source Part B 2014, 9, 315–324. [Google Scholar] [CrossRef]
- Wolde-Rufael, Y. Electricity consumption and economic growth: A time series experience for 17 African countries. Energy Policy 2006, 34, 1106–1114. [Google Scholar] [CrossRef]
- Ogundipe, A.A.; Apata, A. Electricity consumption and economic growth in Nigeria. J. Bus. Manag. Appl. Econ. 2013, 2, 1–14. [Google Scholar]
- Shahbaz, M.; Feridum, M. Electricity consumption and economic growth empirical evidence from Pakistan. Qual. Quant. 2012, 46, 1583–1599. [Google Scholar] [CrossRef]
- Jumbe, C.B.L. Cointegration and causality between electricity consumption and GDP: Empirical evidence from Malawi. Energy Econ. 2004, 26, 61–68. [Google Scholar] [CrossRef]
- Narayan, P.K.; Smyth, R. A panel cointegration analysis of the demand for oil in the Middle East. Energy Policy 2008, 35, 6258–6265. [Google Scholar] [CrossRef]
- Narayan, P.K.; Smyth, R.; Prasad, A. Electricity consumption in G7 countries: A panel cointegrating analysis of residential demand elasticities. Energy Policy 2007, 35, 4485–4494. [Google Scholar] [CrossRef]
- Apergis, N.; Payne, J.E. Energy consumption and economic growth in Central America: Evidence form a panel cointegration and error correction model. Energy Econ. 2009, 31, 211–216. [Google Scholar] [CrossRef]
- Apergis, N.; Payne, J.E. A dynamic panel study of economic development and the electricity consumption-growth nexus. Energy Econ. 2011, 33, 770–781. [Google Scholar] [CrossRef]
- Yoo, S.H. Electricity consumption and economic growth: Evidence from Korea. Energy Policy 2005, 33, 1627–1632. [Google Scholar] [CrossRef]
- Yoo, S.H. The causal relationship between electricity consumption and economic growth in the ASEAN countries. Energy Policy 2006, 34, 3573–3582. [Google Scholar] [CrossRef]
- Yuan, J.H.; Kang, J.G.; Zhao, C.H.; Hu, Z.G. Energy consumption and economic growth: Evidence from China at both aggregate and disaggregate levels. Energy Econ. 2008, 30, 3077–3094. [Google Scholar] [CrossRef]
- Zhang, X.P.; Cheng, X.M. Energy consumption, carbon emissions, and economic growth in China. Ecol. Econ. 2009, 68, 2706–2712. [Google Scholar] [CrossRef]
- Soytas, U.; Sari, R.; Ewing, B.T. Energy consumption, income, and carbon emissions in United States. Ecol. Econ. 2007, 62, 482–489. [Google Scholar] [CrossRef]
- Westerlund, J. Test for error correction in panel data. Oxf. Bull. Econ. Stat. 2007, 69, 709–748. [Google Scholar] [CrossRef]
- Soytas, U.; Sari, R. The relationship between energy and production: Evidence from Turkish manufacturing industry. Energy Econ. 2007, 29, 1151–1165. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Perron, P. Pitfalls and Opportunities: What macroeconomists NBER Macroeconomic Annual; Blanchard, O.J., Fischer, S., Eds.; MIT Press: Cambridge, MA, USA, 1991. [Google Scholar]
- Xu, G.; Pan, Q.Z. The empirical study among energy consumption, economic growth and energy efficiency-based on 6 industries panel cointegration model and parsimonious vector error correction model. J. Cent. Univ. Financ. Econ. 2009, 5, 63–68. [Google Scholar]
- Zhang, C.; Xu, J. Retesting the causality between energy consumption and GDP in China: Evidence from sectoral and regional analyses using dynamic panel data. Energy Econ. 2012, 34, 1782–1789. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, S.Y. The relationship between Energy consumption and Economic Grwoth: Evidence from China’s Industrial Sectors. Energies 2015, 8, 9392–9406. [Google Scholar] [CrossRef]
- Hamit-Haggar, M. Greenhouse gas emissions, energy consumption and economic growth: A panel cointegration analysis from Canadian industrial sector perspective. Energy Econ. 2012, 112, 1483–1492. [Google Scholar] [CrossRef]
- Li, F.; Dong, S.; Li, X.; Liang, Q.; Yang, W. Energy consumption-economic growth relationship and carbon dioxide emissions in China. Energy Policy 2011, 29, 568–574. [Google Scholar]
- Im, K.S.; Pesaran, M.H.; Shin, Y. Testing for unit roots in heterogeneous panels. J. Econom. 2003, 115, 53–74. [Google Scholar] [CrossRef]
- Pesaren, M.H. Time Series and Panel Data Econometrics; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Hurlin, C.; Mignon, V. Une Synthèse des Tests de Cointégration sur Données de Panel. Écon. Prévis. 2007, 180, 241–265. [Google Scholar]
- Pesaran, M.H. A simple panel unit root test in the presence of cross-section dependence. J. Appl. Econ. 2007, 22, 265–312. [Google Scholar] [CrossRef]
- Banerjee, A.; Dolado, J.; Mestre, R. Error-correction mechanism tests for cointegration in a single-equation framework. J. Time Ser. Anal. 1998, 19, 267–283. [Google Scholar] [CrossRef] [Green Version]
- Kremers, J.J.M.; Ericsson, N.R.; Dolado, J.J. The power of cointegration tests. Oxf. Bull. Econ. Stat. 1992, 54, 325–348. [Google Scholar] [CrossRef]
- Persyn, D.; Westerlund, J. Error-correction-based cointegration tests for panel data. Stata J. 2008, 8, 232–241. [Google Scholar]
- Stock, J.; Watson, M. A simple estimator of cointegrating vectors in higher order integrated systems. Econometrica 1993, 61, 783–820. [Google Scholar] [CrossRef]
- Kao, C.; Chiang, M.H. On the estimation and inference of a cointegrated regression in panel data. Adv. Econom. 2000, 15, 179–222. [Google Scholar]
- McCoskey, S.; Kao, C. A residual-based test of the null of cointegration in panel data. Econ. Rev. 1998, 17, 57–84. [Google Scholar] [CrossRef]
- Pesaran, M.H.; Shin, Y.; Smith, R.P. Estimating Long-Run Relationships in Dynamic Heterogeneous Panels; DAE Working Papers Amalgamated Series 9721; University of Cambridge: Cambridge, UK, 1997. [Google Scholar]
- Pesaran, M.H.; Shin, Y.; Smith, R.P. Pooled mean group estimation of dynamic heterogeneous panels. J. Am. Stat. Assoc. 1999, 94, 621–634. [Google Scholar] [CrossRef]
- Taiwan Power Company. Electricity Sales and Production. Available online: http://www.taipower.com.tw/e_content/index.aspx (accessed on 7 April 2015).
- Pedroni, P. Critical Values for cointegration tests in heterogeneous panels with multiple regressors. Oxf. Bull. Econ. Stat. 1999, 61, 653–670. [Google Scholar] [CrossRef]
- Pedroni, P. Fully Modified OLS for Heterogeneous cointegrated panels. Adv. Econom. 2000, 15, 93–130. [Google Scholar]
- Pedroni, P. Panel cointegration: Asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis. Econom. Theor. 2004, 20, 597–625. [Google Scholar] [CrossRef]
| Authors | Method | Data Period | Results | Countries or Industries |
|---|---|---|---|---|
| Abdoli et al. [2] | Panel cointegration and FMOLS estimation | 1980–2011 | Energy consumptionGDP (short-run causality) ElectricityGDP (long-run causality) | OECD countries |
| Apergis and Payne [16] | Dynamic panel data model and causality test | 1990–2007 | In the short-run: ElectricityGDP (in high- and upper-middle-income countries); ElectricityGDP (in low-income countries. In the long-run: ElectricityGDP (in lower-middle, high- and upper-middle-income states) | Four types countries: High-income countries, upper-middle-income countries, lower-middle countries, and low-income countries |
| Aslan [3] | ARDL bound test and Granger causality test | 1968–2008 | ElectricityGDP | Turkey |
| Bayar [4] | Panel cointegration and a Granger causality test | 1970–2011 | ElectricityGDP | 21 emerging countries |
| Chang [5] | VECM, Cointegration and Granger Causality test | 1981–2006 | ElectricityGDP | China |
| Chen et al. [6] | Johansen’s cointegration test and panel causality test | 1971–2001 | GDPEnergy consumption (in the short-run causality); ElectricityGDP (in the long-run causality) | 10 developing Asian countries |
| Jumbe [12] | Granger causality and Error-correction model | 1970–1999 | ElectricityGDP | Malawi |
| Li et al. [29] | Cointegration and DOLS estimation | 1985–2007 | ElectricityGDP | 30 provinces in China |
| Nazlioglu et al. [8] | Bound testing, Cointegration, linear and nonlinear Granger causality test | 1967–2007 | ElectricityGDP (linear Granger causality); There was no causality between electricity and GDP (nonlinear Granger causality) | Turkey |
| Ogundipe and Apata [10] | Johansen Cointegration test and Granger causality test | 1980–2008 | ElectricityGDP | Nigeria |
| Shahbaz and Feridun [11] | ARDL bounds test and Toda Yamamoto causality test | 1971–2008 | GDPElectricity | Pakistan |
| Wolde-Rufael [9] | Granger causality test (Toda and Yamamoto’s method) and cointegration test | 1971–2001 | ElectricityGDP (Benin, Congo, Egypt, Morocco, Gabon, Tunisia); GDPElectricity (Cameroon, Ghana, Zimbabwe, Zambia, Nigeria, Senegal); No causality (Algeria, Kenya, South Africa, Sudan) | 17 African countries |
| Yuan et al. [19] | VECM, Cointegration and Granger Causality test | 1990–2005 | ElectricityGDP Oi consumptionGDP; GDPCoal consumption | China |
| Yoo [17] | Error-correction model | 1970–2002 | ElectricityGDP | Korea |
| Yoo [18] | Hsiao’s Granger causality test | 1971–2002 | ElectricityGDP (Malaysia and Singapore); Electricity (Thailand and Indonesia) | ASEAN 4 countries |
| Zhang and Cheng [20] | VAR and Granger Causality test | 1960–2007 | GDPEnergy consumption | China |
| Variables | Real GDP () | Energy Consumption () | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Maximum | Minimum | Mean | Standard Deviation | Maximum | Minimum | |
| Mining and Quarry | 9.93 | 0.35 | 10.55 | 9.43 | 19.80 | 0.15 | 20.02 | 19.50 |
| Beverages, and Tobacco Manufacturing | 12.01 | 0.08 | 12.12 | 11.89 | 21.92 | 0.09 | 22.06 | 21.77 |
| Textiles Mills Manufacturing | 10.59 | 0.37 | 11.24 | 10.16 | 20.17 | 0.12 | 20.34 | 19.99 |
| Wearing Apparel and Clothing Accessories Manufacturing | 9.83 | 0.12 | 10.01 | 9.63 | 19.43 | 0.12 | 19.59 | 19.20 |
| Wood and Bamboo Products Manufacturing | 9.31 | 0.11 | 9.47 | 9.06 | 19.59 | 0.13 | 19.82 | 19.41 |
| Pulp, Paper and Paper Products Manufacturing | 10.79 | 0.11 | 10.95 | 10.57 | 21.47 | 0.06 | 21.57 | 21.35 |
| Chemical Material Manufacturing | 12.34 | 0.31 | 12.77 | 11.78 | 22.67 | 0.03 | 22.70 | 22.61 |
| Chemical Products Manufacturing | 10.67 | 0.27 | 11.08 | 10.31 | 21.72 | 0.15 | 21.94 | 21.36 |
| Non-metallic Mineral Products Manufacturing | 11.32 | 0.38 | 11.93 | 10.91 | 22.24 | 0.14 | 22.44 | 22.04 |
| Basic Metal Manufacturing | 12.22 | 0.23 | 12.69 | 11.89 | 23.12 | 0.13 | 23.28 | 22.89 |
| Electronic Parts and Components Manufacturing | 13.16 | 0.82 | 14.29 | 11.71 | 23.51 | 0.52 | 24.13 | 22.44 |
| Water Supply | 9.99 | 0.05 | 10.08 | 9.91 | 20.91 | 0.08 | 20.99 | 20.71 |
| Construction | 12.85 | 0.07 | 12.96 | 12.72 | 20.09 | 0.08 | 20.25 | 19.97 |
| Wholesale Trade | 13.97 | 0.24 | 14.27 | 13.52 | 20.48 | 0.14 | 20.60 | 20.09 |
| Food and Beverage Services | 11.96 | 0.15 | 12.20 | 11.73 | 20.84 | 0.10 | 20.96 | 20.63 |
| Accommodation | 12.27 | 0.21 | 12.58 | 11.94 | 20.93 | 0.22 | 21.24 | 20.57 |
| Telcommunications | 12.11 | 0.40 | 13.13 | 11.21 | 20.94 | 1.30 | 21.05 | 20.62 |
| All Industries | CIPS Test | |
|---|---|---|
| Statistic | 5% Critical Values | |
| −2.21 | ||
| −2.21 | ||
| *** | −2.21 | |
| *** | −2.21 | |
| Westerlund Panel Cointegration Test | ||
|---|---|---|
| Statistic | p-Values | |
| *** | ||
| *** | ||
| *** | ||
| Industries | DOLS | |
|---|---|---|
| Coefficient | t-Statistics | |
| Panel | *** | *** |
| Mining and Quarrying | *** | |
| Beverages, and Tobacco Manufacturing | * | |
| Textiles Mills Manufacturing | *** | |
| Wearing Apparel and Clothing Accessories Manufactring | ||
| Wood and Bamboo Products Manufactring | ||
| Pulp, Paper and Paper Products Manufacturing | ||
| Chemical Material Manufacturing | ** | |
| Chemical Products Manufacturing | *** | |
| Non-Metallic Mineral Product Manufacturing | *** | |
| Basic Metal Manufacturing | *** | |
| Electronic Parts and Components Manufacturing | *** | |
| Water Supply | ||
| Construction | ||
| Wholesale Trade | *** | |
| Food and Beverage Services | ||
| Accommodation | ** | |
| Telcommunications | ||
| Source of Causation | |||
|---|---|---|---|
| Short-Run | Long-Run | ||
| Dependent Variable | |||
| *** | *** | ||
| *** | * | ||
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.-C. Electricity Consumption and Economic Growth: Evidence from 17 Taiwanese Industries. Sustainability 2017, 9, 50. https://doi.org/10.3390/su9010050
Lu W-C. Electricity Consumption and Economic Growth: Evidence from 17 Taiwanese Industries. Sustainability. 2017; 9(1):50. https://doi.org/10.3390/su9010050
Chicago/Turabian StyleLu, Wen-Cheng. 2017. "Electricity Consumption and Economic Growth: Evidence from 17 Taiwanese Industries" Sustainability 9, no. 1: 50. https://doi.org/10.3390/su9010050
APA StyleLu, W.-C. (2017). Electricity Consumption and Economic Growth: Evidence from 17 Taiwanese Industries. Sustainability, 9(1), 50. https://doi.org/10.3390/su9010050






