Early Adoption of Innovative Analytical Approach and Its Impact on Organizational Analytics Maturity and Sustainability: A Longitudinal Study from a U.S. Pharmaceutical Company
Abstract
:1. Introduction
2. Pharmaceutical Sales Operations Background
3. Traditional Sales Operations Analytics
4. Data
4.1. Data for a Knowledge-Based Analytical Approach
4.2. Data for Sustainability and Analytics Maturity Assessment
5. An Innovative Knowledge-Based Analytical Approach
5.1. Theoretical Framework for Knowledge and Micromarketing
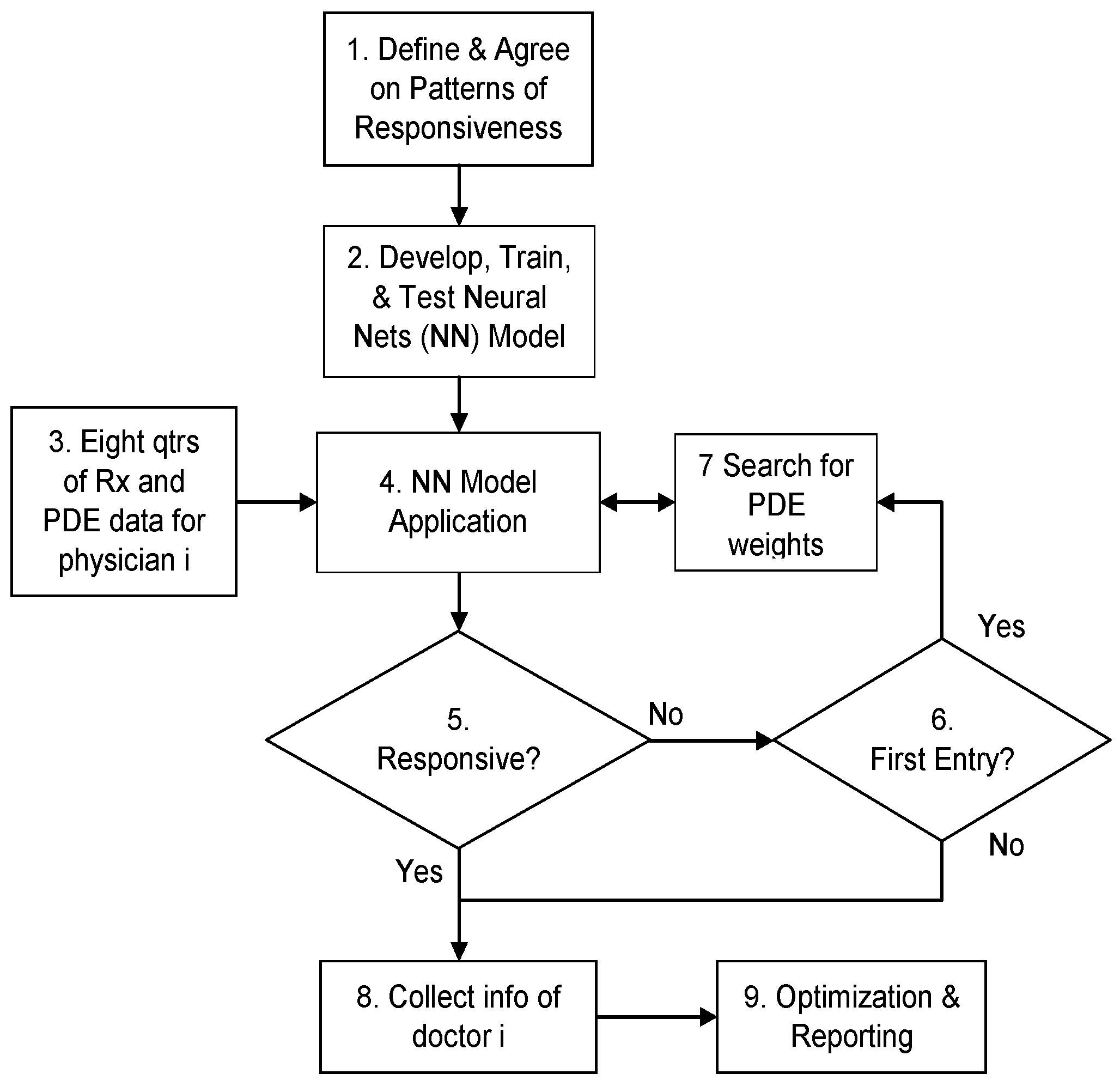
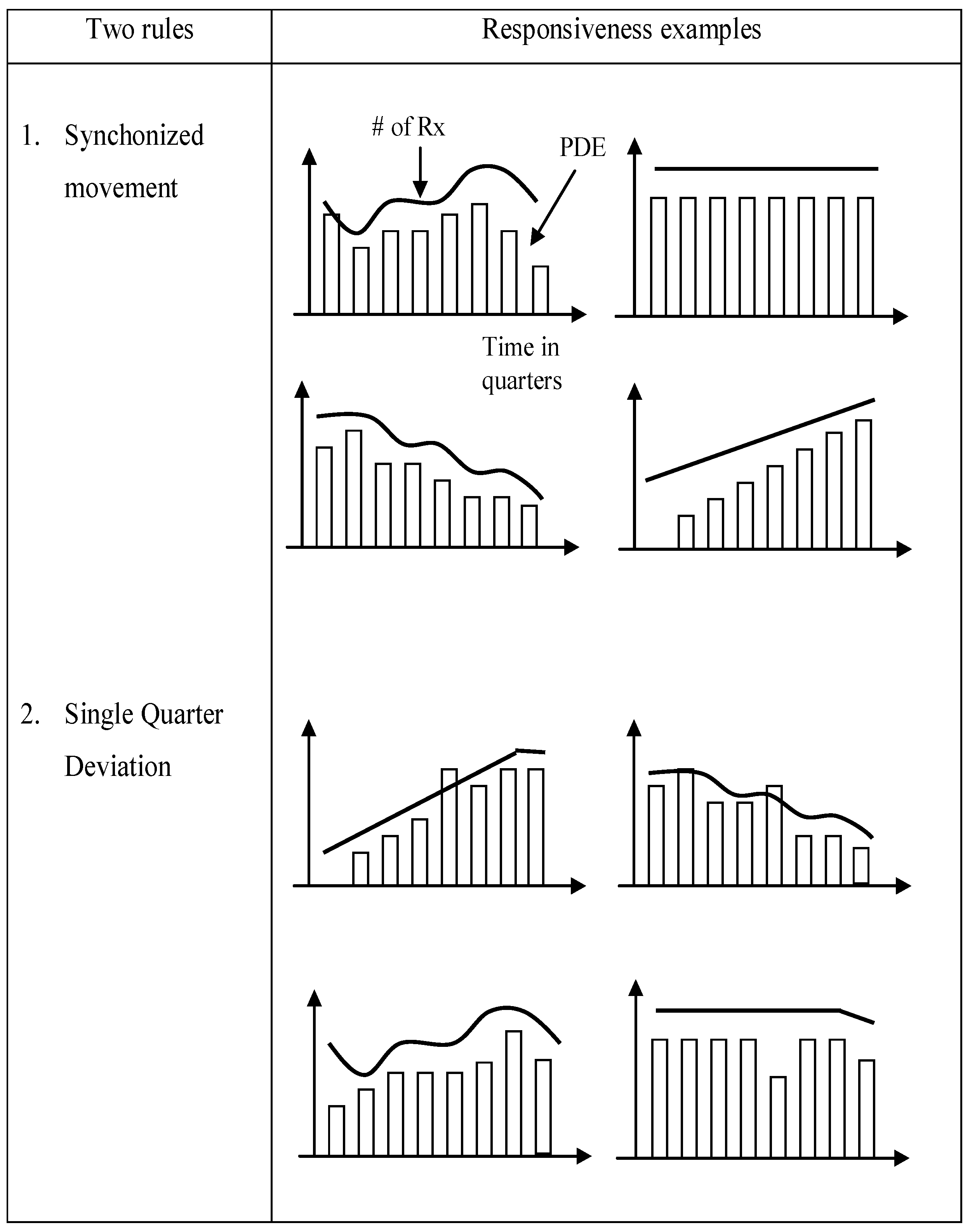
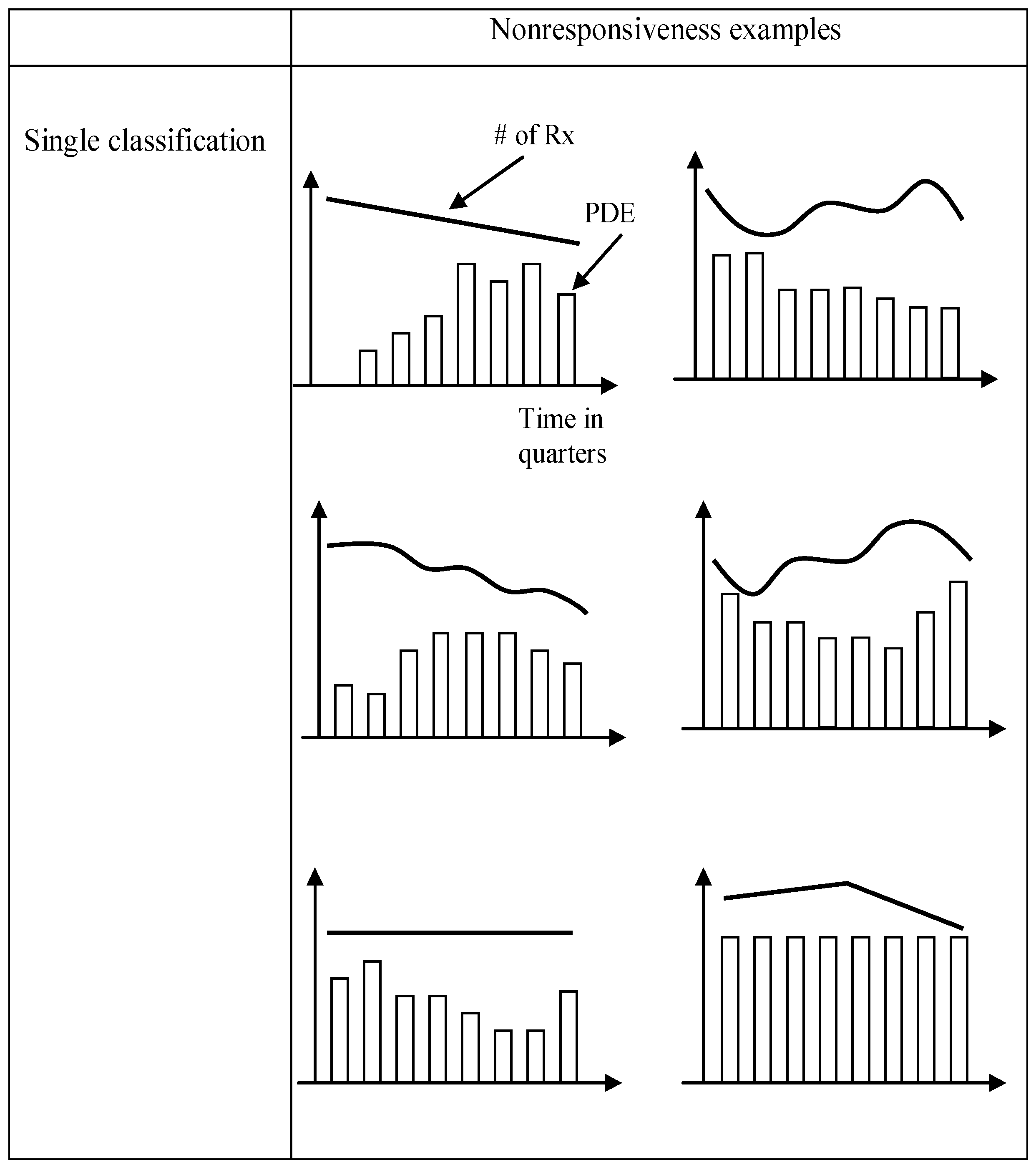
5.2. Process Flow of the Knowledge-Based Analytical Approach
6. Application and Results
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Payer Pressures, Market Access Weigh upon Life Sciences Strategy: KPMG Survey. Available online: http://www.prnewswire.com/news-releases/payer-pressures-market-access-weigh-upon-life-sciences-strategy-kpmg-survey-300122575.html (acessed on 6 May 2016).
- Gagnon, M.-A.; Lexchin, J. The cost of pushing pills: A new estimate of pharmaceutical promotion expenditures in the United States. PLoS Med. 2008. [Google Scholar] [CrossRef] [PubMed]
- IMS Health Forecasts Global Drug Spending to Increase 30 Percent by 2020, to $1.4 Trillion, as Medicine Use Gap Narrows. Available online: http://www.imshealth.com/en/about-us/news/ims-health-forecasts-global-drug-spending-to-increase-30-percent-by-2020 (acessed on 7 May 2016).
- Yi, J.; Anandalingam, G.; Sorrell, L. An expert system to physician-detailing planning. Expert Syst. Appl. 2003, 25, 533–544. [Google Scholar] [CrossRef]
- Claus, B.L.; Underwood, D.J. Discovery informatics: Its evolving role in drug discovery. Drug Discov. Today 2002, 7, 957–966. [Google Scholar] [CrossRef]
- Rivard-Royer, H.; Landry, S.; Beaulieu, M. Hybrid stockless: A case study: Lessons for health-care supply chain integration. Int. J. Oper. Prod. Manag. 2002, 22, 412–424. [Google Scholar] [CrossRef]
- McKone-Sweet, K.E.; Hamilton, P.; Willis, S.B. The ailing healthcare supply chain: A prescription for change. J. Supply Chain Manag. 2005, 41, 4–17. [Google Scholar] [CrossRef]
- Goodman, R.M.; Steckler, A. A model for the institutionalization of health promotion programs. Fam. Community Health 1989, 11, 63–78. [Google Scholar] [CrossRef]
- Rogers, E.M. Diffusion of Innovations; Simon and Schuster: New York, NY, USA, 2010. [Google Scholar]
- Edgeman, R.; Williams, J.A. Enterprise self-assessment analytics for sustainability, resilience and robustness. TQM J. 2014, 26, 368–381. [Google Scholar]
- Yusr, M.M. Innovation capability and its role in enhancing the relationship between TQM practices and innovation performance. J. Open Innov. Technol. Mark. Complex. 2016. [Google Scholar] [CrossRef]
- Rosha, A.; Lace, N. The scope of coaching in the context of organizational change. J. Open Innov. Technol. Mark. Complex. 2016. [Google Scholar] [CrossRef]
- Yi, J. Knowledge-based approach to improving detailing plan in multiple product situations using PDE weights. Expert Syst. Appl. 2011, 38, 3835–3843. [Google Scholar] [CrossRef]
- Nelson, P. Advertising as information. J. Political Econ. 1974, 82, 729. [Google Scholar] [CrossRef]
- Schweitzer, S.O. Pharmaceutical Economics and Policy; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Robinson, J.C. The end of managed care. JAMA 2001, 285, 2622–2628. [Google Scholar] [CrossRef] [PubMed]
- Tenaglia, M. Out of control: the ever increasing price of preferred formulary access. Pharm. Executive 2011, 31, 70–75. [Google Scholar]
- Influence of Managed Care Organizations Increasing within Pharmaceutical Industry. Available online: http://www.prnewswire.com/news-releases/influence-of-managed-care-organizations-increasing-within-pharmaceutical-industry-240912971.html (acessed on 8 May 2016).
- What’s Really Next for Pharma? Available online: http://www.mmm-online.com/features/cannes-roundtable-whats-really-next-for-pharma/article/428481 (accessed on 9 May 2016).
- Malik, N. Key issues in the pharmaceutical industry: Consequences on R&D. Expert Opin. Drug Disc. 2009, 4, 15–19. [Google Scholar]
- Davidson, T.; Sivadas, E. Details drive success. Physicians are responding to electronics sales calls. Mark. Health Serv. 2004, 24, 20–25. [Google Scholar] [PubMed]
- Gönül, F.F.; Carter, F.J. Impact of e-detailing on the number of new prescriptions. Health Care Manag. Sci. 2010, 13, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Barnerjee, S.; Dash, S.K. Effectiveness of e-detailing as an innovative pharmaceutical marketing tool in emerging economies: Views of health care professionals of India. J. Med. Mark. 2011, 11, 204–214. [Google Scholar] [CrossRef]
- Della Corte, V.; Iavazzi, A.; D’Andrea, C. Customer involvement through social media: The cases of some telecommunication firms. J. Open Innov. Technol. Mark. Complex. 2015, 1, 1–10. [Google Scholar] [CrossRef]
- Yi, J. An expert system to derive carryover effect for pharmaceutical sales detailing optimization. Expert Syst. Appl. 2008, 34, 1742–1753. [Google Scholar] [CrossRef]
- Jones, J.P. Ad spending: maintaining market share. Harv. Bus. Rev. 1990, 68, 38–42. [Google Scholar] [PubMed]
- Gonul, F.F.; Carter, F.; Petrova, E.; Srinivasan, K. Promotion of prescription drugs and its impact on physicians’ choice behavior. J. Mark. 2001, 65, 79–90. [Google Scholar] [CrossRef]
- Pesse, M.; Erat, P.; Erat, A. The network is the customer: Setting the stage for fundamental change in pharmaceutical sales and marketing. J. Med. Mark. 2006, 6, 165–171. [Google Scholar] [CrossRef]
- Competing on Analytics. Available online: https://hbr.org/2006/01/competing-on-analytics (acessed on 10 May 2016).
- Shediac-Rizkallah, M.C.; Bone, L.R. Planning for the sustainability of community-based health programs: Conceptual frameworks and future directions for research, practice and policy. Health Educ. Res. 1998, 13, 87–108. [Google Scholar] [CrossRef] [PubMed]
- Scheirer, M.A. The life cycle of an innovation: Adoption versus discontinuation of the fluoride mouth rinse program in schools. J. Health Soc. Behav. 1990, 31, 203–215. [Google Scholar] [CrossRef] [PubMed]
- Evashwick, C.; Ory, M. Organizational characteristics of successful innovative health care programs sustained over time. Fam. Community Health 2003, 26, 177–193. [Google Scholar] [CrossRef] [PubMed]
- Blattberg, R.C.; Hoch, S.J. Database Models and Managerial Intuition: 50% Model + 50% Manager. Manag. Sci. 1990, 36, 887–899. [Google Scholar] [CrossRef]
- Huang, C.-C.; Fan, Y.-N.; Chern, C.-C.; Yen, P.-H. Measurement of analytical knowledge-based corporate memory and its application. Decis. Support Syst. 2013, 54, 846–857. [Google Scholar] [CrossRef]
- Nonaka, I. A dynamic theory of organizational knowledge creation. Organ. Sci. 1994, 5, 14–37. [Google Scholar] [CrossRef]
- Davenport, T.; Prusak, L. Working Knowledge: How Organizations Manage What They Know, 2nd ed.; Harvard Business School Press: Boston, MA, USA, 1998. [Google Scholar]
- Brown, J.; Duguid, P. Organizing knowledge. Calif. Manag. Rev. 1998, 40, 90–111. [Google Scholar] [CrossRef]
- Paladino, A.E. The Power of Unstructured Data: A Study of the Impact of Tacit Knowledge on Business Performance. Ph.D. Thesis, Capella University, Ann Arbor, MI, USA, 2012. [Google Scholar]
- Cai, J. Knowledge Management within collaboration processes: A perspective modeling and analyzing methodology. J. Database Manag. 2006, 17, 33–48. [Google Scholar] [CrossRef]
- Liebowitz, J. ‘Think of others’ in knowledge management: Making culture work for you. Knowl. Manag. Res. Pract. 2008, 6, 47–51. [Google Scholar] [CrossRef]
- Pancholi, S.; Yigitcanlar, T.; Guaralda, M. Public space design of knowledge and innovation spaces: Learnings from Kelvin Grove Urban Village, Brisbane. J. Open Innov. Technol. Mark. Complex. 2015. [Google Scholar] [CrossRef]
- Carrillo, F.J. Knowledge-based development as a new economic culture. J. Open Innov. Technol. Mark. Complex. 2015. [Google Scholar] [CrossRef]
- Coffey, J.W.; Hoffman, R.; Cañas, A. Concept map-based knowledge modeling: Perspectives from information and knowledge visualization. Inform. Visual. 2006, 5, 192–201. [Google Scholar] [CrossRef]
- Yi, J. Knowledge-based approach to improving micromarketing decisions in a data-challenged environment. Expert Syst. Appl. 2008, 35, 1379–1385. [Google Scholar] [CrossRef]
- Leeflang, P.; Wittink, D. Building models for marketing decisions: Past, present and future. Int. J. Res. Mark. 2000, 17, 105–126. [Google Scholar] [CrossRef]
- Zhang, J.; Krishnamurthi, L. Customizing promotions in online stores. Mark. Sci. 2004, 23, 561–578. [Google Scholar] [CrossRef]
- Wright, R.A.; Allen, B.H. Improve the health care macro-system through micro-marketing: A physician/marketer’s viewpoint. In Proceedings of the 1982 Academy of Marketing Science (AMS) Annual Conference; Springer: Berlin/Heidelberg, Germany, 2015; pp. 177–181. [Google Scholar]
- Jain, L.C.; Vemuri, V.R. Industrial Applications of Neural Networks; CRC Press: Boca Raton, FL, USA, 1998; Volume 3. [Google Scholar]
- Kumar, M.; Thenmozhi, M. Stock index return forecasting and trading strategy using hybrid arima-neural network model. Int. J. Financ. Manag. 2012, 2, 1–14. [Google Scholar]
- Livingstone, D.J.; Manallack, D.T.; Tetko, I.V. Data modelling with neural networks: Advantages and limitations. J. Comput. Aided Mol. Des. 1997, 11, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Patra, S.K.; Krishna, V.V. Globalization of R&D and open innovation: Linkages of foreign R&D centers in India. J. Open Innov. Technol. Mark. Complex. 2015, 1, 1–24. [Google Scholar]
- Yun, J.; Won, D.; Park, K. Dynamics from open innovation to evolutionary change. J. Open Innov. Technol. Mark. Complex. 2016, 2, 2–22. [Google Scholar] [CrossRef]
- Jeon, J.-H.; Kim, S.-K.; Koh, J.-H. Historical review on the patterns of open innovation at the national level: The case of the roman period. J. Open Innov. Technol. Mark. Complex. 2015. [Google Scholar] [CrossRef]


| 1st Sequence | 2nd Sequence | 3rd + Sequence | |
|---|---|---|---|
| With single drug | 1.00 | - | - |
| With two drugs | 1.00 | 0.60 | - |
| Three or more drugs | 1.00 | 0.60 | 0.30 |
| 1st Sequence | 2nd Sequence | 3rd + Sequence | |
|---|---|---|---|
| With single drug | 1.00 | - | - |
| With two drugs | 0.82 | 0.68 | - |
| Three or more drugs | 0.70 | 0.41 | 0.02 |
| 1st Sequence | 2nd Sequence | 3rd + Sequence | |
|---|---|---|---|
| With single drug | 1.00 | - | - |
| With two drugs | 0.87 | 0.43 | - |
| Three or more drugs | 0.78 | 0.32 | 0.00 |
| % of Physicians Who Are Responsive | Share of Voice | Duration of Detail | Quarterly Profit | |
|---|---|---|---|---|
| Traditional approach | 30% | 10% | - | - |
| Knowledge-based approach | 47% | 16% | +47% | +12% |
| % of Responsive Physician | SOV | Detailing Duration vs. 2005 | Profitability of Responsive Physicians 2005–2014 | |
|---|---|---|---|---|
| Traditional approach | 19% | 6% | - | - |
| Knowledge-based approach | 35% | 10% | −9% | +23% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, J.C.; Kim, S. Early Adoption of Innovative Analytical Approach and Its Impact on Organizational Analytics Maturity and Sustainability: A Longitudinal Study from a U.S. Pharmaceutical Company. Sustainability 2016, 8, 808. https://doi.org/10.3390/su8080808
Yi JC, Kim S. Early Adoption of Innovative Analytical Approach and Its Impact on Organizational Analytics Maturity and Sustainability: A Longitudinal Study from a U.S. Pharmaceutical Company. Sustainability. 2016; 8(8):808. https://doi.org/10.3390/su8080808
Chicago/Turabian StyleYi, John C., and Sungho Kim. 2016. "Early Adoption of Innovative Analytical Approach and Its Impact on Organizational Analytics Maturity and Sustainability: A Longitudinal Study from a U.S. Pharmaceutical Company" Sustainability 8, no. 8: 808. https://doi.org/10.3390/su8080808
APA StyleYi, J. C., & Kim, S. (2016). Early Adoption of Innovative Analytical Approach and Its Impact on Organizational Analytics Maturity and Sustainability: A Longitudinal Study from a U.S. Pharmaceutical Company. Sustainability, 8(8), 808. https://doi.org/10.3390/su8080808





