Effects of Water Management Strategies on Water Balance in a Water Scarce Region: A Case Study in Beijing by a Holistic Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. The BHIWA Model Description
2.2.1. Irrigation Water Use
2.2.2. Agriculture Water Use Consumption
2.2.3. Groundwater Level
2.3. Scenarios
2.4. Evapotranspiration (ET) Data for the BHIWA Model
2.5. Simulated Evaluation Indexes
3. Results and Discussion
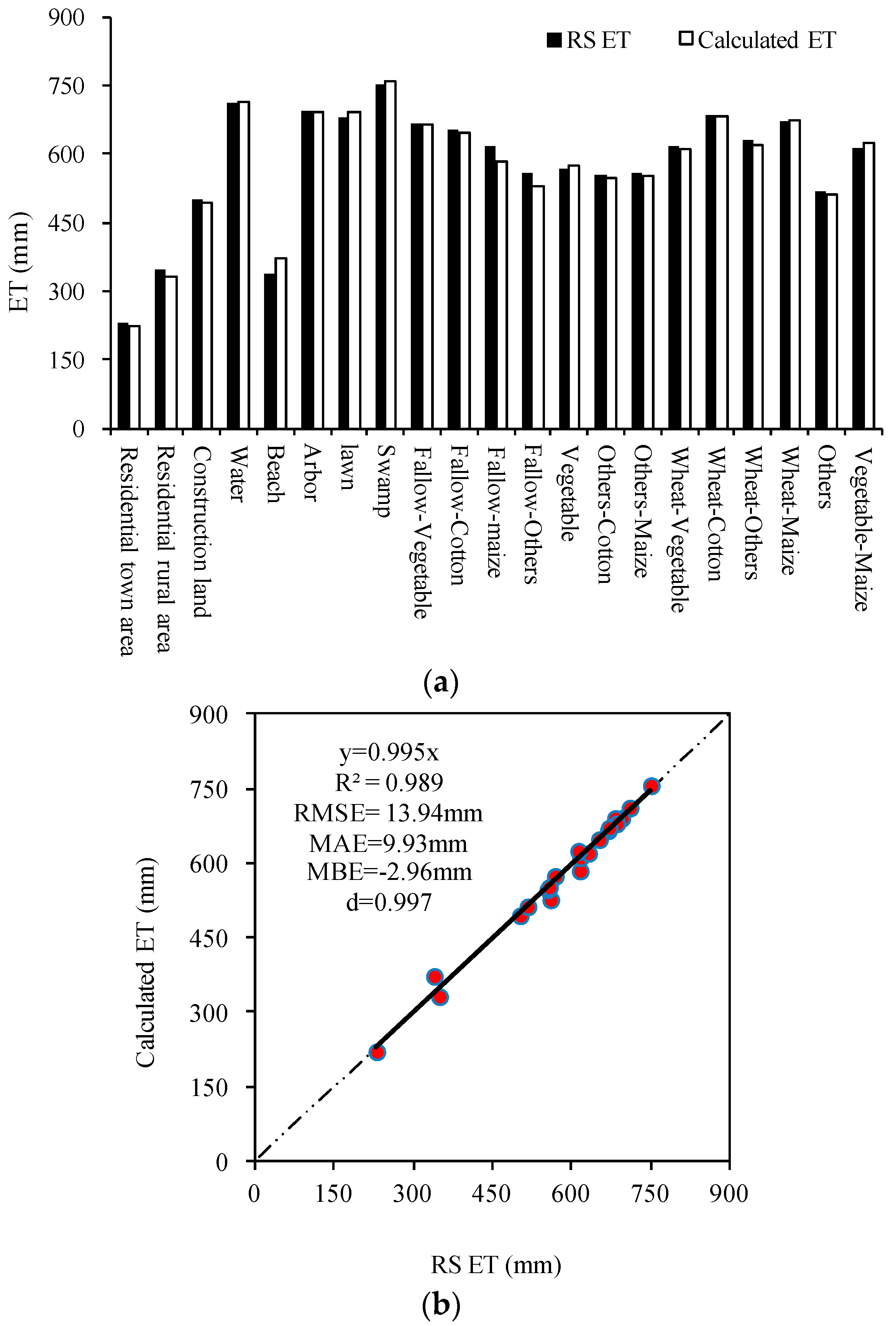
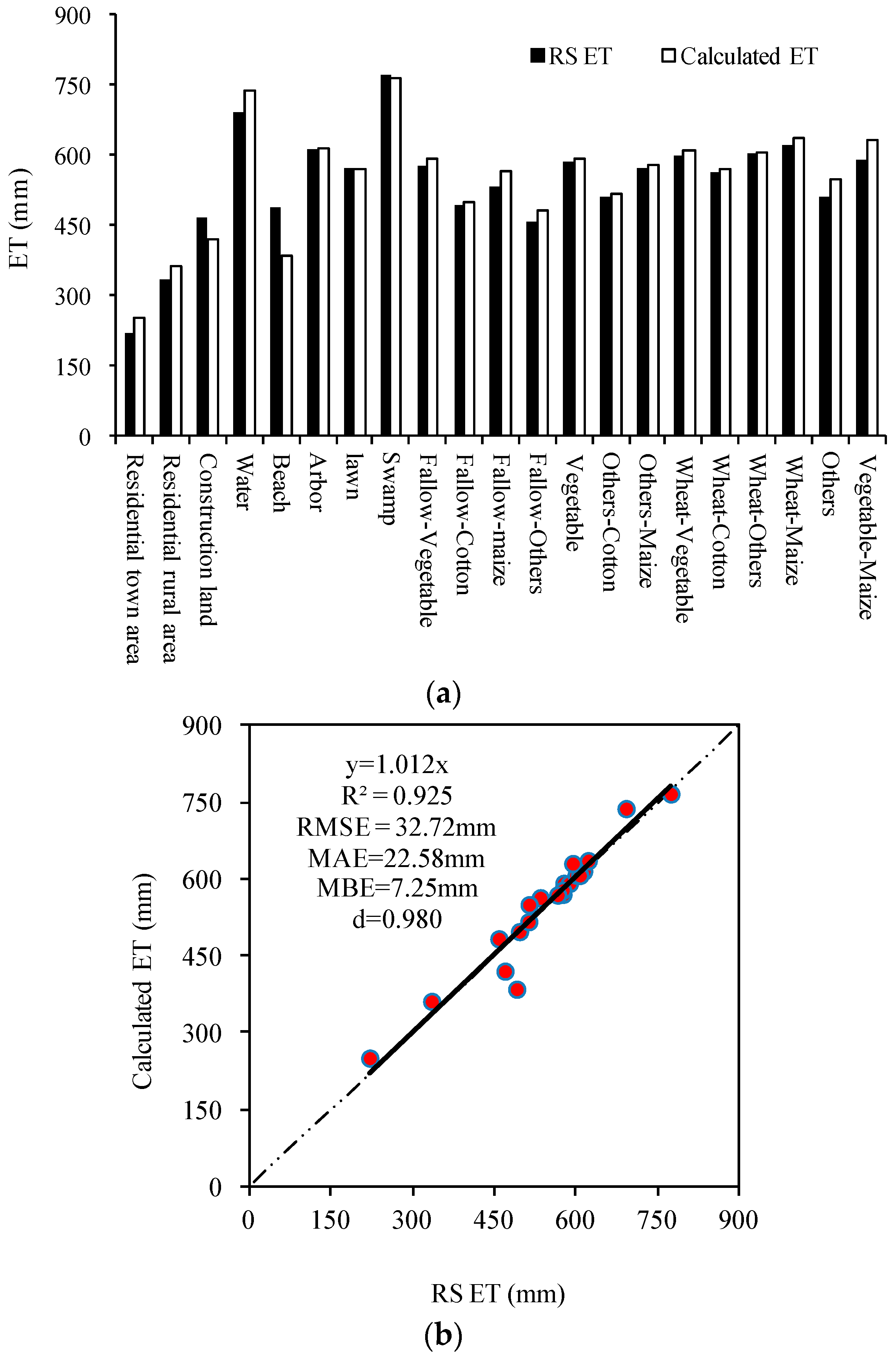
3.1. Calibration and Verification of BHIWA Model
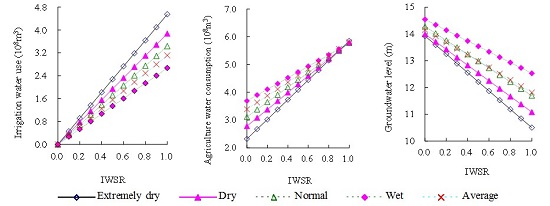
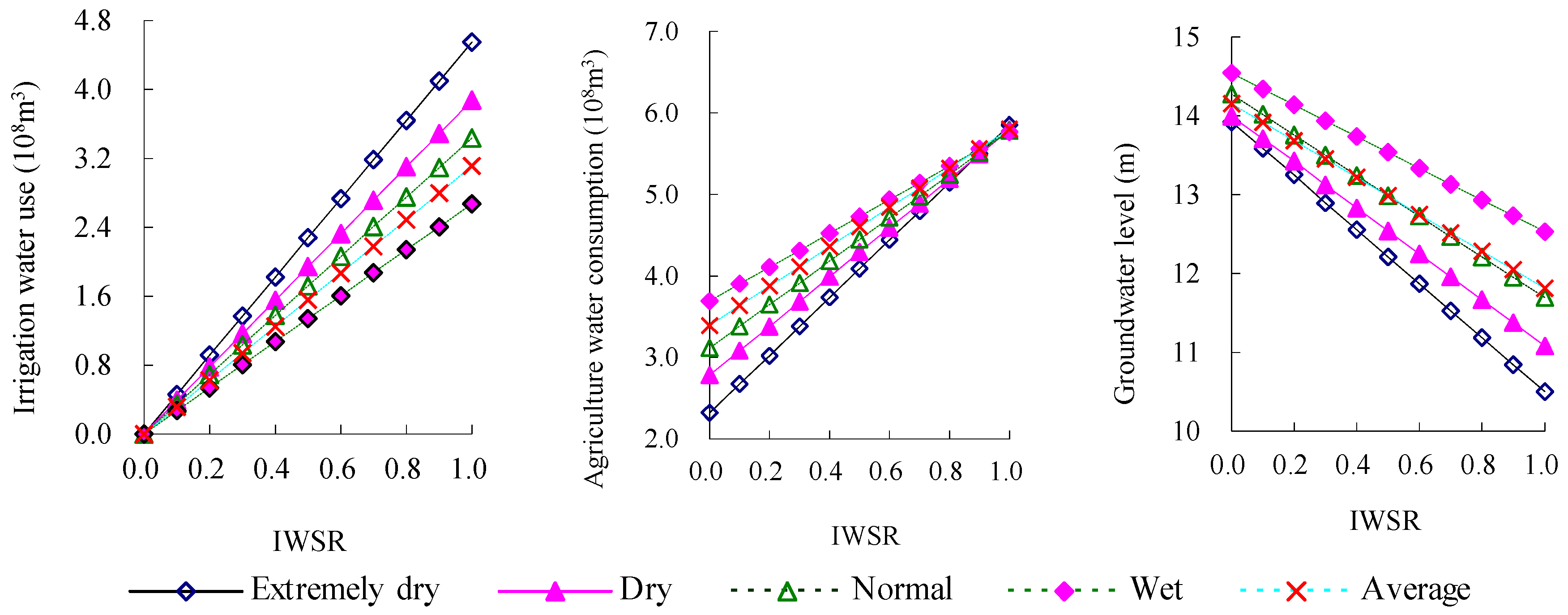
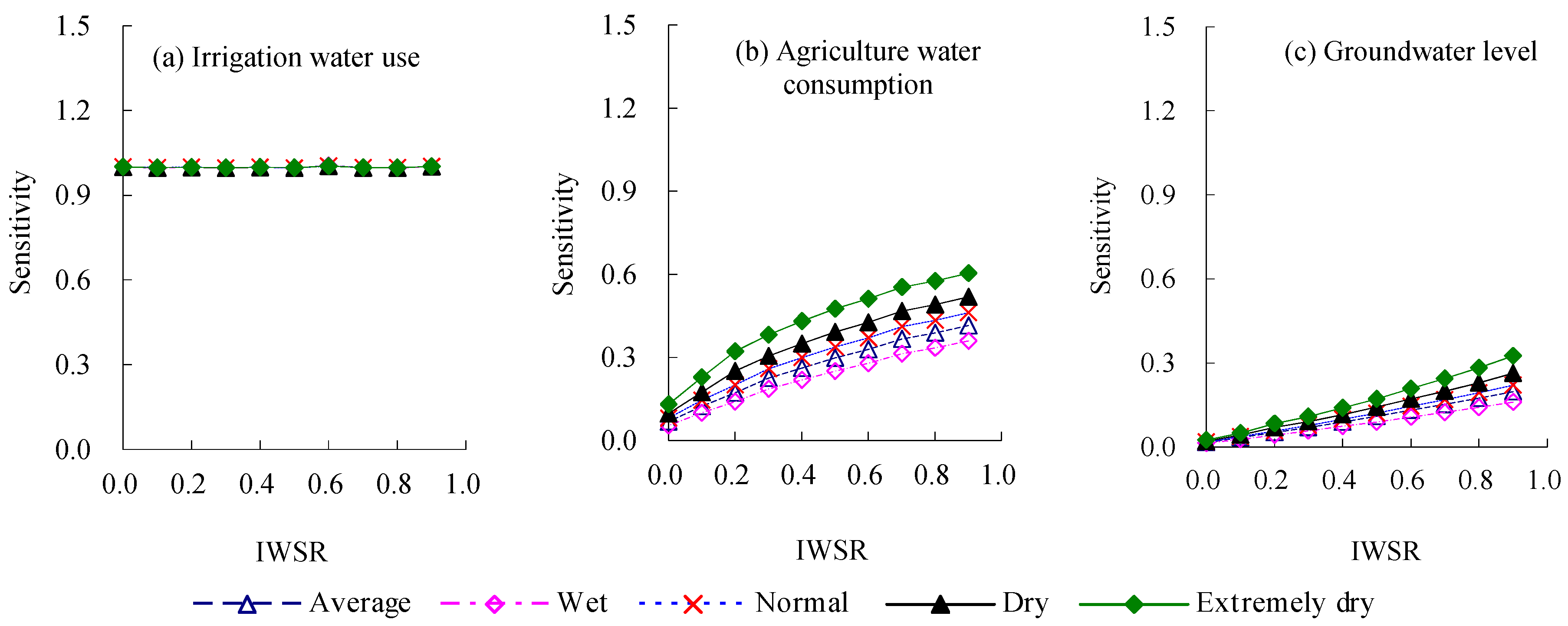
3.2. Effect of the Decrease of IWSR on Regional Irrigation Water Supply, Total Consumption, and Groundwater Level
3.2.1. Variation of Regional Irrigation Water Use and Agriculture Water Consumption
3.2.2. Sensitivity Analysis
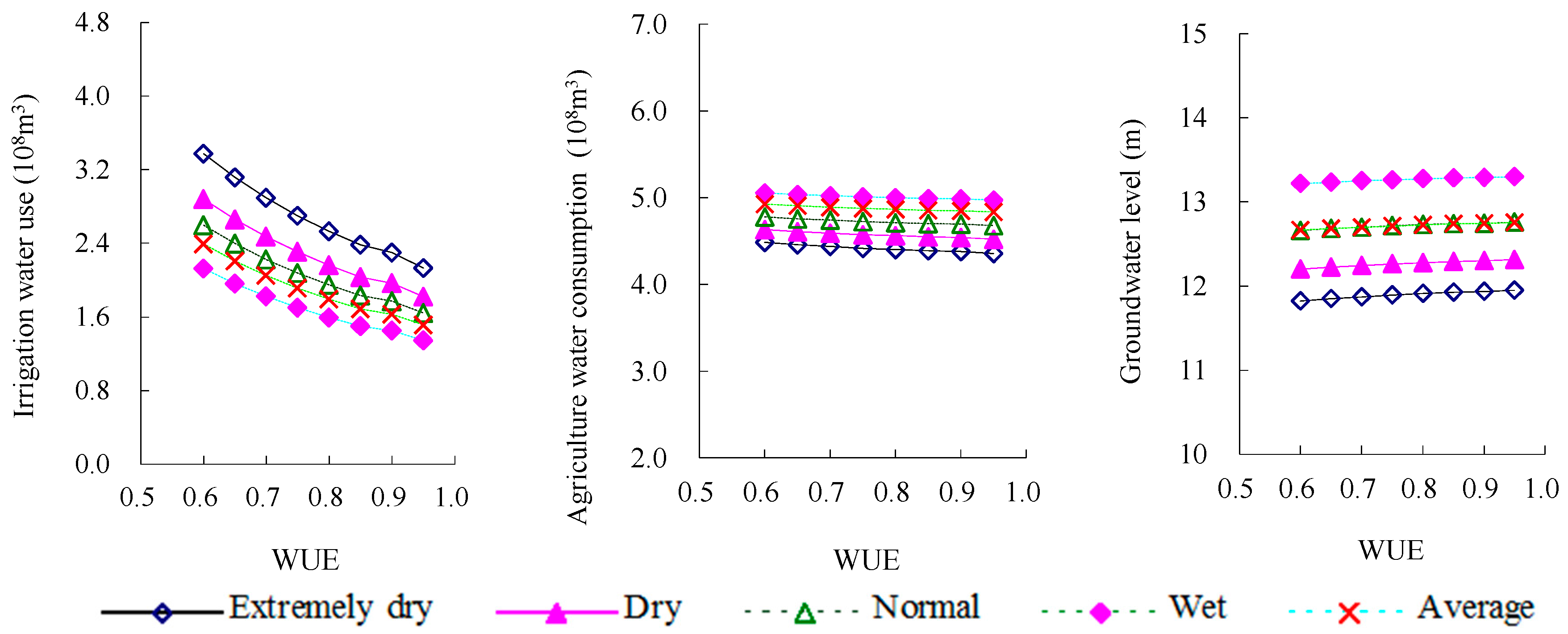
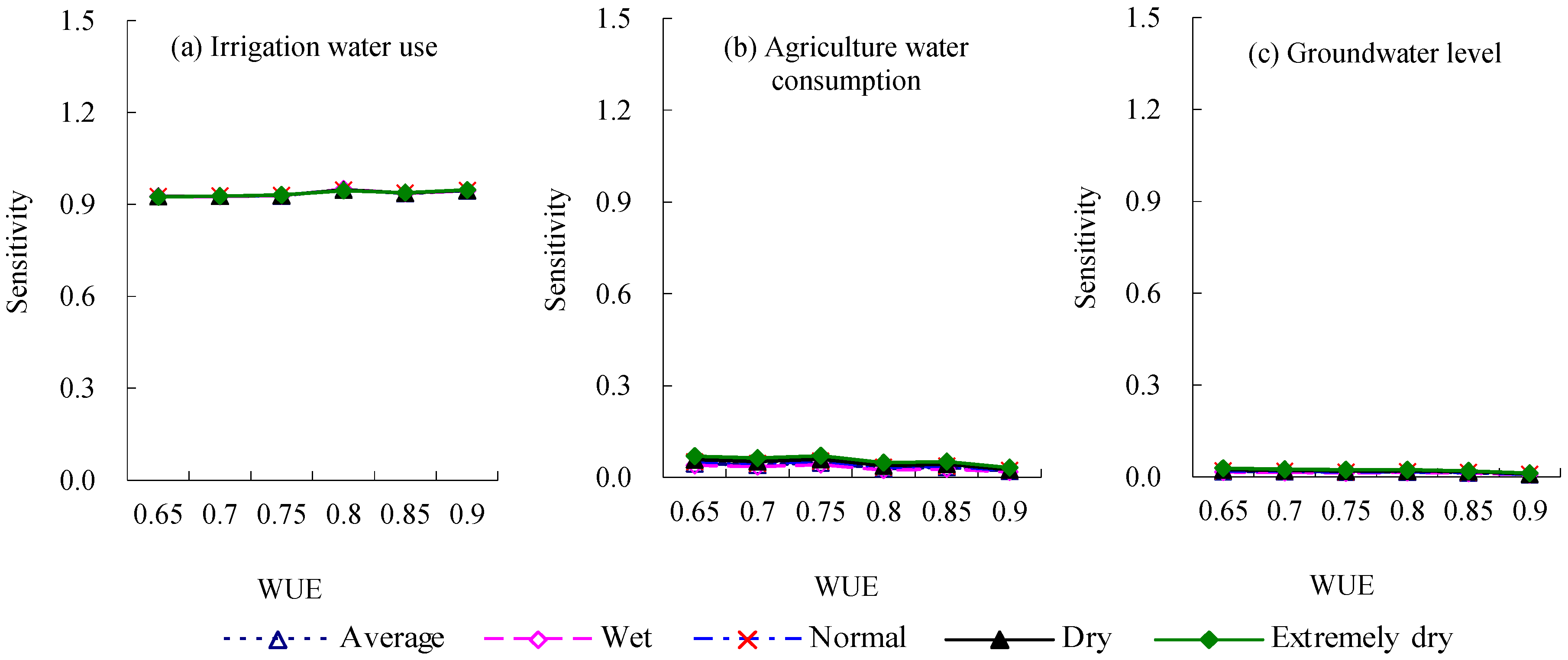
3.3. Effect of the Increase of WUE on Regional Irrigation Water Supply, Agriculture Water Consumption, and Groundwater Level
3.3.1. Variation of Regional Irrigation Water Use and Agriculture Water Consumption
3.3.2. Sensitivity Analysis
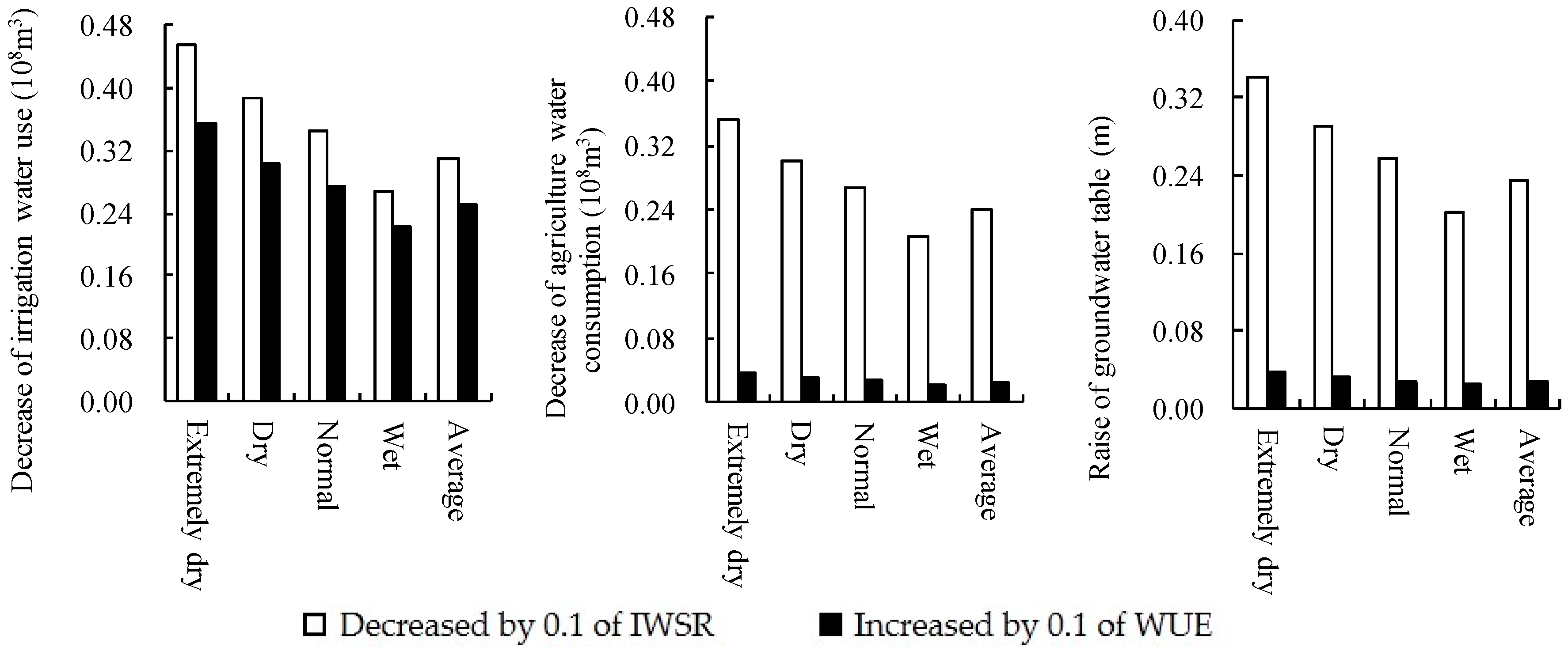
3.4. Effect of Combined Measures on Regional Irrigation Water Use and Water Consumption and Its Sensitivity
3.4.1. Difference of Regional Irrigation Water Use and Water Consumption
3.4.2. Difference of Sensitivity
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bao, C.; Fang, C. Water resources constraint force on urbanization in water deficient regions: A case study of the Hexi Corridor, arid area of NW China. Ecol. Econ. 2007, 62, 508–517. [Google Scholar] [CrossRef]
- Feng, L.; Chen, B.; Hayat, T.; Alsaedi, A.; Ahmad, B. The driving force of water footprint under the rapid urbanization process: A structural decomposition analysis for Zhangye city in China. J. Clean. Prod. 2015. [Google Scholar] [CrossRef]
- Yan, T.; Wang, J.; Huang, J. Urbanization, agricultural water use, and regional and national crop production in China. Ecol. Model. 2015, 318, 226–235. [Google Scholar] [CrossRef]
- Cai, M.; Wei, X.; Su, X. Influence of Irrigation Area Water Consumption Change to Ground Water Balanced. J. Irrig. Drain. 2007, 26, 16–20. (In Chinese) [Google Scholar]
- Lei, J. Study on adjustment and control of agricultural water resource in Luohui trench irrigation district. Groundwater 2010, 32, 68–69. (In Chinese) [Google Scholar]
- Li, Y.; Pang, H.; Chen, F.; Zhang, F.; Lai, X. Analysis on the Guarantee Degree of Irrigation Water Resources and Its Promotion Strategies in Manas River Valley, Xinjiang. J. Nat. Resour. 2010, 25, 2–42. (In Chinese) [Google Scholar]
- Li, G.; Jia, X.; Su, X. Countermeasures of groundwater resources over-exploitation in Hebei Province. China Water Resour. 2010, 5, 36–37, 44. (In Chinese) [Google Scholar]
- Liu, Z.; Zhang, G.; Yan, M.; Wang, J. Impact of Increases in Irrigated Grain Production on Groundwater in the Shijiazhuang Plain. Resour. Sci. 2010, 32, 535–539. (In Chinese) [Google Scholar]
- Beijing Water Authority. Beijing Water Resources Bulletin 2014; Beijing Water Authority: Beijing, China, 2014. (In Chinese)
- Huang, J.; Zhang, H.; Tong, W.; Chen, F. The impact of local crops consumption on the water resources in Beijing. J. Clean. Prod. 2012, 21, 45–50. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, L.; Liu, J.; Li, W.; Zheng, Y. Options of sustainable groundwater development in Beijing Plain, China. Phys. Chem. Earth Parts A/B/C 2012, 47–48, 99–113. [Google Scholar] [CrossRef]
- Li, Y.; Xiong, W.; Zhang, W.; Wang, C.; Wang, P. Life cycle assessment of water supply alternatives in water-receiving areas of the South-to-North Water Diversion Project in China. Water Res. 2016, 89, 9–19. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Huang, K.; Yang, S.; Yu, Y. An input-output approach to evaluate the water footprint and virtual water trade of Beijing, China. J. Clean. Prod. 2013, 42, 172–179. [Google Scholar] [CrossRef]
- Beijing Water Authority. Beijing Water Resources Bulletin 2001; Beijing Water Authority: Beijing, China, 2001. (In Chinese)
- Cao, H.; Ge, D.; Zhao, S.; Liu, Y.; Liu, Y.; Wang, W. Evaluation for applying computer simulation in crop growth and development research. J. Triticeae Crops 2010, 30, 183–187. (In Chinese) [Google Scholar]
- Wang, Y.; He, L. A Review on the Research and Application of Crop Simulation Model. J. Huazhong Agric. Univ. 2005, 24, 529–535. (In Chinese) [Google Scholar]
- Xu, Z. Hydrological models: Past, Present and Future. J. Beijing Norm. Univ. Nat. Sci. 2010, 46, 278–289. (In Chinese) [Google Scholar]
- Gopalakrishnan, M.; Mohile, A.D.; Gupta, L.N.; Kuberan, R.; Kulkarni, S.A. An integrated water assessment model for supporting India water policy. Irrig. Drain. 2006, 55, 33–50. [Google Scholar] [CrossRef]
- Mu, J.; Khan, S.; Gao, Z. Integrated water assessment model for water budgeting under future development scenarios in Qiantang River basin of China. Irrig. Drain. 2008, 57, 369–384. [Google Scholar] [CrossRef]
- Mu, J.; Khan, S.; Liu, Q.; Xu, D.; Xu, J.; Wang, W. A stochastic approach to analyse water management scenarios at the river basin level. Irrig. Drain. 2013, 62, 379–395. [Google Scholar] [CrossRef]
- Mu, J.; Liu, Q.; Gabriel, H.F.; Xu, D.; Xu, J.; Wu, C.; Ren, H. The impacts of climate change on water stress situations in the Yellow River basin, China. Irrig. Drain. 2013, 62, 545–558. [Google Scholar] [CrossRef]
- Peng, Z.; Liu, Y.; Xu, D.; Wang, L.; Zhang, B. Application of CPSP model to agricultural water management in well irrigation region in North China. J. Drain. Irrig. Mach. Eng. 2014, 32, 523–528. (In Chinese) [Google Scholar]
- National Bureau of Statistics of China. China Statistical Yearbook 1997; National Bureau of Statistics of China: Beijing, China, 1997. (In Chinese)
- National Bureau of Statistics of China. China Statistical Yearbook 2014; National Bureau of Statistics of China: Beijing, China, 2014. (In Chinese)
- Peng, Z. Agricultural Water Consumption Management Studies Based on Remote sensing ET Data: A Case Study of Beijing Daxing County; China Institute of Water Resource and Hydropower Research: Beijing, China, 2009; pp. 22–24. (In Chinese) [Google Scholar]
- Gao, Z. Study on China Food Safety and Irrigation Development Measures; China Institute of Water Resource and Hydropower Research: Beijing, China, 2005; pp. 15–22. (In Chinese) [Google Scholar]
- Beven, K. A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates. J. Hydrol. 1979, 44, l69–190. [Google Scholar] [CrossRef]
- Crosetto, M.; Ruiz, J.; Crippa, B. Uncertainty propagation in models driven by remotely sensed data. Remote Sens. Environ. 2001, 76, 373–385. [Google Scholar] [CrossRef]
- Ma, J.; Yan, G.; Li, H.; Guo, S. Sensitivity and uncertainty analysis for Abreu & Johnson numericalvapor intrusion model. J. Hazard. Mater. 2016, 304, 522–531. [Google Scholar] [PubMed]
- Mccuen, R.H. A sensitivity and error analysis of procedures used for estimating evaporation. Water Resour. Bull. 1974, 10, 486–498. [Google Scholar] [CrossRef]
- Médard, B.; Alain, N.R.; Silvio, J.G.; Patrick, G.; Brou, K.; Roger, M. Implementation of an automatic calibration procedure for HYDROTEL based on prior OAT sensitivity and complementary identifiability analysis. Hydrol. Process. 2014, 28, 3947–3961. [Google Scholar]
- Cai, X.; Xu, Z.; Su, B.; Yu, W. Distributed simulation for regional evapotranspiration and verification by using remote sensing. Trans. CSAE 2009, 25, 154–160. (In Chinese) [Google Scholar]
- Immerzeel, W.W.; Droogers, P. Clibration of a distributed hydrological model based on satellite evapotranspiration. J. Hydrol. 2008, 349, 411–424. [Google Scholar] [CrossRef]
- Peng, Z.; Mao, D.; Wang, L.; Liu, Y.; Zhang, J. Establishment of the regional water balance analysis model based on RS ET data and current situation analysis. J. Remote Sens. 2011, 15, 313–317. [Google Scholar]
- Wu, B.; Yan, N.; Xiong, J.; Bastiaanssen, W.G.M.; Zhu, W.; Stein, A. Validation of ETWatch using field measurements at diverse landscapes: A case study in Hai Basin of China. J. Hydrol. 2012, 436–437, 67–80. [Google Scholar] [CrossRef]
- Wu, B.; Xiong, J.; Yan, N. ETWatch: Models and methods. J. Remote Sens. 2010, 15, 224–230. [Google Scholar]
- Wu, B.; Xiong, J.; Yan, N.; Yang, L.; Du, X. ETWatch for monitoring regional evapotranspiration with remote sensing. Adv. Water Sci. 2008, 19, 671–678. [Google Scholar]
- Kahimba, F.C.; Bullock, P.R.; Sri-Ranjan, R.; Cutforth, H.W. Evaluation of the SolarCalc model for simulating hourly and daily incoming solar radiation in the Northern Great Plains of Canada. Can. Biosyst. Eng. 2009, 51, 1–11. [Google Scholar]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Willmott, C.J.; Maasuura, K. Advantages of the meanabsolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
| Precipitation Type | Wet | Normal | Dry | Extremely Dry | Average |
|---|---|---|---|---|---|
| Frequency (%) | 25 | 50 | 75 | 90 | - |
| Annual precipitation (mm) | 551 | 446 | 365 | 310 | 472 |
| Index | Index Range | Value of Index Level Selection |
|---|---|---|
| Irrigation water supply reliability (IWSR) | 0.0~1.0 | 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 |
| Irrigation water use efficiency (WUE) | 0.60~0.90 | 0.60, 0.65, 0.70, 0.75, 0.80, 0.85, 0.90 |
| Precipitation Type | Extremely Dry | Dry | Normal | Wet | Average |
|---|---|---|---|---|---|
| Decrease of irrigation water use (108 m3) | 0.455 | 0.388 | 0.344 | 0.267 | 0.311 |
| Decrease of agriculture water consumption (108 m3) | 0.353 | 0.301 | 0.267 | 0.208 | 0.241 |
| Raise of groundwater level (m) | 0.342 | 0.291 | 0.258 | 0.201 | 0.234 |
| Precipitation Type | Extremely Dry | Dry | Normal | Wet | Average |
|---|---|---|---|---|---|
| Decrease of irrigation water use (108 m3) | 0.355 | 0.303 | 0.273 | 0.223 | 0.251 |
| Decrease of agriculture water consumption (108 m3) | 0.037 | 0.031 | 0.028 | 0.023 | 0.026 |
| Raise of groundwater level (m) | 0.037 | 0.032 | 0.028 | 0.024 | 0.027 |
| Irrigation Water Use | Agriculture Water Consumption | Regional Groundwater Level | ||||
|---|---|---|---|---|---|---|
| IWSR | WUE | IWSR | WUE | IWSR | WUE | |
| Maximum sensitivity | 1.00 | 0.93 | 0.42 | 0.05 | 0.2 | 0.02 |
| Value range with maximum sensitivity | 0.0–1.0 | 0.60–0.90 | 0.9–1.0 | 0.60–0.65 | 0.9–1.0 | 0.60–0.65 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.; Zhang, B.; Cai, X.; Wang, L. Effects of Water Management Strategies on Water Balance in a Water Scarce Region: A Case Study in Beijing by a Holistic Model. Sustainability 2016, 8, 749. https://doi.org/10.3390/su8080749
Peng Z, Zhang B, Cai X, Wang L. Effects of Water Management Strategies on Water Balance in a Water Scarce Region: A Case Study in Beijing by a Holistic Model. Sustainability. 2016; 8(8):749. https://doi.org/10.3390/su8080749
Chicago/Turabian StylePeng, Zhigong, Baozhong Zhang, Xueliang Cai, and Lei Wang. 2016. "Effects of Water Management Strategies on Water Balance in a Water Scarce Region: A Case Study in Beijing by a Holistic Model" Sustainability 8, no. 8: 749. https://doi.org/10.3390/su8080749