Regional Port Productivity in APEC
Abstract
:1. Introduction
2. gMMPI
3. Methodology
- Grouping: We grouped the APEC economies according to their state of economic development.
- Major ports: We defined the major ports of each economy.
- Measurement model: We measured the function between inputs and outputs.
- Analysis: We analyzed the port productivity of the DCs and LDCs.
3.1. Input and Output
3.2. Model
4. Results
4.1. Model of Productivity Analysis
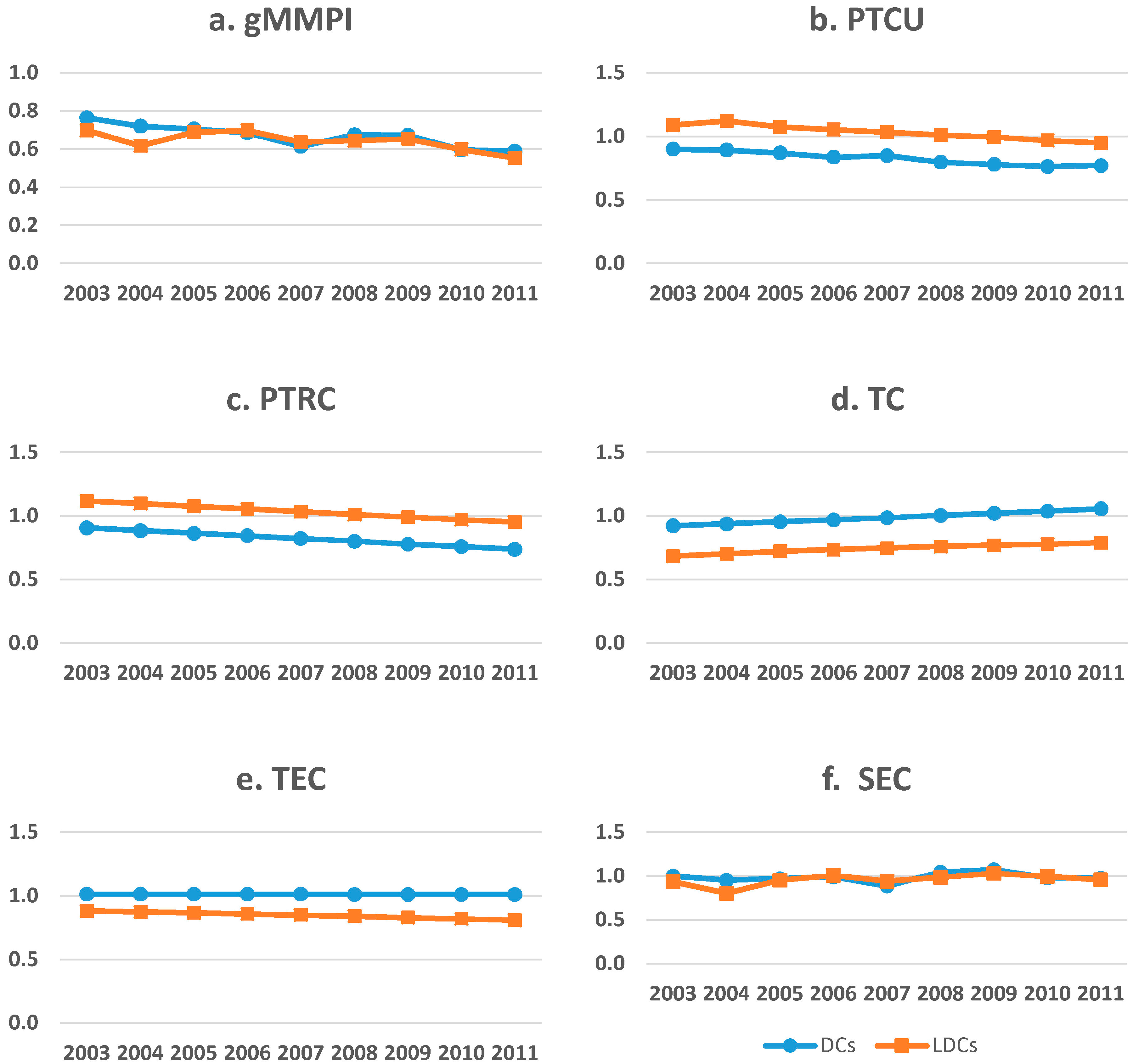
4.2. Trend
4.3. Sources of Impact
5. Conclusions and Discussion
5.1. Implications for Practice
5.2. Implications for Theory
5.3. Limitations and Future Research Direction
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| APEC | Asia-Pacific Economic Cooperation |
| DCs | Developed countries |
| DEA | Data envelopment analysis, |
| gMMPI | generalized metafrontier Malmquist productivity index |
| LDCs | Developing countries |
| PTCU | Pure technological catch-up |
| PTRC | Potential technological relative change |
| SEC | Scale efficiency change |
| SFA | Stochastic frontier analysis |
| TC | Technical change |
| TEC | Technical efficiency change |
| TFP | Total factor productivity |
| TGR | Technology gap ratio |
References
- DFAT. The APEC Region Trade and Investment; Department of Foreign Affairs and Trade (Australia): Barton, Australia, 2015.
- The World Bank. Container Port Traffic; The World Bank: Washington, DC, USA, 2014. [Google Scholar]
- Wilson, R. 26th Annual State of Logistics Report. Fortna President Included in Panel; Council of Supply Chain Management Professionals: Washington, DC, USA, 2015. [Google Scholar]
- Armstrong & Associates. Globaland Regional Infrastructure, Logistics Costs, and Third-Party Logistics Market Trends and Analysis; Armstrong & Associates, Inc.: Milwaukee, WI, USA, 2014. [Google Scholar]
- Walkenhorst, P.; Yasui, T. Quantitative Assessment of the Benefits of Trade Facilitation. In Overcoming Border Bottlenecks: The Costs and Benefits of Trade Facilitation; OECD: Paris, France, 2009; pp. 19–50. [Google Scholar]
- Andersson, D.; Norrman, A. Procurement of logistics services—A minutes work or a multi-year project? Eur. J. Purch. Supply Manag. 2002, 8, 3–14. [Google Scholar] [CrossRef]
- Bichou, K. A two-stage supply chain DEA model for measuring container-terminal efficiency. Int. J. Transp. Logist. Ship. 2011, 3, 6–26. [Google Scholar] [CrossRef]
- Wu, Y.C.J.; Goh, M. Container port efficiency in emerging and more advanced markets. Transp. Res. E Logist. 2010, 46, 1030–1042. [Google Scholar] [CrossRef]
- Wu, Y.C.J.; Lin, C.W. National port competitiveness: Implications for India. Manag. Decis. 2008, 46, 1482–1507. [Google Scholar]
- Jiang, J.; Chew, E.; Lee, L.; Sun, Z. DEA based on strongly efficient and inefficient frontiers and its application on port efficiency measurement. OR Spectr. 2012, 34, 943–969. [Google Scholar] [CrossRef]
- Cheon, S.; Dowall, D.E.; Song, D.-W. Evaluating impacts of institutional reforms on port efficiency changes: Ownership, corporate structure, and total factor productivity changes of world container ports. Transp. Res. E Logist. 2010, 46, 546–561. [Google Scholar] [CrossRef]
- Tongzon, J. Efficiency measurement of selected Australian and other international ports using data envelopment analysis. Transp. Res. A Policy Pract. 2001, 35, 107–122. [Google Scholar] [CrossRef]
- Yuen, A.C.-l.; Zhang, A.; Cheung, W. Foreign participation and competition: A way to improve the container port efficiency in China? Transp. Res. A Policy Pract. 2013, 49, 220–231. [Google Scholar] [CrossRef]
- Figueiredo De Oliveira, G.; Cariou, P. The impact of competition on container port (in) efficiency. Transp. Res. A Policy Pract. 2015, 78, 124–133. [Google Scholar] [CrossRef]
- Tovar, B.; Wall, A. Can ports increase traffic while reducing inputs? Technical efficiency of Spanish Port Authorities using a directional distance function approach. Transp. Res. A Policy Pract. 2015, 71, 128–140. [Google Scholar] [CrossRef]
- Song, B.; Cui, Y. Productivity changes in Chinese Container Terminals 2006–2011. Transp. Policy 2014, 35, 377–384. [Google Scholar] [CrossRef]
- Mentzer, J.T.; Flint, D.J.; Hult, G.T.M. Logistics service quality as a segment-customized process. J. Mark. 2001, 65, 82–104. [Google Scholar] [CrossRef]
- Núñez-Sánchez, R.; Coto-Millán, P. The impact of public reforms on the productivity of Spanish ports: A parametric distance function approach. Transp. Policy 2012, 24, 99–108. [Google Scholar] [CrossRef]
- Chang, V.; Tovar, B. Efficiency and productivity changes for Peruvian and Chilean ports terminals: A parametric distance functions approach. Transp. Policy 2014, 31, 83–94. [Google Scholar] [CrossRef]
- Tovar, B.; Rodríguez-Déniz, H. Classifying ports for efficiency benchmarking: A review and a frontier-based clustering approach. Transp. Rev. 2015, 35, 378–400. [Google Scholar] [CrossRef]
- Martínez-Budría, E.; Díaz-Armas, R.; Navarro-Ibáñez, M.; Ravelo-Mesa, T. A study of the efficiency of Spanish port authorities using data envelopment analysis. Int. J. Transp. Econ. 1999, 26, 237–253. [Google Scholar]
- O’Donnell, C.J.; Rao, D.S.P.; Battese, G.E. Metafrontier frameworks for the study of firm-level efficiencies and technology ratios. Empir. Econ. 2008, 34, 231–255. [Google Scholar] [CrossRef]
- Hausman, W.H.; Lee, H.L.; Subramanian, U. Global Logistics Indicators, Supply Chain Metrics, and Bilateral Trade Patterns; The World Bank: Washington, DC, USA, 2005. [Google Scholar]
- Hung, S.-W.; Lu, W.-M.; Wang, T.-P. Benchmarking the operating efficiency of Asia container ports. Eur. J. Oper. Res. 2010, 203, 706–713. [Google Scholar] [CrossRef]
- Shephard, R.W. Theory of Cost and Production Functions; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Farrell, M.J. The measurement of productive efficiency. J. Roy. Stat. Soc. Ser. A 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Battese, G.E.; Prasada Rao, D.S.; O’Donnell, C.J. A metafrontier production function for estimation of technical efficiencies and technology gaps for firms operating under different technologies. J. Prod. Anal. 2004, 21, 91–103. [Google Scholar] [CrossRef]
- Diewert, W.E. Exact and superlative index numbers. J. Econ. 1976, 4, 115–145. [Google Scholar] [CrossRef]
- Orea, L. Parametric decomposition of a generalized Malmquist productivity index. J. Prod. Anal. 2002, 18, 5–22. [Google Scholar] [CrossRef]
- Song, M.; Zheng, W. Computational analysis of thermoelectric enterprises’ environmental efficiency and Bayesian estimation of influence factors. Soc. Sci. J. 2016, 53, 88–99. [Google Scholar] [CrossRef]
- Chen, K.H. Incorporating risk input into the analysis of bank productivity: Application to the Taiwanese banking industry. J. Bank Financ. 2012, 36, 1911–1927. [Google Scholar] [CrossRef]
- Lin, E.Y.Y.; Chen, P.Y.; Chen, C.C. Measuring green productivity of country: A generlized metafrontier Malmquist productivity index approach. Energy 2013, 55, 340–353. [Google Scholar]
- Ahmed, E.M.; Krishnasamy, G. Are Asian technology gaps due to human capital quality differences? Econ. Model 2013, 35, 51–58. [Google Scholar] [CrossRef]
- IMF. World Economic Outlook Report 2015; IMF: Washington, DC, USA, 2015. [Google Scholar]
- Dowd, T.J.; Leschine, T.M. Container terminal productivity: A perspective. Marit. Policy Manag. 1990, 17, 107–112. [Google Scholar] [CrossRef]
- Yeo, G.-T.; Roe, M.; Dinwoodie, J. Measuring the competitiveness of container ports: Logisticians’ perspectives. Eur. J. Mark. 2011, 45, 455–470. [Google Scholar]
- Cheon, S. Impact of global terminal operators on port efficiency: A tiered data envelopment analysis approach. Int. J. Logist. Res. Appl. 2009, 12, 85–101. [Google Scholar] [CrossRef]
- Cullinane, K.; Wang, T.-F.; Song, D.-W.; Ji, P. The technical efficiency of container ports: Comparing data envelopment analysis and stochastic frontier analysis. Transp. Res. A Policy Pract. 2006, 40, 354–374. [Google Scholar] [CrossRef]
- Rios, L.R.; Maçada, A.C.G. Analysing the relative efficiency of container terminals of Mercosur using DEA. Marit. Econ. Logist. 2006, 8, 331–346. [Google Scholar] [CrossRef]
- Wang, T.F.; Cullinane, K. The efficiency of European container terminals and implications for supply chain management. Marit. Econ. Logist. 2006, 8, 82–99. [Google Scholar] [CrossRef]
- Cullinane, K.; Song, D.-W.; Wang, T. The application of mathematical programming approaches to estimating container port production efficiency. J. Prod. Anal. 2005, 24, 73–92. [Google Scholar] [CrossRef]
- Containerization International. Containerization International Yearbook; Containerization International: London, UK, 2003–2012. [Google Scholar]
- American Association of Port Authorities. World Port Rankings 2011; American Association of Port Authorities: Alexandria, VA, USA, 2011. [Google Scholar]
- CI-Online. Container Traffic; Containerization International: London, UK, 2003–2012. [Google Scholar]
- Cullinane, K.; Wang, T.-F. The efficiency of European container ports: A cross-sectional data envelopment analysis. Int. J. Logist. Res. Appl. 2006, 9, 19–31. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.A.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econ. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; Van Den Broeck, J. Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T.J. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Prod. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Trujillo, L.; Tovar, B. The european port industry: An analysis of its economic efficiency. Marit. Econ. Logist. 2007, 9, 148–171. [Google Scholar] [CrossRef]
- Kalirajan, K.P.; Obwona, M.B.; Zhao, S. A decomposition of total factor productivity growth: The case of chinese agricultural growth before and after reforms. Am. J. Agric. Econ. 1996, 78, 331–338. [Google Scholar] [CrossRef]
- Huang, T.-H.; Chiang, L.-C.; Chen, K.-C.; Chiu, P.H. An application of the meta-frontier cost function to the study of bank efficiencies and technology gaps in 16 European countries. Manag. Rev. 2010, 29, 25–43. [Google Scholar]
- Bray, S.; Caggiani, L.; Dell’Orco, M.; Ottomanelli, M. Features selection based on fuzzy entropy for Data Envelopment Analysis applied to transport systems. Transp. Res. Procedia 2014, 3, 602–610. [Google Scholar] [CrossRef]
- Cullinane, K.; Song, D.-W. Estimating the relative efficiency of European container ports: A stochastic frontier analysis. Res. Trans. E 2006, 16, 85–115. [Google Scholar] [CrossRef]
- Wang, Y.; Cullinane, K. Traffic consolidation in East Asian container ports: A network flow analysis. Transp. Res. A Policy Pract. 2014, 61, 152–163. [Google Scholar] [CrossRef]
- Roll, Y.; Hayuth, Y. Port performance comparison applying data envelopment analysis (DEA). Marit. Policy Manag. 1993, 20, 153–161. [Google Scholar] [CrossRef]
- Mooney, T. Malaysia Developing National Port Strategy with World Bank. Available online: http://www.joc.com/port-news/asian-ports/port-tanjung-pelepas/malaysia-developing-national-port-strategy-world-bank_20151125.html (accessed on 20 April 2016).
- INFOFISH. Mexico Raises a Position in FAO Fishery Prodcution Ranking. Available online: http://infofish.org/v2/index.php/87-mexico-raises-a-position-in-fao-fishery-production-ranking (accessed on 20 June 2016).
- Bain, B. Robust U.S. Market, Foreign Investments behind Rise. Available online: http://www.autonews.com/article/20150206/OEM01/302069972/mexico-auto-exports-forecast-to-hit-record-in-2015 (accessed on 20 June 2016).
- González, M.M.; Trujillo, L. Efficiency measurement in the port industry: A survey of the empirical evidence. J. Transp. Econ. Policy 2009, 43, 157–192. [Google Scholar]
- Bichou, K. An empirical study of the impacts of operating and market conditions on container-port efficiency and benchmarking. Res. Trans. Econ. 2013, 42, 28–37. [Google Scholar] [CrossRef]
| Country | Container Port | Quay Length (m) | Terminal Area (ha) | Capacity (ton) | No. of Containers (TEU) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | ||
| DCs | |||||||||
| Australia | Melbourne | 3502 | 346 | 147 | 9 | 3826 | 449 | 2,009,312 | 351,533 |
| Sydney | 2748 | 677 | 94 | 8 | 2983 | 98 | 1,560,629 | 297,501 | |
| Canada | Montreal | 3936 | 389 | 89 | 11 | 2252 | 429 | 1,267,170 | 132,077 |
| Vancouver BC | 4199 | 475 | 162 | 8 | 2689 | 573 | 2,035,916 | 475,754 | |
| Hong Kong | Hong Kong | 9580 | 2154 | 306 | 51 | 18,269 | 2734 | 22,411,998 | 2,050,206 |
| Japan | Kobe | 7930 | 1111 | 190 | 17 | 4421 | 127 | 2,346,579 | 172,044 |
| Nagoya | 3632 | 236 | 131 | 16 | 4536 | 730 | 2,453,011 | 338,648 | |
| Osaka | 4295 | 245 | 123 | 13 | 2456 | 104 | 1,993,501 | 266,954 | |
| Tokyo | 4242 | 462 | 126 | 34 | 4201 | 613 | 3,829,302 | 512,319 | |
| Yokohama | 5504 | 319 | 199 | 15 | 4607 | 280 | 2,968,394 | 391,328 | |
| New Zealand | Auckland | 1063 | 60 | 41 | 1 | 2122 | 286 | 736,744 | 130,685 |
| Singapore | Singapore | 14,960 | 4603 | 415 | 107 | 30,134 | 12,292 | 24,689,970 | 4,613,651 |
| South Korea | Busan | 12,687 | 1476 | 384 | 60 | 12,519 | 3270 | 12,233,596 | 2,309,898 |
| Gwangyang | 2985 | 1257 | 213 | 309 | 2112 | 1361 | 1,605,088 | 459,862 | |
| Incheon | 2010 | 468 | 47 | 5 | 1005 | 193 | 1,405,936 | 530,070 | |
| Taiwan | Kaohsiung | 6487 | 523 | 148 | 18 | 3210 | 393 | 9,255,783 | 804,964 |
| Keelung | 3362 | 249 | 39 | 7 | 1820 | 170 | 2,026,099 | 228,724 | |
| Taichung | 1864 | 201 | 88 | 17 | 2341 | 602 | 1,246,608 | 73,814 | |
| United States | Charleston | 3102 | 0 | 186 | 10 | 2221 | 472 | 1,600,481 | 320,806 |
| Houston | 1525 | 0 | 78 | 0 | 1456 | 345 | 1,602,306 | 271,445 | |
| Long Beach | 7456 | 475 | 450 | 45 | 4810 | 582 | 6,023,136 | 992,943 | |
| Los Angeles | 8732 | 1176 | 574 | 140 | 5746 | 1822 | 7,406,072 | 1,031,546 | |
| New York/New Jersey | 8251 | 685 | 571 | 30 | 8439 | 1128 | 4,740,355 | 746,186 | |
| Oakland | 6869 | 398 | 307 | 25 | 2884 | 389 | 2,176,142 | 213,793 | |
| Savannah | 2676 | 315 | 476 | 16 | 3071 | 1820 | 2,154,801 | 639,155 | |
| Seattle | 3858 | 412 | 206 | 15 | 1382 | 266 | 1,825,555 | 249,212 | |
| Tacoma | 2680 | 453 | 219 | 35 | 2622 | 895 | 1,732,205 | 253,691 | |
| Virginia | 3894 | 602 | 449 | 58 | 2217 | 415 | 1,860,089 | 235,735 | |
| LDCs | |||||||||
| Brunei | Muara | 765 | 0 | 9 | 2 | 117 | 1 | 88,668 | 16,864 |
| Chile | San Antonio | 1163 | 27 | 46 | 5 | 616 | 47 | 693,283 | 143,197 |
| China | Dalian | 2744 | 1175 | 160 | 60 | 4122 | 1407 | 3,526,890 | 1,688,175 |
| Fuzhou | 1354 | 320 | 94 | 42 | 1341 | 421 | 988,561 | 345,955 | |
| Guangzhou | 3848 | 1878 | 306 | 211 | 3833 | 2156 | 7,712,190 | 4,559,065 | |
| Lianyungang | 540 | 0 | 16 | 0 | 404 | 29 | 2,052,150 | 1,555,327 | |
| Nanjing | 410 | 0 | 20 | 0 | 782 | 61 | 754,954 | 332,160 | |
| Ningbo | 2460 | 679 | 76 | 0 | 1454 | 20 | 7,887,450 | 4,617,521 | |
| Qingdao | 4756 | 1151 | 118 | 17 | 4005 | 897 | 8,058,170 | 3,555,060 | |
| Shanghai | 6899 | 2825 | 621 | 319 | 14,343 | 7734 | 21,114,820 | 8,514,188 | |
| Shenzhen | 9046 | 3842 | 297 | 81 | 10,872 | 4564 | 16,877,284 | 5,990,716 | |
| Tianjin | 3089 | 761 | 132 | 39 | 3720 | 2229 | 6,517,142 | 3,206,334 | |
| Xiamen | 1721 | 676 | 57 | 11 | 1044 | 171 | 4,027,106 | 1,642,391 | |
| Yantai | 1156 | 705 | 58 | 28 | 1263 | 995 | 1,266,185 | 793,099 | |
| Indonesia | Tanjung Perak | 2094 | 444 | 92 | 30 | 2232 | 649 | 1,994,987 | 586,062 |
| Tanjung Priok | 2907 | 451 | 155 | 19 | 4661 | 852 | 3,699,082 | 921,677 | |
| Malaysia | Penang | 1052 | 129 | 75 | 11 | 1885 | 325 | 886,004 | 176,179 |
| Port Klang | 5662 | 907 | 161 | 22 | 10,547 | 1678 | 6,620,973 | 1,947,519 | |
| Tanjung Pelepas | 2376 | 683 | 126 | 19 | 4367 | 1817 | 4,801,387 | 1,966,480 | |
| Mexico | Manzanillo | 1669 | 875 | 27 | 7 | 1037 | 421 | 1,143,002 | 439,051 |
| Peru | Callao | 3821 | 568 | 42 | 15 | 694 | 351 | 950,638 | 363,796 |
| Philippines | Manila | 7768 | 549 | 183 | 29 | 3148 | 625 | 2,809,480 | 298,604 |
| Russia | St. Petersburg | 2154 | 250 | 68 | 35 | 2483 | 1012 | 1,423,794 | 687,832 |
| Thailand | Bangkok | 3958 | 430 | 106 | 57 | 3570 | 1693 | 1,335,638 | 148,976 |
| Laem Chabang | 8420 | 2671 | 337 | 140 | 6658 | 2199 | 4,168,238 | 1,086,971 | |
| Vietnam | Ho Chi Minh | 3842 | 1844 | 167 | 89 | 2991 | 1600 | 2,683,834 | 1,221,260 |
| DCs | LDCs | APEC | Metafrontier | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Constant | 16.170 | *** | (1.449) | 14.895 | *** | (1.162) | 17.470 | *** | (0.967) | 12.965 |
| L | −0.076 | (0.602) | −0.510 | (0.596) | −0.365 | (0.457) | −0.063 | |||
| M | −0.171 | (0.675) | −0.849 | (0.703) | 0.910 | ** | (0.375) | 0.652 | ||
| N | −0.265 | (0.645) | 0.662 | (0.703) | −1.410 | *** | (0.458) | −0.776 | ||
| (lnL)2 | 0.588 | *** | (0.176) | 0.158 | (0.122) | 0.065 | (0.095) | 0.168 | ||
| (lnM)2 | 0.130 | (0.118) | −0.388 | (0.248) | 0.025 | (0.081) | −0.046 | |||
| (lnN)2 | 0.602 | *** | (0.124) | −0.029 | (0.162) | 0.258 | *** | (0.083) | 0.221 | |
| (lnL)(lnM) | −0.067 | (0.079) | 0.122 | (0.106) | −0.002 | (0.065) | −0.004 | |||
| (lnL)(lnN) | −0.532 | *** | (0.142) | −0.143 | (0.094) | 0.030 | (0.065) | −0.093 | ||
| (lnM)(lnN) | 0.007 | (0.083) | 0.217 | (0.178) | −0.121 | * | (0.069) | −0.008 | ||
| t | 0.136 | * | (0.073) | 1.029 | *** | (0.097) | 0.880 | *** | (0.059) | 0.673 |
| t2 | −0.016 | *** | (0.003) | −0.010 | * | (0.006) | −0.009 | ** | (0.003) | 0.022 |
| (lnL)t | 0.015 | (0.012) | −0.049 | *** | (0.015) | −0.053 | *** | (0.009) | −0.103 | |
| (lnM)t | −0.006 | (0.008) | 0.004 | (0.018) | −0.002 | (0.008) | 0.017 | |||
| (lnN)t | −0.016 | * | (0.009) | −0.040 | ** | (0.016) | −0.029 | *** | (0.009) | −0.003 |
| σ2 | 0.340 | *** | (0.043) | 2.13 | *** | (0.480) | 0.956 | *** | (0.075) | |
| γ | 0.955 | *** | (0.010) | 0.975 | *** | 0.007 | 0.954 | *** | (0.007) | |
| μ | 1.139 | ** | (0.163) | 2.882 | *** | (0.456) | 1.910 | *** | (0.153) | |
| η | 0.008 | (0.006) | −0.068 | *** | (0.006) | −0.056 | *** | (0.006) | ||
| Observations | 280 | 260 | 540 | |||||||
| Log likelihood function | 426.773 | −60.819 | −68.537 | |||||||
| Likelihood ratio test | 868.982 *** | |||||||||
| PTCU | PTRC | TC | TEC | SEC | gMMPI | ||
|---|---|---|---|---|---|---|---|
| APEC | 2002–2003 | 0.9912 | 1.0083 | 0.8071 | 0.9497 | 0.9698 | 0.7329 |
| 2003–2004 | 1.0031 | 0.9871 | 0.8241 | 0.9460 | 0.8811 | 0.6710 | |
| 2004–2005 | 0.9689 | 0.9665 | 0.8421 | 0.9421 | 0.9632 | 0.6978 | |
| 2005–2006 | 0.9413 | 0.9452 | 0.8564 | 0.9379 | 0.9994 | 0.6914 | |
| 2006–2007 | 0.9392 | 0.9237 | 0.8710 | 0.9335 | 0.9142 | 0.6253 | |
| 2007–2008 | 0.9004 | 0.9021 | 0.8862 | 0.9289 | 1.0169 | 0.6611 | |
| 2008–2009 | 0.8832 | 0.8807 | 0.9000 | 0.9240 | 1.0539 | 0.6641 | |
| 2009–2010 | 0.8617 | 0.8607 | 0.9128 | 0.9189 | 0.9893 | 0.5970 | |
| 2010–2011 | 0.8564 | 0.8410 | 0.9272 | 0.9135 | 0.9673 | 0.5723 | |
| Average | 0.9273 | 0.9239 | 0.8696 | 0.9327 | 0.9728 | 0.6570 | |
| DCs | 2002–2003 | 0.8999 | 0.9065 | 0.9216 | 1.0122 | 1.0008 | 0.7649 |
| 2003–2004 | 0.8925 | 0.8844 | 0.9377 | 1.0121 | 0.9529 | 0.7206 | |
| 2004–2005 | 0.8702 | 0.8651 | 0.9536 | 1.0120 | 0.9709 | 0.7055 | |
| 2005–2006 | 0.8364 | 0.8437 | 0.9692 | 1.0119 | 0.9913 | 0.6855 | |
| 2006–2007 | 0.8506 | 0.8223 | 0.9859 | 1.0118 | 0.8874 | 0.6145 | |
| 2007–2008 | 0.7970 | 0.8007 | 1.0036 | 1.0117 | 1.0451 | 0.6760 | |
| 2008–2009 | 0.7803 | 0.7784 | 1.0208 | 1.0116 | 1.0738 | 0.6735 | |
| 2009–2010 | 0.7630 | 0.7579 | 1.0381 | 1.0115 | 0.9817 | 0.5956 | |
| 2010–2011 | 0.7716 | 0.7383 | 1.0560 | 1.0114 | 0.9763 | 0.5896 | |
| Average | 0.8291 | 0.8219 | 0.9874 | 1.0118 | 0.9867 | 0.6695 | |
| LDCs | 2002–2003 | 1.0896 | 1.1180 | 0.6837 | 0.8824 | 0.9366 | 0.6984 |
| 2003–2004 | 1.1223 | 1.0978 | 0.7018 | 0.8748 | 0.8038 | 0.6177 | |
| 2004–2005 | 1.0752 | 1.0758 | 0.7221 | 0.8667 | 0.9549 | 0.6896 | |
| 2005–2006 | 1.0544 | 1.0546 | 0.7348 | 0.8582 | 1.0081 | 0.6979 | |
| 2006–2007 | 1.0347 | 1.0329 | 0.7471 | 0.8492 | 0.9431 | 0.6370 | |
| 2007–2008 | 1.0117 | 1.0113 | 0.7597 | 0.8397 | 0.9866 | 0.6451 | |
| 2008–2009 | 0.9940 | 0.9908 | 0.7698 | 0.8297 | 1.0325 | 0.6540 | |
| 2009–2010 | 0.9679 | 0.9714 | 0.7777 | 0.8191 | 0.9976 | 0.5986 | |
| 2010–2011 | 0.9477 | 0.9516 | 0.7886 | 0.8079 | 0.9577 | 0.5537 | |
| Average | 1.0330 | 1.0338 | 0.7428 | 0.8475 | 0.9579 | 0.6436 |
| Decomposition | APEC | DCs | LDCs | |||
|---|---|---|---|---|---|---|
| gMMPI | gMMPI | gMMPI | ||||
| PTCU | 0.131 | *** | 0.242 | *** | 0.201 | *** |
| PTRC | 0.206 | *** | 0.634 | *** | 0.236 | *** |
| TC | −0.005 | −0.482 | *** | 0.071 | ||
| TEC | 0.287 | *** | 0.612 | *** | 0.292 | *** |
| SEC | 0.840 | *** | 0.715 | *** | 0.871 | *** |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.-C.J.; Yuan, C.-H.; Goh, M.; Lu, Y.-H. Regional Port Productivity in APEC. Sustainability 2016, 8, 689. https://doi.org/10.3390/su8070689
Wu Y-CJ, Yuan C-H, Goh M, Lu Y-H. Regional Port Productivity in APEC. Sustainability. 2016; 8(7):689. https://doi.org/10.3390/su8070689
Chicago/Turabian StyleWu, Yen-Chun Jim, Chih-Hung Yuan, M. Goh, and Yung-Hsiang Lu. 2016. "Regional Port Productivity in APEC" Sustainability 8, no. 7: 689. https://doi.org/10.3390/su8070689
APA StyleWu, Y.-C. J., Yuan, C.-H., Goh, M., & Lu, Y.-H. (2016). Regional Port Productivity in APEC. Sustainability, 8(7), 689. https://doi.org/10.3390/su8070689








