A Quantitative Method for Long-Term Water Erosion Impacts on Productivity with a Lack of Field Experiments: A Case Study in Huaihe Watershed, China
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Basic Idea and Research Framework
- Numerical simulation of the natural geography process:
- Relationship between erosion and productivity:
- Logistic fitness model:
2.3. Data
2.4. Methodology
2.4.1. APEX Water Erosion and Localization Parameters
2.4.2. Soil and Water Conservation Measure Scenarios
2.4.3. Soil Erosion and Loss of Productivity
- Productivity simulated by the APEX model:
- Loss of yield index calculation:
- Water erosion intensity calculation:
- Cumulative loss 3D surface fitting:
2.4.4. Statistical Analysis
3. Results
3.1. Productivity Simulation and Verification
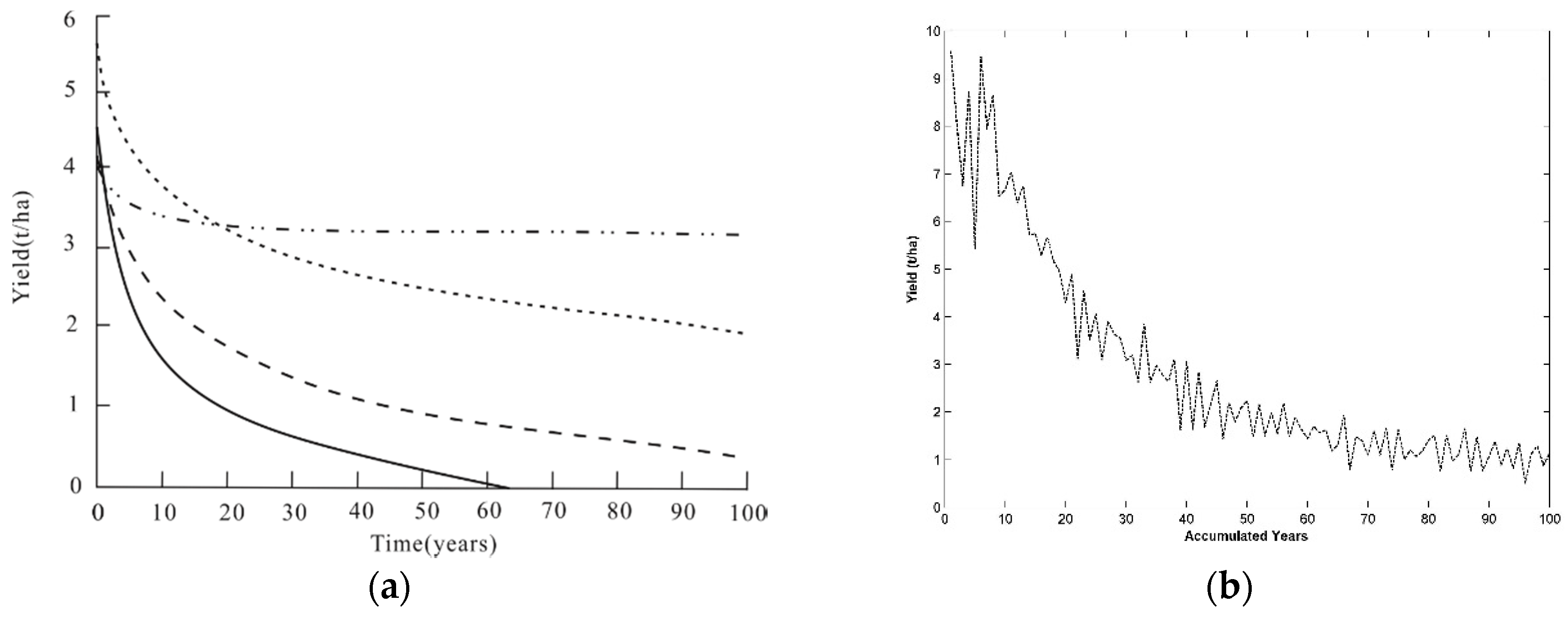
3.2. Comparison of Cumulative Loss 3D Surfaces and 2D Curves
3.3. Cumulative Loss 3D Surface from Long-Term Accumulated Water Erosion
3.4. Spatial Differences in Long-Term Water Erosion Impacts on Productivity
4. Discussion
4.1. Significance of Cumulative Loss 3D Surface
4.2. The Validation and Uncertainty of the Cumulative Loss 3D Surface
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brevik, E.; Cerdà, A.; Mataix-Solera, J.; Pereg, L.; Quinton, J.; Six, J.; Van Oost, K. The interdisciplinary nature of SOIL. Soil 2015, 1, 117. [Google Scholar] [CrossRef]
- Decock, C.; Lee, J.; Necpalova, M.; Pereira, E.; Tendall, D.; Six, J. Mitigating N2O emissions from soil: From patching leaks to transformative action. Soil 2015, 1, 687–694. [Google Scholar] [CrossRef]
- Smith, P.; Cotrufo, M.; Rumpel, C.; Paustian, K.; Kuikman, P.; Elliott, J.; McDowell, R.; Griffiths, R.; Asakawa, S.; Bustamante, M. Biogeochemical cycles and biodiversity as key drivers of ecosystem services provided by soils. Soil Discuss. 2015, 2, 537–586. [Google Scholar] [CrossRef]
- Keesstra, S.D.; Quinton, J.N.; van der Putten, W.H.; Bardgett, R.D.; Fresco, L.O. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111. [Google Scholar] [CrossRef]
- Gang, C.; Zhou, W.; Wang, Z.; Chen, Y.; Li, J.; Chen, J.; Qi, J.; Odeh, I.; Groisman, P.Y. Comparative Assessment of Grassland NPP Dynamics in Response to Climate Change in China, North America, Europe and Australia from 1981 to 2010. J. Agron. Crop Sci. 2015, 201, 57–68. [Google Scholar] [CrossRef]
- Gessesse, B.; Bewket, W.; Bräuning, A. Model-based characterization and monitoring of runoff and soil erosion in response to land use/land cover changes in the Modjo watershed, Ethiopia. Land Degrad. Dev. 2015, 26, 711–724. [Google Scholar] [CrossRef]
- Keesstra, S.; Maroulis, J.; Argaman, E.; Voogt, A.; Wittenberg, L. Effects of controlled fire on hydrology and erosion under simulated rainfall. Cuad. Investig. Geogr. 2014, 40, 269–293. [Google Scholar] [CrossRef]
- Lasanta, T.; Cerdà, A. Long-term erosional responses after fire in the Central Spanish Pyrenees: 2. Solute release. Catena 2005, 60, 81–100. [Google Scholar] [CrossRef]
- Borrelli, P.; Märker, M.; Schütt, B. Modelling Post-Tree-Harvesting Soil Erosion and Sediment Deposition Potential in the Turano River Basin (Italian Central Apennine). Land Degrad. Dev. 2015, 26, 356–366. [Google Scholar] [CrossRef]
- Ochoa-Cueva, P.; Fries, A.; Montesinos, P.; Rodríguez-Díaz, J.A.; Boll, J. Spatial Estimation of Soil Erosion Risk by Land-cover Change in the Andes OF Southern Ecuador. Land Degrad. Dev. 2015, 26, 565–573. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, K.; Dai, H.; Liang, Y. Modeling interrill erosion on unpaved roads in the loess plateau of China. Land Degrad. Dev. 2015, 26, 825–832. [Google Scholar] [CrossRef]
- Department for Environment, Food and Rural Affairs. Safeguarding Our Soils: A Strategy for England; Department for Environment, Food and Rural Affairs: London, UK, 2009; p. 48.
- Kraaijvanger, R.; Veldkamp, T. Grain productivity, fertilizer response and nutrient balance of farming systems in Tigray, Ethiopia: A multi-perspective view in relation to soil fertility degradation. Land Degrad. Dev. 2015, 26, 701–710. [Google Scholar] [CrossRef]
- Erol, A.; Koşkan, Ö.; Başaran, M. Socioeconomic modifications of the universal soil loss equation. Solid Earth 2015, 6, 1025–1035. [Google Scholar] [CrossRef]
- Musinguzi, P.; Ebanyat, P.; Tenywa, J.; Basamba, T.; Tenywa, M.; Mubiru, D. Precision of farmer-based fertility ratings and soil organic carbon for crop production on a Ferralsol. Solid Earth 2015, 6, 1063–1073. [Google Scholar] [CrossRef]
- Wu, S.H.; Zhou, S.L.; Chen, D.X.; Wei, Z.Q.; Dai, L.; Li, X.G. Determining the contributions of urbanisation and climate change to NPP variations over the last decade in the Yangtze River Delta, China. Sci. Total Environ. 2014, 472, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.M.; Chen, X.; Bao, A.M.; Luo, Y. Net Primary Productivity (NPP) of Oasis Changes in Trends in Xinjiang and Responses to Climate Change Analysis in 1981–2000. Adv. Intell. Soft Comput. 2011, 111, 417–424. [Google Scholar]
- Krausmann, F.; Haberl, H.; Schulz, N.B.; Erb, K.-H.; Darge, E.; Gaube, V. Land-use change and socio-economic metabolism in Austria—Part I: Driving forces of land-use change: 1950–1995. Land Use Policy 2003, 20, 1–20. [Google Scholar] [CrossRef]
- Haberl, H.; Fischer-Kowalski, M.; Krausmann, F.; Weisz, H.; Winiwarter, V. Progress towards sustainability? What the conceptual framework of material and energy flow accounting (MEFA) can offer. Land Use Policy 2004, 21, 199–213. [Google Scholar] [CrossRef]
- Evans, I.S. The Selection of Class Intervals. Trans. Inst. Br. Geogr. 1977, 2, 98–124. [Google Scholar] [CrossRef]
- West, P.C.; Gibbs, H.K.; Monfreda, C.; Wagner, J.; Barford, C.C.; Carpenter, S.R.; Foley, J.A. Trading carbon for food: Global comparison of carbon stocks vs. crop yields on agricultural land. Proc. Natl. Acad. Sci. USA 2010, 107, 19645–19648. [Google Scholar] [CrossRef] [PubMed]
- Tenberg, A.; Da Veiga, M.; Dechen, S.C.F.; Stocking, M.A. Modelling the impact of erosion on soil productivity: A comparative evaluation of approaches on data from southern Brazil. Exp. Agric. 1998, 34, 55–71. [Google Scholar] [CrossRef]
- Gao, X.F.; Xie, Y.; Liu, G.; Liu, B.Y.; Duan, X.W. Effects of soil erosion on soybean yield as estimated by simulating gradually eroded soil profiles. Soil Tillage Res. 2015, 145, 126–134. [Google Scholar] [CrossRef]
- Larney, F.J.; Janzen, H.H.; Olson, B.M.; Olson, A.F. Erosion-productivity-soil amendment relationships for wheat over 16 years. Soil Tillage Res. 2009, 103, 73–83. [Google Scholar] [CrossRef]
- Ray, N.; Adams, J. A GIS-based vegetation map of the world at the last glacial maximum (25,000–15,000 BP). Internet Archaeol. 2001. [Google Scholar] [CrossRef]
- Ye, L.M.; Van Ranst, E. Production scenarios and the effect of soil degradation on long-term food security in China. Glob. Environ. Chang. 2009, 19, 464–481. [Google Scholar] [CrossRef]
- Dong, W.; Sullivan, P.; Stout, K. Comprehensive study of parameters for characterising three-dimensional surface topography: III: Parameters for characterising amplitude and some functional properties. Wear 1994, 178, 29–43. [Google Scholar] [CrossRef]
- Yin, Y.; Zhang, X.; Lin, D.; Yu, H.; Shi, P. GEPIC-VR model: A GIS-based tool for regional crop drought risk assessment. Agric. Water Manag. 2014, 144, 107–119. [Google Scholar] [CrossRef]
- Gao, C.; Gemmer, M.; Zeng, X.; Liu, B.; Su, B.; Wen, Y. Projected streamflow in the Huaihe River Basin (2010–2100) using artificial neural network. Stoch. Environ. Res. Risk Assess. 2010, 24, 685–697. [Google Scholar] [CrossRef]
- Yin, L.; Wang, X.; Pan, J.; Gassman, P. Evaluation of APEX for daily runoff and sediment yield from three plots in the Middle Huaihe River Watershed, China. Trans. ASABE 2009, 52, 1833–1845. [Google Scholar] [CrossRef]
- Mitchell, G.; Griggs, R.; Benson, V.; Williams, J. The EPIC Model: Environmental Policy Integrated Climate; Texas Agricultural Experiment Station: Temple, TX, USA, 1998. [Google Scholar]
- Steglich, E.; Williams, J. Agricultural Policy Environmental Extender Model-User’s Manual Version 0806; Blackland Research and Extension Center: Temple, TX, USA, 2013; pp. 1–228. [Google Scholar]
- Lehner, B.; Verdin, K.; Jarvis, A. HydroSHEDS Technical Documentation, version 1.0; World Wildlife Fund US: Washington, DC, USA, 2006; pp. 1–27. [Google Scholar]
- Gassman, P.W.; Williams, J.R.; Wang, X.; Saleh, A.; Osei, E.; Hauck, L.; Izaurralde, C.; Flowers, J. The Agricultural Policy Environmental Extender (APEX) Model: An Emerging Tool for Landscape and Watershed Environmental Analyses; Center for Agricultural and Rural Development (CARD) Publications: Ames, IA, USA, 2009. [Google Scholar]
- Sharpley, A.N.; Williams, J.R. EPIC-Erosion/Productivity Impact Calculator: 1. Model Documentation; United States Department of Agriculture: Washington, DC, USA, 1990.
- Gassman, P.W.; Williams, J.R.; Benson, V.W.; Izaurralde, R.C.; Hauck, L.M.; Jones, C.A.; Atwood, J.D.; Kiniry, J.R.; Flowers, J.D. Historical development and applications of the EPIC and APEX models. In Proceedings of the 2004 ASAE Annual Meeting, Ottawa, ON, Canada, 1–4 August 2004.
- Gruen, A.; Akca, D. Least squares 3D surface and curve matching. ISPRS J. Photogramm. Remote Sens. 2005, 59, 151–174. [Google Scholar] [CrossRef]
- IUCN. UNEP-WCMC, the World Database on Protected Areas (WDPA); UNEP-WCMC: Cambridge, UK, 2015. [Google Scholar]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011. [Google Scholar] [CrossRef]
- Miliaresis, G.C.; Argialas, D. Segmentation of physiographic features from the global digital elevation model/GTOPO30. Comput. Geosci. 1999, 25, 715–728. [Google Scholar] [CrossRef]
- IIASA, FAO. Global Agro-Ecological Zones-Model Documentation (GAEZ v. 3.0); International Institute of Applied Systems Analysis & Food and Agricultural Organization: Laxenburg, Austria; Rome, Italy, 2012. [Google Scholar]
- Batjes, N. ISRIC-WISE Derived Soil Properties on a 5 by 5 Arc-Minutes Global Grid. Version 1.2. Available online: http://www.isric.org/data/isric-wise-derived-soil-properties-5-5-arc-minutes-global-grid-version-12 (accessed on 12 July 2016).
- Warszawski, L.; Frieler, K.; Huber, V.; Piontek, F.; Serdeczny, O.; Schewe, J. The inter-sectoral impact model intercomparison project (ISI–MIP): Project framework. Proc. Natl. Acad. Sci. USA 2014, 111, 3228–3232. [Google Scholar] [CrossRef] [PubMed]
- Vitousek, P.M.; Mooney, H.A.; Lubchenco, J.; Melillo, J.M. Human domination of Earth’s ecosystems. Science 1997, 277, 494–499. [Google Scholar] [CrossRef]
- Sacks, W.J.; Deryng, D.; Foley, J.A.; Ramankutty, N. Crop planting dates: An analysis of global patterns. Glob. Ecol. Biogeogr. 2010, 19, 607–620. [Google Scholar] [CrossRef]
- China Meteorological Administration. China’s Crop Growth and Soil Moisture Late Value Farmland Collection Data. Available online: http://data.cma.cn/data/detail/dataCode/AGME_AB2_CHN_TEN.html (acessed on 14 June 2016).
- Tan, G.; Shibasaki, R. Global estimation of crop productivity and the impacts of global warming by GIS and EPIC integration. Ecol. Model. 2003, 168, 357–370. [Google Scholar] [CrossRef]
- Mueller, N.D.; Gerber, J.S.; Johnston, M.; Ray, D.K.; Ramankutty, N.; Foley, J.A. Closing yield gaps through nutrient and water management. Nature 2012, 490, 254–257. [Google Scholar] [CrossRef] [PubMed]
- Rogelj, J.; den Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 2016, 534, 631–639. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.R.; Izaurralde, R. The APEX model. In Watershed Models; Vijay, P., Donald, K., Eds.; CRC Press: Boca Raton, FL, USA, 2006; pp. 437–482. Available online: https://books.google.co.jp/books?hl=zh-CN&lr=&id=mn8Foj3rAwQC&oi=fnd&pg=PA437&dq=The+APEX+model&ots=o9SMI-FNoz&sig=7D_S58VoOklYkMnuNHvZ7qMsutc#v=onepage&q=The%20APEX%20model&f=false (accessed on 14 June 2016).
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning. Available online: http://naldc.nal.usda.gov/download/CAT79706928/PDF (accessed on 12 July 2016).
- Onstad, C.; Foster, G. Erosion modeling on a watershed (Soil). Trans. ASAE 1975, 18, 288–292. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.; Weesies, G.; McCool, D.; Yoder, D. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); United States Department of Agriculture: Washington, DC, USA, 1997; Volume 703.
- Williams, J.R.; Izaurralde, R.C.; Steglich, E.M. Agricultural Policy/Environmental Extender Model; Theoretical Documentation, Version 0806; Blackland Research and Extension Center: Temple, TX, USA, 2008. [Google Scholar]
- Stoorvogel, J.; Smaling, E.A.; Janssen, B. Calculating soil nutrient balances in Africa at different scales. Fertil. Res. 1993, 35, 227–235. [Google Scholar] [CrossRef]
- Sparovek, G.; Schnug, E. Temporal erosion-induced soil degradation and yield loss. Soil Sci. Soc. Am. J. 2001, 65, 1479–1486. [Google Scholar] [CrossRef]
- Lal, R. Soil erosion and the global carbon budget. Environ. Int. 2003, 29, 437–450. [Google Scholar] [CrossRef]
- Zimmerman, D.W. Teacher’s corner: A note on interpretation of the paired-samples t test. J. Educ. Behav. Stat. 1997, 22, 349–360. [Google Scholar] [CrossRef]
- Lee, G.; Bae, J.W.; Oh, N.; Hong, J.H.; Moon, I.-C. Simulation experiment of disaster response organizational structures with alternative optimization techniques. Soc. Sci. Comput. Rev. 2014. [Google Scholar] [CrossRef]
- Norušis, M.J. IBM SPSS Statistics 19 Guide to Data Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 2011. [Google Scholar]
- Kent State University. SPSS Tutorials Paired Samples t Test. Available online: http://libguides.library.kent.edu/SPSS/PairedSamplestTest (accessed on 12 July 2016).
- De la Rosa, D.; Moreno, J.; Mayol, F.; Bonson, T. Assessment of soil erosion vulnerability in western Europe and potential impact on crop productivity due to loss of soil depth using the ImpelERO model. Agric. Ecosyst. Environ. 2000, 81, 179–190. [Google Scholar] [CrossRef]
- EEA. Environment in the European Union at the Turn of the Century; Office des Publications, European Environment Agency: Luxembourg City, Luxembourg, 1999. [Google Scholar]
- Zhou, K.Q.; Sui, Y.Y.; Liu, X.B.; Zhang, X.Y.; Jin, J.; Wang, G.H.; Herbert, S.J. Crop rotation with nine-year continuous cattle manure addition restores farmland productivity of artificially eroded Mollisols in Northeast China. Field Crops Res. 2015, 171, 138–145. [Google Scholar] [CrossRef]
- Novara, A.; Gristina, L.; Saladino, S.; Santoro, A.; Cerdà, A. Soil erosion assessment on tillage and alternative soil managements in a Sicilian vineyard. Soil Tillage Res. 2011, 117, 140–147. [Google Scholar] [CrossRef]
- Cerdà, A.; González-Pelayo, Ó.; Giménez-Morera, A.; Jordán, A.; Pereira, P.; Novara, A.; Brevik, E.C.; Prosdocimi, M.; Mahmoodabadi, M.; Keesstra, S. Use of barley straw residues to avoid high erosion and runoff rates on persimmon plantations in Eastern Spain under low frequency–high magnitude simulated rainfall events. Soil Res. 2016, 54, 154–165. [Google Scholar] [CrossRef]
- Prosdocimi, M.; Jordán, A.; Tarolli, P.; Keesstra, S.; Novara, A.; Cerdà, A. The immediate effectiveness of barley straw mulch in reducing soil erodibility and surface runoff generation in Mediterranean vineyards. Sci. Total Environ. 2016, 547, 323–330. [Google Scholar] [CrossRef] [PubMed]
- García-Díaz, A.; Allas, R.B.; Gristina, L.; Cerdà, A.; Pereira, P.; Novara, A. Carbon input threshold for soil carbon budget optimization in eroding vineyards. Geoderma 2016, 271, 144–149. [Google Scholar] [CrossRef]
- Yazdanpanah, N.; Mahmoodabadi, M.; Cerdà, A. The impact of organic amendments on soil hydrology, structure and microbial respiration in semiarid lands. Geoderma 2016, 266, 58–65. [Google Scholar] [CrossRef]
- Keesstra, S.; Pereira, P.; Novara, A.; Brevik, E.C.; Azorin-Molina, C.; Parras-Alcántara, L.; Jordán, A.; Cerdà, A. Effects of soil management techniques on soil water erosion in apricot orchards. Sci. Total Environ. 2016, 551, 357–366. [Google Scholar] [CrossRef] [PubMed]
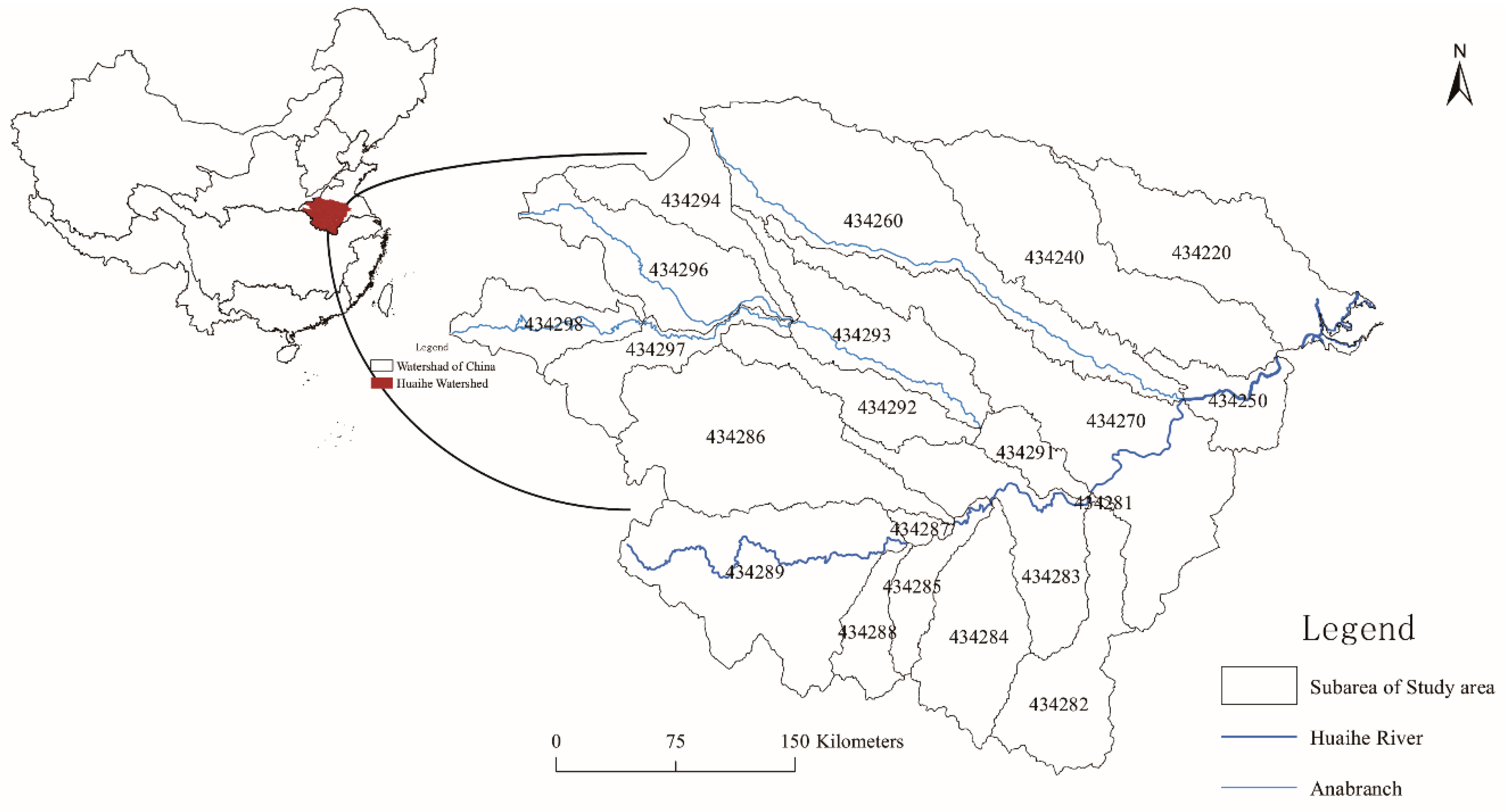
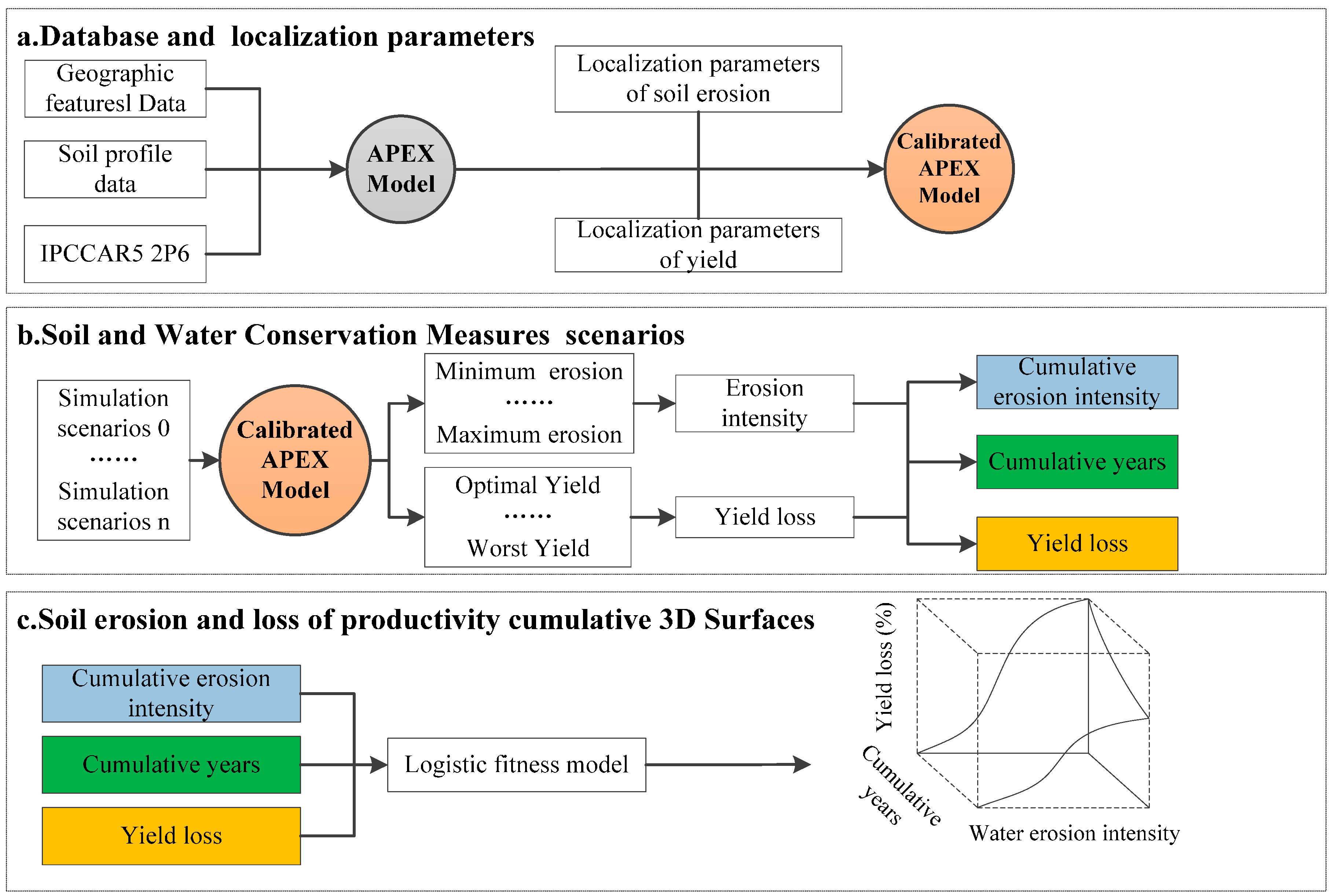
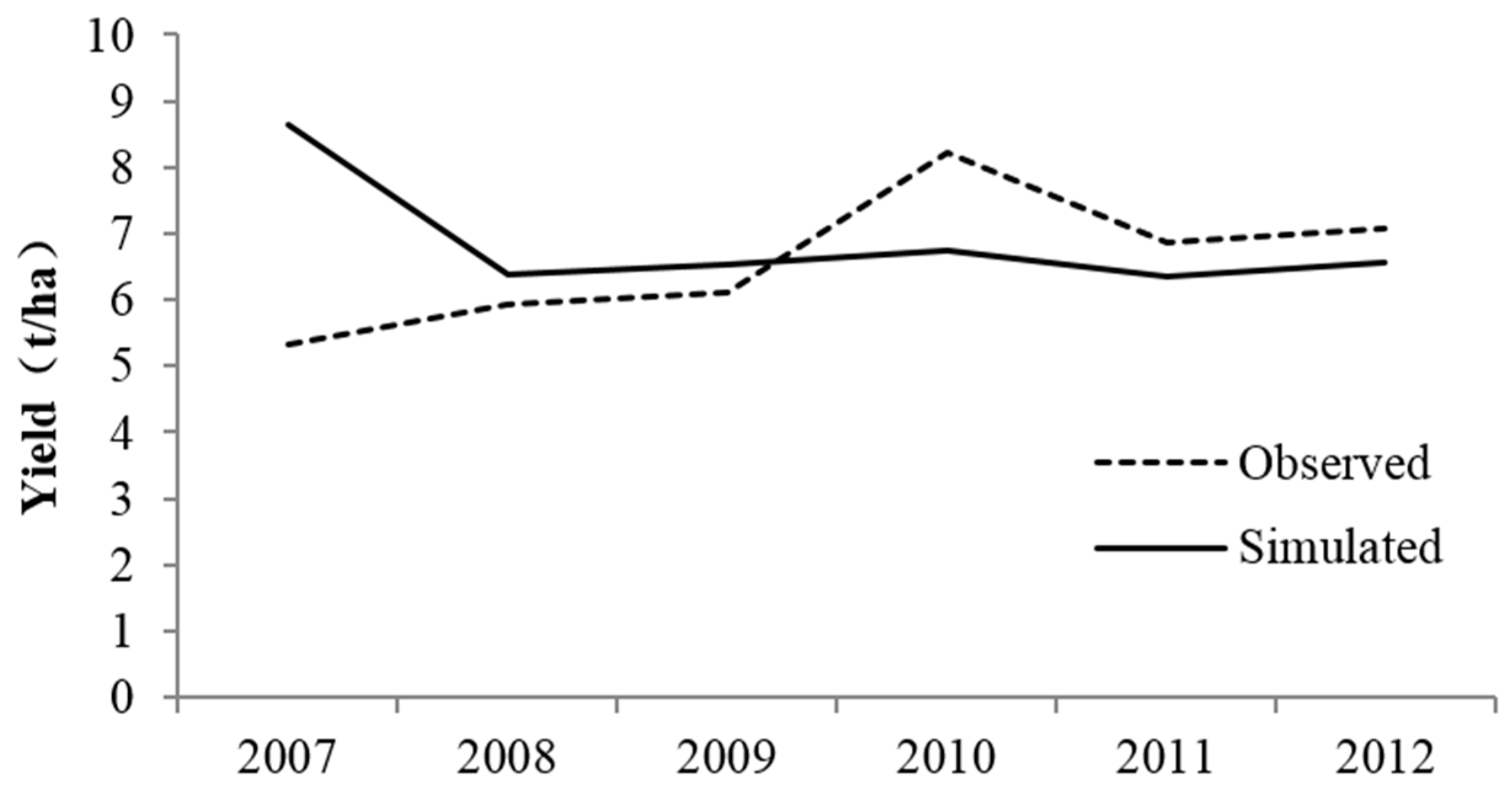
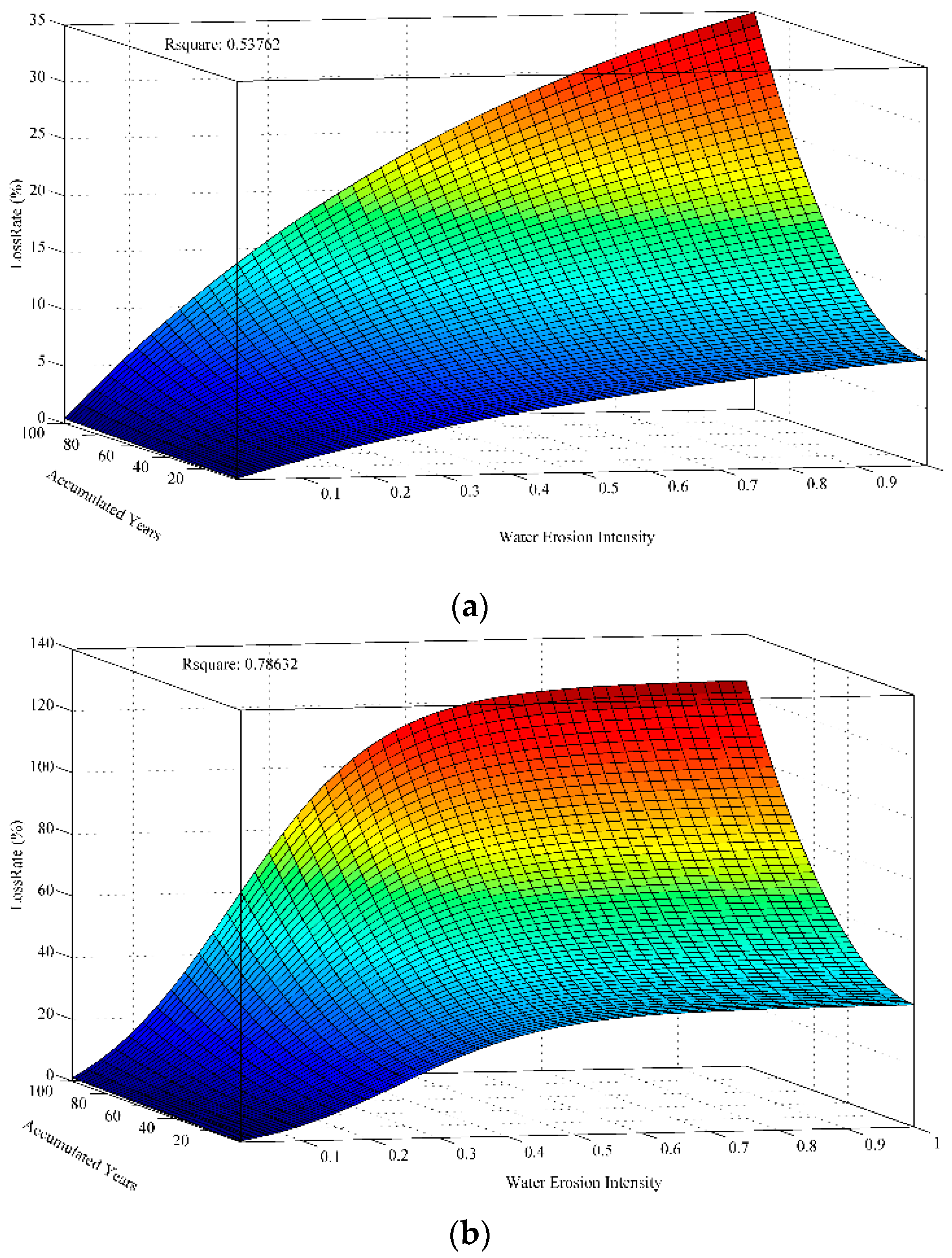
| Data Name | Data Content | Spatial Resolution | Temporal Resolution | Data Sources and url |
|---|---|---|---|---|
| DEM | Global elevation | 0.00833° × 0.00833° | 1997 | USGS [41], ftp://edcftp.cr.usgs.gov/data/gtopo30/global/ |
| Slope | Global slope | 0.0833° × 0.0833° | 1997 | GAEZ [42], http://www.gaez.iiasa.ac.at/ |
| Soil Properties | Global soil distribution raster image and physical and chemical characteristics, such as: pH, soil depth and other information | 0.0833° × 0.0833° | 1995 | ISRIC, http://www.isric.org/data/isric-wise-derived-soil-properties-5-5-arc-minutes-global-grid-version-12 [43] |
| Meteorological | Global precipitation, temperature, solar radiation and other information | 0.5° × 0.5° | 1971–2099 | Inter-Sectoral Impact Model Intercomparison Project RCP2.6 [44], http://pcmdi9.llnl.gov/ |
| Planting Area | Global cultivation crop region | 0.0833° × 0.0833° | 1992 | Sustainability and the Global Environment, University of Wisconsin-Madison [45], http://nelson.wisc.edu/sage/data-and-models/1992-croplands/index.php |
| Growth Period | Planting time and growth period length | 0.0833° × 0.0833° | 2000–2015 | Nelson Institute for Environmental Studies at the University of Wisconsin-Madison [46], http://nelson.wisc.edu/sage/data-and-models/crop-calendar-dataset/index.php; China’s crop growth and soil moisture late value farmland collection data [47], http://data.cma.cn/data/detail/dataCode/AGME_AB2_CHN_TEN.html |
| Irrigation | Global annual irrigation water of agriculture(mm) | 0.5° × 0.5° | 1995 | Institute of Industrial Science, University of Tokyo [48], http://hydro.iis.u-tokyo.ac.jp/GW/result/global/annual/withdrawal/index.html |
| Fertilizer | Global annual fertilizer application for maize | 0.0833° × 0.0833° | 2012 | Earth stat [49], http://www.earthstat.org/data-download/ |
| River basin unit | Global hydrological data | Vector unit | 2010 | HydroSHEDS [33], http://hydrosheds.cr.usgs.gov/index.php |
| Basin Number | Slope (°) | Elevation (m) | Basin Area (ha) | Farming Area (ha) | Soil ID * | Irrigation (mm) |
|---|---|---|---|---|---|---|
| 434220 | 2 | 30 | 936,950 | 5380 | 4339 | 15 |
| 434240 | 2 | 34 | 1,314,620 | 5296 | 4339 | 68 |
| 434250 | 5 | 25 | 312,450 | 3264 | 4329 | 614 |
| 434260 | 2 | 43 | 1,526,660 | 6302 | 4319 | 68 |
| 434270 | 2 | 28 | 1,662,910 | 8386 | 4326 | 83 |
| 434283 | 2 | 23 | 712,520 | 6811 | 4326 | 97 |
| 434282 | 30 | 31 | 672,040 | 10 | 3085 | 0 |
| 434284 | 16 | 56 | 678,050 | 6880 | 3085 | 8 |
| 434285 | 5 | 59 | 240,920 | 550 | 4326 | 1220 |
| 434291 | 2 | 27 | 200,540 | 4115 | 4339 | 310 |
| 434293 | 2 | 52 | 633,070 | 6949 | 4319 | 51 |
| 434292 | 2 | 46 | 406,800 | 4819 | 4319 | 189 |
| 434286 | 2 | 43 | 1,313,270 | 8133 | 4319 | 11 |
| 434287 | 2 | 27 | 56,680 | 4924 | 4326 | 86 |
| 434288 | 5 | 50 | 233,960 | 695 | 4326 | 86 |
| 434289 | 2 | 45 | 1,309,830 | 4966 | 4326 | 48 |
| 434294 | 2 | 88 | 607,860 | 5692 | 4319 | 113 |
| 434297 | 2 | 71 | 388,330 | 2185 | 4319 | 33 |
| 434296 | 2 | 53 | 694,240 | 1450 | 4319 | 2 |
| 434298 | 8 | 52 | 357,500 | 941 | 3085 | 0 |
| 434281 | 5 | 23 | 6830 | 10 | 4326 | 0 |
| Property | Soil Layer | Depth (m) | Bulk Density (Mg·m−3) | Soil Water Content at Field Capacity (mm−1) | Sand (%) | Silt (%) | Soil pH | Organic Carbon (%) | Cation Exchange Capacity (cmol/kg) | Coarse Fragment (%) | Electrical Conductivity (mmho/cm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil ID | ||||||||||||
| 4339 | 1 | 0.2 | 1.35 | 0.17 | 27 | 36 | 6.36 | 24.16 | 28.4 | 4 | 0 | |
| 2 | 0.4 | 1.34 | 0.16 | 29 | 33 | 6.61 | 13.97 | 24.5 | 6 | 0.33 | ||
| 3 | 0.6 | 1.38 | 0.17 | 29 | 33 | 6.73 | 7.06 | 23.8 | 9 | 0.41 | ||
| 4 | 0.8 | 1.38 | 0.19 | 31 | 32 | 6.95 | 4.95 | 21.94 | 10 | 0.51 | ||
| 5 | 1 | 1.39 | 0.19 | 34 | 31 | 7.13 | 3.98 | 19.97 | 9 | 0.38 | ||
| 4329 | 1 | 0.2 | 1.24 | 0.21 | 37 | 34 | 6.02 | 13.12 | 16.09 | 8 | 0 | |
| 2 | 0.4 | 1.37 | 0.16 | 36 | 31 | 6.15 | 5.71 | 15.14 | 11 | 0 | ||
| 3 | 0.6 | 1.4 | 0.15 | 36 | 30 | 6.28 | 4.01 | 14.47 | 14 | 0 | ||
| 4 | 0.8 | 1.43 | 0.15 | 37 | 29 | 6.38 | 3.02 | 14.56 | 16 | 0 | ||
| 5 | 1 | 1.46 | 0.16 | 36 | 29 | 6.48 | 2.79 | 15.18 | 18 | 0 | ||
| 4326 | 1 | 0.2 | 1.24 | 0.21 | 37 | 34 | 6.02 | 13.12 | 16.09 | 8 | 0 | |
| 2 | 0.4 | 1.37 | 0.16 | 36 | 31 | 6.15 | 5.71 | 15.14 | 11 | 0 | ||
| 3 | 0.6 | 1.4 | 0.15 | 36 | 30 | 6.28 | 4.01 | 14.47 | 14 | 0 | ||
| 4 | 0.8 | 1.43 | 0.15 | 37 | 29 | 6.38 | 3.02 | 14.56 | 16 | 0 | ||
| 5 | 1 | 1.46 | 0.16 | 36 | 29 | 6.48 | 2.79 | 15.18 | 18 | 0 | ||
| 4319 | 1 | 0.2 | 1.27 | 0.19 | 35 | 27 | 7.29 | 9.23 | 21.11 | 7 | 1.07 | |
| 2 | 0.4 | 1.55 | 0.16 | 33 | 29 | 7.66 | 4.97 | 16.72 | 9 | 1.84 | ||
| 3 | 0.6 | 1.57 | 0.16 | 39 | 26 | 8.01 | 3.16 | 14.58 | 10 | 1.7 | ||
| 4 | 0.8 | 1.61 | 0.16 | 38 | 25 | 8.06 | 2.16 | 15.75 | 12 | 2.8 | ||
| 5 | 1 | 1.43 | 0.16 | 41 | 24 | 8.31 | 1.91 | 13.51 | 13 | 2.73 | ||
| 3085 | 1 | 0.1 | 1.34 | 0.12 | 47 | 30 | 7.01 | 20.88 | 16.28 | 24 | 1.74 | |
| Mean | N | Standard Deviation | Standard Error Mean | |
|---|---|---|---|---|
| R-square of 3D Surfaces | 0.772 | 21 | 0.078 | 0.017 |
| R-square of 2D Curves | 0.284 | 21 | 0.145 | 0.032 |
| Paired Differences | t | df | Significance (2-Tailed) | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | |||||
| Lower | Upper | |||||||
| R-square of Surface and R-square of Curve | 0.488 | 0.162 | 0.035 | 0.414 | 0.562 | 13.813 | 20 | 0.000 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, D.; Guo, H.; Lian, F.; Gao, Y.; Yue, Y.; Wang, J. A Quantitative Method for Long-Term Water Erosion Impacts on Productivity with a Lack of Field Experiments: A Case Study in Huaihe Watershed, China. Sustainability 2016, 8, 675. https://doi.org/10.3390/su8070675
Lin D, Guo H, Lian F, Gao Y, Yue Y, Wang J. A Quantitative Method for Long-Term Water Erosion Impacts on Productivity with a Lack of Field Experiments: A Case Study in Huaihe Watershed, China. Sustainability. 2016; 8(7):675. https://doi.org/10.3390/su8070675
Chicago/Turabian StyleLin, Degen, Hao Guo, Fang Lian, Yuan Gao, Yaojie Yue, and Jing’ai Wang. 2016. "A Quantitative Method for Long-Term Water Erosion Impacts on Productivity with a Lack of Field Experiments: A Case Study in Huaihe Watershed, China" Sustainability 8, no. 7: 675. https://doi.org/10.3390/su8070675
APA StyleLin, D., Guo, H., Lian, F., Gao, Y., Yue, Y., & Wang, J. (2016). A Quantitative Method for Long-Term Water Erosion Impacts on Productivity with a Lack of Field Experiments: A Case Study in Huaihe Watershed, China. Sustainability, 8(7), 675. https://doi.org/10.3390/su8070675






