1. Introduction
In the past three decades, the cities in developing countries have experienced a rapid increase in the rate of the population growth. According to the world urbanization prospects 2014 revision, the trend in urbanization recently has been focusing on the population transition between urban and rural [
1]. Developing land for an urbanization and migration of people from rural areas is a global phenomenon. The statistical report endorses that about 53 percent of the population live in urban areas in 2015. About 77 percent of those people living in urban areas come from developed countries and 48 percent come from developing countries [
2]. This change in urban population is continuously increasing year by year. By 2035, the world’s population living in urban areas will reach 5000 million, principally in African and Asian countries [
3]. This situation will result in land use, economic, and environmental deterioration problems if each country does not have a suitable approach for better urban planning.
Bangkok Metropolis (BM) is one of the largest primary cities in Southeast Asia [
4]. BM has expanded rapidly in both size and population since the 1960s. Local organizations have tried to improve the management to keep up with the changes; however, it fails to stop the growth. The issue of the primacy of the city of Bangkok is even more pronounced. The main cause is that BM has defined roles in the National Social and Economic Development Plan (NESDP) virtually in every issue for the prosperity of the country in all forms [
5]. It is the administrative center of the country, as well as the center of investment in real estate development, various business services, and industrial center. This results in the expansion of the built-up area in its vicinity and the characteristics of a metropolitan region have become more noticeable.
There is a policy to develop major and minor cities in each region of the NESDP to decentralize BM. In contrast, the NESDP continues to promote the development of the metropolitan region that combines BM and five surrounding provinces called Bangkok Metropolitan Region (BMR). The metropolitan role of the BM focuses on supporting the diversification of production and serves as a residential area to prevent the evacuation of the population. The urbanization pattern in the BMR was initially found along the Chao Phraya River and then expanded itself along the transportation network and centers of minor cities. Nowadays, the major transportation network plays as an important factor in extending the urban areas [
6].
Presently, land use and land cover (LULC) analysis has been extensively used to monitor urban expansion forms in specific space and time. Many satellite images have been used by scientists to comprehend the spatial-temporal evolution of an urban area [
7]. However, they could not account the need for prediction of future LULC without an incorporation of land use models [
8,
9]. These models are powerful techniques that can support the policy making and future land demand evaluation, and simulate the spatial pattern of the land use based on the driving factors [
10]. The LULC simulation models in an urban study are developed from the theories of urban morphology and dynamic process of LULC to forecast the urban expansion in different patterns and scales [
11,
12]. Those models can be categorized into four types: (i) empirical and statistical models such as Markov Chain (MC), logistic regression, etc. [
13,
14]; (ii) dynamic models such as cellular automata (CA), agent-based model (AGB), genetic algorithm (GA), artificial neural network (ANN), system dynamic (SD), etc. [
15,
16,
17,
18,
19,
20,
21]; (iii) integrated models such as conversion of land use and its effects at small regional extent (CLUE-S) and Dyna-CLUE [
22]; and (iv) hybrid models, like Metronamica, land transformation model (LTM), land change modeling (LCM), SLUETH, etc. [
23,
24,
25,
26,
27,
28,
29]. They are composed of the affirmation models, which consider the past changes in the calibration step, and a sigmoidal pattern of the goodness of fit in the change potential function [
30,
31,
32].
To understand the urban expansion phenomena and LULC in BMR, this current study tries to address the complex phenomenon of the urban context by integrating physical, demographic, and economic data into the LULC model to calibrate and simulate the future land use change from the base year 2014. This study also employs a multi-criteria evaluation and multilayer perception to determine the driver factors from the CA-MC and LCM, respectively. Moreover, the projected population and economic growth rates are applied to compute the transition probability by extrapolation, MC, and SD to simulate the urban LULC in 2035.
2. Study Area
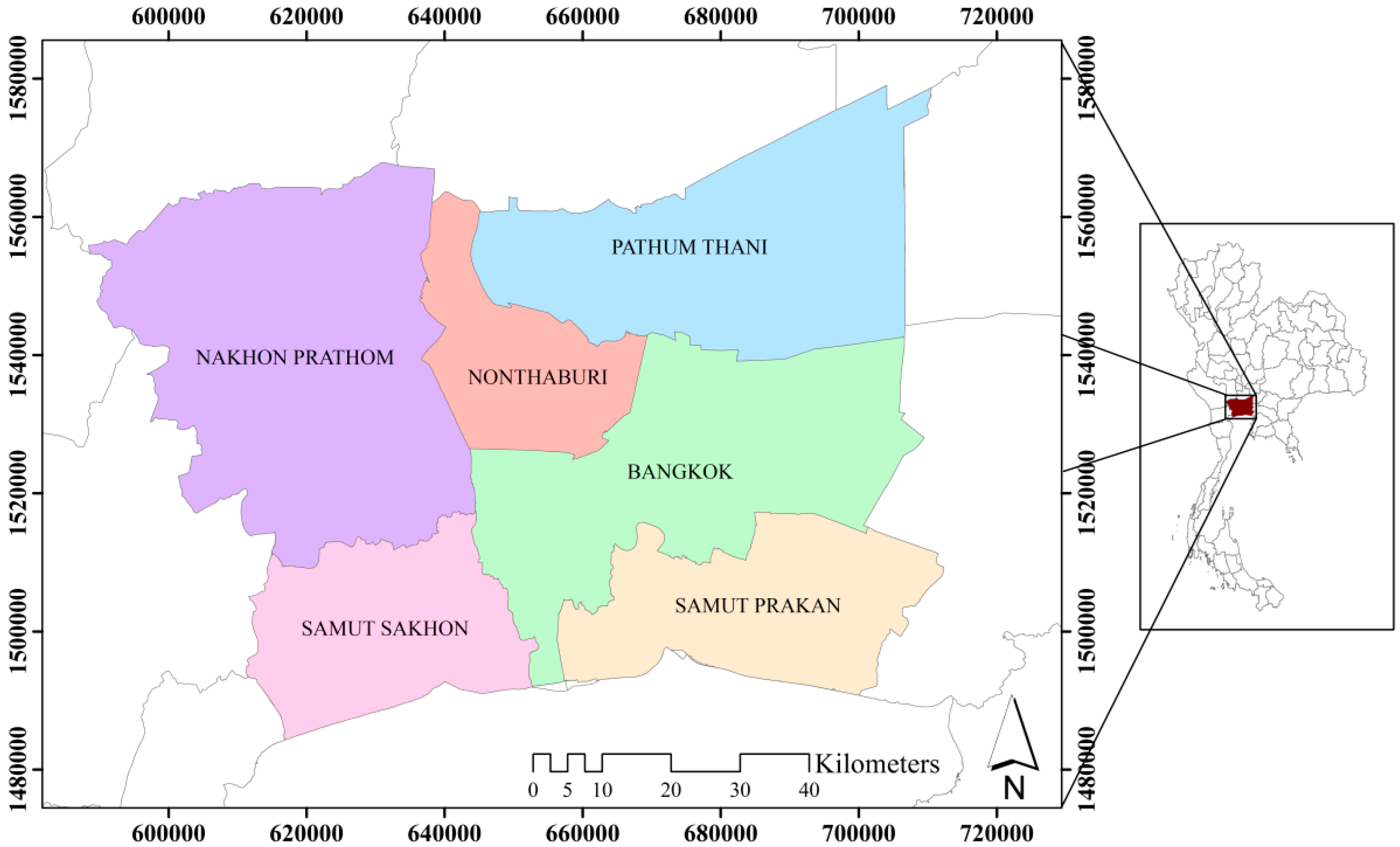
BMR is known as the biggest urban agglomeration in Thailand. It consists of BM and five bordering provinces, Nakhon Pathom, Pathum Thani, Nonthaburi, Samut Prakan and Samut Sakhon, which are located in the lower part of Chao Phaya Delta. The total area covers about 7762.00 km
2 (
Figure 1) [
33].
The registered population in the BMR is about 11 million in 2014. More than half of the population lives in BM with the population density of 5258 people per km
2. Samut Prakan is the second most populous province and it is also a Southeast Asian air transportation hub. The third province is Nonthaburi, which plays an important role as the government center and the major residential zone of the region. Pathum Thani is the center for education and research centers for science and technology as well as industrial and residential zones supporting the population in the Northern part. The other two provinces, Nakhon Pathom and Samut Sakhon, are the least populated. Both cities have a role in supporting the settlement of the population in the East as well as a space for agricultural activities and fishing [
34]. Approximately 75 percent of the land in BMR is utilized for agriculture. The second largest LU is urban and built-up area, accounting for approximately 20 percent. The other LUs are water, miscellaneous, and forest, sequentially. In the case of economics, BMR has a major role in driving the Gross Domestic Product (GDP) of Thailand because it is the center of economic activities. Around 97 percent of Gross Regional Product (GRP) in BMR comes from non-agriculture sections, which BM serves as the primary source [
35].
3. Data and Methodology
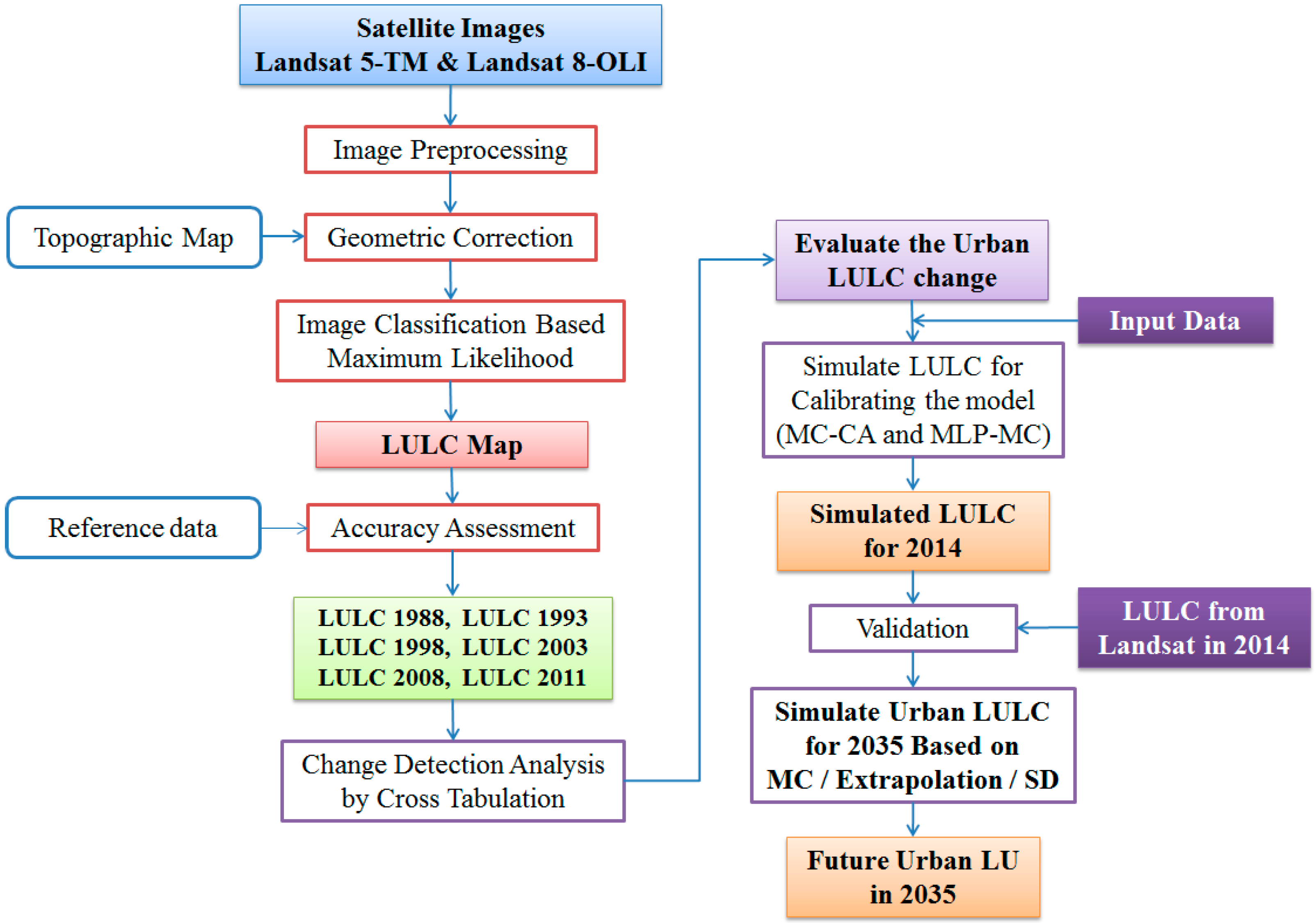
In order to simulate the future urban LULC of BMR, this study implemented four major processes. The first process was the extraction of LULC data from the satellite images for several years. The second process was that of data input preparation for urban LULC modeling. This was the most important step to prepare the data set for each simulation period. In the third process, an analysis of the urban LULC change was taken into account to identify the major classes that had changed in each specific period. The last process was to model the urban LULC change using IDRISI Selva software packet version 17 developed by Clark Labs, Clark University [
36]. The details of these four processes are explained in the following sections, and the overall operation of the methodology is shown in
Figure 2.
3.1. Preparation of Satellite Image and LULC Classification
Extracting LULC information from the satellite images is one of the most important processes in data preparation. Multiple dates of the Landsat data, acquired from the U.S. Geological Survey (USGS) via the USGS Global Visualization Viewer site, were utilized in this study. The five periods of satellite images were generated using the Landsat 5-TM images in November of 1998, 2003, 2008, and 2011 and by Landsat 8-OLI image for 2014 of path/row 129/50 and 129/51. After the mosaic process, a coupler of image in the same year applied a geometric correction and re-projection into a common UTM zone 47 North. The first 2014 Landsat image was geo-reference using topographic map from the Royal Thai Survey Department (RTSD). Then the other images were corrected through an image-to-image rectification method based on the corrected 2014 image. The total root mean square error (RMSE) of each image was assessed to confirm the geometric error, which was less than one pixel. Furthermore, the Landsat images were classified into five classes by the maximum likelihood classification. This method applies the Bayesian theory [
37] to categorize the image data into the interested LULC map. The sets of training data were used to predict the probability of each pixel being classified in each class. Moreover, an accuracy assessment was applied to confirm the quality of the resulted LULC maps by the overall accuracy and Kappa coefficient. The reference data to be used in this process were very high resolution images of IKONOS and QuickBird, Landsat RGB, and ground truth data provided by Land Development Department (LDD) or gathered directly from the field survey. All classified results have an overall accuracy greater than 80% and also a kappa value is higher than 0.8, which shows perfective agreement.
3.2. Data Input for the Urban LULC Modeling
The affirmation satellite data pre-processing was an important step to extract the LULC in each year of study. To model the urban LULC, however, there were many input data to collect, such as demographic, economic data, and other geo-database of physical and environment related to urban features including topography, transportation network, stream, and administrative boundary. These data were created and stored in different formats and scaled according to the data owner. The details of the input data are shown in
Table 1.
Demographic data at the sub-district level and economic data at the provincial level were converted through rasterization, performed using ArcGIS 10.3 (ESRI, Redlands, CA, USA), to produce the raster input maps. Some distance maps were generated such as distance to river, transportation network, agriculture, build-up, forest, and miscellaneous to use in the data analysis step. Finally, all raster inputs were resized into 100-meter resolution.
3.3. Change Analysis
To investigate the changes in an urban area, change analysis is an important process to identify the areas that have changed between the two time periods of interest. Change analysis is based on the historical changes that can be assessed between time 1 and time 2 of the LULC maps. The changes identified are transitions from one LULC state to another within the specific time period. It is likely that with many LULC classes the potential combination of transitions can be complex. In this study, a cross-tabulation analysis from the differential times was applied to determine the LULC change over five periods: 1988–1993, 1993–1998, 1998–2003, 2003–2008, and 2008–2011.
3.4. Urban LULC Modeling
In this section, the study utilized the LULC model to quantify the urban and future LULC changes as shown in
Figure 3. On the whole, the analysis workflow is the following: (i) Cellular Automata-Markov Chain; (ii) Multi-Layer Perceptron-Markov Chain; (iii) Model validation; and (iv) Model application. The details of each part are described in the following subsections.
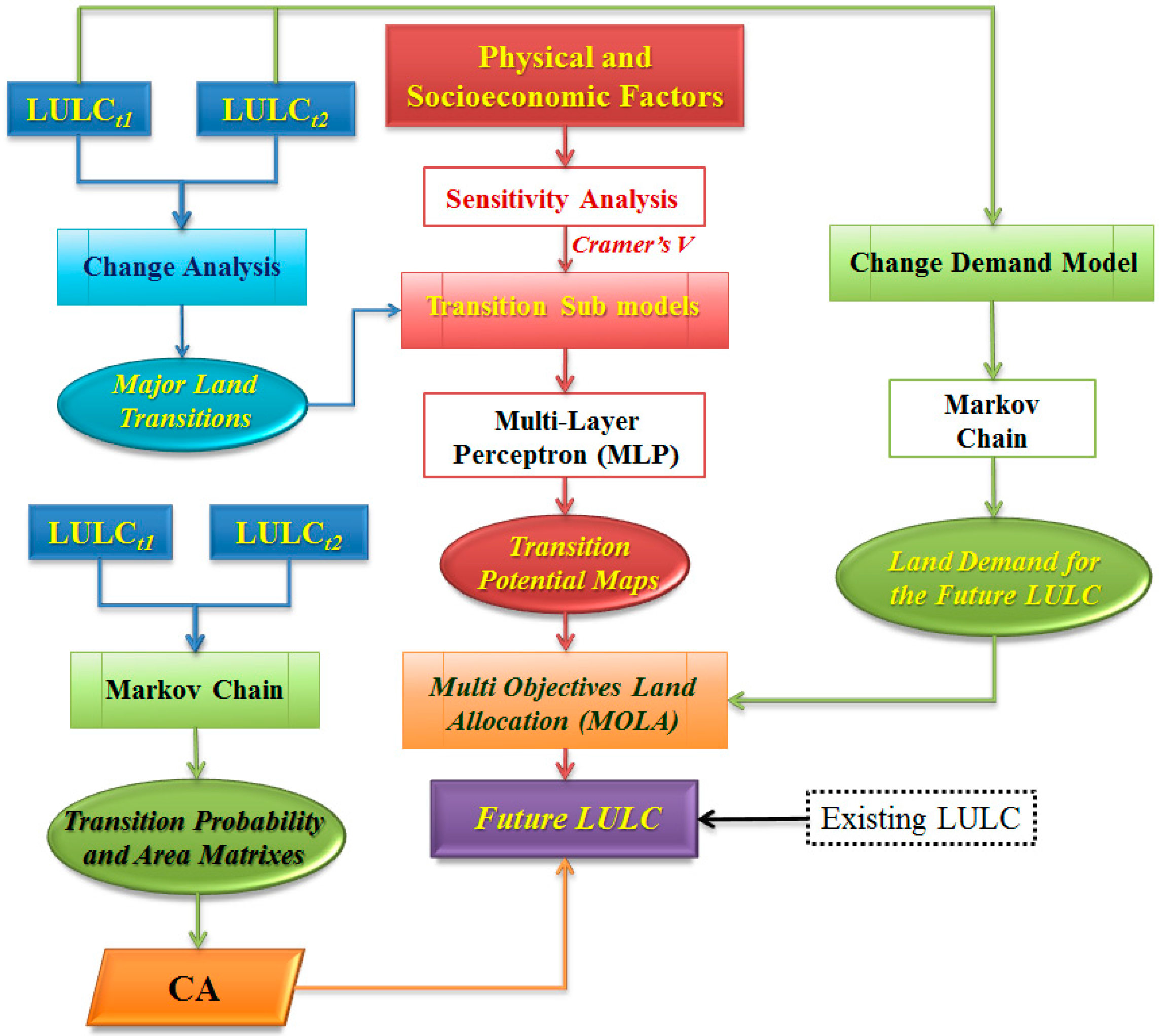
3.4.1. Cellular Automata-Markov Chain (CA-MC)
It is a combination of a sophisticated method between cellular automata (CA) and Markov chain (MC). Firstly, CA is a discrete model from disciplines of physics and biology [
38]. It adopts a natural adaptation from the John Conway’s Game of Life [
36] to simulate and understand a complex behavior [
39]. The CA consists of four important elements: (i) a grid cell, which is a spatial unit in a finite cellular space; (ii) the state, each cell also has an individual state in the system; (iii) a neighborhood, which is a set of surrounding cells in the grid system; and (iv) a transition rule, which applies a change to the cell state based on specific properties of the cell and its neighborhood. Secondly, MC is a stochastic process and widely useful technique in examining LULC changes [
40]. MC uses the knowledge based probability to predict the entire state of a given time (t2) from an earlier time (t1) without historical consideration. A transition probability and area matrix are calculated to illustrate the likelihood of the changes in the pixel status and total area for the next time step [
36]. Moreover, a set of condition probability images is also created to identify the probability that areas will be changed in the next generation. The CA-MC, built in IDRISI Selva version 17 [
36], requires two different periods of LULC maps. The time interval for the future LULC prediction is based on a number of iterations determined by a user. The 5 × 5 mean filter of the contiguity constraint of the CA was used for the future land allocation.
3.4.2. Multi-Layer Perceptron-Markov Chain (MLP-MC)
This method uses the combination between multi-layer perceptron (MLP) and MC to predict the future LULC. The MLP-MC performed in Land Change Modeler (LCM) utilizes three stepwise processes: change analysis, transition potential modeling and change prediction [
28,
36]. The details of each process are examined in detail.
This step comes with two times of LULC maps like change analysis process. It uses these to identify the major transitions that can be modeled separately like sub-model in the next step.
The transition potential analysis is also an important part to determine driver factors that cause a conversion between a pair of LULC classes [
31,
41,
42]. Some affirmation data were passed through the Euclidean distance function to generate distance maps. Statistical data such as slope, population, and economic data are also used to calculate the density and growth rate maps. All of these factors are shown in
Table 2.
In the driving factors identification, Cramer’s
V, a popular nominal scale measurement, based on qui-square, was applied to identify the most associated factors between two categorical maps. Equation (1) shows the formula of Cramer’s
V statistic where
φ (phi) is the coefficient of contingency and t is the smaller of the number of rows minus one or the number of columns minus one [
41].
According to the literature, if the Cramer’s
V value is about 0.15 or higher, it means that the association is useful. Moreover, if its value is greater than 0.4, the association is good [
38].
Once all the explanatory factors were tested in each land transition, the LCM adopted MLP to generate the transition potential maps. The MLP is a feed-forward artificial neural network in which all data are passed from input layers to output layers. Each neuron calculates a combined value that is the result of the multiplication of values in the nodes of the previous layer by the connection weights between the nodes. This combined value is then the input to an activation function of the node, typically a non-linear activation function such as a sigmoid function [
43,
44]. Further, a back propagation training algorithm is typically used for the supervised training of the neural network. The algorithm iteratively changes the weights of the neural connections between the nodes of the different layers in such a manner that the error between the nodes’ outputs and their desired outputs is minimized [
45]. In each land transition sub-model of this study, the MLP generates a random set of sample cells that have and have not experienced the transition. Therefore, each sub-model, consisting of one transition and two examples of classes, including one transition class and one persistence class, was fed. The MLP constructs a network of neurons between two example classes and driving factors, together with a web of connections that consist of sets of weights. Then, the sample cells are divided into two groups. The first 50% of the sample cells are used for training and the second 50% for validation [
31,
45,
46]. This process is to develop the relationship between explanatory factors and activation levels of the transition potential. Thus, the weight has been adjusted to minimize the error to improve accuracy [
46,
47]. When the accuracy rate is more than 80% or reaches the maximum iteration (1000 epochs), the transition potential map of each sub-model, which is an output of the MLP, yields the suitability of LULC classes for the future period.
The LCM uses a change prediction process to determine the quality of the future LULC in specific time modeled by MC. It produces two types of results. The first is a hard prediction model which results from a projected LULC map through a land allocation function [
36]. The second is a soft prediction which is a comprehensive vulnerability map based on the set of transition. Generally, the values of the soft prediction outputs are between 0 and 1 [
28].
3.4.3. Model Validation
The validation is a process to assess the quality of the simulated LULC results by comparing with the reference maps from the classified images in the years of 1998, 2003, 2008, and 2011. This study used the cross tabulation based accuracy assessment to calculate an overall accuracy of each predicted map [
48]. Moreover, the Kappa analysis was also used to examine the quality of results [
49].
3.4.4. Model Application
Once all predicted LULC maps were assessed for acceptable accuracy, the model was used to predict the future LULC in 2014 and 2035. Although the demographic and economic data were introduced as inputs of the model already, much literature [
50,
51,
52,
53] also suggests that it will improve the good performance of the model to incorporate the population and economic growth rate for future predictions. This study considers that reason to integrate both important data to transition rate calculation through the statistical extrapolation and SD.
Statistical extrapolation is a method to estimate the land demand (transition probability) based on the future population. The probabilities of land changes were predicted from an existing LULC and population change. The predicted values were generated by simple linear regression [
31]. In this study, the change in population throughout the specific time period was compared with the change in each LULC category to develop a ratio of the future change using ordinary forecast and trend functions.
SD is a non-spatial simulation technique developed in the late 1950s by Jay W. Forrester of the Massachusetts Institute of Technology. SD was originally applied in the engineering field called “Industrial Dynamics” and also applied in the urban planning field, namely “Urban Dynamics”. It has attracted adequate attention as a tool for system characteristics investigation rather than predictions based on numerical simulations [
54]. To calculate the transition probability of land demand using SD, this study applied the existing and projected population proposed by DOPA and NESDB in 2014 and 2035, respectively, to compute annual growth rates. The economic growth rates, calculated from the GPP, were also used in the model. The process in SD for land demand calculation can be divided into two parts: the first is driving factors module and the second is a land use module. The driving factors module handled the impact of population and economic growth while the land use module paid attention to the interaction and conversions of land use classes that were driven by population and economic data. For example, the demand for the urban class would be increased if the population and GPP growth rates increased. On the other hand, the agriculture and forest classes would decrease because of those factors. This study calculated the land demands using STELLA software from isee system. It was used to design the stocks (land use classes) and flows (driving forces) and to automatically generate relevant equations according to the feedback loop of the land demand in the SD environment. Once all were completed, the model estimated the land demands for each LULC class of the interested year, which were then converted into the transition probability matric.
4. Results and Discussion
In order to understand the LULC changes and dynamics of urban expansion in the BMR, this study divides the results into four sections: (i) LULC classification and accuracy assessment from the satellites images; (ii) Analysis of LULC change in the study periods; (iii) LULC prediction and validation; and (iv) LULC model application.
4.1. LULC Classification and Accuracy Assessment
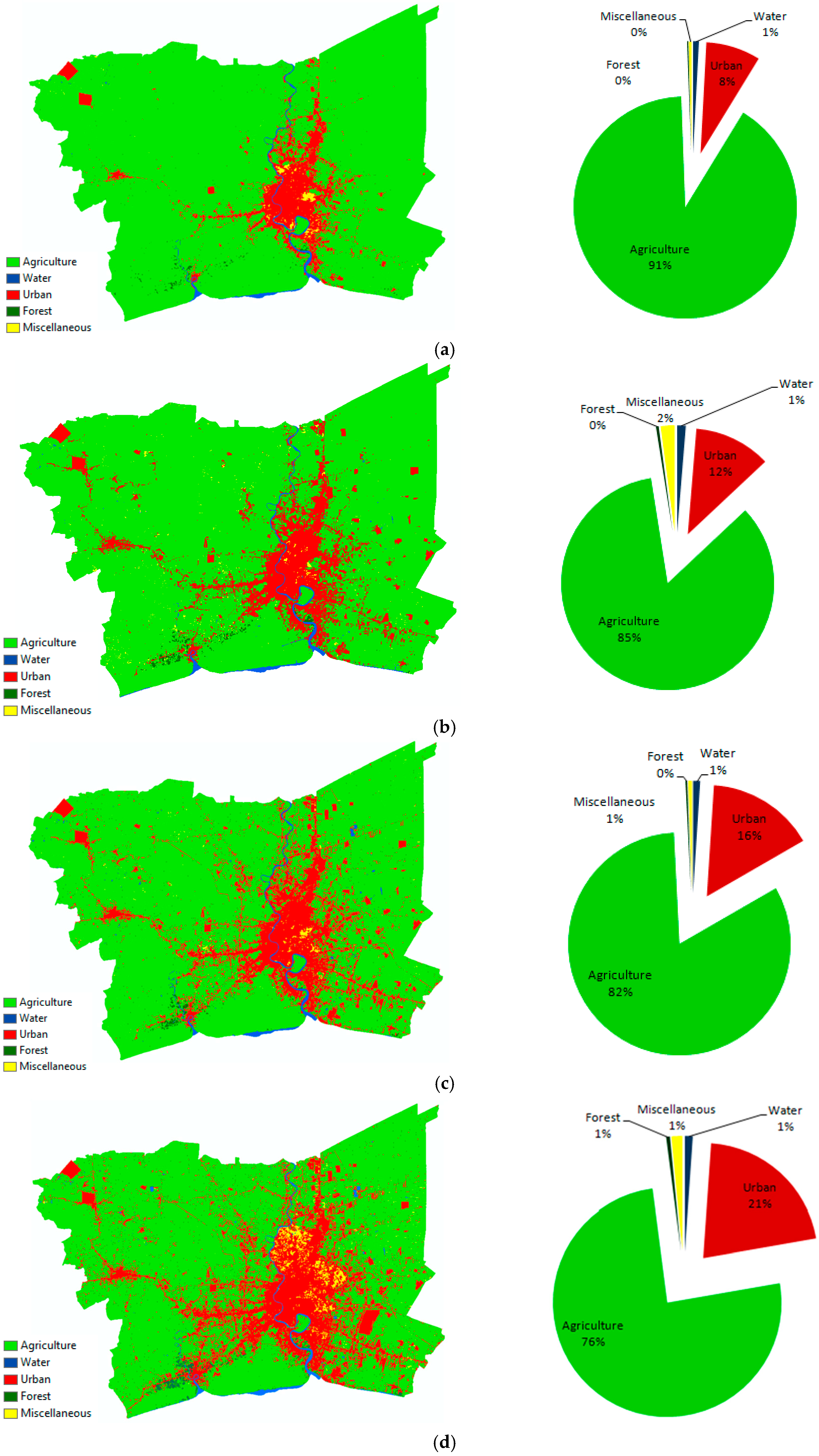
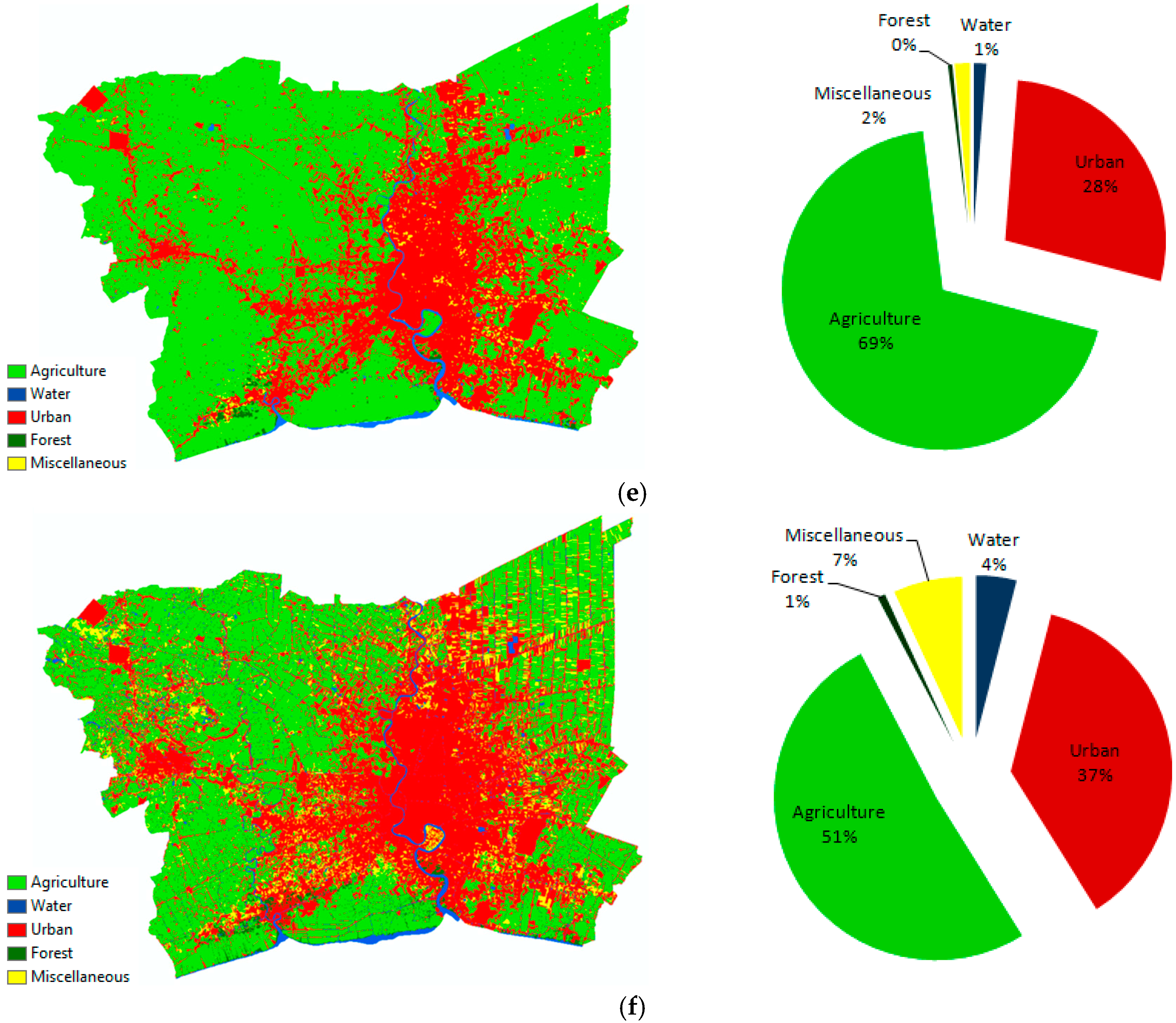
The LULC maps for the six years of the Landsat images, 1988, 1993, 1998, 2003, 2008, and 2011, were analyzed through the maximum likelihood algorithm and improved the map qualities using auxiliary datasets (
Figure 4). The classification results from the six LULC maps indicated that the agricultural class was the predominate land in the BMR throughout the study period. However, its share decreased dramatically. In contrast, urban land seems to be increased continuously due to the land demand for residential and industrial purposes. There was a slight fluctuation in the amount of miscellaneous class. Water and forest areas were relatively stable.
This study employed the advantages of total accuracy value and the kappa value for evaluating the classified LULC maps, as listed in
Table 3. The overall accuracy values of the LULC maps were observed to be 85.19, 86.25, 90.12, 86.95, 87.65, and 89.1 percent for the six time periods, respectively. Furthermore, the kappa values of the maps were 0.80, 0.82, 0.87, 0.83, 0.83, and 0.86, respectively. All values of the overall accuracy and the kappa coefficient were greater than 85 percent and 0.80, which indicated a strong perfect agreement between the classified maps and the ground truth data. Therefore, the accuracy of the LULC maps was satisfactorily accurate for investigating the future urban LULC simulations.
4.2. Change Analysis
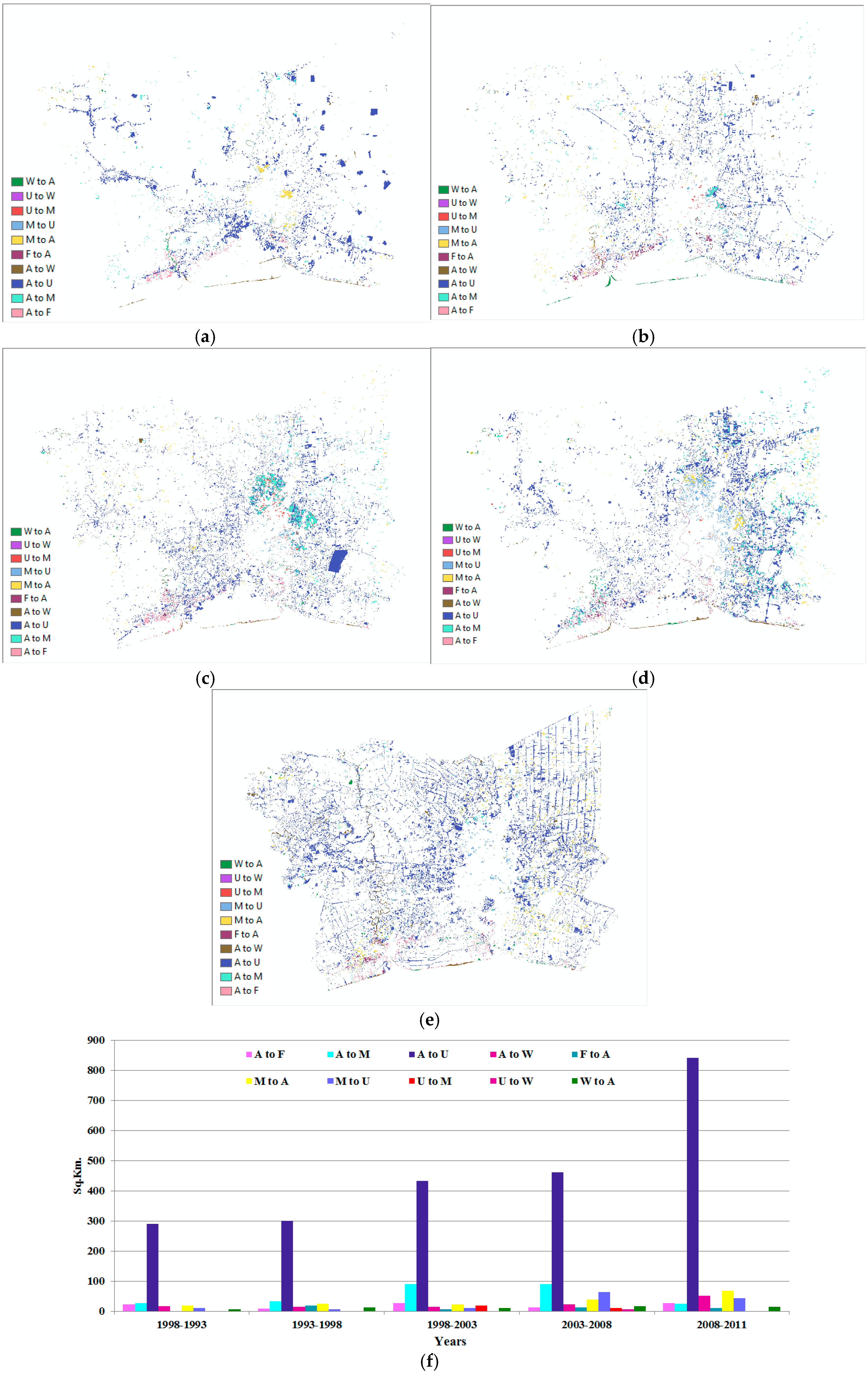
To quantify the changing in an urban area, the LULC is the most important. A cross tabulation process was applied to identify the major changes between two LULC maps of the specified time periods. The LULC change maps together with a number of changes in each class from the five periods are displayed in
Figure 5.
It can illustrate evidently that, firstly, the conversion between agriculture and urban was the most distinctive change of the study period. The amount of change increased gradually from approximately 300 km2 in 1988–1993 to about 850 km2 in 2008–2011. The second was the transition from agriculture to miscellaneous, which could be found from the analysis. The percentage of its change was less than 10 percent from the first four periods. On the other hand, in the last period (2008–2011), a significant increase in this transition was observed. The third was the conversion from miscellaneous to agriculture, which could be detected from the change analysis with a lower rate of change when compared to the second. Moreover, the conversion between miscellaneous land and urban was another influence that could be seen in the LULC change. Nevertheless, the change analysis indicated other transitions in each LULC class, which also had effects on the urban growth and LULC changes in the BMR.
4.3. Urban LULC Prediction
4.3.1. Identification of Driving Factors
After detecting the changes in particular time periods, the identification of the driving factors was investigated regarding the changes in the specific time duration. To determine the association between the changes and the factors for the LULC modeling and simulation, Cramer’s
V values were calculated. The factors that had a Cramer’s
V value higher than 0.15 were selected to generate the transition potential map of land transition in each sub-model based on a root mean square error (RMSE) value less than 0.1 within 10,000 iterations of the MLP neural network parameters.
Table 4 shows the influence factors that were used to generate a transition potential map for each specific period for the simulation.
4.3.2. Transition Probability Analysis
To simulate the future LULC and urban expansion, this study considered a sophisticated method to estimate the rate of land transition in each specific time using the conventional scheme of the MC and application of the projected population to calculate the transition probabilities from statistical extrapolation and SD approach. The details of this analysis are discussed in two separate sections.
The MC was used to quantify the change between a pair of LULC maps. It created a transition probability matrix for each LULC category to be converted to any other categories (
Table 5). The contingency matrix, which displays the relative frequencies of change in a certain time step, was utilized to calculate the transition probability. The resulted matrices were then used with the transition potential map in the next step of the change prediction.
To quantify the future LULC in 2014, this study considered the existing population data collected by DOPA, Ministry of Interior. Based on the population growth calculation between 2011 and 2014, the annual growth rate of population was observed as 0.01 per year. As reported by NESDB, the future population in the BMR would reach up to 16,632,220 in 2035. The increase in the rate of the population when compared with the base year 2014 was 0.15 per year. Moreover, the economic growth rate obtained from the GPP change in the same period would approach a value of 0.12 per year. Here, both data were used to derive the transition probability using simple extrapolation and the non-spatial technique of SD.
Table 6 and
Table 7 show the estimated transition values in 2014 and 2035, respectively. Then, the LULC transitions were applied in the CA-MC and MLP-MC environments to generate the transition potential maps in each sub-model for the simulation.
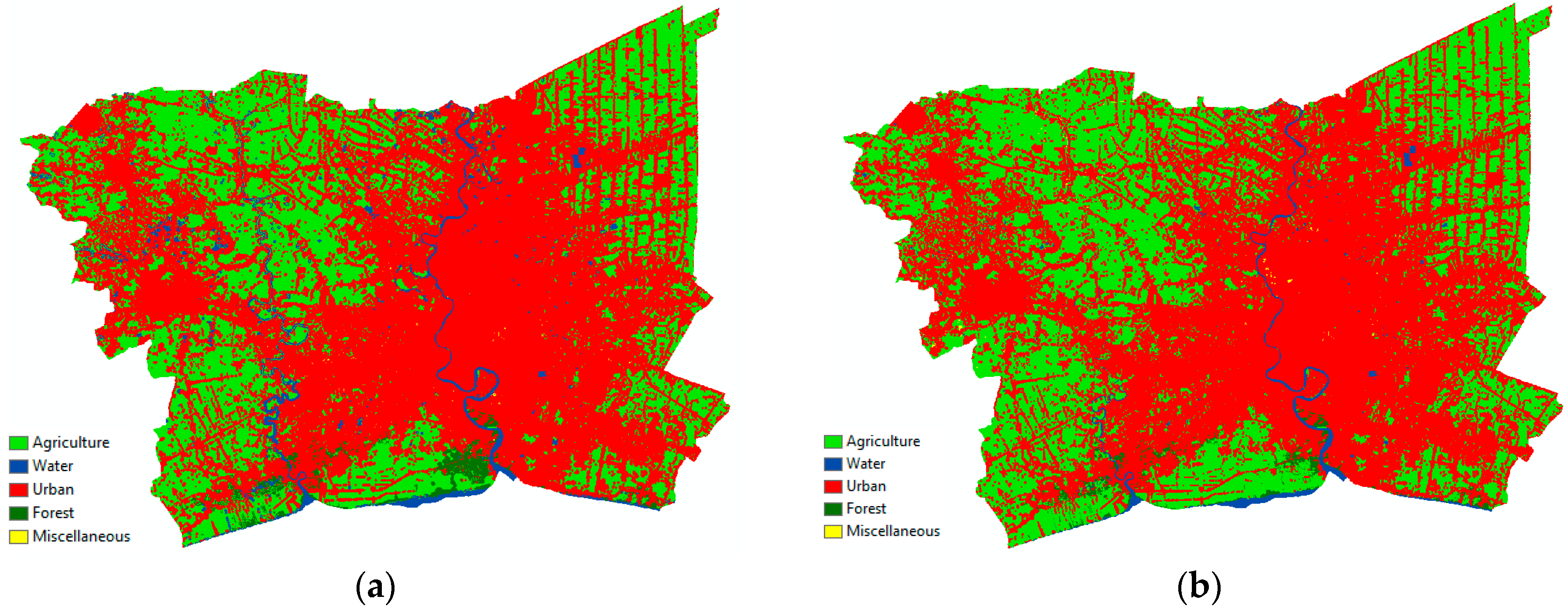
4.3.3. LULC Prediction and Validation
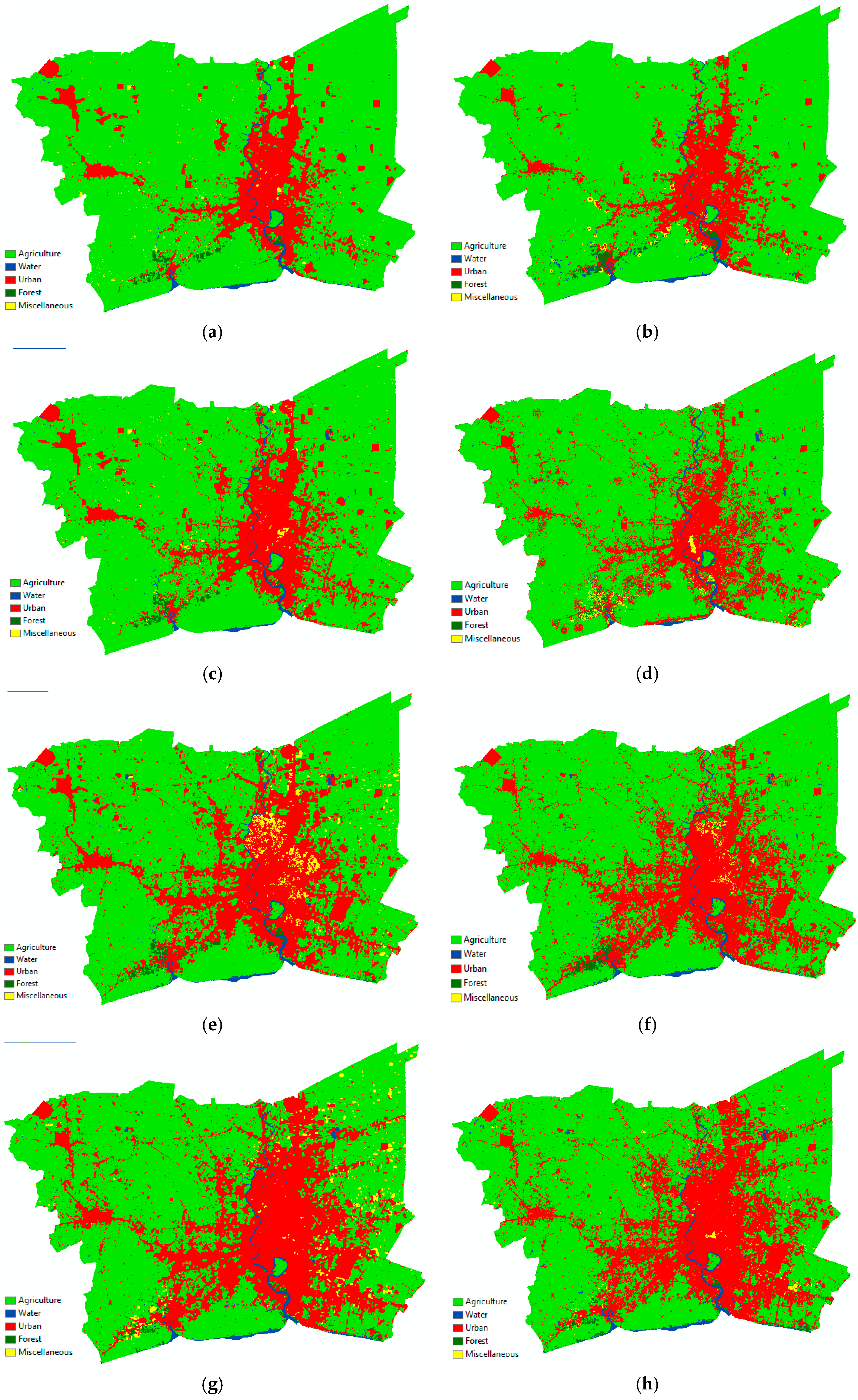
This study considered two different schemes for simulation based on the conventional model to explore the urban LULC and urban expansion in the BMR. The simulated LULC maps in the four time periods 1998, 2003, 2008, and 2011 were generated, as shown in
Figure 6 and
Table 8. The validation procedure was investigated to confirm the reliability and efficiency of the CA-MC and MLP-MC for the LULC prediction. The overall accuracy and several kinds of Kappa coefficients were applied to validate the simulated maps with the LULC maps generated by the maximum likelihood classification. After the superimposing, all simulated maps yielded overall accuracies greater than 80 percent. Furthermore, Kappa coefficients such as Kstandard, Kno, and KlocationStrata were also calculated to assure the accurate result of the simulation, all of which had values higher than 0.8 (
Table 8). However, the accuracy assessment from the simulated LULC maps proved that the MLP-MC method contributed higher accuracy values than CA-MC. Since the MLP-MC deliberated the influence in physical, demographic and economic factors on the LULC conversion, the simulated maps from this method showed a higher accuracy when compared with the CA-MC results (
Table 9 and
Figure 6). CA-MC does not, in contrast, consider the change spatially. This method is not always appropriate to allocate future LULC in suitable locations [
14,
55].
4.3.4. LULC Model Application
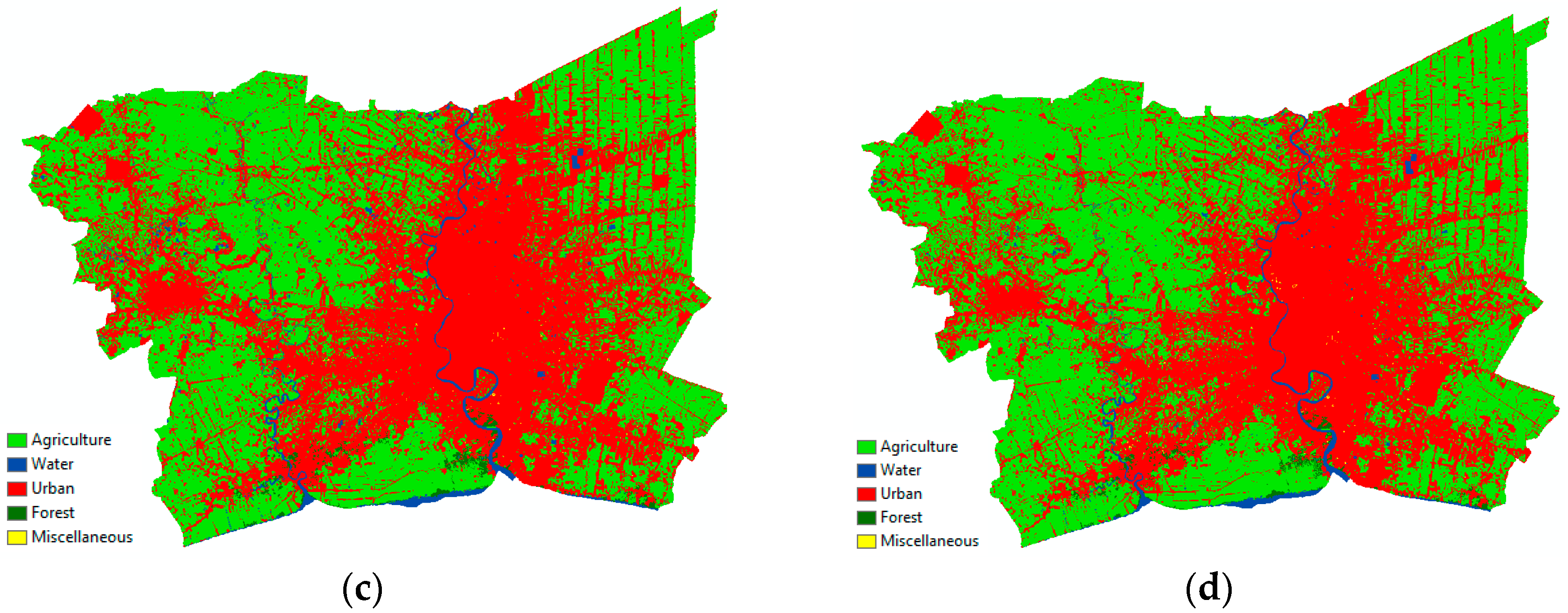
According to the previous section, the accuracy assessment confirms that the MLP-MC method yielded a strong level of perfect agreement between the simulated maps and reference data. The model application in this study adopted the transition rates calculated by MC in CA-MC and MLP-MC methods to simulate the LULC in 2014. The transition probabilities calculated from the population and economics via the extrapolation and SD were also utilized in the MLP as a platform to simulate in 2014. The LULC map in 2011 was used as a base map for the future simulation. The results from all schemes are illustrated in
Figure 7. All values of the overall accuracy and Kappa coefficients illustrated and certify the performance of all schemes that were stratified to simulate the future LULC (
Table 10). The transition rate calculated using the SD displayed the highest accuracy when compared with others. The SD scheme projected the urban area slightly lower than the existing LULC from the Landsat image; however, it showed a strong performance in the simulation (
Table 11). From the extrapolation scheme, its result yielded an overestimation in the urban class and underestimation in agriculture class similar to the results from the conventional MC scheme when performed in CA and MLP environments.
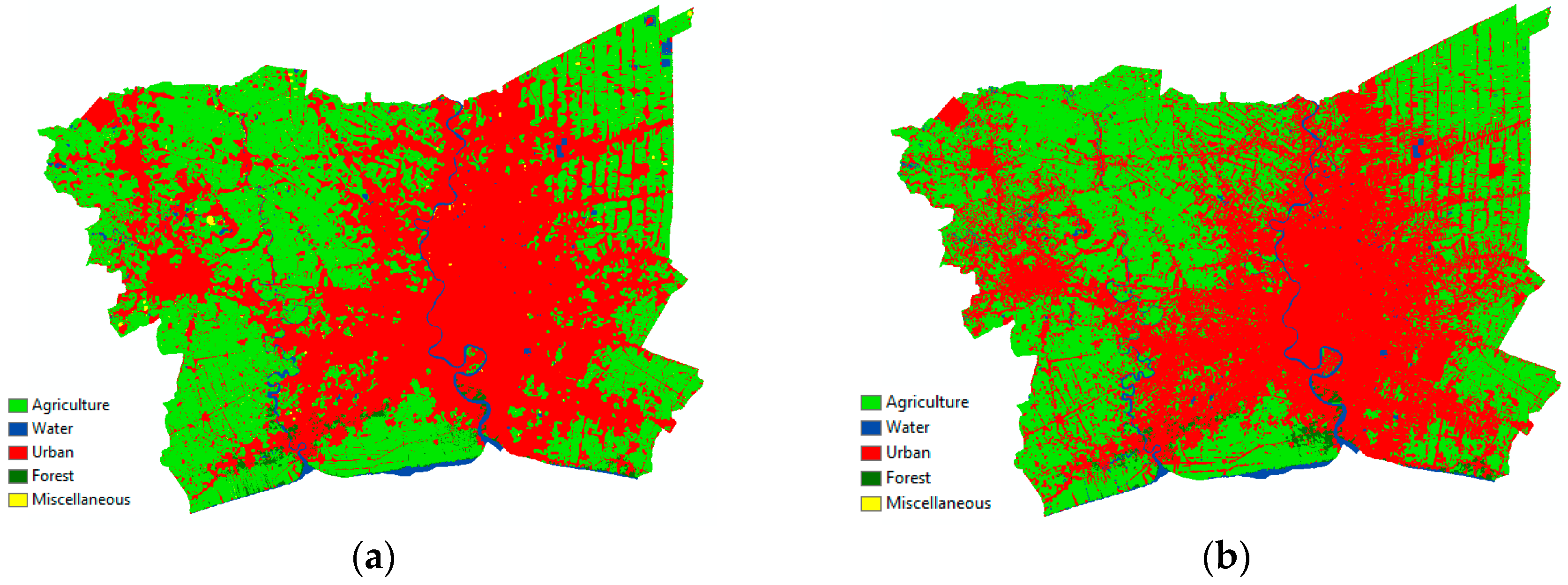
Because of the strong performance of the demographic–economics data, the transition probabilities from the statistic extrapolation and SD schemes were applied to simulate the LULC and urban area. Both transition probabilities were calculated from the estimated population and annual growth rate of 2035. The simulation, in this part, was based on the transition potential map created by the MLP of the LCM model.
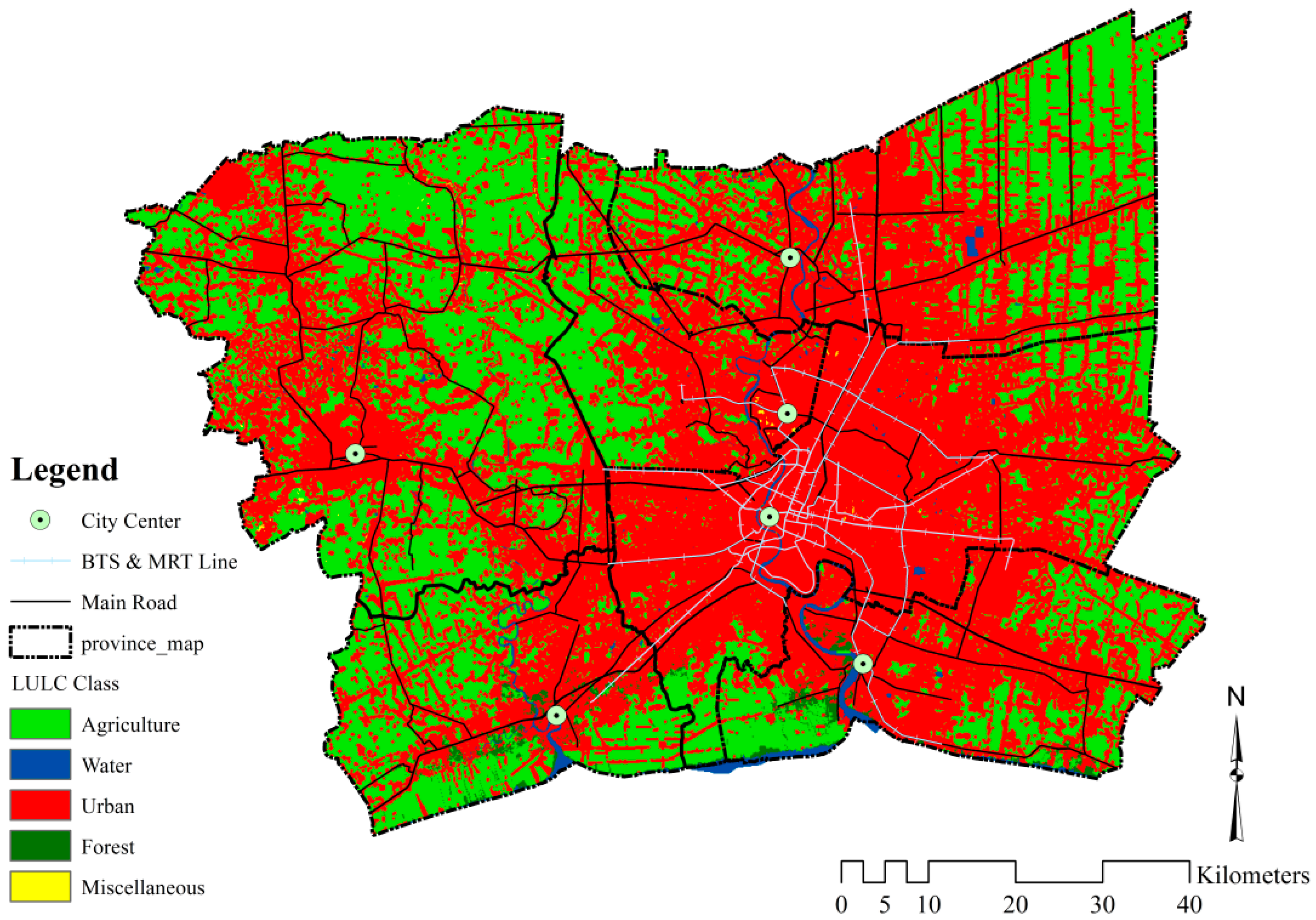
Figure 8 illustrates the simulated results from both methods. It can visualize evidently that, by using the SD scheme, the predicted urban area is 3750.77 km
2 or 48.75 percent of the whole area of the BMR. Agricultural land is almost equal to the urban class. The lands for water, forest, and miscellaneous classes occupy the smallest amounts of land, sequentially (
Table 12). In terms of the simulation from the extrapolation, all of the LULC have a similar trend with the SD scheme. However, the proportion of the LULC is different, especially in the urban class, which occupies around 64 percent of land.
To analyze the urban expansion of the BMR in 2035, this study used the simulated map from the SD scheme to examine the urban extent (
Figure 9). The conversion between agriculture and urban areas plays as a primary role in the LULC change. The large urban agglomeration is located along the Chao Phraya River where the urban and built-up areas have increased dramatically since 1988. The urban area expanded itself over administrative boundaries, particularly in the connected zone between BM and Pathum Thani, Nonthaburi, and Samut Prakan. Those provinces play an important role as residential areas supporting the BM population and also as lands for industrial purposes based on the fundamental function of the city. Moreover, the urban area expands in a linear form along the main roads that connect neighboring provinces to the BM. On the other hand, the center of the BMR remains as most population dene zone where all built up areas will be constructed in response to land demands for business and commercial enterprises. Since the construction of the Bangkok Mass Transit System (BTS) and Mass Rapid Transit (MRT), many condominiums with medium and high classes were built along those lines to respond to the demand for urban lifestyles with reduced commutes to work. Furthermore, there is a different pattern of urban expansion that occurred in Nakhon Pathom. Its urban area has expanded from the center of the province and will continuously extend until 2035. There is also a scattered random pattern in the built-up area, in which farmers occupy the land near agricultural areas. This situation can be found predominantly in Nakhon Pathom. If the spatial planners do not consider this, it will create urban sprawl, which is already a crucial problem in that area.
5. Conclusions
Recently, Thailand faces with the problem of urban expansion due to the national plan policy that was established to confirm BM as the center for all aspects of the country. Moreover, industrialization and innovation in the globalized world have turned BM into a modern city where everyone would like to live. However, BM does not grow by itself, but rather brings about spatial planning problems in the vicinity, which collectively can be called the BMR. This study used scientific methodology to explore the urban expansion and LULC changes in a specific time period based on the innovation of satellite imagery. Landsat images were utilized to generate LULC maps using the sophisticated maximum likelihood classification in different times. Then, the change detection technique was investigated to develop a pair of LULC maps in order to identify the land transformations. From this study, it can noticeably evident that the major land conversion in this area is agriculture to urban. To explore the future LULC and urban expansion in the future, this study applied the integrated methods of CA-MC and MLP-MC to generate transition probabilities and transition rates for the simulations. The simulated results in the years of 1988, 2003, 2008, and 2011 were validated to identify the best method for the predictions. The accuracy of the simulations showed that MLP-MC yielded higher accuracy than CA-MC. Therefore, the simulation in the years of 2014 and 2035 used the MLP as a platform for the prediction.
To project the LULC to the year 2035, even though the physical and economic factors were considered as input layers for the engendering the transition potential in each conversion, the future population and economic growth were applied to control the transition rate of the land conversions. The results from the study evidently confirm that in 2014 the predicted LULC maps from the SD and statistics extrapolation shows reliable results with robust accuracy, particularly the projected result from the SD method. Therefore, the transition probability rates, proposed by the SD method, within the MLP environment were used to explore the urban expansion in 2035. The simulation illustrates that urban and built-up area are the main LULC types and occupy about half of the land in the BMR. Most of the agricultural land would be converted to urban or built-up area if proper measures are not taken. This study shows that integration of the LULC modeling approach, remote sensing data, and demographic and economic data can be professionally used to simulate the future LULC change and, hence, the urban expansion phenomena in spatial distribution, direction, and time can be monitored. Future LULC is crucial information for planners and organizations to allocate important infrastructures and manage sustainable land use in response to the diverse requirements of the people in this region.