A Novel Method for Fast Configuration of Energy Storage Capacity in Stand-Alone and Grid-Connected Wind Energy Systems
Abstract
:1. Introduction
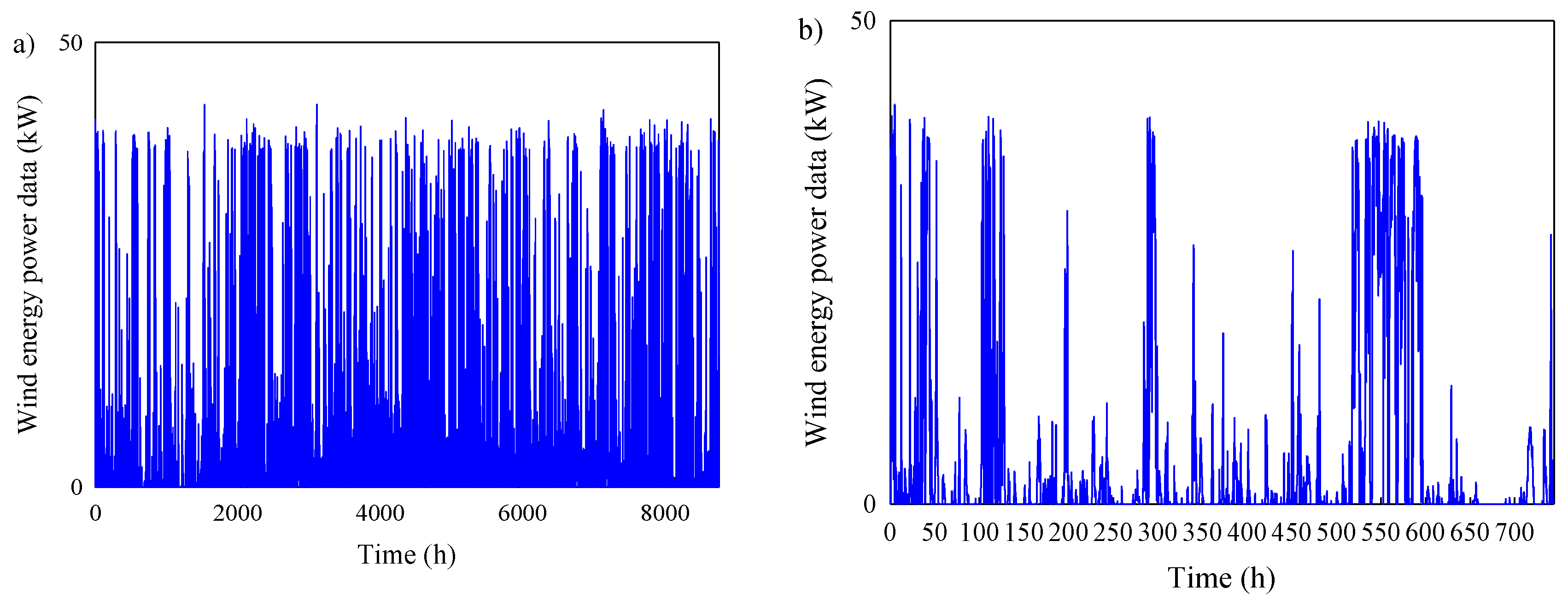
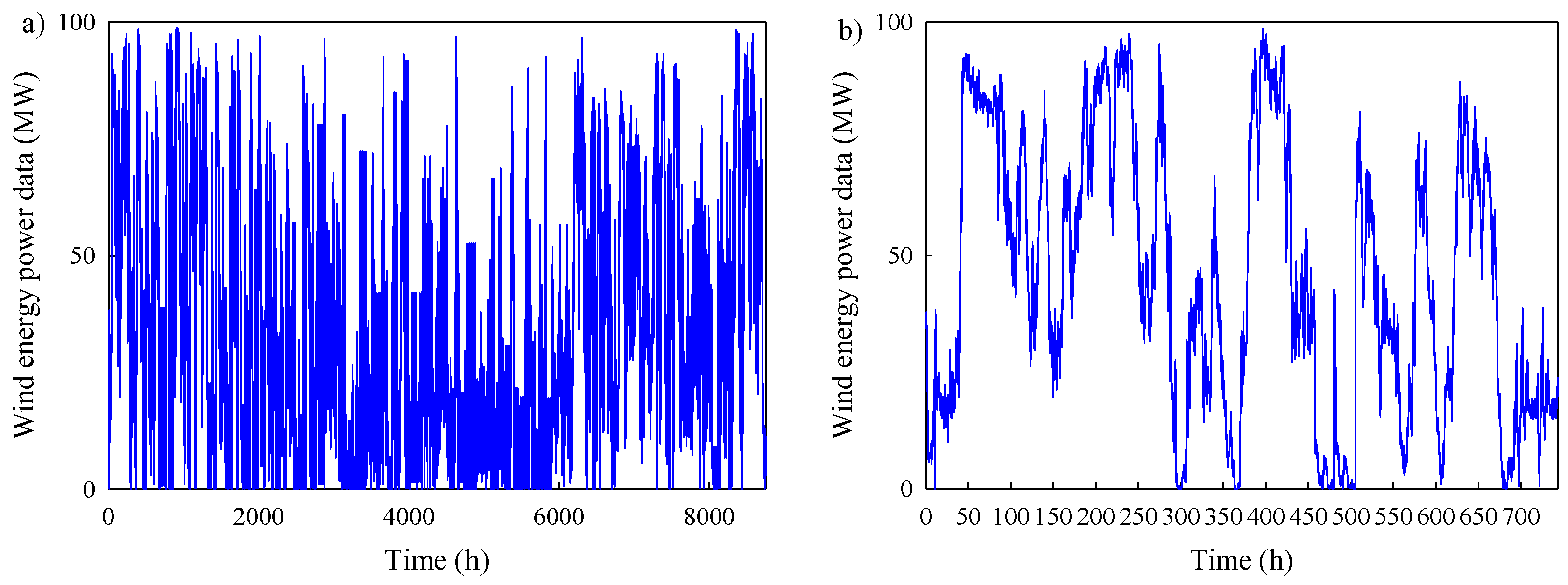
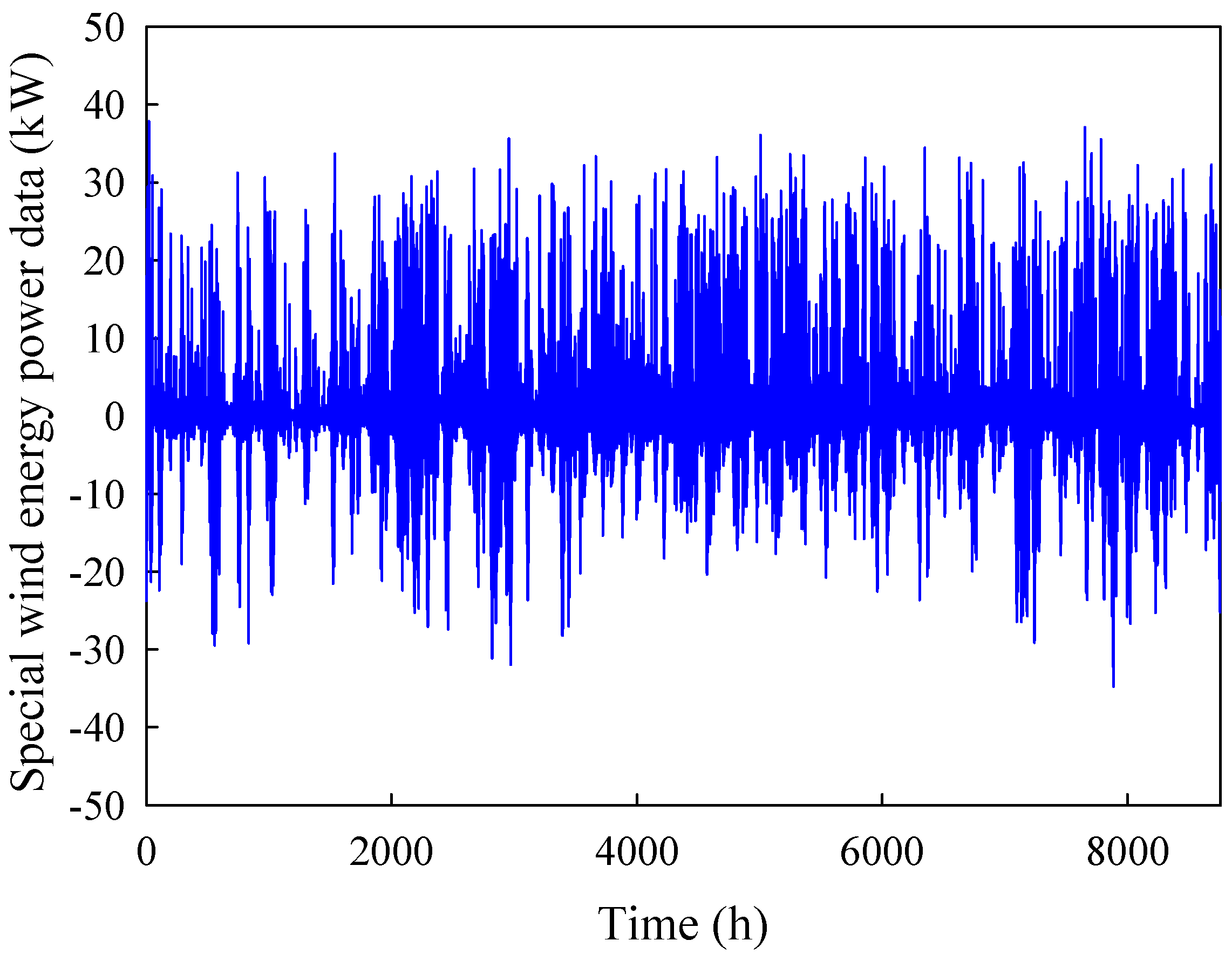
2. Data Used
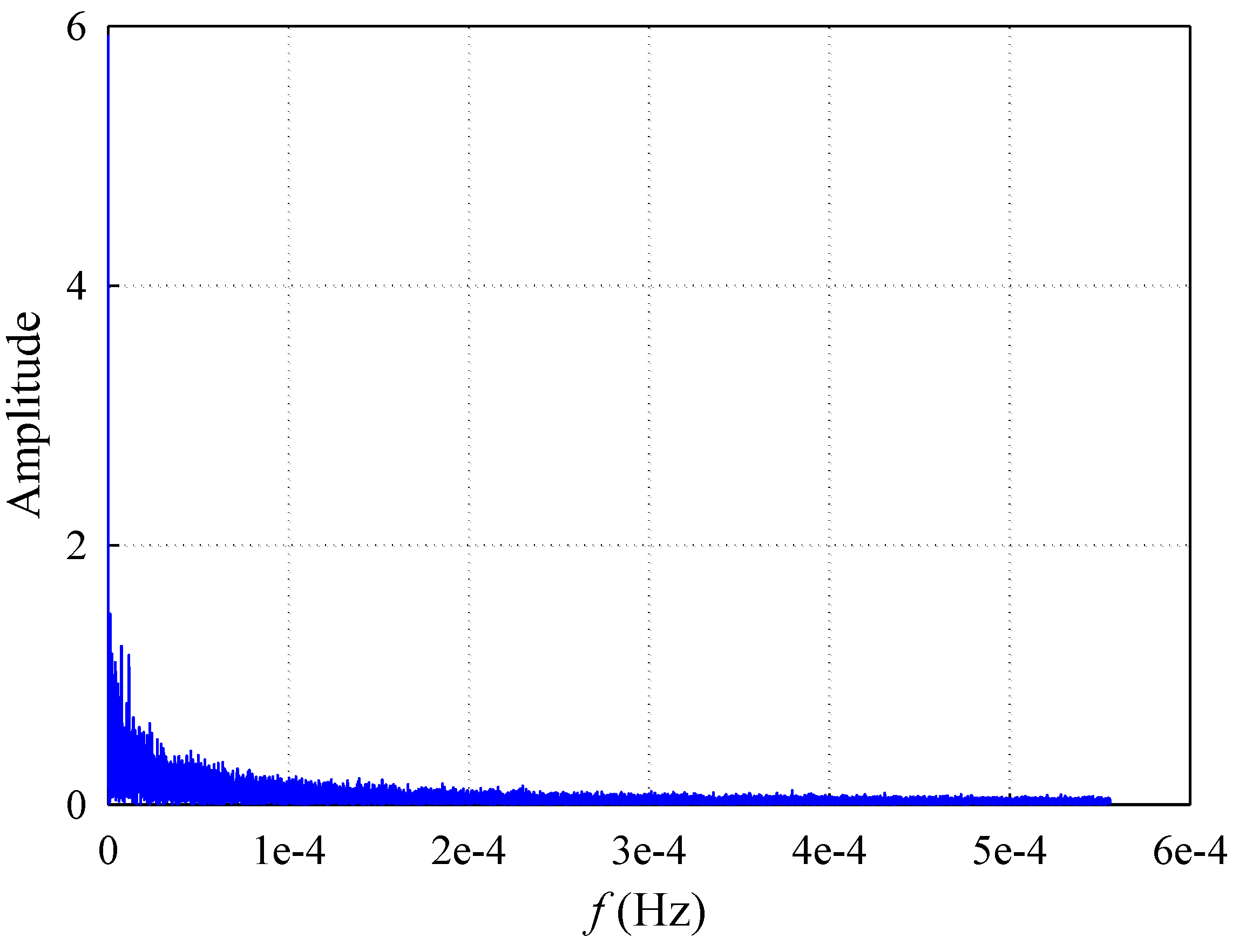
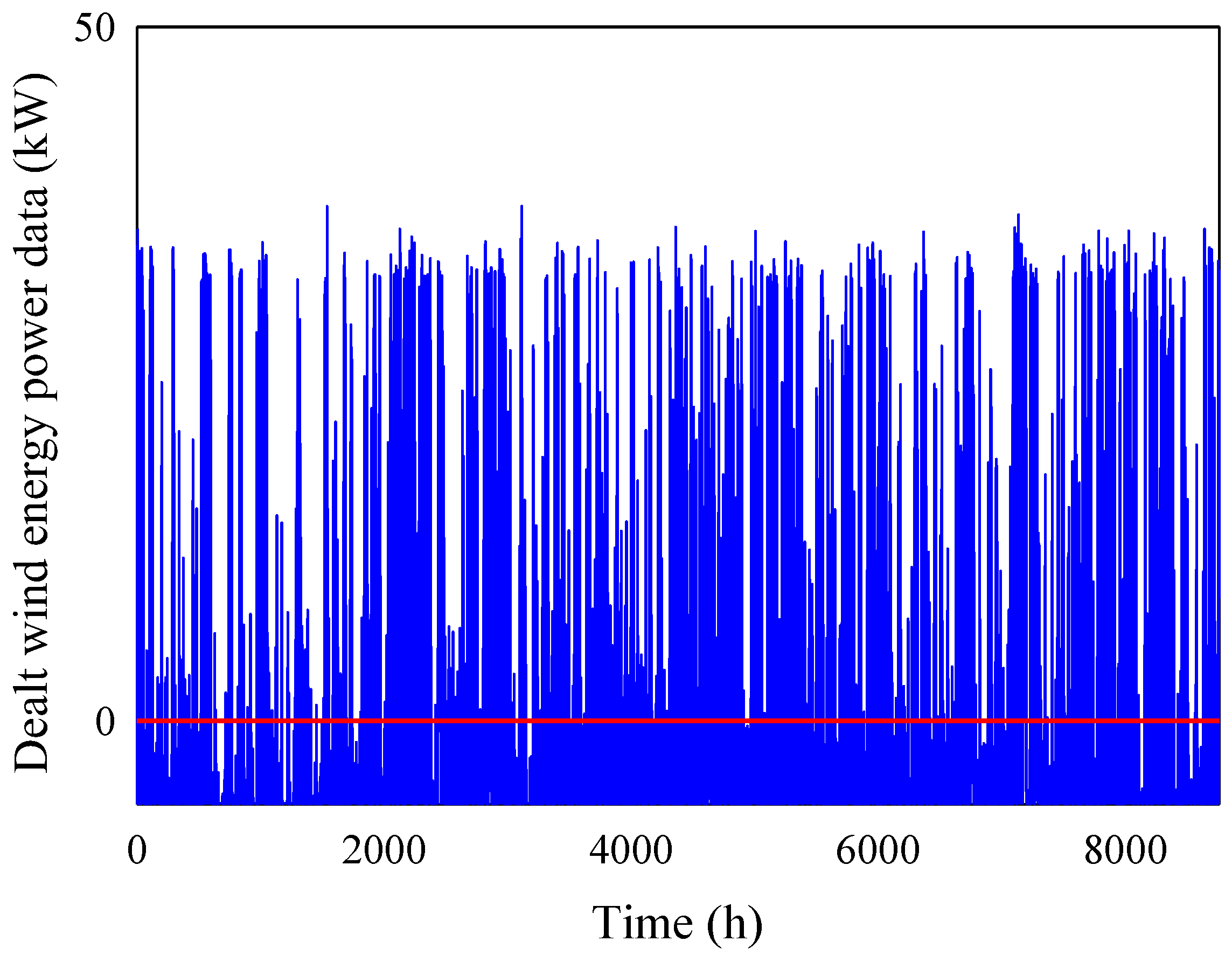
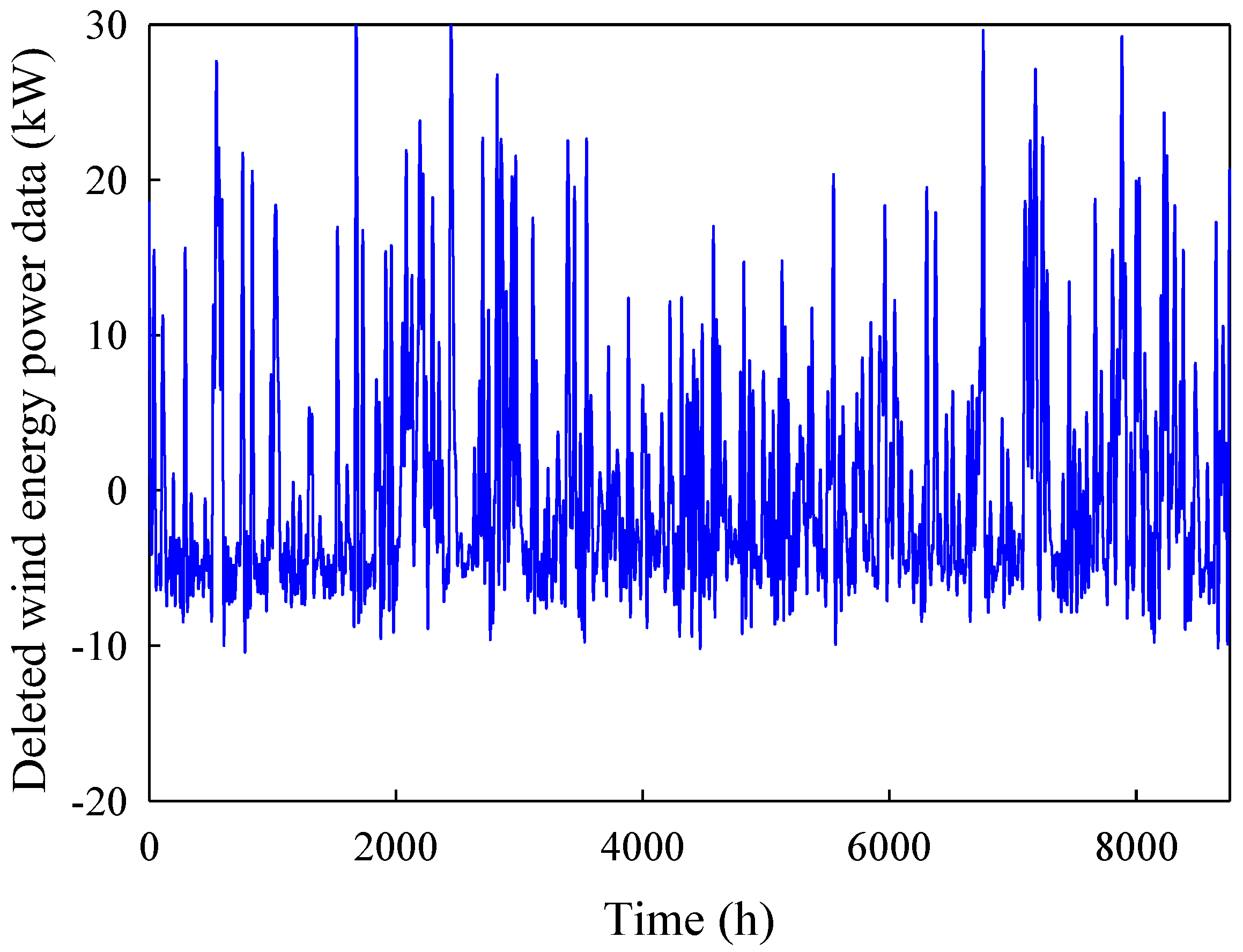
3. Methods Used
- (a)
- Set the energy ratio η0.
- (b)
- Calculate the different P1 by changing the range of the pass band from low (fmin) to high (fmax) according to Equations (4) and (5) shown in the former step. Calculate the energy ratio between energy E1 and the standard energy using Equations (6) and (7).
- (c)
- Determine the computing time T, which is the reception of the compensation frequency f. The program terminates and the final frequency f can be returned when the energy ratio η reaches the predefined value (η − η0 < = 0.005).
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Xu, X.; Niu, D.; Qiu, J.; Wu, M.; Wang, P.; Qian, W.; Jin, X. Comprehensive evaluation of coordination development for regional power grid and renewable energy power supply based on improved matter element extension and TOPSIS method for sustainability. Sustainability 2016, 8, 143. [Google Scholar] [CrossRef]
- Liu, L.Q.; Wang, Z.X.; Zhang, H.Q.; Xue, Y.C. Solar energy development in China-A review. Renew. Sustain. Energy Rev. 2010, 14, 301–311. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R.P. Techno-economic feasibility study on Integrated Renewable Energy System for an isolated community of India. Renew. Sustain. Energy Rev. 2016, 59, 388–405. [Google Scholar] [CrossRef]
- Banos, R.; Manzano-Agugliaro, F.; Montoya, F.; Gil, C.; Alcayde, A.; Gómez, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Cao, M.; Xu, Q.; Zeng, P.; Xu, X.; Yuan, X. An energy storage system configuration method to stabilize power fluctuation in different operation periods. In Proceedings of the 2014 IEEE PES General Meeting Conference & Exposition, Washington, DC, USA, 27–31 July 2014; IEEE: New York, NY, USA, 2014; pp. 1–5. [Google Scholar]
- Cao, M.; Xu, Q.; Bian, H.; Yuan, X.; Du, P. Research on configuration strategy for regional energy storage system based on three typical filtering methods. IET Gener. Transm. Distrib. 2016, 10, 2360–2366. [Google Scholar] [CrossRef]
- Hadjipaschalis, I.; Poullikkas, A.; Efthimiou, V. Overview of current and future energy storage technologies for electric power applications. Renew. Sustain. Energy Rev. 2009, 13, 1513–1522. [Google Scholar] [CrossRef]
- Makarov, Y.V.; Du, P.; Kintner-Meyer, M.C.; Jin, C.; Illian, H.F. Sizing energy storage to accommodate high penetration of variable energy resources. IEEE Trans. Sustain. Energy 2012, 3, 34–40. [Google Scholar] [CrossRef]
- Sreeraj, E.; Chatterjee, K.; Bandyopadhyay, S. Design of isolated renewable hybrid power systems. Sol. Energy 2010, 84, 1124–1136. [Google Scholar] [CrossRef]
- Heide, D.; Greiner, M.; Von Bremen, L.; Hoffmann, C. Reduced storage and balancing needs in a fully renewable European power system with excess wind and solar power generation. Renew. Energy 2011, 36, 2515–2523. [Google Scholar] [CrossRef]
- Chen, S.; Gooi, H.B.; Wang, M. Sizing of energy storage for microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
- Yang, H.; Lu, L.; Zhou, W. A novel optimization sizing model for hybrid solar-wind power generation system. Sol. Energy 2007, 81, 76–84. [Google Scholar] [CrossRef]
- Celik, A.N.; Muneer, T.; Clarke, P. Optimal sizing and life cycle assessment of residential photovoltaic energy systems with battery storage. Prog. Photovolt. Res. Appl. 2008, 16, 69–85. [Google Scholar] [CrossRef]
- Askari, I.B.; Ameri, M. Optimal sizing of photovoltaic—Battery power systems in a remote region in Kerman, Iran. Proc. Inst. Mech. Eng. A J. Power Energy 2009, 223, 563–570. [Google Scholar] [CrossRef]
- Baniasad Askari, I.; Ameri, M. The Effect of Fuel Price on the Economic Analysis of Hybrid (Photovoltaic/Diesel/Battery) Systems in Iran. Energy Sources B Econ. Plan. Policy 2011, 6, 357–377. [Google Scholar] [CrossRef]
- Fossati, J.P.; Galarza, A.; Martín-Villate, A.; Fontán, L. A method for optimal sizing energy storage systems for microgrids. Renew. Energy 2015, 77, 539–549. [Google Scholar] [CrossRef]
- Ogunjuyigbe, A.; Ayodele, T.; Akinola, O. Optimal allocation and sizing of PV/Wind/Split-diesel/Battery hybrid energy system for minimizing life cycle cost, carbon emission and dump energy of remote residential building. Appl. Energy 2016, 171, 153–171. [Google Scholar] [CrossRef]
- Berrada, A.; Loudiyi, K. Operation, sizing, and economic evaluation of storage for solar and wind power plants. Renew. Sustain. Energy Rev. 2016, 59, 1117–1129. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T.; Yona, A.; Funabashi, T. Photovoltaic output power fluctuations smoothing by selecting optimal capacity of battery for a photovoltaic-diesel hybrid system. Electr. Power Compon. Syst. 2011, 39, 621–644. [Google Scholar] [CrossRef]
- Ahmed, N.A.; Miyatake, M.; Al-Othman, A. Power fluctuations suppression of stand-alone hybrid generation combining solar photovoltaic/wind turbine and fuel cell systems. Energy Convers. Manag. 2008, 49, 2711–2719. [Google Scholar] [CrossRef]
- Chengshan, W.; Bo, Y.; Jun, X.; Li, G. Sizing of energy storage systems for output smoothing of renewable energy systems. Proc. CSEE 2012, 32, 1–8. [Google Scholar]
- Abbassi, R.; Chebbi, S. Energy management strategy for a grid-connected wind-solar hybrid system with battery storage: Policy for optimizing conventional energy generation. Int. Rev. Electr. Eng. 2012, 7, 3979. [Google Scholar]
- Vallati, A.; Grignaffini, S.; Romagna, M. A New Method to Energy Saving in a Micro Grid. Sustainability 2015, 7, 13904–13919. [Google Scholar] [CrossRef]
- Park, E.; Kwon, S.J. Solutions for optimizing renewable power generation systems at Kyung-Hee University’s Global Campus, South Korea. Renew. Sustain. Energy Rev. 2016, 58, 439–449. [Google Scholar] [CrossRef]
- Weinstein, S.; Ebert, P. Data Transmission by Frequency-Division Multiplexing Using the Discrete Fourier Transform. IEEE Trans. Commun. Technol. 1971, 19, 628–634. [Google Scholar] [CrossRef]
- Wolf, J. Redundancy, the Discrete Fourier Transform, and Impulse Noise Cancellation. IEEE Trans. Commun. 1983, 31, 458–461. [Google Scholar] [CrossRef]
- Zhongde, W. Fast algorithms for the discrete W transform and for the discrete Fourier transform. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 803–816. [Google Scholar] [CrossRef]
| Energy Ratio | Computing Time/h | Calculated Power/kW | Energy Storage Capacity/kWh |
|---|---|---|---|
| 90% | 130.7 | 5.9 | 771 |
| 80% | 45.1 | 5.9 | 266 |
| 70% | 21.9 | 5.9 | 129 |
| 60% | 10.9 | 5.9 | 64 |
| 50% | 6.0 | 5.9 | 35 |
| 40% | 3.5 | 5.9 | 21 |
| Energy Ratio | Computing Time/h | Calculated Power/MW | Energy Storage Capacity/MWh |
|---|---|---|---|
| 40% | 30.0 | 33.0 | 990.0 |
| 35% | 23.8 | 33.0 | 785.4 |
| 30% | 19.2 | 33.0 | 633.6 |
| 25% | 12.0 | 33.0 | 396.0 |
| 20% | 7.8 | 33.0 | 257.4 |
| 15% | 3.9 | 33.0 | 128.7 |
| 10% | 1.5 | 33.0 | 49.5 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, H.; Guo, M.; Qian, Z.; Wei, Z.; Sun, G. A Novel Method for Fast Configuration of Energy Storage Capacity in Stand-Alone and Grid-Connected Wind Energy Systems. Sustainability 2016, 8, 1336. https://doi.org/10.3390/su8121336
Zang H, Guo M, Qian Z, Wei Z, Sun G. A Novel Method for Fast Configuration of Energy Storage Capacity in Stand-Alone and Grid-Connected Wind Energy Systems. Sustainability. 2016; 8(12):1336. https://doi.org/10.3390/su8121336
Chicago/Turabian StyleZang, Haixiang, Mian Guo, Zeyu Qian, Zhinong Wei, and Guoqiang Sun. 2016. "A Novel Method for Fast Configuration of Energy Storage Capacity in Stand-Alone and Grid-Connected Wind Energy Systems" Sustainability 8, no. 12: 1336. https://doi.org/10.3390/su8121336
APA StyleZang, H., Guo, M., Qian, Z., Wei, Z., & Sun, G. (2016). A Novel Method for Fast Configuration of Energy Storage Capacity in Stand-Alone and Grid-Connected Wind Energy Systems. Sustainability, 8(12), 1336. https://doi.org/10.3390/su8121336







