A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design
Abstract
:1. Introduction
2. Multi-Criteria Decision-Making
2.1. Multi-Attribute Decision-Making
2.1.1. Methods
Complex Proportional Assessment
Technique for Order of Preference by Similarity to Ideal Solution
Data Envelopment Analysis
Analytic Hierarchy Process
Analytic Network Process
Preference Ranking Organization Method for Enrichment Evaluations
Quality Function Deployment
2.1.2. Tools
Monte Carlo Simulation
Delphi
Fuzzy
Grey Numbers
2.2. Multi-Objective Decision-Making
2.3. Limitations of Traditional MCDM Methods
3. Life-Cycle Steps for Bridge
3.1. Planning and Design
3.2. Construction
3.3. Operation and Maintenance
3.4. Demolition or Recycle
4. Discussion
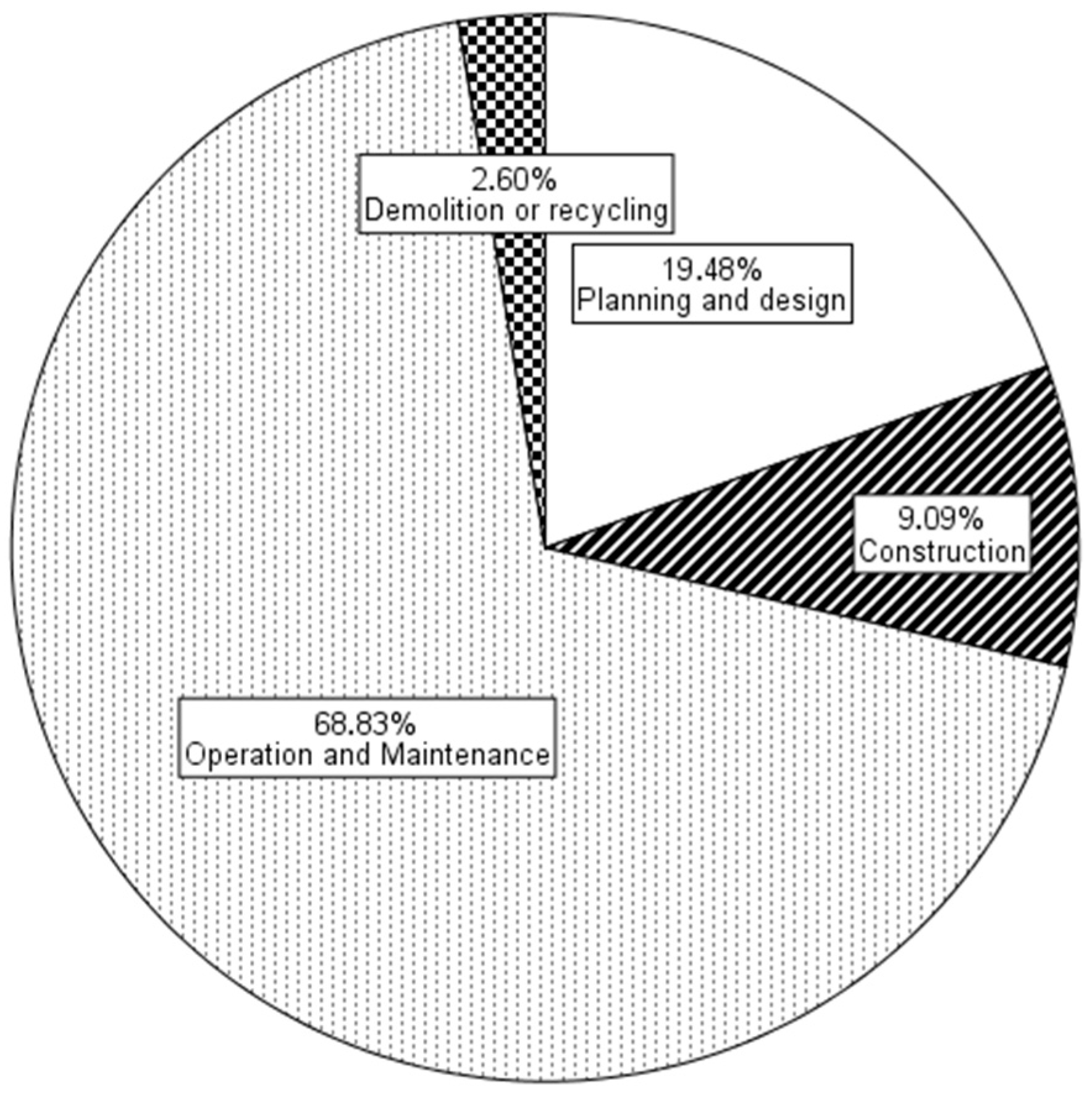
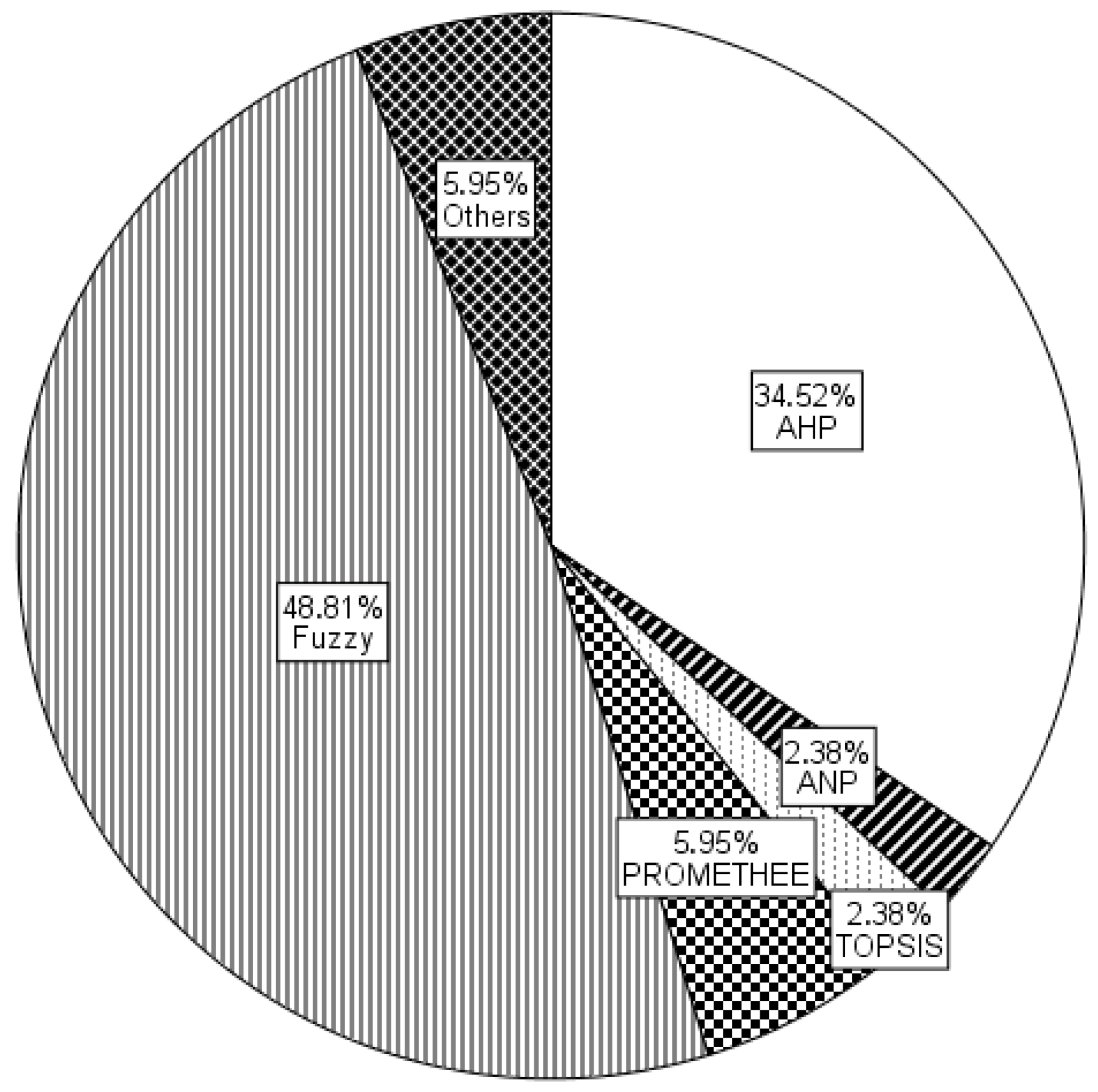
4.1. Overview
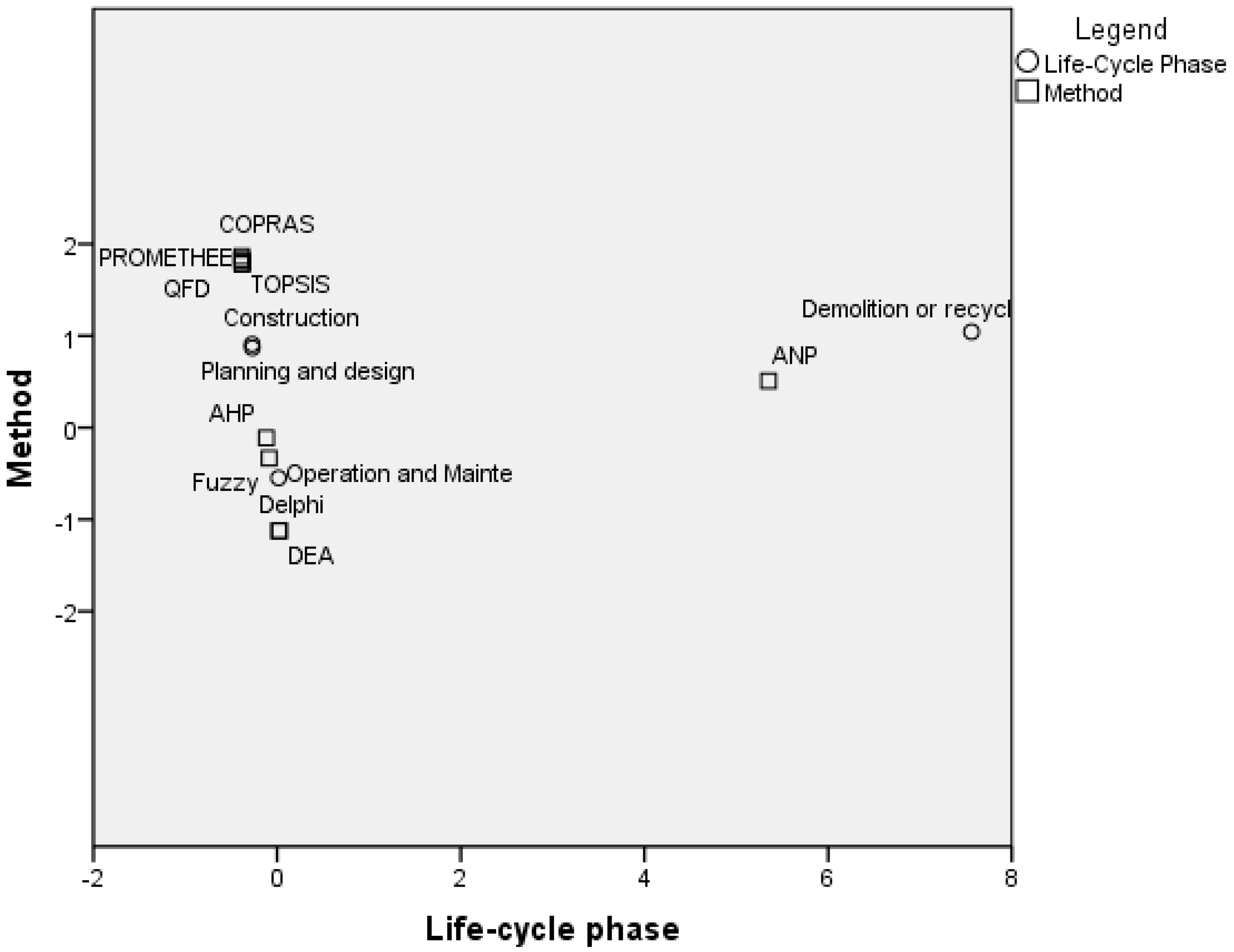
4.2. Statistical Analysis
5. New Concepts and Trends of MCDM
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zastrow, P.; Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Life cycle assessment of cost-optimized buttress earth-retaining walls: A parametric study. J. Clean. Prod. 2017, 140, 1037–1048. [Google Scholar] [CrossRef]
- Sierra, L.A.; Pellicer, E.; Yepes, V. Social sustainability in the lifecycle of chilean public infrastructure. J. Constr. Eng. Manag. 2016, 142, 05015020. [Google Scholar] [CrossRef]
- Pellicer, E.; Sierra, L.A.; Yepes, V. Appraisal of infrastructure sustainability by graduate students using an active-learning method. J. Clean. Prod. 2016, 113, 884–896. [Google Scholar] [CrossRef]
- Waas, T.; Hugé, J.; Block, T.; Wright, T.; Benitez-Capistros, F.; Verbruggen, A. Sustainability Assessment and Indicators: Tools in a Decision-Making Strategy for Sustainable Development. Sustainability 2014, 6, 5512–5534. [Google Scholar] [CrossRef]
- Balali, V.; Mottaghi, A.; Shoghli, O.; Golabchi, M. Selection of appropriate material, construction technique, and structural system of bridges by use of multicriteria decision-making method. Transp. Res. Rec. J. Transp. Res. Board 2014, 2431, 79–87. [Google Scholar] [CrossRef]
- Dutil, Y.; Rousse, D.; Quesada, G. Sustainable buildings: An ever evolving target. Sustainability 2011, 3, 443–464. [Google Scholar] [CrossRef]
- Malekly, H.; Meysam Mousavi, S.; Hashemi, H. A fuzzy integrated methodology for evaluating conceptual bridge design. Expert Syst. Appl. 2010, 37, 4910–4920. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple attributes Decision Making: Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Liou, J.J.H.; Tzeng, G.-H. Comments on “Multiple criteria decision making (MCDM) methods in economics: An overview”. Technol. Econ. Dev. Econ. 2012, 18, 672–695. [Google Scholar] [CrossRef]
- Liou, J.J.H. New concepts and trends of MCDM for tomorrow—In honor of Professor Gwo-Hshiung Tzeng on the occasion of his 70th birthday. Technol. Econ. Dev. Econ. 2013, 19, 367–375. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Shen, K.-Y. New Concepts and Trends of Hybrid Multiple Criteria Decision Making; CRC Press; Taylor and Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; CRC Press; Taylor and Francis Group: Boca Raton, FL, USA, 2011. [Google Scholar]
- Hajkowicz, S.; Collins, K. A review of multiple criteria analysis for water resource planning and management. Water Resour. Manag. 2007, 21, 1553–1566. [Google Scholar] [CrossRef]
- De Brito, M.M.; Evers, M. Multi-criteria decision-making for flood risk management: A survey of the current state of the art. Nat. Hazards Earth Syst. Sci. 2016, 16, 1019–1033. [Google Scholar] [CrossRef]
- Podvezko, V. The Comparative Analysis of MCDA Methods SAW and COPRAS. Eng. Econ. 2011, 22, 134–146. [Google Scholar] [CrossRef]
- Tamiz, M.; Jones, D.; Romero, C. Goal programming for decision making: An overview of the current state-of-the-art. Eur. J. Oper. Res. 1998, 111, 569–581. [Google Scholar] [CrossRef]
- Ballestero, E. Compromise programming: A utility-based linear-quadratic composite metric from the trade-off between achievement and balanced (non-corner) solutions. Eur. J. Oper. Res. 2007, 182, 1369–1382. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Podinovski, V.V. Optimal weights in DEA models with weight restrictions. Eur. J. Oper. Res. 2016, 254, 916–924. [Google Scholar] [CrossRef]
- Görener, A. Comparing AHP and ANP: An application of strategic decisions making in a manufacturing company. Int. J. Bus. Soc. Sci. 2012, 3, 194–208. [Google Scholar]
- Bana e Costa, C.A.; Chagas, M.P. A career choice problem: An example of how to use MACBETH to build a quantitative value model based on qualitative value judgments. Eur. J. Oper. Res. 2004, 153, 323–331. [Google Scholar] [CrossRef]
- Behzadian, M.; Kazemzadeh, R.B.; Albadvi, A.; Aghdasi, M. PROMETHEE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2010, 200, 198–215. [Google Scholar] [CrossRef]
- Govindan, K.; Jepsen, M.B. ELECTRE: A comprehensive literature review on methodologies and applications. Eur. J. Oper. Res. 2016, 250, 1–29. [Google Scholar] [CrossRef]
- Sarabando, P.; Dias, L.C. Simple procedures of choice in multicriteria problems without precise information about the alternatives’ values. Comput. Oper. Res. 2010, 37, 2239–2247. [Google Scholar] [CrossRef]
- Shahin, A. Quality Function Deployment: A Comprehensive Review; Department of Management, University of Isfahan: Isfahan, Iran, 2005; pp. 1–25. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A. Determination of an Efficient Contractor by Using the New Method of Multicriteria Assessment, International Symposium for “The Organization and Management of Construction”. In Shaping Theory and Practice, Vol. 2: Managing the Construction Project and Managing Risk, CIB W 65; Langford, D.A., Retik, A., Eds.; E and FN SPON: London, UK; Weinheim, Germany; New York, NY, USA; Tokyo, Japan; Melbourne, Australia; Madras, India, 1996; pp. 94–104. [Google Scholar]
- Aghdaie, M.H.; Zolfani, S.H.; Zavadskas, E.K. Prioritizing constructing projects of municipalities based on AHP and COPRAS-G: A case study about footbridges in Iran. Balt. J. Road Bridge Eng. 2012, 7, 145–153. [Google Scholar] [CrossRef]
- Liou, J.J.H.; Tamosaitiene, J.; Zavadskas, E.K.; Tzeng, G.-H. New hybrid COPRAS-G MADM Model for improving and selecting suppliers in green supply chain management. Int. J. Prod. Res. 2016, 54, 114–134. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Elhag, T.M.S. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst. Appl. 2006, 31, 309–319. [Google Scholar] [CrossRef]
- Gu, X.; Wang, Y.; Yang, B. Method for selecting the suitable bridge construction projects with interval-valued intuitionistic Fuzzy information. Int. J. Digit. Content Technol. Appl. 2011, 5, 201–206. [Google Scholar]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Liu, J.; Elhag, T.M.S. An integrated AHP-DEA methodology for bridge risk assessment. Comput. Ind. Eng. 2008, 54, 513–525. [Google Scholar] [CrossRef]
- Gervásio, H.; Da Silva, L.S. A probabilistic decision-making approach for the sustainable assessment of infrastructures. Expert Syst. Appl. 2012, 39, 7121–7131. [Google Scholar] [CrossRef]
- Farkas, A. Multi-criteria comparison of bridge designs. Acta Polytech. Hung. 2011, 8, 173–191. [Google Scholar]
- Abu Dabous, S.; Alkass, S. Decision support method for multi-criteria selection of bridge rehabilitation strategy. Constr. Manag. Econ. 2008, 26, 883–893. [Google Scholar] [CrossRef]
- Huang, Q.; Ren, Y.; Lin, Y.-Z. Application of uncertain type of AHP to the condition assessment of cable-stayed bridges 1. J. Southeast Univ. 2007, 23, 599–603. [Google Scholar]
- Torres-Machí, C.; Chamorro, A.; Pellicer, E.; Yepes, V.; Videla, C. Sustainable pavement management: Integrating economic, technical, and environmental aspects in decision making. Transp. Res. Rec. 2015, 2523, 56–63. [Google Scholar] [CrossRef]
- Lu, I.-Y.; Kuo, T.; Lin, T.-S.; Tzeng, G.-H.; Huang, S.-L. Multicriteria decision analysis to develop effective sustainable development strategies for enhancing competitive advantages: Case of the TFT-LCD industry in Taiwan. Sustainability 2016, 8, 646. [Google Scholar] [CrossRef]
- Saaty, T.L.; Takizawa, M. Dependence and independence: From linear hierarchies to nonlinear networks. Eur. J. Oper. Res. 1986, 26, 229–237. [Google Scholar] [CrossRef]
- Lu, S.T.; Lin, C.W.; Ko, P.H. Application of Analytic Network Process (ANP) in assessing construction risk of urban bridge project. In Proceedings of the Second International Conference on Innovative Computing, Information and Control (ICICIC), Kumamoto, Japan, 5–7 September 2007; pp. 1–4.
- Brans, J.P.; Mareschal, B.; Vincke, P. PROMETHEE: A new family of outranking methods in multicriteria analysis. Oper. Res. 1984, 408–421. [Google Scholar]
- Kogure, M.; Akao, Y. Quality function deployment and CWQC in Japan. Qual. Prog. 1983, 16, 25–29. [Google Scholar]
- Osorio Gómez, J.C. Fuzzy QFD for multicriteria decision making—Application example. Prospectiva 2011, 9, 22–29. [Google Scholar]
- Dalkey, N.; Helmer, O. An experimental application of the Delphi method to the use of experts. Manag. Sci. 1963, 9, 458–467. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Theory 1989, 1, 1–24. [Google Scholar]
- Lin, Y.; Chen, M.; Liu, S. Theory of grey systems: Capturing uncertainties of grey information. Kybernetes 2004, 33, 196–218. [Google Scholar] [CrossRef]
- Zavadskas, E.; Kaklauskas, A.; Turskis, Z.; Tamošaitien, J. Multi-attribute decision-making model by applying grey numbers. Inst. Math. Inform. Vilnius 2009, 20, 305–320. [Google Scholar]
- Zavala, G.R.; Nebro, A.J.; Luna, F.; Coello Coello, C.A. A survey of multi-objective metaheuristics applied to structural optimization. Struct. Multidiscip. Optim. 2013, 49, 537–558. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; The MIT Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948.
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man. Cybern. B 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Geem, Z.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Luo, Y.; Hua, Z.-S. A note on group decision-making based on concepts of ideal and anti-ideal points in a fuzzy environment. Math. Comput. Model. 2007, 46, 1256–1264. [Google Scholar] [CrossRef]
- Kuo, M.-S.; Tzeng, G.-H.; Huang, W.-C. Group decision-making based on concepts of ideal and anti-ideal points in a fuzzy environment. Math. Comput. Model. 2007, 45, 324–339. [Google Scholar] [CrossRef]
- Ardeshir, A.; Mohseni, N.; Behzadian, K.; Errington, M. Selection of a bridge construction site using fuzzy analytical hierarchy process in geographic information system. Arab. J. Sci. Eng. 2014, 39, 4405–4420. [Google Scholar] [CrossRef]
- Utomo, C.; Idrus, A. Value—Based Group Decision on Support Bridge Selection. World Acad. Sci. Eng. Technol. 2010, 4, 188–193. [Google Scholar]
- Joshi, P.K.; Sharma, P.C.; Upadhyay, S.; Sharma, S. Multi objective Fuzzy decision making approach for selection of type of caisson for bridge foundation. Indian J. Pure Appl. Math. 2004, 35, 783–791. [Google Scholar]
- Ugwu, O.O.; Kumaraswamy, M.M.; Wong, A.; Ng, S.T. Sustainability appraisal in infrastructure projects (SUSAIP): Part 2: A case study in bridge design. Autom. Constr. 2006, 15, 229–238. [Google Scholar] [CrossRef]
- Moore, C.J.; Miles, J.C.; Rees, D.W.G. Decision support for conceptual bridge design. Artif. Intell. Eng. 1996, 11, 259–272. [Google Scholar] [CrossRef]
- Ohkubo, S.; Dissanayake, P.B.R.; Taniwaki, K. An approach to multicriteria fuzzy optimization of a prestressed concrete bridge system considering cost and aesthetic feeling. Struct. Optim. 1998, 15, 132–140. [Google Scholar] [CrossRef]
- Itoh, Y.; Sunuwar, L.; Hirano, T.; Hammad, A.; Nishido, T. Bridge type selection system incorporating environmental impacts. J. Glob. Environ. Eng. 2000, 6, 81–101. [Google Scholar]
- Wang, H.-L.; Zhang, Z.; Qin, S.-F.; Huang, C.-L. Fuzzy optimum model of semi-structural decision for lectotype. China Ocean Eng. 2001, 15, 453–466. [Google Scholar]
- Jakiel, P.; Fabianowski, D. FAHP model used for assessment of highway RC bridge structural and technological arrangements. Expert Syst. Appl. 2015, 42, 4054–4061. [Google Scholar] [CrossRef]
- Yepes, V.; Martí, J.V.; García-Segura, T. Cost and CO2 emission optimization of precast-prestressed concrete U-beam road bridges by a hybrid glowworm swarm algorithm. Autom. Constr. 2015, 49, 123–134. [Google Scholar] [CrossRef]
- Camp, C.V.; Assadollahi, A. CO2 and cost optimization of reinforced concrete footings using a hybrid big bang-big crunch algorithm. Struct. Multidiscip. Optim. 2013, 48, 411–426. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Martí, J.V.; Alcalá, J. Optimization of concrete I-beams using a new hybrid glowworm swarm algorithm. Latin Am. J. Solids Struct. 2014, 11, 1190–1205. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Alcalá, J.; Pérez-López, E. Hybrid harmony search for sustainable design of post-tensioned concrete box-girder pedestrian bridges. Eng. Struct. 2015, 92, 112–122. [Google Scholar] [CrossRef]
- Martí, J.V.; García-Segura, T.; Yepes, V. Structural design of precast-prestressed concrete U-beam road bridges based on embodied energy. J. Clean. Prod. 2016, 120, 231–240. [Google Scholar] [CrossRef]
- De Medeiros, G.F.; Kripka, M. Optimization of reinforced concrete columns according to different environmental impact assessment parameters. Eng. Struct. 2014, 59, 185–194. [Google Scholar] [CrossRef]
- Martinez-Martin, F.J.; Gonzalez-Vidosa, F.; Hospitaler, A.; Yepes, V. Multi-objective optimization design of bridge piers with hybrid heuristic algorithms. J. Zhejiang Univ. Sci. A 2012, 13, 420–432. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V.; Alcalá, J. Sustainable design using multiobjective optimization of high-strength concrete I-beams. In Proceedings of the 2014 International Conference on High Performance and Optimum Design of Structures and Materials HPSM/OPTI, Ostend, Belgium, 9–11 June 2014; pp. 347–358.
- Yepes, V.; García-Segura, T.; Moreno-Jiménez, J.M. A cognitive approach for the multi-objective optimization of RC structural problems. Arch. Civ. Mech. Eng. 2015, 15, 1024–1036. [Google Scholar] [CrossRef]
- García-Segura, T.; Yepes, V. Multiobjective optimization of post-tensioned concrete box-girder road bridges considering cost, CO2 emissions, and safety. Eng. Struct. 2016, 125, 325–336. [Google Scholar] [CrossRef]
- El-Diraby, T.E.; O’Connor, J.T. Model for evaluationg bridge construction plans. J. Constr. Eng. Manag. 2001, 127, 399–405. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D.; Wang, H. Bidding strategy to support decision-making by integrating Fuzzy AHP and regression-based simulation. Autom. Constr. 2013, 35, 517–527. [Google Scholar] [CrossRef]
- Pan, N.-F. Fuzzy AHP approach for selecting the suitable bridge construction method. Autom. Constr. 2008, 17, 958–965. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Gitinavard, H.; Siadat, A. A new hesitant fuzzy Analytical Hierarchy Process method for decision-making problems under uncertainty. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Piscataway, NJ, USA, 9–12 December 2014; pp. 622–626.
- Chen, Y.; Okudan, G.E.; Riley, D.R. Decision support for construction method selection in concrete buildings: Prefabrication adoption and optimization. Autom. Constr. 2010, 19, 665–675. [Google Scholar] [CrossRef]
- Chen, T.-Y. The extended linear assignment method for multiple criteria decision analysis based on interval-valued intuitionistic fuzzy sets. Appl. Math. Model. 2014, 38, 2101–2117. [Google Scholar] [CrossRef]
- Bitarafan, M.; Arefi, S.L.; Zolfani, S.H.; Mahmoudzadeh, A. Selecting the best design scenario of the smart structure of bridges for probably future earthquakes. Procedia Eng. 2013, 57, 193–199. [Google Scholar] [CrossRef]
- Ei-Mikawi, M.; Mosallam, A.S. A methodology for evaluation of the use of advanced composites in structural civil engineering applications. Compos. Part B 1996, 27, 203–215. [Google Scholar] [CrossRef]
- Sobanjo, J.O.; Stukhart, G.; James, R.W. Evaluation of projects for rehabilitation of highway bridges. J. Struct. Eng. 1994, 120, 81–99. [Google Scholar] [CrossRef]
- Abu Dabous, S.; Alkass, S. A multi-attribute ranking method for bridge management. Eng. Constr. Archit. Manag. 2010, 17, 282–291. [Google Scholar] [CrossRef]
- Yehia, S.; Abudayyeh, O.; Fazal, I.; Randolph, D. A decision support system for concrete bridge deck maintenance. Adv. Eng. Softw. 2008, 39, 202–210. [Google Scholar] [CrossRef]
- Chassiakos, A.P.; Vagiotas, P.; Theodorakopoulos, D.D. A knowledge-based system for maintenance planning of highway concrete bridges. Adv. Eng. Softw. 2005, 36, 740–749. [Google Scholar] [CrossRef]
- Sabatino, S.; Frangopol, D.M.; Dong, Y. Sustainability-informed maintenance optimization of highway bridges considering multi-attribute utility and risk attitude. Eng. Struct. 2015, 102, 310–321. [Google Scholar] [CrossRef]
- Adey, B.; Hajdin, R.; Brühwiler, E. Risk-based approach to the determination of optimal interventions for bridges affected by multiple hazards. Eng. Struct. 2003, 25, 903–912. [Google Scholar] [CrossRef]
- Aktan, A.E.; David, N.F.; Vikram, L.B.; Helmicki, A.J.; Hunt, V.J.; Shelley, S.J. Condition assessment for bridge managment. J. Infrastruct. Syst. 1996, 2, 108–117. [Google Scholar] [CrossRef]
- Al-Wazeer, A.; Harris, B.; Dekelbab, W. Applying Fuzzy concept to bridge managment. Publics Roads 2016, 72, 28–37. [Google Scholar]
- Andrić, J.M.; Lu, D.G. Risk assessment of bridges under multiple hazards in operation period. Saf. Sci. 2016, 83, 80–92. [Google Scholar] [CrossRef]
- Anoop, M.B.; Balaji Rao, K. Application of Fuzzy sets for remaining life assessment of corrosion affected reinforced concrete bridge girders. J. Perform. Constr. Facil. 2007, 21, 166–171. [Google Scholar] [CrossRef]
- Caterino, N.; Iervolino, I.; Manfredi, G.; Cosenza, E. Comparative analysis of multi-criteria decision-making methods for seismic structural retrofitting. Comput. Civ. Infrastruct. Eng. 2009, 24, 432–445. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Hoang, N.-D. Risk score inference for bridge maintenance project using evolutionary Fuzzy least squares support vector machine. J. Comput. Civ. Eng. 2012, 28, 1–9. [Google Scholar] [CrossRef]
- Cheng, J.; Xiao, R. An efficient method for identification of risk factors. Sci. China Ser. E 2009, 52, 3626–3631. [Google Scholar] [CrossRef]
- Dan, D.; Sun, L.; Yang, Z.; Xie, D. The application of a fuzzy inference system and analytical hierarchy process based online evaluation framework to the donghai bridge health monitoring system. Smart Struct. Syst. 2014, 14, 129–144. [Google Scholar] [CrossRef]
- De Brito, J.; Branco, F.A.; Thoft-Christensen, P.; Sørensen, J.D. An expert system for concrete bridge management. Eng. Struct. 1997, 19, 519–526. [Google Scholar] [CrossRef]
- Deng, J.; Li, J.; Fang, X. Condition evaluation of existing long-span bridges using fuzzy based analytic hierarchy process. Adv. Mater. Res. 2011, 163–167, 3328–3331. [Google Scholar] [CrossRef]
- Duchaczek, A.; Skorupka, D. Evaluation of probability of bridge damage as a result of terrorist attack. Arch. Civ. Eng. 2013, 59, 215–227. [Google Scholar] [CrossRef]
- Furuta, H.; Shiraishi, N.; Umano, M.; Kawakami, K. An expert system for damage assessment of a reinforced concrete bridge deck. Fuzzy Sets Syst. 1991, 44, 449–457. [Google Scholar]
- Kawamura, K.; Miyamoto, A. Condition state evaluation of existing reinforced concrete bridges using neuro-Fuzzy hybrid system. Comput. Struct. 2003, 81, 1931–1940. [Google Scholar] [CrossRef]
- Kushida, M.; Miyamoto, A. Modal Logic to evaluate a knowledge-based bridge rating system. Comput. Civ. Infrastruct. Eng. 1998, 13, 227–236. [Google Scholar] [CrossRef]
- Lee, J.; Liu, K.F.R.; Chiang, W. A Fuzzy Petri net-based expert system and its application to damage assessment of bridges. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Piscataway, NJ, USA, 10–12 November 1998; Volume 29, pp. 350–369.
- Li, Q.; Xu, Y.-L.; Zheng, Y.; Guo, A.-X.; Wong, K.-Y.; Xia, Y. SHM-based F-AHP bridge rating system with application to Tsing Ma Bridge. Front. Archit. Civ. Eng. China 2011, 5, 465–478. [Google Scholar] [CrossRef]
- Li, Y.; Wang, T.; Song, X.; Li, G. Optimal resource allocation for anti-terrorism in protecting overpass bridge based on AHP risk assessment model. KSCE J. Civ. Eng. 2015, 20, 309–322. [Google Scholar] [CrossRef]
- Liang, M.-T.; Wu, J.-H.; Liang, C.-H. Applying Fuzzy mathematics to evaluating the membership of existing reinforced concrete bridges in Taipei. J. Mar. Sci. Technol. 2000, 8, 16–29. [Google Scholar]
- Liang, M.-T.; Chu, T.-B.; Tsao, W.-H.; Yeh, C.-J. Determining the repair ranking of existing RC bridges using multi-pole fuzzy pattern recognition evaluation method. J. Mar. Sci. Technol. 2006, 29, 159–173. [Google Scholar]
- Liang, M.-T.; Lin, C.-M.; Yeh, C.-J. Comparison matrix method and its applications to damage evaluation for existing reinforced concrete bridges. J. Mar. Sci. Technol. 2003, 11, 70–82. [Google Scholar]
- Liang, M.-T.; Wu, J.-H.; Liang, C.-H. Multiple layer Fuzzy evaluation for existing reinforced concrete bridges. J. Infrastruct. Syst. 2001, 7, 144–159. [Google Scholar] [CrossRef]
- Lounis, Z. Risk-based maintenance optimization of aging highway bridge decks. Adv. Eng. Struct. Mech. Constr. 2006, 140, 723–734. [Google Scholar]
- Min, Z.; Jingshan, B.; Xiaolei, Z. Quick analysis method for bridge seismic risk based on AHP. In Proceedings of the IEEE International Conference on Electric Technology and Civil Engineering, Piscataway, NJ, USA, 22–24 April 2011; pp. 575–577.
- Moufti, S.A.; Zayed, T.; Dabous, S.A. Fuzzy defect based condition assessment of concrete bridges. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Piscataway, NJ, USA, 24–28 June 2013; pp. 1489–1494.
- Ning, X.-L.; Tan, P.; Huang, D.-Y.; Zhou, F.-L. Application of adaptative fuzzy sliding mode control to a seismically excited highway bridge. Struct. Control Heal. Monit. 2009, 16, 639–656. [Google Scholar] [CrossRef]
- Ozbek, M.E.; De la Garza, J.M.; Triantis, K. Efficiency measurement of bridge maintenance using data envelopment analysis. J. Infrastruct. Syst. 2010, 342, 31–39. [Google Scholar] [CrossRef]
- Park, K.-S.; Koh, H.-M.; Ok, S.-Y.; Seo, C.-W. Fuzzy supervisory control of earthquake-excited cable-stayed bridges. Eng. Struct. 2005, 27, 1086–1100. [Google Scholar] [CrossRef]
- Rashidi, M.; Gibson, P. Proposal of a methodology for bridge condition assessment. In Proceedings of the 2011 Australasian Transport Research Forum, Adelaide, Australia, 28–30 September 2011; pp. 1–15.
- Rashidi, M.; Gibson, P. A methodology for bridge condition evaluation. J. Civ. Eng. Archit. 2012, 6, 1149–1157. [Google Scholar]
- Saito, M.; Sinha, K.C. Delphi study on bridge condition rating and effects of improvements. J. Transp. Eng. 1991, 117, 320–334. [Google Scholar] [CrossRef]
- Sasmal, S.; Ramanjaneyulu, K. Condition evaluation of existing reinforced concrete bridges using Fuzzy based analytic hierarchy approach. Expert Syst. Appl. 2008, 35, 1430–1443. [Google Scholar] [CrossRef]
- Sasmal, S.; Ramanjaneyulu, K.; Gopalakrishan, S.; Lakshmanan, N. Fuzzy logic based condition rating of existing reinforced concrete bridges. J. Perform. Constr. Facil. 2006, 20, 261–273. [Google Scholar] [CrossRef]
- Stewart, M.G. Reliability-based assessment of ageing bridges using risk ranking and life cycle cost decision analyses. Reliab. Eng. Syst. Saf. 2001, 74, 263–273. [Google Scholar] [CrossRef]
- Tarighat, A. Model based damage detection of concrete bridge deck using adaptive neuro-Fuzzy inference system. Int. J. Civ. Eng. 2013, 11, 170–181. [Google Scholar]
- Tarighat, A.; Miyamoto, A. Fuzzy concrete bridge deck condition rating method for practical bridge management system. Expert Syst. Appl. 2009, 36, 12077–12085. [Google Scholar] [CrossRef]
- Chiang, W.; Liu, K.R.R.; Lee, J. Bridge damage assessment through Fuzzy petri net based expert system. 2000, 14, 141–149. [Google Scholar] [CrossRef]
- Ugwu, O.O.; Kumaraswamy, M.M.; Kung, F.; Ng, S.T. Object-oriented framework for durability assessment and life cycle costing of highway bridges. Autom. Constr. 2005, 14, 611–632. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, C. A Fuzzy system for concrete bridge damage diagnosis. Comput. Struct. 2002, 80, 629–641. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Chen, C.Y. Concrete bridge deterioration diagnosis using Fuzzy inference system. J. Adv. Eng. Softw. 2001, 32, 317–325. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Elhag, T.M.S. A Fuzzy group decision making approach for bridge risk assessment. Comput. Ind. Eng. 2007, 53, 137–148. [Google Scholar] [CrossRef]
- Liu, M.; Frangopol, D.M. Optimal bridge maintenance planning based on probabilistic performance prediction. Eng. Struct. 2004, 26, 991–1002. [Google Scholar] [CrossRef]
- Liu, M.; Frangopol, D.M. Multiobjective maintenance planning optimization for deteriorating bridges considering condition, safety, and life-cycle cost. J. Struct. Eng. 2003, 131, 833–842. [Google Scholar] [CrossRef]
- Neves, L.A.C.; Frangopol, D.M.; Cruz, P.J.S. Probabilistic lifetime-oriented multiobjective optimization of bridge maintenance: Single maintenance type. J. Struct. Eng. 2006, 132, 991–1005. [Google Scholar] [CrossRef]
- Kim, S.; Frangopol, D.M.; Zhu, B. Probabilistic optimum inspection/repair planning to extend lifetime of deteriorating structures. J. Perform. Constr. Facil. 2011, 25, 534–545. [Google Scholar] [CrossRef]
- Dong, Y.; Frangopol, D.M.; Saydam, D. Time-variant sustainability assessment of seismically vulnerable bridges subjected to multiple hazards. Earthq. Eng. Struct. Dyn. 2013, 42, 1451–1467. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Soliman, M. Life-cycle of structural systems: Recent achievements and future directions. Struct. Infrastruct. Eng. 2015, 12, 1–20. [Google Scholar] [CrossRef]
- Chen, Z.; Abdullah, A.B.; Anumba, C.J.; Li, H. ANP experiment for demolition plan evaluation. J. Constr. Eng. Manag. 2013, 138, 51–60. [Google Scholar] [CrossRef]
- IBM Corp. IBM SSPS Statics for Windows, version 22.00; IBM Corp.: Armonk, NY, USA, 2013.
- Gölcük, I.; Baykasoglu, A. An analysis of DEMATEL approaches for criteria interaction handling within ANP. Expert Syst. Appl. 2016, 46, 346–366. [Google Scholar] [CrossRef]
- Huang, K.-W.; Huang, J.-H.; Tzeng, G.-H. New hybrid multiple attribute decision-making model for improving competence sets: Enhancing a company’s core competitiveness. Sustainability 2016, 8, 175. [Google Scholar] [CrossRef]
- Yang, Y.-P.O.; Leu, J.-D.; Tzeng, G.-H. A novel hybrid MCDM model combined with DEMATEL and ANP with applications. Int. J. Oper. Res. 2008, 5, 160–168. [Google Scholar]
- Ou Yang, Y.-P.; Shieh, H.-M.; Tzeng, G.-H. A VIKOR technique based on DEMATEL and ANP for information security risk control assessment. Inf. Sci. 2013, 232, 482–500. [Google Scholar] [CrossRef]
- Shen, K.-Y.; Hu, S.-K.; Tzeng, G.-H. Financial modeling and improvement planning for the life insurance industry by using a rough knowledge based hybrid MCDM model. Inf. Sci. 2017, 375, 296–313. [Google Scholar] [CrossRef]
- Liou, J.J.H.; Tsai, C.; Lin, R.; Tzeng, G.-H. A modified VIKOR multiple-criteria decision method for improving domestic airlines service quality. J. Air Transp. Manag. 2011, 17, 57–61. [Google Scholar] [CrossRef]
- Shen, K.-Y.; Yan, M.-R.; Tzeng, G.-H. Combining VIKOR-DANP model for glamor stock selection and stock performance improvement. Knowl.-Based Syst. 2014, 58, 86–97. [Google Scholar] [CrossRef]
- Tsui, C.-W.; Tzeng, G.-H.; Wen, U.-P. A hybrid MCDM approach for improving the performance of green suppliers in the TFT-LCD industry. Int. J. Prod. Res. 2015, 53, 6436–6454. [Google Scholar] [CrossRef]
- Liou, J.J.H.; Chuang, Y.-C.; Tzeng, G.-H. A fuzzy integral-based model for supplier evaluation and improvement. Inf. Sci. 2014, 266, 199–217. [Google Scholar] [CrossRef]
- Canto-Perello, J.; Martinez-Leon, J.; Curiel-Esparza, J.; Martin-Utrillas, M. Consensus in prioritizing river rehabilitation projects through the integration of social, economic and landscape indicators. Ecol. Indic. 2017, 72, 659–666. [Google Scholar] [CrossRef]
- Hu, K.-H.; Chen, F.-H.; Tzeng, G.-H. Evaluating the improvement of sustainability of sports industry policy based on MADM. Sustainability 2016, 8, 606. [Google Scholar] [CrossRef]
- Chang, D.-S.; Chen, S.-H.; Hsu, C.-W.; Hu, A.; Tzeng, G.-H. Evaluation framework for a alternative fuel vehicles: Sustainable development perspective. Sustainability 2015, 7, 11570–11594. [Google Scholar] [CrossRef]
| MADM Group | MADM Method | Reference |
|---|---|---|
| Scoring methods | Simple additive weighting (SAW) | [15] |
| Complex proportional assessment (COPRAS) | [15] | |
| Distance-based methods | Goal programming (GP) | [16] |
| Compromise programming (CP) | [17] | |
| Technique for order of preference by similarity to ideal solution (TOPSIS) | [18] | |
| Multicriteria optimization and compromise solution (VIKOR) | [18] | |
| Data envelopment analysis (DEA) | [19] | |
| Pairwise comparison methods | Analytic hierarchy process (AHP) | [20] |
| Analytic network process (ANP) | [20] | |
| Measuring Attractiveness by a Categorical Based Evaluation Technique (MACBETH) | [21] | |
| Outranking methods | Preference ranking organization method for enrichment of evaluations (PROMETHEE) | [22] |
| Elimination and choice expressing reality (ELECTRE) | [23] | |
| Utility/Valuate methods | Multi-attribute utility theory (MAUT) | [24] |
| Multi-attribute value theory (MAVT) | [24] | |
| Other | Quality function development (QFD) | [25] |
| Reference | MADM Method | Criteria |
|---|---|---|
| [64] | Fuzzy | Cost and aesthetic feeling |
| [65] | Other | Cost, driving comfort, landscape and environmental impact (CO2 and energy) |
| [61] | Fuzzy | Cost, plumbness control, depth, area of site, non-availability of skilled workers, and time required |
| [62] | SUSAIP | Economic (direct cost, indirect cost), environmental (land use, water, air, noise ecology, visual impact, waste management), societal (cultural heritage, public access, public perception), resource utilization (site access, material availability, type, constructability, reusability, quality assurance) health and safety (occupational, public), project administration (contract) and procurement method |
| [60] | AHP (value analysis) | Cost (initial cost and LCC) and function (received load super structure, resist shift super structure, receive force earth quake, allow mini-distortion, resist strike water, resist erosion water, fix element furnish structure, beautify appearance) |
| [7] | Fuzzy QFD and Fuzzy TOPSIS | Design complexity, speed of construction, durability, environment, aesthetics, construction complexity, and geometric design |
| [66] | Fuzzy AHP | Economic rationale (production cost, construction period, production cost), function completeness (deformation adaptability, anti-wind ability), environmental adaptability and advanced technology |
| [36] | AHP and KSIM (Kane Simulation Technique) | Engineering feasibility, capital cost, maintenance, aesthetics, environmental impact and durability |
| [27] | AHP and COPRAS-G | Environmental (traffic related, accident related, average speed limit), socio-economic (rate of transportation of families, children and business dates, situation of area growth in the future, special importance of each road or boulevard to the city, vision of roads or boulevards about issues) and total cost |
| [35] | AHP and PROMETHEE | Environmental (waste production, abiotic, depletion, acidification, eutrophication, global warning, human toxicity, photochemical oxidation, ozone depletion layer, and terrestrial ecotoxicity), economic (construction cost, maintenance cost, and end of life cost), and social (vehicle operation cost, driver delay cost, and safety cost) |
| [59] | Fuzzy AHP in GIS | Transportation (minimizes the total distance traveled), economic, and morphology site |
| [5] | PROMETHEE | Cost, life cycle and durability, thermal influence and ability to build small and lightweight) |
| [5] | PROMETHEE | Cost, span, inspection and maintenance, construction speed, ease of construction, traffic load, dependence on imported technologies, architecture design, irregular geometric, complexity in construction, and symbolic and aesthetics |
| [67] | Fuzzy AHP | Bridge structure geometry adjustable to locality conditions (topography, resistance to natural hazards, and complexity of erection), mitigation of impact upon natural environment (project area minimization, minor interference on landscape and harmoniously integrated into landscape and contamination), structure design technologic ability (complete mechanization of manufacturing and construction process, assembly technology universalism, assembly work in various weather conditions), safety and sustainability of structure (design sub-criterion, structure design safety in challenging topography, structure design safety in natural hazards and contingencies), and economic criterion (total investment cost, project duration, and maintenance costs) |
| Reference | MADM Method | Criteria |
|---|---|---|
| [78] | Other | Safety, accessibility, carrying capacity, schedule, and budget (+project specific factors) |
| [80] | Fuzzy AHP | Quality (durability and sustainability), cost (damage cost and construction cost), safety (traffic conflict and site condition), duration (constructability and weather condition) and shape (landscape, geometry and environmental preservation) |
| [30] | Fuzzy TOPSIS | Quality, cost, safety, and duration |
| [79] | Fuzzy AHP and Monte Carlo | Construction (project complexity, government level, project duration and experience of project staff), environment (site condition, geologic types, climate, and cultural conditions), planning (design concepts, design drawings, construction method and interface management), and estimation (contractors fitness, indirect costs, direct costs and risk assessment) |
| [81] | Fuzzy AHP | Quality, cost, safety, duration and shape |
| [5] | PROMETHEE | Cost, usability in height, construction speed, environmental issues, quality of construction, module installation of deck and traffic interference |
| [83] | Fuzzy PROMETHEE | Durability, damage cost, construction cost, traffic conflict, site condition, weather condition, landscape and environmental effect |
| Reference | MADM Method | Criteria |
|---|---|---|
| [86] | Fuzzy AHP | Ratio of the average daily traffic (ADT) to the project cost (ADT/Cost), expected improvement in structural condition appraisal rating, deck geometry appraisal rating, clearance appraisal rating, load capacity appraisal rating, waterway adequacy appraisal rating, approach roadway alignment appraisal rating and in the expected extension in the bridge’s service life |
| [85] | AHP | Structural performance indicators, economic indicators, environmental aspects, codes and regulations, material availability and architectural aspects |
| [89] | Monte Carlo | Defect type, traffic load, river bed characteristics, environmental conditions, bridge age, foundation type and superstructure type |
| [88] | Other | Age, average daily traffic, corrosion, delamination, cracking and type of repair method (protective and non-protective) |
| [37] | Modified type of AHP | Agency cost (direct cost: material, labor, and equipment), user cost (indirect cost: delay cost, increased vehicle operating cost and, cost of accidents and crashes that may happen during the projects), bridge safety, useful life and environmental impact |
| [87] | AHP | Maximize bridge condition preservation and safety (condition rating, load carrying and capacity and seismic risk), maximize effectiveness of investment (average daily traffic (ADT) and supporting road type), and minimize bridge deficiency [vertical clearance, approach condition and draining system] |
| [84] | AHP | Reduce mortality and vulnerability, possibility of localization of technology, performance speed, performance costs and maintenance |
| [90] | Other | Economy (rebuilding cost), society (extra travel time, extra travel distance, and fatalities), and environment (CO2 emissions and energy consumption) |
| Reference | MADM Method | Criteria |
|---|---|---|
| [138] | ANP | Structure characteristics (type of structure, stability, scope of demolition and usage), conditions (safety risk on/off site, acceptable level of noise, proximity to adjacent structures), cost (machinery and manpower), experiences (familiarity with technologies, availability of equipment, availability of expertise), environmental impact and time (worksite preparation and entire demolition process) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penadés-Plà, V.; García-Segura, T.; Martí, J.V.; Yepes, V. A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design. Sustainability 2016, 8, 1295. https://doi.org/10.3390/su8121295
Penadés-Plà V, García-Segura T, Martí JV, Yepes V. A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design. Sustainability. 2016; 8(12):1295. https://doi.org/10.3390/su8121295
Chicago/Turabian StylePenadés-Plà, Vicent, Tatiana García-Segura, José V. Martí, and Víctor Yepes. 2016. "A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design" Sustainability 8, no. 12: 1295. https://doi.org/10.3390/su8121295
APA StylePenadés-Plà, V., García-Segura, T., Martí, J. V., & Yepes, V. (2016). A Review of Multi-Criteria Decision-Making Methods Applied to the Sustainable Bridge Design. Sustainability, 8(12), 1295. https://doi.org/10.3390/su8121295








