1. Introduction
The necessity of protecting the environment has increased in recent years. Advocating and promoting the use of green products is an effective way of protecting the environment. Consumers also pay attention to green products. A consumer research study indicated that around 80% of American consumers are willing to pay extra for green products [
1]. Consumers are more willing to buy products that are not environmentally harmful [
2]. A survey has shown that a correlation exists between environmental performance and firm’s competitive advantage [
3]. Given this finding, an increasing number of firms are adopting R&D strategies for green products as a powerful and competitive tool in the market. These green products include electric vehicles (EVs) and solar water heating. However, an increasing number of firms encounter problems because of the high R&D risks of green products. Governments exert significant efforts to assist companies involved. The government can promote the development of green product industry through subsidy incentive schemes and/or environmental policies, such as green legislation and fiscal policies (e.g., green taxation and subsidies). Subsidy incentive is common in practice, especially in the automotive industry. In America, President Barack Obama set an annual budget of $2.4 billion to support the development of EVs and batteries [
4]. In the country’s Fiscal Year 2015 budget, the Obama administration also included a provision that increased the maximum tax credit of EVs in 2014 to $10,000 [
5]. In 2010, the Chinese government pledged grants that allocated ¥60,000 for private purchases of new battery electric vehicles and ¥50,000 for plug-in hybrids in five major cities [
6]. Other governments, such as Canada, Germany, and Japan, implemented similar subsidy policies to support the development of EVs. These findings suggest that subsidy policies play an important role in promoting the sales of EVs [
7].
Supply chain management under the subsidy policy of the government has received significant attention from researchers. Previous studies addressed the effects of subsidy policies of the government using game theory [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22]. Despite the availability of these studies, only a few published articles explored the efficienci-es of subsidy policies of the government using game theory. Given this gap in research, we explore the effects of two subsidy policies (subsidizing the cost of greenness and subsidizing unit product) in a vertical supply chain system. The supply chain considered in our study consists of two firms (supplier and manufacturer). The manufacturer produces a final product that consists of two components (one component is provided by the supplier and the other is offered by the manufacturer); this is a fairly common assumption in relevant literature [
23,
24]. The components in our model are characterized by the degree of greenness; a high degree implies that the component if of good quality [
25]. We then incorporate the effects of the degree of greenness of products on the demand function. We utilized game and optimization theories to calculate and compare the optimal decisions for all players in two scenarios: (i) the government subsidizes the cost of manufacturer’s greenness efforts; and (ii) the government grants a per unit subsidy to the manufacturer for the demand for green product. Our model yields the following results: (i) when the value of price sensitivity is large enough, the government will adopt the second subsidy policy; (ii) if the value of price sensitivity is in a mediate level, the government will implement the first subsidy policy; and (iii) when the value of price sensitivity is low, supply chain members might not obtain subsidy from the government.
The remainder of this paper is structured as follows. Previous literature related to our topic is reviewed in the next section.
Section 3 develops the proposed models and discusses the optimal decisions in two different scenarios.
Section 4 offers a numerical analysis. Concluding remarks are presented in
Section 5. Proofs for all propositions are given in the
Appendix A.
2. Literature Review
Our study contributes to several streams of research, each of which is reviewed in this section. The first stream of research is composed of recent studies on sustainable supply chain management under the government subsidy incentive schemes. Many researches focused on the automobile supply chain management under the government subsidy policy. Diamond (2009) examined the relationship between government policies and the adoption of d hybrid-electric vehicles adoption using data from the U.S. [
8]. Huang et al. (2013) focused on two supply chains (i.e., fuel automobile supply chain, electric-and-fuel automobile supply chain), and examined the effects of subsidy policy of the government on the profits and social welfare of supply chain members [
7]. Luo et al. (2014) studied an automobile supply chain that consists of a manufacturer and a retailer, and investigated the effects of the government’s price–discount incentive scheme on the decision making of supply chain member [
9]. Huang et al. (2014) explored the effects of the government’s scrappage program on the optimal decisions of all players’ (i.e., government, manufacturer, and retailer); the results show that a scrappage program with a sufficiently large MSRP cutoff level and proper subsidy can efficiently promote sales [
10]. Zhang (2014) evaluated the effects of consumer trade-offs and government subsidies on EV production decisions [
11].
Researchers also investigated supply chain management under the government subsidy policy in other industries or fields. Mitraa and Webster (2008) focused on supply chain systems that consist of a manufacturer and a competitive remanufacturer and investigated the influences of government subsidies on remanufacturing activities [
12]. Bansal (2008) explored the effects of government subsidy policies in a situation where consumers are environmentally discerning, and their results revealed that the optimal policy depends on the magnitude of damage parameter associated with environmental externality [
13]. Aksen et al. (2009) explored the effects of subsidization agreement on collection and recovery operations; they found that the government should increase subsidy in a supportive model for the same collection rate and profitability ratio [
14]. Sheu (2011) investigated the effects of government intervention on the negotiations of supply chain members; they found that financial intervention of the government has a positive effect on the relative bargaining power of green supply chain members during negotiations [
15]. Sheu and Chen (2012) utilized a stage game theory model to study the influences of governmental taxation and subsidization on competition in a green supply chain [
16]. Ma et al. (2013) studied the influences of the government consumption-subsidy policy on the decisions of members in a dual-channel closed-loop supply chain [
17]. Wang et al. (2014) studied the effects of the government subsidy on the decisions of members in a supply chain for fashion remanufacturing under the two types of channel structure [
18]. Hu et al. (2014) investigated the market and social welfare in a green manufacturing industry, and their results showed that the effectiveness of Pigouvian tax and subsidy policies depend on product characteristics and market structures [
19]. Raz and Ovchinnikov (2015) considered how a government could coordinate the pricing and supply of public interest goods through government rebates and subsidies [
20]. Bi et al. (2016) considered green consumers in the supply chain and investigated the effects of subsidy policy of the government on firm decisions in two different situations [
21]. He et al. (2016) investigated the carbon emissions in a dual channel closed loop supply chain, their research suggested that a government may have to subsidize the e-tailer to maximize the social welfare [
22].
Second, several studies have been conducted to explore the quality cost sharing mechanism between manufacturer and supplier. Balachandran and Radhakrishnan (2005) considered a double moral hazard case in quality efforts and modeled the fixed share rate contract for allocating costs of internal failures [
24]. Zhu et al. (2007) investigated the roles of different channel members in a supply chain in quality improvement; they found that buyer involvement can significantly affect the profits of supply chain members [
26]. Chao et al. (2009) introduced two external quality cost sharing contracts to improve the quality of final product and to coordinate the supply chain [
23]. Lee et al. (2013) considered a supply chain with quality uncertainty and proposed a quality compensation contract to coordinate the supply chain [
27]. He et al. (2016) investigated the quality management of supply chain with the reference effects, and analyzed the decisions of supply chain members under the subsidy policies of manufacturer [
28].
To the best of our knowledge, only a few studies have investigated the effects of government different subsidy policies on supply chain quality management. In the present study, we incorporate the effect of the degree of greenness (or quality) of a product on demand and R&D cooperation between manufacturer and supplier. We also investigate the optimal decisions of all players under the subsidy policies of the government.
3. Model Development
The supply chain system considered in this study consists of two firms (i.e., supplier and manufacturer) and the government. The manufacturer produces and sells a final product that consists of two components. One component is provided by the supplier and the other component is offered by the manufacturer. Both firms are committed to the development of green products. The products are characterized by the degree of greenness [
25]; the green degree of the final product is affected by the degree of its components. We denote
as the green degree of component
offered by the supplier and
as the green degree of component
provided by the manufacturer. Expression
represents the green degree of the final product. Similar to previous studies [
29,
30], we assume that the sales function is linear to the degree of greenness of the final product, which is given by:
where
,
,
, and
are positive constants. In our model, we assume that the demand of the green product is linearly increasing in the degree of greenness. This assumption of linearity with respect to non-price variable is also commonly found in previous literature [
29,
30,
31]. The potential intrinsic demand for the final product is denoted by
, which is irrespective of the green degree of a product. Here, we let
for simplicity.
Similar to [
32], the cost function of greenness efforts is quadratic with respect to green degree as specified by:
Cooperation between supplier and manufacturer on the development of a product or a component is common in practice. For example, GE offered an annual budget of $200 to $400 million for its Six Sigma program, a significant portion of which is allocated for the sole purpose of improving the component quality of its suppliers [
33]. In our study, we consider a subsidy program wherein the manufacturer provides a subsidy rate to the cost of greenness efforts of the supplier. This subsidy program is generally the case in the automotive and other industries [
24,
28].
In the absence of any empirical evidence that shows that innovation positively affects the firm’s production cost [
34], we assume that the supply chain members’ greenness efforts do not affect the channel members’ marginal cost. This assumption is found in the literature [
29,
30,
35]. Without accounting for the cost of greenness efforts, the supplier’s marginal profit is denoted by
, and the manufacturer’s marginal profit is denoted by
. The profit function of the supplier could be given by Equation (3):
and the profit function of the manufacturer is:
Welfare in each country is represented by the sum of consumer surplus and firm profits:
Consumer surplus can be calculated as the maximum price that a consumer is willing to pay minus the actual price; i.e.,
, where
represents inverse demand function, and
denotes the actual price paid by a consumer. The government strives to maximize social welfare. The objective function could then be modified into:
In our model, we assume that product price
in Equations (1) and (6) is kept constant for several reasons. First, the main purpose of this paper is to explore the effects of subsidy policies of the government on the decision of supply chain member and to find an effective subsidy incentive scheme for the government. Second, in practice, firms commonly adopt the same price policy but offer products with different qualities in the market, and this assumption was also found in previous studies [
28,
31].
We consider two subsidy policies of the government: (i) the first subsidy policy (government offers a subsidy rate to the cost of greenness efforts of manufacturer); and (ii) the second subsidy policy (government provides a per unit subsidy to the manufacturer). We then calculate and compare the optimal decisions of all members in two scenarios. We start by analyzing the first scenario, which is denoted by subscript “I”. In the second scenario, the government adopts the second subsidy policy, which is denoted by subscript “II”.
The sequences of decisions are described as follows. (i) The government provides subsidy to manufacturer; (ii) After observing the government’s subsidy, manufacturer offers subsidy rate for the cost of greenness efforts of supplier; (iii) Supplier and manufacturer simultaneously determine their optimal greenness efforts. Therefore, we keep subsidy rates and fixed and calculate the greenness efforts of supplier and manufacturer using optimization theory. We then calculate manufacturer’s optimal subsidy rate and obtain optimal subsidy of the government.
3.1. Scenario I: The Government Provides a Subsidy Rate to the Cost of Greenness Efforts of Manufacturer
In this scenario, the government grants subsidy rate
to the cost of greenness efforts of manufacturer. Manufacturer also provides subsidy rate
to the cost of greenness efforts of supplier. Given fixed subsidy rates
and
, the profit functions for the supplier is represented by the following equation:
and the profit function for the manufacturer is given by:
The government’s objective function could be modified into:
We utilize Equations (7) and (8) for this optimization problem and obtain the following results.
Proposition 1. When the government offers the first subsidy policy and when subsidy rates and are fixed, the optimal greenness efforts of supplier are given by:and the manufacturer’s optimal greenness efforts are given by According to Proposition 1, we study the factors considered by supply chain members when determining their optimal greenness efforts. (i) The first factor is marginal profit. Supply chain member will increase spending on his design of green component as marginal profit increases. If the supply chain member has high level of profitability, a member has strong motivation to increase his greenness efforts to attract consumers to purchase green products; (ii) The second factor is the effect of component on the green degree of the final product. This effect is given as . The significant effect will encourage supply chain members to increase spending on the design or manufacture of his green product. When a supply chain member is a producer of key component, he or she has strong motivation to increase greenness efforts; (iii) The third factor is subsidy rate and . A supply chain member will enhance the degree of greenness of his product as subsidy rate increases. The optimal greenness efforts of supplier are only affected by subsidy rate, which is provided by the manufacturer and do not depend on the subsidy rate of the government. Similarly, the manufacturer’s subsidy program has no effect on his optimal greenness efforts.
We substitute Equations (10) and (11) into Equations (8) and obtain the following profit function of manufacturer:
Under the first government’s subsidy policy, differentiating with the subsidy rate , we get the manufacturer’s optimal subsidy rate, which is given by Proposition 2. In the first subsidy policy of the government, we differentiate with subsidy rate . We then obtain the manufacturer’s optimal subsidy rate, which is given by Proposition 2.
Proposition 2. When the government offers the first subsidy policy, the manufacturer’s optimal subsidy rate is The restraining condition in Equation (13) shows that the manufacturer is willing to provide a subsidy to the supplier if and only if he could obtain enough marginal profit that is no less than half of the supplier’s marginal profit. If the manufacturer does not obtain sufficient marginal profit, his or her motivation to offer a subsidy rate to the supplier decreases. Differentiating with respect to and , and knowing that , we have and . We then obtain the following managerial implications. (i) High marginal profit of manufacturer results in increased subsidy rate to the supplier. By contrast, manufacturer will offer a low subsidy rate if supplier obtains high marginal profit. When supplier has high level of profitability, he will increase spending on the design and manufacture of green product. Thus, manufacturer has low motivation to stimulate the supplier to increase his greenness efforts; (ii) Manufacturer’s optimal subsidy rate is not affected by the subsidy policy of the government. We further prove that the optimal greenness efforts of supplier do not depend on the first subsidy policy of the government.
We substitute Equations (10), (11), and (13) into Equation (9) and obtain social welfare , and differentiate with the subsidy rate , we obtain the government’s optimal subsidy rate, which is given by Proposition 3.
Proposition 3. When the government offers the first subsidy policy, the government’s optimal subsidy rate is The restraining condition implies that the government will provide a subsidy rate to the manufacturer if and only if price sensitivity is high relative to parameter . Differentiating from and , and knowing that , we obtain , which indicates that the government will increase the subsidy rate if the effect of the green degree of a component on that of the final product increases. If the manufacturer is a producer of key component, the government will tend to offer high subsidy rate. In other words, the government tends to offer subsidy to the core member of a supply chain. Differentiating from and , and knowing that , we obtain . The following findings are then obtained. (i) The government will offer a high subsidy rate as the supplier’s marginal profit increases; (ii) The government will provide a low subsidy rate if the manufacturer has a large marginal profit. When the government adopts the first subsidy policy, it tends to provide a high subsidy rate if the manufacturer has a low level of profitability. Differentiating from , and knowing that , we then obtain . We find that increased price sensitivity () will decrease the government’s optimal subsidy rate if the restraining condition holds.
Substituting the Equations (13) and (14) into Equations (10) and (11), respectively, we can get the supply chain member’s optimal greenness efforts as follows:
Equation (15) suggests that manufacturer’s marginal profit positively influences supplier’s optimal greenness efforts if manufacturer’s marginal profit is sufficiently high. The logic behind this conclusion is explained as follows. When condition holds, increased marginal profit of manufacturer will increase subsidy rate, which then increases supplier’s greenness efforts. Equation (16) suggests that if the condition holds: (i) manufacturer will reduce his optimal greenness efforts if the condition is false; (ii) supplier’s marginal profit has a positive effect on the optimal greenness efforts of manufacturer; and (iii) an increase in price sensitivity will decrease manufacturer’s optimal greenness efforts, which means that manufacturer will reduce his greenness efforts if the value of price sensitivity is low.
Together with the Propositions 1–3, we can obtain the profits of two firms, and , and the social welfare, .
3.2. Scenario II: The Government Grants a Per Unit Subsidy to Manufacturer for the Demand for Green Product
The government provides a per unit subsidy
to manufacturer. Manufacturer then offers subsidy rate
to supplier for the cost of his greenness efforts. Given fixed subsidy rates
and
, the profit functions for the supplier is represented by:
and the profit function for the manufacturer is:
The objective function of the government could be changed into:
We apply Equations (17) and (18) for this optimization problem and obtain the following results.
Proposition 4. When the government offers the second subsidy policy, and when the subsidy rates and are fixed, the supplier’s optimal greenness efforts are given byand the manufacturer’s optimal greenness efforts are given by The structure of supplier’s optimal greenness efforts under the second subsidy policy is similar to that under the first subsidy policy. Therefore, we obtain similar managerial implications for supply chain members. Together with Proposition 1, we find that subsidy policies of the government enhance the greenness efforts of manufacturer.
We substitute Equations (20) and (21) into Equation (18) and obtain the following manufacturer’s profit function:
We differentiate with the subsidy rate under the government’s second subsidy policy, we then obtain manufacturer’s optimal subsidy rate, which is given by Proposition 5.
Proposition 5. When the government offers the second subsidy policy, the manufacturer’s optimal subsidy rate is Though the structure of manufacturer’s optimal subsidy rate is similar to that under the first subsidy policy, we also find some new managerial implications. First, we find that manufacturer is willing to provide a subsidy rate to supplier under the government’s second subsidy policy. Even if the manufacturer’s marginal profit is lower than half of the supplier’s marginal profit, the manufacturer may offer a subsidy rate to the supplier if the government adopts the second subsidy policy. This conclusion differs from that under the government’s first subsidy policy. Second, proving that is easy. Manufacturer will offer an identical subsidy rate to supplier under a different subsidy policy if and only if the government does not grant a subsidy to manufacturer. Otherwise, manufacturer will offer a higher subsidy rate to supplier than that under the government’s first subsidy policy. Third, we differentiate with respect to , and knowing that , we have . If the government offers high subsidy to manufacturer, manufacturer may develop strong motivation to offer a high subsidy rate to supplier. This conclusion differs from that obtained under the government’s first subsidy policy.
Substituting Equations (20), (21), and (23) into Equation (19) and obtain social welfare , and differentiating with the subsidy , we obtain the government’s optimal subsidy, which is given by Proposition 6.
Proposition 6. When the government offers the second subsidy policy, the government’s optimal subsidy is Compared with the restraining condition of Equation (14), the subsidy’s restraining condition in Equation (24) is stricter than that in Equation (14). This finding suggests that manufacturer may easily gain subsidy from the government if the first subsidy policy is adopted. Differentiating from , and , and knowing that , we then have , and . Together with the results of Proposition 3, we obtain the following findings. (i) The government tends to offer a subsidy to the core manufacturer regardless of whether the first or second policy is adopted; (ii) The government tends to provide high subsidy if the manufacturer has a high level of profitability.
We substitute Equation (24) into Equation (23) and obtain the following optimal subsidy rate of manufacturer:
where
, and
.
Manufacturer will provide a high subsidy rate to supplier under the government’s second subsidy policy when holds. In this situation, manufacturer has strong motivation to support supplier.
We substitute Equations (25) and (24) into Equations (20) and (21), respectively, and then obtain the optimal greenness efforts of supply chain member under the government’s second subsidy policy:
and
where
, and
.
When holds, supplier’s spending on green product design under the government’s second subsidy policy will be higher than that under the government’s first subsidy policy. Together with the results of Equation (25), we obtain the following conclusion: when the condition is satisfied, the manufacturer will provide a high subsidy rate to the supplier, and the supplier will enhance his greenness efforts within the government’s second subsidy policy.
Together with Propositions 4–6, we can get the profits of two firms, and , and the social welfare, .
4. Numerical Analysis
A numerical analysis of the effects of different subsidy policies of the government on social welfare and profits of supply chain members may allow the government to measure the effects of changes in parameter on social welfare. The government can use such an analysis to determine (i) when to grant the first subsidy policy; (ii) when to grant the second subsidy policy; and (iii) the total budget of subsidies.
Firstly, we study the effects of the parameter on social welfare and profits of supply chain members. Our numerical analysis uses the following values to establish ranges for model parameters: , , , , , . We define the value of axis as , which represents the effect of manufacturer’s component on the green degree of the final product. While if we define the value of axis as (), we can obtain the similar results. A high value of means that the manufacturer’s component has a significant effect on the green degree of the final product, and the green characteristic of the final product then becomes a significant factor that affects the purchase decisions of consumers. The value of will first approach the value of price sensitivity as the value of increases, and the value of will then reach the value of price sensitivity . The government could provide two subsidy policies when the value of price sensitivity is large enough (i.e., ). By contrast, the government will provide only the first subsidy policy if the value of price sensitivity is in a mediate level (i.e., ), and when the value of price sensitivity is low (i.e., is satisfied), the government will not tend to offer a subsidy to manufacturer.
To obtain a qualitative insight on how social welfare and profits of supply members vary when varies in two scenarios, we keep other parameters fixed and draw the relationships in the following figures.
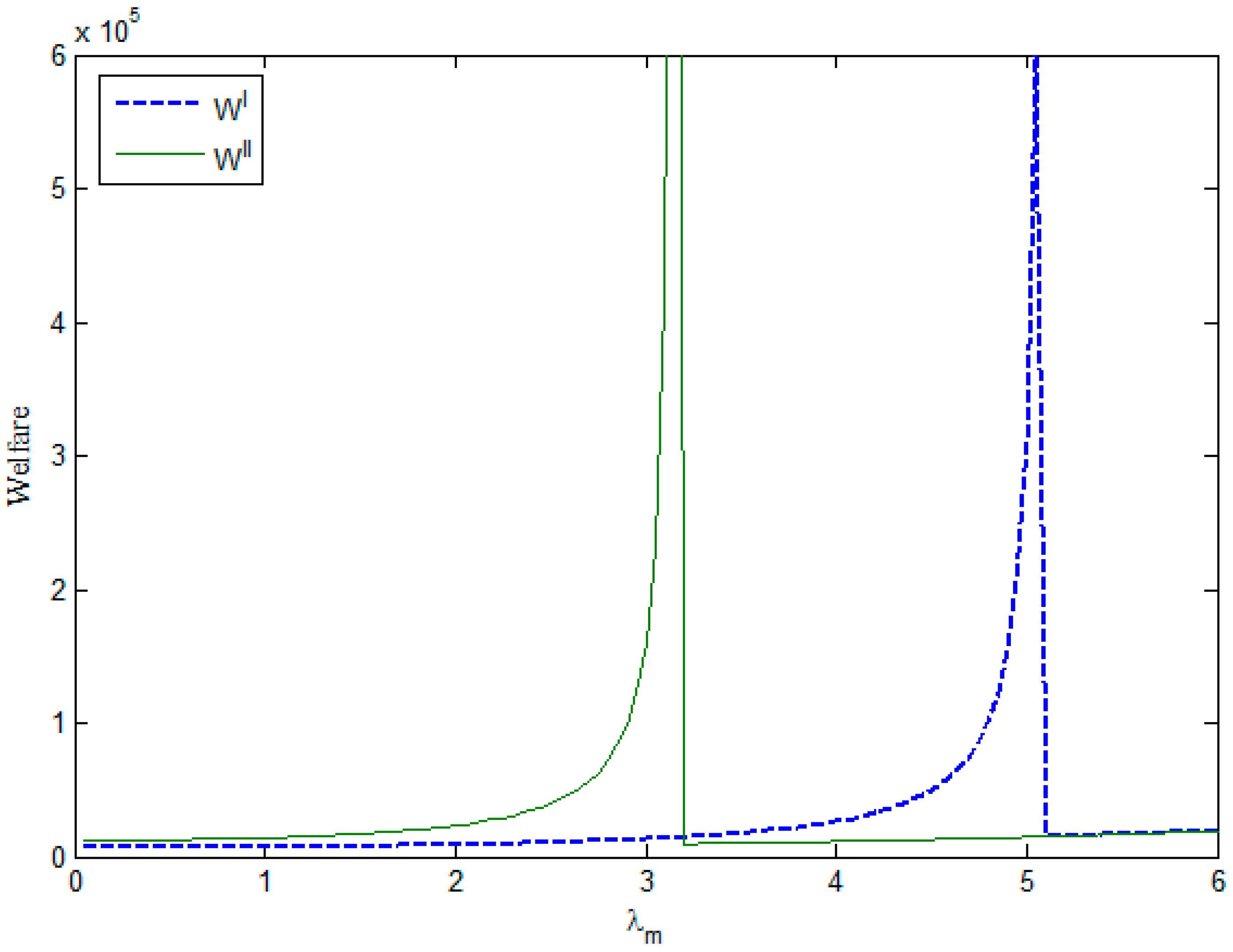
The left part of
Figure 1 shows that the condition
is satisfied, whereas the right part shows that the condition does not hold. The left part of
Figure 1 shows the following implications. (i) All else being equal, social welfare will increase under the government’s two subsidy policies as
increases. Social welfare will increase sharply when
reaches the value of price sensitivity
; (ii) Social welfare under the government’s second subsidy policy is always higher than that under the government’s first subsidy policy if
holds. This finding indicates that when the value of price sensitivity is large enough (i.e.,
), the government should offer the second subsidy policy to maximize social welfare.
The right part of
Figure 1 indicates the following implications. (i) All else being equal, an increase in
will increase social welfare if
holds; (ii) Social welfare under the government’s first subsidy policy is always higher than that under the government’s second subsidy policy if
is satisfied. This finding indicates that the government should offer the first subsidy policy if the value of price sensitivity is in a mediate level (i.e.,
); (iii) When the value of price sensitivity is low (i.e.,
is satisfied), the government might not offer subsidy to manufacturer.
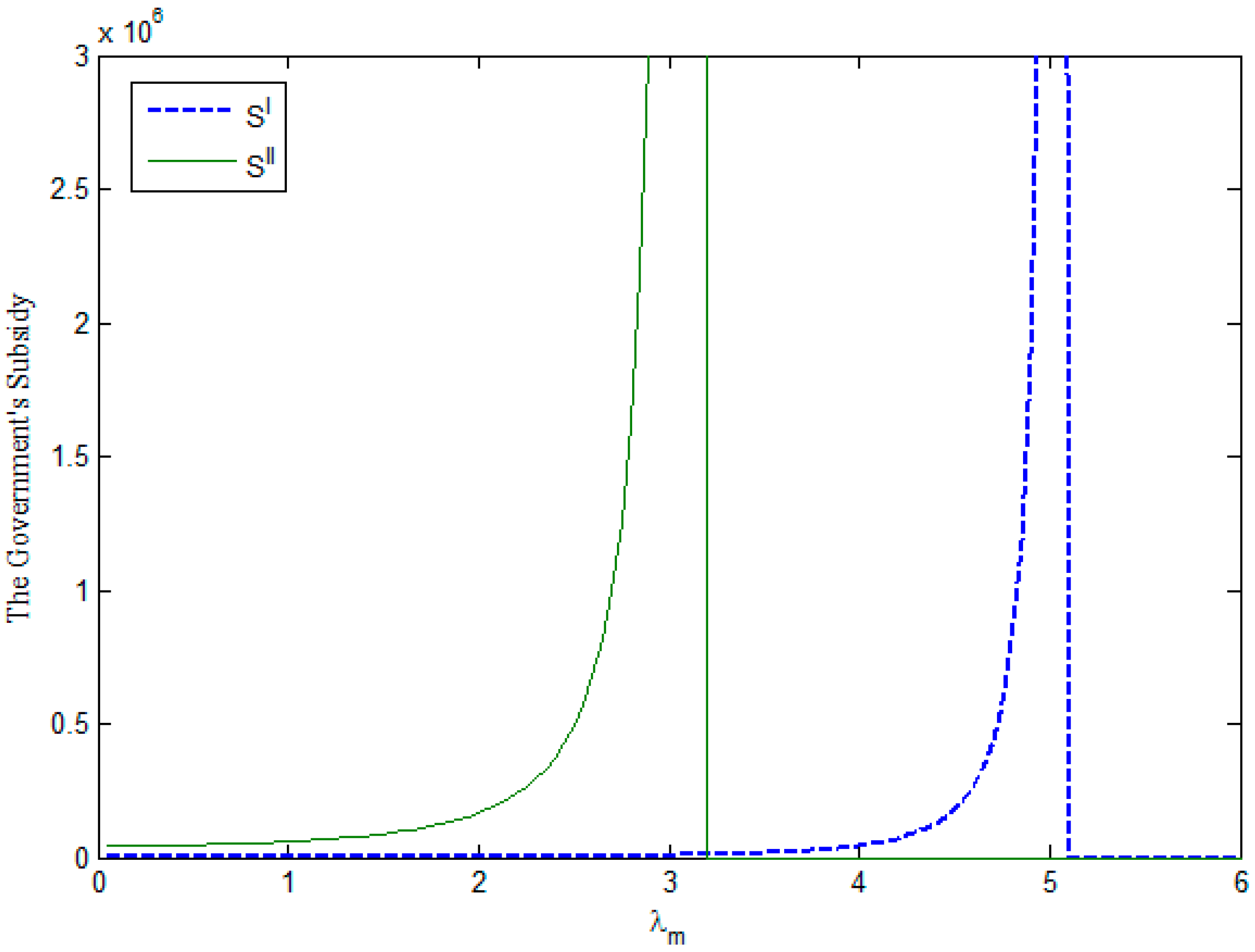
Figure 2 presents the relationships between the government subsidy and parameter
.
Figure 2 offers the following implications. (i) The government will offer a high subsidy budget under the second subsidy policy if
holds; (ii) The government will grant a high subsidy budget under the first subsidy when
is satisfied; (iii) The government will not offer a subsidy budget if
holds. Together with the results of
Figure 1, we also find that social welfare is affected by the government’s subsidy budget, that is, an increase in subsidy budget will increase social welfare.
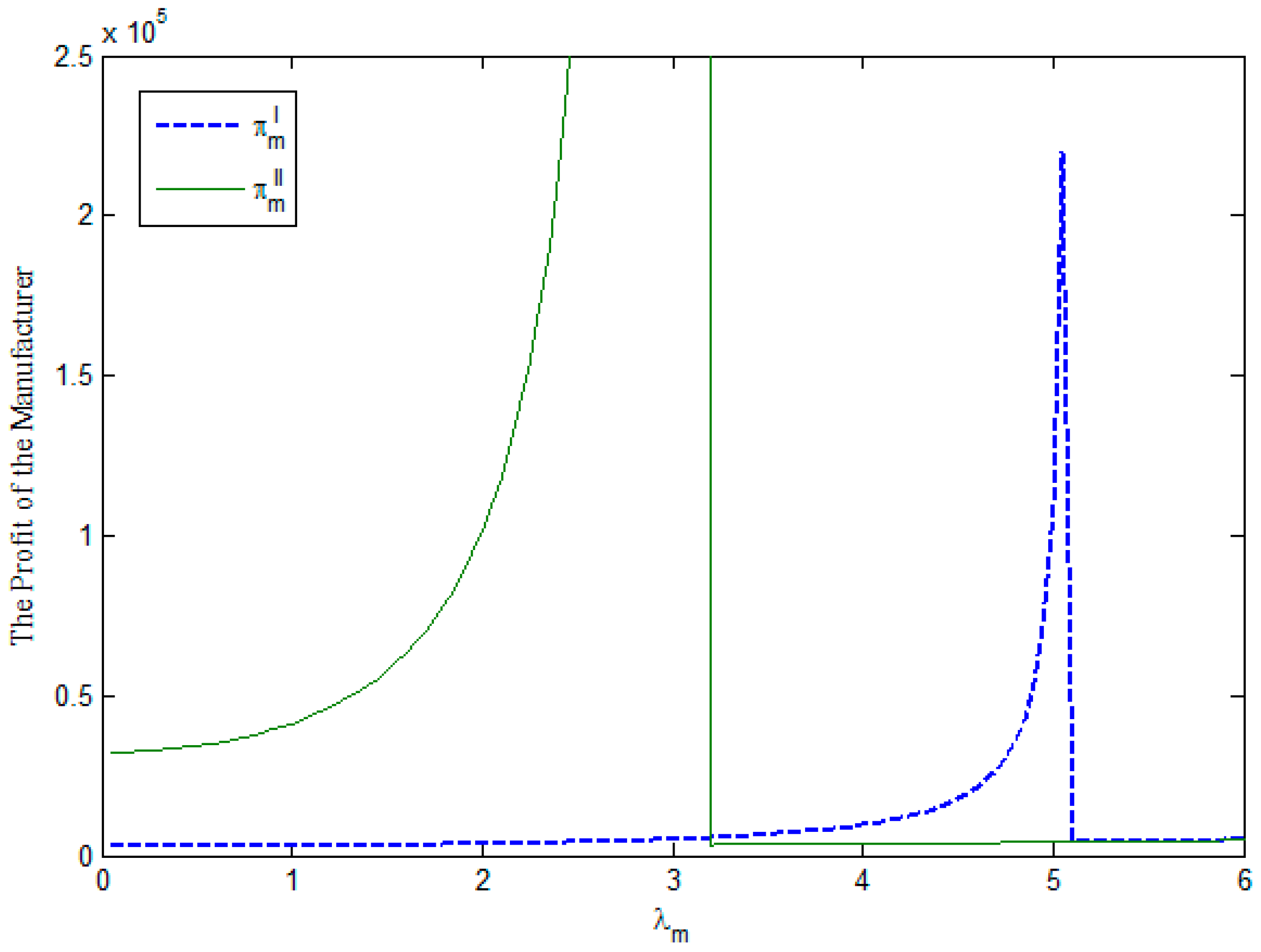
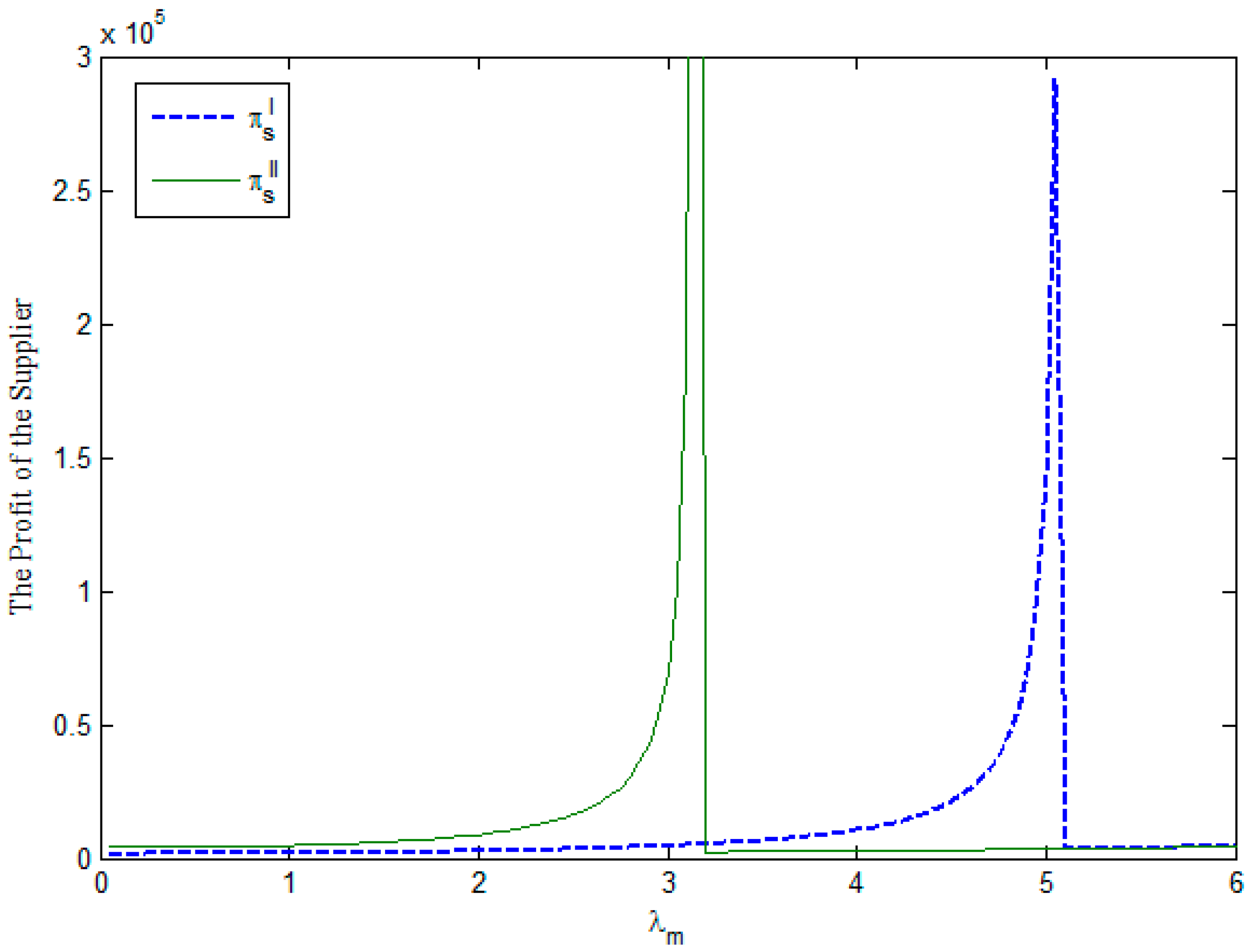
Figure 3 has a similar structure to
Figure 4, and we can obtain similar results for supplier and manufacturer. First, a supply chain member will obtain a higher profit under the second subsidy policy than that under the first subsidy policy if
holds. Second, a supply chain member will obtain increased profit from the government’s first subsidy policy when
is satisfied. Third, if
holds, the profits of supply chain members do not depend on the government’s adoption of the first or second subsidy policies. Fourth, together with the results of
Figure 1 and
Figure 2, we find that increased government subsidy budget will increase social welfare and profits of supply chain members.
Secondly, we investigate the effects of marginal profit on social welfare and profits of supply chain members. Then, we keep the following parameters with values fixed:
,
,
,
,
. We define the value of
axis as
, which represents the supplier’s marginal profit ratio in the whole supply chain. Here, we consider two situations: (i) the condition
is satisfied; and (ii) the condition
holds. Under the first situation, we let
, and then we obtain the following figures (left-hand sides of
Figure 5,
Figure 6 and
Figure 7). Under the second situation, we let
, and then we get the following figures (right-hand sides of
Figure 5,
Figure 6 and
Figure 7).
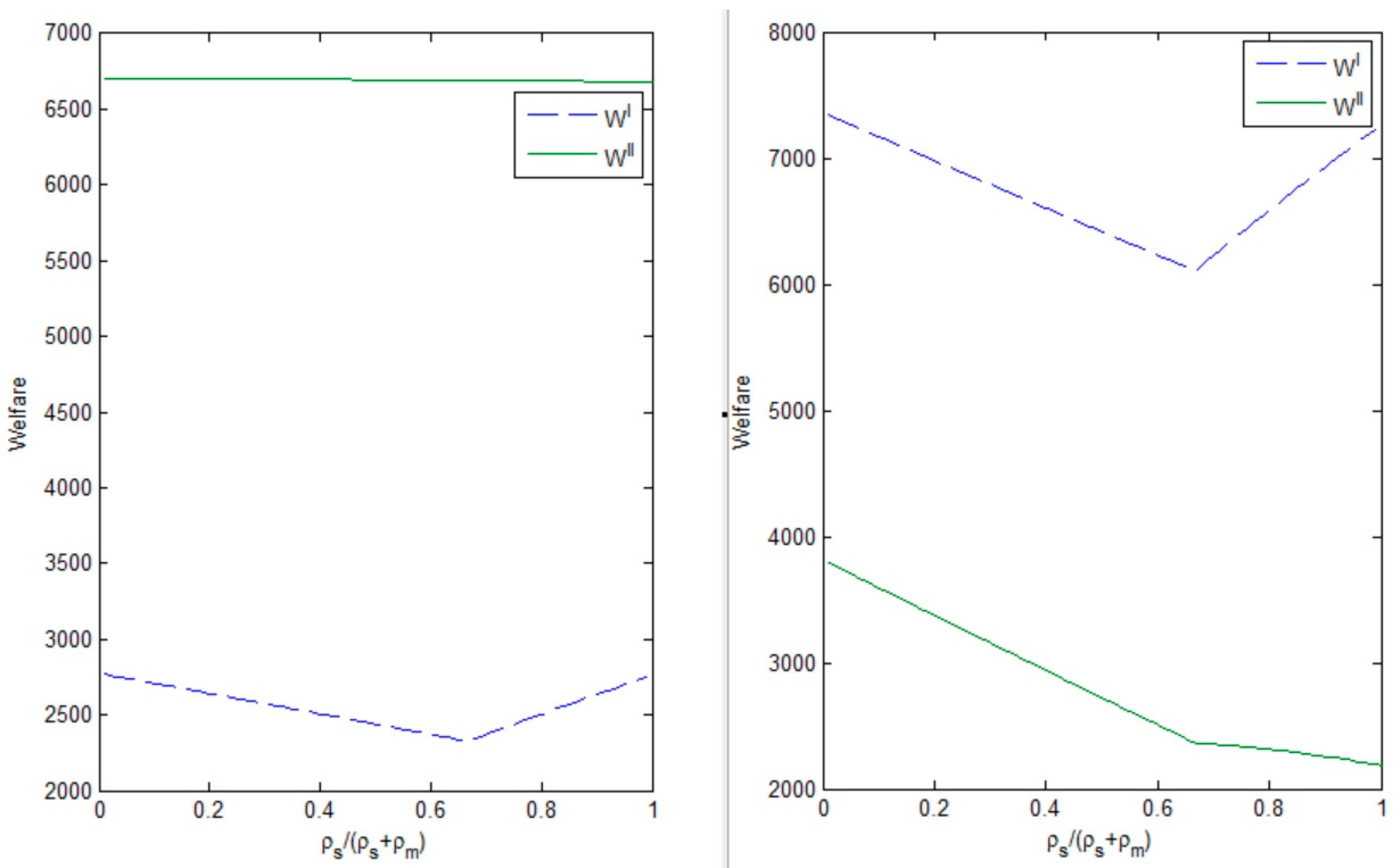
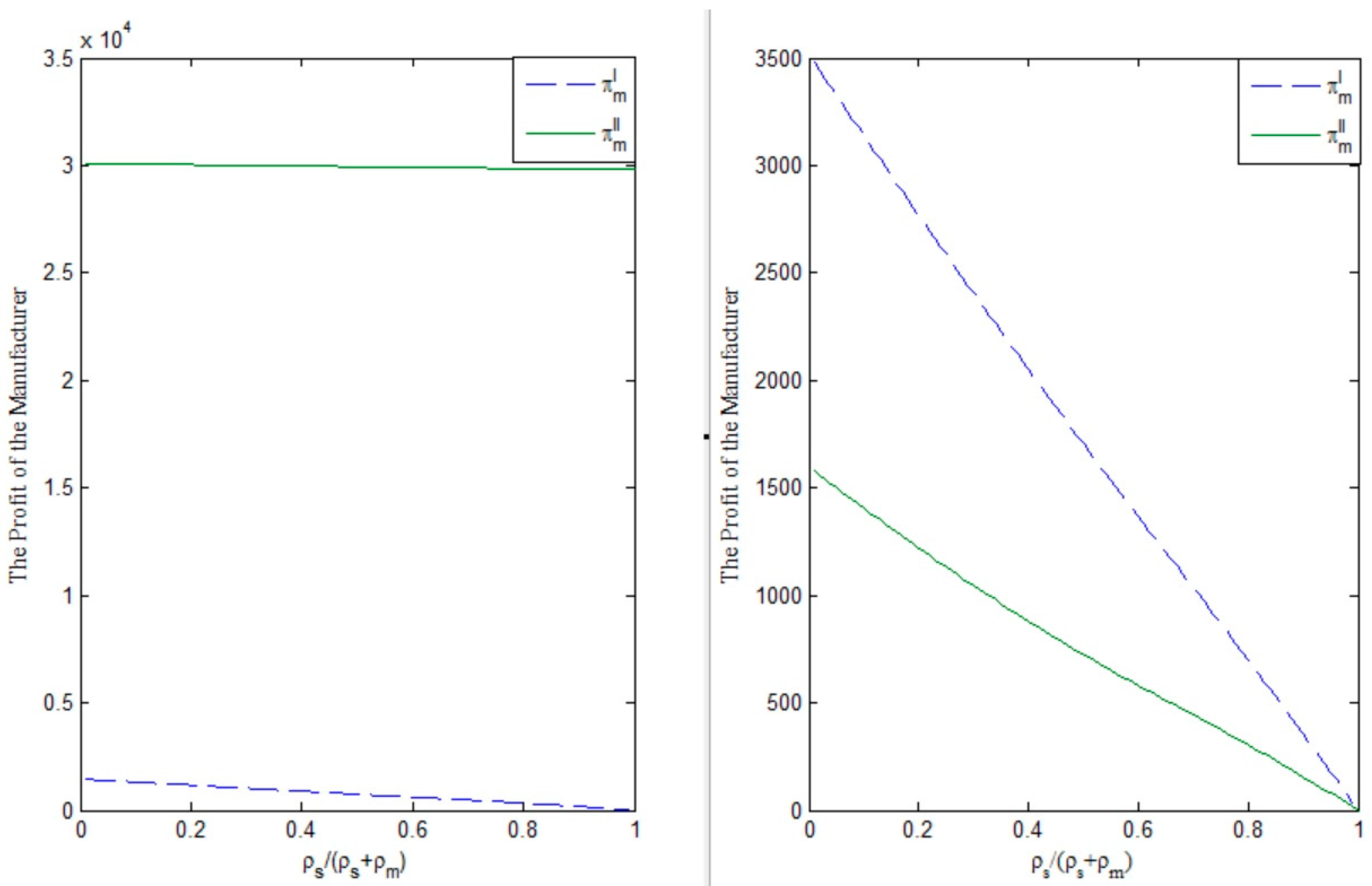
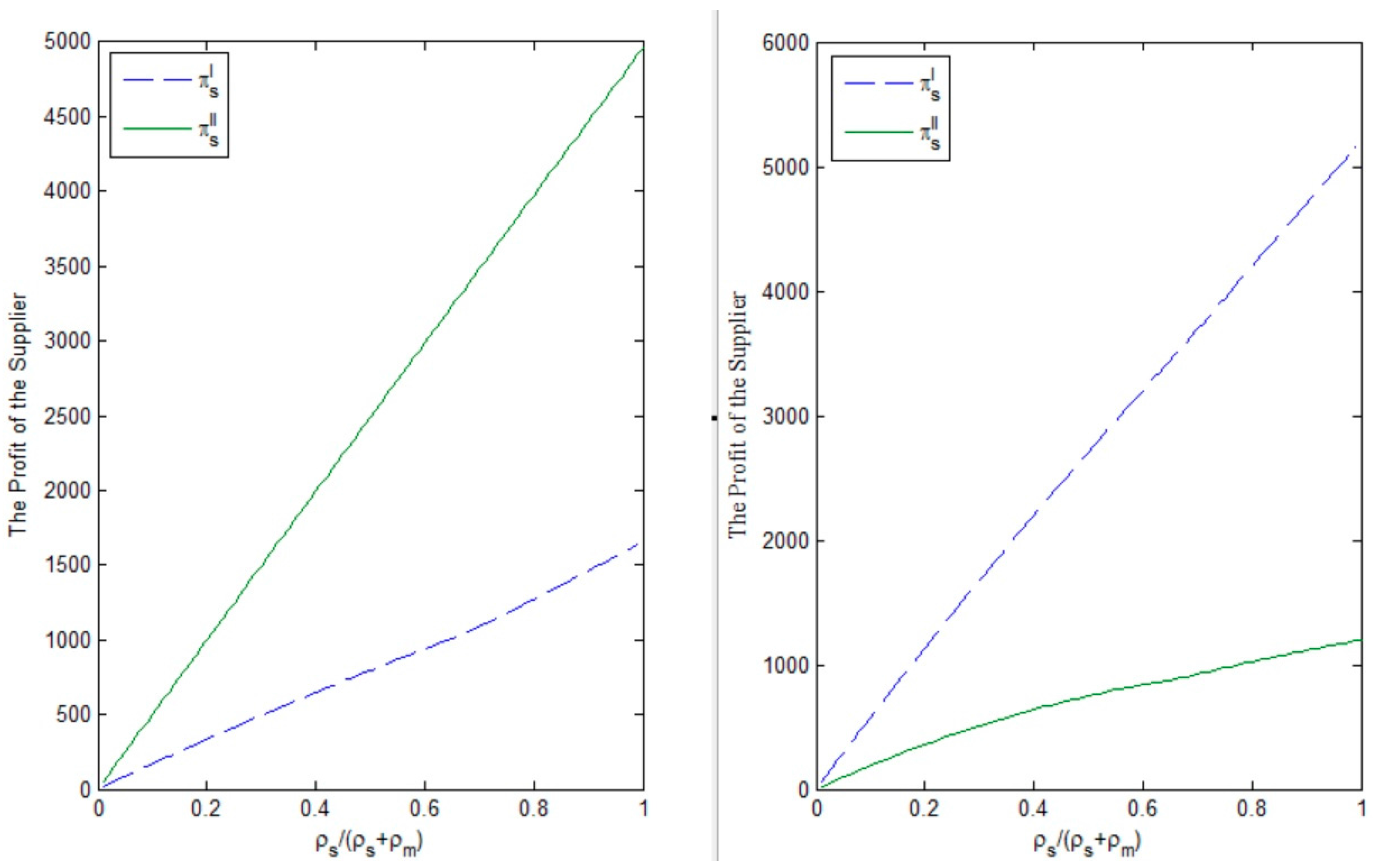
From
Figure 5,
Figure 6 and
Figure 7, we can obtain the following facts. (i) The supplier’s marginal profit has no effect on the government’s selection of subsidy policy. If the condition
is satisfied, no matter how much the supplier’s marginal profit ratio in the whole supply chain is, the government is willing to grant the second subsidy policy, while, if the condition
holds, the government prefers to adopt the first subsidy policy; (ii) For the manufacturer, the supplier’s marginal profit ratio has a negative effect on the manufacturer’s profit. If the condition
is satisfied, the manufacturer can get more profit when the government grants a second subsidy policy, while, if the condition
holds, the manufacturer would expect the government provides the first subsidy policy; (iii) For the supplier, as the marginal profit ratio increases, the supplier’s profit will increase. Similar to the manufacturer, if the condition
holds, the supplier can obtain more profit under the government’s second subsidy policy. When the condition
holds, the supplier always prefers to the government’s first subsidy policy.
5. Conclusions
Today, an increasing number of governments offer subsidy policies to support related firms in producing green products. This paper investigates the effects of two subsidy policies of the government on the decision making of players. The supply chain system discussed in this study consists of supplier, manufacturer, and the government. The optimal decisions of all channel members under two different subsidy policies are calculated and compared using game and optimization theories: (i) the first subsidy policy (government provides a subsidy rate to the cost of greenness efforts of manufacturer); and (ii) the second subsidy policy (government offers a per unit subsidy to manufacturer).
Our major managerial implications are summarized as follows. First, when manufacturer has small marginal profit, the government will offer a high subsidy rate to manufacturer under the first subsidy policy, whereas a low subsidy rate will be offered to manufacturer under the second subsidy policy. Second, if the value of price sensitivity is large enough, the government will adopt the second subsidy policy, and the profit of supply chain members are improved under this situation. Third, when the value of price sensitivity is in a mediate level, the government will provide the first subsidy policy, and improving the profit of supply chain members. Fourth, when the value of price sensitivity is low, the government might not be willing to offer a subsidy to manufacturer.
Our study has a number of limitations that offer directions for future research. First, our models assume that price is constant. Introducing the factors of pricing and advertising into the model may be considered in future research. Second, we consider a supply chain system that includes one supplier and one manufacturer. Further research could extend the supply chain system to a framework involving multiple suppliers and manufacturers.