The Dynamic Enterprise Network Composition Algorithm for Efficient Operation in Cloud Manufacturing
Abstract
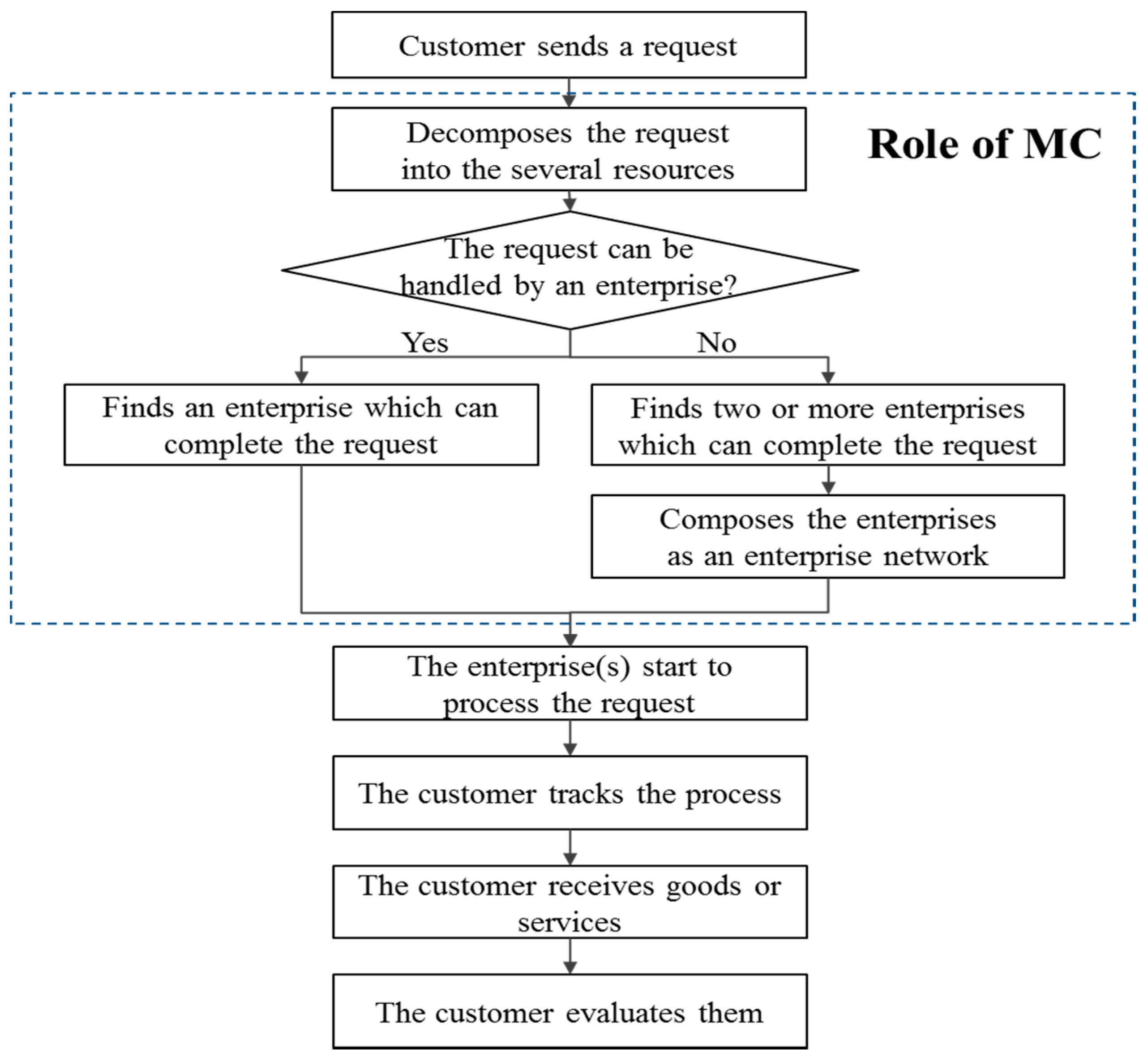
:1. Introduction
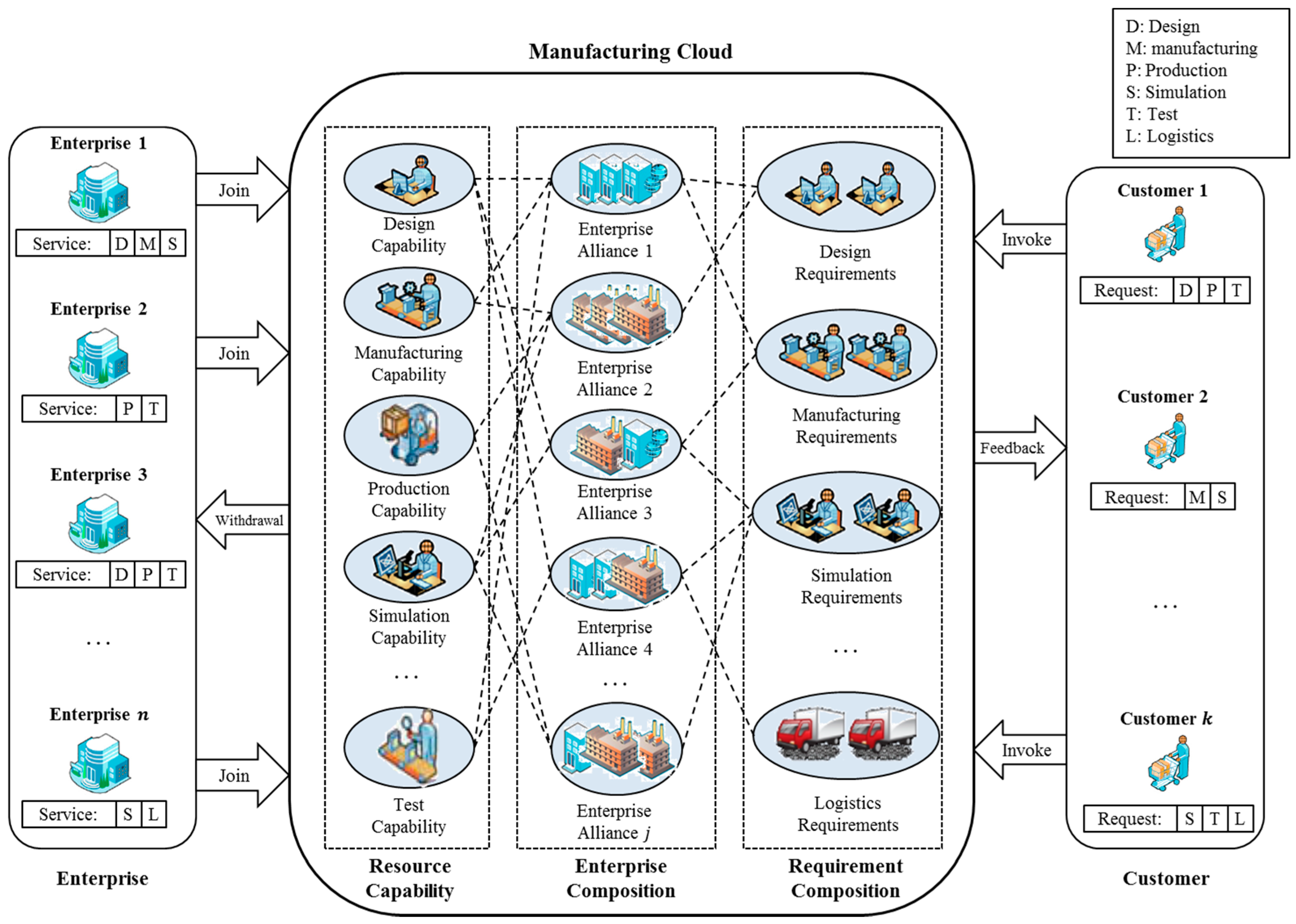
2. Enterprise Network Composition Problem
2.1. Description
2.2. Assumptions and Notations
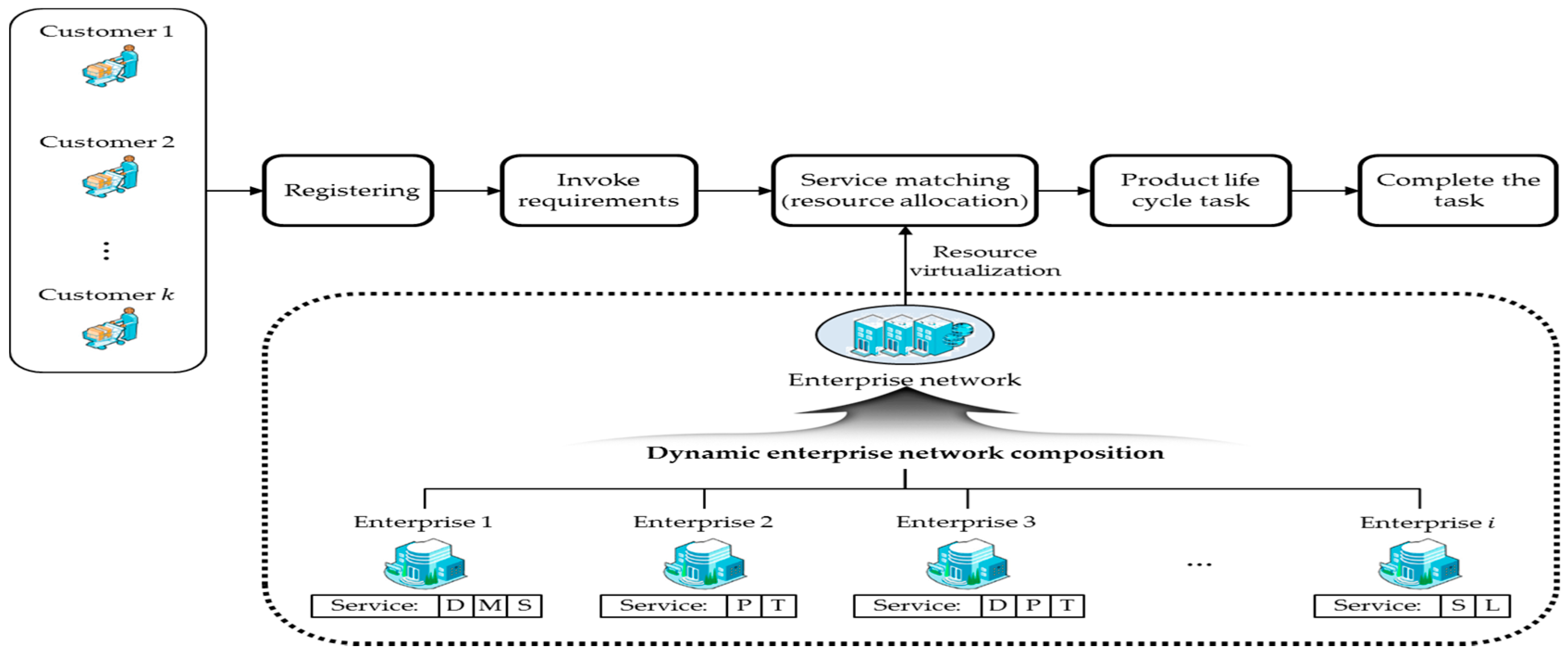
3. Dynamic Enterprise Network Composition Algorithm
3.1. Initial Enterprise Network Composition
3.2. Resource Demand Forecasting
3.3. Conditions of Demand Response
3.4. Enterprise Network Recomposition
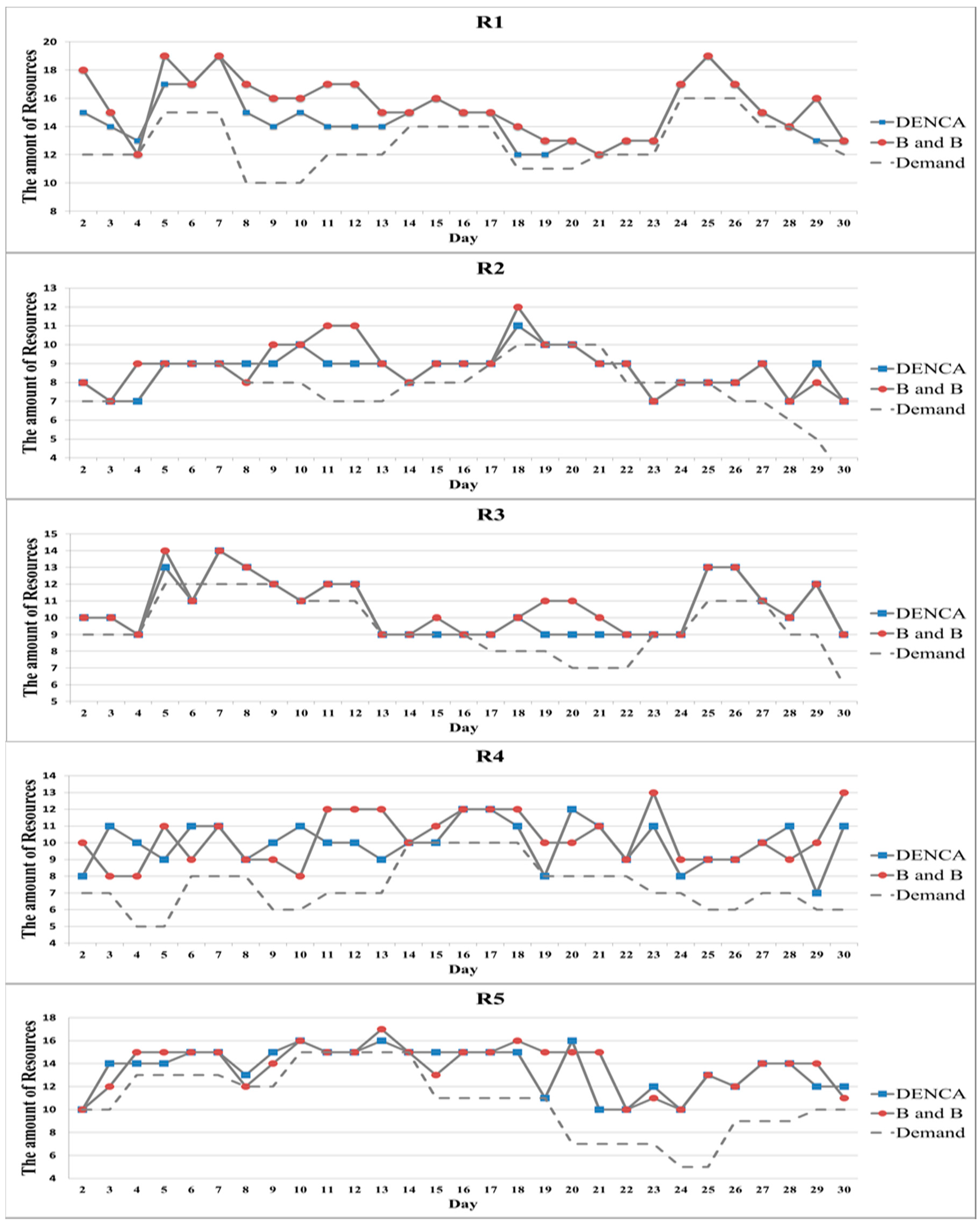
4. Numerical Example
4.1. Data
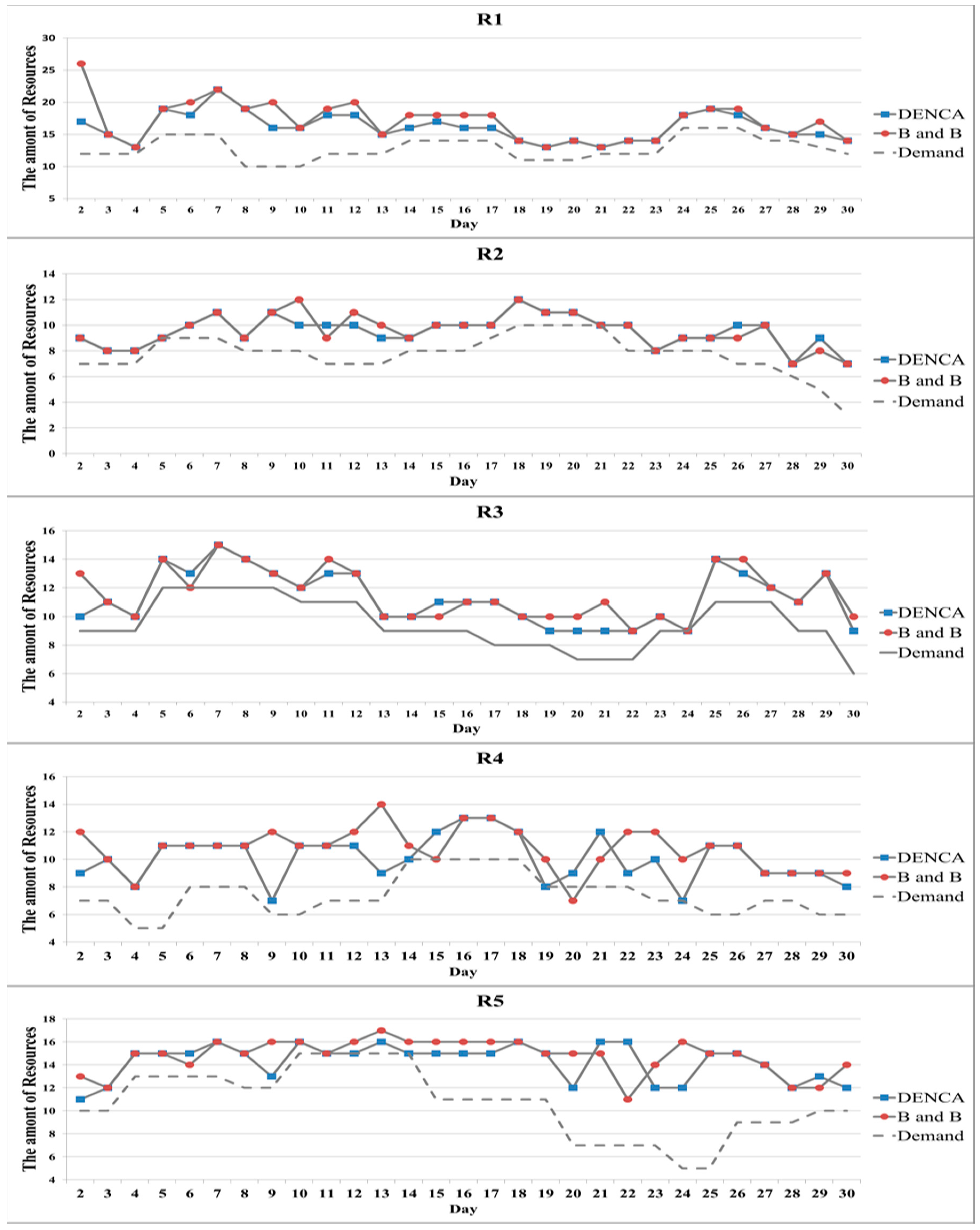
4.2. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Z.; Zhang, M.; Sun, H.; Zhu, G. Effects of standardization and innovation on mass customization: An empirical investigation. Technovation 2016, 48, 79–86. [Google Scholar] [CrossRef]
- Ferguson, S.M.; Olewnik, A.T.; Cormier, P. A review of mass customization across marketing, engineering and distribution domains toward development of a process framework. Res. Eng. Des. 2014, 25, 11–30. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Wang, S.L.; Tao, F.; Cao, J.W.; Jiang, X.D.; Chai, X.D. Cloud manufacturing: A new service-oriented networked manufacturing model. Comput. Integr. Manuf. Syst. 2010, 16, 1–7. [Google Scholar]
- Mell, P.; Grance, T. The NIST Definition of Cloud Computing; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2011. [Google Scholar]
- Wu, D.; Greer, M.J.; Rosen, D.W.; Schaefer, D. Cloud manufacturing: drivers, current status, and future trends. In Proceedings of the ASME 2013 International Manufacturing Science and Engineering Conference Collocated with the 41st North American Manufacturing Research Conference, Madison, WI, USA, 10–14 June 2013.
- Zhang, L.; Luo, Y.; Fan, W.; Tao, F.; Ren, L. Analysis of cloud manufacturing and related advanced manufacturing models. Comput. Integr. Manuf. Syst. 2011, 17, 458–468. [Google Scholar]
- Xu, J.; Chen, P. Study on Objects Ordering for Manufacturing Cloud Platform. In Proceedings of the International Conference on Information Engineering and Applications, London, UK, 26–28 October 2012; pp. 431–437.
- Huang, B.; Li, C.; Yin, C.; Zhao, X. Cloud manufacturing service platform for small-and medium-sized enterprises. Int. J. Adv. Manuf. Technol. 2013, 65, 1261–1272. [Google Scholar] [CrossRef]
- Xu, X. From cloud computing to cloud manufacturing. Robot. Comput.-Integr. Manuf. 2012, 28, 75–86. [Google Scholar] [CrossRef]
- Wu, D.; Rosen, D.W.; Wang, L.; Schaefer, D. Cloud-Based Manufacturing: Old Wine in New Bottles? Procedia CIRP 2014, 17, 94–99. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, L.; Venkatesh, V.C.; Luo, Y.; Cheng, Y. Cloud manufacturing: A computing and service-oriented manufacturing model. J. Eng. Manuf. 2011. [Google Scholar] [CrossRef]
- Laili, Y.; Tao, F.; Zhang, L.; Cheng, Y.; Luo, Y.; Sarker, B.R. A Ranking Chaos Algorithm for dual scheduling of cloud service and computing resource in private cloud. Comput. Ind. 2013, 64, 448–463. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, S.; Kang, L.; Gao, Y. A TQCS-based service selection and scheduling strategy in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2016, 82, 235–251. [Google Scholar] [CrossRef]
- Mai, J.; Zhang, L.; Tao, F.; Ren, L. Customized production based on distributed 3D printing services in cloud manufacturing. Int. J. Adv. Manuf. Technol. 2016, 84, 71–83. [Google Scholar] [CrossRef]
- Li, W.; Zhu, C.; Yang, L.T.; Shu, L.; Ngai, E.C.H.; Ma, Y. Subtask Scheduling for Distributed Robots in Cloud Manufacturing. IEEE Syst. J. 2015, 99, 1–10. [Google Scholar] [CrossRef]
- Wei, X.; Liu, H. A cloud manufacturing resource allocation model based on ant colony optimization algorithm. Int. J. Grid Distrib. Comput. 2015, 8, 55–66. [Google Scholar] [CrossRef]
- Tsai, J.T.; Fang, J.C.; Chou, J.H. Optimized task scheduling and resource allocation on cloud computing environment using improved differential evolution algorithm. Comput. Oper. Res. 2013, 40, 3045–3055. [Google Scholar] [CrossRef]
- Ren, L.; Cui, J.; Wei, Y.; LaiLi, Y.; Zhang, L. Research on the impact of service provider cooperative relationship on cloud manufacturing platform. Int. J. Adv. Manuf. Technol. 2016, 86, 2279–2290. [Google Scholar] [CrossRef]
- Argoneto, P.; Renna, P. Supporting capacity sharing in the cloud manufacturing environment based on game theory and fuzzy logic. Enterp. Inf. Syst. 2016, 10, 193–210. [Google Scholar] [CrossRef]
- Renna, P. Decision model to support the SMEs’ decision to participate or leave a collaborative network. Int. J. Prod. Res. 2013, 51, 1973–1983. [Google Scholar] [CrossRef]
- Rahman, H.F.; Sarker, R.; Essam, D. A real-time order acceptance and scheduling approach for permutation flow shop problems. Eur. J. Oper. Res. 2015, 247, 488–503. [Google Scholar] [CrossRef]
- Lei, H.; Wang, R.; Zhang, T.; Liu, Y.; Zha, Y. A multi-objective co-evolutionary algorithm for energy-efficient scheduling on a green data center. Comput. Oper. Res. 2016, 75, 103–117. [Google Scholar] [CrossRef]
- Ma, J.; Li, W.; Fu, T.; Yan, L.; Hu, G. A Novel Dynamic Task Scheduling Algorithm Based on Improved Genetic Algorithm in Cloud Computing. In Wireless Communications, Networking and Applications; Springer: New Delhi, Germany, 2016; pp. 829–835. [Google Scholar]
- Sethanan, K.; Chamnanlor, C.; Chien, C.; Gen, M. Hybrid Genetic Algorithms for Solving Reentrant Flow-Shop Scheduling with Time Windows. Ind. Eng. Manag. Syst. 2013, 12, 306–316. [Google Scholar]
- Basu, R.; Wright, J. Inventory management. In Total Supply Chain Management; Routledge: London, UK, 2010; pp. 96–108. [Google Scholar]
- Chen, F.; Dou, R.; Li, M.; Wu, H. A flexible QoS-aware Web service composition method by multi-objective optimization in cloud manufacturing. Comput. Ind. Eng. 2016, 99, 423–431. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhao, D.; Hu, A.R.; Luo, Y.L.; Tao, F.; Zhang, L. Multi-view models for cost constitution of cloud service in cloud manufacturing system. In Advances in Computer Science and Education Applications, Proceedings of the International Conference, CSE 2011, Qingdao, China, 9–10 July 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 225–233. [Google Scholar]
- Zhang, Q.; Zhani, M.F.; Zhang, S.; Zhu, Q.; Boutaba, R.; Hellerstein, J.L. Dynamic energy-aware capacity provisioning for cloud computing environments. In Proceedings of the 9th international conference on Autonomic computing, San Jose, CA, USA, 16–20 September 2012; pp. 145–154.

| Notation | Definition |
|---|---|
| Enterprise , | |
| Indicator variable which represents whether the enterprise joins the network at day or not, that is, 0 or 1 | |
| Set of participating enterprises in an enterprise network at day | |
| Participating enterprise in an enterprise network at day | |
| Resource | |
| Demand of at day | |
| Vector of demands at day , | |
| Forecasted demand of at day | |
| ’s capacity of resource | |
| Current enterprise network’s capacity of resource | |
| Internal management cost of MC of | |
| Cloud service invocation cost of | |
| Cloud service aggregation cost of | |
| Participation contract cost of | |
| Contract cancellation cost of | |
| Opportunity cost of production occurring when do not respond demand properly at day t | |
| Unit cost of cloud service invocation for | |
| Unit cost of cloud service aggregation for | |
| Unit cost of participation contract for | |
| Unit cost of contract cancellation for | |
| Unit opportunity cost of production for | |
| Significance level of the risk that demand is unmet (user-defined parameter) | |
| Number of operation days of MC (user-defined parameter) |
| 2 | 0 | 1 | 2 | 1 | |
| 4 | 1 | 2 | 0 | 1 | |
| 3 | 1 | 0 | 3 | 2 | |
| 0 | 2 | 1 | 0 | 5 | |
| 5 | 0 | 2 | 1 | 0 | |
| 1 | 1 | 2 | 2 | 0 | |
| 3 | 2 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 3 | 4 | |
| 2 | 1 | 3 | 1 | 0 | |
| 4 | 0 | 1 | 2 | 2 | |
| 1 | 3 | 1 | 0 | 2 | |
| 2 | 1 | 0 | 1 | 1 | |
| 0 | 4 | 1 | 1 | 3 | |
| 3 | 1 | 2 | 0 | 0 | |
| 0 | 5 | 1 | 2 | 1 |
| (a) Actual Demands | (b) Forecasted Demands | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 12 | 7 | 9 | 7 | 10 | - | - | - | - | - |
| 2 | 12 | 7 | 9 | 7 | 10 | 12 | 7 | 8 | 7 | 9 |
| 3 | 12 | 7 | 9 | 7 | 10 | 13 | 6 | 9 | 7 | 10 |
| 4 | 12 | 7 | 9 | 5 | 13 | 11 | 6 | 8 | 5 | 13 |
| 5 | 15 | 9 | 12 | 5 | 13 | 15 | 6 | 12 | 5 | 13 |
| 6 | 15 | 9 | 12 | 8 | 13 | 16 | 8 | 10 | 7 | 13 |
| 7 | 15 | 9 | 12 | 8 | 13 | 13 | 8 | 13 | 7 | 12 |
| 8 | 10 | 8 | 12 | 8 | 12 | 9 | 7 | 12 | 7 | 11 |
| 9 | 10 | 8 | 12 | 6 | 12 | 8 | 8 | 11 | 5 | 12 |
| 10 | 10 | 8 | 11 | 6 | 15 | 10 | 8 | 10 | 5 | 15 |
| 11 | 12 | 7 | 11 | 7 | 15 | 12 | 6 | 11 | 7 | 14 |
| 12 | 12 | 7 | 11 | 7 | 15 | 11 | 8 | 11 | 6 | 14 |
| 13 | 12 | 7 | 9 | 7 | 15 | 13 | 6 | 8 | 6 | 15 |
| 14 | 14 | 8 | 9 | 10 | 15 | 14 | 7 | 8 | 9 | 14 |
| 15 | 14 | 8 | 9 | 10 | 11 | 15 | 8 | 8 | 9 | 10 |
| 16 | 14 | 8 | 9 | 10 | 11 | 14 | 8 | 8 | 10 | 11 |
| 17 | 14 | 9 | 8 | 10 | 11 | 14 | 8 | 8 | 10 | 10 |
| 18 | 11 | 10 | 8 | 10 | 11 | 9 | 10 | 7 | 10 | 10 |
| 19 | 11 | 10 | 8 | 8 | 11 | 11 | 9 | 6 | 7 | 10 |
| 20 | 11 | 10 | 7 | 8 | 7 | 12 | 9 | 6 | 6 | 6 |
| 21 | 12 | 10 | 7 | 8 | 7 | 10 | 8 | 7 | 8 | 7 |
| 22 | 12 | 8 | 7 | 8 | 7 | 12 | 8 | 6 | 8 | 7 |
| 23 | 12 | 8 | 9 | 7 | 7 | 12 | 6 | 8 | 7 | 6 |
| 24 | 16 | 8 | 9 | 7 | 5 | 16 | 7 | 7 | 6 | 5 |
| 25 | 16 | 8 | 11 | 6 | 5 | 17 | 7 | 12 | 5 | 4 |
| 26 | 16 | 7 | 11 | 6 | 9 | 16 | 7 | 11 | 5 | 8 |
| 27 | 14 | 7 | 11 | 7 | 9 | 14 | 8 | 10 | 8 | 9 |
| 28 | 14 | 6 | 9 | 7 | 9 | 13 | 5 | 9 | 8 | 8 |
| 29 | 13 | 5 | 9 | 6 | 10 | 12 | 3 | 11 | 6 | 10 |
| 30 | 12 | 3 | 6 | 6 | 10 | 12 | 4 | 6 | 6 | 10 |
| 20 | 25 | 20 | 25 | 20 | |
| 20 | 25 | 15 | 25 | 20 | |
| 50 | 60 | 40 | 70 | 60 | |
| 30 | 40 | 30 | 50 | 40 | |
| 60 | 75 | 60 | 80 | 70 |
| 130 | 125 | 340 | 230 | |
| 165 | 155 | 400 | 26 | |
| 200 | 200 | 540 | 360 | |
| 170 | 165 | 460 | 310 | |
| 165 | 155 | 400 | 260 | |
| 135 | 125 | 330 | 230 | |
| 150 | 145 | 370 | 240 | |
| 200 | 195 | 550 | 380 | |
| 150 | 135 | 350 | 240 | |
| 190 | 185 | 500 | 330 | |
| 155 | 150 | 390 | 260 | |
| 110 | 110 | 290 | 190 | |
| 205 | 200 | 530 | 360 | |
| 125 | 115 | 290 | 190 | |
| 215 | 210 | 540 | 370 |
| Day | DENCA | B and B | DENCA | B and B |
|---|---|---|---|---|
| 2 | 12,960 | 13,065 | 12,930 | 12,960 |
| 3 | 13,315 | 13,315 | 13,290 | 13,300 |
| 4 | 13,550 | 13,550 | 13,535 | 13,545 |
| 5 | 13,640 | 13,640 | 13,615 | 13,640 |
| 6 | 13,635 | 13,650 | 13,605 | 13,605 |
| 7 | 13,695 | 13,695 | 13,640 | 13,640 |
| 8 | 13,640 | 13,640 | 13,595 | 13,605 |
| 9 | 13,625 | 13,665 | 13,580 | 13,610 |
| 10 | 13,610 | 13,630 | 13,595 | 13,605 |
| 11 | 13,635 | 13,640 | 13,580 | 13,630 |
| 12 | 13,635 | 13,665 | 13,580 | 13,630 |
| 13 | 13,580 | 13,590 | 13,565 | 13,575 |
| 14 | 13,590 | 13,610 | 13,565 | 13,565 |
| 15 | 13,615 | 13,620 | 13,585 | 13,590 |
| 16 | 13,605 | 13,625 | 13,575 | 13,575 |
| 17 | 13,605 | 13,625 | 13,575 | 13,575 |
| 18 | 13,600 | 13,600 | 13,570 | 13,600 |
| 19 | 13,575 | 13,580 | 13,555 | 13,575 |
| 20 | 13,585 | 13,590 | 13,565 | 13,575 |
| 21 | 13,565 | 13,575 | 13,545 | 13,550 |
| 22 | 13,575 | 13,575 | 13,555 | 13,555 |
| 23 | 13,560 | 13,560 | 13,535 | 13,535 |
| 24 | 13,605 | 13,605 | 13,585 | 13,585 |
| 25 | 13,640 | 13,640 | 13,625 | 13,625 |
| 26 | 13,635 | 13,640 | 13,605 | 13,605 |
| 27 | 13,610 | 13,610 | 13,585 | 13,585 |
| 28 | 13,565 | 13,565 | 13,550 | 13,550 |
| 29 | 13,595 | 13,605 | 13,570 | 13,590 |
| 30 | 13,545 | 13,550 | 13,535 | 13,535 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, G.; Park, Y.-J.; Hur, S. The Dynamic Enterprise Network Composition Algorithm for Efficient Operation in Cloud Manufacturing. Sustainability 2016, 8, 1239. https://doi.org/10.3390/su8121239
Ahn G, Park Y-J, Hur S. The Dynamic Enterprise Network Composition Algorithm for Efficient Operation in Cloud Manufacturing. Sustainability. 2016; 8(12):1239. https://doi.org/10.3390/su8121239
Chicago/Turabian StyleAhn, Gilseung, You-Jin Park, and Sun Hur. 2016. "The Dynamic Enterprise Network Composition Algorithm for Efficient Operation in Cloud Manufacturing" Sustainability 8, no. 12: 1239. https://doi.org/10.3390/su8121239
APA StyleAhn, G., Park, Y.-J., & Hur, S. (2016). The Dynamic Enterprise Network Composition Algorithm for Efficient Operation in Cloud Manufacturing. Sustainability, 8(12), 1239. https://doi.org/10.3390/su8121239







