Production Patterns of Eagle Ford Shale Gas: Decline Curve Analysis Using 1084 Wells
Abstract
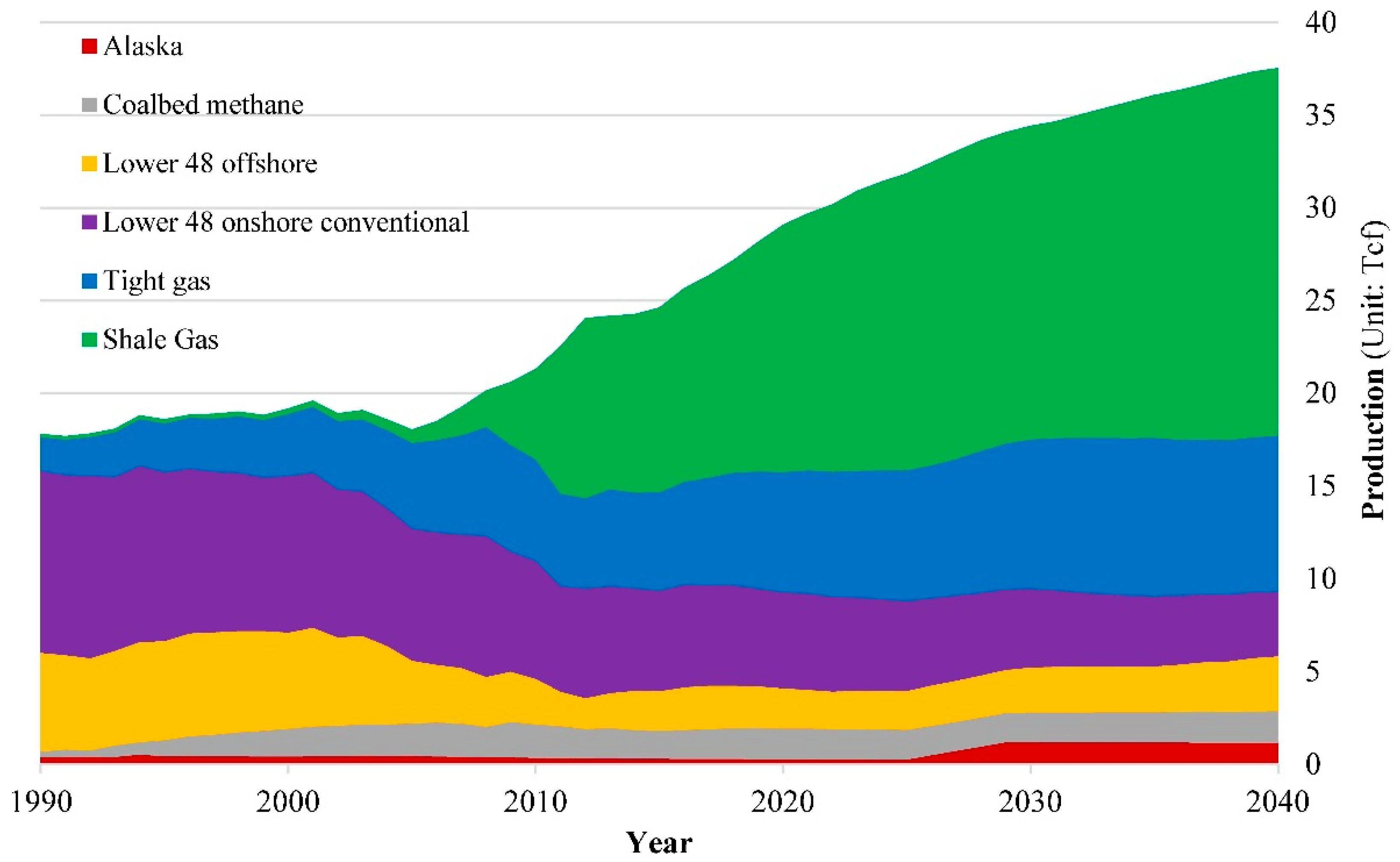
:1. Introduction
2. Methodology
2.1. Decline Curve Models
2.2. Goodness of Fit
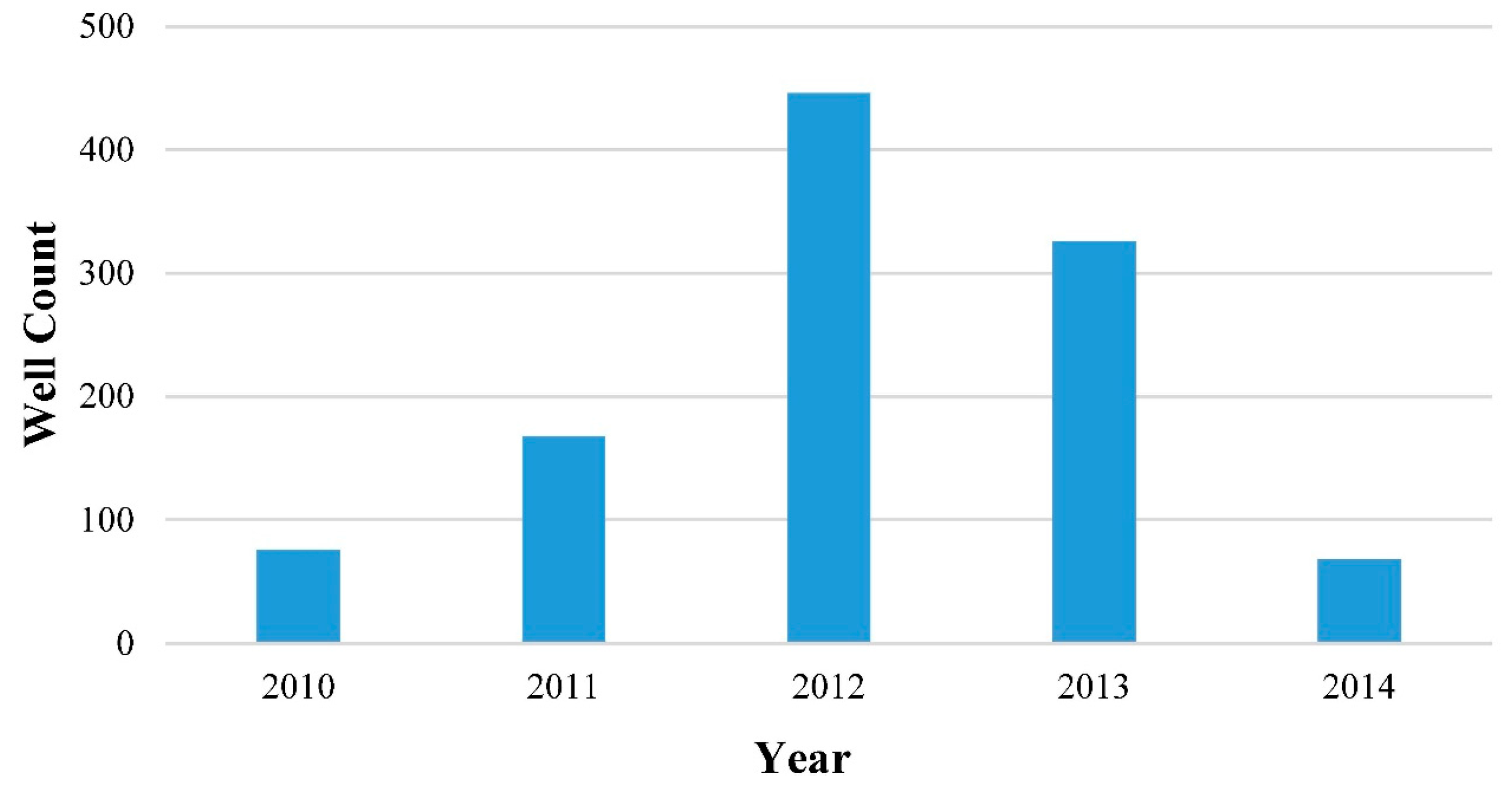
2.3. Data
3. Results
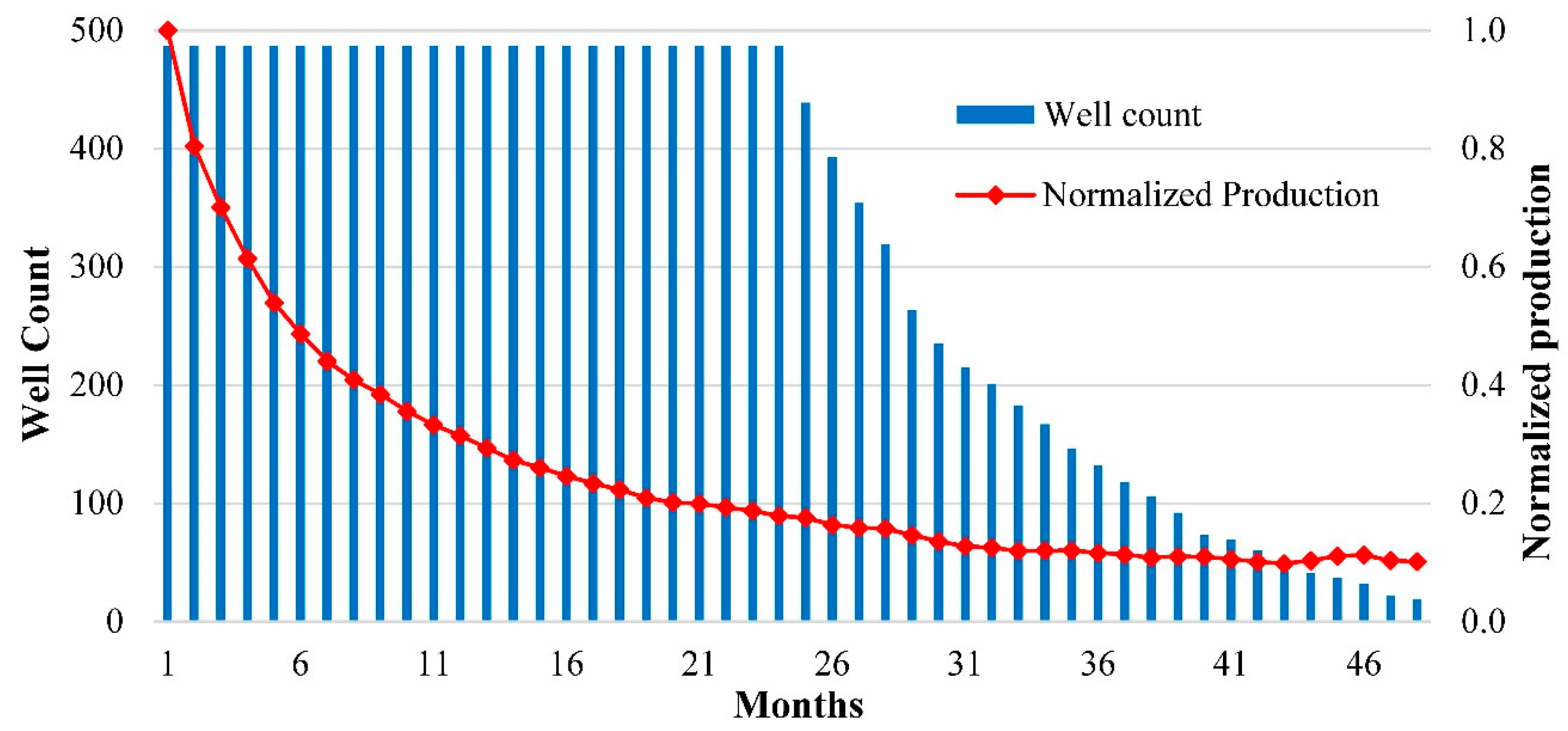
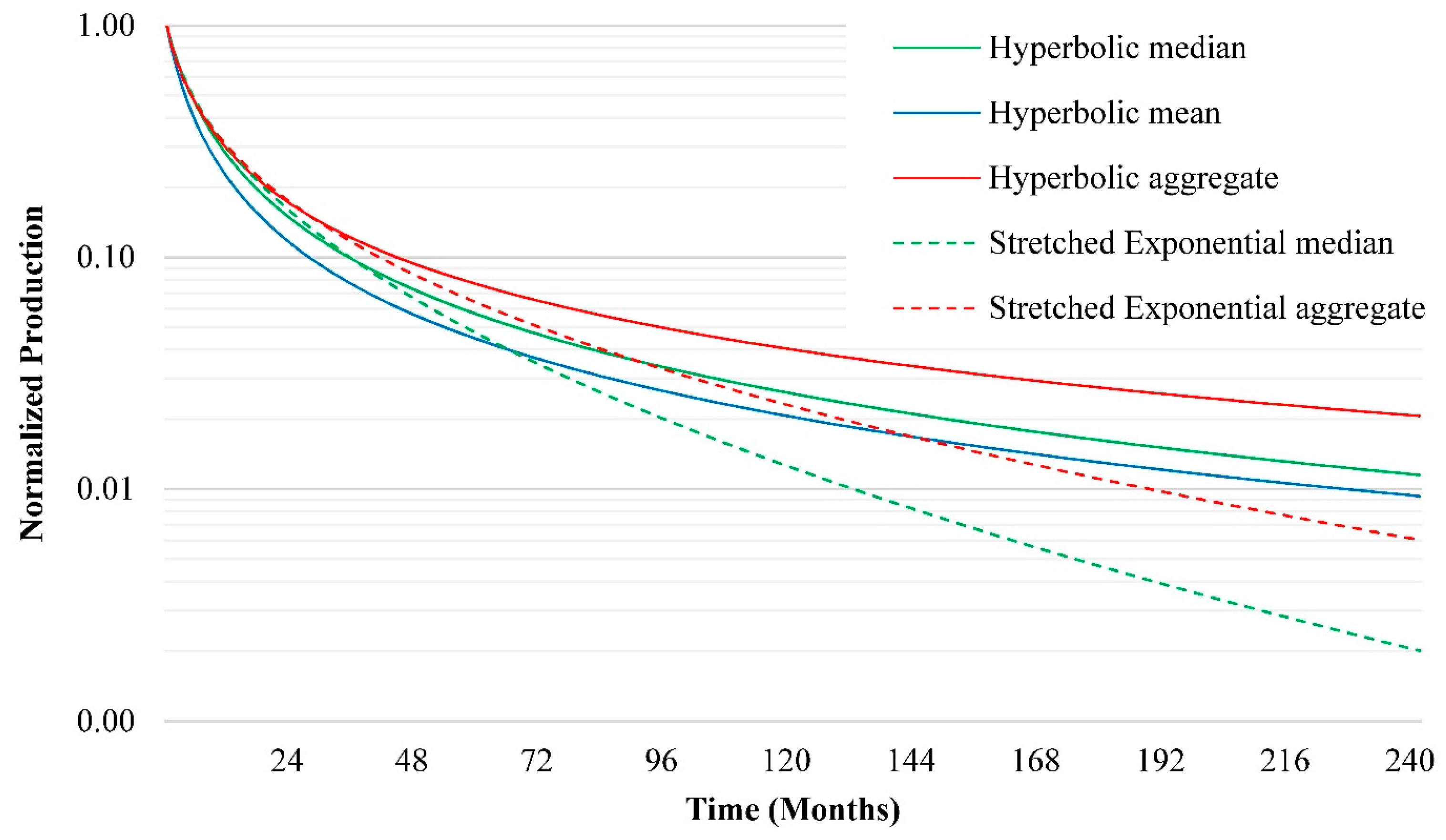
3.1. Aggregate Decline Curves
3.2. Individual Well Decline Curves
3.2.1. Hyperbolic Decline Curve
3.2.2. Stretched Exponential Decline Curve
3.2.3. Summary of Decline Curves
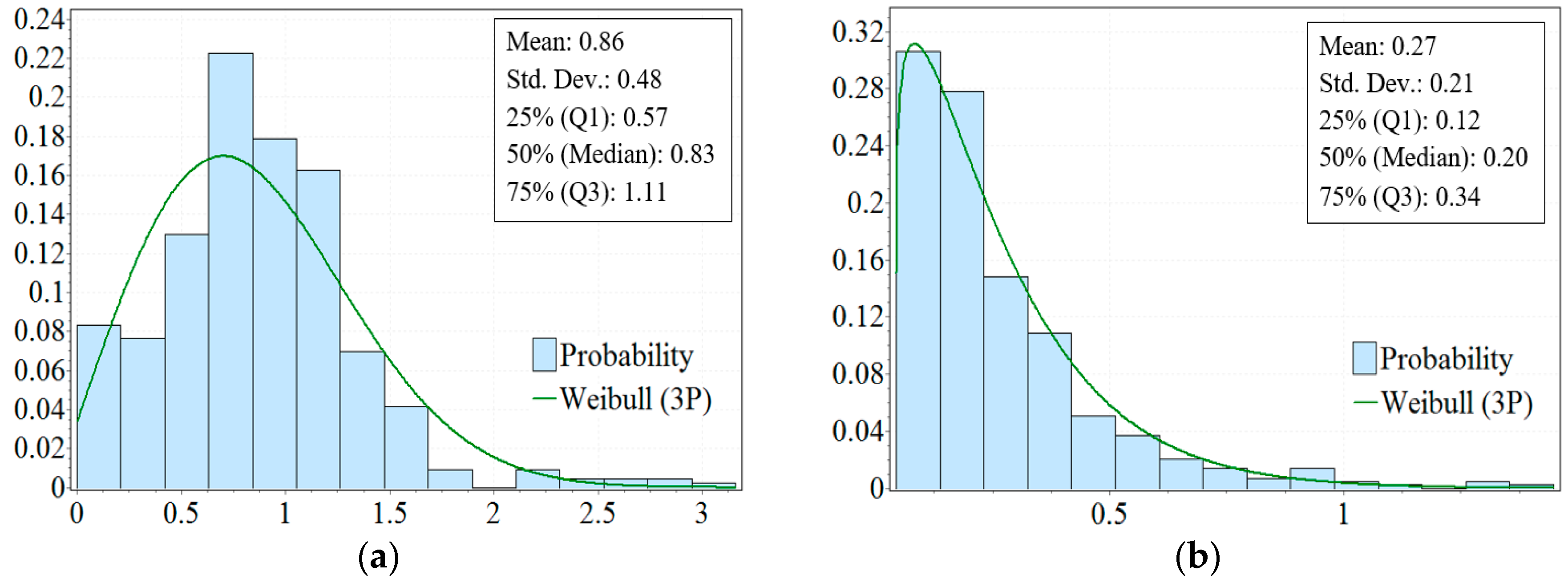
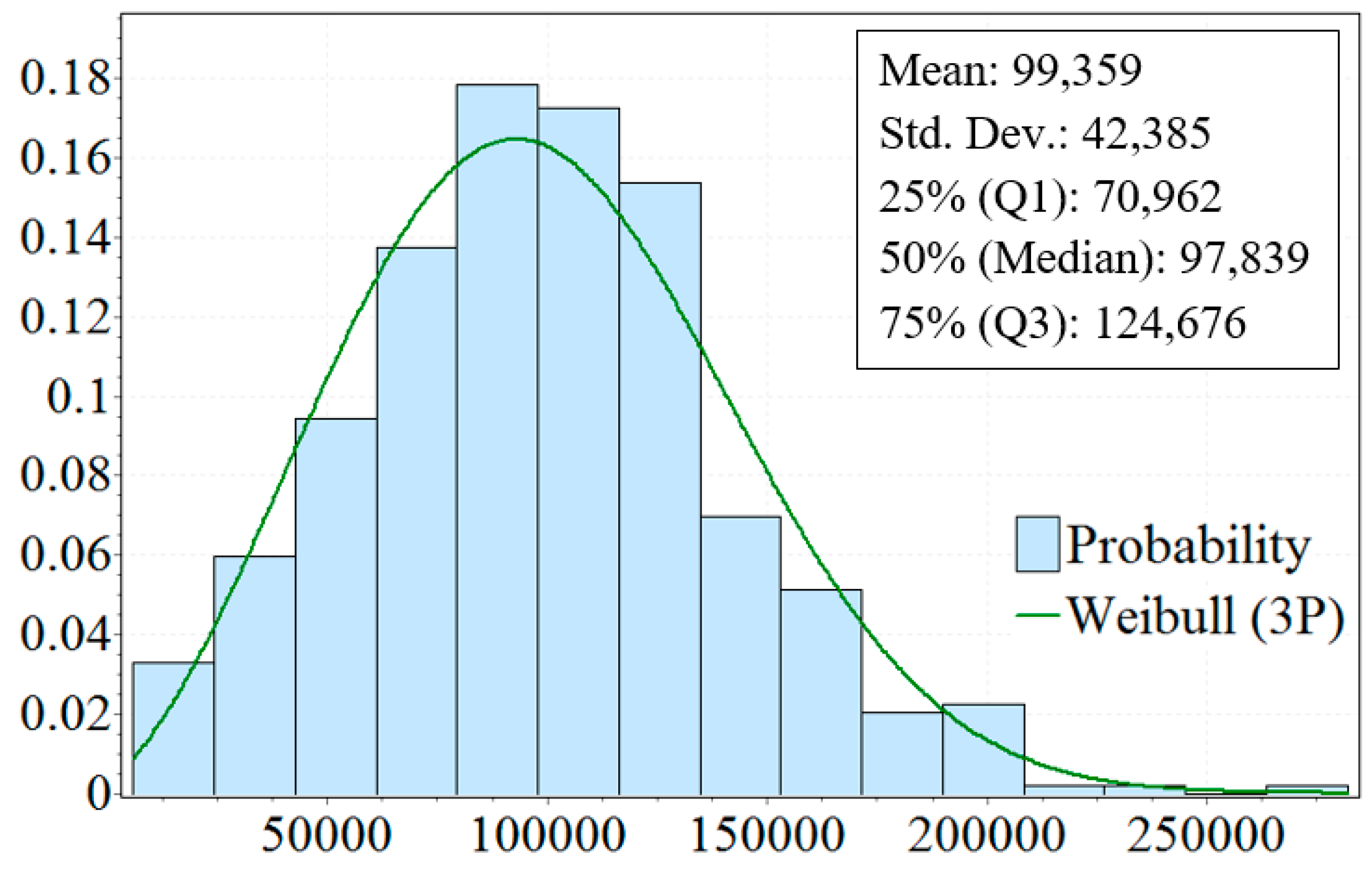
3.3. Initial Production and Decline Rate
3.3.1. Initial Production
3.3.2. Decline Rates in Different Time Phases
3.4. Estimated Cumulative Production
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SE | Stretched Exponential |
| Tcf | Trillion cubic feet |
| Bcf | Billion cubic feet |
| Mcf | Mil cubic feet = Thousand cubic feet |
| URR | Ultimate recoverable resource |
References
- Jackson, J.A. Glossary of Geology, 4th ed.; American Geosciences Institute: Alexandria, WV, USA, 2011. [Google Scholar]
- Technically Recoverable Shale Oil and Shale Gas Resources: An Assessment of 137 Shale Formations in 41 Countries Outside the United States. Available online: http://www.actu-environnement.com/media/pdf/news-23433-rapport-aie.pdf (accessed on 31 July 2015).
- Wang, Z.; Krupnick, A. A Retrospective Review of Shale Gas Development in the United States: What Led to the Boom? Available online: http://www.rff.org/files/sharepoint/WorkImages/Download/RFF-DP-13-12.pdf (accessed on 2 July 2015).
- BP Statistical Review of World Energy 2016. Available online: http://www.bp.com/statisticalreview (accessed on 20 June 2016).
- Erdogdu, E. Bypassing Russia: Nabucco project and its implications for the European gas security. Renew. Sustain. Energy Rev. 2010, 14, 2936–2945. [Google Scholar] [CrossRef]
- Lu, W.; Su, M.; Fath, B.D.; Zhang, M.; Hao, Y. A systematic method of evaluation of the Chinese natural gas supply security. Appl. Energy 2016, 165, 858–867. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration (EIA). Annual Energy Outlook 2014 with Projections to 2040. Available online: http://www.eia.gov/forecasts/archive/aeo14/ (accessed on 7 May 2014).
- Toscano, A.; Bilotti, F.; Asdrubali, F.; Guattari, C.; Evangelisti, L.; Basilicata, C. Recent trends in the world gas market: Economical, geopolitical and environmental aspects. Sustainability 2016, 8, 154. [Google Scholar] [CrossRef]
- Annual Energy Outlook 2016 Early Release: Annotated Summary of Two Cases. Available online: http://www.eia.gov/forecasts/aeo/er/pdf/0383er(2016).pdf (accessed on 10 July 2015).
- Pi, G.; Dong, X.; Dong, C.; Guo, J.; Ma, Z. The status, obstacles and policy recommendations of shale gas development in China. Sustainability 2015, 7, 2353–2372. [Google Scholar] [CrossRef]
- Hu, D.; Xu, S. Opportunity, challenges and policy choices for China on the development of shale gas. Energy Policy 2013, 60, 21–26. [Google Scholar] [CrossRef]
- Höök, M.; Bardi, U.; Feng, L.; Pang, X. Development of oil formation theories and their importance for peak oil. Mar. Petrol. Geol. 2010, 27, 1995–2004. [Google Scholar] [CrossRef]
- Höök, M.; Davidsson, S.; Johansson, S.; Tang, X. Decline and depletion rates of oil production: A comprehensive investigation. Philos. Trans. R. Soc. Lond. Math. Phys. Eng. Sci. 2014, 372, 20120448. [Google Scholar] [CrossRef] [PubMed]
- Khanamiri, H. A non-iterative method of decline curve analysis. J. Pet. Sci. Eng. 2010, 73, 59–66. [Google Scholar] [CrossRef]
- Arps, J.J. Analysis of decline curves. Trans. AIME 1945, 160, 228–247. [Google Scholar] [CrossRef]
- Exponential vs. Hyperbolic Decline in Tight Gas Sands: Understanding the Origin and Implications for Reserve Estimates Using Arps’ Decline Curves. Available online: https://www.researchgate.net/profile/Thomas_Blasingame/publication/254528784_Exponential_vs_Hyperbolic_Decline_in_Tight_Gas_Sands_Understanding_the_Origin_and_Implications_for_Reserve_Estimates_Using_Arps'_Decline_Curves/links/569c06b808ae6169e56278a3.pdf (accessed on 1 July 2015).
- Ahmed, T. Reservoir Engineering Handbook, 3rd ed.; Gulf Professional Burlington: Burlington, MA, USA, 2006. [Google Scholar]
- Bailey. Decline rate in fractured gas wells. Oil Gas J. 1982, 80, 117–118. [Google Scholar]
- Valko, P.P. Assigning value to stimulation in the Barnett Shale: A simultaneous analysis of 7000 plus production histories and well completion records. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 19–21 January 2009.
- Duong, A.N. Rate-Decline Analysis for Fracture-Dominated Shale Reservoirs. Available online: http://www.pe.tamu.edu/blasingame/data/z_zCourse_Archive/P648_15A/P648_15A_Lectures_(working_lectures)/20150420_P648_15A_Lec_19_SPE_137748_[pdf].pdf (accessed on 1 April 2015).
- Wang, J.; Feng, L.; Zhao, L.; Snowden, S.; Wang, X. A comparison of two typical multicyclic models used to forecast the world’s conventional oil production. Energy Policy 2011, 39, 7616–7621. [Google Scholar] [CrossRef]
- Patzek, T.W.; Croft, G.D. A global coal production forecast with multi-Hubbert cycle analysis. Energy 2010, 35, 3109–3122. [Google Scholar] [CrossRef]
- Drillinginfo. Available online: http://info.drillinginfo.com/ (accessed on 20 June 2015).
- Höök, M. Depletion rate analysis of fields and regions: A methodological foundation. Fuel 2014, 121, 95–108. [Google Scholar] [CrossRef]
- Kaiser, M.J.; Yu, Y. Economic limit of field production in Texas. Appl. Energy 2010, 87, 3235–3254. [Google Scholar] [CrossRef]
- Gong, X. Assessment of Eagle Ford Shale Oil and Gas Resources. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, August 2013. [Google Scholar]
- Hughes, J.D. Drill, Baby, Drill: Can Unconventional Fuels Usher in a New Era of Energy Abundance? Post Carbon Institute: Santa Rosa, CA, USA, 2013. [Google Scholar]
- U.S. Geological Survey Oil and Gas Assessment Team. Variability of Distributions of Well-Scale Estimated Ultimate Recovery for Continuous (Unconventional) Oil and Gas Resources in the United States. Available online: http://pubs.usgs.gov/of/2012/1118/OF12-1118.pdf (accessed on 1 June 2012).
- Swindell, G.S. Eagle Ford Shale—An Early Look at Ultimate Recovery. In Proceedings of SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 2012.
- U.S. Energy Information Administration (EIA). Review of Emerging Resources: U.S. Shale Gas and Shale Oil Plays. Available online: https://www.eia.gov/analysis/studies/usshalegas/pdf/usshaleplays.pdf (accessed on 8 July 2011).
- Baihly, J.D.; Altman, R.M.; Malpani, R.; Luo, F. Shale Gas Production Decline Trend Comparison over Time and Basins. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 20–22 September 2010.



| Properties | Hyperbolic | SE |
|---|---|---|
| URR |
| n | |||
|---|---|---|---|
| Mean | 138.95 | 1.39 | 0.49 |
| Std. Deviation | 589.07 | 1.95 | 0.30 |
| Min | 0.86 | <0.01 | 0.06 |
| 25% (Q1) | 1.34 | 0.27 | 0.28 |
| 50% (Median) | 1.84 | 0.58 | 0.45 |
| 75% (Q3) | 4.26 | 1.45 | 0.63 |
| Max | 4608.88 | 8.46 | 2.78 |
| 2010 | 2011 | 2012 | 2010–2012 | |
|---|---|---|---|---|
| First year | 70.58% | 70.40% | 66.76% | 68.54% |
| First two years | 83.72% | 83.74% | 80.57% | 82.09% |
| 10-Year | 15-Year | 20-Year | 30-Year | |||
|---|---|---|---|---|---|---|
| Hyperbolic | Median | q(t) | 85 | 53 | 38 | 23 |
| Q(t) | 1.49 | 1.61 | 1.69 | 1.80 | ||
| Mean | q(t) | 68 | 43 | 31 | 19 | |
| Q(t) | 1.25 | 1.35 | 1.41 | 1.50 | ||
| Aggregate | q(t) | 132 | 90 | 68 | 46 | |
| Q(t) | 1.40 | 1.89 | 2.03 | 2.24 | ||
| SE | Median | q(t) | 41 | 15 | 7 | 2 |
| Q(t) | 1.44 | 1.49 | 1.51 | 1.52 | ||
| Aggregate | q(t) | 76 | 36 | 20 | 8 | |
| Q(t) | 1.58 | 1.68 | 1.73 | 1.78 | ||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Zhang, B.; Aleklett, K.; Höök, M. Production Patterns of Eagle Ford Shale Gas: Decline Curve Analysis Using 1084 Wells. Sustainability 2016, 8, 973. https://doi.org/10.3390/su8100973
Guo K, Zhang B, Aleklett K, Höök M. Production Patterns of Eagle Ford Shale Gas: Decline Curve Analysis Using 1084 Wells. Sustainability. 2016; 8(10):973. https://doi.org/10.3390/su8100973
Chicago/Turabian StyleGuo, Keqiang, Baosheng Zhang, Kjell Aleklett, and Mikael Höök. 2016. "Production Patterns of Eagle Ford Shale Gas: Decline Curve Analysis Using 1084 Wells" Sustainability 8, no. 10: 973. https://doi.org/10.3390/su8100973
APA StyleGuo, K., Zhang, B., Aleklett, K., & Höök, M. (2016). Production Patterns of Eagle Ford Shale Gas: Decline Curve Analysis Using 1084 Wells. Sustainability, 8(10), 973. https://doi.org/10.3390/su8100973





