1. Introduction
Modern business operations are impacted by many variables which imply an increasing level of complexity over time. Globalization as well as the development of new technologies, such as, firstly, information and communication technologies (ICT), make the situation even harder when it comes to identification and handling of all potential business risks [
1,
2]. Methodologies, tools or business standards that are traditionally used by organizations in order to deal with business risks and disruptions seem to be insufficient due to the abovementioned issues. Approximately 200,000 firms go bankrupt each year in the EU. These events have resulted in direct job losses, with a total of 5.1 million over three years [
3], in European Union countries from 2011 until 2014. A significant part of bankruptcy could be addressed by good risk management practices. An important need, which has arisen from the development of a long term economic sustainability perspective [
4], is the opening up of the possibility of organizational resilience assessment and its overall enhancement. The analysis of organizational issues in terms of engineered systems’ resilience [
5,
6] indicates the need for a definition of the enabling conditions of organizational resilience. In this research, the main issues are related to: (1) definition of a model of resilience assessment; (2) definition of appropriate strategies to enable resilience improvement. Motivation for this research is inspired by the fact that there are various resilience assessment models scoped according to different areas of interest, but there is no unique mathematical model for assessment and enhancement of organizational resilience which is widely accepted [
7]. This should enable the presentation of a clear market position of an organization and the possibility to determine an organization’s benchmarks. In the end, learning from other organizations’ experiences may lead to an improved level of long term sustainability [
8].
The model proposed by this paper is oriented to the economic sustainability of the process industry sector SMEs. SMEs represent a very important economic pillar in all parts of Europe. This may be illustrated through the following data: (1) In Serbia, a government strategy highlighted SMEs as a very significant economic factor which needs further development as SMEs together account for 99.4% of all enterprises [
9]; (2) In the UK, SMEs are recognized as the most influential economic actor accounting for 99.9% of all enterprises; (3) In the EU, recent years have brought about certain issues but SMEs have retained their position as the backbone of the European economy, being more than 98% of all enterprises in 2012 [
10]. In the process industry, organizations have to be resilient because of the nature of their business such as the continuous flow of material and connected processes where risk in one process may lead to other unwanted events in other processes. In industries all over Europe, SMEs are recognized as an important sector, especially in the process industry in developing countries [
11].
The aim of this paper is to introduce a two-step model for assessment and enhancement of organizational resilience in SMEs of the process industry in an uncertain environment. In this manner, organizational resilience corresponds to the maximum percentage change given in the worst-case level of performance [
12] that an organization may withstand. Overall organizational resilience of an SME is based on assessment of verified potential factors of organizational resilience (ORPFs) [
13,
14] estimated by using fuzzy sets theory. Since it may be assumed that their value is not subject to change over a predefined period of time, ORPFs are analyzed as static variables.
Finding a near optimal combination of resource usage and ORPFs’ improvement to ensure maximization of overall resilience is based on the proposed genetic algorithm model.
It is closer to the human way of thinking that decision makers should describe uncertainties in the relative importance of ORPFs and their values by linguistic expressions. Depending on the type of uncertainty and quality of available information, linguistic expressions could be modeled by using different mathematical theories. In traditional approaches, modelling of uncertainties is based on dual logic such as Boolean mathematics (BM), which can be extended to n-valued logic [
15]. Often, usage of formal logic does not resemble reality. In literature, many papers can be found which discuss the relationship between fuzzy sets and formal logic [
16,
17]. Fuzzy set theory was extensively used to relax or generalize classical methods from a dichotomous to a gradual character [
18]. The fuzzy sets theory could be the most appropriate way for modelling linguistic expressions [
18], because it supports the subjective natural language descriptors.
Since the membership functions should reflect the knowledge and uncertainty regarding linguistic variables, the authors suggest trapezoidal fuzzy numbers (TrFNs) for modelling uncertainties which exist in the considered problem (by analogy to [
19]).
The determined relative importance of each ORPF for each business process may be given for the target SME of the process industry [
13]. In this paper, the relative importance of ORFPs, considering the level of business, is stated as a fuzzy group decision making problem for a large sample of SMEs. Fuzzy Ordered Weighted Averaging Operator (FOWA) [
20] is used for determination of aggregated values for relative importance of ORPFs for each business process. Accuracy of relative importance of ORPFs for business processes significantly increases, by increasing the specimen of target SMEs of the process industry.
The fuzzy mathematical model for assessment of organizational resilience potential [
13] may be the base for continual resilience improvement. It is known that the Genetic Algorithm (GA) method uses a set of tools based on natural selection and population genetics mechanisms [
21,
22] to find a near optimal solution for specific objective functions, with respect to a set of constraints. It has been shown that a model based on GA can be used for the ranking of SMEs, sub processes of the production process and key performance indicators (KPIs) of the production process [
23]. The proposed GA model introduces two functions: total sum of the overall weighted coefficient of SMEs, sub processes, and KPIs, and the second function is variance of the existing variables. MATLAB—GA toolbox is used for the development of this software solution. Choosing the appropriate strategy for organizational resilience enhancement may be treated as an optimization issue where GA, in recent years, has found many applications [
23,
24]. With respect to the obtained results, an improvement strategy is developed by using GA in this paper.
In this paper, the objective function is defined in order to find the near optimal distribution of the enhancements of ORPFs so that overall resilience could be enhanced for a particular value while respecting constraints that present minimal usage of resources. Constraints of the proposed GA model are obtained respecting the rank of ORPFs and planned overall improvement. The rank of ORPFs is determined by a novel fuzzy Technique for Order Preference by Similarity to Ideal Solution (FTOPSIS) [
25,
26]. The authors have emphasized that the priority of improvement measures which should lead to improvement of the organizational resilience may be based on the obtained rank of ORPFs [
14]. The possible improvement procedure is not proposed in the analyzed papers [
13,
14]. In this paper, the assessment of ORPFs, determination of the organizational resilience of SMEs and enhancement of SMEs’ organizational resilience are considered. It can be considered as the main difference between this paper and the analyzed literature papers.
The paper is organized as follows: a literature review from the reference domains is shown in
Section 2. Modelling of uncertainties, and also method for ranking of ORPFs, based on the fuzzy sets theory and GA method for optimization, with respect to all business processes as well as their weights are described in
Section 3.
Section 4 provides an example with real-life data from SMEs of the process industry that exist in Central Serbia, which illustrates the developed method. Conclusions are presented in
Section 5.
2. Literature Review
Resilience has been analyzed from various perspectives [
7], so it has a lot of similarities and some differences. General resilience may be seen as the capacity of social-ecological systems to adapt or transform in response to unfamiliar, unexpected and extreme shocks [
27]. Engineering resilience may be presented as the ability to sense, recognize, adapt and absorb variations, changes, disturbances, disruptions and surprises [
28]. From an organizational perspective, resilience implies the ability of an organization to withstand systematic discontinuities as well as have the capability to adapt to new risk environments [
29]. Analyzing papers, from the organizational point of view, shows that, chronologically, resilience research has developed into five research streams [
30], and view resilience as: (1) organizational responses to external threats; (2) organizational reliability; (3) employee strengths; (4) the adaptability of business models; or (5) design principles that reduce supply chain vulnerabilities and disruptions. In recent years, research is looking in new directions, such as resilience activation [
31]. In that manner, it is important to detect whether or not an organization has resilience potential, prior to demonstrating a resilient or non-resilient response [
8]. Emerging research trends among recently published papers showed interest in employee resilience and psychological capital development [
32] as well as in developing models for supply chain resilience [
6]. Significant research is dedicated to development of resilience models [
33] with the purpose to measure organizational resilience and manage its factors.
Different issues (e.g., globalization or socio-economic disruptions) have significantly increased market expectations all over the world, so in this manner SMEs have to be capable of innovatively adapting to emerging challenges [
34]. On the other hand, SMEs have a limited approach to resources, firstly, to economic resources, which makes them vulnerable to the environment. In order to assure long term sustainability, they have to define an appropriate business strategy [
35] and wisely manage the resources [
36]. The need to enhance the resilience and competitiveness of SMEs [
37] is extremely important because of SMEs’ significance to the EU economy, accounting for some 20.7 million firms in 2012 [
10]. In the process industry, the concept of resilience is not unknown. As in other industry branches, here it is very important to conduct continuous monitoring of a system and to follow indicators (factors) which will identify the limits and show the position of the system [
38]. The oil and gas industry often use process oriented analysis (e.g., HAZOP) in order to assess potential process deviations, having in mind that different processes are connected in a continuous flow.
In practice, there is a wide range of SMEs that imply the need for a simple and reliable tool for assessment and enhancement of organizational resilience. In the literature, papers can be found which assume that the resilience assessment should be done on the level of organizational processes [
13,
14] with assets that can be influenced by managers in order to keep the measurement consistent over time. In this manner, industrial processes may be assessed from the perspective of the contributing factors of resilience [
14]. A lot of events described with insufficient data may have an influence on resilience of critical processes in an organization. This justifies the employment of fuzzy sets [
18] for modeling resilience and ranking organizational resilience factors in an organization. Relative importance of each identified business process and organizational resilience factors may be stated by fuzzy pair wise comparison matrices. Assessment of values of organizational resilience factors may be assessed by decision makers. All uncertainties may be modeled by fuzzy sets theory. Priority of management initiatives that should be undertaken in order to increase the organizational resilience potential may be based on the obtained rank of the organizational resilience factors in an organization.
In general, the solutions to different management problems can be obtained by using heuristic and/or computer approaches. Based on the available data, managers are making decisions. The values of decision variables obtained in an exact way are less influenced by the subjective attitudes of decision makers. In this way, higher accuracy of available data implies more accurate decision making. There are many approaches oriented to this type of research that employ different techniques. It is shown that GA is a promising technique for obtaining the global near optimal solution [
39,
40].
Organizational resilience of SMEs has been a focus of some recent research [
37], but it is still recognized as an issue for the future research agenda [
33] based on already defined foundations and identified factors. As one of the main issues over time, enhancement of SMEs’ organizational resilience may be achieved by the implementation of a conceptual framework for resilience improvement. The purpose of this framework is to increase the accuracy of the input data and the accuracy of the strategy for ORPFs’ enhancement. The model proposed by this paper for ORPFs’ assessment and for determining an improvement strategy of organizational resilience is novel within the scope of organizational resilience management.
3. The Proposed Fuzzy Model
Uncertainties in: (1) the relative importance of ORPFs for each business process and (2) the ORPFs’ values, are considered. These uncertainties are described by predefined linguistic expressions which are modelled by TrFNs [
18,
41]. This is proposed since TrFNs offer a good compromise between descriptive power and computational simplicity, and fuzzy sets of higher types and levels have not, as yet, played a significant role in applications of fuzzy sets theory [
42].
In this paper, the domains of the defined TrFNs are defined on the scale [0–1]. The value 0 denotes that the existing considered uncertainties have very low importance/value. Value 1 stands for the highest relative importance/value of the considered uncertainties.
3.1. Modelling of the Relative Importance of ORPFs
The relative importance assigned to each ORPF on the business process level is varied due to the high degree of subjective preferences of a management team. Also, they can be considered as unchangeable during the considered period of time (one year).
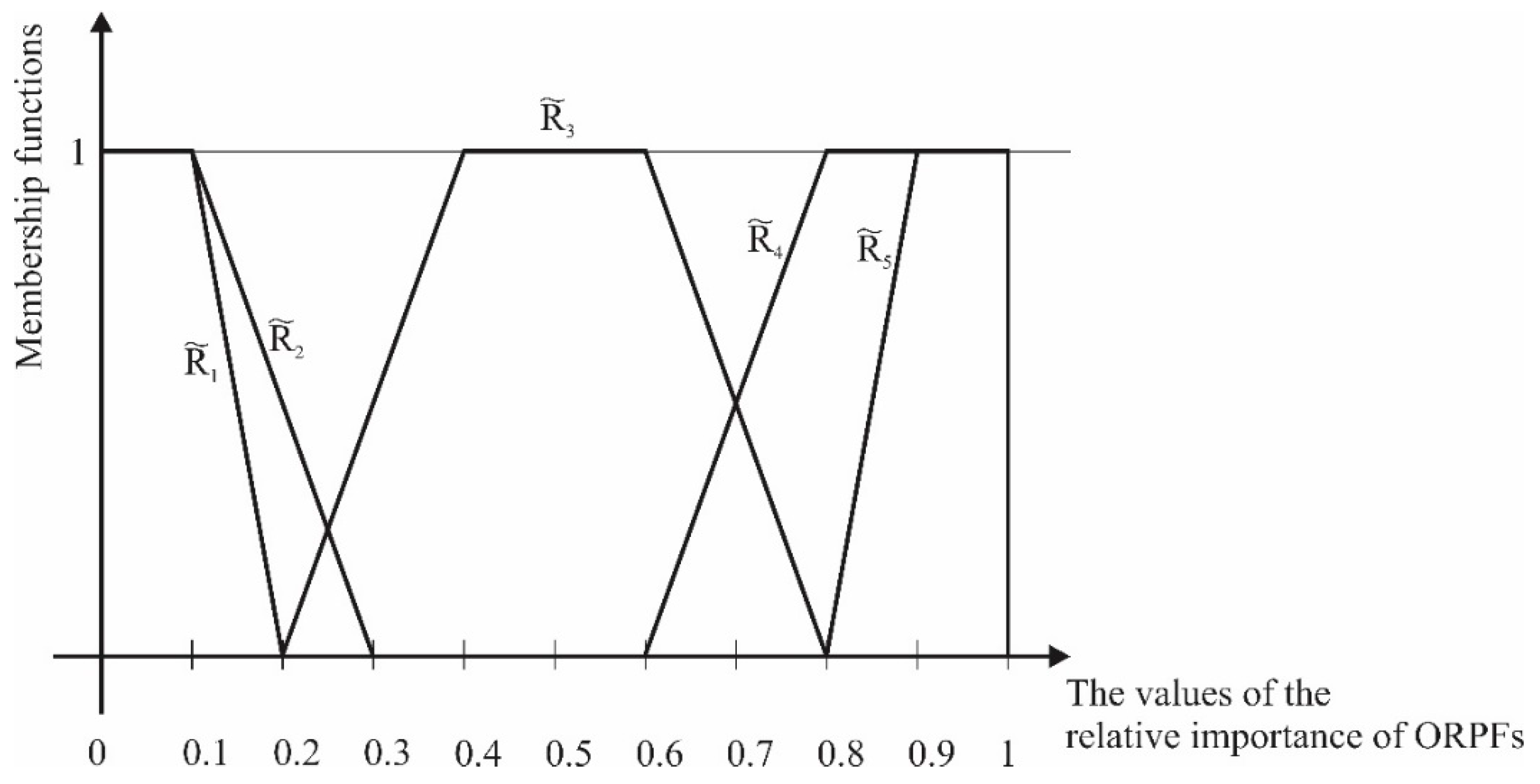
It is assumed that each management team should analyze ORPFs’ importance in the defined business processes. The fuzzy rating of each management team is described by one of the five defined linguistic expressions which can be modelled by TrFN with the lower and upper bounds and modal values , respectively.
These TrFNs are given in the following way, and presented in
Figure 1:
very low importance—
low importance—
moderate importance—
high importance—
very high importance—
Figure 1.
The relative importance of organizational resilience potential factors (ORPFs).
Figure 1.
The relative importance of organizational resilience potential factors (ORPFs).
3.2. Modelling of ORPFs’ Values
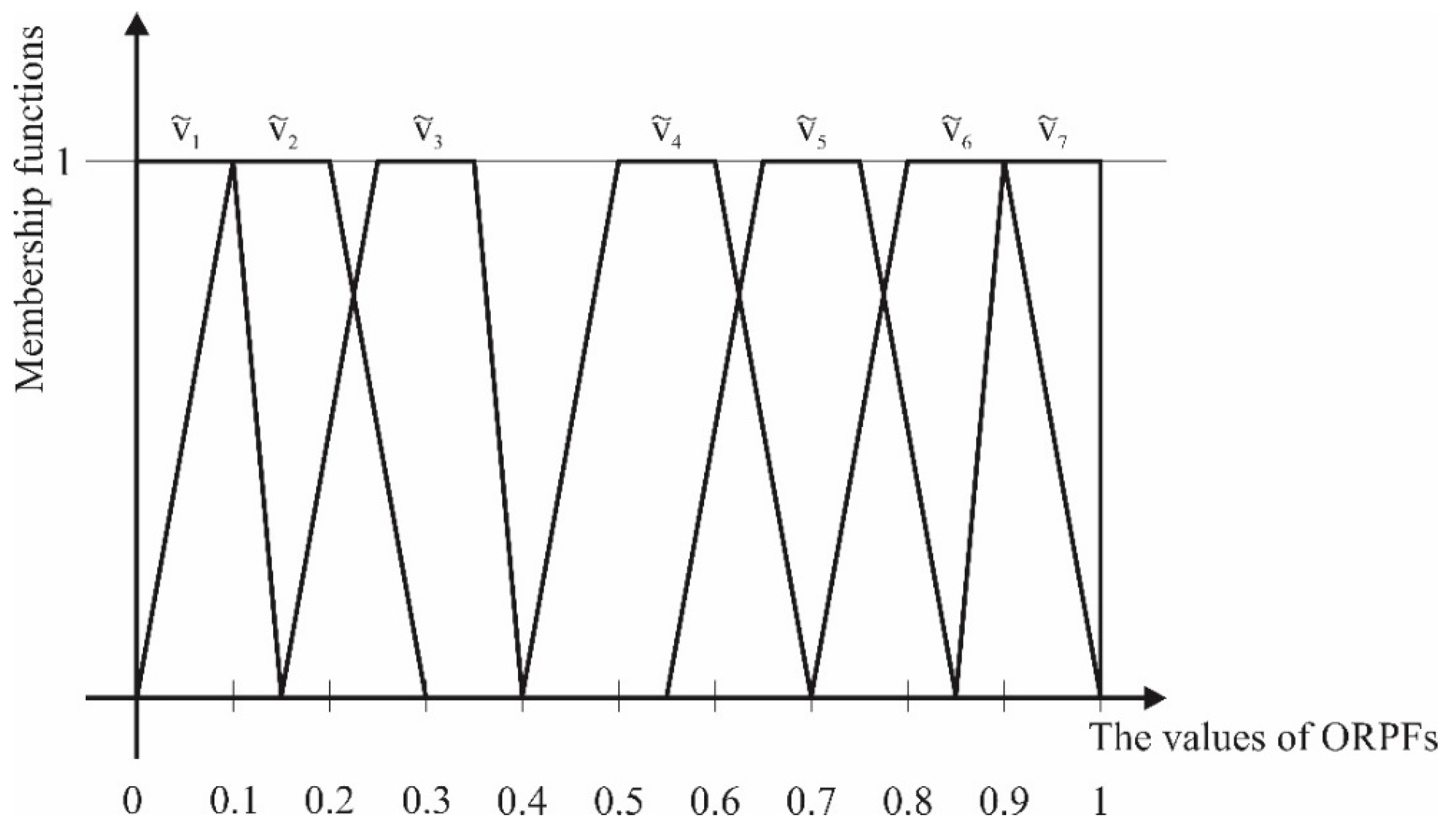
The ORPFs’ values at the level of each business process cannot be stated quantitatively because decision makers most often base their estimates on evidence data, experience, knowledge, etc. These are adequately described by linguistic expressions which can be represented as TrFNs with the lower and upper bounds and modal values , respectively.
For the problem considered in this paper, seven linguistic expressions are proposed, which are modelled by TrFNs as follows, and presented in
Figure 2:
very low value—
low value—
medium low value—
medium value—
medium high value—
high value—
very high value—
Figure 2.
The values of ORPFs.
Figure 2.
The values of ORPFs.
3.3. The Formal Problem Statement
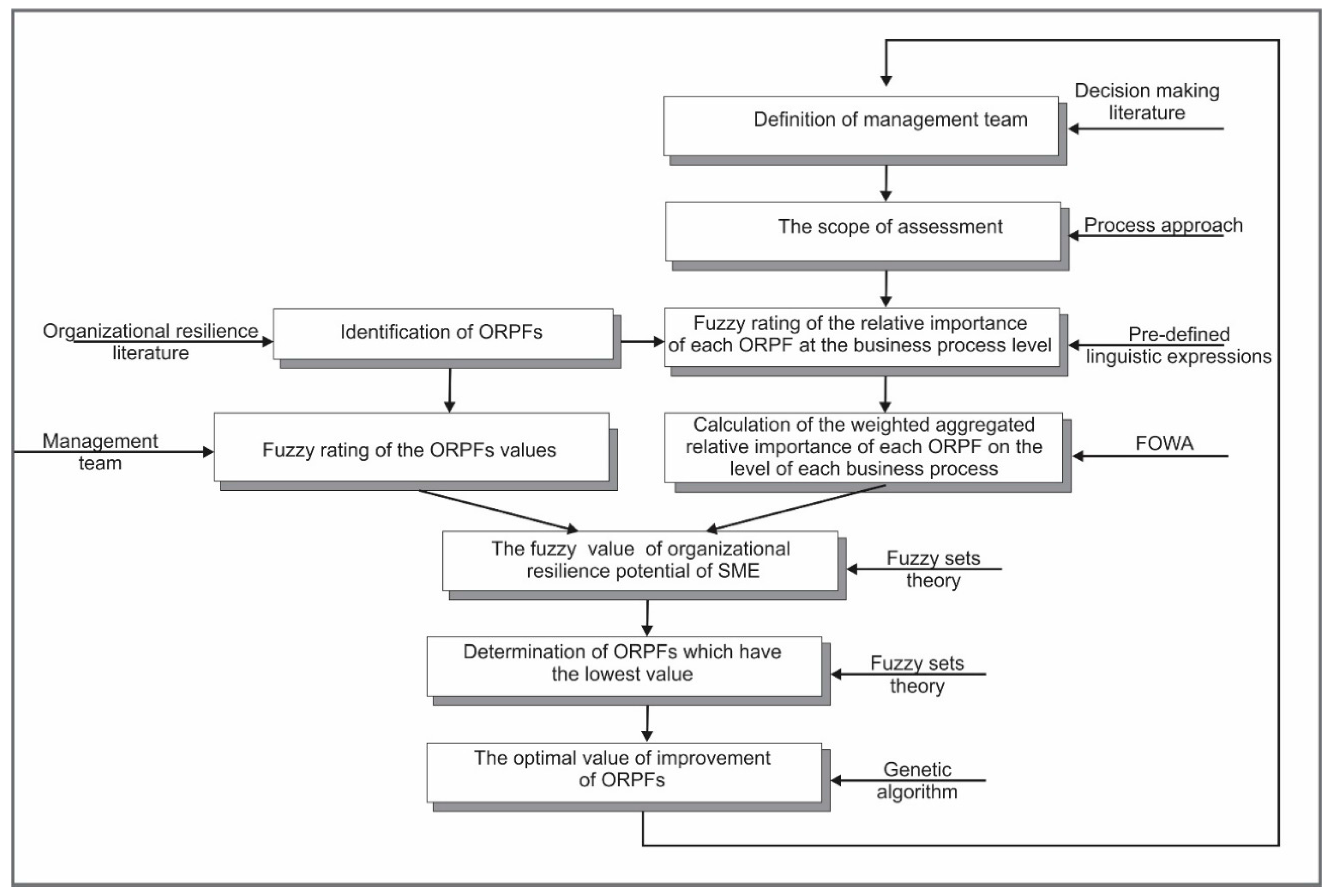
The evaluation framework of the proposed model that is described in this section is summarized in
Figure 3.
Figure 3.
The framework for assessment and enhancement of organizational resilience.
Figure 3.
The framework for assessment and enhancement of organizational resilience.
According to the process approach, an organization is viewed as a network of interrelated processes that are focused towards achieving organizational goals [
43]. In this case, the number, nature and scope of business processes [
43] are identified in the analyzed group of SMEs of the process industry. In general, the business processes, in any enterprise, can be formally denoted by a set of indices Ƿ =
. The index for a business process is denoted as
p, and
P is the total number of business processes.
The ORPFs are presented by a set of indices Ɨ =
. The total number of ORPFs is
I, and
i is the index of these factors. An organization reference model in the process industry is impacted by ORPFs [
13]: (1) planning strategies; (2) capability and capacity of internal resources; (3) internal situation monitoring and reporting; (4) human factors and (5) quality; (6) external situation monitoring and reporting; (7) capability and capacity of external resources; (8) design factor; (9) detection potential; (10) emergency response; and (11) a safety management system.
The assessment of the relative importance of the ORPFs is stated as a fuzzy group decision making problem. Members of the management team are the main manager, the quality manager, and the production manager. These managers do not have equal importance in the decision making process. The importance of each manager
is determined based on the results of good practice in the SMEs of the process industry (by analogy to [
23]).
The fuzzy ratings of the ORPFs’ importance are given by each manager and they are modelled by TrFNs
. These values do not change at all over time. The aggregation of a management team’s opinions into a group consensus is performed by the fuzzy ordered weighted averaging operator (FOWA) [
20]. The relative importance of each of the ORPFs for each business process is denoted as
.
The ORPFs’ values at the process level are assessed by the management team by consensus. The values of the ORPFs are described using linguistic expressions modelled by the TrFNs , .
One of the important tasks of any enterprise management team is to improve the ORPFs’ values in order to increase the organizational resilience. This problem correlates with one of the requirements of ISO 9001:2008 which is defined as continuous improvement [
44]. The objective function minimizes the difference between wanted and accomplished resilience, which was improved for the determined coefficient
. A solution to this issue is found by using a new model which is created in MatLab with given constraints. Considering the type of problem, constraints are determined by opinion of the management team. Generally, GA encodes possible solutions into linear strings that are called chromosomes. In this paper, possible values for ORPFs relevant to the resilience are codified and presented as chromosomes. Chromosomes can be viewed as boxes, arranged in a linear manner [
45], where each box (gene) in the string represents an ORPF that has to be improved. Each box is presented with an index number for the ORPF that has to be enhanced, and the value in the box presents a possible solution for that ORPF. In this case, the group of possible solutions, called population, is randomly selected and given to the GA system. After that, all solutions are evaluated by the objective function; in this way, every solution gets its fitness value according to the Rank selection method, which represents the potential of a solution in terms of its longevity and role in the formation of the next generation, used in GA model iteration process. Selected parent chromosomes are then used to create new offspring with GA operators. GA operators are crossover, which is used to create two new offspring by exchanging parts of two parents between a randomly selected crossing point; and mutation, which creates new offspring by making a random change on a single parent chromosome. These operations are done repetitively through loops (iterations), until the acceptable near optimal solution has been reached or a certain number of generations have been achieved.
3.4. The Proposed Algorithm
The algorithm of the proposed fuzzy model is presented as follows:
Step 1. Calculate the aggregated value of each of the ORPFs:
where
—the importance of each member of management team of considered enterprise.
—fuzzy estimation of relative importance of ORPF i, i = 1,…, I under business process p, p = 1,…, P, by each member of management team e, e = 1, …, E.
Step 2. Calculate the weighted values of the ORPFs,
:
The values of these elements are expressed by approximated values as TrFNs.
Step 3. Calculate the resilience potential of each business process p,
and determine the business process with the least resilience potential
.
Step 4. Determine ORPFs which have the lowest value at the level of each business process p,
p = 1,..,P by using the method in [
46].
Step 5. Determine the representative scalars of TrFNs , .
Step 6. By using GA, determine the near optimal value of improvements of the determined ORPFs, , in regards to the smallest possible resource usage:
The objective function is defined:
where
is the total improvement of the resilience.
Constraints:
and the order of management initiatives being undertaken to improve the value of the indicator
corresponds to the relative importance of business processes, which are assessed with respect to results of good practice.
4. Results and Discussion
The considered SMEs belong to the process industry in Serbia. The analyzed 120 organizations are certified by the requirements of ISO 9001:2008 and have established adequate business processes so their business process structures were employed to provide a unique organization reference model. The proposed model is tested on a randomly selected SME. Reference model of the organization, applied to target SME, may be seen as a group of the following business processes: management (
p = 1), production (
p = 2), marketing and sales (
p = 3), purchase (
p = 4), design and development (
p = 5), and support processes (
p = 6). The considered ORPFs are specified in
Section 3.
The importance of each manager of the management team is based on best practice in the process industry in Central Serbia. Generally speaking, the proposed model could be applicable to any process industry SME all over the world, so this would be the next step in the research. The importance of decision makers in the management team in the domain of organizational resilience is assessed by owners of the target SMEs. Owners’ assessments are based on their experience and best practice. Their assessments are defined on the measurement scale from 0 to 1. The value denotes that the opinion of decision maker almost has no impact, and 1 denotes that they have the greatest impact for the considered problem. In this case, the importance of the main manager, the quality manager, and the production manager is: 0.4, 0.35 and 0.25, respectively.
Fuzzy ratings of the relative importance of ORPFs and the ORPFs’ values are assigned as explained in
Section 4 (
Table 1 and
Table 2).
Table 1.
Fuzzy ratings of the relative importance of ORPFs.
Table 1.
Fuzzy ratings of the relative importance of ORPFs.
| | p = 1 | p = 2 | p = 3 | p = 4 | p = 5 | p = 6 |
|---|
| i = 1 | | | | | | |
| i = 2 | | | | | | |
| i = 3 | | | | | | |
| i = 4 | | | | | | |
| i = 5 | | | | | | |
| i = 6 | | | | | | |
| i = 7 | | | | | | |
| i = 8 | | | | | | |
| i = 9 | | | | | | |
| i = 10 | | | | | | |
| i = 11 | | | | | | |
The fuzzy ratings of ORPFs’ values on the level of a random organization are presented in
Table 2.
Table 2.
Fuzzy ratings of ORPFs’ values.
Table 2.
Fuzzy ratings of ORPFs’ values.
| | p = 1 | p = 2 | p = 3 | p = 4 | p = 5 | p = 6 |
|---|
| i = 1 | | | | | | |
| i = 2 | | | | | | |
| i = 3 | | | | | | |
| i = 4 | | | | | | |
| i = 5 | | | | | | |
| i = 6 | | | | | | |
| i = 7 | | | | | | |
| i = 8 | | | | | | |
| i = 9 | | | | | | |
| i = 10 | | | | | | |
| i = 11 | | | | | | |
The proposed procedure (Step 1 of the proposed algorithm) is illustrated by calculating the aggregated relative importance value of ORPFs’ internal situation monitoring and reporting (
i = 3) for purchase (
p = 4):
By applying the proposed algorithm (from Step 1 to Step 3), the obtained results are presented in
Table 3.
Table 3.
The weighted ORPFs’ values and business process resilience values.
Table 3.
The weighted ORPFs’ values and business process resilience values.
| | p = 1 | p = 2 | p = 3 |
|---|
| i = 1 | (0.560,0.720,0.90,1) | (0.049,0.112,0.247,0.475) | (0.232,0.370,0.540,0.760) |
| i = 2 | (0.289,0.486,0.740,0.870) | (0.525,0.7,0.9,1) | (0.032,0.07,0.145,0.205) |
| i = 3 | (0.066,0.156,0.30,0.510) | (0.08,0.112,0.195,0.332) | (0.187,0.351,0.555,0.739) |
| i = 4 | (0.109,0.216,0.350,0.450) | (0.214,0.325,0.476,0.642) | (0,0.064,0.168,0.276) |
| i = 5 | (0.357,0.536,0.750,0.850) | (0.297,0.455,0.645,0.791) | (0.028,0.07,0.165,0.380) |
| i = 6 | (0.088,0.170,0.30,0.455) | (0.324,0.471,0.645,0.791) | (0.018,0.060,0.140,0.270) |
| i = 7 | (0.493,0.666,0.90,0.950) | (0.24,0.4,0.6,0.7) | (0.125,0.280,0.456,0.615) |
| i = 8 | (0.144,0.280,0.456,0.616) | (0.416,0.599,0.84,0.92) | (0.104,0.190,0.324,0.441) |
| i = 9 | (0.236,0.362,0.516,0.651) | (0.073,0.166,0.294,0.414) | (0,0,0.09,0.142) |
| i = 10 | (0.051,0.135,0.259,0.392) | (0.176,0.32,0.504,0.644) | (0,0.054,0.148,0.261) |
| i = 11 | (0.109,0.216,0.350,0.450) | (0.098,0.194,0.31 5,0.427) | (0,0.036,0.105,0.202) |
| (0.228,0.359,0.529,0.654) | (0.227,0.350,0.515,0.649) | (0.066,0.140,0.258,0.390) |
| | p = 4 | p = 5 | p = 6 |
| i = 1 | (0.281,0.445,0.645,0.791) | (0.357,0.536,0.750,0.850) | (0.012,0.040,0.105,0.209) |
| i = 2 | (0.028,0.07,0.165,0.332) | (0.287,0.404,0.576,0.720) | (0.116,0.182,0.311,0.442) |
| i = 3 | (0.246,0.378,0.585,0.705) | (0.511,0.692,0.90,1) | (0.066,0.160,0.294,0.414) |
| i = 4 | (0.039,0.095,0.189,0.284) | (0.196,0.332,0.504,0.644) | (0,0.054,0.148,0.261) |
| i = 5 | (0.069,0.165,0.301,0.419) | (0,0.064,0.168,0.276) | (0.033,0.085,0.175,0.292) |
| i = 6 | (0,0,0.060,0.120) | (0.30,0.437,0.60,0.70) | (0.018,0.060,0.140,0.270) |
| i = 7 | (0.110,0.260,0.450,0.680) | (0.242,0.390,0.525,0.646) | (0,0,0.060,0.193) |
| i = 8 | (0.176,0.30,0.456,0.704) | (0.275,0.455,0.675,0.808) | (0.023,0.075,0.166,0.304) |
| i = 9 | (0,0.075,0.180,0.285) | (0.136,0.270,0.444,0.609) | (0.039,0.095,0.189,0.302) |
| i = 10 | (0.176,0.272,0.411,0.529) | (0.159,0.286,0.461,0.612) | (0.074,0.166,0.294,0.414) |
| i = 11 | (0.046,0.115,0.222,0.340) | (0.019,0.065,0.149,0.281) | (0.164,0.288,0.444,0.609) |
| (0.106,0.198,0.333,0.472) | (0.226,0.357,0.522,0.649) | (0.049,0.109,0.212,0.337) |
By applying the proposed algorithm (Step 3), it can be concluded that the support processes (p = 6) are denoted as the processes with the lowest organizational resilience potential.
By using the proposed algorithm (Step 4) method, ORPFs which have the lowest value at the level of each business process
p are determined:
The precise values of identified ORPFs are:
, ,
, ,
The near optimal values of enhancement for all ORPFs are determined by using the proposed algorithm (Step 6).
Objective function: ,
Constraints: , and
The relative importance of business processes has been determined based on the decision makers’ experience and best practice. For this kind of enterprises, business processes are sorted from the most to the least important: management (p = 1), development (p = 5), production (p = 2), support processes (p = 6), marketing and sales (p = 3), and purchase (p = 4).
The order of taking management initiatives that will lead to an enhancement in the overall resilience potential corresponds to the ranking of the relative importance of business processes: .
The optimization is done in three search executions with the different values of GA parameters shown in
Table 4.
Table 4.
Different values of GA parameters for three searches.
Table 4.
Different values of GA parameters for three searches.
| Search Case | Population Size | Number of Generations | Mutation Rate |
|---|
| 1 | 100 | 50 | 0.15 |
| 2 | 100 | 100 | 0.10 |
| 3 | 250 | 200 | 0.05 |
Values for enhancement of each highlighted ORPF are obtained and shown in
Table 5, and in
Figure 2 comparative values of the objective function through generations are shown.
Table 5.
Values of enhancement of ORPFs and the value of objective function.
Table 5.
Values of enhancement of ORPFs and the value of objective function.
| Parameters | | | | | | | Value of Objective Function |
|---|
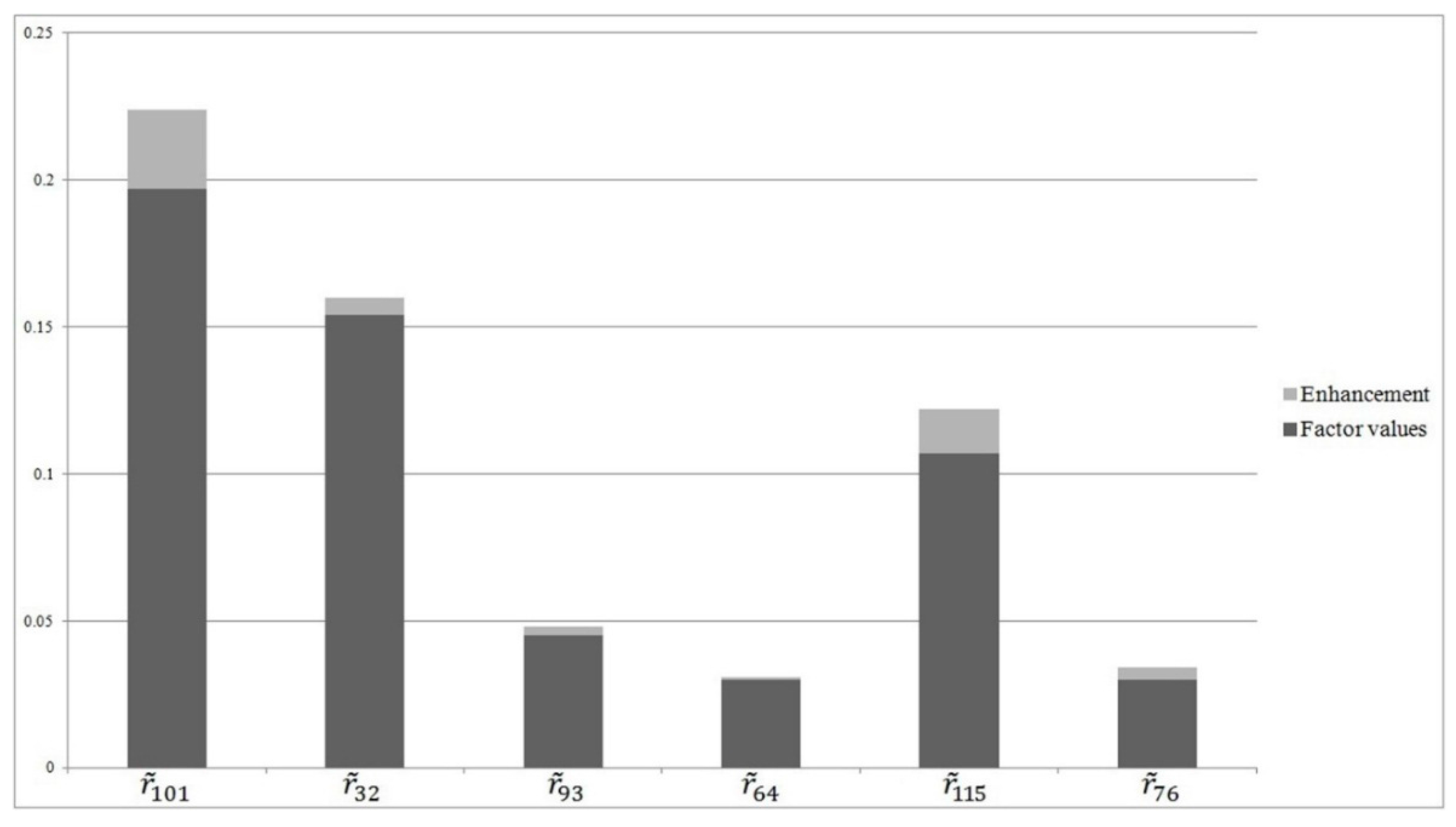
| Current value | 0.197 | 0.154 | 0.045 | 0.03 | 0.107 | 0.03 | 0.0647 |
| Case 1Enhancement | 0.039 | 0.02 | 0.013 | 0.001 | 0.032 | 0.016 | 0.0647 |
| Case 2Enhancement | 0.019 | 0.014 | 0.004 | 0.001 | 0.015 | 0.0013 | 0.002 |
| Case 3Enhancement | 0.027 | 0.006 | 0.003 | 0.001 | 0.015 | 0.004 | 0.0003 |
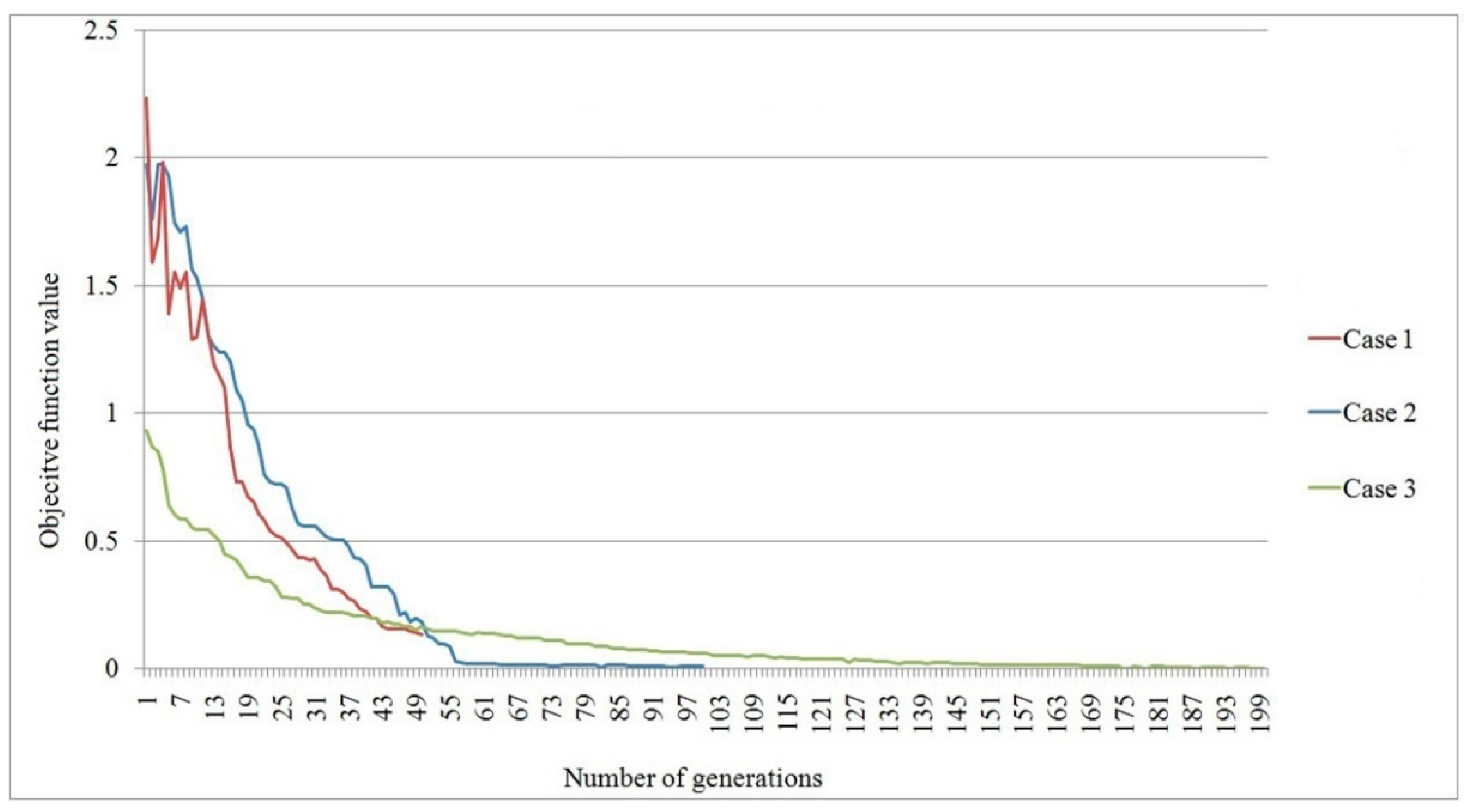
From the data presented in
Table 5, it may be concluded that the objective function has the most optimal value in case 3. Values for the most optimal solution from case 3 are of the objective function shown as enhancement of ORPFs in
Figure 4.
Figure 4.
Values of the objective function through generations for three cases.
Figure 4.
Values of the objective function through generations for three cases.
From the data presented in
Figure 5, it may be concluded that in cases 1 and 2 there is a more rapid decline of near optimal function for the best solution than in case 3 because of the greater mutation rate. In case 3, the population size is bigger, so the objective function has the lowest value at the start, and, because of the greater number of generations, it obtains the most optimal solution at the end.
The proposed solution shows that it addresses all the constraints, especially taking into consideration management initiatives that will lead to an enhancement in the overall resilience by 10%. Compared to the input data, enhancements in percentages for each ORPF are respectively: 13.7%, 3.89%, 6.6%, 3.3%, 14.01% and 13.3%. Re-defining the business strategy on a yearly level is based on the obtained results.
Figure 5.
Values for the objective function in last generations of optimization case 3.
Figure 5.
Values for the objective function in last generations of optimization case 3.
Based on the obtained optimal results for ORPF enhancements, the greatest enhancement could be achieved within the design and development process in regards to the safety management system—factor . In the management process, actions should be defined on a yearly level to enhance emergency responses at the time of disturbance—factor .
5. Conclusions
Having in mind that some of the companies from the process industry are large and multinational with sufficient resources to ensure their organizations are productive and resilient, a significant number of this sector’s organizations belong to the group of SMEs. From the experience of industrial management practice, it may be assumed that organizational resilience in SMEs represents a very relevant issue for long term sustainability. In this manner, ORPFs have to be monitored and improved over time, because in the current turbulent business climate, their decline may lead to business catastrophe.
The main contribution of this paper is the introduction of a two-step model for assessment and enhancement of organizational resilience in SMEs of the process industry in an uncertain environment. The main challenges that are addressed in this research are (1) definition of model for resilience potential assessment in the process industry SMEs; and (2) determination of appropriate strategies that should enable improvement of resilience.
The first step: a model for the resilience assessment is adopted and mathematically improved from the existing literature [
13]. One hundred and twenty organizations who were analyzed have established appropriate business processes, so their business process structures represent a good basisto establish a unique organization reference model. The fuzzy sets theory is a very suitable mathematical tool for the modelling of uncertainties and impreciseness. All of the uncertainties are modelled by TrFNs.
Second step: enhancement of the ORPF values on the process level is performed by using the proposed GA model. The selection of ORPF values which should be improved is based on the determined ranking of ORPF values. Optimization is used so the enhancement of the lowest ORPF values at the business process level could be achieved with the smallest possible amount of resources. The presented approach is novel within the scope of mathematical modelling of organizational resilience assessment and its enhancement.
The main advantage of the presented model is its user friendly assessment methodology which is accomplished by the proposed linguistic expressions, as well as the general output of the model which may significantly facilitate the decisions of managers. The proposed model clearly identifies the weakest ORPFs and proposes the potential for enhancement on the business process level. It should be mentioned that in addressing the discussed issues, the use of less expensive resources may reduce costs, but it may also happen that the desired level of the lowest indicators of resilience is not achieved.
Future research will be directed to the analysis of different organization types which may have different influential ORPFs as well as different organizational resilience benchmarks. In order to be recognized, the proposed model should be tested in different process industry SMEs all over the world. This should enable knowledge transfer amongst organizations that belong to the same industry sector, and, as a final consequence, improve sustainable development.