Sources of China’s Economic Growth: An Empirical Analysis Based on the BML Index with Green Growth Accounting
Abstract
:1. Introduction
2. Literature Review
3. Method
3.1. Environmental Production Technology
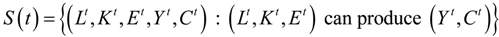

3.2. Biennial Malmquist–Luenberger Index
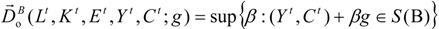
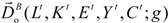 measures the maximum proportional expansion of both desirable and undesirable outputs (Yt, Ct), given the input vector (Lt, Kt, Et) and the biennial technology in the direction g. Following [32], we introduce a TFP index called the biennial Malmquist–Luenberger index (hereafter, BML index). Taking the biennial production technology as a reference, the BML index between period t and t + 1 is given by
measures the maximum proportional expansion of both desirable and undesirable outputs (Yt, Ct), given the input vector (Lt, Kt, Et) and the biennial technology in the direction g. Following [32], we introduce a TFP index called the biennial Malmquist–Luenberger index (hereafter, BML index). Taking the biennial production technology as a reference, the BML index between period t and t + 1 is given by

3.3. Green Growth Accounting Framework

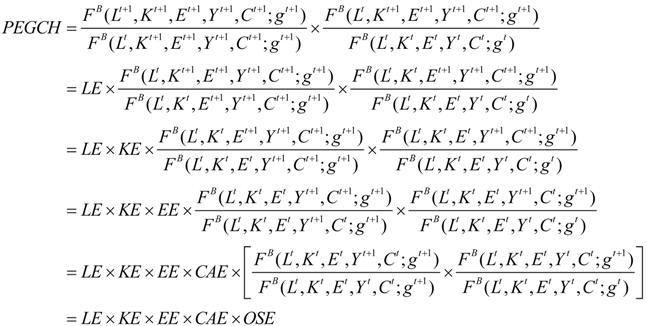
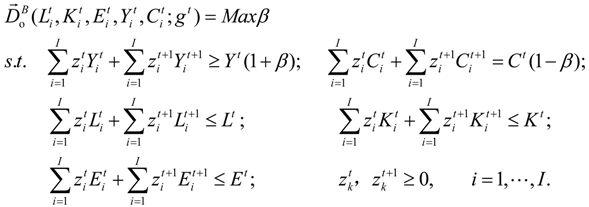
4. Data and Empirical Results
4.1. Data

4.2. Empirical Results
| Variables | Mean | S.D. | Max | Min |
|---|---|---|---|---|
| Gross regional product (100 million CNY) | 6,620.05 | 6,671.37 | 42,860.33 | 223.88 |
| Carbon dioxide emissions (10000 tonnes) | 23,104.14 | 18,408.14 | 106,667.02 | 892.85 |
| Labor (10000 persons) | 2,304.33 | 1,525.40 | 6,288.00 | 230.40 |
| Capital stock (100 million CNY) | 18,642.29 | 17,905.59 | 110,064.98 | 953.54 |
| Energy consumption (10000 tonnes) | 8,797.01 | 6,970.46 | 40,630.76 | 384.48 |
| Provinces | TFP | EFF | TC | OSE | CAE | LE | KE | EE |
|---|---|---|---|---|---|---|---|---|
| Beijing | 1.004 | 0.983 | 1.022 | 1.018 | 1.087 | |||
| 1.031 | 1.002 | 1.029 | 1.002 | 0.998 | 1.079 | 1.037 | 0.964 | |
| Tianjin | 1.034 | 1.014 | 1.019 | 1.015 | 1.090 | |||
| 1.044 | 0.991 | 1.053 | 0.994 | 0.978 | 1.037 | 1.106 | 0.983 | |
| Hebei | 0.982 | 0.986 | 0.995 | 1.005 | 1.126 | |||
| 0.997 | 0.991 | 1.006 | 1.000 | 0.939 | 1.005 | 1.180 | 1.000 | |
| Shanxi | 0.972 | 0.977 | 0.995 | 1.004 | 1.143 | |||
| 0.891 | 0.760 | 1.172 | 0.938 | 0.916 | 1.007 | 1.452 | 0.997 | |
| Inner Mongolia | 0.995 | 0.990 | 1.004 | 1.006 | 1.155 | |||
| 0.979 | 0.751 | 1.303 | 0.899 | 0.879 | 1.022 | 1.485 | 0.986 | |
| Liaoning | 1.029 | 0.997 | 1.032 | 1.009 | 1.076 | |||
| 1.006 | 0.864 | 1.164 | 0.953 | 0.975 | 1.059 | 1.177 | 0.959 | |
| Jilin | 0.988 | 0.986 | 1.002 | 1.005 | 1.130 | |||
| 0.993 | 0.983 | 1.010 | 0.997 | 0.951 | 1.005 | 1.186 | 1.000 | |
| Heilongjiang | 1.007 | 1.011 | 0.996 | 1.005 | 1.094 | |||
| 0.978 | 0.939 | 1.042 | 0.976 | 0.980 | 1.018 | 1.175 | 0.990 | |
| Shanghai | 1.018 | 1.000 | 1.018 | 1.032 | 1.056 | |||
| 1.014 | 1.000 | 1.014 | 0.999 | 1.001 | 1.110 | 1.041 | 0.947 | |
| Jiangsu | 1.036 | 1.005 | 1.031 | 1.008 | 1.076 | |||
| 1.023 | 1.000 | 1.022 | 1.000 | 0.961 | 1.016 | 1.089 | 1.034 | |
| Zhejiang | 1.023 | 0.993 | 1.030 | 1.014 | 1.076 | |||
| 1.010 | 0.994 | 1.016 | 1.000 | 0.921 | 1.012 | 1.130 | 1.049 | |
| Anhui | 0.980 | 1.000 | 0.980 | 1.000 | 1.139 | |||
| 1.006 | 0.999 | 1.007 | 1.000 | 0.938 | 1.000 | 1.182 | 1.000 | |
| Fujian | 1.013 | 0.997 | 1.016 | 1.012 | 1.091 | |||
| 1.005 | 0.987 | 1.018 | 1.000 | 0.975 | 1.020 | 1.049 | 1.067 | |
| Jiangxi | 0.969 | 0.989 | 0.980 | 1.000 | 1.152 | |||
| 1.005 | 0.999 | 1.006 | 1.000 | 0.871 | 1.000 | 1.210 | 1.054 | |
| Shandong | 0.999 | 0.995 | 1.004 | 1.005 | 1.119 | |||
| 0.999 | 0.993 | 1.007 | 1.000 | 0.953 | 1.006 | 1.142 | 1.026 | |
| Henan | 0.959 | 0.974 | 0.984 | 1 | 1.164 | |||
| 1.004 | 0.996 | 1.007 | 1.000 | 0.865 | 1.000 | 1.287 | 0.998 | |
| Hubei | 0.980 | 0.996 | 0.984 | 1.004 | 1.135 | |||
| 1.006 | 1.001 | 1.005 | 1.000 | 0.833 | 1.004 | 1.316 | 1.008 | |
| Hunan | 0.973 | 0.993 | 0.980 | 1.000 | 1.145 | |||
| 1.006 | 1.000 | 1.006 | 1.000 | 0.910 | 1.000 | 1.175 | 1.036 | |
| Guangdong | 1.001 | 1.000 | 1.001 | 1.018 | 1.099 | |||
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.053 | 1.060 | 1.003 | |
| Guangxi | 0.946 | 0.965 | 0.981 | 0.999 | 1.181 | |||
| 0.993 | 0.988 | 1.005 | 1.000 | 0.865 | 1.000 | 1.214 | 1.071 | |
| Hainan | 1.032 | 1.003 | 1.029 | 1.015 | 1.059 | |||
| 0.997 | 0.989 | 1.008 | 1.000 | 0.858 | 1.002 | 1.182 | 1.095 | |
| Chongqing | 0.974 | 0.994 | 0.980 | 1.000 | 1.154 | |||
| 1.009 | 1.004 | 1.005 | 1.000 | 0.837 | 1.000 | 1.254 | 1.061 | |
| Sichuan | 0.981 | 1.001 | 0.980 | 1.000 | 1.141 | |||
| 1.010 | 1.005 | 1.005 | 1.000 | 0.893 | 1.000 | 1.180 | 1.051 | |
| Guizhou | 0.981 | 1.002 | 0.980 | 1.000 | 1.133 | |||
| 1.004 | 1.002 | 1.002 | 1.000 | 0.743 | 1.000 | 1.490 | 1.000 | |
| Yunnan | 0.971 | 0.991 | 0.980 | 1.000 | 1.137 | |||
| 1.000 | 0.995 | 1.004 | 1.000 | 0.741 | 1.000 | 1.433 | 1.040 | |
| Shaanxi | 1.004 | 1.008 | 0.996 | 1.002 | 1.119 | |||
| 1.003 | 0.998 | 1.005 | 1.000 | 0.704 | 1.002 | 1.527 | 1.042 | |
| Gansu | 0.974 | 0.994 | 0.980 | 1.000 | 1.140 | |||
| 1.006 | 1.000 | 1.006 | 1.000 | 0.896 | 1.000 | 1.231 | 1.000 | |
| Qinghai | 1.029 | 1.000 | 1.030 | 1.010 | 1.075 | |||
| 1.008 | 0.998 | 1.009 | 1.000 | 0.649 | 1.006 | 1.618 | 1.051 | |
| Ningxia | 1.018 | 0.995 | 1.023 | 1.010 | 1.085 | |||
| 0.996 | 0.993 | 1.003 | 1.000 | 0.651 | 1.010 | 1.704 | 1.000 | |
| Xinjiang | 1.020 | 0.992 | 1.028 | 1.011 | 1.069 | |||
| 1.004 | 0.991 | 1.014 | 1.000 | 0.801 | 1.011 | 1.355 | 1.000 | |
| Weighted Mean | 0.996 | 0.994 | 1.002 | 1.007 | 1.115 | |||
| 1.001 | 0.974 | 1.032 | 0.992 | 0.883 | 1.016 | 1.256 | 1.017 |
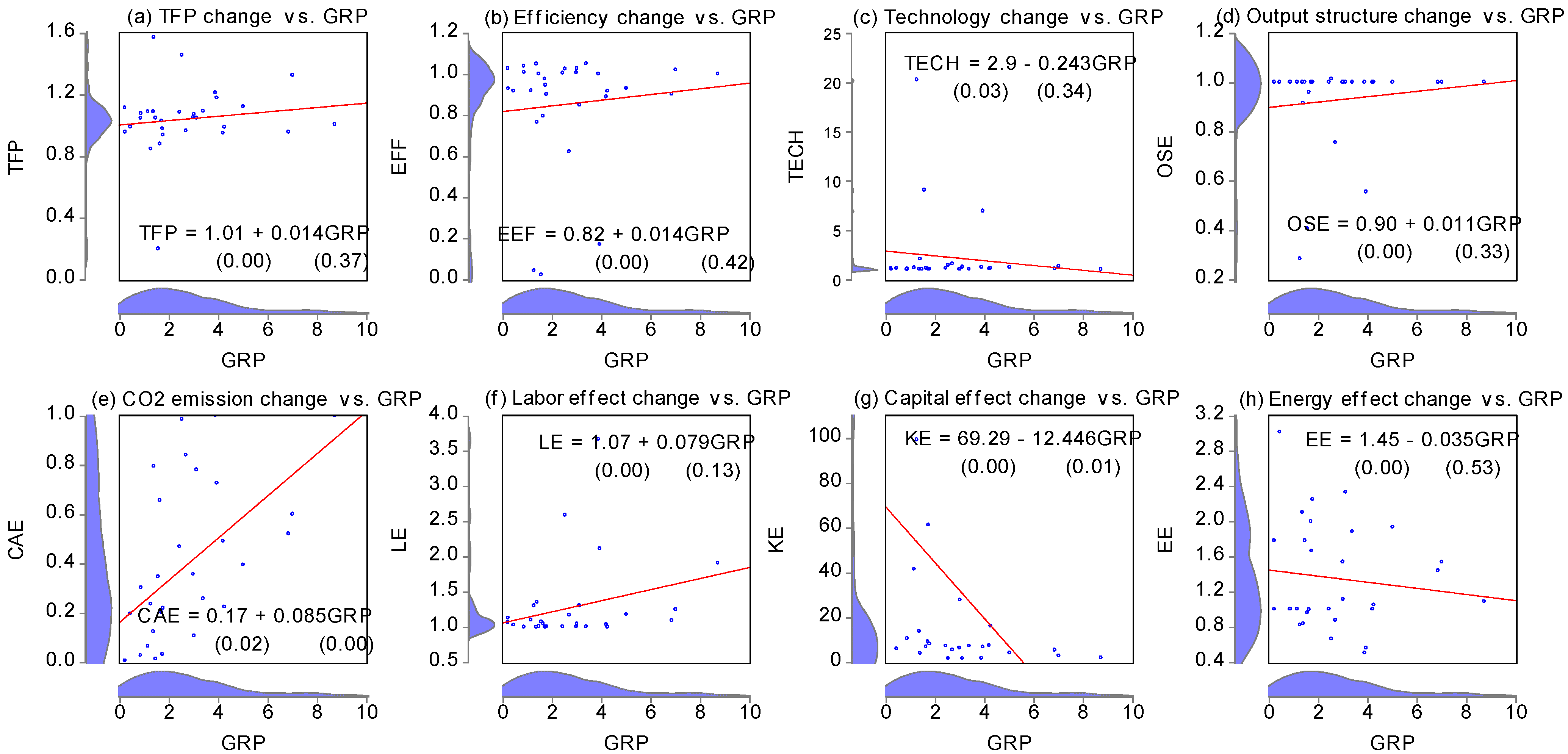
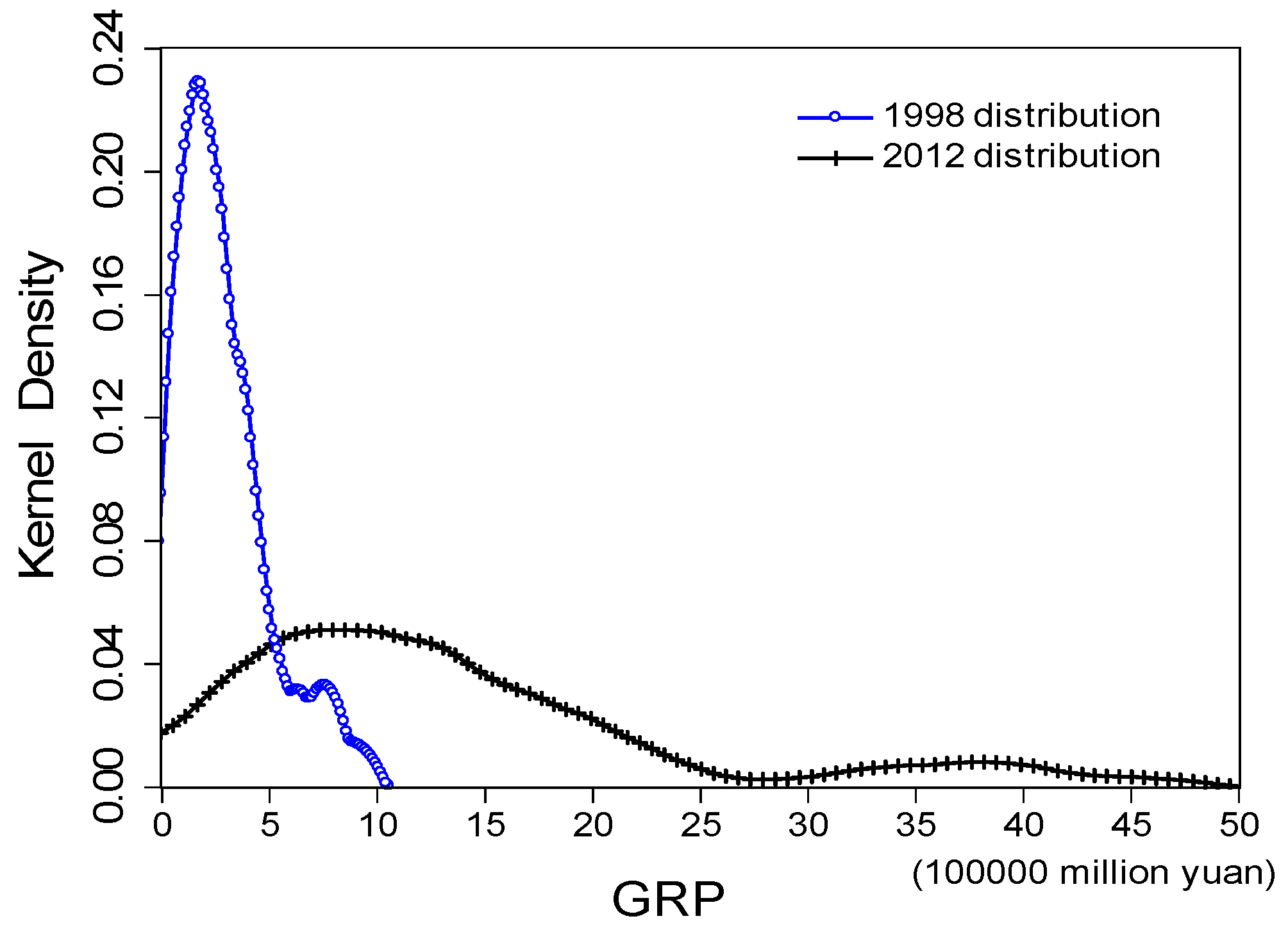
5. Analysis of Distributions Dynamics of Economic Growth
| Distributions | p-values | |
|---|---|---|
| H0: One Mode H1: More than One Mode | H0: Two Modes H1: More than Two Modes | |
| Y98 | 0.262 (H0 not reject) | 0.323 (H0 not reject) |
| Y12 | 0.043 (H0 reject) | 0.523 (H0 not reject) |
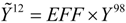
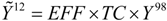
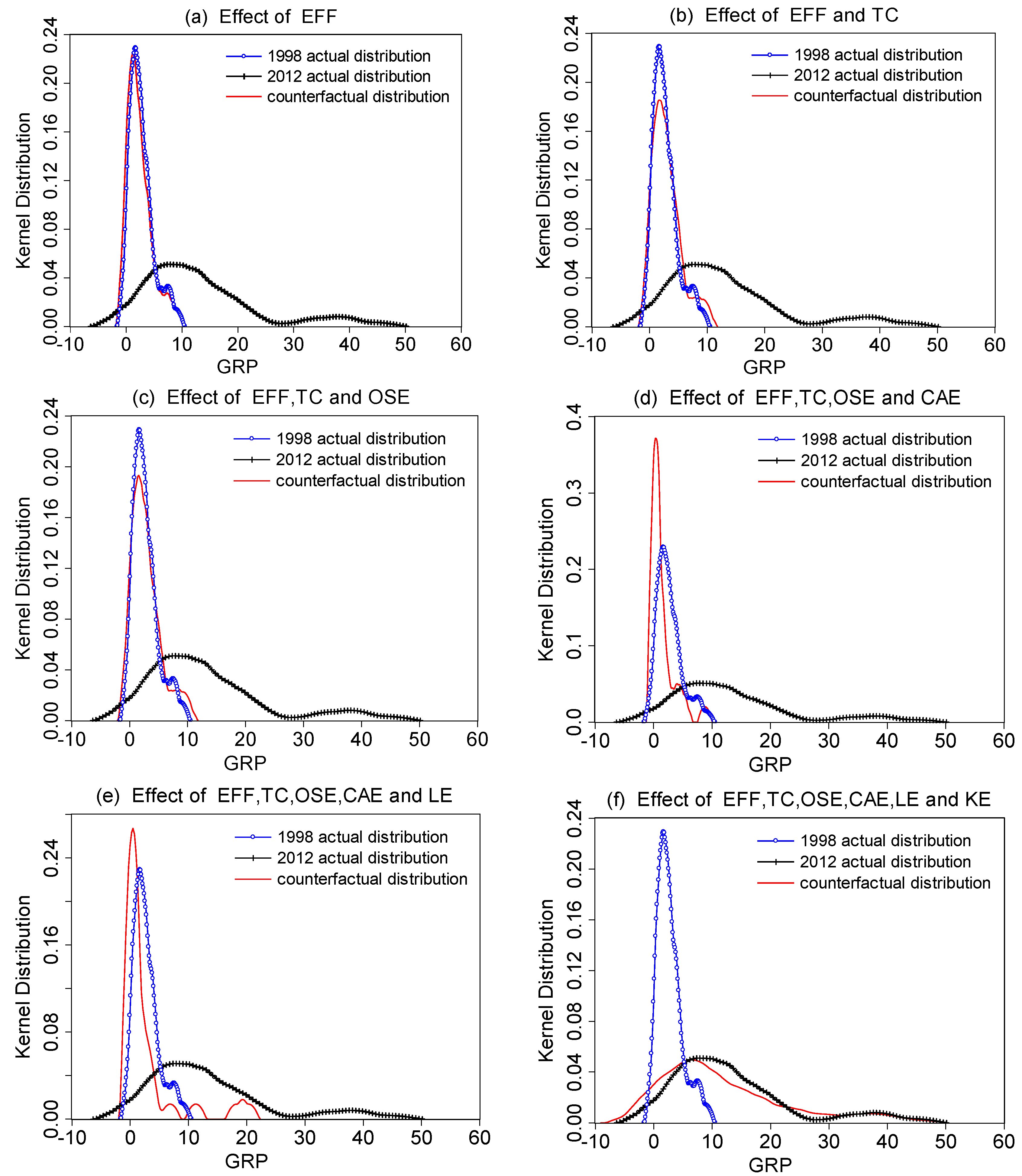
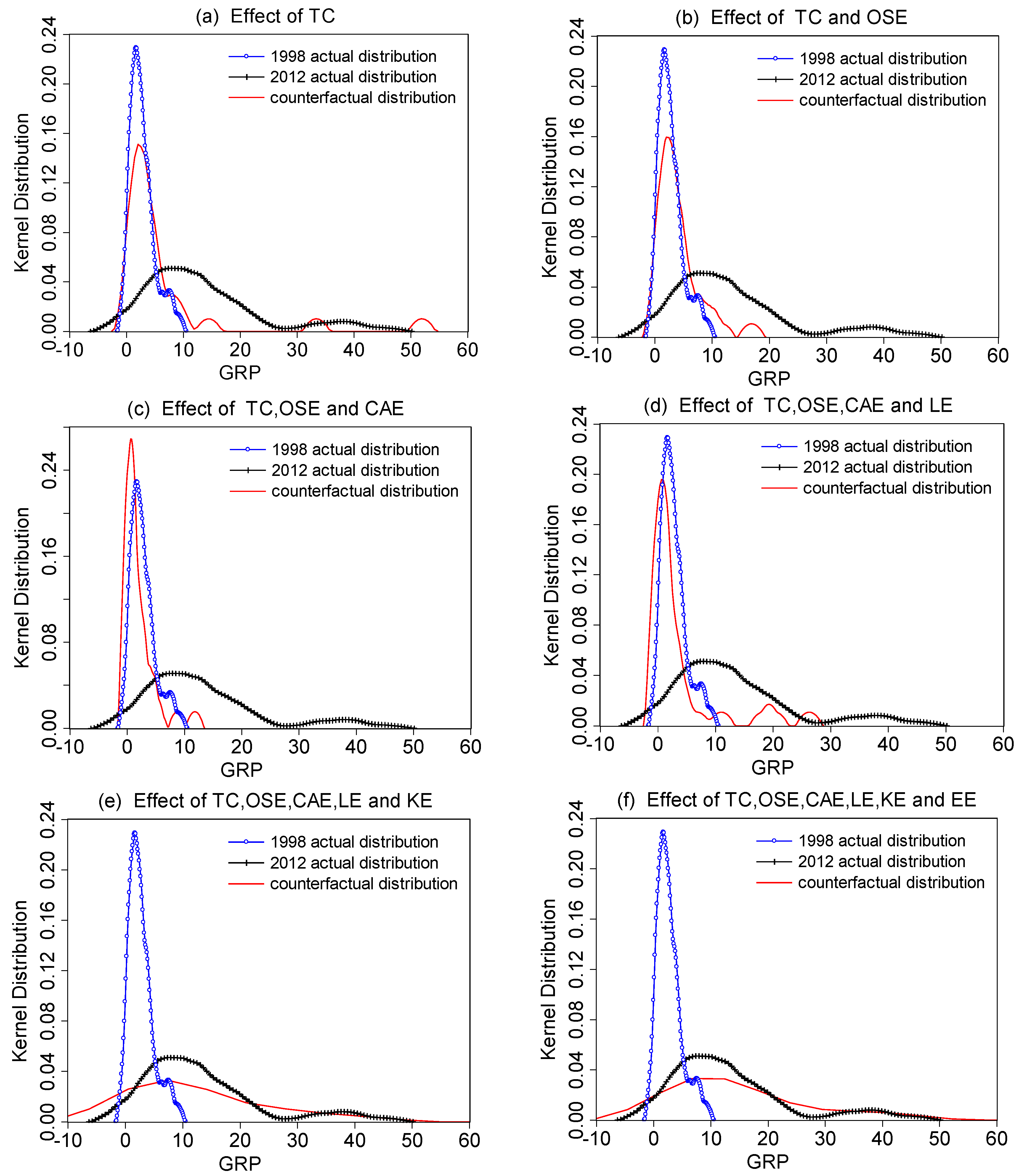
6. Conclusions
Acknowledgments
Author Contributions
Appendix
| Null Hypothesis (H0) | t-Test Statistics | Null Hypothesis (H0) | t-Test Statistics |
|---|---|---|---|
| 1. f(Y12) = g(Y98) | 3.0925 | 43. f(Y12) = g(Y98 × EFF × LE × EE) | 1.6660 * |
| 2. f(Y12) = g(Y98 × EFF) | 3.1722 | 44. f(Y12) = g(Y98 × EFF × KE × EE) | 7.2167 |
| 3. f(Y12) = g(Y98 × TC) | 3.2513 | 45. f(Y12) = g(Y98 × TC × OSE × CAE) | 3.9089 |
| 4. f(Y12) = g(Y98 × OSE) | 3.1999 | 46. f(Y12) = g(Y98 × TC × OSE × LE) | 0.6358* |
| 5. f(Y12) = g(Y98 × CAE) | 4.5551 | 47. f(Y12) = g(Y98 × TC × OSE × KE) | 8.3981 |
| 6. f(Y12) = g(Y98 × LE) | 2.4344 | 48. f(Y12) = g(Y98 × TC × OSE × EE) | 1.5624 * |
| 7. f(Y12) = g(Y98 × KE) | −0.2006 * | 49. f(Y12) = g(Y98 × TC × CAE × LE) | 0.7044 * |
| 8. f(Y12) = g(Y98 × EE) | 2.6783 | 50. f(Y12) = g(Y98 × TC × CAE × KE) | 9.9558 |
| 9. f(Y12) = g(Y98 × EFF × TC) | 2.7458 | 51. f(Y12) = g(Y98 × TC × CAE × EE) | 2.7983 |
| 10. f(Y12) = g(Y98 × EFF × OSE) | 3.1313 | 52. f(Y12) = g(Y98 × TC × LE × KE) | 0.5224 * |
| 11. f(Y12) = g(Y98 × EFF × CAE) | 5.3561 | 53. f(Y12) = g(Y98 × TC × LE × EE) | 0.0716 * |
| 12. f(Y12) = g(Y98 × EFF × LE) | 2.8901 | 54. f(Y12) = g(Y98 × TC × KE × EE) | 9.1998 |
| 13. f(Y12) = g(Y98 × EFF × KE) | 2.8901 | 55. f(Y12) = g(Y98 × OSE × CAE × LE) | 4.1468 |
| 14. f(Y12) = g(Y98 × EFF × EE) | 2.2788 | 56. f(Y12) = g(Y98 × OSE × CAE × KE) | 0.0276* |
| 15. f(Y12) = g(Y98 × TC × OSE) | 2.0906 * | 57. f(Y12) = g(Y98 × OSE × CAE × EE) | 5.1708 |
| 16. f(Y12) = g(Y98 × TC × CAE) | 2.9263 | 58. f(Y12) = g(Y98 × OSE × LE × KE) | 7.7696 |
| 17. f(Y12) = g(Y98 × TC × LE) | −0.0902 * | 59. f(Y12) = g(Y98 × OSE × LE × EE) | 1.8249* |
| 18. f(Y12) = g(Y98 × TC × KE) | 0.2784 * | 60. f(Y12) = g(Y98 × OSE × KE × EE) | 7.5675 |
| 19. f(Y12) = g(Y98 × TC × EE) | 0.9731 * | 61. f(Y12) = g(Y98 × CAE × LE × KE) | 9.1998 |
| 20. f(Y12) = g(Y98 × OSE × CAE) | 4.8776 | 62. f(Y12) = g(Y98 × CAE × LE × EE) | 3.3905 |
| 21. f(Y12) = g(Y98 × OSE × LE) | 2.5605 | 63. f(Y12) = g(Y98 × CAE × KE × EE) | 0.0212* |
| 22. f(Y12) = g(Y98 × OSE × KE) | 8.1129 | 64. f(Y12) = g(Y98 × LE × KE × EE) | 8.7493 |
| 23. f(Y12) = g(Y98 × OSE × EE) | 2.4269 | 65. f(Y12) = g(Y98 × EFF × TC × OSE × CAE) | 4.5586 |
| 24. f(Y12) = g(Y98 × CAE × LE) | 3.7703 | 66. f(Y12) = g(Y98 × EFF × TC × OSE × LE) | 2.1208 * |
| 25. f(Y12) = g(Y98 × CAE × KE) | −0.0399 * | 67. f(Y12) = g(Y98 × EFF × TC × OSE × KE) | 8.6480 |
| 26. f(Y12) = g(Y98 × CAE × EE) | 4.9706 | 68. f(Y12) = g(Y98 × EFF × TC × OSE × EE) | 2.3043 * |
| 27. f(Y12) = g(Y98 × LE × KE) | 0.5651 * | 69. f(Y12) = g(Y98 × EFF × TC × CAE × LE) | 3.2199 |
| 28. f(Y12) = g(Y98 × LE × EE) | 1.9149 * | 70. f(Y12) = g(Y98 × EFF × TC × CAE × KE) | −0.1126 * |
| 29. f(Y12) = g(Y98 × KE × EE) | 8.7209 | 71. f(Y12) = g(Y98 × EFF × TC × CAE × EE) | 4.6026 |
| 30. f(Y12) = g(Y98 × EFF × TC × OSE) | 2.9007 | 72. f(Y12) = g(Y98 × EFF × TC × LE × KE) | 1.6153 * |
| 31. f(Y12) = g(Y98 × EFF × TC × CAE) | 4.2116 | 73. f(Y12) = g(Y98 × EFF × TC × LE × EE) | 1.3714 * |
| 32. f(Y12) = g(Y98 × EFF × TC × LE) | 1.9787 * | 74. f(Y12) = g(Y98 × EFF × TC × KE × EE) | 7.6552 |
| 33. f(Y12) = g(Y98 × EFF × TC × KE) | 8.5744 | 75. f(Y12) = g(Y98 × EFF × OSE × CAE × LE) | 4.7471 |
| 34. f(Y12) = g(Y98 × EFF × TC × EE) | 2.4802 | 76. f(Y12) = g(Y98 × EFF × OSE × CAE × KE) | 0.7412 * |
| 35. f(Y12) = g(Y98 × EFF × OSE × CAE) | 5.4615 | 77. f(Y12) = g(Y98 × EFF × OSE × CAE × EE) | 5.2877 |
| 36. f(Y12) = g(Y98 × EFF × OSE × LE) | 2.8215 | 78. f(Y12) = g(Y98 × EFF × OSE × LE × KE) | 7.9339 |
| 37. f(Y12) = g(Y98 × EFF × OSE × KE) | 8.3418 | 79. f(Y12) = g(Y98 × EFF × OSE × LE × EE) | 1.5858 * |
| 38. f(Y12) = g(Y98 × EFF × OSE × EE) | 2.2165 * | 80. f(Y12) = g(Y98 × EFF × OSE × KE × EE) | 7.1302 |
| 39. f(Y12) = g(Y98 × EFF × CAE × LE) | 4.7027 | 81. f(Y12) = g(Y98 × EFF × CAE × LE × KE) | −0.0305 * |
| 40. f(Y12) = g(Y98 × EFF × CAE × KE) | 0.7840 * | 82. f(Y12) = g(Y98 × EFF × CAE × LE × EE) | 3.9011 |
| 41. f(Y12) = g(Y98 × EFF × CAE × EE) | 5.2502 | 83. f(Y12) = g(Y98 × EFF × CAE × KE × EE) | 0.0233 * |
| 42. f(Y12) = g(Y98 × EFF × LE × KE) | −0.0651 * | 84. f(Y12) = g(Y98 × EFF × LE × KE × EE) | 7.2847 |
| 85. f(Y12) = g(Y98 × TC × OSE × CAE × LE) | 2.1985 * | 107. f(Y12) = g(Y98 × EFF × TC × CAE × LE × EE) | 2.8757 |
| 86. f(Y12) = g(Y98 × TC × OSE × CAE × KE) | 6.5094 | 108. f(Y12) = g(Y98 × EFF × TC × CAE × KE × EE) | −0.0267 * |
| 87. f(Y12) = g(Y98 × TC × OSE × CAE × EE) | 3.9165 | 109. f(Y12) = g(Y98 × EFF × TC × LE × KE × EE) | 7.7859 |
| 88. f(Y12) = g(Y98 × TC × OSE × LE × KE) | 8.1778 | 110. f(Y12) = g(Y98 × EFF × OSE × CAE × LE × KE) | 0.0060 * |
| 89. f(Y12) = g(Y98 × TC × OSE × LE × EE) | 0.8540 * | 111. f(Y12) = g(Y98 × EFF × OSE × CAE × LE × EE) | 3.9147 |
| 90. f(Y12) = g(Y98 × TC × OSE × KE × EE) | 8.5051 | 112. f(Y12) = g(Y98 × EFF × OSE × CAE × KE × EE) | −0.0191 * |
| 91. f(Y12) = g(Y98 × TC × CAE × LE × KE) | 10.2244 | 113. f(Y12) = g(Y98 × EFF × OSE × LE × KE × EE) | 7.1642 |
| 92. f(Y12) = g(Y98 × TC × CAE × LE × EE) | 1.0477 * | 114. f(Y12) = g(Y98 × EFF × CAE × LE × KE × EE) | −0.0649* |
| 93. f(Y12) = g(Y98 × TC × CAE × KE × EE) | 9.8342 | 115. f(Y12) = g(Y98 × TC × OSE × CAE × LE × KE) | 2.1411 |
| 94. f(Y12) = g(Y98 × TC × LE × KE × EE) | 8.9758 | 116. f(Y12) = g(Y98 × TC × OSE × CAE × LE × EE) | 2.2456 * |
| 95. f(Y12) = g(Y98 × OSE × CAE × LE × KE) | −0.1248 * | 117. f(Y12) = g(Y98 × TC × OSE × CAE × KE × EE) | 5.1559 |
| 96. f(Y12) = g(Y98 × OSE × CAE × LE × EE) | 3.6693 | 118. f(Y12) = g(Y98 × TC × OSE × LE × KE × EE) | 8.8583 |
| 97. f(Y12) = g(Y98 × OSE × CAE × KE × EE) | –0.1008 * | 119. f(Y12) = g(Y98 × TC × CAE × LE × KE × EE) | 9.9377 |
| 98. f(Y12) = g(Y98 × OSE × LE × KE × EE) | 7.5982 | 120. f(Y12) = g(Y98 × OSE × CAE × LE × KE × EE) | −0.0889 * |
| 99. f(Y12) = g(Y98 × CAE × LE × KE × EE) | 0.5346 * | 121. f(Y12) = g(Y98 × EFF × TC × OSE × CAE × LE × KE) | −0.1959 * |
| 100. f(Y12) = g(Y98 × EFF × TC × OSE × CAE × LE) | 3.5822 | 122. f(Y12) = g(Y98 × EFF × TC × OSE × CAE × LE × EE) | 3.1966 |
| 101. f(Y12) = g(Y98 × EFF × TC × OSE × CAE × KE) | 0.3618 * | 123. f(Y12) = g(Y98 × EFF × TC × OSE × CAE × KE × EE) | 0.1709 * |
| 102. f(Y12) = g(Y98 × EFF × TC × OSE × CAE × EE) | 4.8423 | 124. f(Y12) = g(Y98 × EFF × TC × OSE × LE × KE × EE) | 7.1949 |
| 103. f(Y12) = g(Y98 × EFF × TC × OSE × LE × KE) | 7.6422 | 125. f(Y12) = g(Y98 × EFF × TC × CAE × LE × KE × EE) | 0.1431 * |
| 104. f(Y12) = g(Y98 × EFF × TC × OSE × LE × EE) | 1.4114 * | 126. f(Y12) = g(Y98 × EFF × OSE × CAE × LE × KE × EE) | −0.0987 * |
| 105. f(Y12) = g(Y98 × EFF × TC × OSE × KE × EE) | 7.2751 | 127. f(Y12) = g(Y98 × TC × OSE × CAE × LE × KE × EE) | 2.1060 * |
| 106. f(Y12) = g(Y98 × EFF × TC × CAE × LE × KE) | 0.1907 * | 128. f(Y12) = g(Y98 × EFF × TC × OSE ×CAE × LE × KE × EE) | 0.00 * |
Conflicts of Interest
References and Notes
- Krugman, P. The myth of Asia’s miracle. Foreign Aff. 1994, 73, 62–78. [Google Scholar]
- Han, G.F.; Kalirajan, K.; Singh, N. Productivity and economic growth in East Asia: Innovation, efficiency and accumulation. Jpn. World Econ. 2002, 14, 401–424. [Google Scholar]
- Wang, Y.; Yao, Y.D. Sources of China’s economic growth 1952–1999: Incorporating human capital accumulation. China Econ. Rev. 2003, 14, 32–52. [Google Scholar]
- Zhao, C.W.; Du, J. Capital formation and economic growth in western China. Chin. Econ. 2009, 42, 7–26. [Google Scholar] [CrossRef]
- Chow, G.C. Capital formation and economic growth in China. Q. J. Econ. 1993, 108, 809–842. [Google Scholar] [CrossRef]
- Kim, J.I.; Lau, L.J. The sources of economic growth of the East Asian newly industrialized countries. J. Jpn. Int. Econ. 1994, 8, 235–271. [Google Scholar] [CrossRef]
- Young, A. Gold into base metals: Productivity growth in the People’s Republic of China during the reform period. J. Polit. Econ. 2003, 111, 1220–1261. [Google Scholar] [CrossRef]
- Arayama, Y.; Miyoshi, K. Regional diversity and sources of economic growth in China. World Econ. 2004, 27, 1583–1607. [Google Scholar] [CrossRef]
- Islam, N.; Dai, E.; Sakamoto, H. Role of TFP in China’s growth. Asian Econ. J. 2006, 20, 127–159. [Google Scholar]
- Jefferson, G.H.; Hu, A.G.Z.; Su, J. The sources and sustainability of China’s economic growth. Brook. Pap. Econ. Act. 2006, 2, 1–47. [Google Scholar] [CrossRef]
- Borensztein, E.; Ostry, D.J. Accounting for China’s growth performance. Am. Econ. Rev. 1996, 86, 224–228. [Google Scholar]
- Hu, Z.F.; Khan, M.S. Why is China growing so fast? Staff. Pap. Int. Monet. Fund 1997, 44, 103–131. [Google Scholar] [CrossRef]
- Chow, G.C.; Li, K.W. China’s economic growth: 1952–2010. Econ. Dev. Cult. Chang. 2002, 51, 247–256. [Google Scholar] [CrossRef]
- Ding, S.; Knight, J. Why has China grown so fast? The role of structural change. Available online: http://www.economics.ox.ac.uk/materials/working_papers/paper415.pdf (access on 1 September 2014).
- Nadiri, M.I.; PruchaI, R. Dynamic Factor Demand Models and Productivity Analysis. In New Developments in Productivity Analysis; Hulten, C.R., Dean, E.R., Harper, M., Eds.; University of Chicago Press: Chicago, IL, USA, 2001. [Google Scholar]
- Gong, B.; Sickles, R. Finite sample evidence on the performance of stochastic frontiers and data envelopment analysis using panel data. J. Econ. 1992, 51, 259–284. [Google Scholar]
- Shiu, A.; Lam, P.L. Electricity consumption and economic growth in China. Energy Policy 2004, 32, 47–54. [Google Scholar] [CrossRef]
- Zhou, G.; Chau, K.W. Short and long-run effects between oil consumption and economic growth in China. Energy Policy 2006, 34, 3644–3655. [Google Scholar] [CrossRef]
- Yuan, J.H.; Kang, J.G.; Zhao, C.H.; Hu, Z.G. Energy consumption and economic growth: Evidence from China at both aggregated and disaggregated levels. Energy Econ. 2008, 30, 3077–3094. [Google Scholar] [CrossRef]
- Yalta, A.T.; Cakar, H. Energy consumption and economic growth in China: A reconciliation. Energy Policy 2012, 41, 666–675. [Google Scholar] [CrossRef]
- Koop, G. Carbon dioxide emissions and economic growth: A structural approach. J. Appl. Stat. 1998, 25, 489–515. [Google Scholar] [CrossRef]
- Chang, C.C. A multivariate causality test of carbon dioxide emissions, energy consumption and economic growth in China. Appl. Energy 2010, 87, 3533–3537. [Google Scholar] [CrossRef]
- Wang, S.S.; Zhou, D.Q.; Zhou, P.; Wang, Q.W. CO2 emissions, energy consumption and economic growth in China: A panel data analysis. Energy Policy 2011, 39, 4870–4875. [Google Scholar] [CrossRef]
- Kareem, S.D.; Kari, F.; Alam, G.M.; Adewale, A.; Oke, O.K. Energy consumption, pollutant emissions and economic growth: China experience. Int. J. Appl. Econ. Financ. 2012, 6, 136–147. [Google Scholar] [CrossRef]
- Grossman, G.M.; Krueger, A.B. Economic growth and the environment. Q. J. Econ. 1995, 110, 353–377. [Google Scholar] [CrossRef]
- Hailu, A.; Veeman, T.S. Environmentally sensitive productivity analysis of the Canadian pulp and paper industry, 1959–1994: An input distance function approach. J. Environ. Econ. Manag. 2000, 40, 251–274. [Google Scholar] [CrossRef]
- Coelli, T.; Lauwers, L.G.; Huylenbroeck, V. Formulation of Technical, Economic and Environmental Efficiency Measures that are Consistent with the Materials Balance Condition; CEPA Working Paper Series, No WP062005. The University of Queensland: Brisbane, Australia, 2005. Available online: http://www.uq.edu.au/economics/cepa/docs/WP/WP062005.pdf (access on 1 September 2014).
- Chung, Y.H.; Färe, R.; Grosskopf, S. Productivity and undesirable outputs: A directional distance function approach. J. Environ. Manag. 1997, 51, 229–240. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Margaritis, D. APEC and the Asian economic crisis: Early signals from productivity trends. Asian Econ. J. 2001, 15, 325–342. [Google Scholar] [CrossRef]
- Jeon, B.M.; Sickles, R.C. The role of environmental factors in growth accounting. J. Appl. Econ. 2004, 19, 567–591. [Google Scholar] [CrossRef]
- Kumar, S. Environmentally sensitive productivity growth: A global analysis using Malmquist–Luenberger index. Ecol. Econ. 2006, 56, 280–293. [Google Scholar] [CrossRef]
- Pastor, J.T.; Asmild, M.; Lovell, C.A. The biennial Malmquist productivity change index. Soc. Econ. Plan. Sci. 2011, 45, 10–15. [Google Scholar] [CrossRef]
- Luenberger, D.G. New optimality principles for economic efficiency and equilibrium. J. Optim. Theory Appl. 1992, 75, 221–264. [Google Scholar] [CrossRef]
- Chambers, R.G.; Chung, Y.; Färe, R. Benefit and distance functions. J. Econ. Theory 1996, 70, 407–419. [Google Scholar] [CrossRef]
- Wei, C.; Ni, J.; Du, L. Regional allocation of carbon dioxide abatement in China. China Econ. Rev. 2012, 23, 552–565. [Google Scholar] [CrossRef]
- Choi, Y.; Zhang, N.; Zhou, P. Efficiency and abatement costs of energy-related CO2 emissions in China: A Slacks-based Efficiency Measure. Appl. Energy 2012, 98, 198–208. [Google Scholar] [CrossRef]
- National Bureau of Statistics. China Statistical Yearbook; China Statistical Press: Beijing, China, 2011. [Google Scholar]
- Department of Industry and Transport Statistics; National Bureau of Statistics (NBS); Energy Bureau; National Development and Reform Commission (NDRC) (Eds.) China Energy Statistical Yearbook; China Statistical Press: Beijing, China, 2011. (in Chinese)
- Wu, Y. Openness, productivity and growth in the APEC economies. Empir. Econ. 2004, 29, 593–604. [Google Scholar] [CrossRef]
- Wu, Y. China’s contribution to productivity growth: New estimates. China Econ. Q. 2008, 3, 827–842. [Google Scholar]
- Eggleston, H.S.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K. IPCC Guidelines for National Greenhouse Gas Inventories in 2006; IGES: Kanagawa, Japan, 2006. [Google Scholar]
- These values are on weighted mean by GRP proportion of each province mean between 1998 and 2012.
- Kumar, S.; Russell, R.R. Technological change, technological catch-up, and capital deepening: Relative contributions to growth and convergence. Am. Econ. Rev. 2002, 92, 527–548. [Google Scholar] [CrossRef]
- Henderson, J.D.; Russell, R.R. Human capital and convergence: A production-frontier approach. Int. Econ. Rev. 2005, 46, 1167–1205. [Google Scholar] [CrossRef]
- Kumar and Russell and Henderson and Russell use the same regression to describe labor productivity and its components growth rates. We also employ generalized least squares because the error term is likely to be heteroskedastic. These results are consistent with White test of OLS.
- Silverman, B.W. Using kernel density estimates to investigate multimodality. J. R. Stat. Soc. 1981, 43, 97–99. [Google Scholar]
- Bianchi, M. Testing for convergence: Evidence from non-Parametric multimodality tests. J. Appl. Econ. 1997, 12, 393–409. [Google Scholar] [CrossRef]
- The proposed test was first applied to an OECD economic research by Bianchi, M.
- Li, Q. Nonparametric testing of closeness between two unknown distribution functions. Econ. Rev. 1996, 15, 261–274. [Google Scholar] [CrossRef]
- Fan, Y.; Ullah, A. On goodness-of-fit tests for weekly dependent processes using kernel method. J. Nonparametric Stat. 1999, 11, 337–360. [Google Scholar] [CrossRef]
- Wang, C.H. Sources of energy productivity growth and its distribution dynamics in China. Resour. Energy Econ. 2011, 33, 279–292. [Google Scholar] [CrossRef]
- Parteka, A.; Wolszczak-Derlacz, J. Dynamics of productivity in higher education: Cross-european evidence based on bootstrapped Malmquist indices. J. Product. Anal. 2013, 40, 67–82. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P. Estimating and bootstrapping Malmquist indices. Eur. J. Oper. Res. 1999, 115, 459–471. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Du, M.; Wang, B.; Wu, Y. Sources of China’s Economic Growth: An Empirical Analysis Based on the BML Index with Green Growth Accounting. Sustainability 2014, 6, 5983-6004. https://doi.org/10.3390/su6095983
Du M, Wang B, Wu Y. Sources of China’s Economic Growth: An Empirical Analysis Based on the BML Index with Green Growth Accounting. Sustainability. 2014; 6(9):5983-6004. https://doi.org/10.3390/su6095983
Chicago/Turabian StyleDu, Minzhe, Bing Wang, and Yanrui Wu. 2014. "Sources of China’s Economic Growth: An Empirical Analysis Based on the BML Index with Green Growth Accounting" Sustainability 6, no. 9: 5983-6004. https://doi.org/10.3390/su6095983
APA StyleDu, M., Wang, B., & Wu, Y. (2014). Sources of China’s Economic Growth: An Empirical Analysis Based on the BML Index with Green Growth Accounting. Sustainability, 6(9), 5983-6004. https://doi.org/10.3390/su6095983






