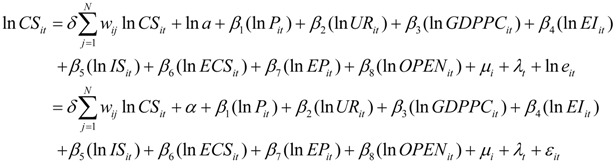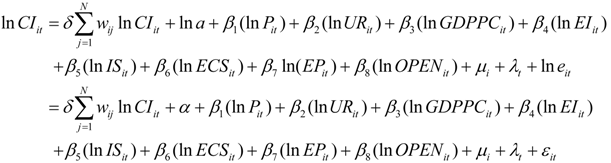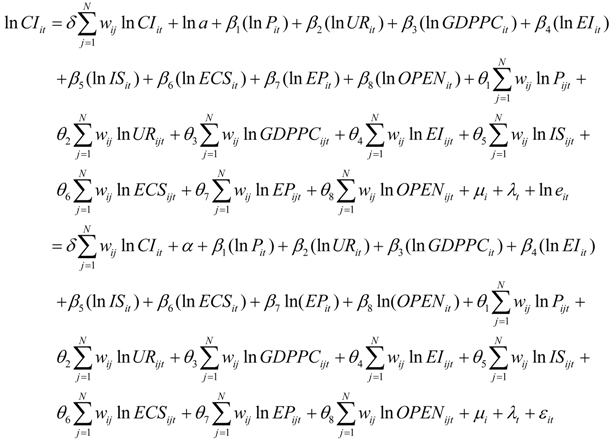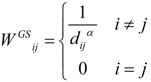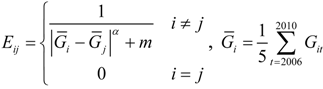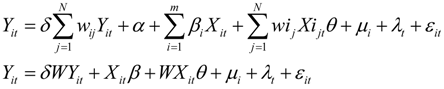Next Article in Journal
Can Environmental Laws Fulfill Their Promise? Stories from Canada
Next Article in Special Issue
Sustainable E-Governance: The Relationship among Trust, Digital Divide, and E-Government
Previous Article in Journal / Special Issue
Sources of China’s Economic Growth: An Empirical Analysis Based on the BML Index with Green Growth Accounting
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 6
Issue 9
10.3390/su6096005
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Carbon Emissions in China: A Spatial Econometric Analysis at the Regional Level

by
Yu Liu
1,
Hongwei Xiao
2,*,
Precious Zikhali
3 and
Yingkang Lv
4
1
Institute of Policy and Management, Chinese Academy of Sciences, Beijing 100190, China
2
Economic Forecasting Department, State Information Center, Beijing 100045, China
3
Postnet Suite 122, Private Bag X1, Die Wilgers 0041, Pretoria, South Africa
4
College of Economics and Management, China Agricultural University, Beijing 100083, China
*
Author to whom correspondence should be addressed.
Sustainability 2014, 6(9), 6005-6023; https://doi.org/10.3390/su6096005
Submission received: 23 July 2014 / Revised: 1 September 2014 / Accepted: 2 September 2014 / Published: 5 September 2014
(This article belongs to the Special Issue Special issue of Sustainable Asia Conference 2014)
Versions Notes

Abstract

:
An extended Stochastic Impacts by Regression on Population, Affluence and Technology (STIRPAT) model, incorporating factors that drive carbon emissions, is built from the regional perspective. A spatial Durbin model is applied to investigate the factors, including population, urbanization level, economic development, energy intensity, industrial structure, energy consumption structure, energy price, and openness, that impact both the scale and intensity of carbon emissions. After performing the model, we find that the revealed negative and significant impact of spatial-lagged variables suggests that the carbon emissions among regions are highly correlated. Therefore, the empirical results suggest that the provinces are doing an exemplary job of lowering carbon emissions. The driving factors, with the exception of energy prices, significantly impact carbon emissions both directly and indirectly. We, thus, argue that spatial correlation, endogeneity and externality should be taken into account in formulating polices that seek to reduce carbon emissions in China. Carbon emissions will not be met by controlling economic development, but by energy consumption and low-carbon path.

1. Introduction

The challenge of climate change continues to put pressure on countries to shift to a low-carbon economy, which is loosely defined as an economy that produces minimal greenhouse gas (GHG) emissions. As a result, most developed or emerging countries have created their own strategies to save energy and reduce GHG emissions. As the world’s biggest GHG emitter driven largely by energy use as the population and economy continue to expand, the importance of China’s participation to reducing global emissions cannot be overemphasized. The growth in China’s economy at an unprecedented average of 10.4 percent per year between 1990 and 2010 was accompanied by a tripling of the country’s carbon dioxide emissions. By 2010, China’s carbon emissions constituted 24 percent of global emissions. Projections indicate that China, together with India, will continue to lead not only future global economic growth, but, also, future growth in energy demand, making up 34 percent of projected total world energy consumption in 2040.
The importance of China reducing its global emissions has attracted the attention of many researchers as they attempt to identify factors that may determine the country’s transition towards a low-carbon economy. This research has benefited from the development of spatial econometrics, which allows for analyses of China’s trends and drivers of carbon emissions that permit variation both in the patterns and drivers across regions. Some impressive studies have applied spatial panel models to analyze China’s regional or industrial environmental Kuznets curve [1,2,3,4,5,6,7,8,9,10]. However, most of these studies tend to focus on the impact of economic growth and foreign direct investment (FDI) on carbon emission, while the impacts of other factors, such as population size, urbanization, and energy price, are often ignored. Secondly, most of the researchers opt for either a fixed-effects model or a spatial lag and spatial error model, which usually give different empirical results and thus lead to some discrepancies. Although studies have used spatial econometric techniques to analyze carbon emissions, most of the models used generally face selection bias problems associated with the choice of a spatial lag model or spatial error model, fixed-effects or random-effects model, spatial heterogeneity model, and the construction of a spatial weight matrix.
This paper seeks to contribute to the literature that studies patterns and drivers of growth in China’s carbon emissions using spatial econometric techniques that incorporate spatial effects, thereby making the estimates more effective. This can guide policy makers in designing carbon emissions policies and respond to climate change through a transition towards low-carbon economies.

2. Expanded Stochastic Impacts by Regression on Population, Affluence and Technology (STIRPAT) Carbon Emission Model

The Impacts of Population, Affluence, and Technology (IPAT) equation, originally proposed by Ehrlich et al. [11], is often used to study the impact of human activities on the environment. Its simplicity and ability to connect factors that impact environmental quality have resulted in its being widely used in studies of environmental problems (see, for example, Harrison [12], Raskin [13], York [14], Shi [15], Cole [16], Rosa [17], among others). IPAT is an accounting identity that is expressed as follows:
I = PAT
where I represents environmental impact, P is population size, A is affluence or wealth per capita (measured by GDP per capital), and T is technology level (measured by environmental impact per unit of GDP). The IPAT equation allows for the investigation of the role of a specific factor on environmental change while keeping other factors constant.
The equation has been criticized for not allowing room for diagnostic analysis. This has led to an evolution of the IPAT equation. One modification was proposed by Waggoner and Ausubel [18]: adding “consumption” C as a fourth variable on the right-hand side of Equation 1 to create the ImPACT model. C represents the intensity of energy use. The fact that the IPAT and ImPACT equations are mathematical identities under which the concerned factors impact the environment proportionally, thus limits the application of the models. Moreover, the relationship between the driving factors and carbon emissions is usually nonlinear and disproportionate, rendering the application of IPAT and ImPACT problematic.
In response to these limitations, Dietz and Rosa [19] proposed another variation—the Stochastic Impacts by Regression on Population, Affluence and Technology (STIRPAT) model. They present the IPAT equation in a stochastic manner under which carbon emissions are modeled stochastically via regressing it on population, wealth, and technology. The STIRPAT is expressed as follows:
I = aPbAcTde
where a represents model coefficient, b, c and d are the coefficients for population, wealth and technology, respectively, and e is the error term. Environmental pressure is represented by I, population size by P, wealth by A, and finally, technology by T. Since a = b = c = d = 1, STIRPAT is simplified to the IPAT equation. The inclusion of the coefficients in STIRPAT ensures that the disproportional impacts of factors driving carbon emissions can be modeled. Taking a natural logarithm on both sides gives:
InI = Ina + b(InP) + c(InA) + d(InT) + Ine
Each coefficient in Equation 3 is interpreted as an elasticity between the independent variables and the dependent variable, i.e., they show the percentage of change of the dependent variable due to a percentage changes of the dependent variable. STIRPAT allows both the estimation of the coefficients as well as decomposition of factors affecting environmental quality. Several studies have been conducted based on the model and its adjustment (see, for example, Dietz and Rosa [20], York et al. [21], among others). This paper extends STIRPAT by including variables such as urbanization, industry structure, energy consumption structure, energy price and openness. The extended STIRPAT model is expressed as in Equations (4) and (5).
ln CS = ln a + β1(ln P) + β2(ln UR) + β3(ln GDPPC) + β4(ln EI) + β5(ln IS) + β6(ln ECS) + β7ln(EP) + β8ln(OPEN) + ln e = α + β1(ln P) + β2(ln UR) + β3(ln GDPPC) + β4(ln EI) + β5(ln IS) + β6(ln ECS) + β7(ln EP) + β8ln(OPEN) + ε
ln CI = ln a + β1(ln P) + β2(ln UR) + β3(ln GDPPC) + β4(ln EI) + β5(ln IS) + β6(ln ECS) + β7ln(EP) + β8ln(OPEN) + ln e = α + β1(ln P) + β2(ln UR) + β3(ln GDPPC) + β4(ln EI) + β5(ln IS) + β6(ln ECS) + β7(ln EP) + β8ln(OPEN) + ε
where CS denotes the level or scale of carbon emissions (measured in 10,000 tons of carbon emission), CI is carbon intensity (CO2 emission per unit of GDP, measured by in 10,000 Yuan/ton), P represents population (population size, in 10,000), UR denotes the urbanization level (measured by the percentage of urban population in total population), GDPPC denotes economic development (measured by GDP per capital), EI is energy intensity (measured by energy consumption per unit of GDP), IS represents industrial structure (measured by the secondary industry share of GDP), ECS represents energy consumption structure (measured by the percentage of coal in total energy consumption), EP is energy price (measured by producer’s price index for manufactured products), and OPEN is openness (measured by the gross investment the registered foreign-funded enterprises by region at the year-end).

3. Construction of Carbon Emission Spatial Econometric Model and Spatial Weight Matrix

The State Council has issued the 12th Five-Year Work Plan for Controlling Greenhouse Gas Emissions, setting a goal of reducing CO2 emissions per unit of GDP by 17 percent in 2015 compared to 2010. Plans to reduce CO2 emissions need to be included by the regions in their plans for economic and social development and the yearly plan, making carbon emissions an important indicator of development. In addition, in 2011, the National Development and Reform Commission issued Notice Regarding the Development of Carbon Emissions Trading Pilot, whose aim is to implement a pilot trading of carbon emissions rights in seven provinces, including Beijing, Tianjin, Shanghai, Chongqing, Guangdong, Hubei, and Shenzhen. These regions are required to draft a regulation and formulate the rules for the pilot carbon emissions trading and to set a regional GHG emissions reduction target. This makes the scale of carbon emissions an important monitoring indicator of regional carbon emissions. In line with this, this paper uses two variables—the scale and intensity of carbon emissions—as independent variables to obtain a comprehensive result.
Based on the extended STIRPAT, the papers build a spatial econometric model by taking into account the fact that carbon emissions are heterogeneous and spatially correlated across regions and industries. A spatial panel data econometric model, which integrates spatial econometrics (spatial effects) and panel data (time effects), makes spatial econometric analysis more efficient. The spatial panel data econometric model includes three basic models: the spatial lag panel data model, spatial error panel data model, and spatial Durbin panel data model. These models are further discussed below.

3.1. Spatial Lag Panel Data Model (SLPDM)

Where InCSit and InCIit denote scale and intensity of carbon emissions of the ith region at time t, respectively. ΣwijInCSit and ΣwijInCIit represent the spatial correlation between InCSit and InCIit of the region i and that of its adjacent regions. InPit, InURit, InGDPPCit, InEIit, InISit, InECSit, InEPit and InOPENit are independent variables of region i at time t. δ is spatial auto-correlation index, wij is an element of the spatial weight matrix representing the spatial relations between region i and j. α is the constant term, β is are coefficients to be estimated, μi is the individual-fixed effect and λt is the time-fixed effect.
Sustainability 06 06005 i001
Sustainability 06 06005 i002

3.2. Spatial Error Panel Data Model (SEPDM)

The Spatial Error Panel Data model (SEPDM) is specified as follows:
Sustainability 06 06005 i003
Sustainability 06 06005 i004
where InCSit, InCIit, α, β, μi, λt, εit, InPit, InURit, InGDPPCit, InEIit, InISit, InECSit, InEPit and InOPENit are defined same as in (6) and (7). ϕit denotes spatial error auto-correlation, ρ is spatial auto-correlation index.

3.3. Spatial Durbin Panel Data Model (SDPDM)

The Spatial Durbin Panel Data model (SDPDM) is specified as follows:
Sustainability 06 06005 i005
Sustainability 06 06005 i006
where InCSit, InCIit, InPit, InURit, InGDPPCit, InEIit, InISit, InECSit, InEPit, InOPENit, α, μi, λt are defined the same as in (6) and (7). θ is a vector of coefficients to be estimated. We test the hypothesis H0 : θ = 0 and H0 : θ + δβ = 0. The reject of the hypothesis indicates that SDPDM best fits the data.
The extended STIRPAT model examines not only the impacts of the aforementioned independent variables on scale and intensity of regions’ carbon emissions, but it also determines the impacts of the independent variables of the adjacent regions on carbon emissions scale and extent. It also measures the impact of the carbon emissions scale and intensity of the adjacent regions on the region’s carbon emissions scale and extent.

3.4. Spatial Weight Matrix

A spatial weight matrix needs to be constructed to reflect spatial correlation among regions. A proper spatial weight matrix is of substantial importance to get a sound spatial econometric result. The construction of the spatial weight matrix influences whether a spatial correlation exists, as well as spatial econometric model selection and the empirical results. To improve model credibility, we consider both geographical and non-geographical spatial correlation among the regions.
We opt for both geographical and economical spatial weighted matrix. The former is constructed by the inverse distance method.
Sustainability 06 06005 i007
where dij is the distance between regional i and j, which is calculated from their longitudes and latitudes.
The economic spatial weight matrix W* is a product of W. and the economic weight matrix, E.
Sustainability 06 06005 i008
where Git denotes per capita GDP, representing the income level of region i at time t (Deflated by the price index in 2006). Thus, W* incorporates economic development into the weight matrix. α is the adjustable parameters of economic weight, usually 1 or 2. When two different geo-spatial locate at the same level of economic development with the same period of time, the denominator is zero. To avoid the zero distance problem, when there are any two different locations in the same period geospatial economic variables are the same, m take 1. When any two different locations in the same period geospatial economic variables are not the same, m is taken to 0.
The calculation of regional carbon emissions takes into account the spatial–temporal dynamics of regional carbon emissions from electricity and thermo. The regional carbon emissions from electricity are elicited under the Origination Principle. The dynamic energy conversion coefficient of energy resources is used. The data is from the China Energy Statistical Yearbook 2011 [22].

4. Model Selection

Two Lagrange Multiplier tests (LM-Lag and LM-Error tests) are applied to choose which model, described in Sections 3.1 to Sections 3.3, best fits the data. In classical panel data models, there are four categories of fixed effects, namely individual-fixed effects, time-fixed effects, individual and time-fixed effects, and no fixed effects. We test the four kinds of fixed-effect models through the LM test. Table 1 and Table 2 show the LM test statistics for Model 1 and Model 2, in which the dependent variable is Log(CS) and Log(CI), respectively.
Table
Table 1. LM test for Model 1 (dependent variable: Log(CS)).
Table 1. LM test for Model 1 (dependent variable: Log(CS)).
VariablePooled MLIndividual-Fixed EffectsTime-Fixed EffectsIndividual and Time-Fixed Effects
Constant–3.3551 *** (–5.8748)——————
Log(P)0.9307 *** (21.2903)0.7383 *** (3.9259)0.9269 *** (21.0747)1.2101 *** (4.5873)
Log(UR)–0.2600 (–1.2142)0.1818 (0.8779)–0.1983 (–0.8826)0.4890 ** (2.2189)
Log(GDPPC)0.8992 *** (9.6115)0.9090 *** (8.0765)0.8583 *** (8.2249)1.1905 *** (6.6064)
Log(EI)1.1225 *** (15.1500)1.1579 *** (4.6128)1.1284 *** (15.1838)1.1928 *** (4.2843)
Log(IS)0.1321 (1.0852)0.2492 ** (2.2930)0.1208 (0.9918)0.1563 (1.3847)
Log(ECS)0.2847 *** (3.4521)0.2583 *** (2.6862)0.2901 *** (3.5199)0.2952 *** (3.0436)
Log(EP)–0.0611 (–0.2379)–0.1480 ** (–2.2421)0.3289 (0.6455)0.0590 (0.4786)
Log(OPEN)0.0804 ** (2.4207)0.0556 *** (2.7728)0.0895 *** (2.6282)0.0554 *** (2.6780)
σ20.00690.00040.00680.0003
R20.94320.83410.94310.4882
Adjusted R20.94000.82590.94030.4630
Durbin–Watson2.03121.87042.06611.9776
Log-Likelihood164.6880382.5538165.5679390.1138
LM Spatial Lag25.6397 (0.000)6.9517 (0.008)25.0131 (0.000)8.5919 (0.003)
Robust LM Spatial Lag31.6000 (0.000)3.6978 (0.054)31.2468 (0.000)0.3639 (0.546)
LM Spatial Error1.1145 (0.291)3.4387 (0.064)1.3975 (0.237)9.5364 (0.002)
Robust LM Spatial Error7.0748 (0.008)0.1847 (0.667)7.6311 (0.006)1.3083 (0.253)
Joint Test of Significance LRFixed-EffectsStatisticsdfp-value
Individual-Fixed Effects449.0918300.0000
Time-Fixed Effects15.120050.0099
Note: t or z-values are in parentheses, p-values in the parentheses under the coefficients of the LM tests, * represents significance at 10%, ** 5%, and *** 1%, respectively.
Table
Table 2. LM test for Model 2 (dependent variable: Log(CI)).
Table 2. LM test for Model 2 (dependent variable: Log(CI)).
VariablePooled MLIndividual-Fixed EffectsTime-Fixed EffectsIndividual and Time-Fixed Effects
Constant0.6449 (1.1291)——————
Log(P)–0.0693 (–1.5858)–0.2616 (–1.3914)–0.0731* (–1.6609)0.2101 (0.7963)
Log(UR)–0.2600 (–1.2142)0.1818 (0.8779)–0.1983 (–0.8826)0.4890 ** (2.2189)
Log(GDPPC)–0.1008 (–1.0772)–0.0910 (–0.8083)–0.1417 (–1.3574)0.1905 (1.0571)
Log(EI)1.1225 *** (15.1500)1.1579 *** (4.6128)1.1284 *** (15.1838)1.1928 *** (4.2843)
Log(IS)0.1321 (1.0852)0.2492 ** (2.2930)0.1208 (0.9918)0.1563 (1.3847)
Log(ECS)0.2847 *** (3.4521)0.2583 *** (2.6862)0.2901 ***3.5199)0.2952 *** (3.0436)
Log(EP)–0.0611 (–0.2379)–0.1480 ** (–2.2421)0.3289 (0.6455)0.0590 (0.4786)
Log(OPEN)0.0804 ** (2.4208)0.0556 *** (2.7728)0.0895 *** (2.6282)0.0554 *** (2.6780)
σ20.00690.00040.00680.0003
R20.89420.80130.89320.3492
Adjusted R20.88820.79150.88790.3171
Durbin–Watson2.03121.87042.06611.9776
Log-Likelihood164.6880382.5538165.5679390.1138
LM Spatial Lag12.3664 (0.000)4.8069 (0.028)11.8219 (0.001)10.6239 (0.001)
Robust LM Spatial Lag12.6202 (0.000)1.4754 (0.224)11.2804 (0.001)1.1991 (0.274)
LM Spatial Error1.1145 (0.291)3.4387 (0.064)1.3975 (0.237)9.5364 (0.002)
Robust LM Spatial Error1.3684 (0.242)0.1072 (0.743)0.8561 (0.355)0.1116 (0.738)
Joint Test of Significance (LR)Fixed-EffectsStatisticsdfp-Value
Individual-Fixed Effects449.0918300.0000
Time-Fixed Effects15.120050.0099
Note: t or z-values are in parentheses, p-values in parentheses under the coefficients of the LM tests, * represents significance at 10%, ** 5%, and *** 1%, respectively.
Table 1 and Table 2 show that for both models, the LM tests with the four kinds of fixed effects (pooled-effects, individual-fixed effect, time-fixed effect, and individual and time-fixed effect) all support the spatial lag model at the five percent significance level. Similarly, the LM test with individual and time-fixed effect supports the spatial error model. Thus, the hypothesis that spatial correlations do not exist can be rejected. Furthermore, the LR tests reject the hypothesis that individual-fixed effect and time-fixed effect do not exist, indicating that the individual and time-fixed effects model outperforms its alternatives. We further determine which model (SLPDM, SEPDM, and SDPDM) is more appropriate by means of a Wald and LR test.

5. Spillover Effects of Regional Carbon Emissions

It is common to use point estimate from one or more spatial regression to test the existence of spillover effects. Lesage and Pace [23], however, argue that the point estimate of multiple spatial regression will bias its prediction of the spillover effect. They further break down spillover effects into direct and indirect effects.
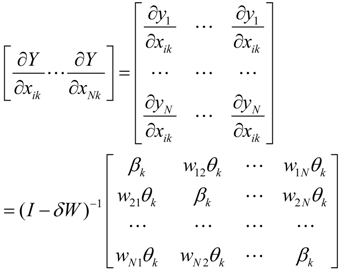
The SDPDM model (13) can be rearranged as (14) and (15).
Sustainability 06 06005 i009
Yit = (I − δW)−1(Xitβ + WXitθ) + (I − δW)−1μi + (I − δW)−1λt + (I − δW)−1εit
where Yit is the dependent variable of region i at time t, Xit is a vector of independent variables of region i at time t, α is the constant term, θ is similar to β, which is a K × 1 vector of coefficients, μi is individual-fixed effect, λt is time-fixed effect. Taking partial derivatives of the kth independent variable X in both sides results in the following:
Sustainability 06 06005 i010
where wij is the (i, j) element of the matrix W. The direct effect is defined as the sum of the diagonal elements in the right matrix while the indirect effect is defined as the average of all the elements other than the diagonal elements (Lesage and Pace, 2009). Calculation of the direct and indirect effects by this method has a drawback because calculation (I − δW)−1 is time consuming. To solve this, Lesage and Pace (2009) propose another method as follows:
(I − δW)−1 = I + δW + δ2W2 + δ3W3 + …
The estimates of direct and indirect effects from (16) are denoted as Method 1 and Method 2 for (17). Table 3 and Table 4 displays the direct and indirect effect estimates through Method 1 and Method 2, respectively, for Model 5 with Log(CS) being dependent variable. The results differ slightly across Method 1 and Method 2. All the variables have direct and indirect effects. P, GDPPC, EI, IS, impact the scale of carbon emission positively and significantly, while UR impacts significantly and negatively. Although the direct effects of ECS, EP, and OPEN are insignificant, their signs are in line with expectation.
Table 5 and Table 6 display the direct and indirect effects estimates for Model 5 with Log(CI) being the dependent variable. The chosen from Method 1 and Method 2 do not differ from results. All the variables have direct and indirect effects. The direct effect of EI, IS, and ECS on the carbon intensity is positive, whereas it is negative for P, UR. Moreover, the direct effect of GDPPC, EP, and OPEN on the carbon intensity is insignificant, though their signs are as expected. From the perspective of indirect effects, all of the variables except for energy price have significant indirect effects. We can thus argue that spillover effects do exist. Spillover effects mean the independent variables affect the dependent variable via the spatial lagged variables. The differences of direct and indirect effects of all the control variables are substantial, indicating that failing to explicitly account for spatial correlation leads to estimation bias.
Table
Table 3. Direct, indirect and total effect of the spatial Durbin model (Method 1, dependent variable: Log(CS)).
Table 3. Direct, indirect and total effect of the spatial Durbin model (Method 1, dependent variable: Log(CS)).
VariableDirect EffectIndirect EffectTotal Effect
Log(P)0.8695 *** (17.5550)0.2562 *** (3.5963)1.1257 *** (16.9993)
Log(UR)–0.6102 *** (–2.6245)1.4454 *** (4.8198)0.8352 *** (4.0497)
Log(GDPPC)1.1107 *** (9.2912)–0.6206 *** (–3.9366)0.4901 *** (4.3048)
Log(EI)1.3005 *** (10.6820)–0.4729 *** (–2.6714)0.8276 *** (6.1398)
Log(IS)0.3498 *** (3.8936)0.7305 *** (5.2446)1.0804 *** (7.0120)
Log(ECS)0.1102 (1.4101)–0.2659 ** (–2.2764)–0.1558 (–1.1617)
Log(EP)–0.0464 (–0.3767)0.0799 (0.3984)0.0335 (0.1862)
Log(OPEN)0.0004 (0.0206)–0.0528 ** (–2.2098)–0.0524 (–1.7280)
Note: t-values are in parentheses, * represents significance at 10%, ** 5%, and *** 1%, respectively.
Table
Table 4. Direct, indirect and total effect of the spatial Durbin model (Method 2, dependent variable: Log(CS)).
Table 4. Direct, indirect and total effect of the spatial Durbin model (Method 2, dependent variable: Log(CS)).
VariableDirect EffectIndirect EffectTotal Effect
Log(P)0.8680 *** (16.9634)0.2573 *** (3.7798)1.1253 *** (16.8913)
Log(UR)–0.5950 ** (–2.5072)1.4454 *** (4.7180)0.8404 *** (4.0538)
Log(GDPPC)1.1075 *** (9.0225)–0.6203 *** (–3.6545)0.4872 *** (4.2317)
Log(EI)1.3057 *** (10.4525)–0.4845 ** (–2.6801)0.8212 *** (5.9779)
Log(IS)0.3525 *** (3.8938)0.7284 *** (5.3623)1.0809 *** (6.9873)
Log(ECS)0.1053 (1.3456)–0.2625 ** (–2.2113)–0.1572 (–1.1692)
Log(EP)–0.0451 (–0.3586)0.0834 (0.4056)0.0383 (0.2008)
Log(OPEN)0.0003 (0.0139)–0.0536 ** (–2.3221)–0.0534 * (–1.7624)
Note: t-values are in parentheses, * represents significance at 10%, ** 5%, and *** 1%, respectively.
Table
Table 5. Direct, indirect and total effect of the spatial Durbin model (Method 1, dependent variable: Log(CI)).
Table 5. Direct, indirect and total effect of the spatial Durbin model (Method 1, dependent variable: Log(CI)).
VariableDirect EffectIndirect EffectTotal Effect
Log(P)–0.1333 ** (–2.5375)0.2570 *** (3.8721)0.1237 * (1.9022)
Log(UR)–0.6072 *** (–2.6125)1.4402 *** (4.8072)0.8331 *** (4.1424)
Log(GDPPC)0.1172 (0.9877)–0.6246 *** (–3.7793)–0.5075 *** (–4.4427)
Log(EI)1.3100 *** (10.9563)–0.4772 *** (–2.7687)0.8328 *** (6.1855)
Log(IS)0.3433 *** (3.9225)0.7147 *** (5.5172)1.0580 *** (7.4353)
Log(ECS)0.1115 ** (1.4542)–0.2536 ** (–2.3062)–0.1421 (–1.1075)
Log(EP)–0.0452 (–0.3634)0.0797 (0.4023)0.0345 (0.1890)
Log(OPEN)0.0010 (0.0524)–0.0506 ** (–2.2070)–0.0496 (–1.6861)
Note: t-values are in parentheses, * represents significance at 10%, ** 5%, and *** 1%, respectively.

6. The Spatial Durbin Panel Data Model (SDPDM) for Carbon Emission

We consider three Durbin models: (i) individual and time-fixed effects model (Model 3), (ii) both time and individual effects with bias correction borrowed from Lee and Yu [24] (Model 4), (iii) individual random effects and time-fixed effects (Model 5). The models with Log(CS) and Log (CI) as dependent variables are reported in Table 3 and Table 4, respectively. Model 3 and Model 4 show that the coefficients for P, UR, GDPPC, EI, IS, ECS, EP, OPEN, and σ2 changed slightly after bias correction, while the coefficients for the spatial lagged dependent and independent variables are sensitive to it. Thus, the bias correction is necessary for the spatial Durbin model with both individual and time-fixed effects. The SDPDM has two hypotheses: H0 : θ = 0 and H0 : θ + δβ = 0. Rejection of both hypotheses indicates that SDPDM fits the data best. Both the Wald and LR tests reject the two hypotheses, thereby suggesting that both SLPDM and SEPDM are rejected. We thus opt for SDPDM. Meanwhile, the Houseman test points to (Model 5), of which the coefficients are in line with expectation, and the square correlation coefficient is greater than that of (Model 4).
Table
Table 6. Direct, indirect and total effect of the spatial Durbin model (Method 2, dependent variable: Log(CI)).
Table 6. Direct, indirect and total effect of the spatial Durbin model (Method 2, dependent variable: Log(CI)).
VariableDirect EffectIndirect EffectTotal Effect
Log(P)–0.1331 ** (–2.4595)0.2598 *** (3.9424)0.1267 ** (1.9568)
Log(UR)–0.6056 ** (–2.5655)1.4450 *** (4.6130)0.8394 *** (4.0677)
Log(GDPPC)0.1181 (0.9869)–0.6269 *** (–3.8520)–0.5089 *** (–4.5164)
Log(EI)1.3078 *** (10.7349)–0.4754 *** (–2.8265)0.8324 *** (6.2488)
Log(IS)0.3486 *** (3.8477)0.7194 *** (5.4372)1.0680 *** (6.8492)
Log(ECS)0.1116 (1.4192)–0.2601 ** (–2.2649)–0.1485 (–1.1442)
Log(EP)–0.0507 (–0.3953)0.0924 (0.4544)0.0418 (0.2324)
Log(OPEN)0.0008 (0.0423)–0.0525 ** (–2.2719)–0.0517 * (–1.7145)
Note: t-values are in parentheses, * represents significance at 10%, ** 5%, and *** 1%, respectively.
We only report the results of Model 5, which are in column four in Table 3 and Table 4, respectively, for the two dependent variables. The empirical results show that coefficients for most of the independent variables are significant and the signs are as expected. The coefficients for the spatial lagged variable are negative and significant in both models (line 1, column 4 in Table 7 and Table 8), indicating that carbon emissions among regions are correlated. A region’s carbon emission level is estimated to decrease by 0.2 percent if the scale and intensity of carbon emissions of its neighbors increase by one percent. Therefore, provinces which successfully pursuing a low carbon strategy plays an important role in building a low-carbon economy for the whole country, they will drive other provinces to increase their emissions reduction. An effective regional emission reduction strategy plus government's support will lead the regional emission reduction to a virtuous cycle, and make the carbon emissions reduce effectively. Below, we discuss the impacts of the independent variables on carbon emission.
Population. The significant and positive coefficient (line 3, column 4 in Table 7) for population size P suggests that population growth increases the scale of China’s carbon emissions. The demand for energy increases dramatically with population growth, which in turn raises CO2 emissions. In carbon intensity estimation, P impacts the carbon intensity negatively and significantly (line 3, column 4 in Table 8), indicating that population growth did not enlarge the carbon intensity. Saving energy and reducing emissions have become important aspects in adjusting the structure of China’s economy and the path to development. Thus we have seen a declining trend in carbon intensity. For instance, in the 2009 United Nations Climate Change Conference, held in Copenhagen, Denmark, the Chinese government committed to reduce 40 to 50 percent of its CO2 emissions by 2020 compared to 2005. Considering the fact that China is still undergoing urbanization and industrialization, as well as a surge of population and consumption per capita, a decrease of the carbon intensity has become the priority. China should follow the principle of “shared but differentiated responsibility” to develop its low-carbon economy in a sustainable way. The spatial lagged variable W × Log(P) impacts both the scale and intensity of carbon emissions significantly and positively, proving that there are carbon emissions spillover effects of population size. One should also note that the spillover effect of population is stronger at the scale of carbon emissions than carbon intensity. The possible reason is that spillover effects are generated by flow of population, such as interregional and rural–urban migration, and by a surge of CO2 emissions from infrastructure development and household consumption.
Table
Table 7. The spatial Durbin model with both individual and time-fixed effect (dependent variable: Log(CS)).
Table 7. The spatial Durbin model with both individual and time-fixed effect (dependent variable: Log(CS)).
VariableSpatial and Time-fixed EffectBoth Time and Individual Effects (Bias Corrected)Spatial Random Effect and Time-Fixed Effect
W × Log(CS)–0.2290 *** (–2.7392)–0.1978 ** (–2.2988)–0.2020 ** (–2.4198)
Log(P)1.1820 *** (3.9562)1.1880 *** (3.4908)0.8871 *** (17.6901)
Log(UR)–0.2978 (–1.1976)–0.3110 (–1.1002)–0.4915 ** (–2.2262)
Log(GDPPC)1.3010 *** (7.6561)1.3101 *** (6.7802)1.0642 *** (9.5461)
Log(EI)0.8258 *** (3.4713)0.8429 *** (3.1212)1.2663 *** (11.2678)
Log(IS)0.2827 *** (2.6770)0.2755 ** (2.2968)0.4039 *** (4.4186)
Log(ECS)0.1940 ** (2.2499)0.1964 ** (1.9999)0.0900 (1.1606)
Log(EP)–0.0565 (–0.5608)–0.0548 (–0.4775)–0.0348 (–0.2952)
Log(OPEN)0.0108 (0.6195)0.0113 (0.5677)–0.0030 (–0.1595)
W × Log(P)0.6424 (1.4861)0.6118 (1.2460)0.4634 *** (4.2059)
W × Log(UR)1.8219 *** (5.1834)1.8099 *** (4.5221)1.4938 *** (4.8326)
W × Log(GDPPC)–0.0443 (–0.1559)–0.0787 (–0.2454)–0.4749 ** (–2.5301)
W × Log(EI)–1.2913*** (–3.1092)–1.3385 *** (–2.8564)–0.2720 (–1.3163)
W × Log(IS)0.7874 *** (4.4070)0.7861 *** (3.8624)0.8859 *** (6.0133)
W × Log(ECS)–0.2082 (–1.4987)–0.2113 (–1.3356)–0.2700 ** (–2.0940)
W × Log(EP)–0.0378 (–0.2028)–0.0360 (–0.1695)0.0828 (0.3832)
W × Log(OPEN)–0.0319 (–1.2736)–0.0325 (–1.1394)–0.0588 ** (–2.2985)
teta————0.1256 *** (5.5030)
σ20.00020.00030.0003
R20.99820.99820.9974
Square Correlation Coefficient0.65730.65660.9615
Log-Likelihood422.9826422.9826333.4740
Wald Test Spatial Lag68.7413 (0.000)52.9481 (0.000)71.8871 (0.000)
LR Test Spatial Lag56.5236 (0.000)56.5236 (0.000)NA
Wald Test Spatial Error65.5395 (0.000)51.4416 (0.000)63.8144 (0.000)
LR Test Spatial Error52.4984 (0.000)52.4984 (0.000)NA
Hausman testStatisticsdfp-Value
11.1632170.8480
Note: t or z-values are in parentheses, p-values in parentheses under the coefficients of the LM and Wald tests. * represents significance at 10%, ** 5%, and *** 1%, respectively.
Table
Table 8. Spatial Durbin model with both individual and time-fixed effect (dependent variable: Log(CI)).
Table 8. Spatial Durbin model with both individual and time-fixed effect (dependent variable: Log(CI)).
VariableSpatial and Time-Fixed EffectBoth Time and Individual Effects (Bias Corrected)Spatial Random Effect and Time-Fixed Effect
W × Log(CI)–0.2290 *** (–2.7499)–0.1980 ** (–2.3095)–0.2220 *** (–2.6778)
Log(P)0.1820 (0.6092)0.1879 (0.5522)–0.1105 ** (–2.2183)
Log(UR)–0.2978 (–1.1977)–0.3109 (–1.0999)–0.4819 ** (–2.1899)
Log(GDPPC)0.3010 * (1.7715)0.3100 * (1.6045)0.0593 (0.5332)
Log(EI)0.8258 *** (3.4718)0.8428 *** (3.1211)1.2646 *** (11.3236)
Log(IS)0.2827 *** (2.6774)0.2756 ** (2.2975)0.4093 *** (4.4913)
Log(ECS)0.1940 ** (2.2500)0.1964 ** (1.9997)0.0890 (1.1512)
Log(EP)–0.0565 (–0.5608)–0.0549 (–0.4777)–0.0393 (–0.3332)
Log(OPEN)0.0108 (0.6195)0.0113 (0.5675)–0.0035 (–0.1831)
W × Log(P)0.4135 (0.9741)0.4141 (0.8563)0.2617 *** (3.6790)
W × Log(UR)1.8219 *** (5.1836)1.8100 *** (4.5226)1.4948 *** (4.8508)
W × Log(GDPPC)–0.2733 (–1.0161)–0.2764 (–0.9023)–0.6770 *** (–4.0574)
W × Log(EI)–1.2913 *** (–3.1103)–1.3382 *** (–2.8563)–0.2474 (–1.2043)
W × Log(IS)0.7874 *** (4.4070)0.7862 *** (3.8625)0.8877 *** (6.0435)
W × Log(ECS)–0.2082 (–1.4987)–0.2113 (–1.3354)–0.2651 ** (–2.0601)
W × Log(EP)–0.0378 (–0.2028)–0.0361 (–0.1696)0.0849 (0.3932)
W × Log(OPEN)–0.0319 (–1.2736)–0.0325 (–1.1393)–0.0577 ** (–2.2615)
teta————0.1266 *** (5.5034)
σ20.00020.00030.0003
R20.99670.99670.9951
Square Correlation Coefficient0.56420.56340.9282
Log-Likelihood422.9334422.9334333.6113
Wald Test Spatial Lag66.1930 (0.000)51.3633 (0.000)65.0033 (0.000)
LR Test Spatial Lag54.5750 (0.000)54.5750 (0.000)NA
Wald Test Spatial Error65.5435 (0.000)51.4385 (0.000)63.7257 (0.000)
LR Test Spatial Error52.3998 (0.00)52.3998 (0.000)NA
Hausman TestStatisticsdfP-Value
0.9612171.0000
Note: t or z-values are in parentheses, P-values in parentheses under the coefficients of the LM and Wald tests, * represents significance at 10%, ** 5%, and *** 1%, respectively.
Urbanization. Population impacts carbon emission via human production and consumption. The population factor affects carbon emissions not only through its size, but also via urbanization. Urbanization levels affect both the scale of carbon emissions and carbon intensity positively and significantly, indicating the acceleration of urbanization restrains the increase of carbon emissions scale and carbon intensity. In the past decade, China’s urbanization rate has been one percent per year, reaching 50 percent in 2011 and 51.27 percent by the end of 2011. The variable W × Log(UR) positively and significantly affects both the level and intensity of carbon emissions. This suggests that spillover effects of urbanization on carbon emissions do exist and that the spillover effect of urbanization on the scale of carbon emission is similar to that on the carbon intensity. This is due to the competition for homogeneity among regions. The differentiated levels of urbanization of different regions accelerate the urbanization process for the lagging regions that aim to “catch up” with regions with higher urbanization level. This extensive urbanization model leads to negative consequences such as low land use efficiency, imperfect infrastructure and improper urban planning and so on. All these factors lead to growth in carbon emissions.
Per capita GDP. China is in an era of rapid industrialization and urbanization, which translates into CO2 emissions growth from economic growth and energy consumption. The positive and significant impact of per capita GDP on the scale and intensity of carbon emissions indicates that China’s unprecedented economic growth is the main driver of carbon emissions growth. Rising carbon emissions are to some extent unavoidable in maintaining a high growth rate. Thus, the carbon emissions reduction target is not likely to be met by controlling economic development, but by adjusting the structure of energy consumption and following the low-carbon path. We argue that economic growth and carbon emissions reduction can both be achieved. The negative and significant coefficient of the spatial lagged variable W × Log(GDPPC) shows that the economic growth in some regions can affect carbon emissions of other regions through spillover effects. The results also indicate that the spillover effect of economic development on the carbon intensity is greater than on the scale of carbon emission. This is explained by the fact that the provinces are competing to develop lower carbon economies in the 11th Five-Year period. The provinces have attempted to save energy and reduce emissions by adjusting the structure of economic growth and shifting towards low-carbon development paths. As a result, the effect of economic growth on carbon emissions has been alleviated.
Energy intensity. The decrease in energy intensity is mainly from technological innovation, affecting both the scale and intensity of carbon emissions. We found a significant and positive impact of energy intensity on the level and intensity of carbon emissions, indicating that China’s technological innovation and the associated decrease in energy intensity contributes to the reduction of carbon emissions. Since adjusting industry and energy consumption structure is difficult, China needs to search for other ways—as with technological innovation—to improve energy efficiency and reduce carbon emissions. The low-carbon technologies, including clean energy alternative technologies, renewable energy technologies, and new energy technologies, which are currently in the stages of energy exploration, transformation and application, give substantial support to meeting the 2020 carbon emissions reduction target. However, no spatial spillover effect is found for energy intensity on carbon emissions, since the coefficient for W × Log(EI) is negative but insignificant. This is because the flow of carbon emissions technology from one region to another is hard to fulfill. The imitation of developing carbon emissions reduction technologies is to a large extent influenced by regional economic development and innovation capability. The large differences on research capabilities among regions block diffusion of those technologies.
Industry structure. Industrial structure refers to the percentage of the secondary industry which includes manufacturing and construction sectors. Those are energy-intensive industries. However, the secondary industry is still the main industry of China’s economy, which is in the phase of urbanization and industrialization. Under such circumstances, the scale and intensity of carbon emissions are influenced by the current economic structure. This is supported by the results that IS effects scale and intensity of carbon emissions positively and significantly. This means the change in industry structure is not successful in reducing high energy consumption and emissions and increasing energy efficiency, because China is historically concentrated on heavy industries. To meet the emissions reduction target, China should adjust its economic structure and develop high-tech and modern service industries, which have far lower carbon emissions. On the other hand, the spillover effect by industry structure on carbon emissions levels is found to be positive but insignificant, suggesting that, in the short term, changes in industry structure are unlikely to reduce levels of carbon emissions. However, we confirm there is a spillover effect of industrial structure on the intensity of carbon emissions. The reason is that the carbon intensity target is allocated by the central government to the provinces that compete to meet the carbon emissions target. Different carbon intensity indicators in the energy production and consumption phases give the provinces incentives to adjust their industrial structures and strategies of energy production and consumption, which again leads to carbon emissions reduction.
Structure of energy consumption. In the long run, China ought to transform its traditional coal-intensive energy structure to an oil- and gas-intensive one. However, given current resource status and the high consumption rate of coal, the coal-intensive structure will remain for a long period of time. ECS is positive but insignificant in affecting both the levels and intensity of carbon emissions, indicating that change in energy consumption structure does not play a role. To strengthen the role of changes in the energy consumption structure, it is necessary to increase, in proportional terms, the use of non-fossil energies such as wind, hydro, nuclear, solar and biomass. The use of gas should also be increased through adjusting industrial policy and international trade policies. Moreover, W × Log(ECS) impacts the scale and intensity negatively and significantly, suggesting the presence of spillover effects of the structure of energy consumption. The spillover is due to the competition among the regions in optimizing energy consumption structure and developing non-fossil energies. It is necessary to build a mechanism under which the scale and intensity of energy consumption is controlled and provincial energy structures are correlated in an optimal way.
Energy price. In this paper, energy price refers to producer’s price index for manufactured products. In theory, factor prices negatively correlate with factor demands. The coefficient for energy price is negative but insignificant in affecting both the level and intensity of carbon emissions, indicating that although the role of energy price in affecting carbon emission is not statistically significant, but important. To meet the increasing demand for energy, a market-oriented price mechanism needs to be formed to reflect resource scarcity. While the government decides the price for electricity transmission and distribution, the price for electricity producers and consumers is determined by the market-oriented price mechanism. We do not find evidence that the spillover effect of the energy price exists, because the release of regional energy price information is inefficient. When energy price in one region increases, producers in this region will purchase energy from its adjacent regions, thereby causing an increase of total carbon emission. Therefore, China is in need of a sounder price information system.
Openness. Under the trend of globalization, China’s opening up policy has been pushing its economy forward; many achievements have been made as a result. In recent years, the need for a low-carbon economy has made it necessary to import advanced technologies from abroad, with a preference for sustainable ones. Thus, openness decreases carbon emissions. However, this hypothesis is rejected by the model results. We find OPEN effects carbon emissions to impact negatively but insignificantly. Nonetheless, China needs to import low-carbon technologies and welcome FDI in developing low-carbon technologies, since the spillover effect of FDI lowers scale and intensity of carbon emissions. The coefficient for W × Log(OPEN) is negative and significant, confirming the presence of a spillover effect. The spillover effect is from the competition among regions on absorbing FDI. Not only cities along the coast have increased the intensity of their policies to open their borders for trade and investment, but also the provinces from Central and Western China have accelerated the pace of opening up, supporting the transition towards a low-carbon economy.

7. Conclusions and Policy Recommendations

An extended Stochastic Impacts by Regression on Population, Affluence and Technology (STIRPAT) model for the regional level is created to investigate factors that drive the scale and intensity of carbon emissions in China. Based on provincial panel data from 2006 to 2010, a spatial Durbin model is applied to test the impacts of the driving factors on the scale and intensity of carbon emissions and to examine spatial correlation of carbon emissions and the spillover effects of the determinants. The main conclusions from the analysis are as follows:
First, most of the factors impact the level and intensity of carbon emissions significantly and with expected signs. The revealed negative and significant impact of spatial-lagged variables suggests that the carbon emissions among regions are highly correlated. As a result, the exemplary role of the provinces with low-carbon emission is of great importance in developing a nationwide low-carbon economy.
Second, the driving factors impact carbon emission both directly and indirectly. From the perspective of indirect effects, all of the variables except for energy price have significant indirect effects. We can, thus, argue that spillover effects do exist. The transitional panel data model will bias the estimation. The spillover effect refers to the independent variables that affect the dependent variable via the spatial-lagged variables. The differences of direct and indirect effects of the control variables are substantial, indicating that failure to account for spatial correlation leads to estimation bias.
The analyses show that spatial correlation, heterogeneity and externality need to be taken into account when formulating policies. Carbon emissions will not be met by controlling economic development, but energy consumption and low-carbon path. Considering the fact that carbon emissions among regions and industries are different, we propose the following strategies to reduce carbon emission while maintaining economic growth: Accelerating the process of urbanization, to fully realize its function of reducing carbon emissions, fostering technological innovation, optimizing industry structure, moderately increasing energy prices, and extending opening up policies for trade and foreign investment while choosing FDI with low-carbon technologies.

Acknowledgments

This research is supported by the National Natural Science Foundation of China “A Research on the Operating Mechanism and Economic Impact of the Pilot Regional Carbon Trading—Based on the Term-Co2 Model (No.71473242)”, National Basic Research Program of China (No. 2012CB955700) and Chinese Academy of Science Strategic technology Special Project “Climate Change and Carbon budget Certification related issue (XDA.05140300)”.

Author Contributions

Yu Liu performed research, analyzed the data and wrote the paper. Hongwei Xiao contributed to the conceptual framework of the methodology and interpreted the results. Precious Zikhali drafted and revised the manuscript. Yingkang Lv performed the calculations and analyzed the data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Huang, Y.; Wang, L.; Li, G.; Jiang, D. An empirical analysis for the environmental Kuznets curve in China based on spatial penal models . South China J. Econ. 2009, 10, 59–68. (in Chinese). [Google Scholar]
  2. Su, Z.; Hu, R.; Lin, S. Spatial econometric analysis of Kuznets’ relationship between environmental quality and economic growth. Geogr. Res. 2009, 2, 303–310. (in Chinese). [Google Scholar]
  3. Zhu, P.; Yuan, J.; Zen, W. Analysis of Chinese Industry Environmental Kuznets Curve—Empirical Study Based on Spatial Panel Model. China Ind. Econ. 2010, 6, 65–74. (in Chinese). [Google Scholar]
  4. Wang, L.; Guan, J.; Zhang, J. Environmental Pollution and Economic Growth in China: A Dynamic Spatial Panel Data Model. Geogr. Res. 2010, 6, 818–825. (in Chinese). [Google Scholar]
  5. Yao, Y.; Ni, Q. The impact of foreign direct investment on carbon intensity empirical study based on Chinese provincial dynamic panel data. Econ. Geogr. 2011, 9, 1432–1438. (in Chinese). [Google Scholar]
  6. Yu, Y. Innovation Cluster, Government Support and the Technological Innovation Efficiency: Based on Spatial Econometrics of Panel Data with Provincial Data. Econ. Rev. 2011, 2, 93–101. (in Chinese). [Google Scholar]
  7. Zheng, Z.; Huang, H. Spatial panel statistical analysis on local government behavior and environmental pollution. Stat. Inf. Forum 2011, 10, 52–57. (in Chinese). [Google Scholar]
  8. Chen, D.; Zhang, J. An empirical study on the environmental Kuznets curve for China’s carbon emission: Based on Spatial Panel model. Stat. Inf. Forum 2011, 5, 48–53. (in Chinese). [Google Scholar]
  9. Xu, H.; Deng, Y. Does FDI lead to environment pollution in China? A spatial econometric analysis based on provincial panel data. Manag. World 2012, 2, 30–43. (in Chinese). [Google Scholar]
  10. Wang, H.; Teng, Y. Economic Development and Environmental Pollution Space Panel Data Analysis. Technol. Econ. Manag. Res. 2013, 2, 85–89. (in Chinese). [Google Scholar]
  11. Ehrlich, P.R.; Holdren, J.P. Impact of population growth. Science 1971, 3977, 1212–1217. [Google Scholar]
  12. Harrison, P. Inside the Third World: The Anatomy of Poverty; Penguin Books: New York, NY, USA, 1981. [Google Scholar]
  13. Raskin, P.D. Methods for estimating the population contribution to environmental change. Ecol. Econ. 1995, 3, 225–233. [Google Scholar]
  14. York, R.; Rosa, E.A.; Dietz, T. Bridging environmental science with environmental policy: Plasticity of population, affluence, and technology. Soc. Sci. Q. 2002, 1, 18–34. [Google Scholar]
  15. Shi, A. The impact of population pressure on global carbon dioxide emissions, 1975–1996: Evidence from pooled cross-country data. Ecol. Econ. 2003, 1, 29–42. [Google Scholar] [CrossRef]
  16. Cole, M.A.; Neumayer, E. Examining the impact of demographic factors on air pollution. Popul. Environ. 2004, 1, 5–21. [Google Scholar] [CrossRef]
  17. Rosa, E.A.; York, R.; Dietz, T. Tracking the anthropogenic drivers of ecological impacts. AMBIO A. J. Hum. Environ. 2004, 8, 509–512. [Google Scholar]
  18. Waggoner, P.E.; Ausubel, J.H. A framework for sustainability science: A renovated IPAT identity. Proc. Nat. Acad. Sci. USA 2002, 12, 7860–7865. [Google Scholar] [CrossRef]
  19. Dietz, T.; Rosa, E.A. Rethinking the environmental impacts of population, affluence and technology. Hum. Ecol. Rev. 1994, 1, 277–300. [Google Scholar]
  20. Dietz, T.; Rosa, E.A. Effects of population and affluence on CO2 emissions. Proc. Nat. Acad. Sci. USA 1997, 1, 175–179. [Google Scholar] [CrossRef]
  21. York, R.; Rosa, E.A.; Dietz, T. STIRPAT, IPAT and ImPACT: Analytic tools for unpacking the driving forces of environmental impacts. Ecol. Econ. 2003, 3, 351–365. [Google Scholar] [CrossRef]
  22. National Bureau of Statistics of People’s Republic of China. China Energy Statistical Yearbook 2011; China Statistics Press: Beijing, China, 2012.
  23. LeSage, J.P.; Pace, R.K. An Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009; pp. 19–44. [Google Scholar]
  24. Lee, L.; Yu, J. Estimation of spatial autoregressive panel data models with fixed effects. J. Econ. 2010, 2, 165–185. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Liu, Y.; Xiao, H.; Zikhali, P.; Lv, Y. Carbon Emissions in China: A Spatial Econometric Analysis at the Regional Level. Sustainability 2014, 6, 6005-6023. https://doi.org/10.3390/su6096005

AMA Style

Liu Y, Xiao H, Zikhali P, Lv Y. Carbon Emissions in China: A Spatial Econometric Analysis at the Regional Level. Sustainability. 2014; 6(9):6005-6023. https://doi.org/10.3390/su6096005

Chicago/Turabian Style

Liu, Yu, Hongwei Xiao, Precious Zikhali, and Yingkang Lv. 2014. "Carbon Emissions in China: A Spatial Econometric Analysis at the Regional Level" Sustainability 6, no. 9: 6005-6023. https://doi.org/10.3390/su6096005

APA Style

Liu, Y., Xiao, H., Zikhali, P., & Lv, Y. (2014). Carbon Emissions in China: A Spatial Econometric Analysis at the Regional Level. Sustainability, 6(9), 6005-6023. https://doi.org/10.3390/su6096005

Article Metrics

Back to TopTop