Energy Costs of Energy Savings in Buildings: A Review
Abstract
:1. Introduction
2. Energy Return on Investment: A Revised Concept
2.1. Energy Production

2.2. Energy Saved

2.3. The Energy Ratio: Energy Return on Investment


2.4. Differences and Similarities in EROI

2.5. A Schematic Representation of the EROI Complete Concept
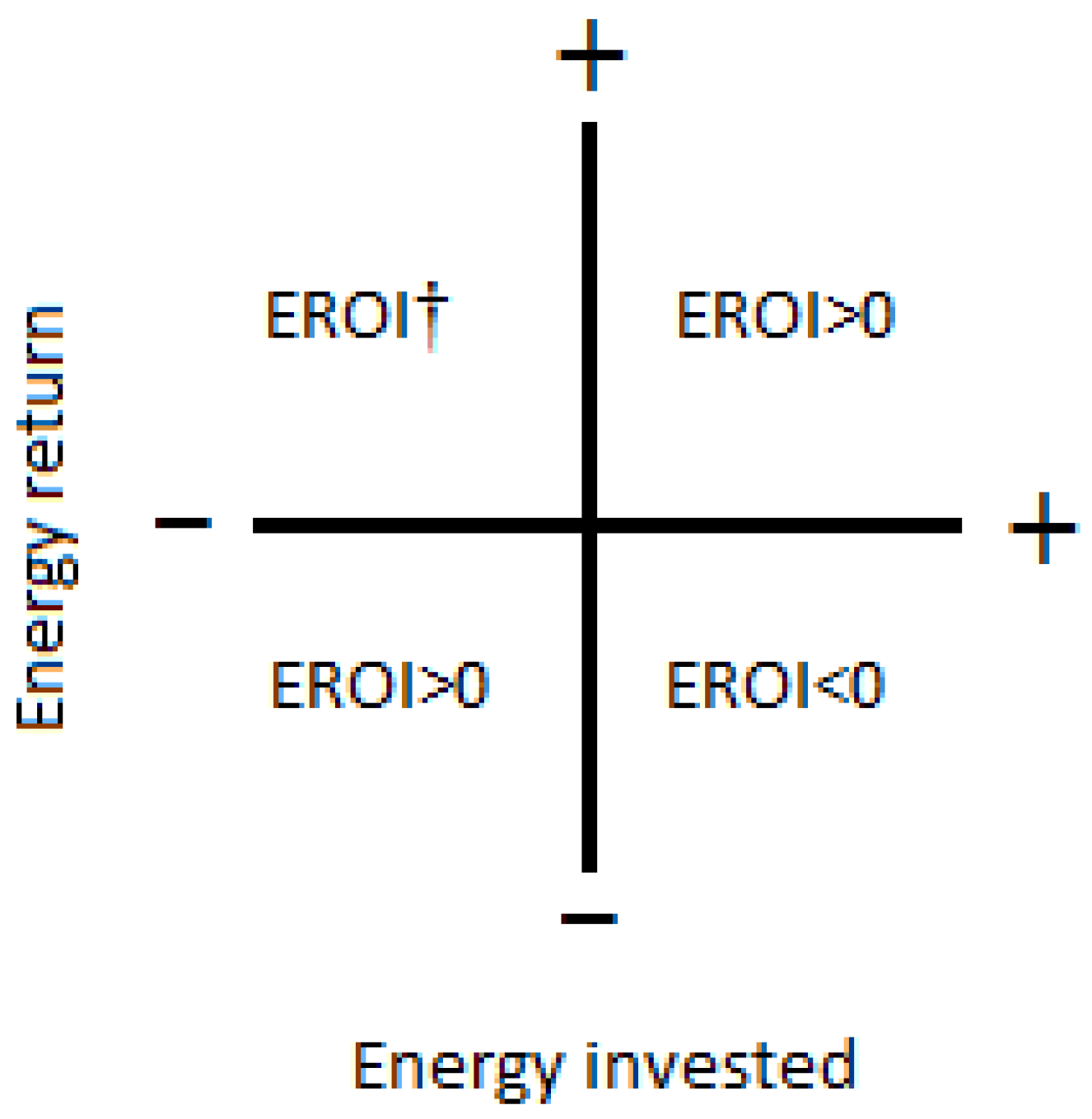
2.6. Additional Considerations
2.7. The Energy Payback Time (EPT)

2.8. Other Factors
3. Discussion Related to Specific Applications: Insulation and Windows
3.1. Insulation













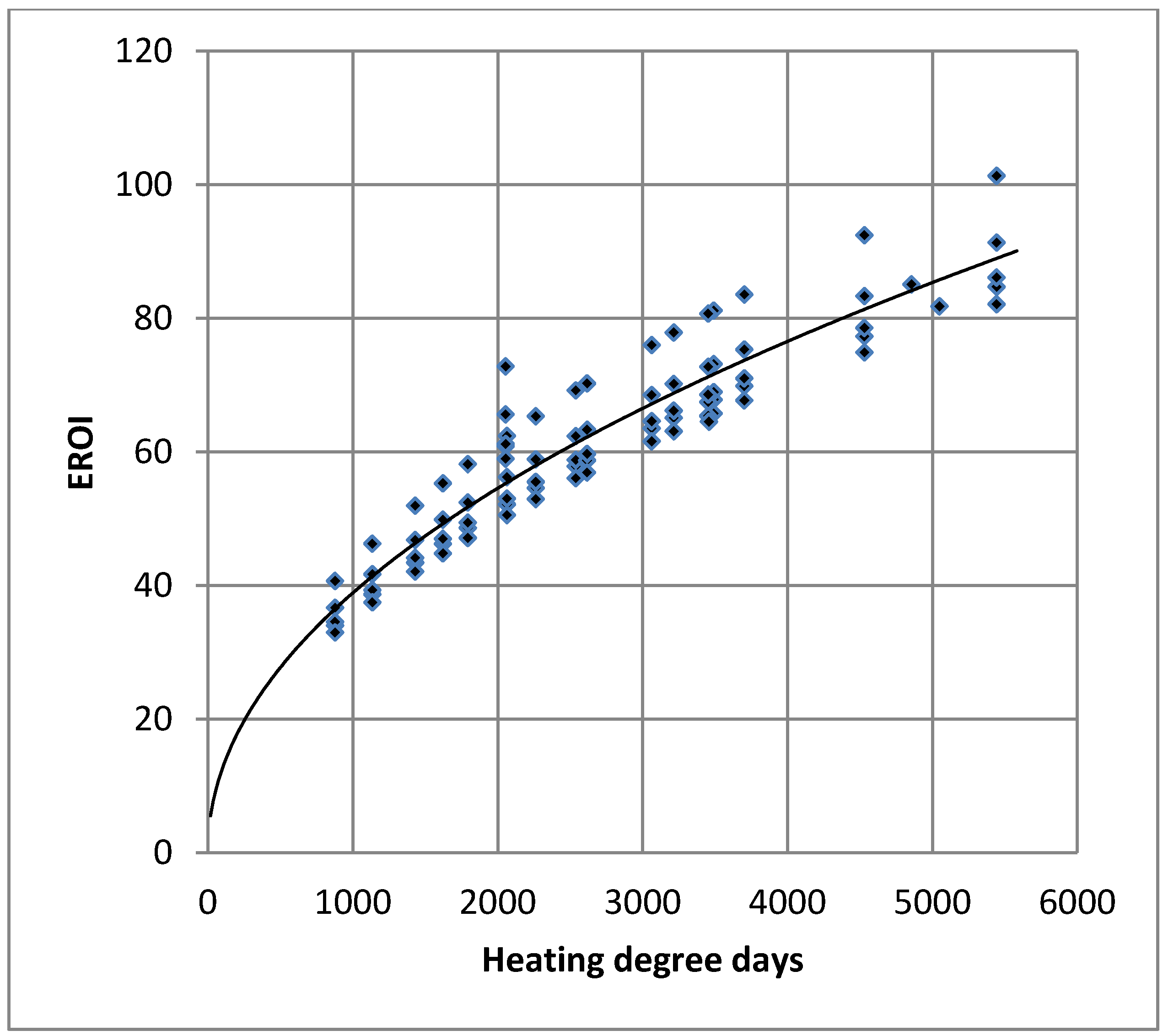
3.2. Windows
- • Addition of low-e coating on a double glazed window: EPT = 17–22 days, EROI = 592–758
- • Addition of argon to a low-e coated and doubled glazed window: EPT < 1 day, EROI = 125,000–134,000
- • Addition of krypton to a low-e coated and doubled glazed window: EPT = 4.25–11 yr, EROI = 3.2–8.2
- • Addition of a third glazing and an additional low-e coating to a low-e coated and doubled glazed window with argon filling: EPT = 1.4–1.9 yr, EROI = 18–25
- • Addition of a third glazing and an additional low-e coating and krypton to a low-e coated and doubled glazed window with argon filling: EPT = 9.6–12.8 yr, EROI = 2.7–3.6
3.3. Whole Building
4. Conclusions
Conflict of Interest
References
- IPCC, Climate Change 2007: Mitigation; Contribution of Working Group III to the Fourth Assessment Report; Cambridge University Press: Cambridge, UK, 2007.
- Kesselring, P.; Winter, C.J. World Energy Scenarios: A Two-kilowatt Society, Plausible Future or Illusion? In Proceedings of the Energietage 94, Villigen, Switzerland, 10-12 November 1994.
- Pfeiffer, A.; Koschenz, M.; Wokaum, A. Energy and building technology for the 2000 W society—Potential of residential buildings in Switzerland. Energy Build. 2005, 37, 1158–1174. [Google Scholar]
- Schulz, T.F.; Kypreos, S.; Barreto, L.; Wokaum, A. Intermediate steps towards the 2000 W society in Switzerland: An energy-economic scenario analysis. Energy Policy 2008, 36, 1303–1317. [Google Scholar] [CrossRef]
- Dixit, M.K.; Fernández-Solís, J.L.; Lavy, S.; Culp, C.H. Identification of parameters for embodied energy measurement: A literature review. Energy Build. 2010, 42, 1238–1247. [Google Scholar] [CrossRef]
- Arena, A.P.; de Rosa, C. Life cycle assessment of energy and environmental implications of the implementation of conservation technologies in school buildings in Mendoza-Argentina. Build. Environ. 2003, 38, 359–368. [Google Scholar] [CrossRef]
- Horvath, A. Construction materials and the environment. Annu. Rev. Energy Environ. 2004, 29, 181–204. [Google Scholar]
- Urge-Vorsatz, D.; Novikova, A. Opportunities and Costs of Carbon Dioxide Mitigation in the Worlds Domestic Sector. In Proceedings of the International Energy Efficiency in Domestic Appliances and Lighting Conference ’06, London, UK, 21-23 June 2006.
- Langston, Y.L.; Langston, C.A. Reliability of building embodied energy modeling: An analysis of 30 Melbourne case studies. Constr. Manag. Econ. 2008, 26, 147–160. [Google Scholar] [CrossRef]
- Lippiatt, B.C. Selecting cost effective green building products: BEES approach. J. Constr. Eng. Manag. 1999, 125, 448–455. [Google Scholar] [CrossRef]
- Tommerup, H.; Rose, J.; Svendsen, S. Energy-efficient houses built according to the energy performance requirements introduced in Denmark in 2006. Energy Build. 2007, 39, 1123–1130. [Google Scholar] [CrossRef]
- Ding, G. The Development of a Multi-criteria Approach for the Measurement of Sustainable Performance for Built Projects and Facilities. Ph.D. Thesis, University of Technology, Sydney, Australia, 2004. [Google Scholar]
- Asif, M.; Muneer, T.; Kelley, R. Life cycle assessment: A case study of a dwelling home in Scotland. Build. Environ. 2007, 42, 1391–1394. [Google Scholar] [CrossRef]
- Campogrande, D. The European Construction Industry—Facts and Trends. In Proceedings of the ERA Convention; European Construction Industry Federation (FIEC), Berlin, Germany: 5-6 June 2007.
- European Parliament, Report on the Proposal for a Directive of the European Parliament and of the Council on the Energy Performance of Buildings (Recast); COM(2008)0780-C6-0413/2008-2008/0223(COD); European Parliament: Bruxelles, Belgium, 2009 April 6.
- Règlementation Thermique. 2012. Available online: http://www.rt-batiment.fr/batiments-neufs/reglementation-thermique-2012/presentation.html (accessed on 4 July 2012).
- A National Programme for Energy Efficiency and Energy-Smart Construction. Swedish Government Bill. 2005. Available online: http://www.regeringen.se/sb/d/574/a/63635 (accessed on 4 July 2012).
- Harvey, L.D.D. Reducing energy use in the buildings sector: Measures, costs, and example. Energy Effic. 2009, 2, 139–163. [Google Scholar] [CrossRef]
- Hall, C.A.S. Migration and metabolism in a temperate stream ecosystem. Ecology 1972, 53, 585–604. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Cleveland, C.J. Petroleum drilling and production in the U.S.: Yield per effort and net energy analysis. Science 1981, 211, 576–579. [Google Scholar]
- Cleveland, C.J.; Costanza, R.; Hall, C.A.S.; Kaufmann, R. Energy and the U.S. economy: A biophysical perspective. Science 1984, 225, 890–897. [Google Scholar]
- Hall, C.A.S.; Cleveland, C.J.; Kaufmann, R. Energy and Resource Quality: The Ecology of the Economic Process; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Hall, C.A.S.; Powers, R.; Schoenberg, W. Peak Oil, EROI, Investments and the Economy in an Uncertain Future. In Renewable Energy Systems: Environmental and Energetic Issues; Pimentel, D., Ed.; Elsevier: London, UK, 2008; pp. 113–136. [Google Scholar]
- Huijbregts, M.A.; Hellweg, S.; Frischknecht, R.; Hendriks, H.W.; Hungerbühler, K.; Hendriks, A.J. Cumulative energy demand as predictor for the environmental burden of commodity production. Environ. Sci. Technol. 2010, 44, 2189–2196. [Google Scholar]
- Ulgiati, S.; Raugei, M.; Bargigli, S. Overcoming the inadequacy of single-criterion approaches to Life Cycle Assessment. Ecol. Model. 2006, 190, 432–442. [Google Scholar] [CrossRef]
- Svensson, N.; Roth, L.; Eklund, M.; Mårtensson, A. Environmental relevance and use of energy indicators in environmental management and research. J. Clean. Prod. 2006, 14, 134–145. [Google Scholar] [CrossRef]
- Mulder, K.; Hagens, N.J. Energy return on investment: Toward a consistent framework. AMBIO 2008, 37, 74–79. [Google Scholar] [CrossRef]
- Gagnon, L. Civilisation and energy payback. Energy Policy 2008, 36, 3317–3322. [Google Scholar] [CrossRef]
- Hall, C.A.S.; Balogh, S.; Murphy, D.J.R. What is the minimum EROI that a sustainable society must have? Energies 2009, 2, 25–47. [Google Scholar] [CrossRef]
- Polimeni, J.M.; Mayumi, K.; Giampietro, M.; Alacott, B. The Myth of Resource Efficiency; Earthscan: London, UK, 2009. [Google Scholar]
- Hammond, G.; Jones, C. Embodied Carbon - The Inventory of Carbon and Energy (ICE); Lowrie, F., Tse, P., Eds.; University of Bath with BSRIA: Bath, UK, 2011. [Google Scholar]
- Hernandez, P.; Kenny, P. Zero Energy Houses and Embodied Energy: Regulatory and Design Considerations. In Proceedings of the American Society of Mechanical Engineering 2nd International Conference on Energy Sustainability; Jacksonville, FL, USA: 10-14 August 2008.
- Hernandez, P.; Kenny, P. Defining Zero Energy Buildings—A life cycle perspective. In Proceedings of the PLEA 2008—25th Conference on Passive and Low Energy Architecture, Dublin, Ireland, 22-24 October 2008.
- Kellenberger, D.; Althaus, H.G. Relevance of simplifications in LCA of building components. Build. Environ. 2009, 44, 818–825. [Google Scholar] [CrossRef]
- ISO, Buildings and Constructed Assets—Service-Life Planning—Part 8: Reference Service Life and Service-Life Estimation; ISO 15686-8:2008; International Organization for Standardization (ISO): Geneva, Switzerland, 2008.
- Sartori, I.; Hestnes, A.G. Energy use in the life cycle of conventional and low-energy buildings: A review article. Energy Build. 2007, 39, 249–257. [Google Scholar] [CrossRef]
- Massachusetts Institute of TechnologyEnergy LaboratoryEnergy Technology Availability: Review of Longer Term Scenarios for Development and Deployment of Climate-Friendly Technologies; Massachusetts Institute of Technology, Energy Laboratory: Cambridge, MA, USA, 1997.
- Gregory, A.N.; Yost, P. A transparent, interactive software environment for communicating life cycle assessment results: An application to residential windows. J. Ind. Ecol. 2002, 5, 15–28. [Google Scholar]
- Paulsen, J.H.; Borg, M. A building sector related procedure to assess the relevance of the usage phase. Int. J. Life Cycle Assess. 2003, 8, 142–150. [Google Scholar] [CrossRef]
- Johnston, D. A Physically Based Energy and Carbon Dioxide Emission Model of the UK Housing Stock. Ph.D. Thesis, Leeds Metropolitan University, Leeds, UK, 2003. [Google Scholar]
- Khasreen, M.M.; Banfill, P.F.G.; Menzies, G.F. Life-cycle assessment and the environmental impact of buildings: A review. Sustainability 2009, 1, 674–701. [Google Scholar] [CrossRef]
- Guinée, J.B. Life Cycle Assessment: An Operational Guide to the ISO Standards; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Van Oers, L.; de Koning, A.; Guinée, J.B.; Huppes, G. Improving Characterisation Factors for Abiotic Resource Depletion as Recommended in the New Dutch LCA Handbook; Roads and Hydraulic Engineering Institute: Leiden, The Netherlands, 2002. [Google Scholar]
- Habert, G.; Bouzidi, Y.; Chen, C.; Jullien, A. Development of a depletion indicator for natural resources used in concrete. Resour. Conserv. Recy. 2010, 54, 364–376. [Google Scholar] [CrossRef]
- Habert, G.; Castillo, E.; Morel, J.C. Sustainable Indicators for Resources and Energy in Building Construction. In Proceedings of the Second International Conference on Sustainable Construction Materials and Technologies, Ancona, Italy, 28-30 June 2010.
- Muncey, R.W. Optimum thickness of insulation for Australian houses. Aust. J. Appl. Sci. 1955, 6, 486–495. [Google Scholar]
- Molnar, J.; Armitage, J.B. Determination of economic thickness of insulation. J. Inst. Engng. Ans. 1968, 40, 129. [Google Scholar]
- Barnhart, J.M. Economic thickness of thermal insulation. Chem. Eng. Prog. 1974, 70, 50. [Google Scholar]
- Brundrett, G.W. Some effects of thermal insulation on design. Appl. Energy 1975, 1, 7–30. [Google Scholar] [CrossRef]
- Probert, S.D.; Giani, S. Economics of thermal insulation. Appl. Energy 1976, 2, 189–204. [Google Scholar] [CrossRef]
- Probert, S.D.; Thirst, T.J. Thermal insulation provided by triangular sectioned attic spaces. Appl. Energy 1977, 3, 41–50. [Google Scholar] [CrossRef]
- Anani, A.; Jibril, Z. Role of thermal insulation in passive designs of buildings. Sol. Wind Techchnol. 1988, 5, 303–313. [Google Scholar] [CrossRef]
- Hasan, A. Optimizing insulation thickness for buildings using life cycle cost. Appl. Energy 1999, 63, 115–124. [Google Scholar] [CrossRef]
- Gustafsson, G. Optimisation of insulation measures on existing buildings. Energy Build. 2000, 33, 49–55. [Google Scholar] [CrossRef]
- Chaumont, D.; Angers, J.-F.; Frigon, A.; Pacher, G.; Roy, R. Évolution des Conditions Climatiques au Québec, Développement d’un Scenario Climatique Utilisé à des Fins de Prévision de la Demande d’Électricité au Québec sur l’Horizon 2030 (in French); Consortium Ouranos: Montreal, QC, Canada, 2007. [Google Scholar]
- Frank, T. Climate change impacts on building heating and cooling energy demand in Switzerland. Energy Build. 2005, 37, 1175–1185. [Google Scholar] [CrossRef]
- Gaterell, M.R.; McEvoy, M.E. The impact of energy externalities on the cost effectiveness of energy efficiency measures applied to dwellings. Energy Build. 2005, 37, 1017–1027. [Google Scholar] [CrossRef]
- Wang, X.; Chen, D.; Ren, Z. Assessment of climate change impact on residential building heating and cooling energy requirement in Australia. Build. Environ. 2010, 45, 1663–1682. [Google Scholar] [CrossRef]
- De Wilde, P. The implications of a changing climate for buildings. Build. Environ. 2012, 55, 1–7. [Google Scholar] [CrossRef]
- De Wilde, P.; Tian, W. Management of thermal performance risks in buildings subject to climate change. Build. Environ. 2012, 55, 167–177. [Google Scholar] [CrossRef]
- Feist, W. Life-Cycle Energy Balances Compared: Low-Energy House,Passiv House,Self-Sufficient House. In Proceedings of the International Symposium of CIB W67, International Council for Building Research, Vienna, Austria, 4-10 August 1996; pp. 183–190.
- Szalay, A.Z.-Z. What is missing from the concept of the new European Building Directive. Build. Environ. 2006, 42, 1781–1769. [Google Scholar]
- Comaklı, K.; Yüksel, B. Optimum insulation thickness of external walls for energy saving. Appl. Therm. Eng. 2003, 23, 473–479. [Google Scholar] [CrossRef]
- Bolattürk, A. Determination of optimum insulation thickness for building walls with respect to various fuels and climate zones in Turkey. Appl. Therm. Eng. 2006, 26, 1301–1309. [Google Scholar] [CrossRef]
- Dombaycı, Ö.A.; Gölcü, M.; Pancar, Y. Optimization of insulation thickness for external walls using different energy-sources. Appl. Energy 2006, 83, 921–928. [Google Scholar] [CrossRef]
- Kurt, H. The usage of air Gap in the composite wall for energy saving and air pollution. Environ. Prog. Sustain. Energy 2011, 30, 450–458. [Google Scholar] [CrossRef]
- Daouas, N.; Hassen, Z.; Ben Aissia, H. Analytical periodic solution for the study of thermal performance and optimum insulation thickness of building walls in Tunisia. Appl. Therm. Eng. 2010, 30, 319–326. [Google Scholar] [CrossRef]
- Daouas, N. A study on optimum insulation thickness in walls and energy savings in Tunisian buildings based on analytical calculation of cooling and heating transmission loads. Appl. Energy 2011, 88, 156–164. [Google Scholar] [CrossRef]
- Mahlia, T.M.I.; Iqbal, A. Cost benefits analysis and emission reductions of optimum thickness and air gaps for selected insulation materials for building walls in Maldives. Energy 2010, 35, 2242–2250. [Google Scholar] [CrossRef]
- Harvey, L.D.D. Net climatic impact of solid foam insulation produced with halocarbon and non-halocarbon blowing agents. Build. Environ. 2007, 42, 2860–2879. [Google Scholar] [CrossRef]
- Bribián, I.Z.; Uséon, A.A.; Scarpellini, S. Life cycle assessment in buildings: State-of-the-art and simplified LCA methodology as a complement for building certification. Build. Environ. 2009, 44, 2510–2520. [Google Scholar] [CrossRef]
- Masoso, O.T.; Grobler, L.J. A new and innovative look at anti-insulation behaviour in building energy consumption. Energy Build. 2008, 40, 1889–1894. [Google Scholar] [CrossRef]
- Huberman, N. Life Cycle Energy Costs of Building Materials: Alternatives for a Desert Environment. M.Sc. Thesis, Ben-Gurion University of the Negev, Beer-Sheva, Israel, 2007. [Google Scholar]
- Pulselli, R.M.; Simoncini, E.; Marchettini, N. Energy and emergy based cost-benefit evaluation of building envelopes relative to geographical location and climate. Build. Environ. 2009, 44, 920–928. [Google Scholar] [CrossRef]
- Utama, A.; Gheewala, S.H. Indonesian residential high rise buildings: A life cycle energy assessment. Energy Build. 2009, 41, 1263–1268. [Google Scholar] [CrossRef]
- Saito, M.; Shukuya, M. Energy and material use in the production of insulating glass windows. Solar Energy 1996, 58, 247–252. [Google Scholar] [CrossRef]
- Weir, G. Life Cycle Assessment of Multi-Glazed Windows. Ph.D. Thesis, Napier University, Napier, Australia, 1998. [Google Scholar]
- Weir, G.; Muneer, T. Energy and environmental impact analysis of double-glazed windows. Energy Convers. Manag. 1998, 39, 243–256. [Google Scholar] [CrossRef]
- Baumert, K.; Selman, M. Heating and Cooling Degree Days; World Resources Institute: Washington, DC, USA, 2003. [Google Scholar]
- Menzies, G.F.; Wherrett, J.R. Multiglazed windows: Potential for savings in energy, emissions and cost. Build. Serv. Eng. Res. Technol. 2005, 26, 249–258. [Google Scholar] [CrossRef]
- Asif, M.; Muneer, T.; Kubie, J. Sustainability analysis of window frames. Build. Serv. Eng. Res. Technol. 2005, 26, 71–87. [Google Scholar] [CrossRef]
- Sedovic, W.; Gorrhelf, J.H. What replacement windows can’t replace: The real cost of removing historic windows. APT Bull. J. Preserv. Technol. 2005, 36, 25–29. [Google Scholar]
- Recio, J.M.B.; Narvaez, R.P.; Guerrero, P.J. Estimate of energy consumption and CO2 emission associated with the production, use and final disposal of PVC, aluminium, and wooden windows. Département de Projectes d’Engineyeria, Universitat Politecnica de Catalunya, Environmental Modelling Lab., Barcelona, Spain, 2005. Available online: http://www.pvcinfo.be/bestanden/Baldasano%20study_windows.pdf (accessed on 4 July 2012).
- Dahlstrøm, O. Modern Highly Effective Windows; Report; NTNU: Trondheim, Sweden, 2010. [Google Scholar]
- Ramesh, T.; Prakash, R.; Shukla, K.K. Life cycle energy analysis of buildings: An overview. Energy Build. 2010, 42, 1592–1600. [Google Scholar] [CrossRef]
- Keoleian, G.A.; Blanchard, S.; Reppe, P. Life-cycle energy, costs, and strategies for improving a single-family house. J. Ind. Ecol. 2001, 4, 135–156. [Google Scholar]
- Uzsilaityte, L.; Martinaitis, V. Impact of the Implementation Energy Saving Measure on the Life Cycle Energy Consumption of the Building. In Proceedings of the 7th International Conference Environmental Engineering, Vilnius Gediminas Technical University, Vilnius, Lithuania, 22-23 May 2008.
- Yohanis, Y.G.; Norton, B. Life-cycle operational and embodied energy for a generic single-storey office building in the UK. Energy 2002, 27, 77–92. [Google Scholar] [CrossRef]
- Verbeeck, G.; Hens, H. Life cycle inventory of buildings: A contribution analysis. Build. Environ. 2010, 45, 964–967. [Google Scholar] [CrossRef]
- Gustavsson, L.; Joelsson, A. Life cycle primary energy analysis of residential buildings. Energy Build. 2010, 42, 210–220. [Google Scholar] [CrossRef]
- Ardente, F.; Beccali, M.; Cellura, M.; Mistretta, M. Energy and environmental benefits in public buildings as a result of retrofit actions. Renew. Sustain. Energy Rev. 2011, 15, 460–470. [Google Scholar] [CrossRef]
- Fay, R.; Treloar, G.; Iyer-Raniga, U. Life-cycle energy analysis of buildings: A case study. Build. Res. Inf. 2000, 28, 31–41. [Google Scholar] [CrossRef]
- Karlsson, J.F.; Moshfegh, B. A comprehensive investigation of a low-energy building in Sweden. Renew. Energy 2007, 32, 1830–1841. [Google Scholar] [CrossRef]
- Hernandez, P.; Cavanagh, S.; Brophy, V.; Futcher, J.; Szalay, Z.; Kenney, P. The Challenge of Refurbishing recentely Built Apartments: A Life Cycle Perspective. In Proceedings of the Paper Presented at the SB10mad: International Sustainable Building Conference, Madrid, Spain, 28-30 April 2010.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dutil, Y.; Rousse, D. Energy Costs of Energy Savings in Buildings: A Review. Sustainability 2012, 4, 1711-1732. https://doi.org/10.3390/su4081711
Dutil Y, Rousse D. Energy Costs of Energy Savings in Buildings: A Review. Sustainability. 2012; 4(8):1711-1732. https://doi.org/10.3390/su4081711
Chicago/Turabian StyleDutil, Yvan, and Daniel Rousse. 2012. "Energy Costs of Energy Savings in Buildings: A Review" Sustainability 4, no. 8: 1711-1732. https://doi.org/10.3390/su4081711
APA StyleDutil, Y., & Rousse, D. (2012). Energy Costs of Energy Savings in Buildings: A Review. Sustainability, 4(8), 1711-1732. https://doi.org/10.3390/su4081711



