Design and Evaluation of a CO₂ Liquefaction and Liquid-Phase Compression System for Decarbonized Coal-Fired Power Plants

Abstract

This study investigates the energy performance and preliminary turbomachinery design of post-combustion CO₂ compression systems integrated into an ultra-supercritical coal-fired power plant with carbon capture and storage (CCS). To enable pipeline transport, CO₂ must be delivered at 150 bar and 15 °C, i.e., in liquid phase. Unlike conventional configurations that compress CO₂ entirely in the gaseous/supercritical phase before final cooling, two alternative layouts are proposed, introducing an intermediate liquefaction step prior to liquid-phase compression. Each layout uses a chiller system that operates at CO₂ condensation temperatures of 10 °C and 20 °C. The energy performance and the system layout architecture are evaluated and compared with the conventional gaseous-phase compression configuration. An in-depth sensitivity analysis, which varies the flow coefficient, the working coefficient, and the degree of reaction, confirms that the turbomachinery preliminary design, based on input parameters related to the specific speed, is a high-efficiency design. The results indicate that the 10 °C liquefaction layout requires the least compression power (60 MW), followed by the 20 °C layout (62.5 MW) and the conventional system (67 MW). Including the consumption of the chiller, the proposed systems require an additional power of 11–12 MW, compared to just over 1 MW for the conventional layout with simple CO₂ cooling. These results highlight the significant influence of the integration of the chiller on the overall power requirement of the system. Although the proposed configurations result in a larger equipment footprint, the integrated capture and compression/liquefaction system allows for very low CO₂ emissions, making the power plant more sustainable.

1. Introduction

The consequences of climate change constitute one of the foremost global challenges of the 21st century, necessitating transformative mitigation and adaptation measures to strengthen system resilience and facilitate the transition to a low-carbon economy [1,2]. Addressing this complex challenge requires not only substantial emission reductions and large-scale deployment of renewable energy, but also the adoption of complementary strategies aimed at enhancing sustainability, fostering a structural transformation of the energy system, and ensuring progress toward international climate goals [1,3]. Meeting the “net-zero emissions” target outlined in the Paris Agreement (2015) [3] requires going beyond conventional mitigation strategies, by integrating carbon capture solutions combined with utilization and/or storage (CCUS) [4]. Industrial emissions are particularly challenging, as growing demand for industrial products is expected to increase GHG emissions while abatement options remain limited [5]. Efficiency improvements and low-carbon energy inputs (e.g., electrification or hydrogen) can reduce energy-related emissions, but not process-related ones, making industry a hard-to-abate sector [6]. CCUS offers a promising solution, capable of removing up to 90–99% of energy-related and process emissions, and its limited deployment has prompted strong investment from governments, industry, and research institutions to accelerate its development [6,7,8]. In Europe, significant financial resources have been allocated to support the development and deployment of CCUS technologies [9]. This commitment is exemplified by several high-profile projects, such as the Northern Lights project [10], the 3D initiative by ArcelorMittal [11], the HyNet cluster in Northwest England [12], and the Ravenna Hub led by SNAM and ENI [13], reflecting the region’s proactive efforts to advance large-scale decarbonization through carbon capture, utilization, and storage. Furthermore, Celanese Corporation, in partnership with Mitsui & Co., Ltd., has launched a CCU initiative under the Fairway Methanol joint venture [14]. In parallel, major CO₂ storage projects such as Bifrost in Denmark [15], Aramis in the Netherlands [16] and Iroko in Norway [17] are currently under development.

CCUS technology involves three sequential stages. The first stage is carbon capture, which can be achieved through various approaches, including pre-combustion, post-combustion, and oxy-fuel combustion [2]. The second stage involves compressing CO₂ to make it ‘transport-ready’, typically at a temperature of 15 °C and a pressure of 150 absolute bar [18]. Finally, the third stage concerns either the utilization of CO₂ (CCU) or its storage (CCS) or both (CCUS) [19,20]. With respect to CCU, it is well established that captured CO₂ can be converted into e-fuels [21].

The authors have pursued an extensive research agenda in the power generation field, with a particular focus on the rigorous performance characterization of plants integrating CO₂-mitigation frameworks. Their investigations have encompassed both traditional and advanced thermodynamic configurations [22]. In these investigations, the CO₂ capture and compression/liquefaction units were assessed through a black-box analysis framework. Nevertheless, a comprehensive evaluation of the compression and liquefaction processes is crucial, considering their substantial influence on the overall energy performance of the plant and the spatial demands of their implementation.

Another critical component of CCUS systems relates to the transportation of CO₂ from emission sources to storage or utilization sites. Existing studies indicate that pipeline-based CO₂ conveyance, particularly when operated in the supercritical regime, constitutes the most robust and cost-effective option for transporting large mass flows across intermediate distances, generally below approximately 1000 km [18,23]. Regarding the compression phase, CO₂ can be pressurized through different pathways. For instance, in the previous study [24], the authors developed a preliminary design of turbomachinery based on multi-stage gaseous compression, ultimately achieving supercritical conditions. On the other hand, the compression pathway may involve liquefaction of CO₂ at a specified pressure after the initial stages, with the subsequent compression performed in the liquid phase to reach the pressure required for ‘transport-ready’ conditions. Implementation of this pathway requires the integration of a chiller system into the compression process. In relation to the chiller system, various solutions are currently available, differing in the type of working fluid and the thermodynamic cycle employed, such as transcritical or subcritical configurations [25,26]. Selecting the working fluid is critical for both chiller performance and reducing its impact on climate change [27]. In fact, according to Montreal protocol [28], the selection of refrigerants must take into account their ODP and GWP values [27]. Natural refrigerants have recently emerged as very promising alternatives, particularly in the context of mitigating climate change [26]. Among the most widely recognized natural refrigerants are carbon dioxide (R-744) and ammonia (R-717) [29,30]. Water (R-718) and air (R-729) are also environmentally benign refrigerants; however, their practical application is limited by the large size of system components required and the relatively low coefficients of performance (COP) that can be achieved [30]. Therefore, in this work, the authors selected ammonia as the refrigerant, operating in a subcritical cycle. In addition to its positive environmental effects, the use of ammonia is characterized by very low power consumption and the ability to provide a significant cooling/heating capacity [31].

Based on these considerations, this paper focuses on exploring alternative compression pathways within the context of CCS applications integrated into a power plant (Figure 1). Two different pathways are proposed, both of which involve the liquefaction of CO₂ following an initial compression phase. The main distinction between these two alternatives is the CO₂ condensing pressure, which influences the system performance and design requirements of compressors and pumps to achieve the CO₂ ‘transport-ready’ condition. Compared to existing literature, this study reports the complete outcomes of the preliminary compressor and pump design, outlining the kinematic and thermodynamic parameters of each turbomachinery stage, the geometric parameters to assess the spatial requirements of the proposed solutions, and the isentropic efficiency. In addition, a sensitivity analysis was carried out on the centrifugal compressors designed to evaluate the influence of key parameters, including flow rate coefficients, blade loading coefficients, and degree of reaction, on compressor performance. Finally, the alternative proposed in the previous work [24], based on IGC solution, is compared with those presented in this paper in order to identify the optimal compression/liquefaction configuration for achieving the CO₂ ‘transport-ready’ condition in terms of energy consumption.

The case study focuses on an advanced ultra-supercritical steam power plant, RDK8 Rheinhafen-Dampfkraftwerk in Karlsruhe, Germany, which features a nominal net thermal efficiency of 47.5% and a net electrical output of 919 MW. Among coal-fired steam power plants in operation today, RDK8 exhibits the highest efficiency worldwide. It is assumed that the power plant is equipped with a post-combustion capture unit capable of capturing 90% of the CO₂ emissions.

Figure 1. Scheme of CCS process integrated in a power plant [24].

Figure 1. Scheme of CCS process integrated in a power plant [24].

The authors implemented custom MATLAB 2024b codes and integrated NIST Refprop [32] sub-routine to accurately evaluate the thermodynamic properties of the process working fluids. The paper is organized as follows. Section 2 first provides a brief description of the case study, then presents the thermodynamic analysis, followed by the preliminary design of the pumps, and concludes by highlighting the main design parameters and assumptions used to evaluate the refrigeration systems. 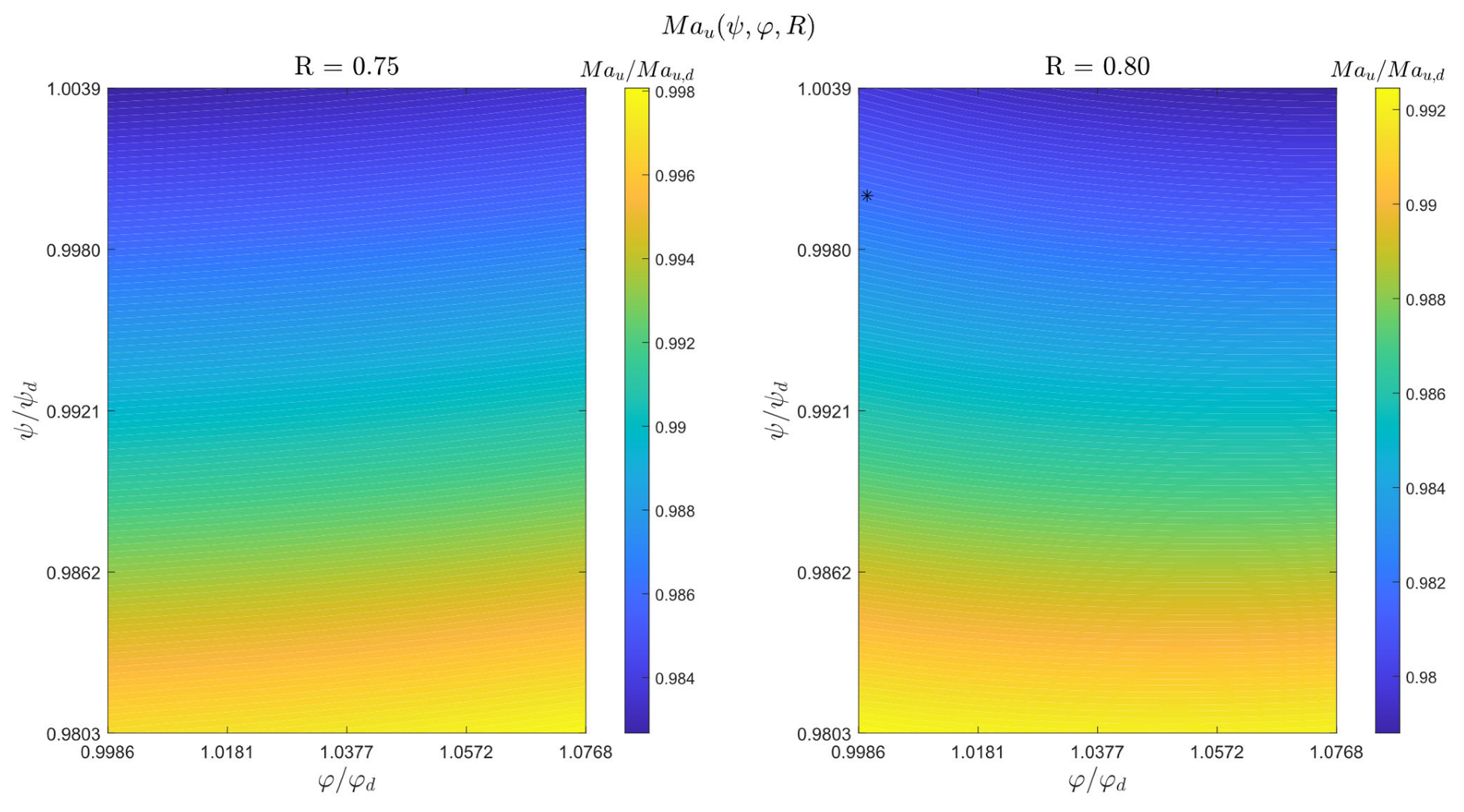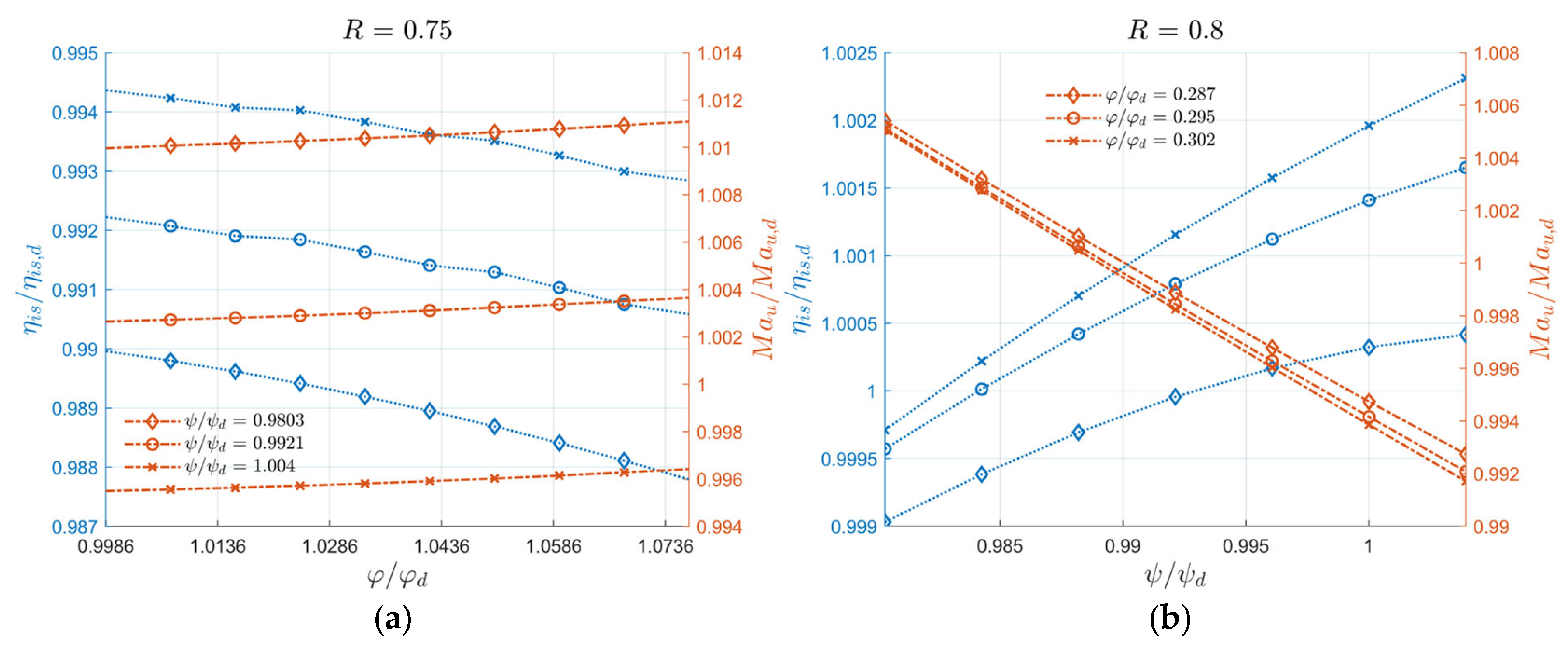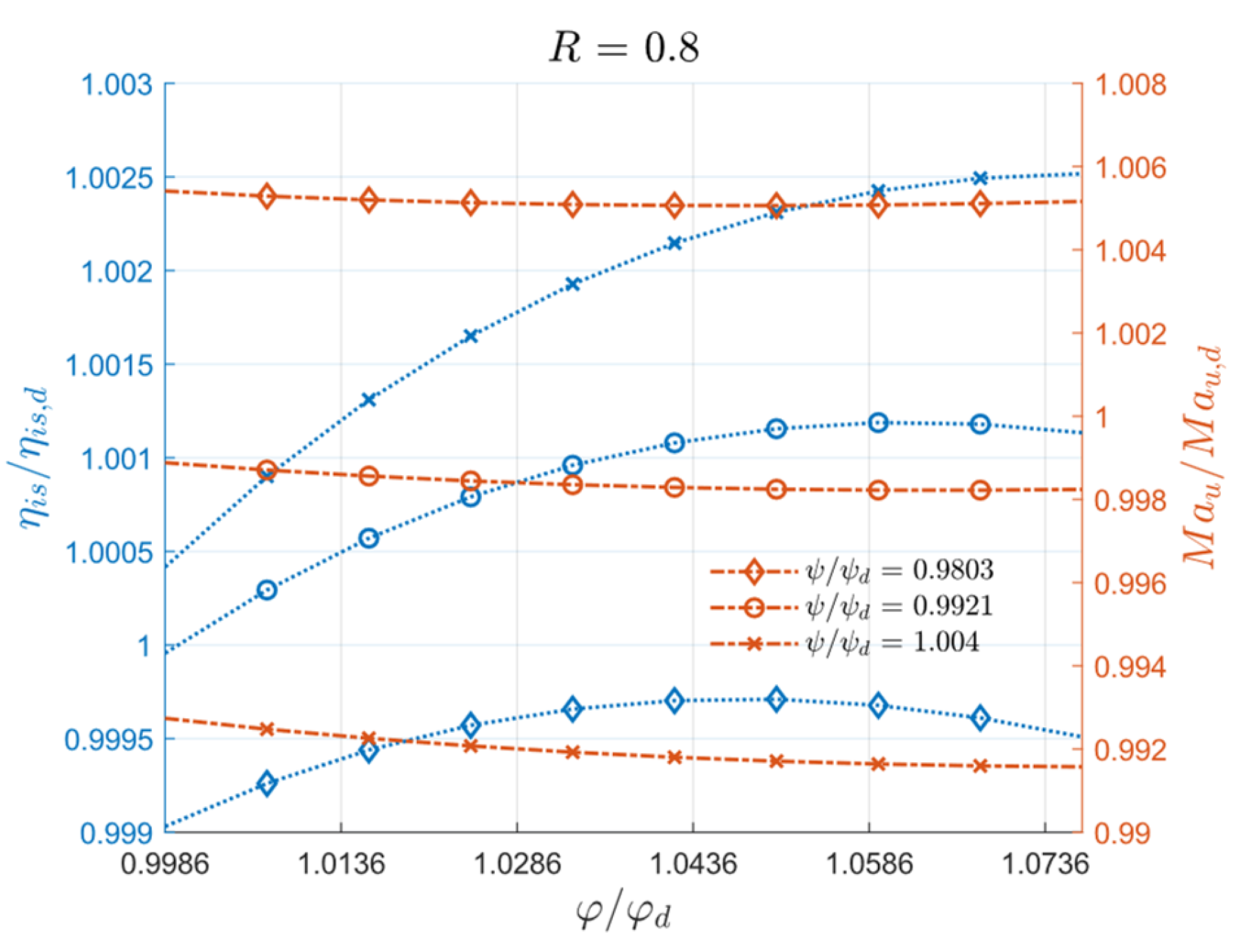Section 3 presents the results, beginning with the selection of compressors and pumps, followed by the preliminary pump design. It then reports the performance of the refrigeration systems for the three compression pathways and concludes with a sensitivity analysis on turbomachinery design, focusing on peripheral Mach number, isentropic efficiency, and Mach at inlet conditions, and the energy balance of the proposed layouts.

2. Materials and Methods

2.1. Case Study

As outlined in the introduction, this paper examines the CO₂ compression system of an advanced ultra-supercritical coal-fired steam power plant, specifically the RDK8 Rhein-hafen-Dampfkraftwerk located in Karlsruhe, Germany [33]. It is important to highlight that the CO₂ separation process employed corresponds to post-combustion capture technology (Figure 1). The parameters used for quantifying the amount of CO₂ generated and subsequently separated are summarized in

Table 1. RDK8’s performance and operational parameters (adapted from [34]).

RDK8 Steam Power
Power (MW)	P	919
Annual net thermal efficiency (%)	${\eta }_{net}$	46.5
Annual boiler efficiency (%)	${\eta }_{boiler}$	92
Equivalent operating hours	EOH	7000
Carbon dioxide emission factor (t/TJ)	EF	104.55

.

The CO₂ mass flow rate in the compression system has been evaluated in the previous work [24] and it is approximately equal to 200 kg/s.

2.2. Thermodynamic Analysis

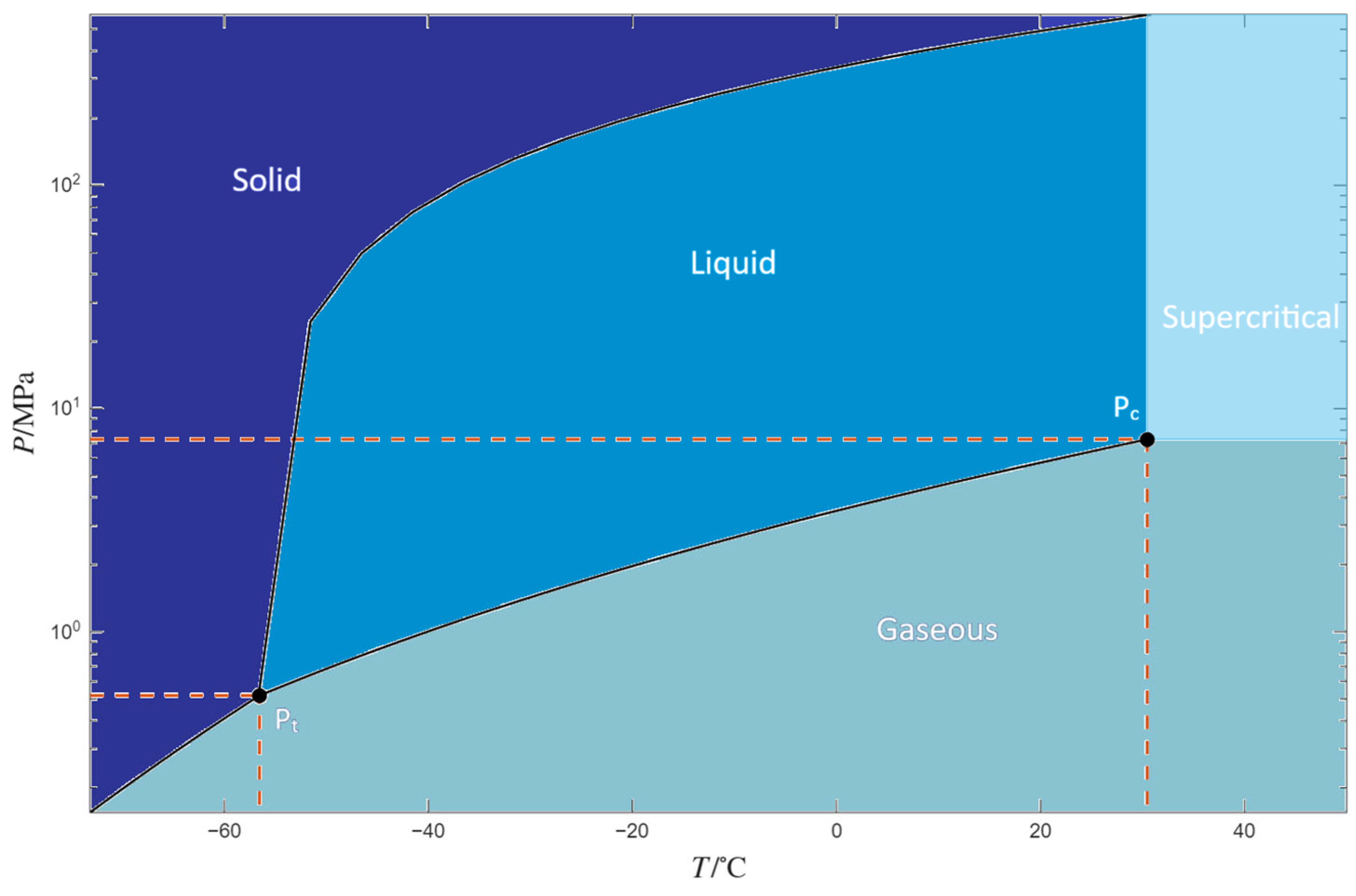
To achieve transport-ready conditions, CO₂ must be in the liquid phase. In the authors’ previous work, the compression process was analyzed under supercritical gaseous conditions, since the minimum temperature was set at 35 °C. Figure 2 shows the CO₂ phase diagram. In the present study, the effect of CO₂ liquefaction at an intermediate pressure—ranging between 40 and 60 absolute bar—is investigated to assess the system’s energy consumption and the complexity of the plant layout (in terms of the number of machines and compression stages).

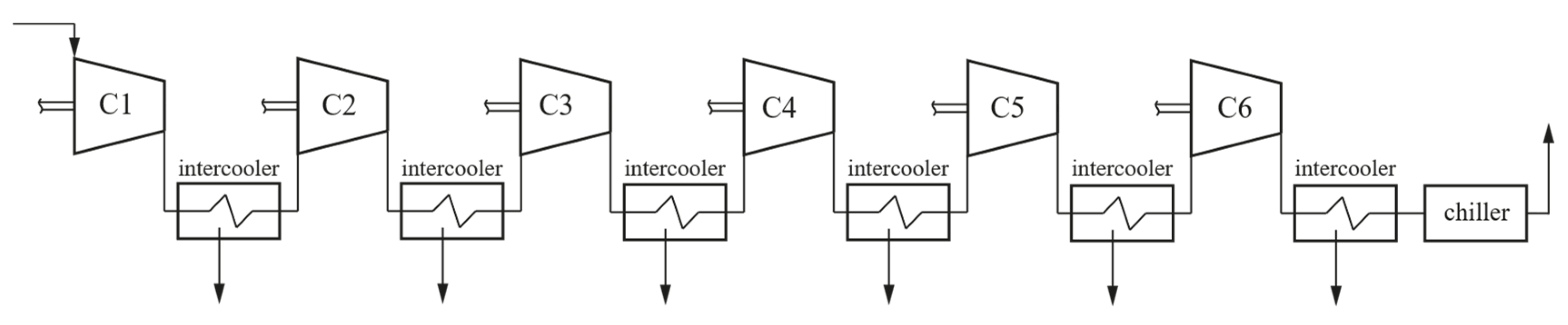
To enable a fair comparison between the configurations analyzed in this study and those presented in the previous work, the same arrangement of the first four compressors in the six-stage scheme has been maintained (Figure 3). In addition, it is worth noting that only the IGC configuration has been considered, as previous work [24] demonstrated advantages such as compactness with respect to both dimensions and stages.

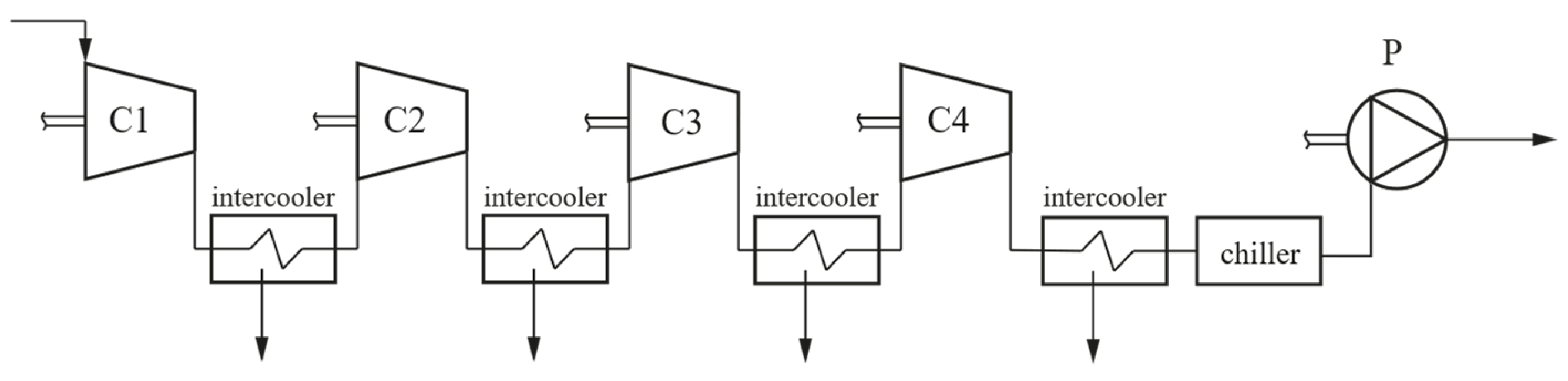
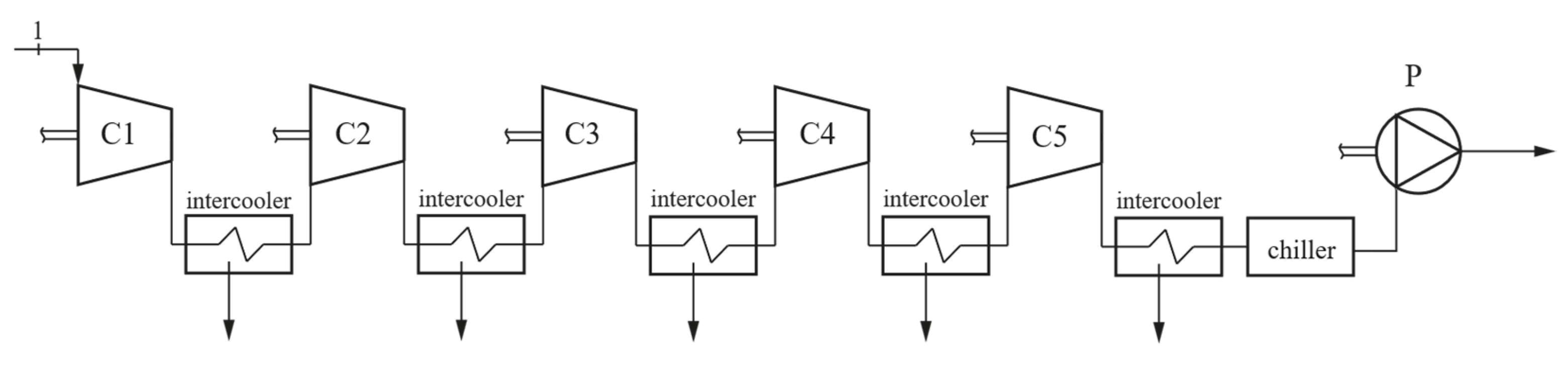
Two alternative system configurations have been proposed. In the first one (Figure 4), the transport-ready condition is achieved through an intercooled phase following the fourth compression phase, a chiller system, and a pump. In the second configuration (Figure 5), an additional compression process in gaseous phase and an intercooled phase are introduced before the chiller system and the final pumping process. Therefore, the main difference between the two proposed configurations lies in the distinct CO₂ condensation temperatures, set at 10 °C for the first configuration and 20 °C for the second, both values being compatible with refrigeration systems.

Figure 2. CO₂ phase diagram.

Figure 2. CO₂ phase diagram.

Figure 3. Analyzed plant layout scheme 0.

Figure 3. Analyzed plant layout scheme 0.

Figure 4. Analyzed plant layout scheme 1.

Figure 4. Analyzed plant layout scheme 1.

Figure 5. Analyzed plant layout scheme 2.

Figure 5. Analyzed plant layout scheme 2.

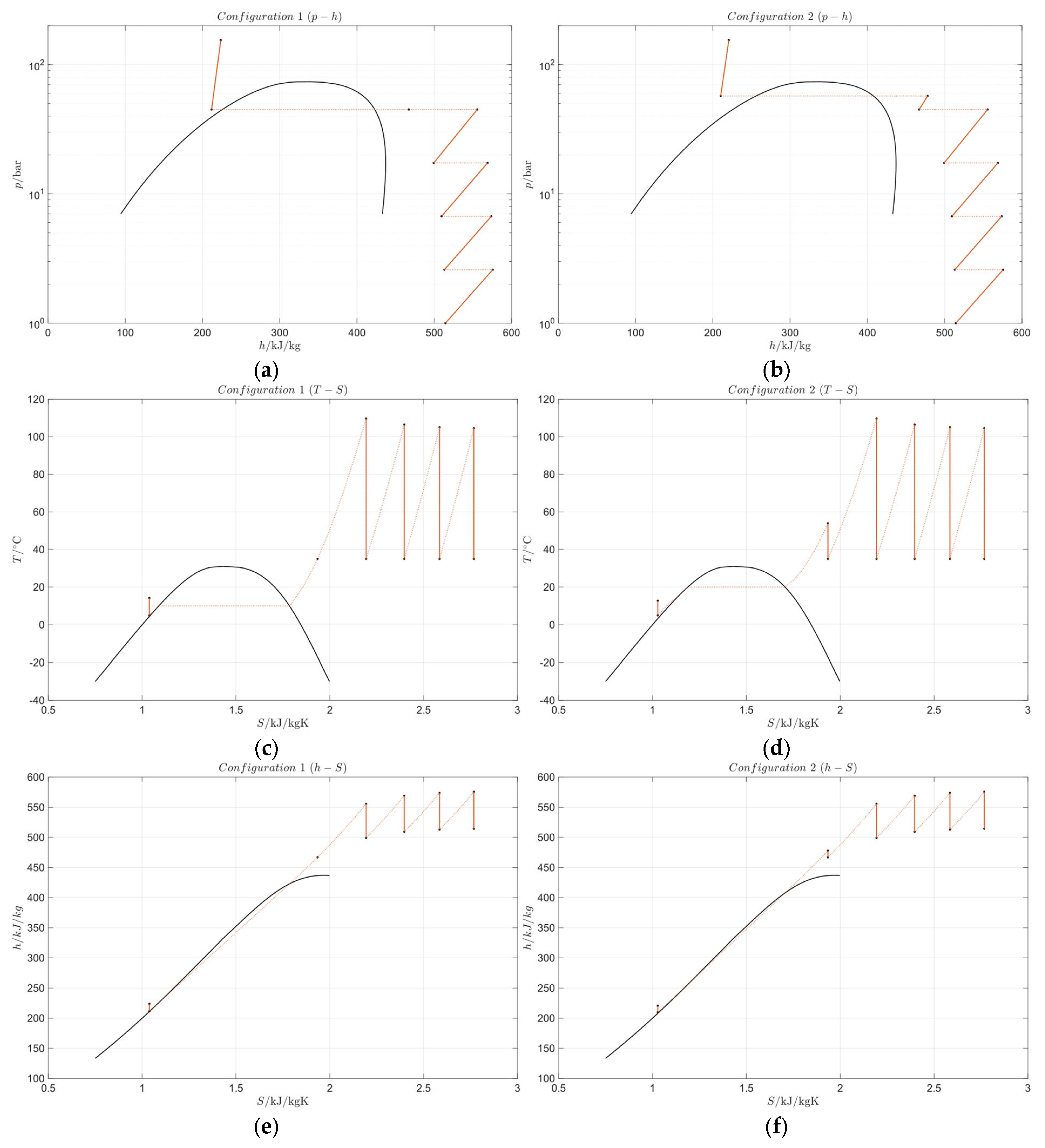
Figure 6 illustrates the transformations involving CO₂ as represented on the thermodynamic charts. It is important to emphasize that ideal transformations were initially assumed as a starting point for the preliminary design, in order to divide the overall compression ratio among the individual compressors in a consistent manner. As highlighted in the previous study [24] the thermophysical behavior of CO₂ ensures a relatively uniform distribution of specific compression work across the first four stages within the considered pressure range between 1 and 45 absolute bar.

In Layout 2, in addition to the pump, a gas-phase compression is required, for which the enthalpy change (reversible work) through compressor C5_2 is comparable to that of the pump P_2.

2.3. Selection and Preliminary Design Pump

It is worth highlighting that this section only presents the selection and preliminary design procedure of pumps, as that concerning the compressors has already been described in a previous work [24].

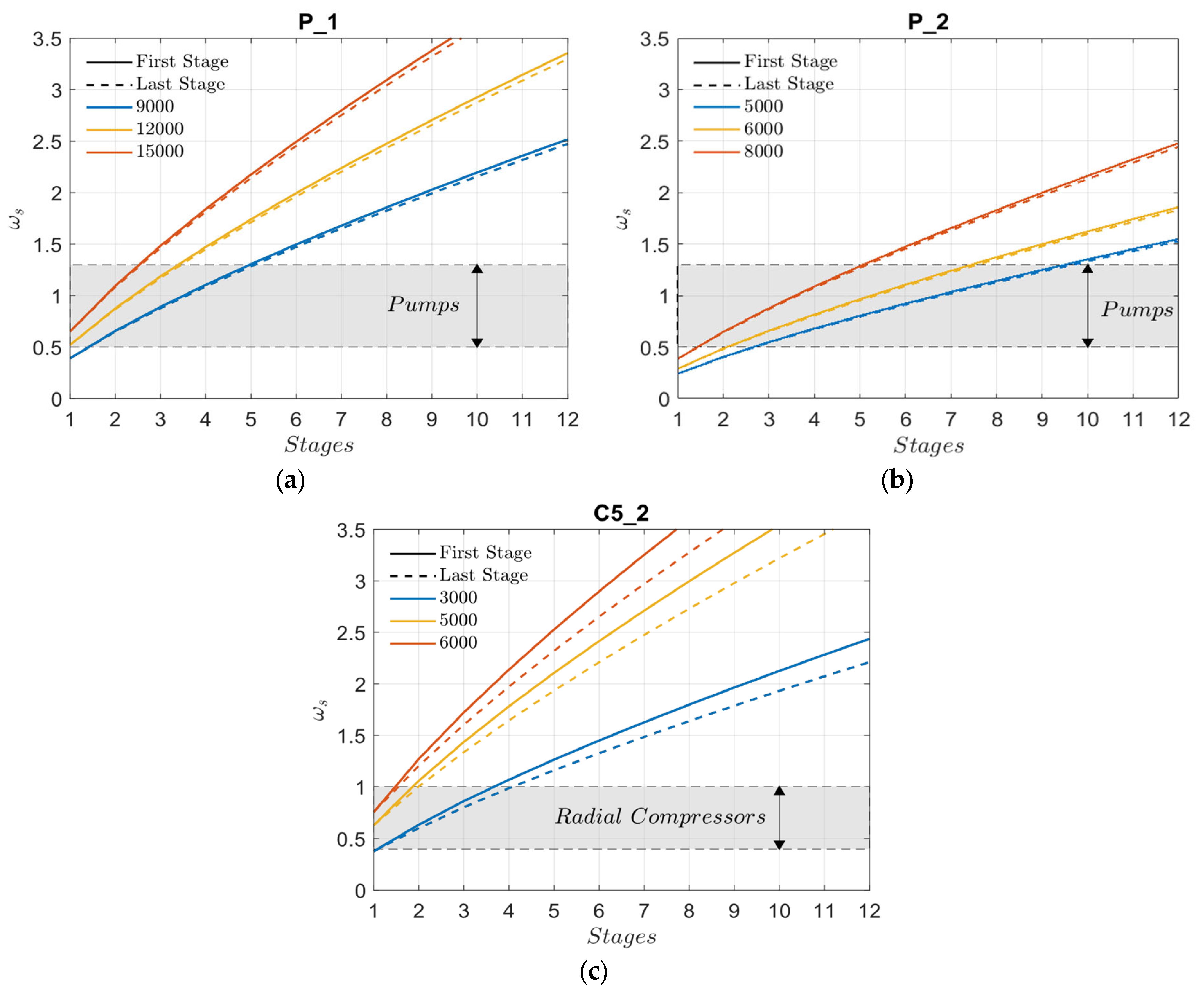
The similarity theory, particularly as formulated through the Baljé method, provides a fundamental approach for classifying turbomachines (axial, radial, or mixed flow) according to their specific application. Baljé’s diagrams, in particular, enable the identification of characteristic ranges of specific speed that define the suitability of each turbomachine type [35].

Accordingly, selecting the appropriate turbomachine type requires a preliminary estimation of the specific speed, based on the available operating data, which includes:

• The working fluid;
• m: mass flow rate (kg/s);
• T_in: inlet temperature of the fluid (°C);
• p_in: inlet pressure of the fluid (bar);
• p_out: outlet pressure of the fluid (bar).

These quantities allow to evaluate the ideal specific work of the machine, which corresponds to the head in hydraulic machines, $\Delta H$. In addition, the pump head has been considered in the evaluation of the specific speed which also depends on the rotational speed ($\omega$, rad $s^{-1}$, or rpm), number of stages $z$ and the volumetric inlet flow rate $V_{in}$. For pumps, the specific speed is expressed as:

$${\omega }_s=\omega \cdot {\displaystyle \frac{V_{in}^{1/2}}{{(g\cdot \Delta H_{stage})}^{3/4}}}$$

(1)

In this context, it is necessary to establish a criterion for distributing the reversible work of the entire machine among its individual stages. Once this distribution has been defined, the volumetric flow rate at the inlet of each pump stage can be evaluated. This evaluation is performed by calculating the pressures and temperatures upstream and downstream of each stage based on the ideal head increment $\Delta H_{\mathrm{stage}}$, and subsequently determining the associated volumetric flow rates. It is important to note that, in pumps, the volumetric flow rate varies only slightly between the inlet and the outlet due to the relatively small change in fluid density. For this reason, selecting a specific number of stages, the specific speeds at the first and last stages are approximately equal.

This step in the pump selection process determines the feasible values of the rotational speed ($n$) and the number of stages ($z$) that ensure an appropriate specific speed, that would be within the range of values for high-hydraulic efficiency pumps which falls in 0.5–1.3, consistent with the desired machine size and compliant with possible rotational-speed constraints, such as cavitation limits.

The preliminary design of the centrifugal pump is carried out stage by stage, following the sequential order below [36]:

1.

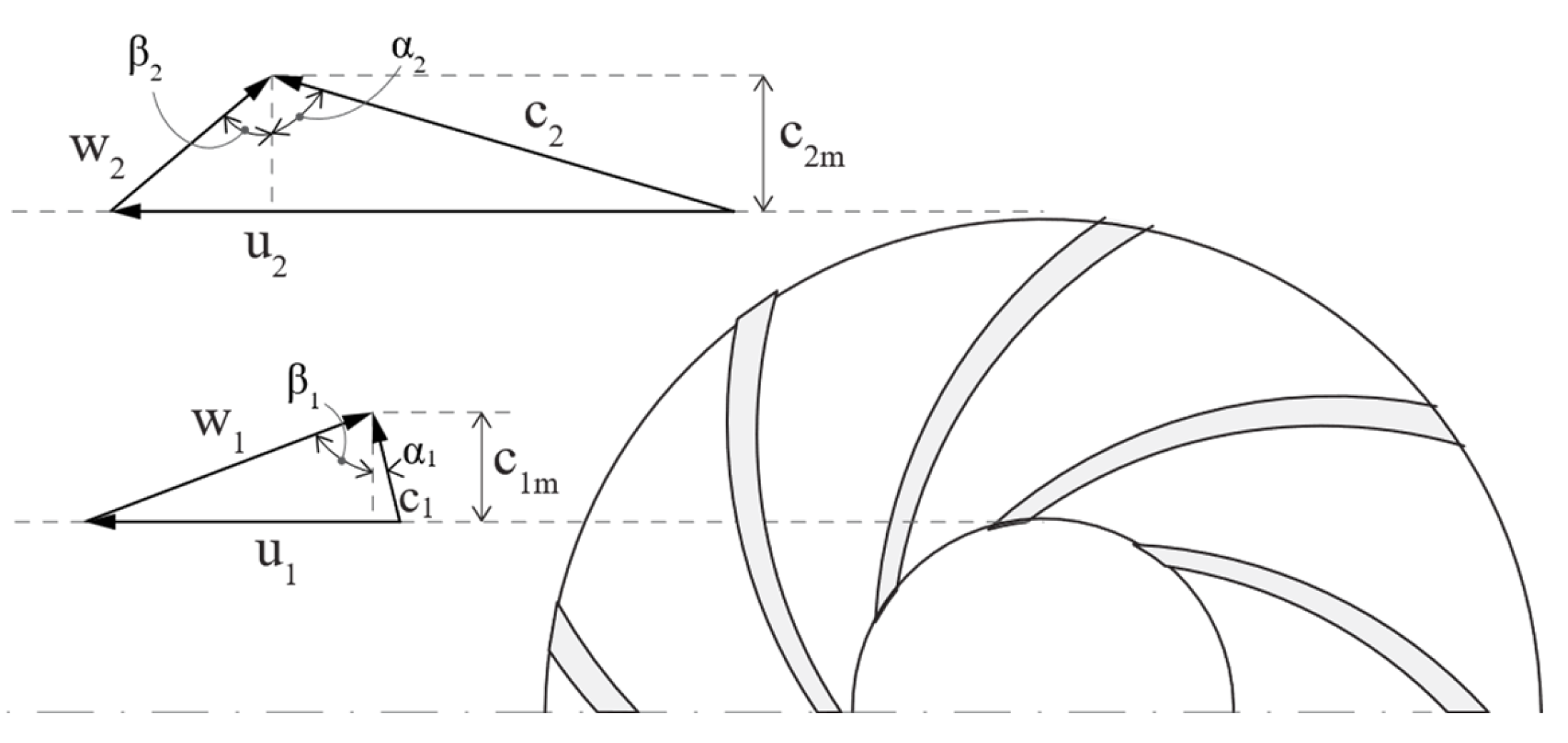
Evaluation of kinematic parameters: The kinematic angles at the rotor inlet and outlet (${\alpha }_2, {\beta }_1, {\beta }_2$, Figure 7) are determined by setting the following five independent parameters:

• The flow coefficient, here defined as $\phi =c_{1m}/u_2$;
• The work coefficient, here defined as $\psi =W/u_2^2 =g\cdot \Delta H/{ \eta }_{hyd}\cdot u_2^2$;
• The rotor meridional velocity ratio: $\xi =c_{2m}/c_{1m}$;
• The rotor tip diameter ratio: ${\delta }_t=D_{1t}/D_2=u_{1t}/u_2$;
• The angle ${\alpha }_1$.

Thus, the following is obtained:

$$\mathit{tan}{\alpha }_2={\displaystyle \frac{\psi }{\xi \cdot \phi }}+{\displaystyle \frac{{\delta }_t}{\xi }} ·\mathit{tan}{\alpha }_1$$

(2)

$$\mathit{tan}{\beta }_1={\displaystyle \frac{{\delta }_t}{\phi }}-\mathit{tan}{\alpha }_1$$

(3)

$$\mathit{tan}{\beta }_2={\displaystyle \frac{1}{\xi \cdot \phi }}\cdot \left(1-\psi \right)-{\displaystyle \frac{{\delta }_t}{\xi }}-\mathit{tan}{\alpha }_1$$

(4)

Therefore, the peripheral velocity $u_2$ can be used to define the stage kinematics fully. To calculate $u_2$, the parameter $\psi$ must be specified, along with an initial estimate of the hydraulic efficiency, which will be updated once the stage is fully defined.

Figure 7. Velocity triangles in a radial pump stage (adapted from [36]).

Figure 7. Velocity triangles in a radial pump stage (adapted from [36]).

2.

Evaluation of thermodynamic parameters: Knowing the pressure and temperature at the stage inlet, along with the pressure at the stage outlet, allows the determination of the thermodynamic states at the rotor inlet and at the stator inlet and outlet.

In this case if the density can be considered almost constant throughout each stage, the pressure at the rotor outlet can be calculated using the rotor hydraulic efficiency, defined as:

$${\overline{\eta }}_{hyd,R}={\displaystyle \frac{\Delta p_R / \rho \cdot g}{\Delta p_R / \rho \cdot g+Z_{H, R}}}$$

(5)

If, in addition to the six input previously introduced parameters, an initial estimate of the rotor hydraulic efficiency is provided (which will be updated once the stage is fully characterized), all thermodynamic properties of the stage can then be calculated.

3.

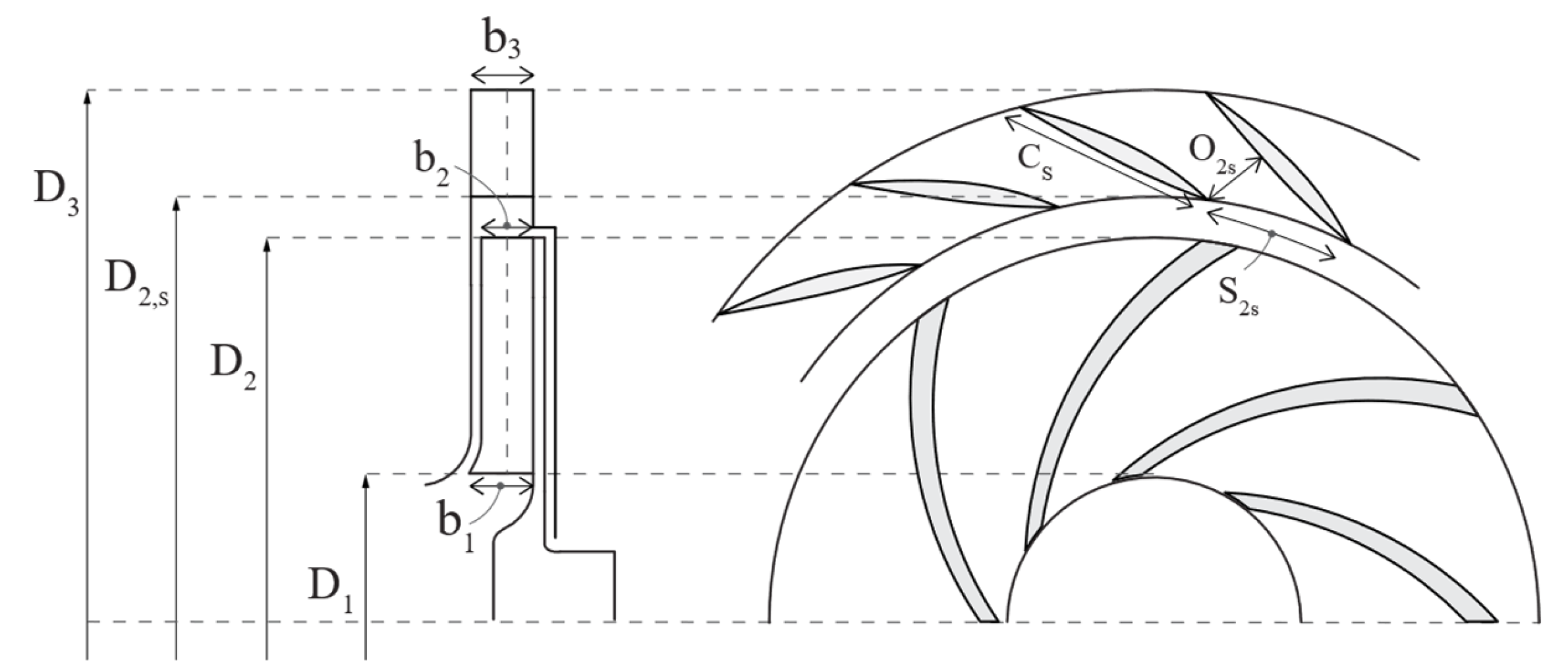
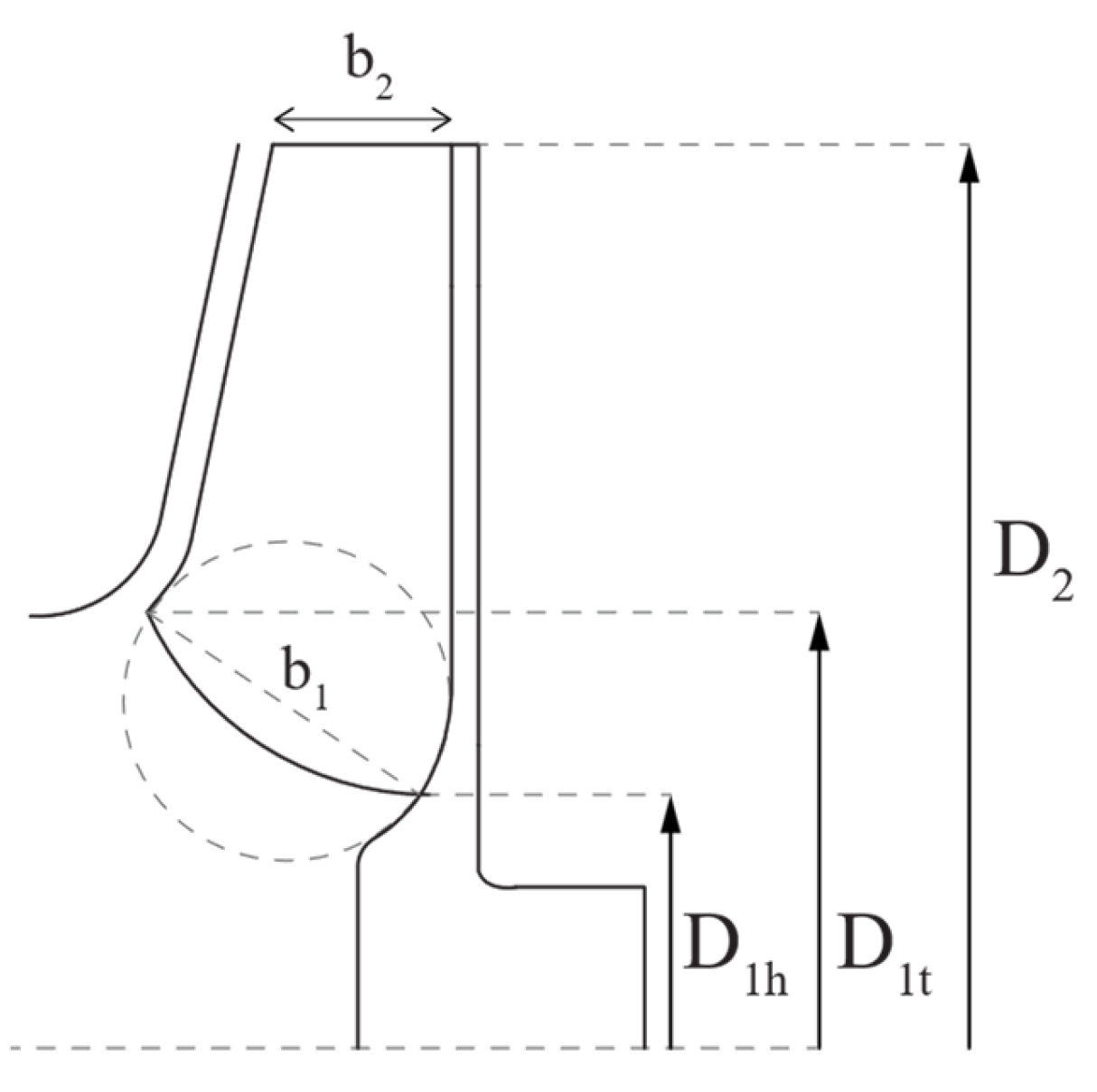
Assessment of geometric parameters: Figure 8 and Figure 9 illustrate the key geometric parameters of a radial stage, corresponding to radial inlet flow and mixed inlet flow, respectively. It is worth noting that the evaluation of geometric parameters involves defining an equivalent rotor channel with a circular section characterized by a hydraulic diameter and a hydraulic length. The outlet flow angle differs from the blade angle, since the fluid does not perfectly follow the geometry defined by the blades. By expressing the slip factor as a function of the outlet flow angle and the number of blades, and using additional correlations suggested by Gulich [37], the outlet flow angle has been defined. At the rotor outlet, the stator typically consists of a vaneless diffuser followed by a vaned diffuser. Following Gulich’s recommendations [37], the geometries of both the vaned and vaneless diffusers can be defined, nevertheless some constraints must be satisfied: for example, the number of stator blades can be selected in correlation with the number of rotor blades in order to limit pressure pulsations and vibrations.

4.

Losses and stage efficiency evaluation: For any type of turbomachinery, the authors [38] have extensively described the main sources of losses and the corresponding loss models suitable for preliminary design. In this paper, the loss model proposed by Gulich is adopted [37], where losses are expressed in terms of head (meters). The losses within the stator and rotor of a radial stage—where $Z_{H,S}$ represent stator losses and $Z_{H,R}$ rotor losses—are influenced by the kinematic, thermodynamic, and geometric parameters of the stage. After determining these losses, the rotor and overall stage efficiencies can be easily derived as functions of the stage work input and the corresponding energy losses. Then:

$${\overline{\eta }}_{hyd,R}=1-{\displaystyle \frac{Z_{H,R}}{\frac{u_2^2-u_1^2}{2 \cdot g}+\frac{w_1^2-w_2^2}{2 \cdot g}}}$$

(6)

$${\eta }_{hyd}=1-{\displaystyle \frac{g\cdot Z_H}{W}}$$

(7)

If the calculated stage efficiency satisfies the design specifications, the sizing procedure can be considered complete; otherwise, the input parameters should be modified and a new sizing iteration carried out.

Figure 8. Impeller inlet geometry: radial (adapted from [36]).

Figure 8. Impeller inlet geometry: radial (adapted from [36]).

Figure 9. Impeller inlet geometry: mixed (adapted from [36]).

Figure 9. Impeller inlet geometry: mixed (adapted from [36]).

For multistage pumps, the same calculation procedure is repeated for each stage. Between two consecutive stages, a volute is assumed in which the total enthalpy, mass flow rate, and angular momentum remain constant, provided that frictional effects are negligible. Based on these assumptions, the subsequent stages can be assessed by appropriately redefining the six input parameters.

Although summarized here, the procedure highlights that the design of a centrifugal pump stage essentially depends on six main input parameters, given the fluid type, mass flow rate, inlet temperature and pressure, outlet pressure, rotational speed, and number of stages. As noted in [36], the previously introduced parameters ($\phi , \psi , R, {\eta }_{hyd}, {\alpha }_1, {\delta }_h=D_{1h}/D_2)$ correspond exactly to another parameter set (${\psi }_{id}=g\cdot \Delta H/u_2^2, {\delta }_t, {\delta }_b=b_2/D_2, {\eta }_{hyd}, {\alpha }_1, {\delta }_h)$, designated as set B. In the latter, the first four quantities can be expressed as functions of the stage specific speed, whereas the remaining two parameters can be reasonably fixed at 0° and 0.30, as suggested in [36]. Within Set B, the two rotor diameter ratios—${\delta }_t$ and ${\delta }_b$—replace the flow coefficient as independent input parameters. In this regard, Gulich [37] suggested evaluating the optimum value of ${\delta }_t$ for the cavitation avoiding, whereas ${\delta }_b$ as a function of the specific speed:

$${\delta }_t=f\left({\omega }_s\right)$$

(8)

$${\delta }_b={\displaystyle \frac{b_2}{D_2}}=f\left({\omega }_s\right)$$

(9)

Nevertheless, introducing the parameter ${\phi }^{\prime }=V_{in}/u_2·D_2^2$ and ${\psi }_{id}$, it is possible to determine the flow coefficient as function of ${\omega }_s$:

$$\left\{\begin{array}{c}{\phi }^{\prime }={\displaystyle \frac{\pi }{4}}\cdot \left({\delta }_t^2-{\delta }_h^2\right)\cdot \phi \\ {\phi }^{\prime }=f\left({\omega }_s,{\psi }_{id}\right)\end{array}\right.\Rightarrow \phi =f\left({\omega }_s,{\psi }_{id}\right)=f\left({\omega }_s\right)$$

(10)

Therefore, having established the optimal ranges of the specific speed for high-efficiency centrifugal pump stages [35] the design procedure for the single stage based on set B requires knowledge of only two input parameters, thus becoming a guided procedure. Following the design stage, it is essential to perform a thorough validation of the resulting parameters to ensure they lie within the optimal ranges reported in the relevant technical literature.

2.4. Chiller Design Assumptions

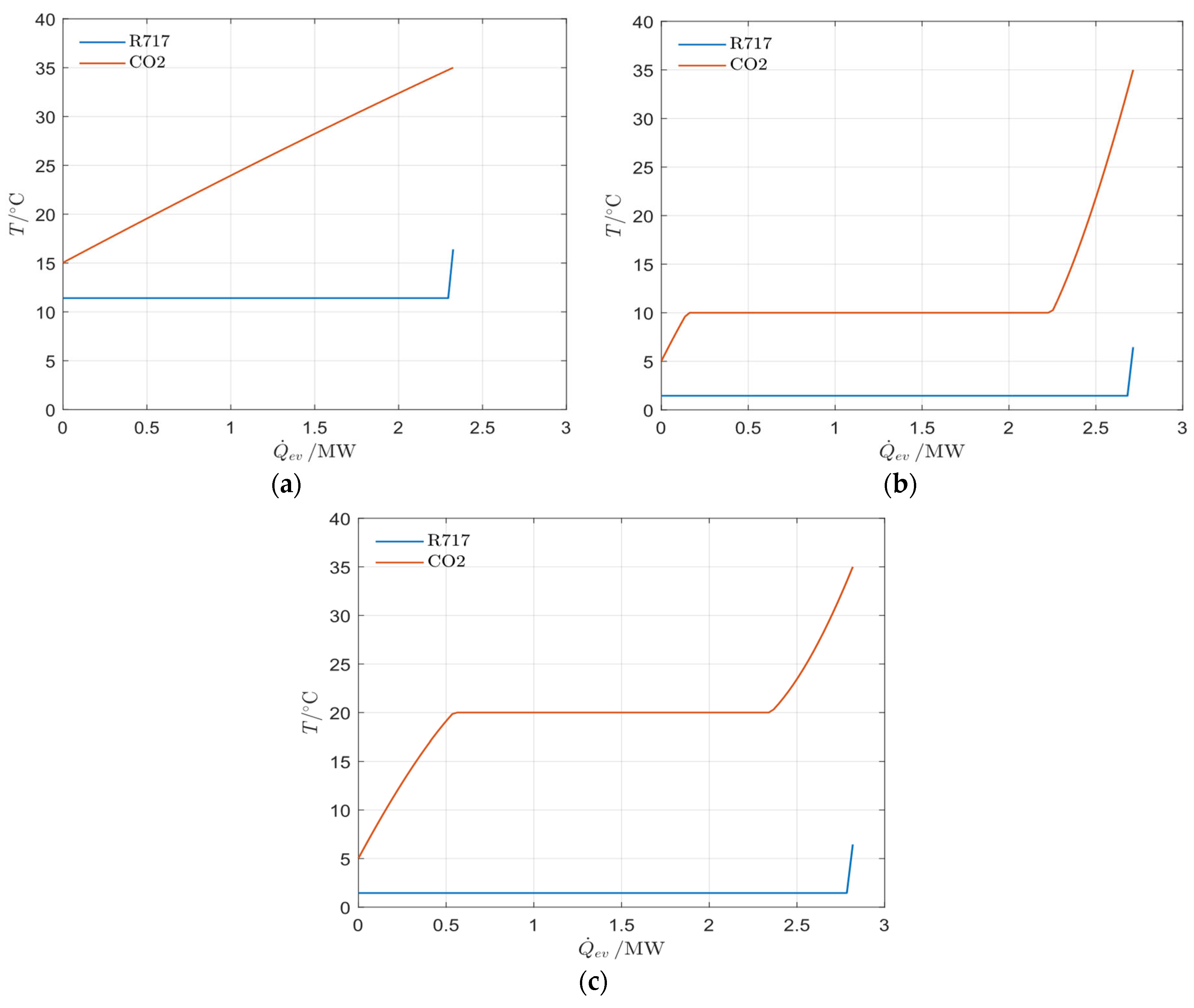
This section summarizes the main design parameters and assumptions used to evaluate the performance of the subcritical reverse cycles. First, as highlighted in the Introduction, ammonia (R-717) was selected as the working fluid. This decision followed a preliminary assessment comparing a subcritical ammonia cycle with a transcritical CO₂ cycle. Starting from the external fluid, the following

Table 2. External fluid parameters, Chiller 0.

Chiller 0	Fluid	Temperature (In-Out)/°C	Pressure/MPa	Cooling Capacity/MW
Condenser	Air	25–40	0.12	-
Evaporator	CO2	35–15	15.5	9.290

,

Table 3. External fluid parameters, Chiller 1.

Chiller 1	Fluid	Temperature (In-Out)/°C	Pressure/MPa	Cooling Capacity/MW
Condenser	Air	25–40	0.12	-
Evaporator	CO2	35–5	4.50	51.57

and

Table 4. External fluid parameters, Chiller 2.

Chiller 2	Fluid	Temperature (In-Out)/°C	Pressure/MPa	Cooling Capacity/MW
Condenser	Air	25–40	0.12	-
Evaporator	CO2	35–5	5.73	47.91

report the inlet and outlet temperatures, pressures, and cooling capacities. For all chillers considered, the external fluid in the condenser is air at ambient pressure with an identical temperature profile, whereas in the evaporator, the CO₂ outlet temperature varies depending on the specific case.

With respect to the evaporation temperature, it is determined by the external fluid temperature profile, the degree of superheating ($∆T_{SH}$), and the minimum temperature difference between the fluids in the evaporator ($∆T_{ev}$), which is specified as a design parameter. Moreover, the location of the minimum temperature difference depends on the temperature decrease in the external fluid ($∆T_{ext}$) and the degree of superheating. Specifically, the minimum temperature difference occurs either at the hot end or at the cold end according to the following conditions:

$$\Delta T^{ext}\ge \Delta T_{SH}\Rightarrow \Delta T_{ce}=\Delta T_{ev}\Rightarrow T_{ev}={T_{in}}^{ext}-\Delta T^{ext}-\Delta T_{ev}$$

(11)

$$\Delta T^{ext}\le \Delta T_{SH}\Rightarrow \Delta T_{he}=\Delta T_{ev}\Rightarrow T_{ev}={T_{in}}^{ext}-\Delta T_{SH}-\Delta T_{ev}$$

(12)

In all cases, the degree of superheating was set to 5 °C, while the temperature difference in the CO₂ varies depending on the specific operating conditions. In addition, the minimum temperature difference in the evaporator was fixed at 3 °C. On the other hand, in the condenser, four key temperature differences can be distinguished: the temperature differences between the refrigerant and the external cooling fluid at the cold and hot ends ($∆T_{ce}$ and $∆T_{he}$), the temperature difference at the pinch point ($∆T_{pp}$), where the refrigerant reaches the condensing temperature $T_{cnd}$, and the subcooling temperature difference ($∆T_{sc}$) between the condensing and outlet temperatures, which has been set to 5 °C in the analyzed cases. The temperature profile of the external fluid and the pinch-point temperature difference determine the condensing temperature, which can be expressed as follows:

$$T_{cnd}={T_{in}}^{ext}-\Delta T_{pp}^{ext}-\Delta T_{min, cnd}$$

(13)

where $\Delta T_{pp}^{ext}$ represents the temperature increase in the external fluid from the condenser inlet to the pinch point and $∆T_{min,cnd}$ is the minimum temperature difference between the two fluids, which has been set to 3 °C. However, determining the precise location of the pinch point requires an iterative calculation, since it depends on the heat rate necessary to cool the superheated vapor to saturation conditions. This, in turn, is influenced by the refrigerant inlet temperature, which depends on the pressure ratio, itself governed by the condensing pressure and, consequently, by the condensing temperature. Finally, the condensing and evaporation pressures can then be found as the saturation pressures corresponding to the condensing and evaporation temperatures:

$$p_{ev}=p_{sat}\left(T_{ev}\right)$$

(14)

$$p_{cnd}=p_{sat}\left(T_{cnd}\right)$$

(15)

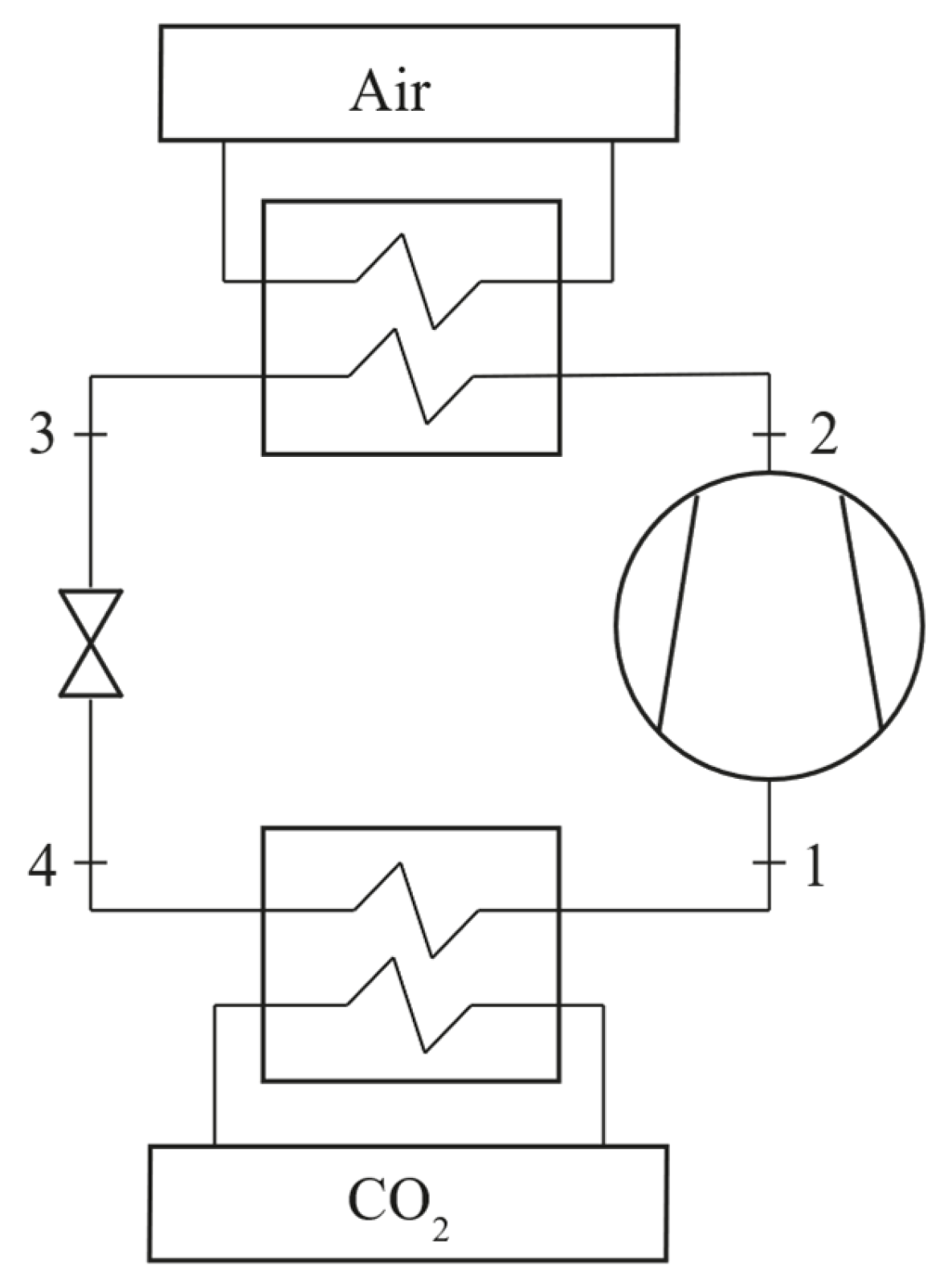
Determining the thermodynamic cycle also requires isentropic and mechanical efficiencies. In this study, the isentropic efficiency was assumed to be 0.8, reflecting the use of a volumetric compressor, while the mechanical efficiency was set to 0.9. These values were applied consistently to all three chillers considered. The chiller performance indicator is the Energy Efficiency Ratio ($EER$) defined as follows:

$$EER = {\displaystyle \frac{{\dot{Q}}_{ev}}{P}}$$

(16)

where the numerator is the cooling capacity, while P represents the power required by the compressor. Finally, the chiller schematic layout has been reported in Figure 10.

3. Results and Discussion

3.1. Turbomachinery Selection

As discussed in Section 2, the first four compressors—originally designed in the earlier work based on a six-stage compression process—have been retained in the two newly proposed configurations. Accordingly, this section focuses on the selection of the two pumps and the fifth compressor, in accordance with the case study described in Section 2.1 and the plant layouts presented in Section 2.2. The inlet parameters of each compressor and pump, including the flow rate, inlet pressure and temperature, as well as the discharge pressure, are summarized in Table 5 and Table 6. The reported values account for an assumed 3% pressure loss between successive compression stages and a final intercooling temperature of 35 °C. Therefore, the turbomachinery selection procedure outlined in Section 2.3 for the pumps, together with that adopted in the previous work for the compressors, was employed [24].

As the IGC configuration enables the installation of two impellers on each pinion, the rotational speed can be optimized to reduce the total number of compression stages. From the simulations carried out, the selected values of n and z used in the preliminary design of the compressor and pumps for the IGC solution are summarized in Table 7 and Table 8. The simulations performed involved the sizing of the turbomachinery and the verification of compliance with multiple functional parameters (kinematic, geometric, mechanical, and others). The data presented here results from an in-depth comparative analysis of the possible design alternatives. These solutions therefore represent one of the feasible configurations, which can be further refined by adjusting the individual input parameters of each machine to assess potential performance improvements. The aim of this paper is to provide a preliminary design of the compression train involved in the analyzed schemes, and the selected n and z values are consistent with this objective.

The results are graphically presented in Figure 11. In these figures, the optimal specific speed range for radial compressor and pump stages is highlighted in gray. By selecting appropriate rotational speeds, the specific speeds of the first and last stages were computed as a function of the number of stages (shown on the x-axis). These plots provide crucial insights for determining the optimal combination of rotational speed and stage count for each compression phase.

The IGC configuration enables the installation of two pump impellers on a new pinion designed to operate at a predetermined rotational speed (9000 rpm) in the first configuration analyzed. In the second configuration, two new pinions are implemented. At a rotational speed of 5000 rpm, the first pinion supports the rotor of the fifth single stage compressor and that of the first stage of the pump, whereas the second pinion accommodates the final two impellers of the pump. Once again, numerous simulations for the sizing of compressors and pumps, along with checks on compliance with functional parameters, were carried out; the data presented here result from a comprehensive comparative analysis of the available options.

Table 5. Data for each compressor and pump related to Configuration 1.

	m (kg/s)	pin (bar)	Tin (°C)	pout (bar)
C1_1	202.1	1.0	35.0	2.670
C2_1	202.1	2.590	35.0	6.916
C3_1	202.1	6.708	35.0	17.91
C4_1	202.1	17.37	35.0	46.39
P_1	202.1	45.0	5.00	155.0

Table 5. Data for each compressor and pump related to Configuration 1.

	m (kg/s)	pin (bar)	Tin (°C)	pout (bar)
C1_1	202.1	1.0	35.0	2.670
C2_1	202.1	2.590	35.0	6.916
C3_1	202.1	6.708	35.0	17.91
C4_1	202.1	17.37	35.0	46.39
P_1	202.1	45.0	5.00	155.0

Table 6. Data for each compressor and pump related to Configuration 2.

	m (kg/s)	pin (bar)	Tin (°C)	pout (bar)
C1_2	202.1	1.000	35.0	2.670
C2_2	202.1	2.590	35.0	6.916
C3_2	202.1	6.708	35.0	17.91
C4_2	202.1	17.37	35.0	46.39
C5_2	202.1	45.00	35.0	57.00
P_2	202.1	57.00	5.00	155.0

Table 6. Data for each compressor and pump related to Configuration 2.

	m (kg/s)	pin (bar)	Tin (°C)	pout (bar)
C1_2	202.1	1.000	35.0	2.670
C2_2	202.1	2.590	35.0	6.916
C3_2	202.1	6.708	35.0	17.91
C4_2	202.1	17.37	35.0	46.39
C5_2	202.1	45.00	35.0	57.00
P_2	202.1	57.00	5.00	155.0

In the first configuration, the pump operates with inlet pressure and temperature values (Table 5) below the critical point of CO₂, where the working fluid is in the liquid phase. Conversely, in the second configuration, the compressor (C5) operates with an inlet temperature above the critical temperature (Table 6), such that the working fluid enters in a gaseous state, while at the pump inlet the CO₂ is in liquid phase.

Table 7. Data for the pump in Configuration 1.

	n (rpm)	z (–)	ωs
P_1	9000	2	0.66–0.65

Table 7. Data for the pump in Configuration 1.

	n (rpm)	z (–)	ωs
P_1	9000	2	0.66–0.65

Table 8. Data for the compressor and the pump in Configuration 2.

	n (rpm)	z (–)	ωs
C5_2	5000	1	0.63
P_2	5000	3	0.54–0.54–0.53

Table 8. Data for the compressor and the pump in Configuration 2.

	n (rpm)	z (–)	ωs
C5_2	5000	1	0.63
P_2	5000	3	0.54–0.54–0.53

Figure 11. Specific speed in relation to the number of stages for the considered turbomachinery: (a) pump in Configuration 1; (b) pump in Configuration 2; (c) C5 compressor in Configuration 2.

Figure 11. Specific speed in relation to the number of stages for the considered turbomachinery: (a) pump in Configuration 1; (b) pump in Configuration 2; (c) C5 compressor in Configuration 2.

3.2. Pumps and Compressor Preliminary Design

Based on the methodology outlined in Section 2.3 and the results presented in Section 3.1, the sizing of the two pumps and the fifth compressor was performed. As previously described, the two configurations share the first four compressors. Accordingly,

Table 9. Pump in Configuration 1 (a), compressor C5 and pump in Configuration 2 (b): main results.

(a)				(b)
P_1				C5_2			P_2
Input f(ωs)		Fist stage	Last stage	Input f(ωs)			Input f(ωs)			Fist stage	Last stage
ψid		0.4629	0.4642	ψis		0.4888	ψid			0.4853	0.4865
δt		0.6103	0.6077	δt		0.5647	δt			0.5661	0.5636
δb		0.0971	0.0966	α2	°	72.48	δb			0.0848	0.0843
Assumptions				Assumptions			Assumptions
α1	°	0	0	α1M	°	0	α1		°	0	0
δh		0.30	0.30	δh		0.35	δh			0.30	0.30
Outputs				Outputs			Outputs
Dimensionless parameters				Dimensionless parameters			Dimensionless parameters
ψ		0.5185	0.5202	ψ	0.5603		ψ			0.5460	0.5475
ϕ		0.1528	0.1518	ϕ	0.2197		ϕ			0.1363	0.1354
Kinematics				Kinematics			Kinematics
ξ		0.7155	0.7133	ξ		0.8049	ξ			0.6733	0.6706
R		0.7517	0.7508	R		0.7350	R			0.7363	0.7354
α2	°	78.09	78.24	β1M	°	64.34	α2		°	80.46	80.58
β1,t	°	75.94	75.97	β2	°	68.09	β1,t		°	76.46	76.49
β2	°	77.21	77.28	u2	m/s	159.1	β2		°	78.57	78.65
Operation				Operation			Operation
Pin	bar	45.00	99.48	Pin	bar	45.00	Pin		bar	57.30	122.1
Tin	°C	5.000	10.13	Tin	°C	35.00	Tin		°C	5.000	10.71
Pout	bar	99.48	155.0	Pout	bar	59.00	Pout		bar	89.52	155.0
Tout	°C	10.13	14.82	Tout	°C	57.58	Tout		°C	7.930	13.37
Geometry				Geometry			Geometry
D1t	cm	14.7	14.7	D1t	cm	34.3	D1t		cm	18.4	18.3
D2	cm	24.1	24.1	D2	cm	60.8	D2		cm	32.5	32.5
D3	cm	34.9	34.8	D3	cm	96.8	D3		cm	45.0	44.9
b1	cm	3.7	3.7	b1	cm	6.5	b1		cm	4.3	4.3
b2	cm	2.3	2.3	b2	cm	3.2	b2		cm	2.8	2.7
SF		0.8304	0.8307	SF		0.8299	SF			0.8383	0.8388
Dhyd,R	cm	2.9	2.9	Dhyd,R	cm	4.2	Dhyd,R		cm	3.4	3.4
Lhyd,R	cm	22.2	22.3	Lhyd,R	cm	54.0	Lhyd,R		cm	33.5	33.7
Dhyd,vaned	cm	2.9	2.9	Dhyd,vaned	cm	4.4	Dhyd,vaned		cm	3.4	3.3
Lhyd,vaned	cm	14.0	13.8	Lhyd,vaned	cm	40.1	Lhyd,vaned		cm	17.9	17.8
NB,R		5	5	La	cm	16.4	NB,R			5	5
NB,S		8	8	NB,R		13	NB,S			8	8
				NB,S		12
Dimensionless coefficients				Dimensionless coefficients			Dimensionless coefficients
Re1		1.52 × 107	1.46 × 107	Ma1t		0.406	Re1			1.25 × 107	1.20 × 107
Re2,S		1.54 × 107	1.50 × 107	Ma2,S		0.382	Re2,S			1.41 × 107	1.37 × 107
				Re1		2.08 × 107
				Re2,S		2.61 × 107
Performances				Performances			Performances
P	MW	2.71		P	MW	2.87	P		MW		2.39
ηhyd		0.8918		ηis		0.8724	ηhyd				0.8877

present the main parameters of the pump for the first configuration, and of the compressor and pump for the second configuration, respectively. For completeness, the parameters of the IGC configuration proposed in the previous work are reported in Appendix A in

Table A1. Configuration 0: main results [24].

		C1_0	C2_0	C3_0	C4_0	C5_0	C6_0
Input f(ωs)
ψis		0.4527	0.5045	0.4474	0.5004	0.4677	0.4864
δt		0.6054	0.5481	0.6114	0.5524	0.5882	0.5674
α2	°	70.44	73.12	70.07	72.97	71.39	72.37
Assumptions
α1M	°	0	0	0	0	0	0
δh		0.35	0.35	0.35	0.35	0.35	0.35
Outputs
Dimensionless coefficients
ψ		0.5080	0.5836	0.5121	0.5902	0.5421	0.5916
ϕ		0.2879	0.1801	0.2955	0.1911	0.2631	0.2253
Kinematics
ξ		0.6269	0.9831	0.6282	0.9461	0.6936	0.8346
R		0.7955	0.7091	0.7956	0.7082	0.7621	0.7172
β1M	°	58.92	68.14	58.42	67.04	60.71	63.85
β2	°	69.85	66.96	69.17	66.19	68.27	65.28
u2	m/s	374.2	353.1	371.2	341.5	257.2	156.8
Thermodynamics
p2	bar	2.265	5.463	15.26	36.76	75.53	138.6
T2	°C	99.4	94.6	101.7	97.76	78.8	51.3
p3	bar	2.670	6.916	17.91	46.39	86.10	159.8
T3	°C	115.3	117.9	118.0	122.0	91.3	56.3
Geometry
D1t	cm	144.2	123.2	54.18	45.02	24.08	14.16
D2	cm	238.2	224.8	88.62	81.52	40.94	24.96
D3	cm	386.0	355.6	143.9	129.2	65.86	39.81
b1	cm	30.4	22.3	11.6	8.2	4.9	2.7
b2	cm	12.4	5.7	4.7	2.2	2.2	1.3
SF		0.8397	0.8214	0.8383	0.8203	0.8348	0.8361
Dhyd,R	cm	16.5	11.7	6.29	4.4	2.9	1.7
Lhyd,R	cm	194.6	203.1	70.2	70.3	33.8	20.5
Dhyd,vaned	cm	16.2	9.0	6.1	3.5	3.0	1.8
Lhyd,vaned	cm	191.9	126.2	70.9	47.2	31.1	16.1
La	cm	59.4	56.5	21.9	20.5	10.7	6.7
NB,R		15	12	15	12	14	14
NB,S		14	11	14	11	13	13
Dimensionless coefficients
Ma1t		0.919	0.750	0.938	0.765	0.698	0.437
Ma2,S		0.679	0.733	0.690	0.743	0.5727	0.300
Re1		3.86 × 106	5.82 × 106	10.1 × 106	15.4 × 106	24.9 × 106	18.9 × 106
Re2,S		5.42 × 106	8.09 × 106	14.0 × 106	20.6 × 106	31.2 × 106	15.6 × 106
Performances
P	MW	14.37	14.70	14.26	13.91	7.25	2.94
ηis		0.8910	0.8645	0.8737	0.8479	0.8628	0.8221

. For each turbomachinery stage, the work and flow coefficient parameters are reported, demonstrating that they remain within the limits required for achieving high efficiency in compressors and pumps [35]. Further results regarding the thermodynamic and kinematic performance of the stages, along with their geometric features, are also presented.

In all configurations analyzed, the compressor peripheral velocity $u_2$(tip speed) remains within the optimal range recommended for this class of applications [35]. Particular attention should be given to the stator outlet temperature in compressor C5_2 ($T_{\mathrm{out}}$). The findings reveal that, when operating near the critical point, the compression process exhibits limited temperature variation, which confirms the predominantly liquid-like thermodynamic behavior of the working fluid compared with that of an ideal gas. The geometry will subsequently be evaluated. The pumps feature impeller outlet diameters of 24 cm and 32 cm for the two configurations, respectively, whereas compressor C5_2 exhibits an outlet diameter about 61 cm. Overall, all components display a high degree of compactness. Lastly, the power and isentropic/hydraulic efficiency of pump P_1, compressor C5_2, and pump P_2 are reported. Pump performance is comparable in the two configurations, with high hydraulic efficiencies of roughly 89%. Likewise, compressor C5_2 achieves an efficiency similar to that of the four compressors analyzed in the system configuration reported in the previous study [24]. In configuration 1, the gaseous compression process requires only four stages, implying that each compressor operates as a single-stage unit, while the pump consists of two stages. In contrast, in configuration 2, the fifth compressor operates as a single stage and the pump comprises three stages.

3.3. Chiller

In this section, the main results related to the chiller systems are presented and discussed in detail. The analysis of the heat exchange profiles at the evaporator indicates that, for all cases considered, the pinch point occurs at the cold end of the heat exchanger. This behavior can be attributed to the selected degree of superheating, which is lower than the temperature difference in the external fluid. Consequently, the pinch-point is located at the colder end, in agreement with Equations (11) and (12). The corresponding heat exchange diagrams are presented in Figure 12.

With respect to the Energy Efficiency Ratio ($EER$), the results show that Chiller 3 exhibits the highest value. This behavior is fully consistent with that of a reverse thermodynamic cycle, in which an increase in the evaporation pressure, at constant condenser pressure, leads to an improvement in the $EER$. As for the other two chillers, they display identical $EER$ values, since they operate at the same pressure levels within the cycle. It is worth highlighting that, due to the high cooling power required by CO₂, it was necessary to use different modules to achieve the respective thermal capacities. In particular, the subdivision was carried out with the aim of ensuring that the modules of the three chillers could dissipate approximately the same thermal load at the evaporator. For this reason, in Figure 13, in addition to the $EER$, the corresponding number of modules and their respective thermal capacities are also reported.

Figure 12. Heat exchange diagrams: (a) Chiller 0; (b) Chiller 1; (c) Chiller 2.

Figure 12. Heat exchange diagrams: (a) Chiller 0; (b) Chiller 1; (c) Chiller 2.

Figure 13. EER, Cooling power and number of modules for each chiller.

Figure 13. EER, Cooling power and number of modules for each chiller.

As expected, chillers 1–2 require a higher number of modules (considering approximately the same thermal power at the evaporator) compared to chiller 3 and therefore need a larger installation space.

3.4. Sensitivity Analysis

The results of the conducted sensitivity analysis are reported in this section. The first objective of this analysis is to examine the influence of key parameters—work coefficient ψ, flow coefficient φ, and degree of reaction R—on the peripheral Mach number Ma_u, isentropic efficiency η_is, and tip inlet Mach number Ma₁. The second objective is to verify whether the preliminary design, developed according to the procedure based on specific rotational speed and, consequently, the parameters grouped in Set B [39], leads to an optimal solution. In this paper, the authors have solely reported the results obtained of the first compressor, whose preliminary design was presented in the previous work [24], with the corresponding data provided in the table reported in the Appendix A. Moreover, in the respective figures presented later, the set of values obtained from the previous design is marked with a black marker. The ranges considered for each parameter are summarized in

Table 10. Range of values considered for the sensitivity analysis.

Parameter	Range	Step
ψ/ψd 1	0.9803–1.0039	0.0040
ϕ/ϕd 1	0.9986–1.0768	0.0025
R	0.7500–0.7956	0.0456

¹ Ratio between the imposed value of ψ/ϕ and the value of ψ/ϕ in the preliminary design (see Table A1).

. Specifically, the parameters ψ and φ have been normalized using the respective values obtained from the preliminary design. These ranges are fully consistent with the design limits for radial compressors reported in the available literature [39].

Starting from the normalized results obtained with the respective values ${\mathrm{Ma}}_u=1.379$, ${\eta }_{is}=0.891$, and ${\mathrm{Ma}}_{1t}=0.919$, and with the degree of reaction fixed at 0.75, it can be observed from Figure 14 that for relatively low values of the work coefficient, high values of the peripheral Mach number are achieved as the flow coefficient increases. Conversely, increasing the coefficient ψ, while keeping the flow coefficient fixed, a decrease in the peripheral Mach number is observed. These trends highlight the strong interaction between the work coefficient and the flow coefficient in determining the peripheral Mach number, which is critical for optimizing the aerodynamic performance of the machine. In fact, it should also be emphasized that the peripheral Mach number represents a fundamental aerodynamic constraint, with a value of 1.4 corresponding to its upper limit, as reported in the literature [40]. This occurs because an increase in the peripheral Mach number leads to a decrease in the stage’s isentropic efficiency and a reduction in its operating range. The aforementioned observations are confirmed by the results obtained in terms of isentropic efficiency, reported in Figure 15. In fact, in regions characterized by high peripheral Mach numbers, lower efficiency values are observed compared to regions where the Mach number is lower, leading to an overall increase in efficiency. To avoid redundancies, the complete set of figures has been included in Appendix B, as they help to better illustrate these patterns. Figure A1 reports the trends of the peripheral Mach number and the isentropic efficiency. In particular, in Figure A1a, the work coefficient is held constant while the flow coefficient is varied, whereas in Figure A1b, φ is fixed and ψ is varied.

Focusing now on the influence of the degree of reaction, the results show that increasing its value leads to a decrease in the peripheral Mach number and, consequently, to an increase in isentropic efficiency. This effect can be attributed to rotor and stator losses. Specifically, for example, by fixing the work coefficient and allowing the flow coefficient to vary, an increase in the degree of reaction leads to lower rotor losses, while diffuser losses increase. However, the increase in stator losses does not offset the reduction in rotor losses, resulting in an overall decrease in stage losses. To provide further insight into this pattern, Figure A2 presents the trend for $R=0.8$, which, when compared with that shown in Figure A1a, highlights this aspect by focusing directly on the trends of the peripheral Mach number and the isentropic efficiency, with the work coefficient held constant and the flow coefficient varying.

Figure 14. Peripheral Mach number.

Figure 14. Peripheral Mach number.

Figure 15. Isentropic efficiency.

Figure 15. Isentropic efficiency.

Turning to the second objective of the sensitivity analysis defined earlier, it can be concluded that the preliminary design obtained using Set B leads to an optimal solution in terms of isentropic efficiency. As shown in Figure 15, the maximum achievable isentropic efficiency obtained by varying the parameters ψ and φ is only about 0.25% higher than the proposed solution. This confirms that the preliminary design based on Set B provides a configuration very close to the global optimum among the possible design alternatives.

To provide a complete picture, the Mach number at the inlet tip was also analyzed to verify whether sonic conditions were reached across the range of the three parameters considered. The results, presented in Figure 16, indicate that for any combination of the three parameters considered, the Mach number at the inlet tip does not exceed unity. Moreover, when the work coefficient ψ is kept constant, an increase in the coefficient φ leads to a reduction in the tip inlet Mach number.

3.5. Energy Balance Assessment

The aim of this section is to compare the three proposed layouts in terms of the power required, in order to identify which configuration offers the greatest potential for energy saving. It is important to note that the analysis was conducted without considering the first four compressors, since they are common to all the layouts examined. Consequently,

Table 11. Power required for each layout.

Power/MW [Layout 0]	Power/MW [Layout 1]	Power/MW [Layout 2]
C5_0 = 7.25	P_1 = 2.71	C5_2 = 2.87
C6_0 = 2.94	-	P_2 = 2.39
Chiller 0 = 1.51	Chiller 1 = 11.83	Chiller 2 = 10.99

summarizes only the power demand of each new turbomachine and chiller.

Focusing solely on the power required by new turbomachinery, Layout 1 can be identified as the least energy-intensive compression configuration, since it includes only a single pump which demands very low power. In fact, compared to Layout 0, the turbomachinery power requirement of Layout 1 is approximately 73.4% lower. Layout 2 is also advantageous compared to Layout 0, showing a reduction in power demand of approximately 48.4%.

On the other hand, when considering in addition the chiller systems in each layout, as illustrated in Figure 17, it can be observed that, although Layout 0 includes two additional compressors compared to Layout 1 and one more than Layout 2, it nonetheless requires the lowest additional power. The main reason for this behavior lies in the compression work associated with the chillers which is significantly lower in Layout 0. This difference highlights the strong influence of the chiller compression stages on the overall energy performance of the system. Overall, the comparison reveals that Layout 1 requires approximately 24.3% more additional power than the first configuration, while Layout 2 demonstrates the highest additional power demand, with an increase of 38.9% compared to Layout 0.

4. Conclusions

In this study, the authors focused on the CO₂ compression stage within CCUS systems and proposed two alternative pathways to achieve transport-ready conditions. The analysis included the preliminary design of each pump and the development of a new compressor required by the second configuration, in which the chiller operates at a higher condensing temperature. The proposed approach was applied to a case study based on the advanced ultra-supercritical steam power plant RDK8 (Rheinhafen-Dampfkraftwerk, Karlsruhe, Germany). This choice is particularly relevant, as the power and heat generation sector represents one of the major sources of CO₂ emissions, where substantial opportunities for decarbonization can be achieved. The authors carried out the preliminary design of the additional turbomachinery required by the two alternative layouts, namely the pumps and the additional compressor C5_2 in the second configuration. Furthermore, a thermodynamic calculation was implemented to evaluate the Energy Efficiency Ratio of each chiller. In addition, the authors performed parametric analyses to highlight the influence of three main parameters—the work coefficient, the flow coefficient, and the degree of reaction—on the performance of the centrifugal compressor and to verify whether the preliminary design based on Set B, and therefore on the use of specific speed, leads to high-efficiency turbomachinery configurations. The key findings of the analysis can be summarized as follows:

• Among all the layouts analyzed, Layout 1, which involves CO₂ liquefaction at 10 °C, exhibits the lowest overall turbomachinery power requirement, 59.95 MW, followed by Layout 2 (62.50 MW) and Layout 0 (67.43 MW), which operates without CO₂ condensation. When the chiller power is included, the new layouts require an additional power approximately equal to 11–12 MW, while Layout 0, with the simple CO₂ cooling, requires only slightly more than one tenth of this power.
• Considering the entire compression schemes, Layout 0 requires a total power consumption of 68.94 MW, followed by Layout 1 (71.78 MW) and Layout 2 (73.49 MW). Comparing the total power demand, it can be observed that Layout 1 requires approximately 4.1% more power than Layout 0, whereas Layout 2 requires approximately 6.7% more. These results show that the process used to achieve the CO₂ transport-ready conditions is energy-intensive.
• The sensitivity analysis highlights the relationship between the three parameters considered—the flow coefficient, the work coefficient, and the degree of reaction—and the performance of the centrifugal compressors under investigation, both in terms of isentropic efficiency and the aerodynamic limit represented by the peripheral Mach number. The analysis quantifies changes in the compressor’s isentropic efficiency and the peripheral Mach number varying these input parameters.
• The preliminary compressor design, developed using input parameters related to the specific speed, leads to a high-efficiency configuration; it should be noted that, varying input parameters, other solutions can be designed but the maximum isentropic efficiency attained is about 0.25% higher than the proposed configuration.

The authors are currently working on constructing a centrifugal compressor map based on the preliminary design proposed in this paper and in [39], to study the off-design conditions of compressors. Moreover, to complete the assessment of the proposed system, a detailed techno-economic analysis will be carried out. Finally, the integration of the chiller condenser with the existing water-cooled condenser of the USC power plant should be analyzed in order to identify a configuration that could significantly enhance the overall performance.