Study on Carbon Emissions from Road Traffic in Ningbo City Based on LEAP Modelling
Abstract
1. Introduction
2. Methods
2.1. Prediction Method of Car Ownership
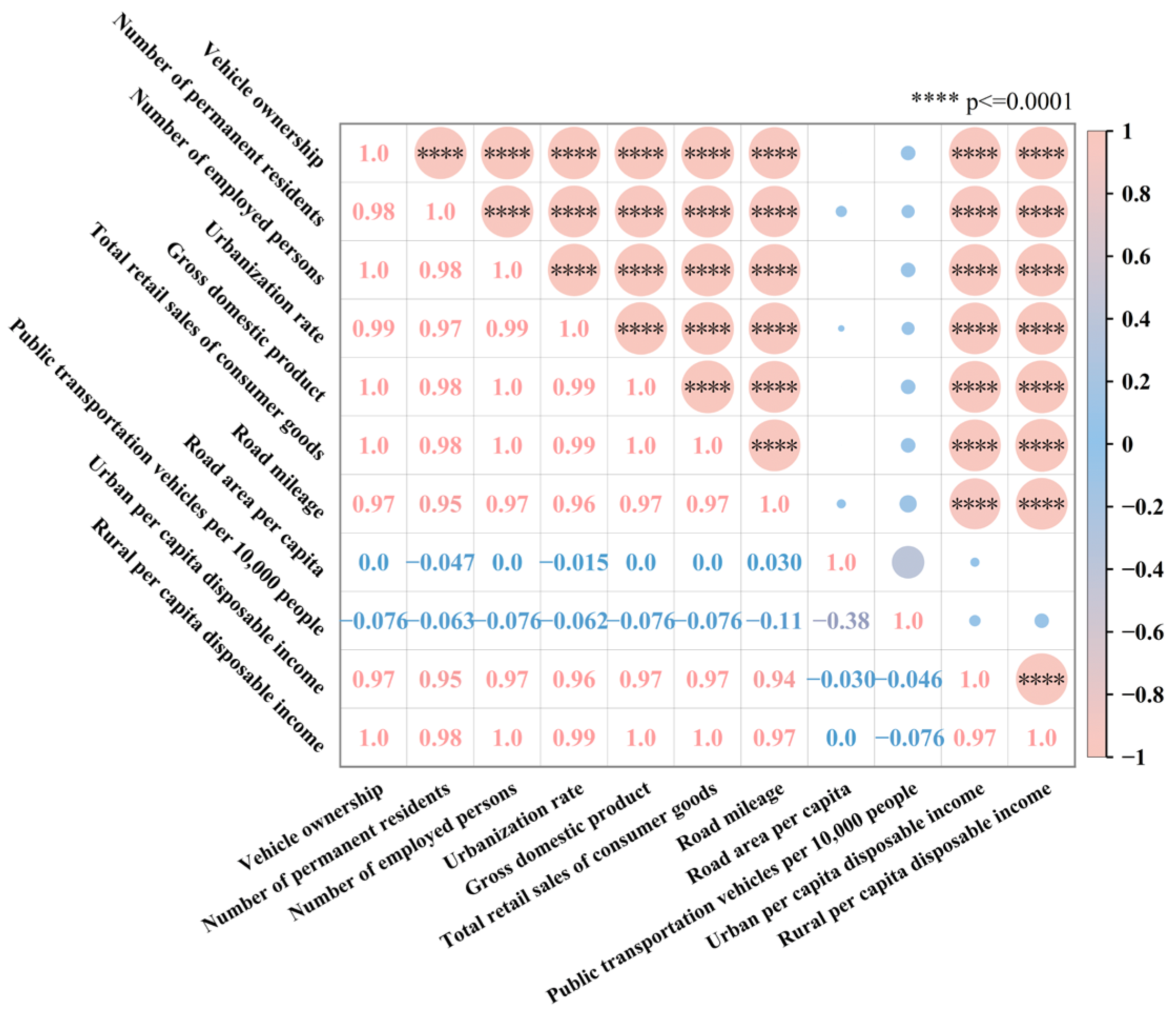
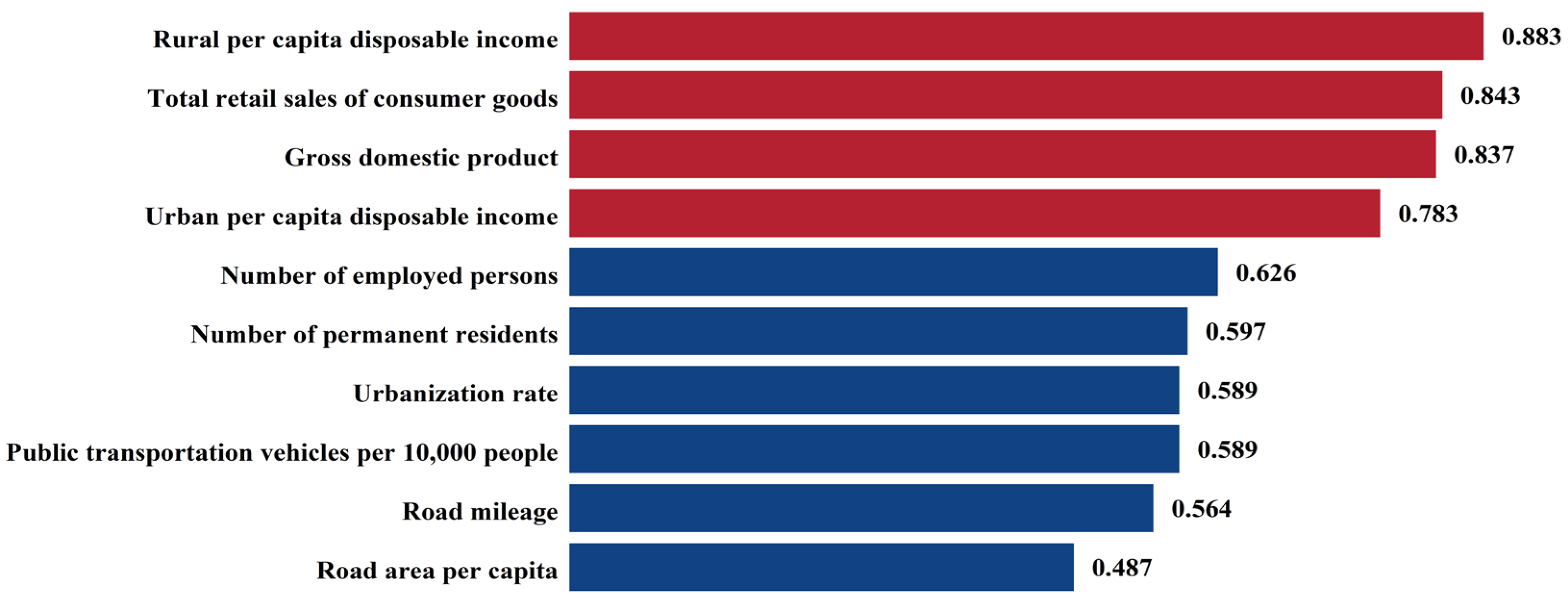
2.1.1. Influential Factor Analysis
- (1)
- Kendall’s correlation coefficient
- (2)
- Grey correlation analysis
- where , are the discriminant coefficients.
- (1)
- Normality: When condition equals and, if it equals , then condition must also be met.
- (2)
- Proximity: The smaller the value of condition , the greater is the value of condition .
- (3)
- Integrity: For condition , when condition is satisfied, condition must exist.
- (4)
- Even Symmetry: When condition is present and condition is met, symmetric pairwise relationships hold.
2.1.2. Data Preprocessing
- (1)
- Missing Value Processing
- (2)
- Data Standardization
- (3)
- Dataset Partitioning
2.1.3. Implementation of the LSSA-GRNN Model
- (1)
- GRNN model
- (2)
- SSA algorithm
- (3)
- Levy Flight Strategy
2.2. Modeling of Carbon Emissions
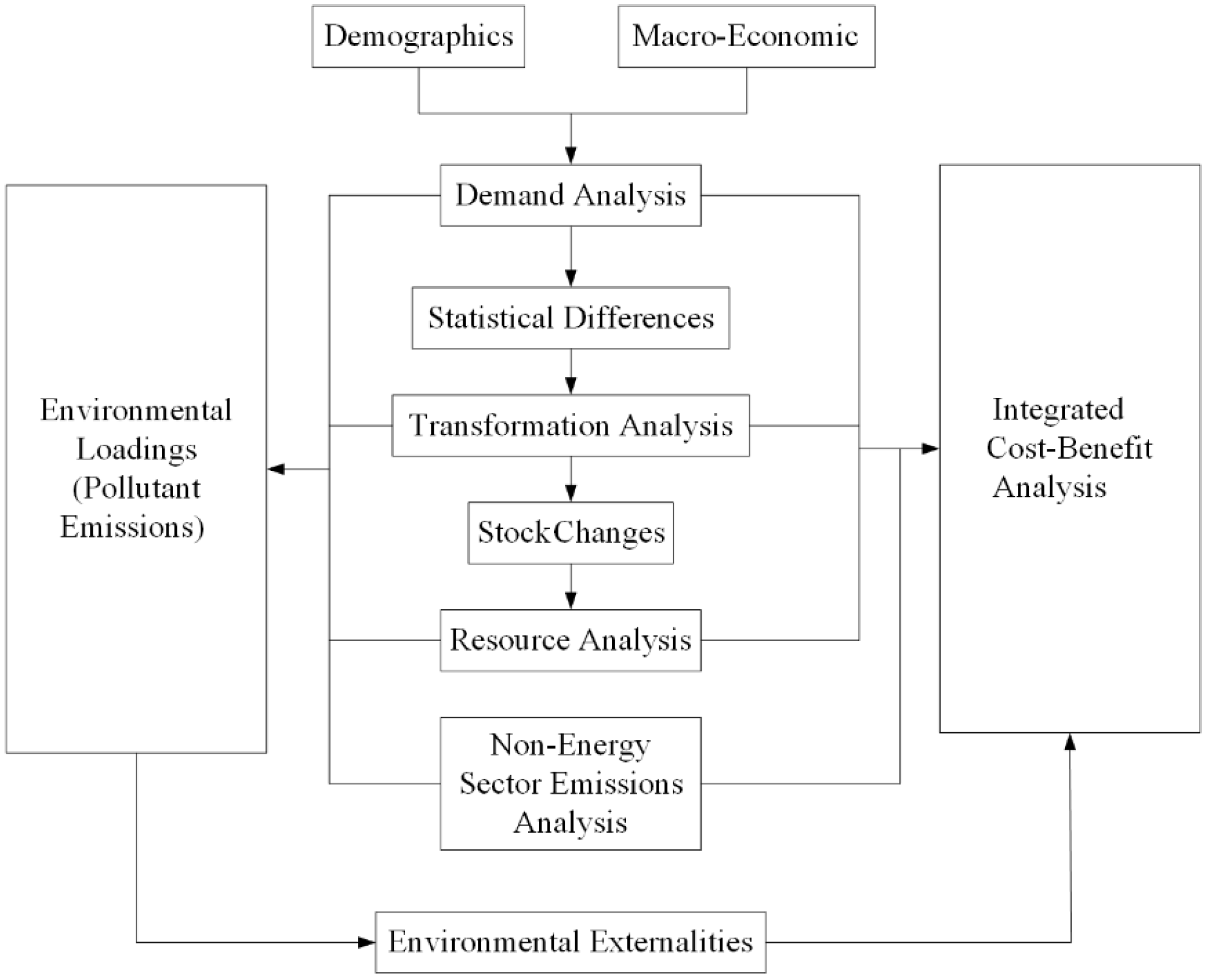
2.2.1. LEAP Model
- (1)
- Identification of the Research Domain
- (2)
- Development of the Data Structure
- (3)
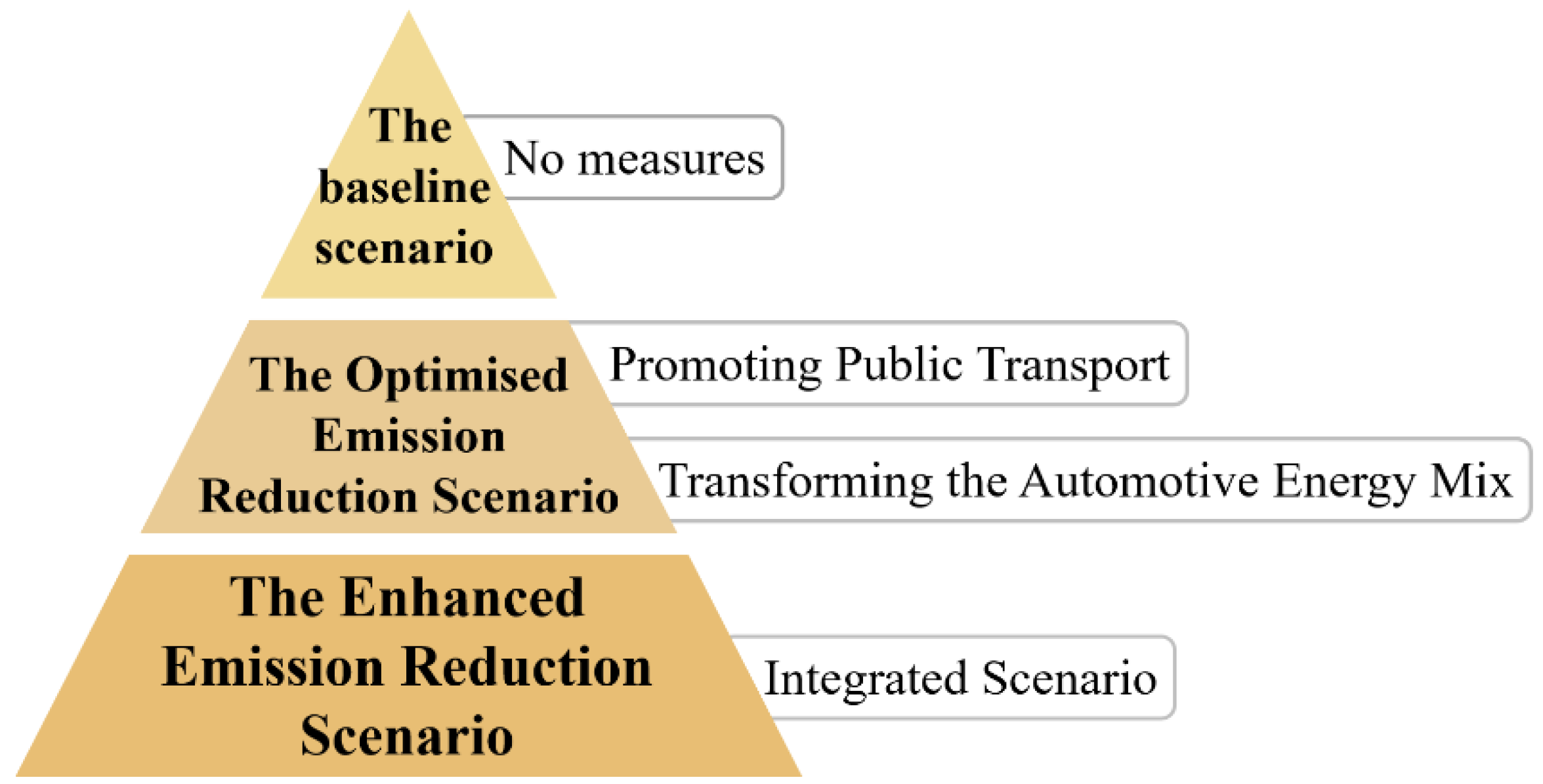
- Scenario Design
- (4)
- Results Analysis
2.2.2. Calculation of Carbon Emissions
- —Total CO2 emissions from conventional fuel vehicles;
- —Type of vehicle used for transport, e.g., car, taxi, bus, etc;
- —Type of energy used for transport, e.g., petrol, diesel, natural gas, etc;
- —Number of vehicles of type i models using type j energy (units);
- —Average consumption per unit kilometer for the i model of vehicle using the j energy source (L/100 km, m3/100 km);
- —Average annual mileage of the i model using the j energy source (km);
- —Carbon dioxide emission factor of the j energy source.
- —CO2 emissions of electric vehicles.
- —The number of electric vehicles of the i type (units).
- —Average consumption per unit kilometer of type i electric vehicles (kw·h/100 km).
- —Average annual mileage of the i electric vehicle (km).
- —Carbon dioxide emission factor of electric power.
- —Efficiency of electricity transportation.
- —Charging efficiency of electric vehicles.
3. Construction of the Model
3.1. Car Ownership LSSA-GRNN Forecasting Model
3.1.1. Analysis of Influencing Factors
3.1.2. Analysis of Projected Results
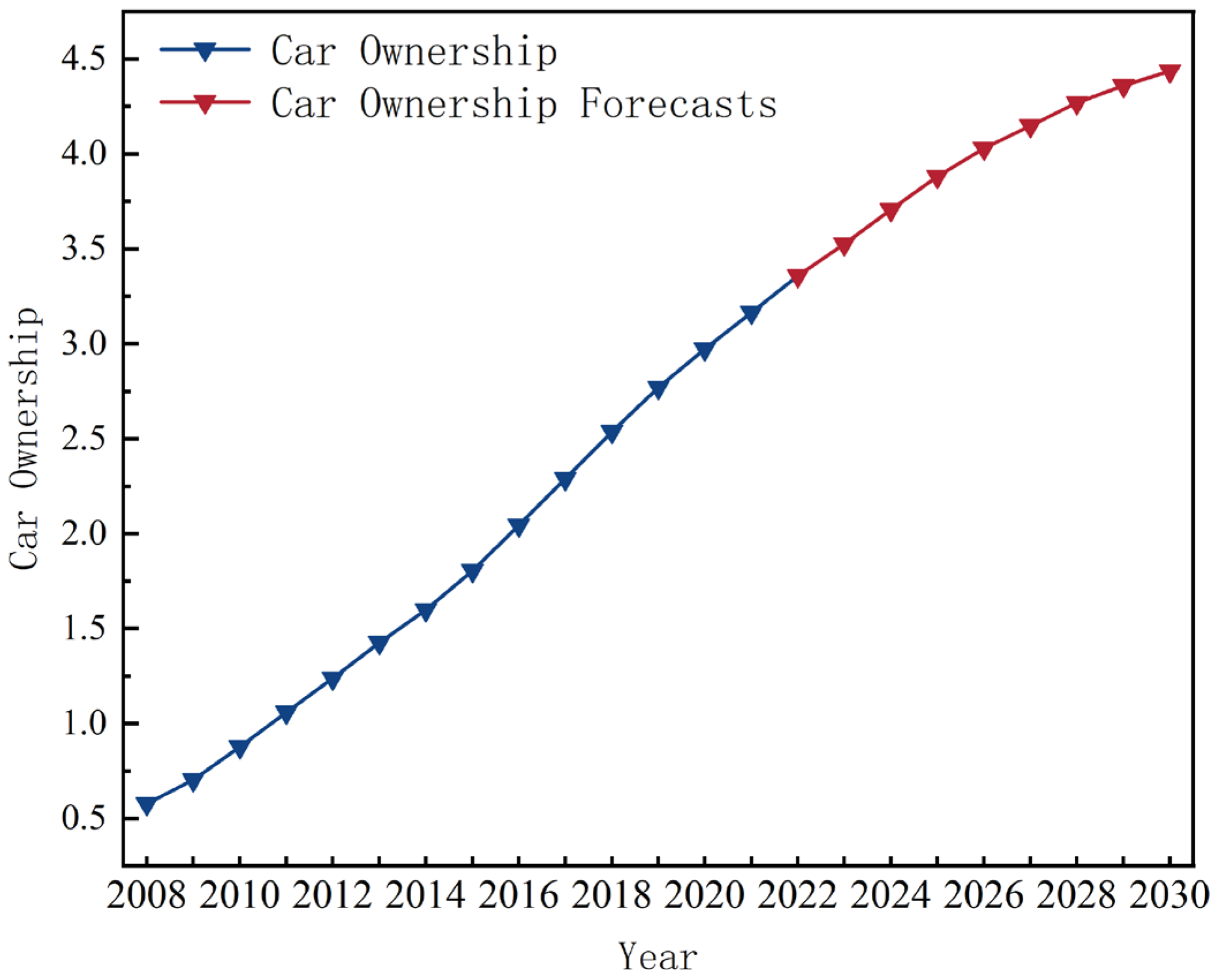
3.1.3. Projections for Future Years
3.2. Urban Transport Carbon Emission Modeling
3.2.1. Structural Division of Carbon Emissions
3.2.2. Baseline Parameter Setting
3.2.3. Scenario Design
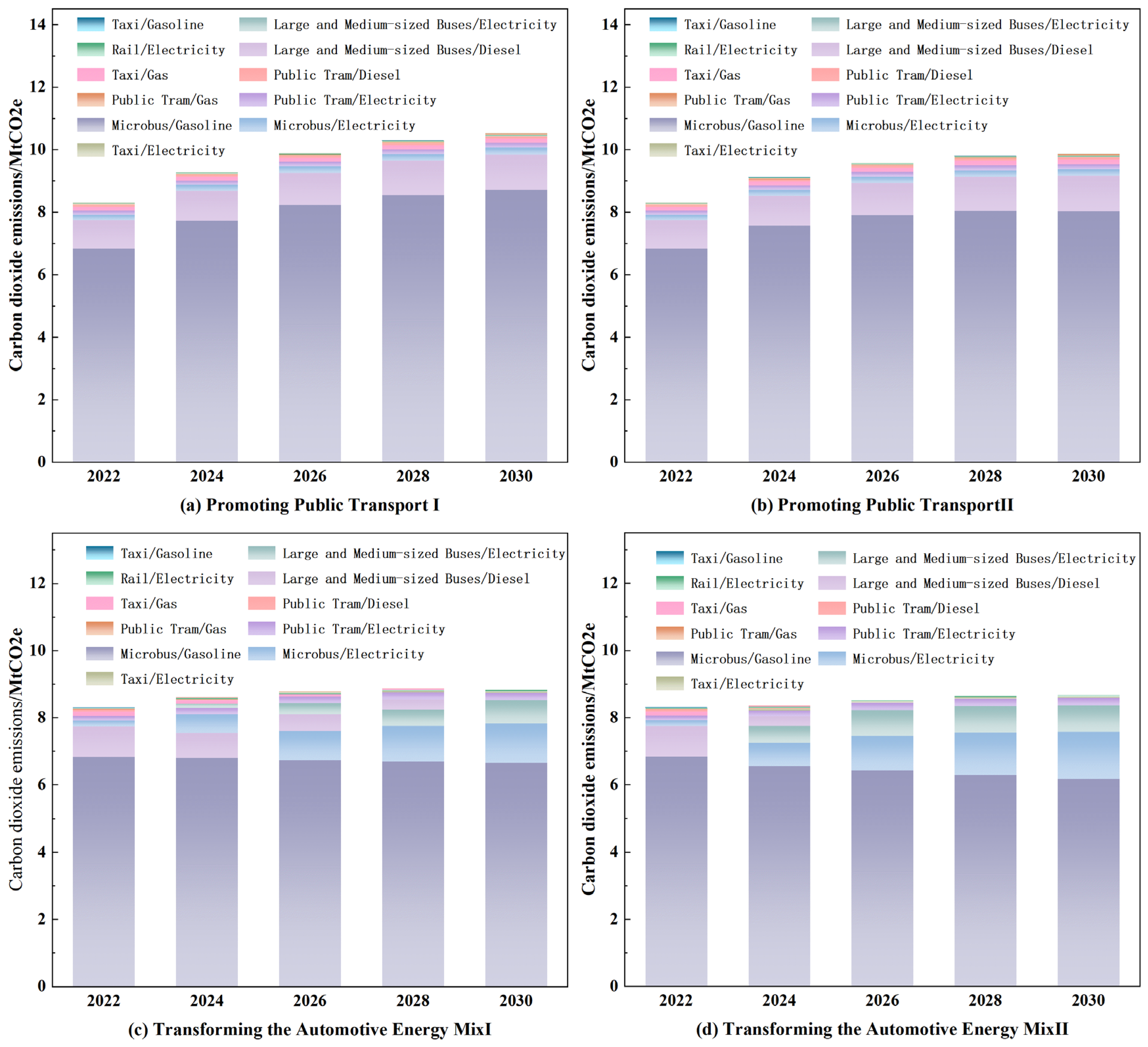
- ➀
- Promoting Public Transport Ⅰ: The average annual mileage of individual transport is reduced by 1% per year relative to the base year, while the average mileage of public transport increases by 1% annually.
- ➁
- Promoting Public Transport Ⅱ: The average annual mileage of individual transport is reduced by 2% per year relative to the base year, with a corresponding 2% annual increase in the average mileage of public transport.
- ➂
- Transforming the Automotive Energy Mix Ⅰ: By 2025, all new vehicle sales in Ningbo will be purely electric, and all public transport vehicles will transition to clean or new energy sources. By 2030, the number of new energy vehicles will reach 800,000, with 100% electrification of public transport vehicles. Additionally, the energy intensity of each vehicle type will be reduced by 1% annually from the base year level, in alignment with national targets for automotive energy efficiency.
- ➃
- Transforming the Automotive Energy Mix Ⅱ: By 2025, new energy vehicles will constitute 20% of Ningbo’s total vehicle stock, with complete electrification of public transport. From the base year, energy intensity for all non-electric fuels will be reduced by 1% annually, while the energy intensity of electricity will decline by 1.5% annually. By 2030, all newly sold vehicles will be fully electric.
4. Results
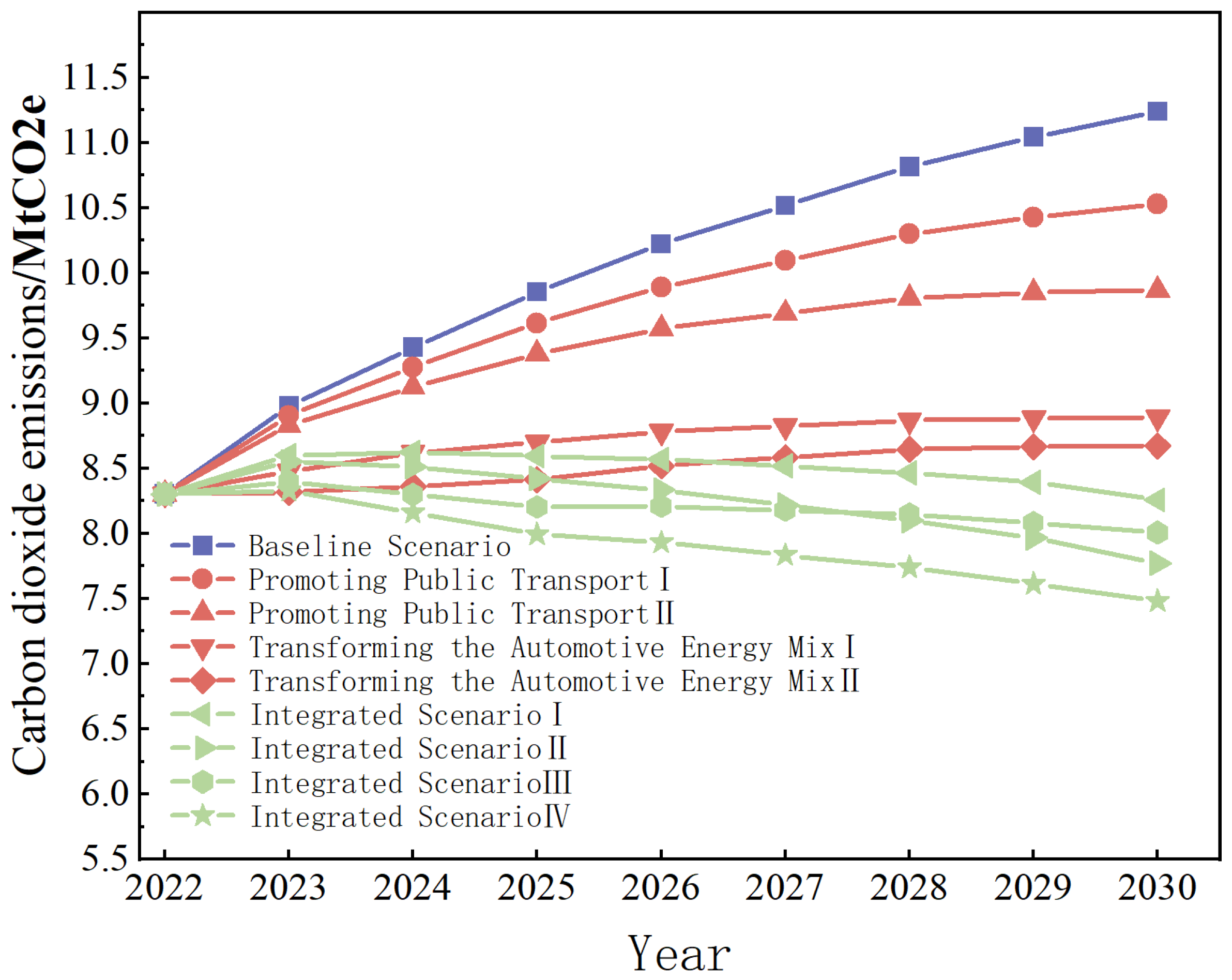
4.1. Analysis of Carbon Emission Results by Scenario
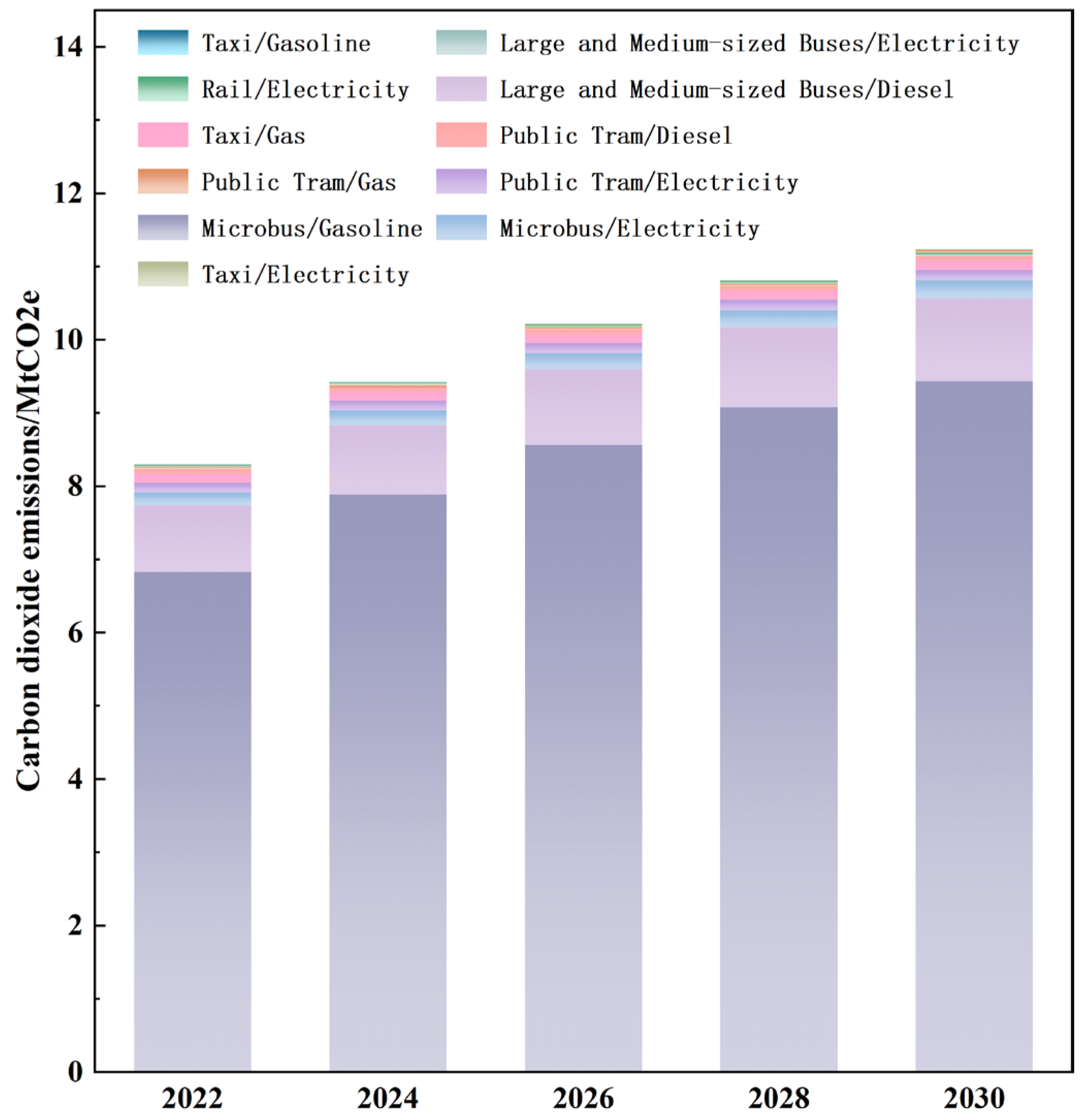
4.1.1. Baseline Scenario
4.1.2. Optimization of Low-Carbon Scenarios
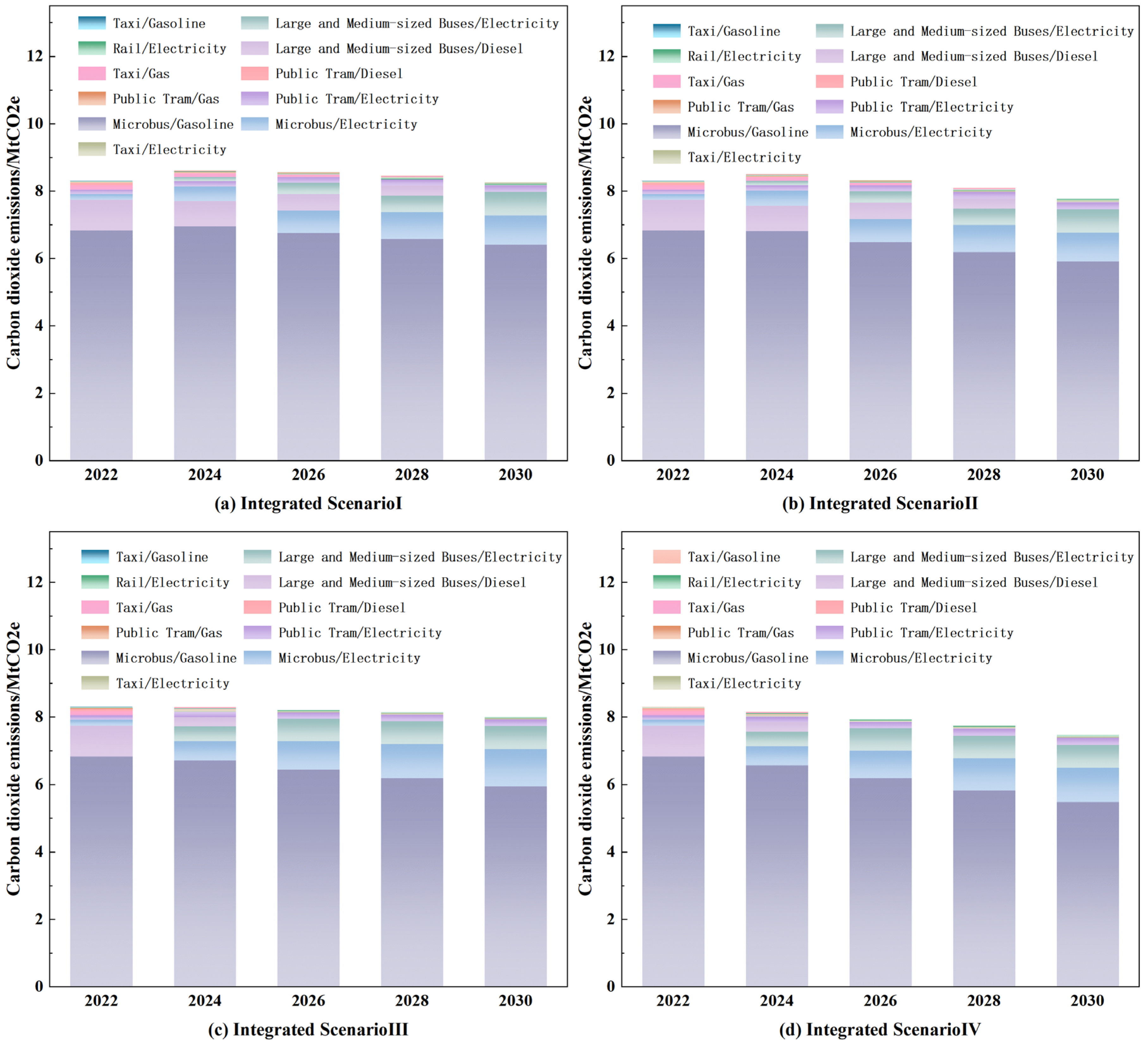
4.1.3. Enhanced Low-Carbon Scenarios
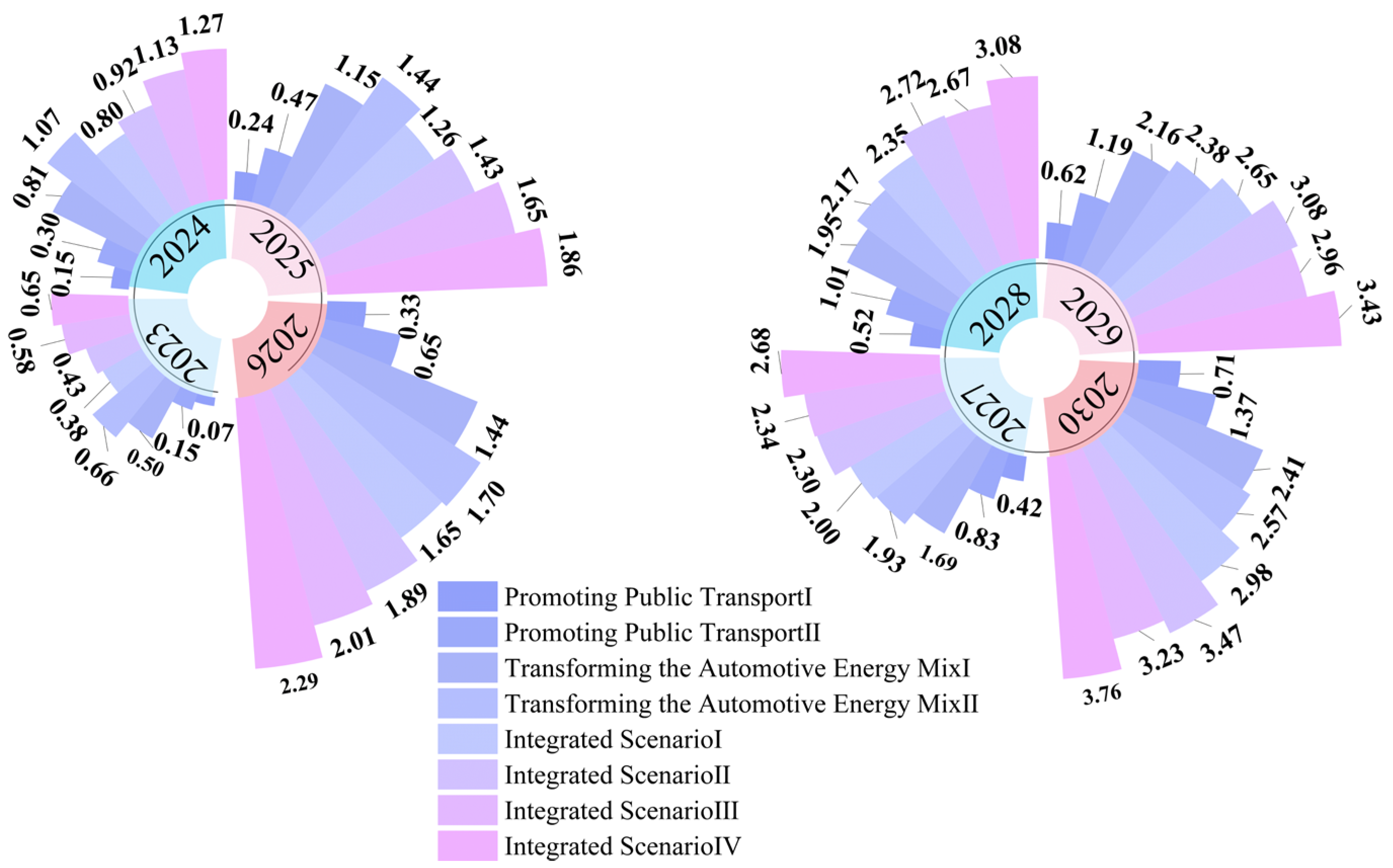
4.2. Sub-Scenario Carbon Reduction Potential Analysis
5. Conclusions
- (1)
- Under the Baseline Scenario, Ningbo will not achieve carbon peaking in the transport sector by 2030, with annual emissions rising to 11,239,100 tonnes.
- (2)
- Under the Optimized Low-Carbon Scenario, the implementation of targeted carbon reduction measures leads to reduced emissions. Within this scenario, the sub-scenario that promotes public transport exhibits a lower potential for reducing carbon emissions, reaching 9,867,400 tonnes in 2030 and yielding an annual reduction of up to 13,700 tonnes. In contrast, the sub-scenario focusing on transforming the automotive energy structure shows stronger emission reduction potential, with 2030 emissions estimated at no more than 8,671,500 tonnes and achieving a reduction of 14,400 tonnes in 2025. Despite its higher potential, the energy structure transformation measures face challenges related to the widespread adoption of new energy vehicles and enhancing the performance of conventional vehicles. Notably, none of the scenarios achieve carbon peaking by 2030.
- (3)
- Under the Enhanced Low-Carbon Scenario, which integrates and intensifies measures from the optimized low-carbon scenario, the overall emission reduction effect is more pronounced. In this integrated scenario, the maximum total carbon emissions in 2030 are projected to be 8,258,000 tonnes, with annual emission reductions ranging from 29,800 to 37,600 tonnes, signifying a significant improvement over the other scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Significance of Symbol |
| Sample data column of Kendall correlation coefficient | |
| Sample data column of Kendall correlation coefficient | |
| Pairwise dataset of Kendall correlation coefficient | |
| Kendall correlation coefficient value | |
| A Factor Data Series in Grey Relational Analysis. | |
| A reference data sequence | |
| A comparison data sequence. | |
| Discriminant coefficients in grey relational analysis | |
| Correlation coefficient of grey correlation analysis | |
| Value of grey relational analysis | |
| The min–max normalized original data value | |
| Min-Max Normalizes the minimum value of the original data. | |
| Min-Max Normalizes the maximum value of the original data. | |
| The min–max normalized data value | |
| Input data of GRNN model | |
| Output data of GRNN model | |
| The output at node | |
| Smoothing factor of GRNN model | |
| Transfer function of GRNN arithmetic summation neuron | |
| Transfer function of GRNN weighted summation neurons | |
| B | Sparrow population |
| Fitness of sparrow population | |
| Fitness of each sparrow | |
| Maximum number of iterations | |
| Vigilance values of sparrow population | |
| Safety values of sparrow population | |
| The worst search position of the iterative process | |
| The best search position of the iterative process | |
| The best fitness value for this iterative process | |
| The worst fitness value for this iterative process. | |
| The current fitness value of this iterative process | |
| A step control parameter | |
| A random step size | |
| Total CO2 emissions from conventional fuel vehicles | |
| Number of vehicles of type i models using type j energy | |
| Average consumption per unit kilometer for the i model of vehicle using the j energy source | |
| Average annual mileage of the i model using the j energy source | |
| Carbon dioxide emission factor of the j energy source | |
| Carbon dioxide emissions from electric vehicles | |
| Number of Type i electric vehicles | |
| Average consumption per unit kilometer of type i electric vehicles | |
| Average annual mileage of Type i electric vehicles | |
| Carbon dioxide emission factor of electric power | |
| Efficiency of electricity transportation | |
| Charging efficiency of electric vehicles | |
| Abbreviations | Full Form |
| LSSA | Lévy-flight-enhanced Sparrow Search Algorithm |
| GRNN | Generalized Regression Neural Network |
| LSSA-GRNN | Levy flight-improved Sparrow Search Algorithm optimized Generalized Regression Neural Network |
| LEAP | Long-range Energy Alternatives Planning System |
| SSA-GRNN | Sparrow Search Algorithm optimized Generalized Regression Neural Network |
| RDD | Regression Discontinuity Design |
| BLR | Binary Logistic Regression |
| SR | Symbolic Regression |
| NE-SR | Novel Equation Symbolic Regression |
| PCA | Principal Components Analysis |
| GM(1,1) | Grey models |
| MLP | Multilayer Perceptron |
| LCA | Life Cycle Assessment |
| EKC | Environmental Kuznets Curve |
| MFD | Macro Fundamental Diagram |
| TSCV | Time Series Cross-Validation |
| SEI | Stockholm Environment Institute |
| BRI | Boston Research Institute |
References
- Dargay, J.M.; Vythoulkas, P.C. Estimation of a dynamic car ownership model: A pseudo-panel approach. J. Transp. Econ. Policy 1999, 33, 287–301. [Google Scholar]
- Lo, K.L.; Fan, Y.; Zhang, C.; Mi, J.J. Factors for China’s Automobile Demand Structure: Petroleum Prices or Tax Policies? In Proceedings of the 8th International Conference on Information Technology and Quantitative Management (ITQM)—Developing Global Digital Economy After COVID-19, Chengdu, China, 9–11 July 2021; pp. 1136–1143. [Google Scholar]
- Liu, F.; Zhao, F.; Liu, Z.; Hao, H. The Impact of Purchase Restriction Policy on Car Ownership in China’s Four Major Cities. J. Adv. Transp. 2020, 2020, 7454307. [Google Scholar] [CrossRef]
- Baldwin Hess, D.; Ong, P.M. Traditional neighborhoods and automobile ownership. Transp. Res. Rec. 2002, 1805, 35–44. [Google Scholar] [CrossRef]
- Sefriyadi, I.; Andani, I.G.A.; Raditya, A.; Belgiawan, P.F.; Windasari, N.A. Private car ownership in Indonesia: Affecting factors and policy strategies. Transp. Res. Interdiscip. Perspect. 2023, 19, 100796. [Google Scholar] [CrossRef]
- Dargay, J.; Gately, D. Income’s effect on car and vehicle ownership, worldwide: 1960–2015. Transp. Res. Part A Policy Pract. 1999, 33, 101–138. [Google Scholar] [CrossRef]
- Lian, L.; Tian, W.; Xu, H.; Zheng, M. Modeling and Forecasting Passenger Car Ownership Based on Symbolic Regression. Sustainability 2018, 10, 2275. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Y. Private car ownership forecasting considering the factor of new energy vehicles. In Proceedings of the Sixth International Conference on Traffic Engineering and Transportation System (ICTETS 2022), Guangzhou, China, 16 February 2023. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Yan, L. Prediction Model of Car Ownership Based on Back Propagation Neural Network Optimized by Particle Swarm Optimization. Sustainability 2023, 15, 2908. [Google Scholar] [CrossRef]
- Wang, S.; Huang, X.; Li, J. Forecasting Car Ownership in China Based on an Improved GM (1,1)-MLP Model. In Proceedings of the 2024 IEEE 4th International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 24–26 May 2024. [Google Scholar]
- Del Pero, F.; Delogu, M.; Pierini, M. Life Cycle Assessment in the automotive sector: A comparative case study of Internal Combustion Engine (ICE) and electric car. Procedia Struct. Integr. 2018, 12, 521–537. [Google Scholar] [CrossRef]
- Guo, Z.; Li, T.; Peng, S.; Wang, X.; Zhang, H. When will China’s passenger vehicle sector reach CO2 emissions peak? A life cycle approach based on system dynamics. Sustain. Prod. Consum. 2022, 33, 508–519. [Google Scholar] [CrossRef]
- Yan, W.; Yeow, E.C.H.; Wang, Z.; Foo, C.K.; Tan, D.Z.L.; Chiam, S.Y.; Teo, Z.; Ng, J.K.H.; Meng, F.S.; Yeo, Z.; et al. Assessing the environmental benefits of passenger cars electrification in metropolises: A case study of Singapore. Int. J. Sustain. Transp. 2024, 1–13. [Google Scholar] [CrossRef]
- Meng, L.; Li, M.; Asuka, J. A scenario analysis of the energy transition in Japan’s road transportation sector based on the LEAP model. Environ. Res. Lett. 2024, 19, 044059. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, L.; Chen, J. Measurement Models for Carbon Dioxide Emission Factors of Passenger Cars Considering Characteristics of Roads and Traffic. Int. J. Environ. Res. Public Health 2021, 18, 1594. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Wang, M.; Du, W. Prediction on Peak Values of Carbon Dioxide Emissions from the Chinese Transportation Industry Based on the SVR Model and Scenario Analysis. J. Adv. Transp. 2020, 2020, 8848149. [Google Scholar] [CrossRef]
- Hou, L.; Wang, Y.; Zheng, Y.; Zhang, A. The impact of vehicle ownership on carbon emissions in the transportation sector. Sustainability 2022, 14, 12657. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, J.; Huang, Y.; Shen, H.; He, K.; Chen, H. Investigating the effect of dynamic traffic distribution on network-wide traffic emissions: An empirical study in Ningbo, China. PLoS ONE 2024, 19, e0305481. [Google Scholar] [CrossRef]
- Yu, Z.; Li, W.; Liu, Y.; Zeng, X.; Zhao, Y.; Chen, K.; Zou, B.; He, J. Quantification and management of urban traffic emissions based on individual vehicle data. J. Clean. Prod. 2021, 328, 129386. [Google Scholar] [CrossRef]
- Ravi, S.S.; Osipov, S.; Turner, J.W.G. Impact of Modern Vehicular Technologies and Emission Regulations on Improving Global Air Quality. Atmosphere 2023, 14, 1164. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Zhang, Y. Research on Carbon Emissions of Road Traffic in Chengdu City Based on a LEAP Model. Sustainability 2022, 14, 5625. [Google Scholar] [CrossRef]
- Liora, N.; Poupkou, A.; Kontos, S.; Meleti, C.; Chrysostomou, K.; Aifadopoulou, G.; Zountsa, S.; Kalogirou, C.; Chacartegui, R.; Liguori, F. Estimating road transport pollutant emissions under traffic-congested conditions with an integrated modelling tool—Emissions reduction scenarios analysis. Emiss. Control Sci. Technol. 2021, 7, 137–152. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, H.; Li, S.; Liu, Y. How road network transformation may be associated with reduced carbon emissions: An exploratory analysis of 19 major Chinese cities. Sustain. Cities Soc. 2023, 95, 104575. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, L.; Ma, J. Carbon dioxide emission reduction-oriented optimal control of traffic signals in mixed traffic flow based on deep reinforcement learning. Sustainability 2023, 15, 16564. [Google Scholar] [CrossRef]
- Litchfield, J.T., Jr.; Wilcoxon, F. Rank correlation method. Anal. Chem. 1955, 27, 299–300. [Google Scholar] [CrossRef]
- Li, S. Research and Application of Desert Seismic Noise Properties Based on Kendall Rank Correlation Coefficient. Ph.D. Thesis, Jilin University, Changchun, China, 2020. (In Chinese). [Google Scholar] [CrossRef]
- Zhou, W.; Zeng, B. A Research Review of Grey Relational Degree Model. Stat. Decis. 2020, 36, 29–34. (In Chinese) [Google Scholar] [CrossRef]
- Sun, K.H.G.B.H. Research on improved MVO GRNN neural network rockburst prediction model. J. Saf. Environ. 2023, 24, 923–932. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, H. Research on Wind Power Prediction Based on Sparrow SearchAlgorithm and Gated Recurrent Unit Neural Network. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2022. (In Chinese). [Google Scholar]
- Xiao, S. Tree Seed Optimization Algorithm Based on Levy Flight and ITS Application in Image Segmentation. Ph.D. Thesis, Guangxi University for Nationalities, Nanning, China, 2019. (In Chinese). [Google Scholar]
- Tian, P.; Chen, S.; Mao, B.; Zhou, Q.; Huang, J.; Tong, R. Impact of new energy vehicles on carbon emissions of private cars in China. J. Change Univ. (Nat. Sci. Ed.) 2023, 43, 88–98. (In Chinese) [Google Scholar] [CrossRef]
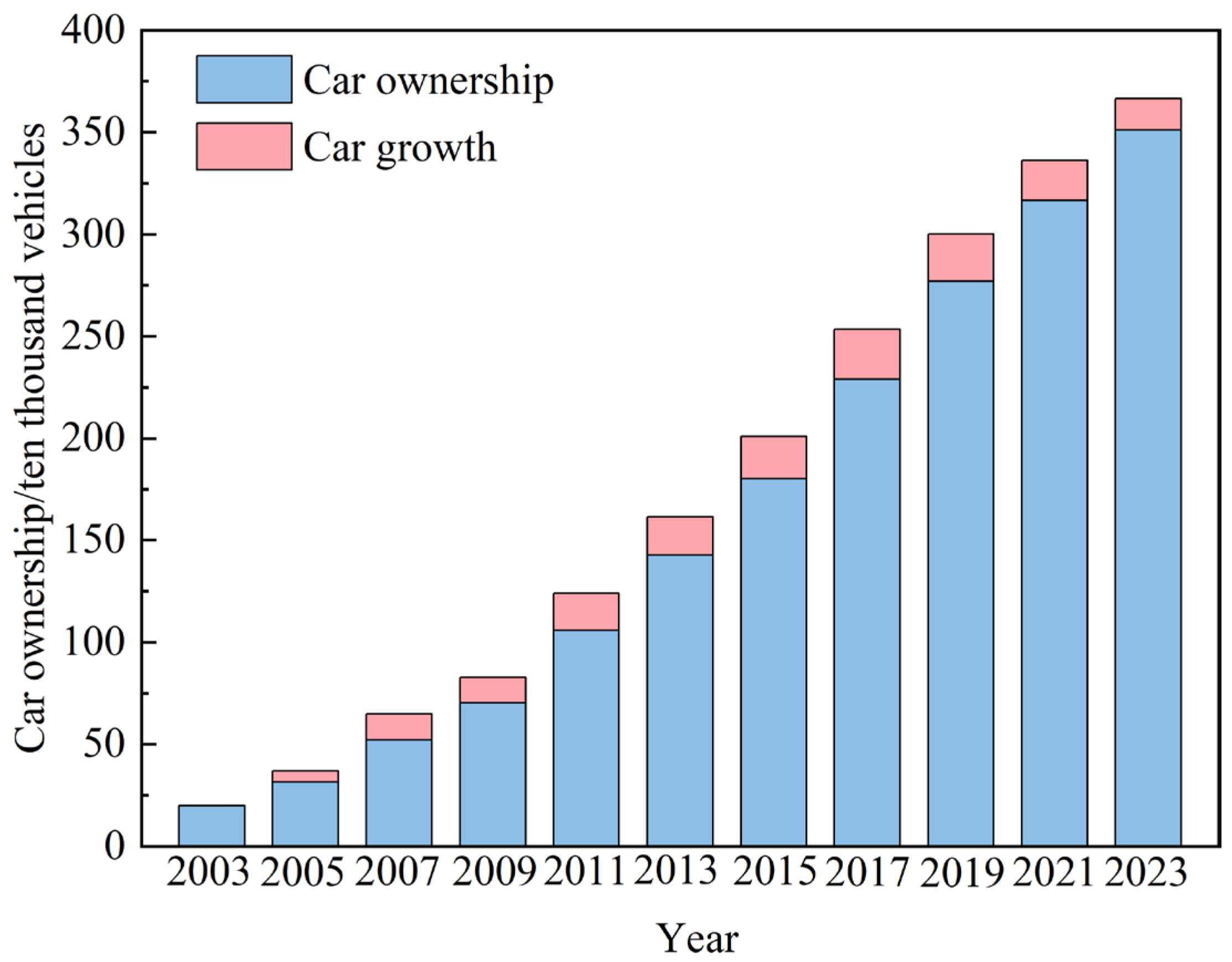
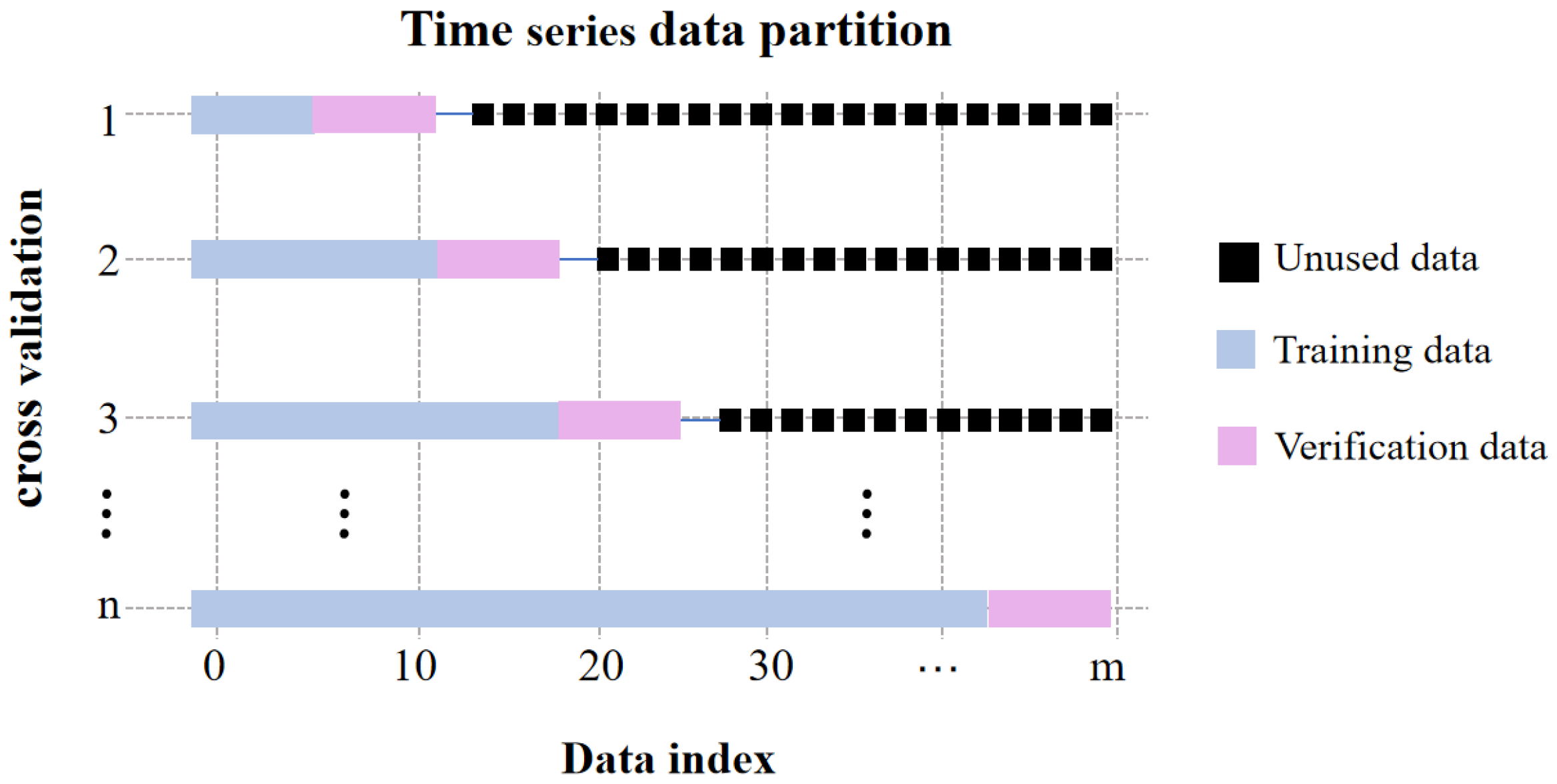
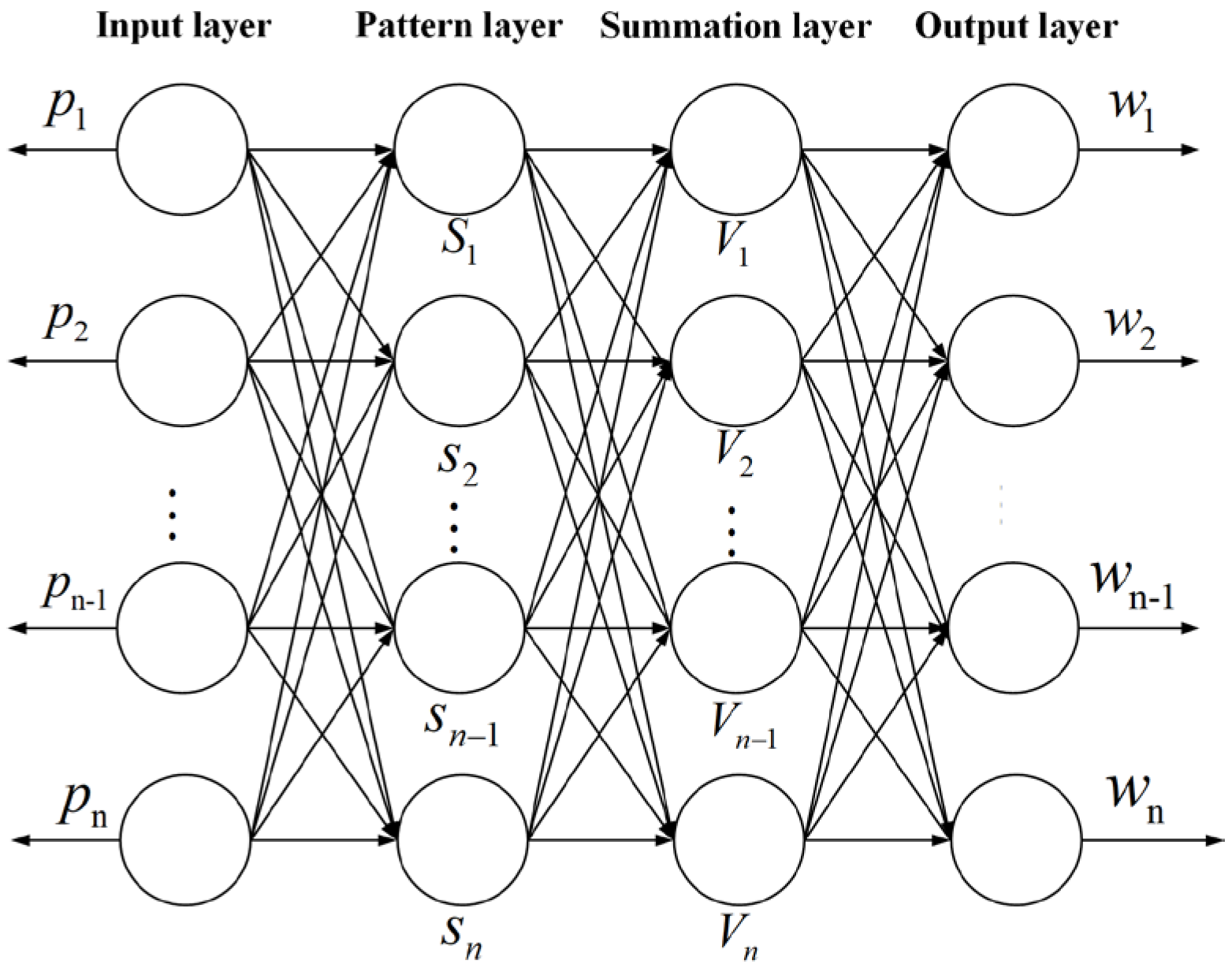
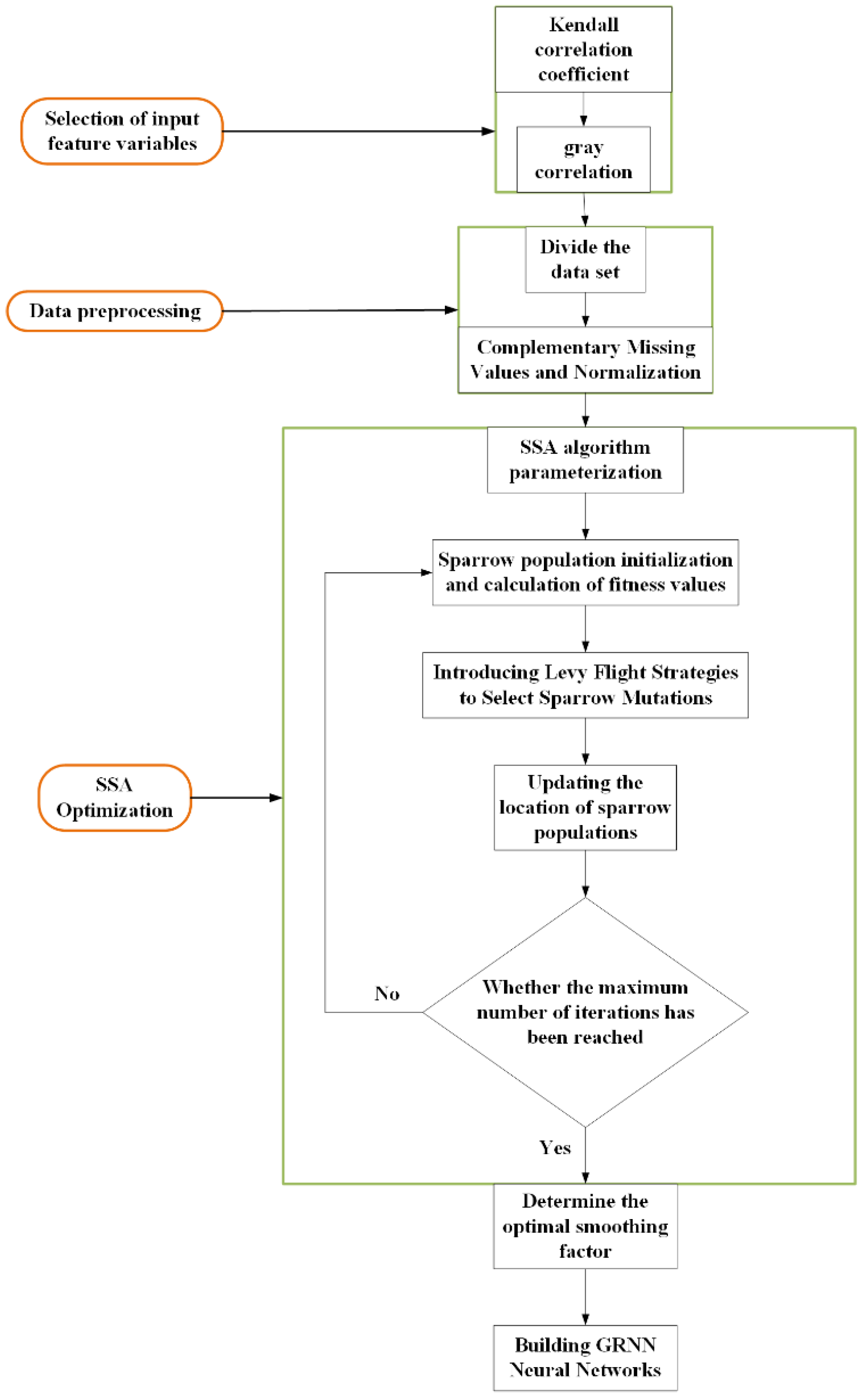
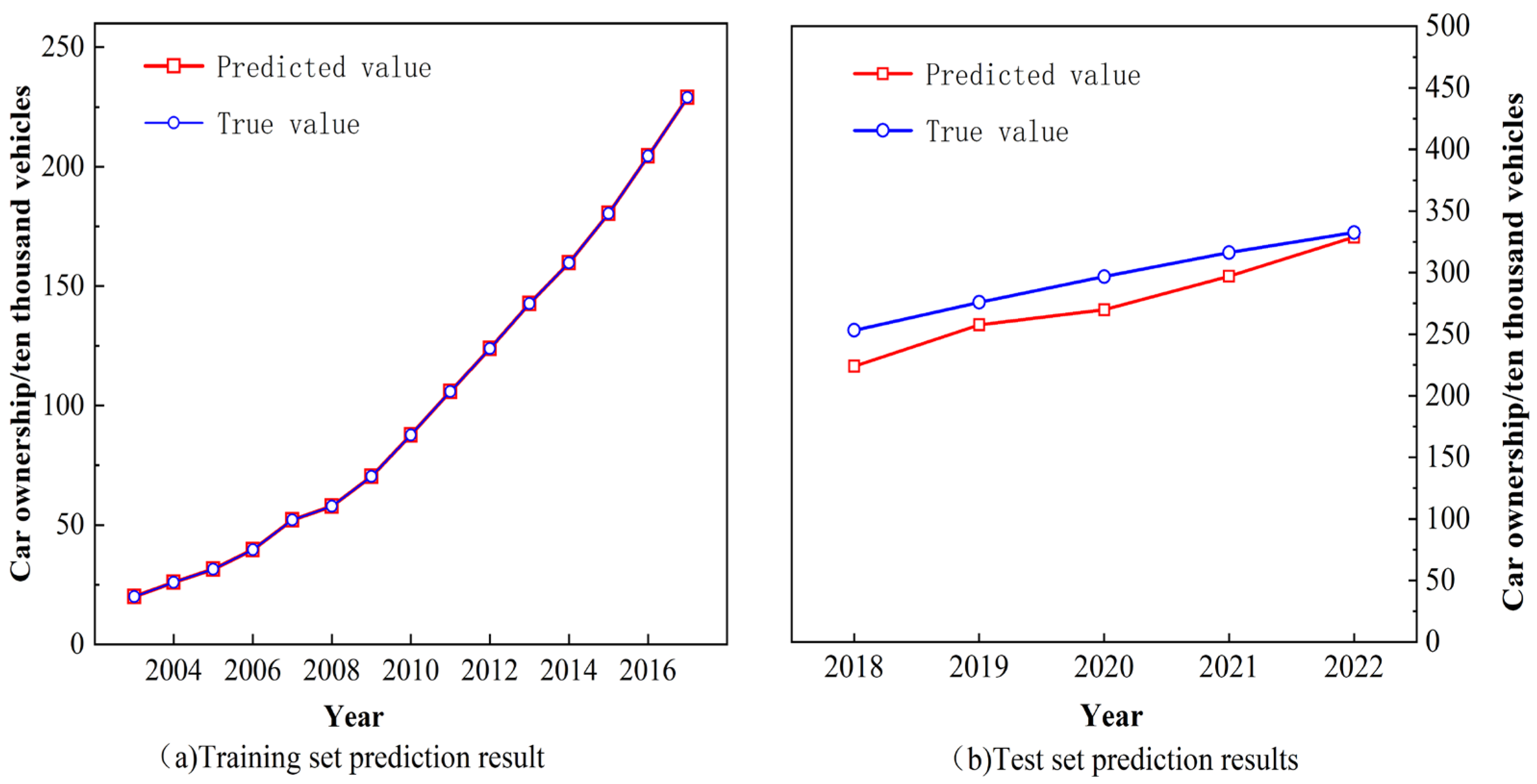
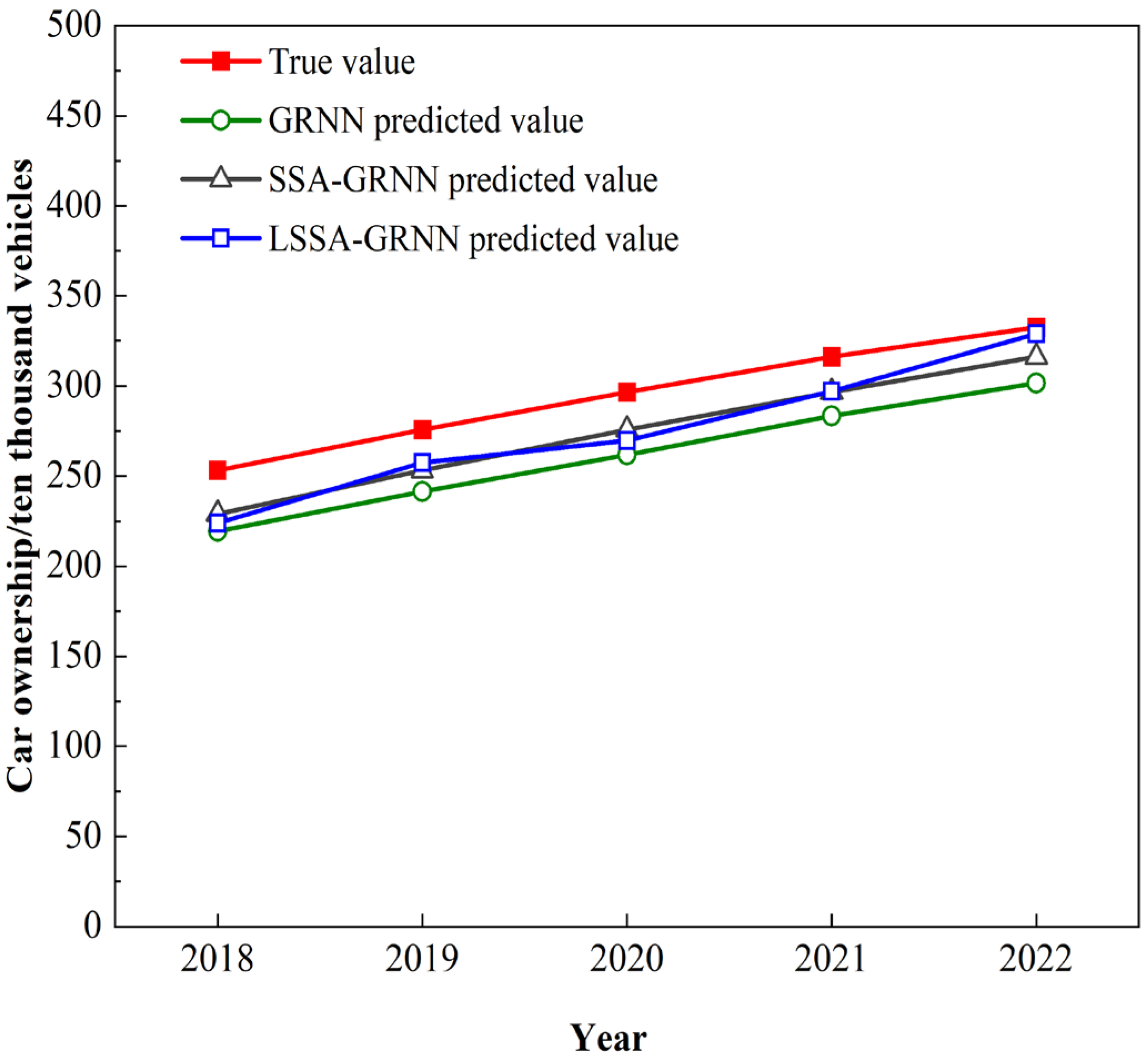
| Year | Ture Value | GRNN Predicted Value | SSA-GRNN Predicted Value | LSSA-GRNN Predicted Value |
|---|---|---|---|---|
| 2018 | 253.83 | 219.26 | 229.01 | 223.98 |
| 2019 | 277.02 | 241.53 | 253.09 | 257.60 |
| 2020 | 297.14 | 261.73 | 275.81 | 269.76 |
| 2021 | 316.58 | 283.30 | 296.72 | 297.08 |
| 2022 | 335.71 | 301.63 | 316.23 | 328.86 |
| Year | Ture Value | RMSE of GRNN | RMSE of SSA-GRNN | RMSE of LSSA-GRNN |
|---|---|---|---|---|
| 2018 | 253.83 | 0.1337 | 0.9512 | 0.0645 |
| 2019 | 277.02 | 0.1243 | 0.08238 | 0.0616 |
| 2020 | 297.14 | 0.1146 | 0.0704 | 0.0438 |
| 2021 | 316.58 | 0.1041 | 0.0617 | 0.0396 |
| 2022 | 335.71 | 0.0928 | 0.0489 | 0.0287 |
| Year | Urban per Capita Disposable Income/Yuan | Rural per Capita Disposable Income/Yuan | Total Retail Sales of Consumer Goods/Billion Yuan | GDP/Billion Yuan |
|---|---|---|---|---|
| 2023 | 81,759.20 | 48,753.97 | 5347.27 | 17,068.20 |
| 2024 | 86,758.19 | 53,001.04 | 5768.46 | 18,700.41 |
| 2025 | 92,179.26 | 57,644.43 | 6228.92 | 20,454.93 |
| 2026 | 97,921.53 | 62,721.30 | 6727.62 | 22,386.43 |
| 2027 | 104,028.69 | 68,266.77 | 7266.56 | 24,500.67 |
| 2028 | 110,517.64 | 74,320.96 | 7848.69 | 26,814.84 |
| 2029 | 117,412.62 | 80,928.31 | 8474.03 | 29,347.67 |
| 2030 | 124,738.43 | 88,137.71 | 9152.03 | 32,119.80 |
| System | Subsectors | Terminal Equipment | Consumption of Energy |
|---|---|---|---|
| Passenger transport | Individual transport | Microbus | Petrol |
| Electricity | |||
| Public transport | Medium and large buses | Diesel | |
| Electricity | |||
| Public Trams | Natural Gas | ||
| Diesel | |||
| Electricity | |||
| Taxi | Petrol | ||
| Natural gas | |||
| Electricity | |||
| Railway | Electricity |
| Terminal Equipment | Ownership (Vehicles) | Average Annual Mileage (km) | Energy Consumption | Fuel Share (%) | Energy Consumption per 100 km |
|---|---|---|---|---|---|
| Microbus | 2,891,345 | 12,222.88 | Petrol | 94.5 | 8.82 L/100 km |
| Electricity | 5.5 | 15.1 kw·h/100 km | |||
| Medium and large buses | 35,546 | 43,333 | Diesel | 100 | 20 L/100 km |
| Electricity | 0 | 64.5 kw·h/100 km | |||
| Public Trams | 9063 | 52,118.64 | Natural Gas | 11 | 33.18 m3/100 km |
| Diesel | 16 | 30.2 L/100 km | |||
| Electricity | 73 | 64.5 kw·h/100 km | |||
| Taxi | 6135 | 79,198.43 | Petrol | 76 | 16.45 m3/100 km |
| Natural gas | 2 | 8.62 L/100 km | |||
| Electricity | 22 | 15.1 kw·h/100 km | |||
| Railway | 1056 | 23,287 | Electricity | 100 | 184.33 kw·h/100 km |
| Fuel Type | Carbon Content per Unit t C/GJ | Carbon Oxidation Rate% | Carbon Dioxide Emission Factor Kg CO2/GJ or kg CO2/kW·h |
|---|---|---|---|
| Petrol | 0.0189 | 98 | 67.92 kg CO2/GJ |
| Diesel | 0.0202 | 98 | 72.64 kg CO2/GJ |
| Natural Gas | 0.0153 | 99 | 55.56 kg CO2/GJ |
| Electricity | / | / | 0.5153 kg CO2/kW·h |
| Scenario Name | Intensity of Measures to Promote Public Transport | Intensity of Measures to Change the Energy Mix of Vehicles |
|---|---|---|
| Integrated Scenario Ⅰ | Promoting Public Transport Ⅰ | Transforming the Automotive Energy Mix Ⅰ |
| Integrated Scenario Ⅱ | Promoting Public Transport Ⅱ | Transforming the Automotive Energy Mix Ⅰ |
| Integrated Scenario III | Promoting Public Transport Ⅰ | Transforming the Automotive Energy Mix Ⅱ |
| Integrated Scenario Ⅳ | Promoting Public Transport Ⅱ | Transforming the Automotive Energy Mix Ⅱ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Guo, L.; Xiao, R. Study on Carbon Emissions from Road Traffic in Ningbo City Based on LEAP Modelling. Sustainability 2025, 17, 3969. https://doi.org/10.3390/su17093969
Lu Y, Guo L, Xiao R. Study on Carbon Emissions from Road Traffic in Ningbo City Based on LEAP Modelling. Sustainability. 2025; 17(9):3969. https://doi.org/10.3390/su17093969
Chicago/Turabian StyleLu, Yan, Lin Guo, and Runmou Xiao. 2025. "Study on Carbon Emissions from Road Traffic in Ningbo City Based on LEAP Modelling" Sustainability 17, no. 9: 3969. https://doi.org/10.3390/su17093969
APA StyleLu, Y., Guo, L., & Xiao, R. (2025). Study on Carbon Emissions from Road Traffic in Ningbo City Based on LEAP Modelling. Sustainability, 17(9), 3969. https://doi.org/10.3390/su17093969






