Analysis of Sustainable Municipal Solid Waste Management Alternatives Based on Source Separation Using the Analytic Hierarchy Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Deciding on MSW Management Alternatives and Scenarios
2.2. Deciding on Criteria Influencing Decision Points
2.3. Decision Making with Analytic Hierarchy Process
2.4. Attaining Opinions of Experts
3. Results
3.1. Pairwise Comparison of Sub-Criteria Based on Selected Source Separation Methods
3.2. Pairwise Comparison of Sub-Criteria Based on MSW Management Scenarios
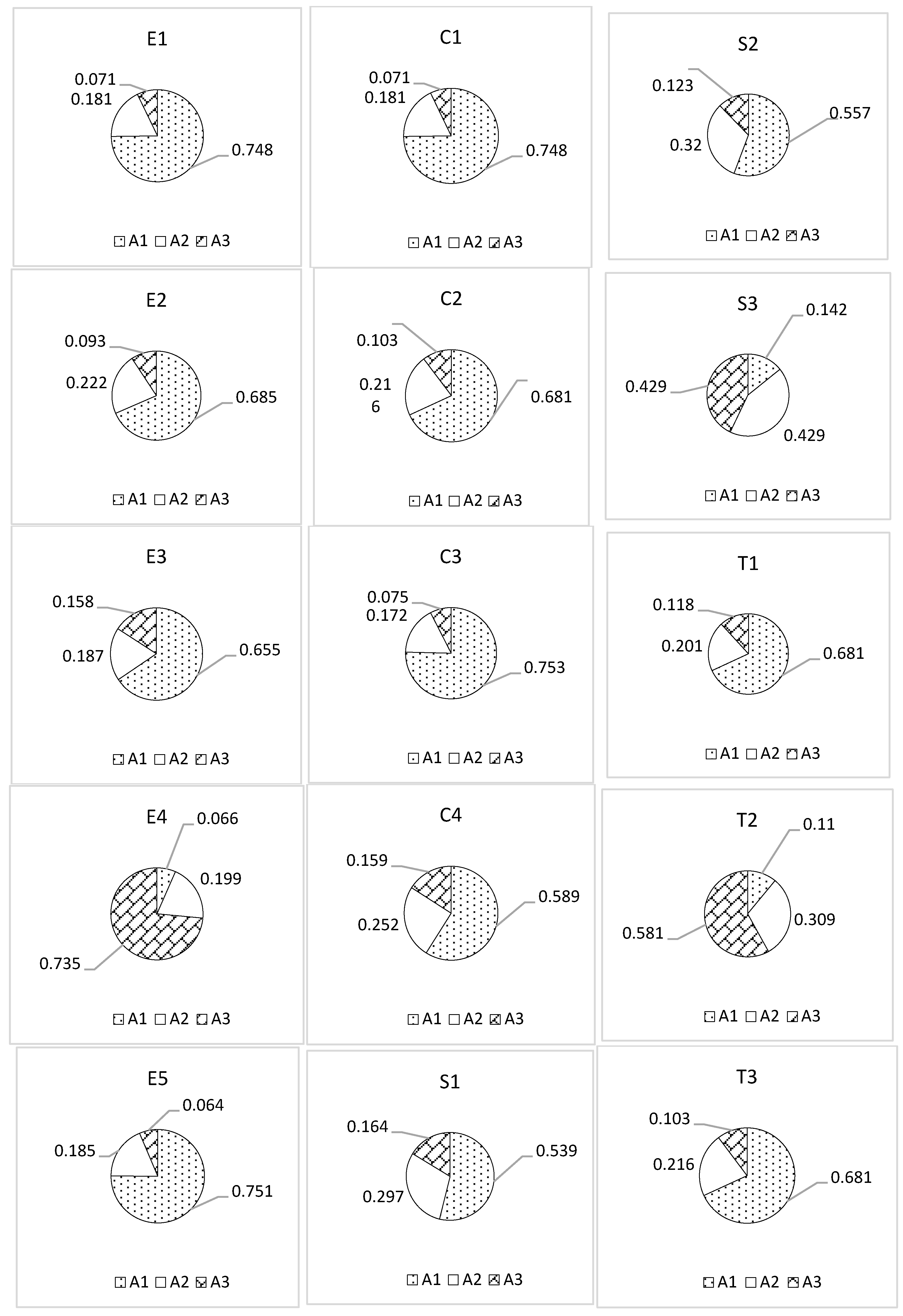
3.3. Decision of MSW Management Scenarios for Each Sub-Criterion Based on Source Separation Methods
3.4. Sensitivity Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Mixed | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | 1 | 3 | 4 | 5 |
| C2 | 1/3 | 1 | 3 | 4 |
| C3 | 1/4 | 1/3 | 1 | 2 |
| C4 | 1/5 | 1/4 | 1/2 | 1 |
| Sum | 1.78 | 4.58 | 8.50 | 12 |
| Mixed | C1 | C2 | C3 | C4 | Priority Vector |
|---|---|---|---|---|---|
| C1 | 0.561 | 0.655 | 0.470 | 0.417 | 0.526 |
| C2 | 0.187 | 0.218 | 0.353 | 0.333 | 0.273 |
| C3 | 0.140 | 0.073 | 0.118 | 0.167 | 0.124 |
| C4 | 0.112 | 0.054 | 0.059 | 0.083 | 0.077 |
| Σ = 1.000 | |||||
| λmax = 4.12, CI = 0.038, RI = 0.9, CR = 0.043 < 0.1 OK | |||||
| Mixed | S1 | S2 | S3 |
|---|---|---|---|
| S1 | 1 | 2 | 6 |
| S2 | 1/2 | 1 | 4 |
| S3 | 1/6 | 1/4 | 1 |
| Sum | 1.67 | 3.25 | 11 |
| Mixed | S1 | S2 | S3 | Priority Vector |
|---|---|---|---|---|
| S1 | 0.600 | 0.615 | 0.545 | 0.587 |
| S2 | 0.300 | 0.308 | 0.364 | 0.324 |
| S3 | 0.100 | 0.077 | 0.091 | 0.089 |
| Σ = 1.000 | ||||
| λmax = 3.01, CI = 0.005, RI = 0.58, CR = 0.008 < 0.1 OK | ||||
| Mixed | T1 | T2 | T3 |
|---|---|---|---|
| T1 | 1 | 3 | 4 |
| T2 | 1/3 | 1 | 2 |
| T3 | 1/4 | 1/2 | 1 |
| Sum | 1.58 | 4.50 | 7 |
| Mixed | T1 | T2 | T3 | Priority Vector |
|---|---|---|---|---|
| T1 | 0.632 | 0.667 | 0.571 | 0.623 |
| T2 | 0.211 | 0.222 | 0.286 | 0.240 |
| T3 | 0.157 | 0.111 | 0.143 | 0.137 |
| Σ = 1.000 | ||||
| λmax = 3.02, CI = 0.009, RI = 0.58, CR = 0.016 < 0.1 OK | ||||
| S@2S | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | 1 | 1/3 | 1/6 | 3 |
| C2 | 3 | 1 | 1/4 | 4 |
| C3 | 6 | 4 | 1 | 7 |
| C4 | 1/3 | 1/4 | 1/7 | 1 |
| Sum | 10.30 | 5.58 | 1.56 | 15 |
| S@2S | C1 | C2 | C3 | C4 | Priority Vector |
|---|---|---|---|---|---|
| C1 | 0.097 | 0.060 | 0.107 | 0.200 | 0.116 |
| C2 | 0.290 | 0.179 | 0.160 | 0.267 | 0.224 |
| C3 | 0.581 | 0.716 | 0.641 | 0.467 | 0.601 |
| C4 | 0.032 | 0.045 | 0.092 | 0.066 | 0.059 |
| Σ = 1.00 | |||||
| λmax = 4.18, CI = 0.06, RI = 0.9, CR = 0.07 < 0.1 OK | |||||
| S@2S | S1 | S2 | S3 |
|---|---|---|---|
| S1 | 1 | 1 | 5 |
| S2 | 1 | 1 | 4 |
| S3 | 1/5 | 1/4 | 1 |
| Sum | 2.20 | 2.25 | 10 |
| S@2S | S1 | S2 | S3 | Priority Vector |
|---|---|---|---|---|
| S1 | 0.455 | 0.444 | 0.500 | 0.466 |
| S2 | 0.455 | 0.444 | 0.400 | 0.433 |
| S3 | 0.090 | 0.112 | 0.100 | 0.101 |
| Σ = 1.00 | ||||
| λmax = 3.01, CI = 0.003, RI = 0.58, CR = 0.005 < 0.1 OK | ||||
| S@2S | T1 | T2 | T3 |
|---|---|---|---|
| T1 | 1 | 3 | 1/4 |
| T2 | 1/3 | 1 | 1/7 |
| T3 | 4 | 7 | 1 |
| Sum | 5.33 | 11 | 1.39 |
| S@2S | T1 | T2 | T3 | Priority Vector |
|---|---|---|---|---|
| T1 | 0.188 | 0.273 | 0.179 | 0.213 |
| T2 | 0.062 | 0.091 | 0.103 | 0.085 |
| T3 | 0.750 | 0.636 | 0.718 | 0.702 |
| Σ = 1.00 | ||||
| λmax = 3.03 CI = 0.02, RI = 0.58, CR = 0.03 < 0.1 OK | ||||
| S@3S | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| C1 | 1 | 1/4 | 1/7 | 3 |
| C2 | 4 | 1 | 1/4 | 5 |
| C3 | 7 | 4 | 1 | 9 |
| C4 | 1/3 | 1/5 | 1/9 | 1 |
| Sum | 12.33 | 5.45 | 1.50 | 18 |
| S@3S | C1 | C2 | C3 | C4 | Priority Vector |
|---|---|---|---|---|---|
| C1 | 0.081 | 0.046 | 0.095 | 0.167 | 0.097 |
| C2 | 0.324 | 0.183 | 0.166 | 0.277 | 0.238 |
| C3 | 0.567 | 0.734 | 0.665 | 0.500 | 0.617 |
| C4 | 0.027 | 0.037 | 0.074 | 0.056 | 0.048 |
| Σ = 1.00 | |||||
| λmax = 4.18, CI = 0.061, RI = 0.9, CR = 0.068 < 0.1 OK | |||||
| S@3S | S1 | S2 | S3 |
|---|---|---|---|
| S1 | 1 | 1 | 6 |
| S2 | 1 | 1 | 5 |
| S3 | 1/6 | 1/5 | 1 |
| Sum | 2.17 | 2.20 | 12 |
| S@3S | S1 | S2 | S3 | Priority Vector |
|---|---|---|---|---|
| S1 | 0.461 | 0.455 | 0.500 | 0.472 |
| S2 | 0.461 | 0.455 | 0.417 | 0.444 |
| S3 | 0.078 | 0.091 | 0.083 | 0.084 |
| Σ = 1.00 | ||||
| λmax = 3.004, CI = 0.002, RI = 0.58, CR = 0.003 < 0.1 OK | ||||
| S@3S | T1 | T2 | T3 |
|---|---|---|---|
| T1 | 1 | 2 | 1/3 |
| T2 | 1/2 | 1 | 1/5 |
| T3 | 3 | 5 | 1 |
| Sum | 4.50 | 8 | 1.53 |
| S@3S | T1 | T2 | T3 | Priority Vector |
|---|---|---|---|---|
| T1 | 0.222 | 0.250 | 0.217 | 0.230 |
| T2 | 0.111 | 0.125 | 0.130 | 0.122 |
| T3 | 0.667 | 0.625 | 0.653 | 0.648 |
| Σ = 1.00 | ||||
| λmax = 3.004, CI = 0.002, RI = 0.58, CR = 0.003 < 0.1 OK | ||||
Appendix B
| E1 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 5 | 9 |
| A2 | 1/5 | 1 | 3 |
| A3 | 1/9 | 1/3 | 1 |
| Sum | 1.31 | 6.33 | 13 |
| E1 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.763 | 0.789 | 0.692 | 0.748 |
| A2 | 0.153 | 0.158 | 0.231 | 0.181 |
| A3 | 0.084 | 0.053 | 0.077 | 0.071 |
| Σ = 1.00 | ||||
| λmax = 3.03, CI = 0.015, RI = 0.58, CR = 0.025 < 0.1 OK | ||||
| E2 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 4 | 6 |
| A2 | 1/4 | 1 | 3 |
| A3 | 1/6 | 1/3 | 1 |
| Sum | 1.42 | 5.33 | 10 |
| E2 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.706 | 0.75 | 0.6 | 0.685 |
| A2 | 0.176 | 0.188 | 0.3 | 0.222 |
| A3 | 0.118 | 0.062 | 0.1 | 0.093 |
| Σ = 1.00 | ||||
| λmax = 3.054, CI = 0.027, RI = 0.58, CR = 0.047 < 0.1 OK | ||||
| E3 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 3 | 5 |
| A2 | 1/3 | 1 | 1 |
| A3 | 1/5 | 1 | 1 |
| Sum | 1.53 | 5 | 7 |
| E3 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.652 | 0.6 | 0.714 | 0.655 |
| A2 | 0.217 | 0.2 | 0.143 | 0.187 |
| A3 | 0.131 | 0.2 | 0.143 | 0.158 |
| Σ = 1.00 | ||||
| λmax = 3.03, CI = 0.015, RI = 0.58, CR = 0.025 < 0.1 OK | ||||
| E4 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 1/4 | 1/9 |
| A2 | 4 | 1 | 1/5 |
| A3 | 9 | 5 | 1 |
| Sum | 14 | 6.25 | 1.31 |
| E4 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.071 | 0.04 | 0.084 | 0.066 |
| A2 | 0.286 | 0.16 | 0.153 | 0.199 |
| A3 | 0.643 | 0.8 | 0.763 | 0.735 |
| Σ = 1.00 | ||||
| λmax = 3.07, CI = 0.036, RI = 0.58, CR = 0.062 < 0.1 OK | ||||
| E5 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 6 | 9 |
| A2 | 1/6 | 1 | 4 |
| A3 | 1/9 | 1/4 | 1 |
| Sum | 1.28 | 7.25 | 14 |
| E5 | A1 | A2 | A3 | Priority vector |
|---|---|---|---|---|
| A1 | 0.783 | 0.828 | 0.643 | 0.751 |
| A2 | 0.13 | 0.138 | 0.286 | 0.185 |
| A3 | 0.087 | 0.034 | 0.071 | 0.064 |
| Σ = 1.00 | ||||
| λmax = 3.11, CI = 0.055, RI = 0.58, CR = 0.096 < 0.1 OK | ||||
| C1 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 5 | 9 |
| A2 | 1/5 | 1 | 3 |
| A3 | 1/9 | 1/3 | 1 |
| Sum | 1.31 | 6.33 | 13 |
| C1 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.763 | 0.789 | 0.692 | 0.748 |
| A2 | 0.152 | 0.158 | 0.231 | 0.181 |
| A3 | 0.085 | 0.053 | 0.077 | 0.071 |
| Σ = 1.00 | ||||
| λmax = 3.03, CI = 0.015, RI = 0.58, CR = 0.025 < 0.1 OK | ||||
| C2 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 3 | 7 |
| A2 | 1/3 | 1 | 2 |
| A3 | 1/7 | 1/2 | 1 |
| Sum | 1.48 | 4.5 | 10 |
| C2 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.677 | 0.667 | 0.7 | 0.681 |
| A2 | 0.226 | 0.222 | 0.2 | 0.216 |
| A3 | 0.097 | 0.111 | 0.1 | 0.103 |
| Σ = 1.00 | ||||
| λmax = 3.003, CI = 0.0013, RI = 0.58, CR = 0.0023 < 0.1 OK | ||||
| C3 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 6 | 8 |
| A2 | 1/6 | 1 | 3 |
| A3 | 1/8 | 1/3 | 1 |
| Sum | 1.29 | 7.33 | 12 |
| C3 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.774 | 0.818 | 0.667 | 0.753 |
| A2 | 0.129 | 0.136 | 0.25 | 0.172 |
| A3 | 0.097 | 0.046 | 0.083 | 0.075 |
| Σ = 1.00 | ||||
| λmax = 3.08, CI = 0.037, RI = 0.58, CR = 0.065 < 0.1 OK | ||||
| C4 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 3 | 3 |
| A2 | 1/3 | 1 | 2 |
| A3 | 1/3 | 1/2 | 1 |
| Sum | 1.67 | 4.5 | 6 |
| C4 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.600 | 0.667 | 0.5 | 0.589 |
| A2 | 0.200 | 0.222 | 0.333 | 0.252 |
| A3 | 0.200 | 0.111 | 0.167 | 0.159 |
| Σ = 1.000 | ||||
| λmax = 3.05, CI = 0.027, RI = 0.58, CR = 0.046 < 0.1 OK | ||||
| S1 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 2 | 3 |
| A2 | 1/2 | 1 | 2 |
| A3 | 1/3 | 1/2 | 1 |
| Sum | 1.83 | 3.50 | 6 |
| S1 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.545 | 0.571 | 0.500 | 0.539 |
| A2 | 0.273 | 0.286 | 0.333 | 0.297 |
| A3 | 0.182 | 0.143 | 0.167 | 0.164 |
| Σ = 1.000 | ||||
| λmax = 3.01, CI = 0.005, RI = 0.58, CR = 0.008 < 0.1 OK | ||||
| S2 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 2 | 4 |
| A2 | 1/2 | 1 | 3 |
| A3 | 1/4 | 1/3 | 1 |
| Sum | 1.75 | 3.33 | 8 |
| S2 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.571 | 0.600 | 0.500 | 0.557 |
| A2 | 0.286 | 0.300 | 0.375 | 0.320 |
| A3 | 0.143 | 0.100 | 0.125 | 0.123 |
| Σ = 1.00 | ||||
| λmax = 3.02, CI = 0.009, RI = 0.58, CR = 0.016 < 0.1 OK | ||||
| S3 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 1/3 | 1/3 |
| A2 | 3 | 1 | 1 |
| A3 | 3 | 1 | 1 |
| Sum | 7 | 2.33 | 2.33 |
| S3 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.1429 | 0.1428 | 0.1428 | 0.142 |
| A2 | 0.4285 | 0.4285 | 0.4286 | 0.429 |
| A3 | 0.4286 | 0.4286 | 0.4286 | 0.429 |
| Σ = 1.000 | ||||
| λmax = 3.06, CI = 0.028, RI = 0.58, CR = 0.048 < 0.1 OK | ||||
| T1 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 4 | 5 |
| A2 | 1/4 | 1 | 2 |
| A3 | 1/5 | 1/2 | 1 |
| Sum | 1.6 | 5.5 | 6 |
| T1 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.690 | 0.727 | 0.625 | 0.681 |
| A2 | 0.172 | 0.182 | 0.250 | 0.201 |
| A3 | 0.138 | 0.091 | 0.125 | 0.118 |
| Σ = 1.00 | ||||
| λmax = 3.03, CI = 0.012, RI = 0.58, CR = 0.021 < 0.1 OK | ||||
| T2 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 1/3 | 1/5 |
| A2 | 3 | 1 | 1/2 |
| A3 | 5 | 2 | 1 |
| Sum | 9 | 3.33 | 1.70 |
| T2 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.111 | 0.100 | 0.118 | 0.110 |
| A2 | 0.333 | 0.300 | 0.294 | 0.309 |
| A3 | 0.556 | 0.600 | 0.588 | 0.581 |
| Σ = 1.00 | ||||
| λmax = 3.004, CI = 0.002, RI = 0.58, CR = 0.003 < 0.1 OK | ||||
| T3 | A1 | A2 | A3 |
|---|---|---|---|
| A1 | 1 | 3 | 7 |
| A2 | 1/3 | 1 | 2 |
| A3 | 1/7 | 1/2 | 1 |
| Sum | 1.48 | 4.50 | 10 |
| T3 | A1 | A2 | A3 | Priority Vector |
|---|---|---|---|---|
| A1 | 0.677 | 0.667 | 0.700 | 0.681 |
| A2 | 0.226 | 0.222 | 0.200 | 0.216 |
| A3 | 0.097 | 0.111 | 0.100 | 0.103 |
| Σ = 1.00 | ||||
| λmax = 3.003, CI = 0.001, RI = 0.58, CR = 0.002 < 0.1 OK | ||||
Appendix C
| Alternatives | E1 (0.390) | E2 (0.162) | E3 (0.318) | E4 (0.078) | E5 (0.052) | Overall Priority Vector |
|---|---|---|---|---|---|---|
| A1 | 0.748 | 0.685 | 0.655 | 0.065 | 0.751 | 0.655 |
| A2 | 0.180 | 0.221 | 0.187 | 0.199 | 0.185 | 0.191 |
| A3 | 0.072 | 0.094 | 0.158 | 0.736 | 0.064 | 0.154 |
| Σ = 1.000 |
| Alternatives | C1 (0.525) | C2 (0.273) | C3 (0.124) | C4 (0.078) | Overall Priority Vector |
|---|---|---|---|---|---|
| A1 | 0.748 | 0.681 | 0.753 | 0.589 | 0.699 |
| A2 | 0.181 | 0.216 | 0.172 | 0.251 | 0.200 |
| A3 | 0.071 | 0.103 | 0.075 | 0.160 | 0.101 |
| Σ = 1.000 |
| Alternatives | S1 (0.587) | S2 (0.324) | S3 (0.089) | Overall Priority Vector |
|---|---|---|---|---|
| A1 | 0.539 | 0.557 | 0.142 | 0.510 |
| A2 | 0.297 | 0.320 | 0.429 | 0.316 |
| A3 | 0.164 | 0.123 | 0.429 | 0.174 |
| Σ = 1.000 |
| Alternatives | T1 (0.623) | T2 (0.239) | T3 (0.137) | Overall Priority Vector |
|---|---|---|---|---|
| A1 | 0.681 | 0.110 | 0.681 | 0.544 |
| A2 | 0.201 | 0.309 | 0.216 | 0.229 |
| A3 | 0.118 | 0.581 | 0.103 | 0.227 |
| Σ = 1.000 |
| Alternatives | E1 (0.046) | E2 (0.098) | E3 (0.160) | E4 (0.258) | E5 (0.438) | Overall Priority Vector |
|---|---|---|---|---|---|---|
| A1 | 0.748 | 0.685 | 0.655 | 0.065 | 0.751 | 0.553 |
| A2 | 0.180 | 0.221 | 0.187 | 0.199 | 0.185 | 0.192 |
| A3 | 0.072 | 0.094 | 0.158 | 0.736 | 0.064 | 0.255 |
| Σ = 1.000 |
| Alternatives | C1 (0.116) | C2 (0.224) | C3 (0.601) | C4 (0.059) | Overall Priority Vector |
|---|---|---|---|---|---|
| A1 | 0.748 | 0.681 | 0.753 | 0.589 | 0.673 |
| A2 | 0.181 | 0.216 | 0.172 | 0.252 | 0.217 |
| A3 | 0.071 | 0.103 | 0.075 | 0.159 | 0.110 |
| Σ = 1.000 |
| Alternatives | S1 (0.466) | S2 (0.433) | S3 (0.101) | Overall Priority Vector |
|---|---|---|---|---|
| A1 | 0.539 | 0.557 | 0.142 | 0.507 |
| A2 | 0.297 | 0.320 | 0.429 | 0.320 |
| A3 | 0.164 | 0.123 | 0.429 | 0.173 |
| Σ = 1.000 |
| Alternatives | T1 (0.213) | T2 (0.085) | T3 (0.702) | Overall Priority Vector |
|---|---|---|---|---|
| A1 | 0.681 | 0.110 | 0.681 | 0.632 |
| A2 | 0.201 | 0.309 | 0.216 | 0.221 |
| A3 | 0.118 | 0.581 | 0.103 | 0.147 |
| Σ = 1.000 |
| Alternatives | E1 (0.035) | E2 (0.082) | E3 (0.147) | E4 (0.252) | E5 (0.484) | Overall Priority Vector |
|---|---|---|---|---|---|---|
| A1 | 0.748 | 0.685 | 0.655 | 0.065 | 0.751 | 0.558 |
| A2 | 0.181 | 0.221 | 0.187 | 0.200 | 0.185 | 0.192 |
| A3 | 0.071 | 0.094 | 0.158 | 0.735 | 0.064 | 0.250 |
| Σ = 1.000 |
| Alternatives | C1 (0.097) | C2 (0.238) | C3 (0.617) | C4 (0.048) | Overall Priority Vector |
|---|---|---|---|---|---|
| A1 | 0.748 | 0.681 | 0.753 | 0.589 | 0.669 |
| A2 | 0.180 | 0.216 | 0.172 | 0.252 | 0.219 |
| A3 | 0.072 | 0.103 | 0.075 | 0.159 | 0.112 |
| Σ = 1.00 |
| Alternatives | S1 (0.472) | S2 (0.444) | S3 (0.084) | Overall Priority Vector |
|---|---|---|---|---|
| A1 | 0.539 | 0.557 | 0.142 | 0.514 |
| A2 | 0.297 | 0.320 | 0.429 | 0.318 |
| A3 | 0.164 | 0.123 | 0.429 | 0.168 |
| Σ = 1.000 |
| Alternatives | T1 (0.230) | T2 (0.122) | T3 (0.648) | Overall Priority Vector |
|---|---|---|---|---|
| A1 | 0.681 | 0.110 | 0.681 | 0.611 |
| A2 | 0.201 | 0.309 | 0.216 | 0.224 |
| A3 | 0.118 | 0.581 | 0.103 | 0.165 |
| Σ = 1.000 |
References
- Zaman, A.; Ahsan, T. Zero-Waste: Reconsidering Waste Management for the Future; Routledge: New York, NY, USA, 2020. [Google Scholar]
- Tchobanoglous, G.; Theisen, H.; Vigil, S.A. Integrated Solid Waste Management: Engineering Principles and Management Issues; McGraw Hill Inc.: New York, NY, USA, 1993. [Google Scholar]
- Apaydin, Ö.; Han, G.S.A. Analysis of Municipal Solid Waste Collection Methods Focusing on Zero-Waste Management Using an Analytical Hierarchy Process. Sustainability 2023, 15, 13184. [Google Scholar] [CrossRef]
- Anagnostopoulos, T.; Zaslavsky, A.; Kolomvatsos, K.; Medvedev, A.; Amirian, P.; Morley, J.; Hadjieftymiades, S. Challenges and Opportunities of Waste Management in IoT-Enabled Smart Cities: A Survey. IEEE Trans. Sustain. Comput. 2017, 2, 275–289. [Google Scholar] [CrossRef]
- Esmaeilian, B.; Wang, B.; Lewis, K.; Duarte, F.; Ratti, C.; Behdad, S. The future of waste management in smart and sustainable cities: A review and concept paper. Waste Manag. 2018, 81, 177–195. [Google Scholar] [CrossRef] [PubMed]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Modell. 1987, 9, 161–176. [Google Scholar] [CrossRef]
- Saaty, T.L. That is not the analytical hierarchical process: What the AHP is and what it is not. J. Multi Criteria Decis. Anal. 1998, 6, 320–329. [Google Scholar]
- Saaty, T.L. Rank from comparisons and from ratings in the analytic hierarchy/network processes. Eur. J. Oper. Res. 2006, 168, 557–570. [Google Scholar] [CrossRef]
- Demircan, B.G.; Yetilmezsoy, K. Ahybrid fuzzy AHP-TOPSIS approach for implementation of smart sustainable waste management strategies. Sustainability 2023, 15, 6256. [Google Scholar] [CrossRef]
- Tamasila, M.; Prostean, G.; Ivascu, L.; Cioca, L.I.; Draghici, A.; Diaconescu, A. Evaluating and prioritizing municipal solid waste management-related factors in Romania using fuzzy AHP and TOPSIS. J. Intell. Fuzzy Syst. 2020, 38, 6111–6127. [Google Scholar] [CrossRef]
- Shahnazari, A.; Pourdej, H.; Kharage, M.D. Ranking of organic fertilizer production from solid municipal waste systems using analytic hierarchy process (AHP) and VIKOR models. Biocatal. Agric. Biotechnol. 2021, 32, 101946. [Google Scholar] [CrossRef]
- Xi, H.; Li, Z.; Han, J.; Shen, D.; Li, N.; Long, Y.; Chen, Z.; Xu, L.; Zhang, X.; Niu, D.; et al. Evaluating the capability of municipal solid waste separation in China based on AHP-EWM, BP neural network. Waste Manag. 2022, 139, 208–216. [Google Scholar] [CrossRef]
- AlHumid, H.A.; Haider, H.; AlSaleem, S.S.; Shafiquzamman, M.; Sadiq, R. Performance indicators for municipal solid waste management systems in Saudi Arabia: Selection and ranking using fuzzy AHP and PROMETHEE II. Arab. J Geosci. 2019, 12, 491. [Google Scholar] [CrossRef]
- Zhou, X.; Xiang, X.; Wang, C.; Deng, Z.; Peng, D.; Li, Y.; Zhou, J. Study on evaluation method for the rural solid waste fixed bed gasification using the AHP-FCE based on exergy analysis. Int. J. Exergy 2023, 40, 365–391. [Google Scholar] [CrossRef]
- Ampofo, S.; Issifu, J.S.; Kusibu, M.M.; Mohammed, A.S.; Adiali, F. Selection of the final solid waste disposal site in the Bolgatanga municipality of Ghana using analytical hierarchy process (AHP) and multi-criteria evaluation (MCE). Heliyon 2023, 9, e18558. [Google Scholar] [CrossRef]
- Karimzadeh, K.; Tehrani, G.M.; Khaloo, S.S.; Vaziri, M.H.; Ardeh, S.A.; Saeedi, R. Quantitative assessment of health, safety, and environment (HSE) resilience based on the Delphi method and analytic hierarchy process (AHP) in municipal solid waste management system: A case study in Tehran. Environ. Health Eng. Manag. J. 2023, 10, 237–247. [Google Scholar] [CrossRef]
- Torkayesh, A.E.; Rajaeifar, M.A.; Rostom, M.; Malmir, B.; Yazdani, M.; Suh, S.; Heidrich, O. Integrating life cycle assessment and multi criteria decision making for sustainable waste management: Key issues and recommendations for future studies. Renew. Sustain. Energy Rev. 2022, 168, 112819. [Google Scholar] [CrossRef]
- Kumar, A.; Dixit, G. A novel hybrid MCDM framework for WEEE recycling partner evaluation on the basis of green competencies. J. Clean. Prod. 2019, 241, 118017. [Google Scholar] [CrossRef]
- Çoban, A.; Firtina Ertiş, I.; Ayvaz Cavdaroglu, N. Municipal solid waste management via multi-criteria decision making methods: A case study in Istanbul, Turkey. J. Clean. Prod. 2018, 180, 159–167. [Google Scholar] [CrossRef]
- Khan, I.; Kabir, Z. Waste-to-energy generation technologies and the developing economies: A multi-criteria analysis for sustainability assessment. Renew. Energy 2020, 150, 320–333. [Google Scholar] [CrossRef]
- Topaloglu, M.; Yarkin, F.; Kaya, T. Solid waste collection system selection for smart cities based on a type-2 fuzzy multi-criteria decision technique. Soft Comput. 2018, 22, 4879–4890. [Google Scholar] [CrossRef]
- Singh, A. Solid waste management through the applications of mathematical models. Resour. Conserv. Recycl. 2019, 151, 104503. [Google Scholar] [CrossRef]
- Al-Harbi, K.M.A.S. Application of the AHP in project management. Int. J. Proj. Manag. 2001, 19, 19–27. [Google Scholar] [CrossRef]
- Thomas, L.; Saaty, T.L.; Vargas, L.G. Models, Methods, Concepts and Applications of the Analytic Hierarchy Process, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- 1000minds. Decision-Making/Multi-Criteria Decision Analysis (MCDA/MCDM). Available online: https://www.1000minds.com/decision-making/what-is-mcdm-mcda (accessed on 21 March 2025).
- Goyal, S.; Garg, D.; Luthra, S. Sustainable production and consumption: Analysing barriers and solutions for maintaining green tomorrow by using fuzzy-AHP–fuzzy-TOPSIS hybrid framework. Environ. Dev. Sustain. 2021, 23, 16934–16980. [Google Scholar] [CrossRef]
- Alqaraleh, L.; Abu Hajar, H.A.; Matarneh, S. Multi-criteria sustainability assessment of solid waste management in Jordan. J. Environ. Manag. 2024, 366, 121929. [Google Scholar] [CrossRef]
- Syed, A.S.; Sierra-Sosa, D.; Kumar, A.; Elmaghraby, A. 2021 IoT in smart cities: A survey of technologies, practices and challenges. Smart Cities 2021, 4, 429–475. [Google Scholar] [CrossRef]
- Gopikumar, S.; Raja, S.; Robinson, Y.H.; Shanmuganathan, V.; Rho, S. A method of landfill leachate management using internet of things for sustainable smart city development. Sustain. Cities Soc. 2020, 66, 102521. [Google Scholar] [CrossRef]
- Sheng, T.J.; Islam, M.S.; Misran, N.; Baharuddin, M.H.; Arshad, H.; Islam, R.; Chowdhury, M.E.H.; Rmili, H. An internet of things based smart waste management system using lora and tensorflow deep learning model. IEEE Access 2020, 8, 148793–148811. [Google Scholar] [CrossRef]
- Gupta, Y.S.; Mukherjee, S.; Dutta, R.; Bhattacharya, S. A blockchain-based approach using smart contracts to develop a smart waste management system. Int. J. Environ. Sci. Technol. 2022, 19, 7833–7856. [Google Scholar] [CrossRef]
- Chauhan, A.; Jakhar, S.K.; Chauhan, C. The interplay of circular economy with industry 4.0 enabled smart city drivers of healthcare waste disposal. J. Clean. Prod. 2021, 279, 123854. [Google Scholar] [CrossRef]
- Seker, S. IoT based sustainable smart waste management system evaluation using MCDM model under interval-valued q-rung orthopair fuzzy environment. Technol. Soc. 2022, 71, 102100. [Google Scholar] [CrossRef]
- Apaydin, Ö.; Gönüllü, M.T. Emission control with route optimization in solid waste collection process: A case study. Sadhana-Acad. Proc. Eng. Sci. 2008, 33, 71–82. [Google Scholar] [CrossRef]
- Rhvner, C.R.; Schwartz, L.J.; Wenger, R.B.; Kohrell, M.G. Waste Management and Resource Recovery, 1st ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Tanner, R. Die Entwicklung der Von Roll Müllverbrennungsanlagen. Schweiz. Bauztg. 1965, 16, 251–260. [Google Scholar]
- Öztürk, İ. Katı Atık Yönetimi ve AB Uygulamaları; Teknik Kitaplar Serisi 2; İSTAÇ AŞ: Istanbul, Türkiye, 2010. [Google Scholar]
- Henaien, A.; Ben Elhadj, H.; Fourati, L.C. A sustainable smart IoT-based solid waste management system. Future Gener. Comput. Syst. Int. J. Sci. 2024, 157, 587–602. [Google Scholar] [CrossRef]
- Mujtaba, M.A.; Munir, A.; Imran, S.; Nasir, M.K.; Muhayyuddin, M.G.; Javed, A.; Mehmood, A.; Habila, M.A.; Fayaz, H.; Qazi, A. Evaluating sustainable municipal solid waste management scenarios: A multicriteria decision making approach. Heliyon 2024, 10, e25788. [Google Scholar] [CrossRef] [PubMed]




| Methods | Descriptions |
|---|---|
| Material recovery facility, MRF | These are the facilities where the separation of materials according to material group, size reduction process, supply of organic matter to compost processes, waste compression, temporary storage, and marketing operations is carried out (e.g., S@3S or S@2S). The more waste that is separated into components at the source and collected separately, the better it will be for these facilities. Thanks to these facilities, it is possible to integrate waste into secondary raw material processes and sustainable waste management, and thus, minimize natural resource use. |
| Composting process, CP | Thanks to this process, compost is produced from organic materials, which is an environmentally beneficial product that improves the soil structure and contributes to sustainable solid waste management. Source separation methods, in which organic substances are collected separately (e.g., S@3S), make a positive contribution to this process. |
| Biological methane process, BMP | Thanks to this process, organic substances are biologically transformed in an oxygen-free environment and methane is produced. Although the controlled transfer of methane via energy conversion processes is considered positive, if it is not controlled, negative greenhouse gas effects may occur. Source separation methods (e.g., S@3S), in which organic substances are collected separately, make a positive contribution to this process. |
| Thermal process, TP | The separate collection of materials with a high calorific value at the source makes a significant contribution to this process (e.g., S@2S or S@3S). It is known that mixed waste coming to this process will create negative processing processes. At the end of TPs, negative effects of flue gas formation and greenhouse gas formation are expected. For this reason, control costs related to the resulting flue gas, leachate, and ash come to the fore and require higher unit costs compared to other disposal processes. |
| Sanitary landfill, SLF | SLF, also known as the final disposal method, is negatively affected by the waste collected in a mixed manner per unit time, when viewed from the perspective of the waste hierarchy. Because waste is not separated at the source, more waste is disposed of in SLF facilities, resulting in a rapid decrease in SLF capacity. The integration of recyclable waste into secondary production processes is disrupted. If methane gas, which is likely to form under anaerobic conditions in SLF plants, cannot be controlled, it causes negative consequences due to the greenhouse effect. |
| MSW Management Scenarios and Methods | Source Separation Methods (Main Criteria) 1 | |||
|---|---|---|---|---|
| Scenarios | Methods | S@3S | S@2S | Mixed |
| A1 | MRF + SLF | + | + | - |
| A2 | MRF + CP + BMP + SLF | + | + | - |
| A3 | TP + CP + BMP + SLF | + | + | - |
| Sub-Criteria 1 | Sub-Criteria 2 |
|---|---|
| Environmental (E) | E1: Atmospheric emissions E2: Surface water pollution E3: Soil pollution E4: Energy recovery E5: Natural resource recovery |
| Economic (C) | C1: Initial investment costs C2: Operational costs C3: Maintenance costs C4: Transportation costs |
| Social (S) | S1: Increased awareness of sustainable city S2: Increased quality of life in the city S3: New job creation |
| Technical (T) | T1: Operational feasibility T2: Innovativeness T3: Need for qualified personnel |
| Scale | Degree of Preference |
|---|---|
| 1 | Equal importance |
| 3 | Moderate importance of one factor over another |
| 5 | Strong or essential importance |
| 7 | Very strong importance |
| 9 | Extreme importance |
| 2, 4, 6, 8 | Values for inverse comparison |
| Mixed | E1 | E2 | E3 | E4 | E5 |
|---|---|---|---|---|---|
| E1 | 1 | 3 | 2 | 4 | 5 |
| E2 | 1/3 | 1 | 1/3 | 3 | 4 |
| E3 | 1/2 | 3 | 1 | 5 | 6 |
| E4 | 1/4 | 1/3 | 1/5 | 1 | 2 |
| E5 | 1/5 | 1/4 | 1/6 | 1/2 | 1 |
| Sum | 2.28 | 7.58 | 3.70 | 13.50 | 18 |
| Mixed | E1 | E2 | E3 | E4 | E5 | Priority Vector |
|---|---|---|---|---|---|---|
| E1 | 0.050 | 0.029 | 0.037 | 0.049 | 0.066 | 0.389 |
| E2 | 0.150 | 0.088 | 0.074 | 0.083 | 0.092 | 0.162 |
| E3 | 0.200 | 0.177 | 0.148 | 0.124 | 0.153 | 0.318 |
| E4 | 0.250 | 0.265 | 0.296 | 0.248 | 0.230 | 0.079 |
| E5 | 0.350 | 0.441 | 0.445 | 0.496 | 0.459 | 0.052 |
| Σ = 1.000 | ||||||
| λmax = 5.20, CI = 0.051, RI = 1.12, CR = 0.046 < 0.1 OK | ||||||
| S@2S | E1 | E2 | E3 | E4 | E5 |
|---|---|---|---|---|---|
| E1 | 1 | 1/3 | 1/4 | 1/5 | 1/7 |
| E2 | 3 | 1 | 1/2 | 1/3 | 1/5 |
| E3 | 4 | 2 | 1 | 1/2 | 1/3 |
| E4 | 5 | 3 | 2 | 1 | 1/2 |
| E5 | 7 | 5 | 3 | 2 | 1 |
| Sum | 20 | 11.33 | 6.75 | 4.03 | 2.18 |
| S@2S | E1 | E2 | E3 | E4 | E5 | Priority Vector |
|---|---|---|---|---|---|---|
| E1 | 0.050 | 0.029 | 0.037 | 0.049 | 0.066 | 0.047 |
| E2 | 0.150 | 0.088 | 0.074 | 0.083 | 0.092 | 0.097 |
| E3 | 0.200 | 0.177 | 0.148 | 0.124 | 0.153 | 0.160 |
| E4 | 0.250 | 0.265 | 0.296 | 0.248 | 0.230 | 0.258 |
| E5 | 0.350 | 0.441 | 0.445 | 0.496 | 0.459 | 0.438 |
| Σ = 1.00 | ||||||
| λmax = 5.08, CI = 0.02, RI = 1.12, CR = 0.0018 < 0.1 OK | ||||||
| S@3S | E1 | E2 | E3 | E4 | E5 |
|---|---|---|---|---|---|
| E1 | 1 | 1/4 | 1/5 | 1/6 | 1/9 |
| E2 | 4 | 1 | 1/3 | 1/4 | 1/6 |
| E3 | 5 | 3 | 1 | 1/3 | 1/4 |
| E4 | 6 | 4 | 3 | 1 | 1/3 |
| E5 | 9 | 6 | 4 | 3 | 1 |
| Sum | 25 | 14.25 | 8.50 | 4.80 | 1.86 |
| S@S3 | E1 | E2 | E3 | E4 | E5 | Priority Vector |
|---|---|---|---|---|---|---|
| E1 | 0.04 | 0.018 | 0.023 | 0.035 | 0.060 | 0.035 |
| E2 | 0.16 | 0.070 | 0.039 | 0.053 | 0.090 | 0.082 |
| E3 | 0.20 | 0.211 | 0.117 | 0.070 | 0.134 | 0.147 |
| E4 | 0.24 | 0.281 | 0.352 | 0.211 | 0.179 | 0.252 |
| E5 | 0.36 | 0.420 | 0.469 | 0.631 | 0.537 | 0.484 |
| Σ = 1.00 | ||||||
| λmax = 5.29, CI = 0.072, RI = 1.12, CR = 0.065 < 0.1 OK | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Apaydın, Ö. Analysis of Sustainable Municipal Solid Waste Management Alternatives Based on Source Separation Using the Analytic Hierarchy Process. Sustainability 2025, 17, 3868. https://doi.org/10.3390/su17093868
Apaydın Ö. Analysis of Sustainable Municipal Solid Waste Management Alternatives Based on Source Separation Using the Analytic Hierarchy Process. Sustainability. 2025; 17(9):3868. https://doi.org/10.3390/su17093868
Chicago/Turabian StyleApaydın, Ömer. 2025. "Analysis of Sustainable Municipal Solid Waste Management Alternatives Based on Source Separation Using the Analytic Hierarchy Process" Sustainability 17, no. 9: 3868. https://doi.org/10.3390/su17093868
APA StyleApaydın, Ö. (2025). Analysis of Sustainable Municipal Solid Waste Management Alternatives Based on Source Separation Using the Analytic Hierarchy Process. Sustainability, 17(9), 3868. https://doi.org/10.3390/su17093868






