A Hybrid Prospect–Regret Decision-Making Method for Green Supply Chain Management Under the Interval Type-2 Trapezoidal Fuzzy Environment
Abstract
1. Introduction
- (i)
- The proposed model, which integrates the interval type-2 trapezoidal fuzzy set (IT2TFS) into cross-entropy, is applied to determine the weight distribution of the GSCM index.
- (ii)
- A novel approach for multi-criteria decision analysis, which utilizes the prospect theory incorporating the regret method under the IT2TFS environment, is applied to consider people’s psychological changes and further rank the GSCM schemes.
- (iii)
- The feasibility and applicability of the research methodology are demonstrated using the scheme of GSCM.
2. Literature Reviews
2.1. MCDM Methods in GSCM
2.2. Prospect and Regret Theory
2.3. Fuzzy Theory in GSCM
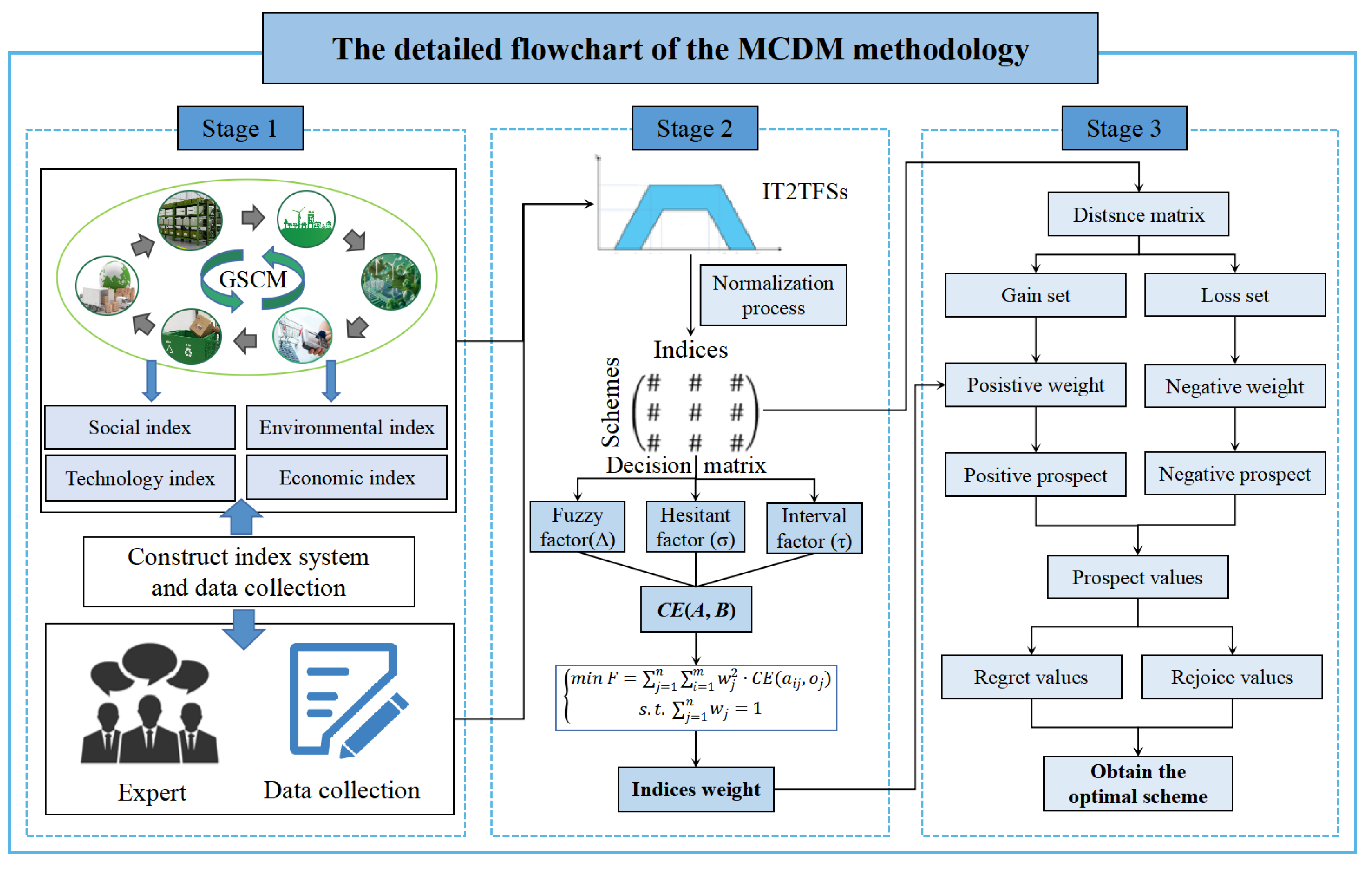
3. Method
3.1. Interval Type-2 Fuzzy Set
3.2. Fuzzy Cross-Entropy of IT2TFSs
3.3. The Framework of the Proposed Approach
3.4. Prospect–Regret Theory of IT2TFSs
4. Experimental Result and Discussion
4.1. Case Study
4.1.1. Background
4.1.2. Data Collection
4.1.3. Case Study
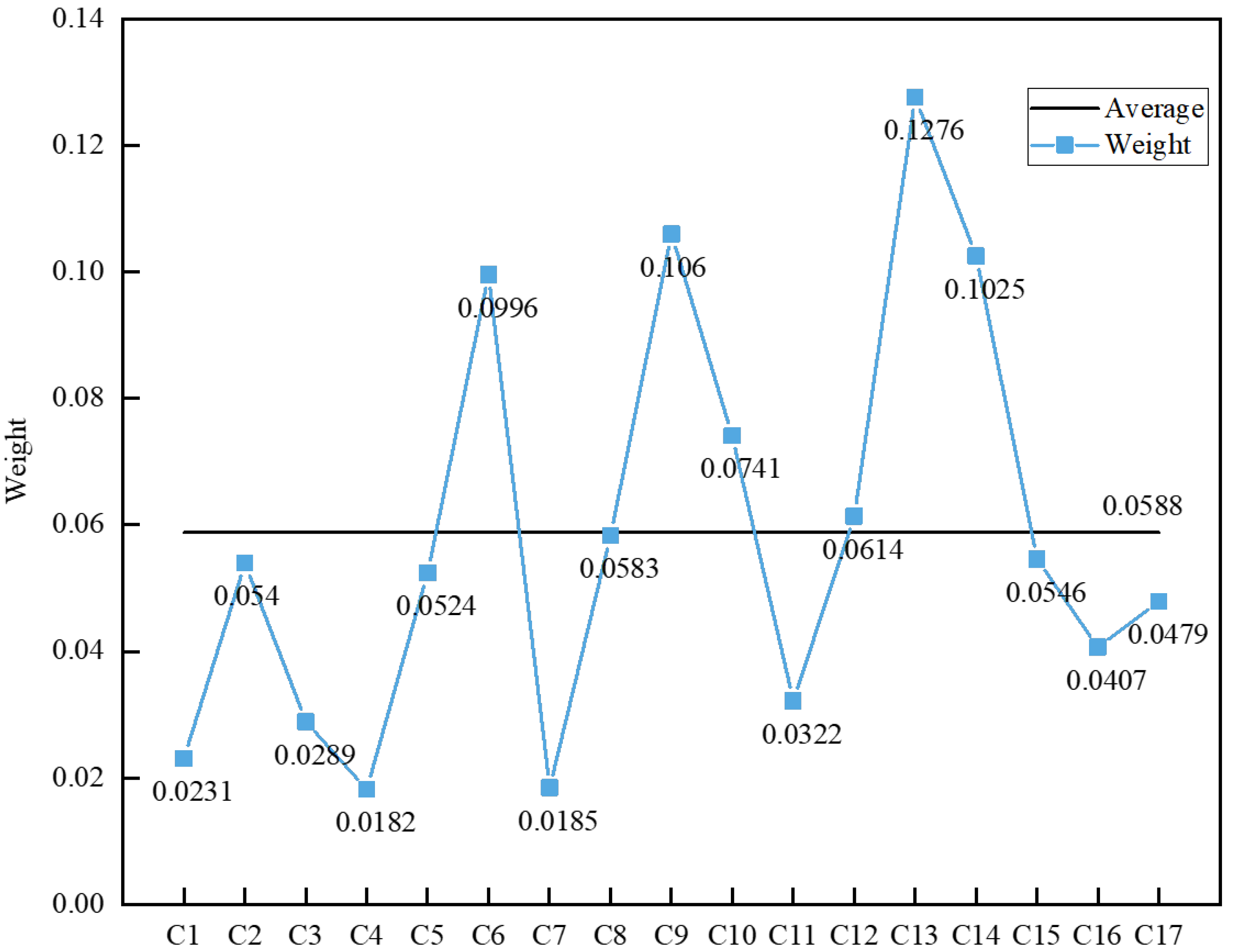
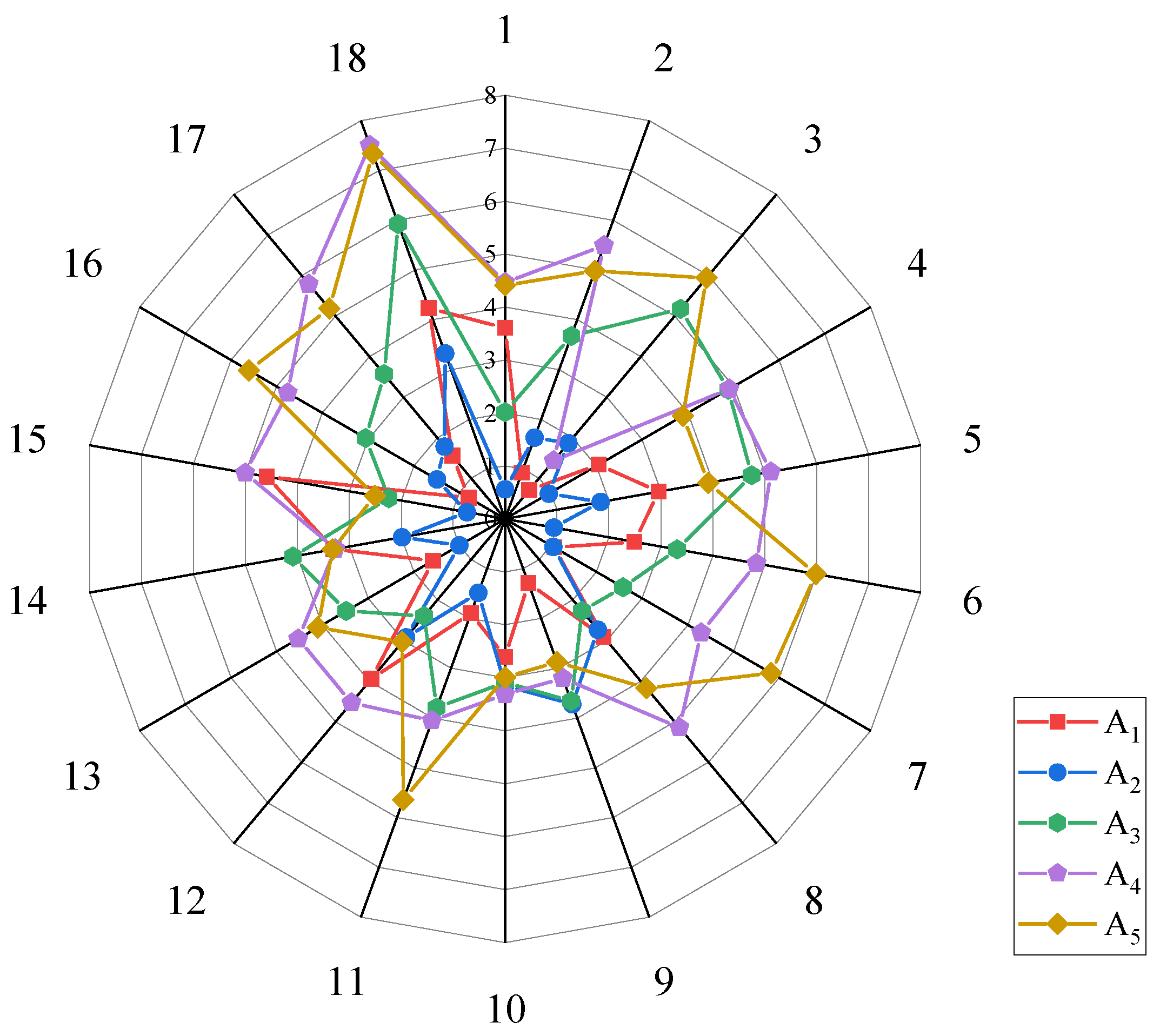
4.2. Sensitivity Analysis
4.3. Comparative Analysis
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, J.; Li, Q.; Zhao, Q.; Liou, J.; Li, C. From bytes to green: The impact of supply chain digitization on corporate green innovation. Energy Econ. 2024, 139, 107942. [Google Scholar] [CrossRef]
- Tseng, M.L.; Lim, M.; Wu, K.J.; Zhou, L.; Bui, D.T.D. A novel approach for enhancing green supply chain management using converged interval-valued triangular fuzzy numbers-grey relation analysis. Resour. Conserv. Recycl. 2018, 128, 122–133. [Google Scholar] [CrossRef]
- Zhang, H.H.; Huang, Z.W.; Tian, G.D.; Wang, W.J.; Li, Z.W. A hybrid QFD-based human-centric decision making approach of disassembly schemes under interval 2-tuple q-rung orthopair fuzzy sets. IEEE Trans. Autom. Sci. Eng. 2025, 22, 724–735. [Google Scholar] [CrossRef]
- Huang, Z.W.; Zhang, H.H.; Wang, D.Q.; Yu, H.; Wang, L.Y.; Yu, D.T.; Peng, Y. Preference-based multi-attribute decision-making method with spherical-Z fuzzy sets for green product design. Eng. Appl. Artif. Intell. 2023, 126, 106767. [Google Scholar] [CrossRef]
- My, L.T.D.; Wang, C.N.; Thanh, N.V. Fuzzy MCDM for improving the performance of agricultural supply chain. Cmc-Comput. Mater. Contin. 2022, 73, 4003–4015. [Google Scholar]
- Mohammed, A.; Harris, I.; Govindan, K. A hybrid MCDM-FMOO approach for sustainable supplier selection and order allocation. Int. J. Prod. Econ. 2019, 217, 171–184. [Google Scholar] [CrossRef]
- Chen, R.; Lepori, G.M.; Tai, C.C.; Sung, M.-C. Explaining cryptocurrency returns: A prospect theory perspective. J. Int. Financ. Mark. Inst. Money 2022, 79, 101599. [Google Scholar] [CrossRef]
- Zhao, Q.; Ju, Y.B.; Martinez, L.; Pedrycz, W.; Dong, P.; Wang, A. SMAA-Bicapacity-Choquet-Regret model for Heterogeneous linguistic MCDM with interactive criteria with bipolar ccale and 2-Tuple aspirations. IEEE Trans. Fuzzy Syst. 2022, 30, 4384–4398. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W.; Pedrycz, W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. Eur. J. Oper. Res. 2017, 258, 626–638. [Google Scholar]
- Qin, J.D.; Liu, X.W.; Pedrycz, W. A multiple attribute interval type-2 fuzzy group decision making and its application to supplier selection with extended LINMAP method. Soft Comput. 2017, 21, 3207–3226. [Google Scholar] [CrossRef]
- Ali, Z.; Mahmood, T.; Gwak, J.; Jan, N. A novel extended Portuguese of interactive and multi-criteria decision making and archimedean Bonferroni mean operators based on prospect theory to select green supplier with complex q-rung orthopair fuzzy information. Caai Trans. Intell. Technol. 2023, 8, 177–191. [Google Scholar]
- Zhao, Y.J.; Zhou, H. Remanufacturing vs. greening: Competitiveness and harmony of sustainable strategies of supply chain under uncertain yield. Comput. Ind. Eng. 2023, 179, 109233. [Google Scholar]
- Mumtaz, U.; Ali, Y.; Petrillo, A.; De Felice, F. Identifying the critical factors of green supply chain management: Environmental benefits in Pakistan. Sci. Total Environ. 2018, 640, 144–152. [Google Scholar]
- Liu, S.; Chang, Y.T. Manufacturers’ closed-loop orientation for green supply chain management. Sustainability 2017, 9, 222. [Google Scholar] [CrossRef]
- Zhang, D.; Shi, L.; Liu, G. Supply chain in transition navigating economic growth and environmental sustainability through education. Environ. Sci. Pollut. Res. 2024, 31, 12321–12339. [Google Scholar]
- Zhang, H.H.; Huang, Z.W.; Wang, D.Q.; Tian, G.D.; Wang, W.J. U-shaped disassembly line balancing problem under interval Type-2 trapezoidal fuzzy set: Modeling and solution method. Eng. Appl. Artif. Intell. 2025, 145, 110211. [Google Scholar]
- Tian, G.; Zhang, C.; Fathollahi-Fard, A.M.; Li, Z.; Zhang, C.; Jiang, Z. An enhanced social engineering optimizer for solving an energy-efficient disassembly dine balancing problem based on bucket brigades and cloud theory. IEEE Trans. Ind. Inf. 2023, 19, 7148–7159. [Google Scholar]
- Huang, Z.W.; Zhang, H.H.; Tian, G.D.; Yang, M.Z.; Wang, D.Q.; Li, Z.W. Energy-efficient human-robot collaborative U-shaped disassembly line balancing problem considering turn on-off strategy: Uncertain modeling and solution method. J. Manuf. Syst. 2025, 80, 38–69. [Google Scholar]
- Xu, J.; Meng, Q.; Chen, Y.; Zhao, J. Dual-channel pricing decisions for product recycling in green supply chain operations: Considering the impact of consumer loss aversion. Int. J. Environ. Res. Public Health 2023, 20, 1792. [Google Scholar] [CrossRef]
- Dorfeshan, Y.; Jolai, F.; Mousavi, S.M. A new risk quantification method in project-driven supply chain by MABACODAS method under interval type-2 fuzzy environment with a case study. Eng. Appl. Artif. Intell. 2023, 119, 105729. [Google Scholar]
- Qu, G.; Zhang, Z.; Qu, W.; Xu, Z. Green supplier selection based on green practices evaluated using fuzzy approaches of TOPSIS and ELECTRE with a case study in a Chinese internet company. Int. J. Environ. Res. Public Health 2020, 17, 3268. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.M.; Bin, Z.L.; Shi, B.; Cao, W. Sustainable supplier selection based on regret theory and QUALIFLEX method. Int. J. Comput. Intell. Syst. 2020, 13, 1120–1133. [Google Scholar] [CrossRef]
- Nie, S.; Liao, H.; Wu, X.; Xu, Z. Green supplier selection with a continuous interval-valued linguistic TODIM method. IEEE Access 2019, 7, 124315–124328. [Google Scholar] [CrossRef]
- Tian, X.L.; Niu, M.L.; Zhang, W.K.; Li, L.; Herrera-Viedma, E. A novel TODIM based on prospect theory to select green supplier with q-rung orthopair fuzzy set. Technol. Econ. Dev. Econ. 2021, 27, 284–310. [Google Scholar] [CrossRef]
- Chithambaranathan, P.; Subramanian, N.; Gunasekaran, A.; Palaniappan, P.K. Service supply chain environmental performance evaluation using grey based hybrid MCDM approach. Int. J. Prod. Econ. 2015, 166, 163–176. [Google Scholar]
- Liou, J.J.H.; Chang, M.H.; Lo, H.W.; Hsu, M.-H. Application of an MCDM model with data mining techniques for green supplier evaluation and selection. Appl. Soft Comput. 2021, 109, 107534. [Google Scholar] [CrossRef]
- Liou, J.J.H.; Chuang, Y.C.; Zavadskas, E.K.; Tzeng, G.-H. Data-driven hybrid multiple attribute decision-making model for green supplier evaluation and performance improvement. J. Clean. Prod. 2019, 241, 118321. [Google Scholar]
- Xie, G.; Zhu, W.; Xiang, J.; Li, T.; Wu, X.; Peng, Y.; Zhang, H.; Wang, K. A behavior three-way decision approach under interval-valued triangular fuzzy numbers with application to the selection of additive manufacturing composites. Eng. Appl. Artif. Intell. 2024, 137, 109214. [Google Scholar]
- Song, W.; Chen, Z.Y.; Liu, A.J.; Zhu, Q.; Zhao, W.; Tsai, S.-B.; Lu, H. A Study on Green Supplier Selection in Dynamic Environment. Sustainability 2018, 10, 1226. [Google Scholar] [CrossRef]
- Liao, N.N.; Cai, Q.; Garg, H.; Wei, G.; Xu, X. Novel gained and lost dominance score method based on cumulative prospect theory for group decision-making problems in probabilistic hesitant fuzzy environment. Int. J. Fuzzy Syst. 2023, 25, 1414–1428. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, T.Y. An integrated multicriteria group decision-making approach for green supplier selection under Pythagorean fuzzy scenarios. IEEE Access 2020, 8, 165216–165231. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Yildizbasi, A.; Ustunyer, P. Intuitionistic Fuzzy TOPSIS method for green supplier selection problem. Soft Comput. 2020, 24, 2215–2228. [Google Scholar] [CrossRef]
- Liu, P.D.; Gao, H.; Ma, J.H. Novel green supplier selection method by combining quality function deployment with partitioned Bonferroni mean operator in interval type-2 fuzzy environment. Inf. Sci. 2019, 490, 292–316. [Google Scholar] [CrossRef]
- Panja, S.; Mondal, S.K. Sustainable production inventory management through bi-level greening performance in a three-echelon supply chain. Oper. Res. 2023, 23, 16. [Google Scholar] [CrossRef]
- Pei, H.L.; Liu, Y.K.; Li, H.L. Robust pricing for a dual-channel green supply chain under fuzzy demand ambiguity. IEEE Trans. Fuzzy Syst. 2023, 31, 53–66. [Google Scholar] [CrossRef]
- Wu, Q.; Zhou, L.G.; Chen, Y.; Chen, H. An integrated approach to green supplier selection based on the interval type-2 fuzzy best-worst and extended VIKOR methods. Inf. Sci. 2019, 502, 394–417. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Amiri, M.; Esmaeili, A. Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets. J. Clean. Prod. 2016, 137, 213–229. [Google Scholar] [CrossRef]
- Liu, L.M.; Cao, W.Z.; Shi, B.; Tang, M. Large-Scale Green Supplier Selection Approach under a Q-Rung Interval-Valued Orthopair Fuzzy Environment. Processes 2019, 7, 573. [Google Scholar] [CrossRef]
- Mousakhani, S.; Nazari-Shirkouhi, S.; Bozorgi-Amiri, A. A novel interval type-2 fuzzy evaluation model based group decision analysis for green supplier selection problems: A case study of battery industry. J. Clean. Prod. 2017, 168, 205–218. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.; Feilong, L. Interval Type-2 fuzzy logic systems made simple. IEEE Trans. Fuzzy Syst. 2006, 14, 808–821. [Google Scholar] [CrossRef]
- Yao, D.B.; Wang, C.C. Interval type-2 fuzzy information measures and their applications to attribute decision-making approach. J. Intell. Fuzzy Syst. 2017, 33, 1809–1821. [Google Scholar]
- Tsai, J.F.; Shen, S.P.; Lin, M.H. Applying a hybrid MCDM model to evaluate green supply chain management practices. Sustainability 2023, 15, 2148. [Google Scholar] [CrossRef]
- Haseli, G.; Sheikh, R.; Wang, J.Q.; Tomaskova, H.; Tirkolaee, E.B. A novel approach for group decision making based on the Best-Worst method (G-BWM): Application to supply chain management. Mathematics 2021, 9, 1881. [Google Scholar] [CrossRef]
- Lu, M.T.; Tsai, J.F.; Shen, S.P.; Lin, M.-H.; Hu, Y.-C. Estimating sustainable development performance in the electrical wire and cable industry: Applying the integrated fuzzy MADM approach. J. Clean. Prod. 2020, 277, 122440. [Google Scholar]
- Buyukozkan, G.; Cifci, G. A novel hybrid MCDM approach based on fuzzy DEMATEL, fuzzy ANP and fuzzy TOPSIS to evaluate green suppliers. Expert. Syst. Appl. 2012, 39, 3000–3011. [Google Scholar]
- Deng, X.; Jiang, W. Evaluating green supply chain management practices under fuzzy environment: A novel method based on D number theory. Int. J. Fuzzy Syst. 2019, 21, 1389–1402. [Google Scholar]
- Han, Y.T.; Zheng, H.X.; Huang, Y.C.; Li, X.W. Considering Consumers’ Green Preferences and Government Subsidies in the Decision Making of the Construction and Demolition Waste Recycling Supply Chain: A Stackelberg Game Approach. Buildings 2022, 12, 832. [Google Scholar] [CrossRef]
- Song, Y.; Dong, Y. Influence of resource compensation and complete information on green sustainability of semiconductor supply chains. Int. J. Prod. Econ. 2024, 271, 109227. [Google Scholar]
- Guarnieri, P.; Trojan, F. Decision making on supplier selection based on social, ethical, and environmental criteria: A study in the textile industry. Resour. Conserv. Recycl. 2019, 141, 347–361. [Google Scholar]
- Ghadikolaei, A.S.; Parkouhi, S.V.; Saloukolaei, D.D. Extension of a hybrid MABAC-DANP method under gray environment for green supplier selection. Int. J. Inf. Technol. Decis. Mak. 2022, 21, 755–788. [Google Scholar]
- Freeman, J.; Chen, T. Green supplier selection using an AHP-Entropy-TOPSIS framework. Supply Chain. Manag. Int. J. 2015, 20, 327–340. [Google Scholar] [CrossRef]
- He, J.; Lei, Y.; Fu, X. Do consumer’s green preference and the reference price effect improve green innovation? A theoretical model using the food supply chain as a case. Int. J. Environ. Res. Public Health 2019, 16, 5007. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, H. Green supply chain management of automotive manufacturing industry considering multiperspective indices. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 1787–1795. [Google Scholar] [CrossRef]
- Wang, D.Q.; Deng, W.G.; Hu, L.; Huang, Z.; Lu, Y.; Zhang, H. Safety assessment of intelligent vehicles considering drivers’ risk perception information under interval 2-tuple q-rung orthopair fuzzy sets. Appl. Soft Comput. 2025, 175, 112919. [Google Scholar]
| Symbol | Definition | |
|---|---|---|
| IT2TFS | Interval type-2 trapezoidal fuzzy set (IT2TFS) | |
| Upper trapezoidal bounds of membership function | ||
| Lower trapezoidal bounds of membership function | ||
| Heights of upper and lower membership functions | ||
| Cross-Entropy | Fuzzy factor (ambiguity in IT2TFS membership) | |
| Hesitant factor (deviation from mean membership) | ||
| Interval factor (gap between upper and lower membership means) | ||
| Cross-entropy between IT2TFSs A and B | ||
| Prospect–Regret Theory | Gain deviation (positive difference from reference point) | |
| Loss deviation (negative difference from reference point) | ||
| , | Risk aversion coefficients for gains () and losses () | |
| Loss aversion multiplier (typically > 1) | ||
| Weight functions for gains and losses | ||
| Prospect values for gains and losses | ||
| Regret and rejoice values between alternatives and |
| Linguistic Variables | IT2TFSs |
|---|---|
| Very dissatisfied (VD) | [(0,0,0,0.1;1), (0,0,0,0.05;0.9)] |
| Dissatisfied (D) | [(0,0.1,0.2,0.31;1), (0.05,0.12,0.18,0.2;0.9)] |
| Lower dissatisfied (LD) | [(0.1,0.3,0.4,0.5;1), (0.2,0.32,0.38,0.4;0.9)] |
| Middle (M) | [(0.3,0.5,0.6,0.7;1), (0.4,0.52,0.58,0.6;0.9)] |
| Lower satisfied (LS) | [(0.5,0.7,0.8,0.9;1), (0.6,0.72,0.78,0.8;0.9)] |
| Satisfied (S) | [(0.7,0.9,0.95,1;1), (0.8,0.92,0.93,0.95;0.9)] |
| Very satisfied (VS) | [(0.9,1,1,1.1;1), (0.95,1,1,1;0.9)] |
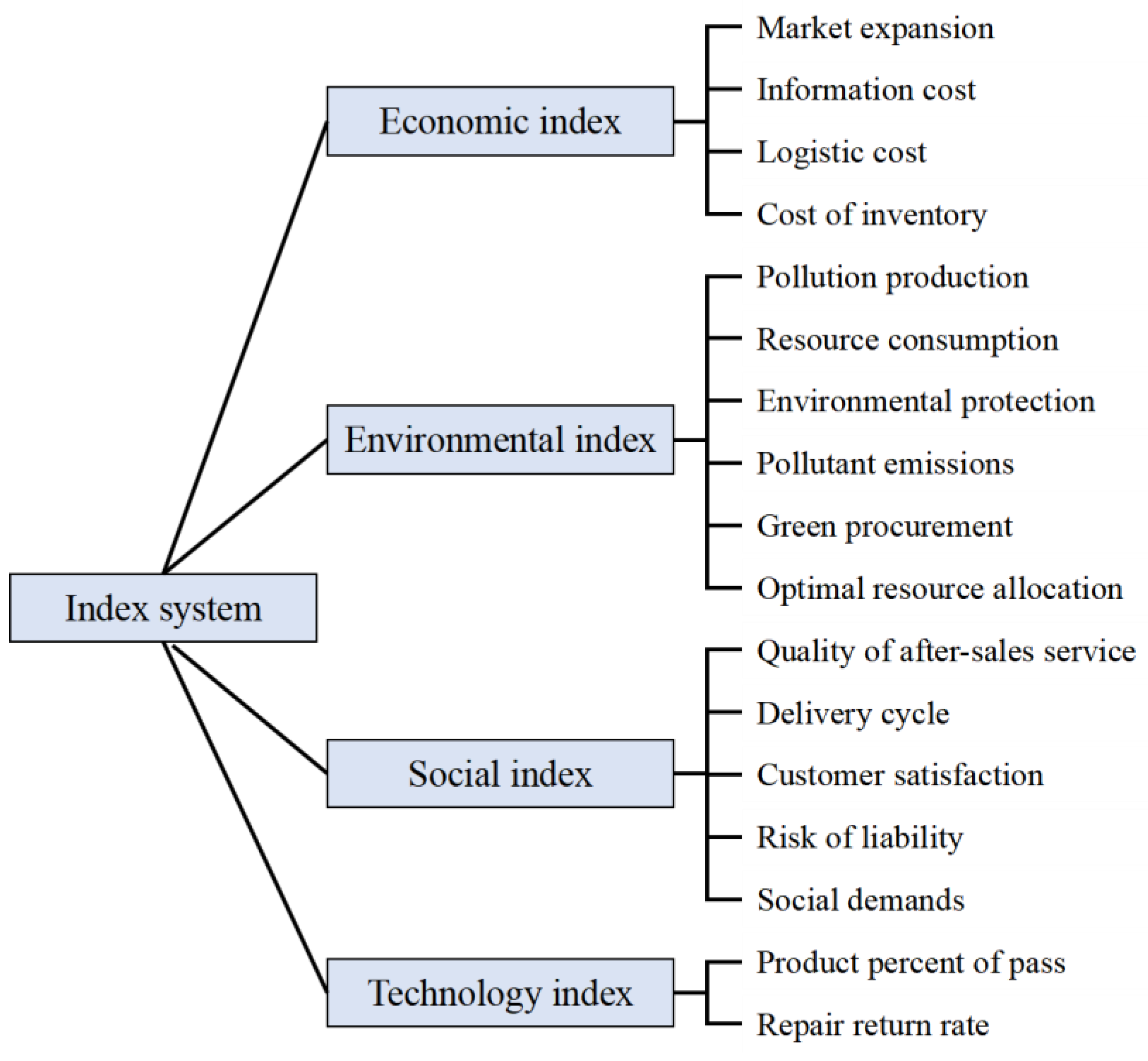
| Attribute Level | IT2TFSs | Code | References |
|---|---|---|---|
| Economic index (P1) | Market expansion | C1 | [2,26,37,47] |
| Information cost | C2 | [2,21,42,43,45] | |
| Logistic cost | C3 | [42,44] | |
| Cost of inventory | C4 | [32,36,45] | |
| Environmental index (P2) | Pollution production | C5 | [2,32,46,50,51] |
| Resource consumption | C6 | [47,48,52] | |
| Environmental protection | C7 | [26,42] | |
| Pollutant emissions | C8 | [42,43,49] | |
| Green procurement | C9 | [26,46] | |
| Social index (P3) | Optimal resource allocation | C10 | [23,46] |
| Quality of after-sales service | C11 | [2,26,37,47] | |
| Delivery cycle | C12 | [2,21,42,43] | |
| Customer satisfaction | C13 | [42,44] | |
| Risk of liability | C14 | [32,36,45] | |
| Social demands | C15 | [2,32,46,50,51] | |
| Technology index (P4) | Product percent of pass | C16 | [47,48,52] |
| Repair return rate | C17 | [26,42] |
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 | C16 | C17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| π+ | 0.088 | 0.137 | 0.099 | 0.077 | 0.135 | 0.186 | 0.078 | 0.142 | 0.192 | 0.161 | 0.105 | 0.146 | 0.210 | 0.189 | 0.138 | 0.118 | 0.129 |
| π− | 0.068 | 0.117 | 0.079 | 0.059 | 0.115 | 0.170 | 0.059 | 0.123 | 0.176 | 0.142 | 0.085 | 0.127 | 0.197 | 0.173 | 0.118 | 0.098 | 0.109 |
| Alt. | v+ | v− | v |
|---|---|---|---|
| 1 | [(−0.649, 0.320, 0.863, 1.468; 1); (0.170, 0.551, 0.760, 1.075; 0.9)] | [(−2.669, −1.267, −0.169, 1.454; 1); (−1.251, −0.967, −0.535, 0.143; 0.9)] | [(−3.318, −0.948, 0.694, 2.922; 1); (−1.080, −0.416, 0.225, 1.217; 0.9)] |
| 2 | [(−0.625, 0.352, 0.913, 1.545; 1); (0.192, 0.581, 0.798, 1.115; 0.9)] | [(−2.652, −1.240, −0.082, 1.609; 1); (−1.218, −0.935, −0.478, 0.209; 0.9)] | [(−3.278, −0.888, 0.831, 3.154; 1); (−1.026, −0.354, 0.320, 1.324; 0.9)] |
| 3 | [(−0.699, 0.219, 0.743, 1.362; 1); (0.056, 0426, 0.644, 0.964; 0.9)] | [(−2.748, −1.466, −0.440, 1.247; 1); (−1.466, 1.228, −0.797, −0.099; 0.9)] | [(−3.447, −1.247, 0.303, 2.609; 1); (−1.410, −0.802, −0.152, 0.865; 0.9)] |
| 4 | [(−0.749, 0.120, 0.678, 1.345; 1); (−0.022, 0.327, 0.553, 0.879; 0.9)] | [(−2.854, −1.614, −0.585, 1.209; 1); (−1.614, −1.397, −0.974, −0.305; 0.9)] | [(−3.603, −1.494, 0.093, 2.554; 1); (−1.635, −1.070, −0.421, 0.575; 0.9)] |
| 5 | [(−0.749, 0.150, 0.699, 1.374; 1); (0.003, 0.352, 0.565, 0.896; 0.9)] | [(−2.834, −1.557, −0.507, 1.248; 1); (−1.559, −1.312, −0.894, −0.248; 0.9)] | [(−3.583, −1.407, 0.1915, 2.621; 1); (−1.556, −0.960, −0.330, 0.648; 0.9)] |
| No. | Weights | DRG Value | Ranking | ||||
|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | |||
| 1 | wC1 = 0.68, wC2–17 = 0.02 | 3.606 | 0.560 | 2.017 | 4.462 | 4.410 | A4 A5 A1 A3 A2 |
| 2 | wC2 = 0.68, wC1,C3–17 = 0.02 | 0.928 | 1.631 | 3.675 | 5.491 | 4.979 | A4 A5 A3 A2 A1 |
| 3 | wC3 = 0.68, wC1–2,C4–17 = 0.02 | 0.713 | 1.866 | 5.179 | 1.436 | 5.941 | A5 A3 A2 A4 A1 |
| 4 | wC4 = 0.68, wC1–3,C5–17 = 0.02 | 2.048 | 0.954 | 4.884 | 4.908 | 3.894 | A4 A3 A5 A1 A2 |
| 5 | wC5 = 0.68, wC1–4,C6–17 = 0.02 | 2.958 | 1.839 | 4.748 | 5.118 | 3.914 | A4 A3 A5 A2 A1 |
| 6 | wC6 = 0.68, wC1–5,C7–17 = 0.02 | 2.489 | 0.938 | 3.313 | 4.839 | 5.983 | A5 A4 A3 A2 A1 |
| 7 | wC7 = 0.68, wC1–6,C8–17 = 0.02 | 1.078 | 1.056 | 2.580 | 4.295 | 5.827 | A5 A4 A3 A1 A2 |
| 8 | wC8 = 0.68, wC1–7,C9–17 = 0.02 | 2.909 | 2.734 | 2.271 | 5.144 | 4.167 | A5 A4 A1 A2 A3 |
| 9 | wC9 = 0.68, wC1–8,C10–17 = 0.02 | 1.293 | 3.726 | 3.664 | 3.202 | 2.880 | A2 A3 A4 A5 A1 |
| 10 | wC10 = 0.68, wC1–9,C11–17 = 0.02 | 2.605 | 3.146 | 3.085 | 3.317 | 2.991 | A4 A2 A3 A5 A1 |
| 11 | wC11 = 0.68, wC1–10,C12–17 = 0.02 | 1.896 | 1.487 | 3.792 | 4.052 | 5.647 | A5 A4 A3 A1 A2 |
| 12 | wC12 = 0.68, wC1–11,C13–17 = 0.02 | 3.945 | 2.920 | 2.392 | 4.530 | 3.032 | A4 A1 A5 A2 A3 |
| 13 | wC13 = 0.68, wC1–12,C14–17 = 0.02 | 1.576 | 0.999 | 3.477 | 4.531 | 4.100 | A4 A5 A3 A1 A2 |
| 14 | wC14 = 0.68, wC1–13,C15–17 = 0.02 | 3.300 | 1.985 | 4.085 | 3.271 | 3.324 | A3 A5 A1 A4 A2 |
| 15 | wC15 = 0.68, wC1–14,C16–17 = 0.02 | 4.586 | 0.734 | 2.241 | 5.003 | 2.507 | A4 A1 A5 A3 A2 |
| 16 | wC16 = 0.68, wC1–15,C17 = 0.02 | 0.798 | 1.489 | 3.053 | 4.757 | 5.612 | A5 A4 A3 A2 A1 |
| 17 | wC17 = 0.68, wC1–16 = 0.02 | 1.553 | 1.784 | 3.567 | 5.789 | 5.185 | A4 A5 A3 A2 A1 |
| 18 | wC1–17 = 0.059 | 4.235 | 3.326 | 5.927 | 7.502 | 7.340 | A4 A5 A3 A1 A2 |
| MCDM Methods | The Values of Schemes | Ranking | ||||
|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | ||
| IT2TFS–prospect | 0.1366 | 0.3048 | 0.7808 | 1.2828 | 1.0858 | A4 A5 A3 A2 A1 |
| IT2TFS–regret | 0.4000 | 0.2925 | 0.7738 | 0.9863 | 0.7800 | A4 A5 A3 A1 A2 |
| The proposed method | 4.0937 | 3.7922 | 5.4538 | 6.6269 | 6.2321 | A4 A5 A3 A1 A2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Meng, Z.; Huang, Z.; Zhang, H.; Wang, D. A Hybrid Prospect–Regret Decision-Making Method for Green Supply Chain Management Under the Interval Type-2 Trapezoidal Fuzzy Environment. Sustainability 2025, 17, 3323. https://doi.org/10.3390/su17083323
Zhou S, Meng Z, Huang Z, Zhang H, Wang D. A Hybrid Prospect–Regret Decision-Making Method for Green Supply Chain Management Under the Interval Type-2 Trapezoidal Fuzzy Environment. Sustainability. 2025; 17(8):3323. https://doi.org/10.3390/su17083323
Chicago/Turabian StyleZhou, Shaodong, Zilong Meng, Zhongwei Huang, Honghao Zhang, and Danqi Wang. 2025. "A Hybrid Prospect–Regret Decision-Making Method for Green Supply Chain Management Under the Interval Type-2 Trapezoidal Fuzzy Environment" Sustainability 17, no. 8: 3323. https://doi.org/10.3390/su17083323
APA StyleZhou, S., Meng, Z., Huang, Z., Zhang, H., & Wang, D. (2025). A Hybrid Prospect–Regret Decision-Making Method for Green Supply Chain Management Under the Interval Type-2 Trapezoidal Fuzzy Environment. Sustainability, 17(8), 3323. https://doi.org/10.3390/su17083323








