A Robust Sustainability Assessment Methodology for Aircraft Parts: Application to a Fuselage Panel
Abstract
1. Introduction
- The methodology is holistic as it efficiently combines environment, cost, and performance.
- The methodology is robust as all combinations of MCDM, and weighting methods consistently identify the most sustainable options.
- The methodology evaluates diverse assessment criteria using various MCDM methods, particularly the novel R-TOPSIS method and employs five different objective weighting methods to examine their influence on ranking outcomes.
- It integrates SimaPro software with the Ecoinvent 3 database, a reliable combination, to conduct both lifecycle analysis (LCA) and lifecycle costing (LCC).
- These innovations contribute to a more nuanced and adaptable approach to sustainability assessment in the field of aircraft structural design.
2. The Technological Problem
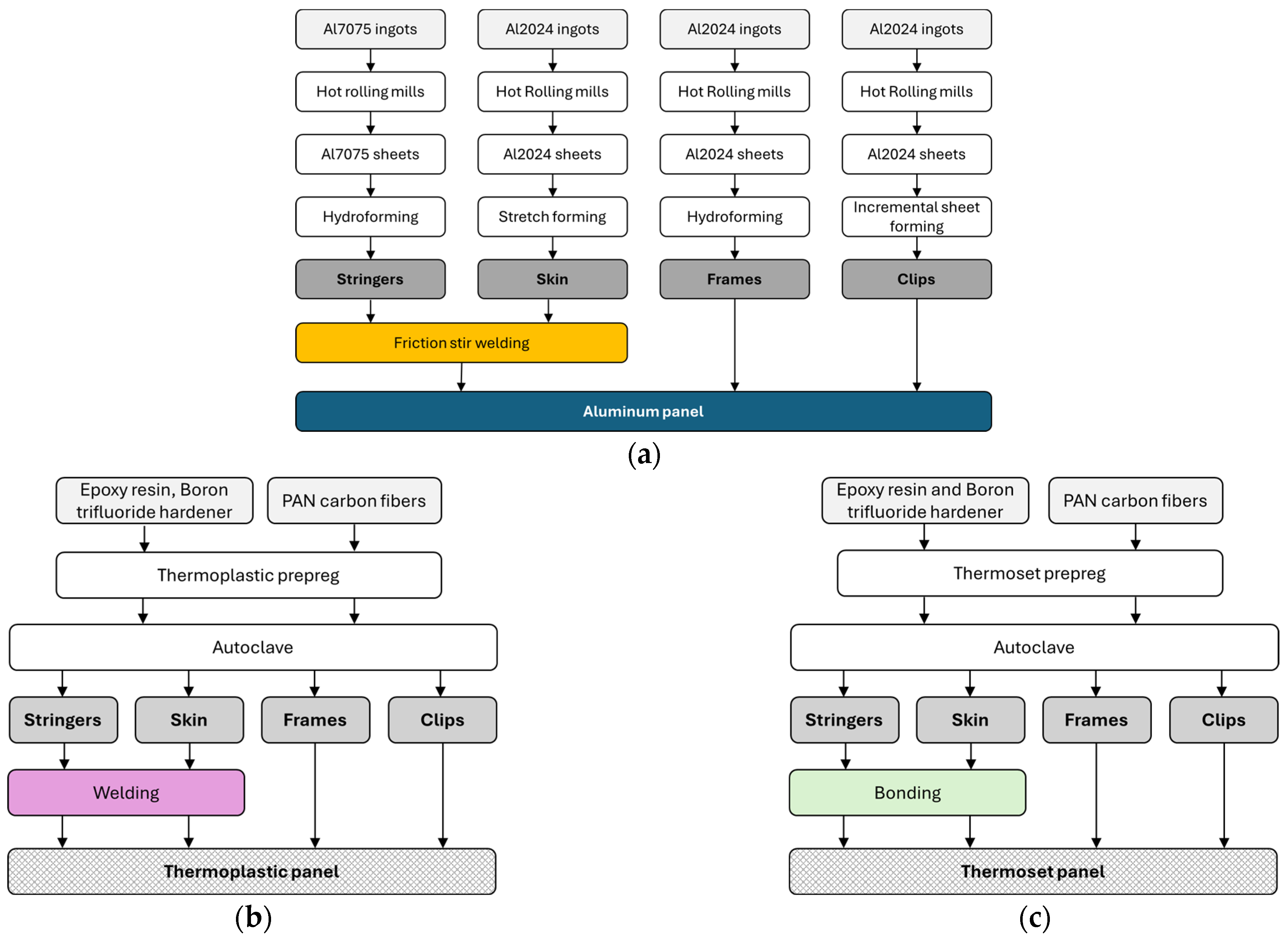
Different Configurations of the Fuselage Panel
- Aluminum 2024 (Al2024), manufactured using stretch forming;
- Aluminum 7075 (Al7075), manufactured using hydroforming;
- Thermosetting (TS) composite material, manufactured using autoclave;
- Thermoplastic (TP) composite material, manufactured using autoclave;
- Welding for aluminum and TP;
- Bonding for TS.
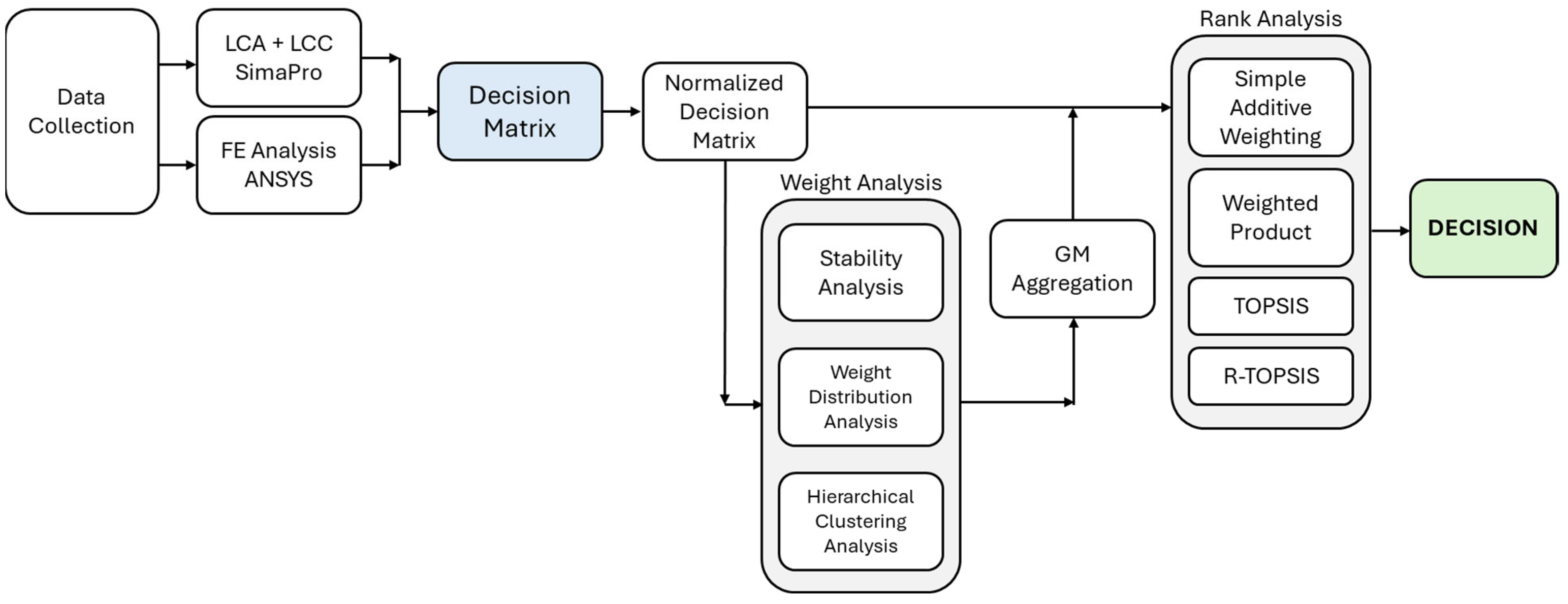
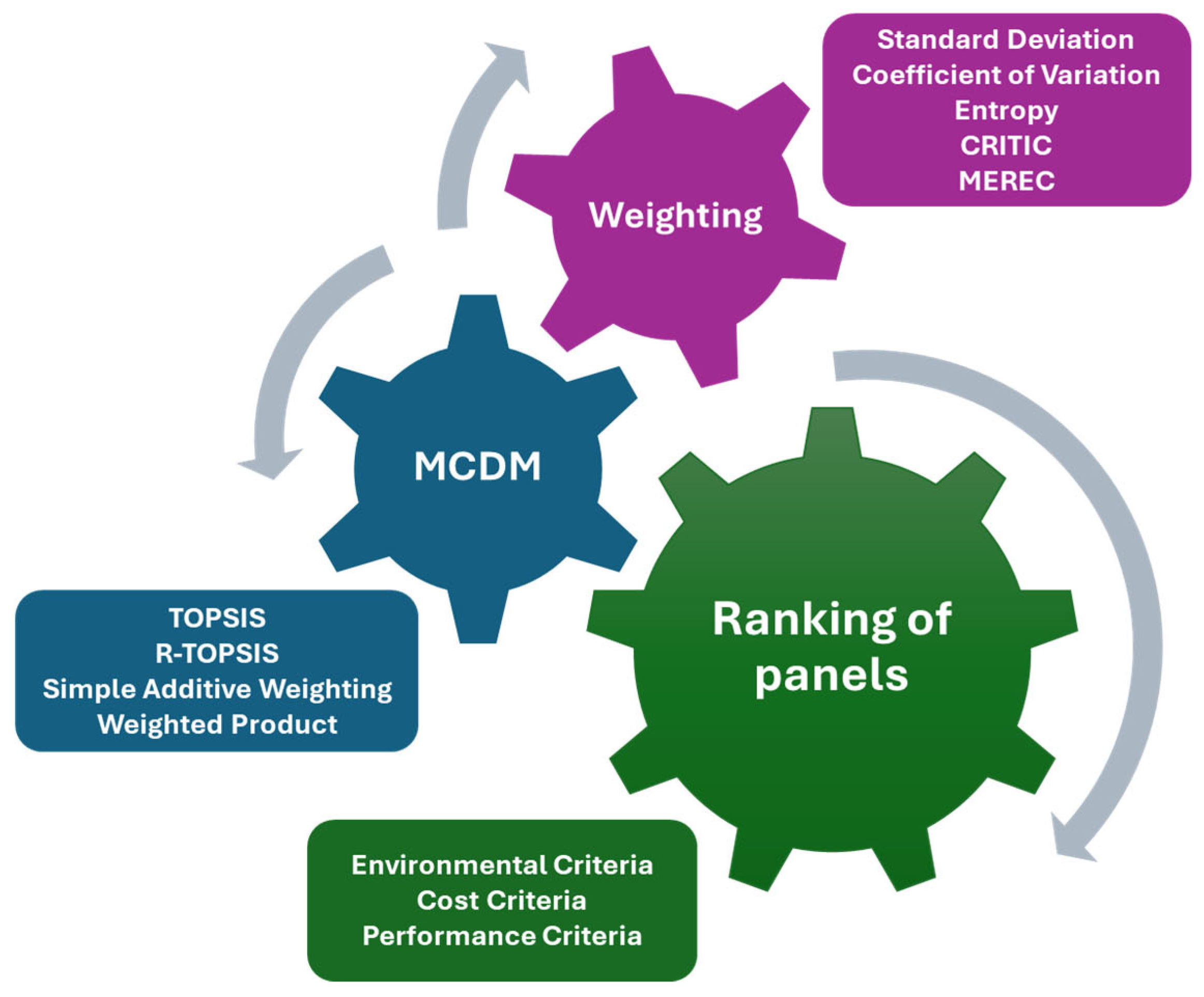
3. The Sustainability Assessment Methodology
3.1. Related Work
3.2. The Methodology
3.2.1. Criteria
Environment
- Definition of goal and scope: The first step of an LCA involves outlining the purpose and scope of the assessment, including the functional unit under study, the system boundaries, and the assumptions and limitations.
- Inventory analysis: The second step requires the collection of data.
- Impact assessment: In this step are chosen the environmental categories that we want to interpret. This is performed by selecting the appropriate method in SimaPro.
- Interpretation: The last step of an LCA is where the results are discussed.
- Stiffeners: Al7075 ingots are passed through rolling mills to form sheets, which are then used to produce the stiffeners and clips through the hydroforming process.
- Skin: Al2024 ingots are passed through rolling mills to form sheets, which then are used to produce the skin through the stretch forming process.
- Frames: Al2024 ingots are passed through rolling mills to form sheets, which are then used to produce the stiffeners and clips through the hydroforming process.
- Clips: Al2024 ingots are passed through rolling mills to form sheets, which then are used to produce the stiffeners and clips through the incremental sheet forming process.
- Polyphenylene powder, a thermoplastic resin, is added to the PAN carbon fiber fabric and the prepreg is constructed. Then, using an autoclave, the skin, stiffeners, frames, and clips are manufactured. Finally, the stiffeners are welded to the skin.
- The process is similar to the process of thermoplastic composite with different joining method. Epoxy resin with Boron trifluoride hardener is added to the PAN carbon fiber fabric and the prepreg is constructed. Then, using an autoclave, the skin, stiffeners, frames, and clips are manufactured. Finally, the stiffeners are bonded to the skin. Data for the bonding can be found in Table A5.
- Human health (C1): Measured as disability adjusted life years (DALYs), representing the combined years of life lost and years lived with disability.
- Ecosystems (C2): Assessed based on species loss over a specific area and time period.
- Resource scarcity (C3): Evaluated as the additional future production costs of resources over an infinite timeframe, with constant annual production and a 3% discount rate applied.
- Global warming potential (GWP) (C4): Climate change factors of IPCC method with a timeframe of 100 years, where carbon dioxide uptake is implicitly included.
Cost
- Energy cost (C6): Accounts for energy consumption throughout the production and manufacturing processes.
- Use cost (C7): Includes kerosene consumption for transporting the panel throughout the entire operational lifetime of the A319.
- End of life (EoL) cost (C8): Accounts for the cost of EoL services (recycling, landfill, incineration, etc.).
Performance
3.3. MCDM Analysis
3.3.1. Normalization Methods
- Benefit criterion (to be maximized): C10 (Specific stiffness)
- Cost criteria (to be minimized): C1–C9 environmental impacts (human health, ecosystems, resources, global warming potential), costs (material, energy, use-phase, end-of-life), and mass efficiency.
3.3.2. Objective Weighting Methods
3.3.3. MCDM Methods
4. Results
4.1. Construction and Normalization of the Decision Matrix
4.2. Weighting Methods Analysis and Selection
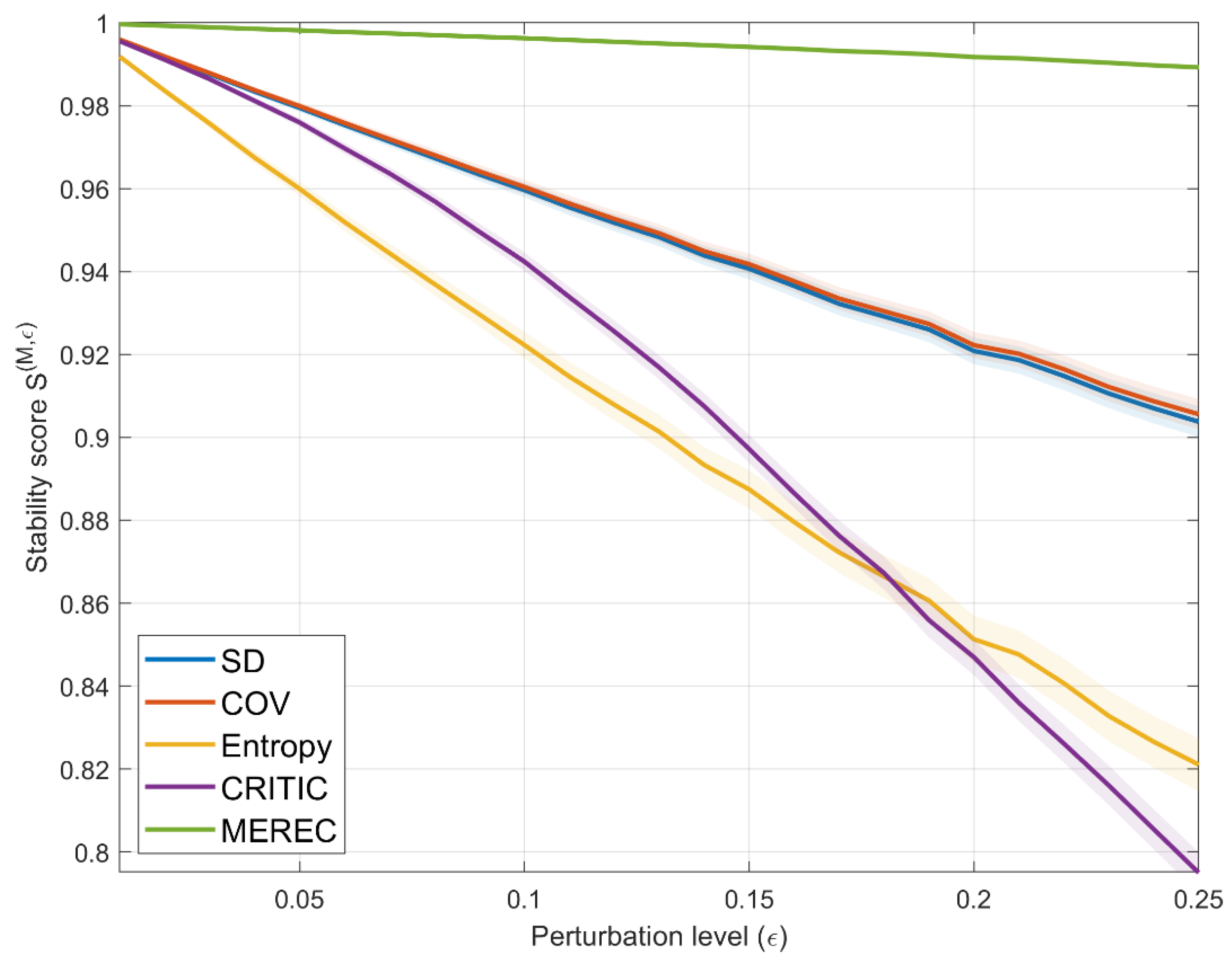
4.2.1. Stability Analysis
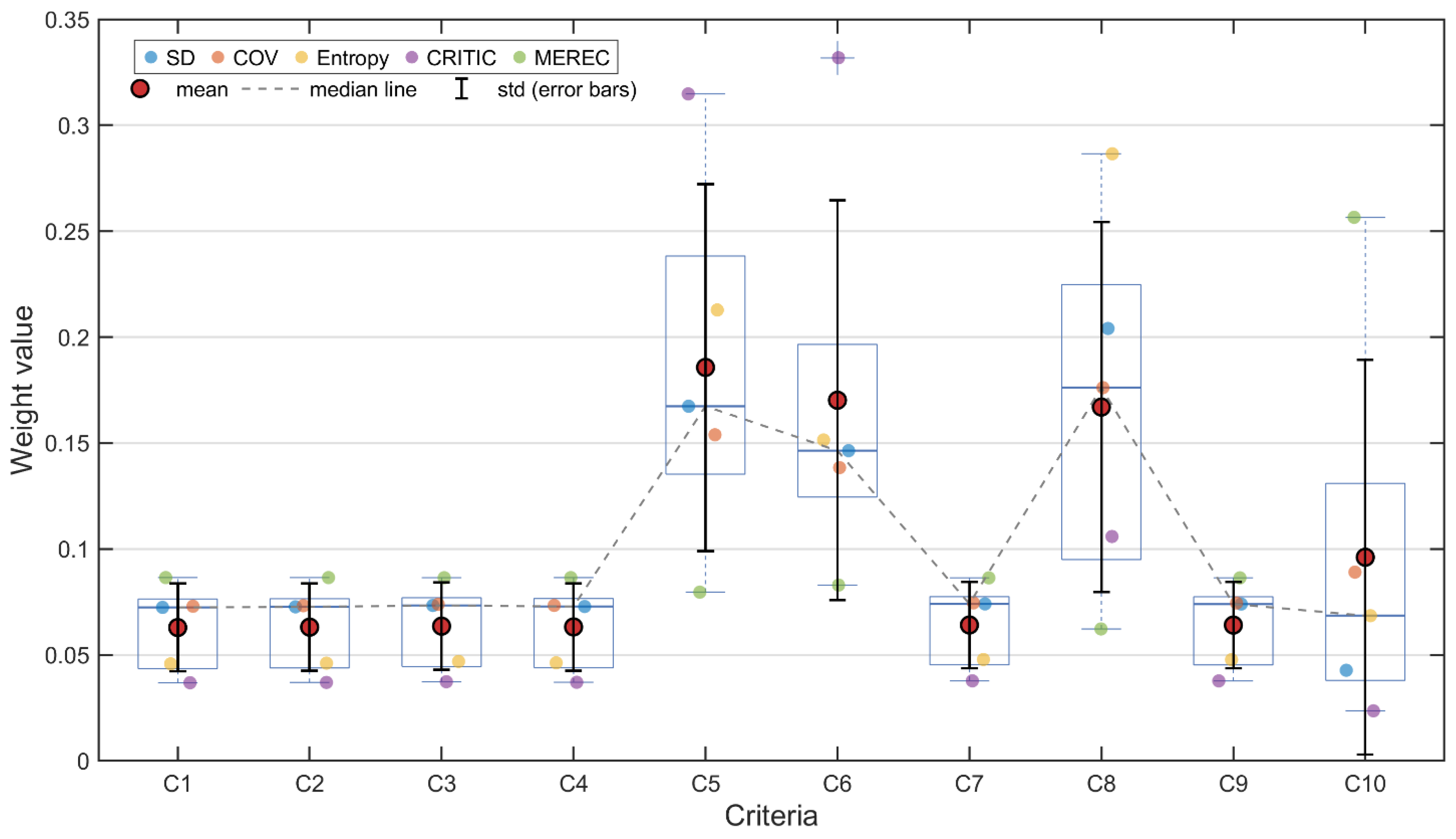
4.2.2. Weight Distribution Analysis
4.2.3. Hierarchical Clustering Analysis
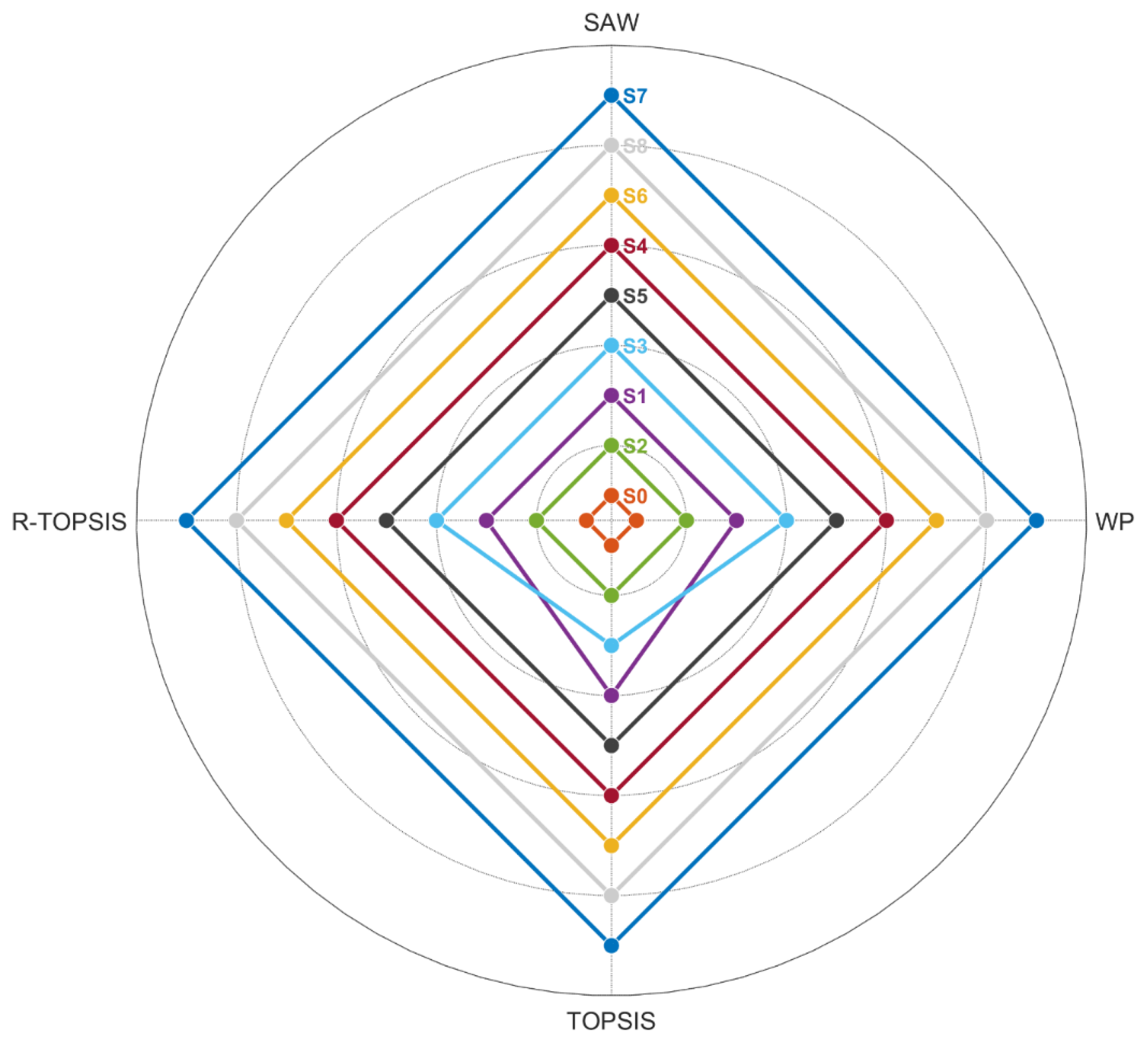
4.3. Rank Analysis Using Aggregated Weights
5. Conclusions
- The application of specific software packages, e.g., SimaPro along with the Ecoinvent 3 database, supported LCA and LCC analyses as well as ANSYS to evaluate the structural behavior of the component, which allows assessing all the sustainability criteria of the component throughout its lifecycle on environmental, economic, and technical perspectives. Such systematic methods, with the use of established industry standards, enhance the validity of the data and the results obtained, which is very important in enhancing the validity of sustainability assessment in aviation.
- Utilizing numerous MCDM methods and objective weighting methods, we were able to show the following:
- The GM of the weights of the three most stable methods, that is, SD, COV, and MEREC, results in a more balanced set of weights with a max/min ratio of 1.6979, which prevents the assessment from being driven by any one aspect of sustainability. Moreover, the categorical analysis of weight distributions shows that traditional methods (SD and COV) tend to prioritize the cost category of the criteria set (54–59%), but on the other hand, the MEREC suggests a more balanced distribution across environmental (34.59%), cost (31.12%), and performance (34.29%) categories. The GM somehow reduces these extremes and provides a more reasonable approach to making design decisions from the sustainability perspective.
- The methodology shows notable robustness through consistent ranking results obtained by applying four different MCDM methods (SAW, WP, TOPSIS, and R-TOPSIS). This consistency validates not only the aggregation of weights but also confirms the reliability of the overall assessment framework. Remarkably, thermoplastic CFRP panel configuration S7 was the best option in all the methods applied, followed by the S8 panel configuration and S6, while the reference aluminum panel S0 always ranked last.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MCDM | Multi-Criteria Decision-Making |
| CFRP | Carbon Fiber-Reinforced Polymer |
| LCA | Lifecycle Analysis |
| LCC | Lifecycle Costing |
| R-TOPSIS | Robust Technique for Order of Preference by Similarity to Ideal Solution |
| EU | European Union |
| 3D | Three Dimensional |
| MRO | Maintenance Repair and Operations |
| SMR | Short-to-Medium Range |
| Al2024 | Aluminum 2024 |
| Al7075 | Aluminum 7075 |
| TS | Thermosetting |
| TP | Thermoplastic |
| NGO | Non-Governmental Organizations |
| AHM | Analytical Hierarchy Method |
| WSM | Weighted Sum Model |
| LW | Laser Welding |
| ECM | Electro Chemical Machining |
| ISO | International Organization for Standardization |
| CF | Carbon Fiber |
| PAN | Polyacrylonitrile |
| DALYs | Disability Adjusted Life Years |
| IPCC | Intergovernmental Panel on Climate Change |
| GWP | Global Warming Potential |
| H | Hierarchist |
| CO2 | Carbon Dioxide |
| EoL | End of Life |
| FEM | Finite Element Model |
| USD | United States Dollar |
| SD | Standard Deviation |
| COV | Coefficient of Variance |
| CRITIC | Criteria Importance Through Inter-Criteria Correlation |
| MEREC | Method Based on the Removal Effects of Criteria |
| SAW | Simple Additive Weighting |
| WP | Weighted Product |
| TOPSIS | Technique for Order Preference by Similarity to Ideal |
| PIS | Positive Ideal Solution |
| NIS | Negative Ideal Solution |
| Max | Maximum |
| Min | Minimum |
| GM | Geometric Mean |
Appendix A
Appendix A.1. Materials
| Material | Content |
|---|---|
| Aluminum | 92.81% |
| Chromium | 0.05% |
| Iron | 0.25% |
| Magnesium | 0.5% |
| Manganese | 0.6% |
| Silicon | 0.25% |
| Titanium | 0.07% |
| Zinc | 0.125% |
| Copper | 4.36% |
| Material | Content |
|---|---|
| Aluminum | 88% |
| Chromium | 0.2% |
| Iron | 0.3% |
| Magnesium | 2.5% |
| Manganese | 0.1% |
| Silicon | 0.35% |
| Titanium | 0.15% |
| Zinc | 6% |
| Copper | 1.5% |
| Material | Content |
| Epoxy resin and Boron trifluoride hardener for 1 kg CFRP | 0.423 kg |
| Epoxy resin for 1 kg resin | 0.66 kg |
| Boron trifluoride for 1 kg resin | 0.33 kg |
| PAN carbon fibers for 1 kg thermoset CFRP | 0.577 kg |
| Acrylonitrile (production of 1 kg PAN carbon fibers) | 2.25 kg |
| Dimethylacetamide (production of 1 kg PAN carbon fibers) | 0.031 kg |
| Polyurethane (production of 1 kg PAN carbon fibers) | 0.02 kg |
| Embodied energy (prepreg) | 40 MJ |
| Electricity (production of 1 kg PAN carbon fibers) | 58 kWh |
| Heat (production of 1 kg PAN carbon fibers) | 257.3 MJ |
| Material | Content |
|---|---|
| Thermoplastic resin (Polyphenylene sulfidepowder) | 0.43 kg |
| Plastic micronizer machine (milling the resin pellets)/consumption for 1 kg of pellets | 0.2 kWh |
| PAN carbon fibers for 1 kg thermoplastic CFRP | 0.57 kg |
| Composite density | 1550 kg/m3 |
| Bisphenol A epoxy-based vinyl ester resin | 0.66 kg |
| Ethylenediamine | 0.33 kg |
Appendix A.2. Processes
| Subprocess | Energy (kWh/kg) |
|---|---|
| Stretch forming | 3.95 |
| Incremental sheet forming | 12.91 |
| Hydroforming | 4 |
| Hot rolling mills | 0.07 |
| Process | Energy (kwh/800 mm) |
|---|---|
| Friction stir welding | 0.07056 |
| Process | Energy |
|---|---|
| Vacuum generation | 10.2 MJ |
| Autoclave curing | 294.3 kWh |
Appendix A.3. Cost
| Material | Cost (EUR/kg) |
|---|---|
| Al2024 | 5 |
| Al7075 | 7 |
| Boron Trifluoride | 341.66 |
| Epoxy resin | 9.15 |
| PAN carbon fibers | 30 |
| Permabond adhesive | 693.5 |
| Polyphenylene sulfide | 20 |
| Polyurethane sizing | 3.58 |
| Energy | Cost (EUR/kWh) |
|---|---|
| Electricity Europe | 0.2847 |
Appendix A.4. Use-Phase of the Panel
| Total distance in A319 lifetime | 20,188,120.8 km |
| Kerosene consumption per kg of transportation | 6729.374 kg kerosene/kg transportation |
| Kerosene cost | 0.658 EUR/kg |
Appendix A.5. End-of-Life of the Panel
| Aluminum panel | 85% recycling and 15% landfill |
| CFRP panel | 100% landfill |
| Landfill cost | 0.06 EUR/kg |
| Recycling cost | 1.04 EUR/kg |
References
- Vogiantzi, C.; Tserpes, K. On the Definition, Assessment, and Enhancement of Circular Economy across Various Industrial Sectors: A Literature Review and Recent Findings. Sustainability 2023, 15, 16532. [Google Scholar] [CrossRef]
- Drohomeretski, E.; Da Costa, S.E.G.; De Lima, E.P.; De Oliveira Neves, T.R. The Application of Sustainable Practices and Performance Measures in the Automotive Industry: A Systematic Literature Review. Eng. Manag. J. 2015, 27, 32–44. [Google Scholar] [CrossRef]
- Ramadugu, S.; Ledella, S.R.K.; Gaduturi, J.N.J.; Pinninti, R.R.; Sriram, V.; Saxena, K.K. Environmental Life Cycle Assessment of an Automobile Component Fabricated by Additive and Conventional Manufacturing. Int. J. Interact. Des. Manuf. IJIDeM 2024, 18, 847–858. [Google Scholar] [CrossRef]
- Pinheiro Melo, S.; Barke, A.; Cerdas, F.; Thies, C.; Mennenga, M.; Spengler, T.S.; Herrmann, C. Sustainability Assessment and Engineering of Emerging Aircraft Technologies—Challenges, Methods and Tools. Sustainability 2020, 12, 5663. [Google Scholar] [CrossRef]
- Swastanto, G.A.; Johnson, M.E. Exploratory Study of Sustainability Practices in Worldwide Major Aircraft Maintenance, Repair, and Overhaul Companies. Transp. Res. Rec. J. Transp. Res. Board 2024, 2678, 1060–1078. [Google Scholar] [CrossRef]
- Filippatos, A.; Markatos, D.; Tzortzinis, G.; Abhyankar, K.; Malefaki, S.; Gude, M.; Pantelakis, S. Sustainability-Driven Design of Aircraft Composite Components. Aerospace 2024, 11, 86. [Google Scholar] [CrossRef]
- Katsiropoulos, C.V.; Pantelakis, S.G. A Novel Holistic Index for the Optimization of Composite Components and Manufacturing Processes with Regard to Quality, Life Cycle Costs and Environmental Performance. Aerospace 2020, 7, 157. [Google Scholar] [CrossRef]
- Balli, O.; Caliskan, N.; Caliskan, H. Aviation, Energy, Exergy, Sustainability, Exergoenvironmental and Thermoeconomic Analyses of a Turbojet Engine Fueled with Jet Fuel and Biofuel Used on a Pilot Trainer Aircraft. Energy 2023, 263, 126022. [Google Scholar] [CrossRef]
- Akdeniz, H.Y.; Balli, O.; Caliskan, H. Energy, Exergy, Thermoecologic, Environmental, Enviroeconomic and Sustainability Analyses and Assessments of the Aircraft Engine Fueled with Biofuel and Jet Fuel. J. Therm. Anal. Calorim. 2023, 148, 3585–3603. [Google Scholar] [CrossRef]
- Akdeniz, H.Y. Systematic Benchmarking of Performance, Environmental and Sustainability Impacts of Utilization of Alternative Cleaner Fuel in an Aircraft Gas Turbine Engine. Environ. Sci. Pollut. Res. 2022, 29, 51012–51029. [Google Scholar] [CrossRef]
- Markowska, K.; Sękala, A.; Stecuła, K.; Kawka, T.; Sirovitskiy, K.; Pankova, O.; Vnukova, N.; Shulyak, M.; Kharchenko, S.; Shchur, T.; et al. Comparison of the Sustainability and Economic Efficiency of an Electric Car and an Aircraft—A Case Study. Sustainability 2023, 15, 1238. [Google Scholar] [CrossRef]
- Barbosa, C.; Malarranha, C.; Azevedo, A.; Carvalho, A.; Barbosa-Póvoa, A. A Hybrid Simulation Approach Applied in Sustainability Performance Assessment in Make-to-Order Supply Chains: The Case of a Commercial Aircraft Manufacturer. J. Simul. 2023, 17, 32–57. [Google Scholar] [CrossRef]
- Karpuk, S.; Radespiel, R.; Elham, A. Assessment of Future Airframe and Propulsion Technologies on Sustainability of Next-Generation Mid-Range Aircraft. Aerospace 2022, 9, 279. [Google Scholar] [CrossRef]
- Aygun, H. Exergo-Sustainability Behavior of High by-Pass Turbofan Engine of a Passenger Aircraft during Main Flight Phases. Energy Sources Part Recovery Util. Environ. Eff. 2021, 46, 1127–1144. [Google Scholar] [CrossRef]
- Fera, M.; Abbate, R.; Caterino, M.; Manco, P.; Macchiaroli, R.; Rinaldi, M. Economic and Environmental Sustainability for Aircrafts Service Life. Sustainability 2020, 12, 10120. [Google Scholar] [CrossRef]
- Cardeal, G.; Höse, K.; Ribeiro, I.; Götze, U. Sustainable Business Models–Canvas for Sustainability, Evaluation Method, and Their Application to Additive Manufacturing in Aircraft Maintenance. Sustainability 2020, 12, 9130. [Google Scholar] [CrossRef]
- Lin, C.-W.; Chen, T. 3D Printing Technologies for Enhancing the Sustainability of an Aircraft Manufacturing or MRO Company—A Multi-Expert Partial Consensus-FAHP Analysis. Int. J. Adv. Manuf. Technol. 2019, 105, 4171–4180. [Google Scholar] [CrossRef]
- Baklacioglu, T.; Turan, O.; Aydin, H. Metaheuristic Approach for an Artificial Neural Network: Exergetic Sustainability and Environmental Effect of a Business Aircraft. Transp. Res. Part Transp. Environ. 2018, 63, 445–465. [Google Scholar] [CrossRef]
- Raj, A.; Srivastava, S.K. Sustainability Performance Assessment of an Aircraft Manufacturing Firm. Benchmarking Int. J. 2018, 25, 1500–1527. [Google Scholar] [CrossRef]
- Balli, O. Exergy Modeling for Evaluating Sustainability Level of a High By-Pass Turbofan Engine Used on Commercial Aircrafts. Appl. Therm. Eng. 2017, 123, 138–155. [Google Scholar] [CrossRef]
- Somerville, A.; Marino, M.; Baxter, G.; Wild, G. Understanding Box Wing Aircraft: Essential Technology to Improve Sustainability in the Aviation Industry. Aviation 2016, 20, 129–136. [Google Scholar] [CrossRef]
- Sabaghi, M.; Cai, Y.; Mascle, C.; Baptiste, P. Sustainability Assessment of Dismantling Strategies for End-of-Life Aircraft Recycling. Resour. Conserv. Recycl. 2015, 102, 163–169. [Google Scholar] [CrossRef]
- Aydın, H.; Turan, Ö.; Karakoç, T.H.; Midilli, A. Exergo-Sustainability Indicators of a Turboprop Aircraft for the Phases of a Flight. Energy 2013, 58, 550–560. [Google Scholar] [CrossRef]
- Barke, A.; Thies, C.; Melo, S.P.; Cerdas, F.; Herrmann, C.; Spengler, T.S. Socio-Economic Life Cycle Assessment of Future Aircraft Systems. Procedia CIRP 2020, 90, 262–267. [Google Scholar] [CrossRef]
- Munk, D.J.; Miller, J.D. Topology Optimization of Aircraft Components for Increased Sustainability. AIAA J. 2022, 60, 445–460. [Google Scholar] [CrossRef]
- Anagnostopoulou, A.; Sotiropoulos, D.; Floros, G.; Tserpes, K. Towards the Development of an Eco-Design Approach for Aircraft Components. Eng. Proc. 2025, 90, 81. [Google Scholar] [CrossRef]
- Passos Neto, G.D.M.; Alencar, L.H.; Valdes-Vasquez, R. Multiple-Criteria Methods for Assessing Social Sustainability in the Built Environment: A Systematic Review. Sustainability 2023, 15, 16231. [Google Scholar] [CrossRef]
- Ziemba, P. Application Framework of Multi-Criteria Methods in Sustainability Assessment. Energies 2022, 15, 9201. [Google Scholar] [CrossRef]
- Negrin, I.; Kripka, M.; Yepes, V. Multi-Criteria Optimization for Sustainability-Based Design of Reinforced Concrete Frame Buildings. J. Clean. Prod. 2023, 425, 139115. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; Yepes, V. Multi-Criteria Decision-Making Applied to the Sustainability of Building Structures Based on Modern Methods of Construction. J. Clean. Prod. 2022, 330, 129724. [Google Scholar] [CrossRef]
- Bhat, P.; Agrawal, C.; Khanna, N. Development of a Sustainability Assessment Algorithm and Its Validation Using Case Studies on Cryogenic Machining. J. Manuf. Mater. Process. 2020, 4, 42. [Google Scholar] [CrossRef]
- Khalili, N.R.; Duecker, S. Application of Multi-Criteria Decision Analysis in Design of Sustainable Environmental Management System Framework. J. Clean. Prod. 2013, 47, 188–198. [Google Scholar] [CrossRef]
- Jasiński, D.; Meredith, J.; Kirwan, K. A Comprehensive Framework for Automotive Sustainability Assessment. J. Clean. Prod. 2016, 135, 1034–1044. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining Objective Weights in Multiple Criteria Problems: The Critic Method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Markatos, D.N.; Malefaki, S.; Pantelakis, S.G. Sensitivity Analysis of a Hybrid MCDM Model for Sustainability Assessment—An Example from the Aviation Industry. Aerospace 2023, 10, 385. [Google Scholar] [CrossRef]
- Sharma, A.K.; Aravindan, N.; Ignatia, K.M.J.; Areche, F.O.; Loganathan, G.B.; Taha, A.H.; Dwivedi, P.; Yellapragada, R.K. Hybrid Multi Criteria Decision Making Methodology for Improving Sustainability of the Manufacturing Sector. Int. J. Interact. Des. Manuf. IJIDeM 2024, 19, 695–704. [Google Scholar] [CrossRef]
- Peirow, S.; Razi Astaraei, F.; Saifoddin Asl, A. Techno-Economic and Environmental Assessment of a Hybrid Renewable Energy System for a Hospital Using Multi-Criteria Decision-Making Method. Energies 2023, 16, 1916. [Google Scholar] [CrossRef]
- Moro, C. Comparative Analysis of Multi-Criteria Decision Making and Life Cycle Assessment Methods for Sustainable Evaluation of Concrete Mixtures. Sustainability 2023, 15, 12746. [Google Scholar] [CrossRef]
- ISO 14044; Environmental Management—Life Cycle Assessment—Requirements and Guidelines. ISO: Geneva, Switzerland, 2006.
- ISO 14040:2006; Environmental Management—Life Cycle Assessment—Principles and Framework. ISO: Geneva, Switzerland, 2006.
- Jahan, A.; Edwards, K.L. A State-of-the-Art Survey on the Influence of Normalization Techniques in Ranking: Improving the Materials Selection Process in Engineering Design. Mater. Des. 1980–2015 2015, 65, 335–342. [Google Scholar] [CrossRef]
- Milani, A.S.; Shanian, A.; Madoliat, R.; Nemes, J.A. The Effect of Normalization Norms in Multiple Attribute Decision Making Models: A Case Study in Gear Material Selection. Struct. Multidiscip. Optim. 2005, 29, 312–318. [Google Scholar] [CrossRef]
- Zanakis, S.H.; Solomon, A.; Wishart, N.; Dublish, S. Multi-Attribute Decision Making: A Simulation Comparison of Select Methods. Eur. J. Oper. Res. 1998, 107, 507–529. [Google Scholar] [CrossRef]
- Zelený, M. Multiple Criteria Decision Making; McGraw-Hill Series in Quantitative Methods for Management; McGraw-Hill Book: New York, NY, USA, 1982; ISBN 978-0-07-072795-3. [Google Scholar]
- Wang, Y.-M.; Luo, Y. Integration of Correlations with Standard Deviations for Determining Attribute Weights in Multiple Attribute Decision Making. Math. Comput. Model. 2010, 51, 1–12. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1981; Volume 186, ISBN 978-3-540-10558-9. [Google Scholar]
- Keshavarz-Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. Determination of Objective Weights Using a New Method Based on the Removal Effects of Criteria (MEREC). Symmetry 2021, 13, 525. [Google Scholar] [CrossRef]
- Keshavarz-Ghorabaee, M. Assessment of Distribution Center Locations Using a Multi-Expert Subjective–Objective Decision-Making Approach. Sci. Rep. 2021, 11, 19461. [Google Scholar] [CrossRef]
- Triantaphyllou, E.; Lin, C.-T. Development and Evaluation of Five Fuzzy Multiattribute Decision-Making Methods. Int. J. Approx. Reason. 1996, 14, 281–310. [Google Scholar] [CrossRef]
- Yeh, C. A Problem-based Selection of Multi-attribute Decision-making Methods. Int. Trans. Oper. Res. 2002, 9, 169–181. [Google Scholar] [CrossRef]
- Triantaphyllou, E. Multi-Criteria Decision Making Methods: A Comparative Study; Applied Optimization; Springer: Boston, MA, USA, 2000; Volume 44, ISBN 978-1-4419-4838-0. [Google Scholar]
- Aires, R.F.D.F.; Ferreira, L. A New Approach to Avoid Rank Reversal Cases in the TOPSIS Method. Comput. Ind. Eng. 2019, 132, 84–97. [Google Scholar] [CrossRef]
- Murtagh, F.; Legendre, P. Ward’s Hierarchical Agglomerative Clustering Method: Which Algorithms Implement Ward’s Criterion? J. Classif. 2014, 31, 274–295. [Google Scholar] [CrossRef]
- Kimes, P.K.; Liu, Y.; Hayes, D.N.; Marron, J.S. Statistical Significance for Hierarchical Clustering. Biometrics 2017, 73, 811–821. [Google Scholar] [CrossRef]
- Aczél, J.; Saaty, T.L. Procedures for Synthesizing Ratio Judgements. J. Math. Psychol. 1983, 27, 93–102. [Google Scholar] [CrossRef]





| Alternative | Skin Material | Stiffener Material | Frame Material | Clip Material | Joining Method | Skin Thickness (mm) | Stiffener Thickness (mm) | Frame Thickness (mm) |
|---|---|---|---|---|---|---|---|---|
| S0 | Al2024 | Al7075 | Al2024 | Al2024 | Welding | 2.8 | 2.4 | 1.6 |
| S1 | Al2024 | Al7075 | Al2024 | Al2024 | Welding | 2.5 | 2.2 | 1.5 |
| S2 | Al2024 | Al7075 | Al2024 | Al2024 | Welding | 2.8 | 2.4 | 1.6 |
| S3 | TS | TS | TS | TS | Bonding | 2.8 | 2.4 | 1.6 |
| S4 | TS | TS | TS | TS | Bonding | 2.5 | 2.2 | 1.5 |
| S5 | TS | TS | TS | TS | Bonding | 2.8 | 2.4 | 1.5 |
| S6 | TP | TP | TP | TP | Welding | 2.8 | 2.4 | 1.6 |
| S7 | TP | TP | TP | TP | Welding | 2.5 | 2.2 | 1.5 |
| S8 | TP | TP | TP | TP | Welding | 2.8 | 2.4 | 1.6 |
| Part | Material | Manufacturing Process |
|---|---|---|
| Skin Panel | Al2024 | Stretch forming |
| Stringer | Al7075 | Hydroforming |
| Clip | Al2024 | Incremental sheet forming |
| Frame | Al2024 | Hydroforming |
| Part | Material | Manufacturing Process |
|---|---|---|
| Skin Panel | TS prepreg 57.7% wt. cf. | Autoclave |
| Stringer | TS prepreg 57.7% wt. cf. | Autoclave |
| Clip | TS prepreg 57.7% wt. cf. | Autoclave |
| Frame | TS prepreg 57.7% wt. cf. | Autoclave |
| Part | Material | Manufacturing Process |
|---|---|---|
| Skin Panel | TP prepreg 57% wt. cf. | Autoclave |
| Stringer | TP prepreg 57% wt. cf. | Autoclave |
| Clip | TP prepreg 57% wt. cf. | Autoclave |
| Frame | TP prepreg 57% wt. cf. | Autoclave |
| Criteria | Description | Category | Impact Type |
|---|---|---|---|
| C1 | Human health (DALYs) | Environment | Minimize |
| C2 | Ecosystems (species. year) | Environment | Minimize |
| C3 | Resources (USD 2013) | Environment | Minimize |
| C4 | Global warming potential (kg CO2) | Environment | Minimize |
| C5 | Material cost | Cost | Minimize |
| C6 | Energy cost | Cost | Minimize |
| C7 | Use cost | Cost | Minimize |
| C8 | EoL cost | Cost | Minimize |
| C9 | Mass | Performance | Minimize |
| C10 | Specific stiffness | Performance | Maximize |
| Method | Benefit Criteria (Max) | Cost Criteria (Min) | Description |
|---|---|---|---|
| Vector normalization | Transforms using Euclidean norm, with cost criteria inverted | ||
| Linear scale | Scales relative to maximum for benefits and minimum for costs | ||
| Min-max | Scales to [0,1] range with appropriate direction |
| Alternative | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
|---|---|---|---|---|---|---|---|---|---|---|
| S0 | 1.3300 | 3.430 × 10−3 | 1.160 × 105 | 8.130 × 105 | 164 | 38.30 | 1.340 × 105 | 27.0 | 30.2308 | 4931.845 |
| S1 | 1.2000 | 3.100 × 10−3 | 1.050 × 105 | 7.350 × 105 | 153 | 35.90 | 1.210 × 105 | 25.2 | 27.3357 | 4897.502 |
| S2 | 1.3000 | 3.360 × 10−3 | 1.140 × 105 | 7.950 × 105 | 161 | 36.80 | 1.310 × 105 | 26.4 | 29.5650 | 5037.188 |
| S3 | 0.7560 | 1.950 × 10−3 | 6.560 × 104 | 4.610 × 105 | 1540 | 1490 | 7.540 × 104 | 1.02 | 17.0330 | 7355.105 |
| S4 | 0.6840 | 1.760 × 10−3 | 5.930 × 104 | 4.170 × 105 | 1430 | 1350 | 6.820 × 104 | 0.924 | 15.4010 | 7306.868 |
| S5 | 0.7560 | 1.950 × 10−3 | 6.560 × 104 | 4.610 × 105 | 1520 | 1460 | 7.380 × 104 | 0.999 | 16.6570 | 7515.834 |
| S6 | 0.7460 | 1.920 × 10−3 | 6.480 × 104 | 4.550 × 105 | 430 | 1440 | 7.450 × 104 | 1.010 | 16.8160 | 6999.713 |
| S7 | 0.6750 | 1.740 × 10−3 | 5.860 × 104 | 4.110 × 105 | 389 | 1310 | 6.730 × 104 | 0.912 | 15.2050 | 6952.876 |
| S8 | 0.7300 | 1.880 × 10−3 | 6.340 × 104 | 4.450 × 105 | 421 | 1410 | 7.280 × 104 | 0.987 | 16.4450 | 7152.875 |
| Alternative | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 |
|---|---|---|---|---|---|---|---|---|---|---|
| S0 | 0.5314 | 0.5316 | 0.5313 | 0.5311 | 0.9394 | 0.9889 | 0.5289 | 0.4061 | 0.5293 | 0.2510 |
| S1 | 0.5772 | 0.5766 | 0.5758 | 0.5761 | 0.9434 | 0.9896 | 0.5746 | 0.4457 | 0.5744 | 0.2492 |
| S2 | 0.5420 | 0.5411 | 0.5394 | 0.5415 | 0.9405 | 0.9894 | 0.5395 | 0.4193 | 0.5396 | 0.2563 |
| S3 | 0.7336 | 0.7337 | 0.7349 | 0.7341 | 0.4307 | 0.5691 | 0.7349 | 0.9776 | 0.7348 | 0.3743 |
| S4 | 0.7590 | 0.7596 | 0.7604 | 0.7595 | 0.4713 | 0.6096 | 0.7603 | 0.9797 | 0.7602 | 0.3718 |
| S5 | 0.7336 | 0.7337 | 0.7349 | 0.7341 | 0.4381 | 0.5778 | 0.7406 | 0.9780 | 0.7406 | 0.3825 |
| S6 | 0.7372 | 0.7378 | 0.7382 | 0.7376 | 0.8410 | 0.5836 | 0.7381 | 0.9778 | 0.7382 | 0.3562 |
| S7 | 0.7622 | 0.7624 | 0.7632 | 0.7630 | 0.8562 | 0.6211 | 0.7634 | 0.9799 | 0.7632 | 0.3538 |
| S8 | 0.7428 | 0.7433 | 0.7438 | 0.7433 | 0.8444 | 0.5922 | 0.7441 | 0.9783 | 0.7439 | 0.3640 |
| Method | Mean | Median | std | Variance | Min | Max |
|---|---|---|---|---|---|---|
| SD | 0.9486 | 0.9479 | 0.0282 | 0.9040 | 0.9958 | |
| COV | 0.9495 | 0.9488 | 0.0276 | 0.9059 | 0.9959 | |
| Entropy | 0.9026 | 0.9006 | 0.0522 | 0.8213 | 0.9917 | |
| CRITIC | 0.9083 | 0.9157 | 0.0633 | 0.7956 | 0.9956 | |
| MEREC | 0.9948 | 0.9950 | 0.0032 | 0.9892 | 0.9996 |
| Criteria | SD | COV | Entropy | CRITIC | MEREC |
|---|---|---|---|---|---|
| C1 | 0.0724 | 0.0730 | 0.0458 | 0.0369 | 0.0865 |
| C2 | 0.0727 | 0.0732 | 0.0461 | 0.0370 | 0.0865 |
| C3 | 0.0733 | 0.0739 | 0.0469 | 0.0374 | 0.0864 |
| C4 | 0.0728 | 0.0734 | 0.0463 | 0.0371 | 0.0865 |
| C5 | 0.1674 | 0.1539 | 0.2128 | 0.3148 | 0.0796 |
| C6 | 0.1464 | 0.1384 | 0.1515 | 0.3319 | 0.0829 |
| C7 | 0.0741 | 0.0746 | 0.0478 | 0.0378 | 0.0864 |
| C8 | 0.2041 | 0.1762 | 0.2865 | 0.1059 | 0.0623 |
| C9 | 0.0740 | 0.0745 | 0.0478 | 0.0377 | 0.0864 |
| C10 | 0.0428 | 0.0891 | 0.0685 | 0.0236 | 0.2566 |
| max/min | 4.7736 | 2.4138 | 6.2586 | 14.0570 | 4.1207 |
| Criterion | SD | COV | MEREC | GM |
|---|---|---|---|---|
| C1 | 0.0724 | 0.0730 | 0.0865 | 0.0818 |
| C2 | 0.0727 | 0.0732 | 0.0865 | 0.0820 |
| C3 | 0.0733 | 0.0739 | 0.0864 | 0.0825 |
| C4 | 0.0728 | 0.0734 | 0.0865 | 0.0821 |
| C5 | 0.1674 | 0.1539 | 0.0796 | 0.1350 |
| C6 | 0.1464 | 0.1384 | 0.0829 | 0.1263 |
| C7 | 0.0741 | 0.0746 | 0.0864 | 0.0830 |
| C8 | 0.2041 | 0.1762 | 0.0623 | 0.1390 |
| C9 | 0.0740 | 0.0745 | 0.0864 | 0.0830 |
| C10 | 0.0428 | 0.0891 | 0.2566 | 0.1054 |
| max/min | 4.7736 | 2.4138 | 4.1207 | 1.6979 |
| Category | SD | COV | MEREC | GM |
|---|---|---|---|---|
| Environmental (C1–C4) | 29.13% | 29.34% | 34.59% | 32.85% |
| Cost (C5–C8) | 59.19% | 54.30% | 31.12% | 48.32% |
| Performance (C9–C10) | 11.68% | 16.36% | 34.29% | 18.83% |
| max/min | 5.07 | 3.32 | 1.11 | 2.57 |
| Panel | SAW | WP | TOPSIS | R-TOPSIS | Mean | Rank |
| S0 | 9 | 9 | 9 | 9 | 9.00 | 9 |
| S1 | 7 | 7 | 6 | 7 | 6.75 | 7 |
| S2 | 8 | 8 | 8 | 8 | 8.00 | 8 |
| S3 | 6 | 6 | 7 | 6 | 6.25 | 6 |
| S4 | 4 | 4 | 4 | 4 | 4.00 | 4 |
| S5 | 5 | 5 | 5 | 5 | 5.00 | 5 |
| S6 | 3 | 3 | 3 | 3 | 3.00 | 3 |
| S7 | 1 | 1 | 1 | 1 | 1.00 | 1 |
| S8 | 2 | 2 | 2 | 2 | 2.00 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anagnostopoulou, A.; Sotiropoulos, D.; Tserpes, K. A Robust Sustainability Assessment Methodology for Aircraft Parts: Application to a Fuselage Panel. Sustainability 2025, 17, 3299. https://doi.org/10.3390/su17083299
Anagnostopoulou A, Sotiropoulos D, Tserpes K. A Robust Sustainability Assessment Methodology for Aircraft Parts: Application to a Fuselage Panel. Sustainability. 2025; 17(8):3299. https://doi.org/10.3390/su17083299
Chicago/Turabian StyleAnagnostopoulou, Aikaterini, Dimitris Sotiropoulos, and Konstantinos Tserpes. 2025. "A Robust Sustainability Assessment Methodology for Aircraft Parts: Application to a Fuselage Panel" Sustainability 17, no. 8: 3299. https://doi.org/10.3390/su17083299
APA StyleAnagnostopoulou, A., Sotiropoulos, D., & Tserpes, K. (2025). A Robust Sustainability Assessment Methodology for Aircraft Parts: Application to a Fuselage Panel. Sustainability, 17(8), 3299. https://doi.org/10.3390/su17083299







