An Integrated Approach to Schedule Passenger Train Plans and Train Timetables Economically Under Fluctuating Passenger Demands
Abstract
1. Introduction
- The arrival and departure time, origin and destination stations, running time, and maximum passenger capacity of the trains in the full-schedule timetable are known.
- The passenger demands are known, and all passengers are aware of their travel information in advance and can board and get off trains efficiently, without considering the impact of waiting, boarding, and alighting processes on passenger service quality.
- It is assumed that the train operation time is strictly in accordance with the timetable, without considering the impact of train delays on passenger service quality.
- It is assumed that the operating costs generated by each stop are the same.
- For the trains that operate on more than one railway line, which we call “cross-line trains”, we only consider the portion operating on the current railway line to simplify the problem.
- An integrated approach is proposed to synergistically schedule the passenger train plan and train timetable, containing measures of selecting operating trains, adjusting the train stopping scheme, and adjusting the train operation sequence.
- A two-objective model is established to integrally optimize the timetable and passenger train plan, aiming to minimize train operation costs and maximize passenger service quality, and an algorithm based on NSGA-II is designed to solve the model.
- Two key acceleration techniques, which utilize overtaking chromosomes and parallel computing, are designed to accelerate the algorithm.
2. Literature Review
- In terms of research scope, most research handles the passenger train plan and train timetable independently, such as [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. However, there exists a strong interrelation between them, and independent studies may make it difficult to optimize train operation from an overall perspective. Some research focuses on the integrated scheduling of train stopping plans and train timetables by adopting a two-stage collaborative optimization model, such as [20,21]. However, when the passenger demands decrease, in addition to adjusting the train stopping plan, the number of operating trains should also be adjusted, so as to reduce operational costs and energy consumption. The research in this field is relatively limited.
- In terms of objectives, some research adopts one objective. However, the train operation process is complex, and it is difficult to handle train operation optimization with one objective under different scenarios. Some research adopts multiple objectives and sums them up with weighted coefficients, which makes it difficult to reflect the interrelationships between the objectives and obtain diverse results. Thus, more research is needed to explore more diverse methods to address multiple objectives in train operation optimization issues, and the research within this domain is relatively restricted.
- Based on the limitations of the integrated scheduling of passenger train plans and train timetables, instead of scheduling the passenger train plan and train timetable separately or adopting a two-stage approach, an integrated approach is proposed to synergistically schedule the passenger train plan and train timetable, containing measures of selecting operating trains, adjusting the train stopping scheme, and adjusting the train operation sequence.
- Based on the limitations of handling multi-objective optimization, we formulate a model with two objectives: minimizing train operation costs to reduce energy consumption and maximizing passenger service quality to enhance travel experience. Instead of weighing the two objectives, we designed an algorithm based on NSGA-II to yield a Pareto front containing a set of non-dominated results, from which the railway operators can select suitable solutions under specific scheduling scenarios.
- To accelerate the algorithm, we have designed two key acceleration techniques. Firstly, a chromosome coding method based on initial train sequence and train overtaking is employed to describe the train operation sequence. Secondly, parallel computing technology is utilized to concurrently solve each independent process of the algorithm.
3. Integrated Scheduling Model Formulation
3.1. Notations
3.2. Objective Functions
- Operation costs
- 2.
- Passenger service quality
3.3. Constraints
3.3.1. Constraints of Operating Trains
3.3.2. Constraints of Headway
3.3.3. Constraints of Train Stopping Scheme
3.3.4. Constraints of Operation Time
3.3.5. Constraints of Passenger Assignment Plan
3.3.6. Constraints of Cross-Line Trains
3.3.7. Constraints of Maximum Deviation of Departure and Arrival Time
4. Algorithm Based on NSGA-II
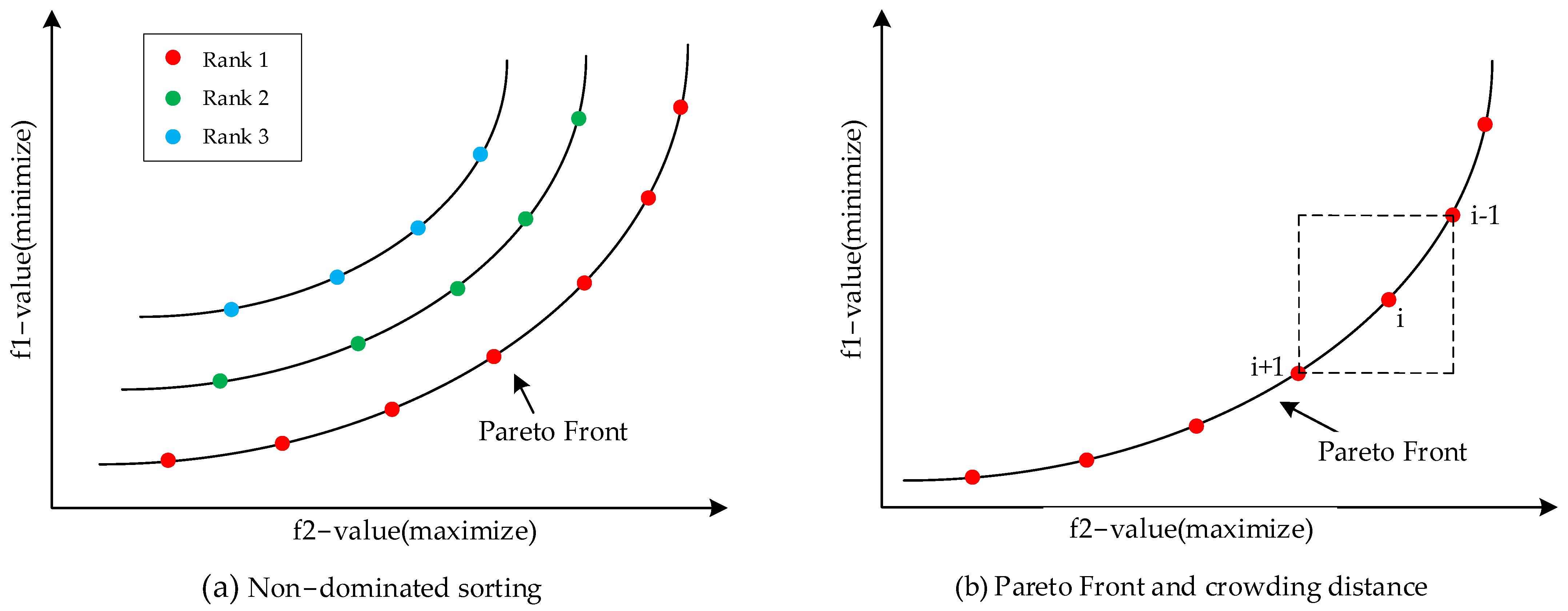
4.1. Conceptions About Pareto
4.1.1. Pareto Dominance
4.1.2. Non-Dominated Sorting
4.1.3. Crowding Distance
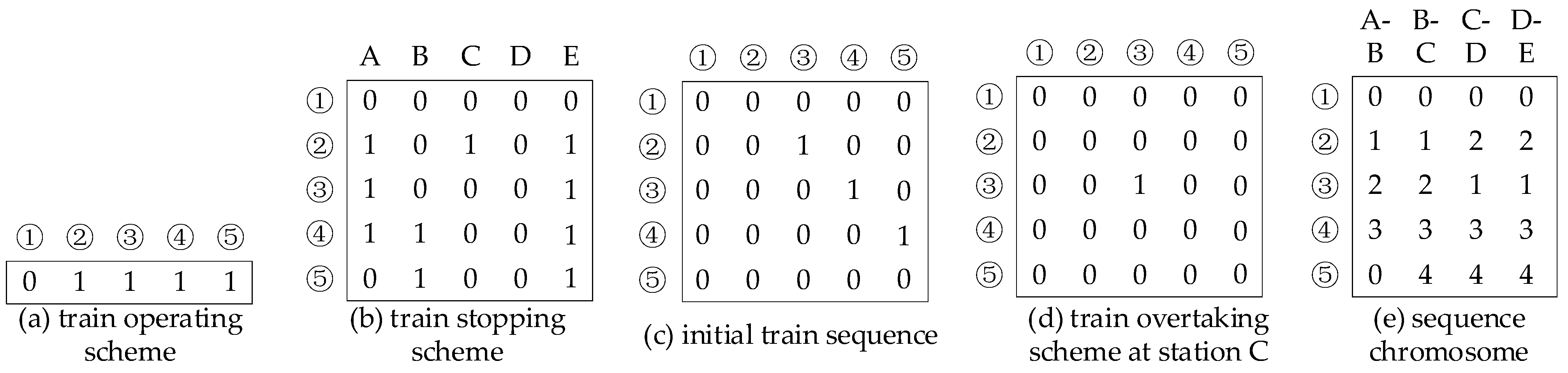
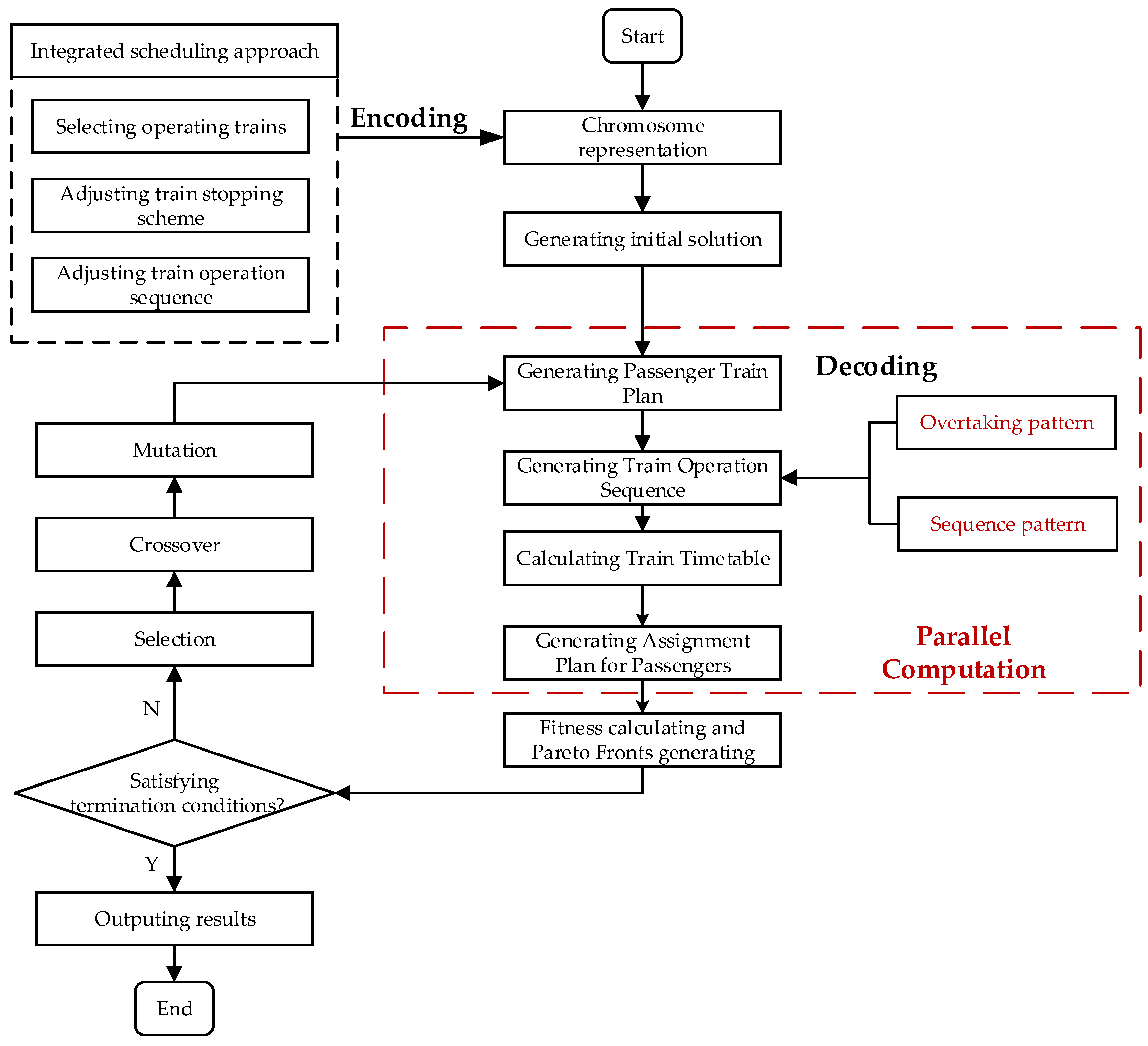
4.2. Chromosome Encoding Method
4.3. Generating Initial Solution
4.4. Feasibility of Solutions
- If the value of the gene in Chromosome I equals 0, signifying train is not selected to operate, each value of the genes in the row within Chromosome II must also be modified to 0, signifying train does not stop at any stations; values of genes in column and row in Chromosome III must also be modified to 0, signifying train does not operate before or after other trains; values of genes in column and row in Chromosome IV must also be modified to 0, signifying train does not overtake or be overtaken by other trains in any station; and values of genes in row in Chromosome IV must also be modified to 0, signifying train has no operation sequence in any section.
- In Chromosome II, if station is a compulsory stop station of train , the value of should be set to 1. If the stop frequency of train exceeds the maximum number, some stops that are not compulsory stops should be randomly canceled; that is, the corresponding values should be set to 0.
- In Chromosome V, the operation sequences in the sections should be adjusted to the consecutive sequence of positive integers. For example, the sequences in a section of 1-1-3-2-4 should be adjusted to 1-2-4-3-5; the sequences in another section of 0-1-4-3-0 should be adjusted to 0-1-3-2-0.
4.5. Chromosomes Decoding Method
4.5.1. Generating Passenger Train Plan
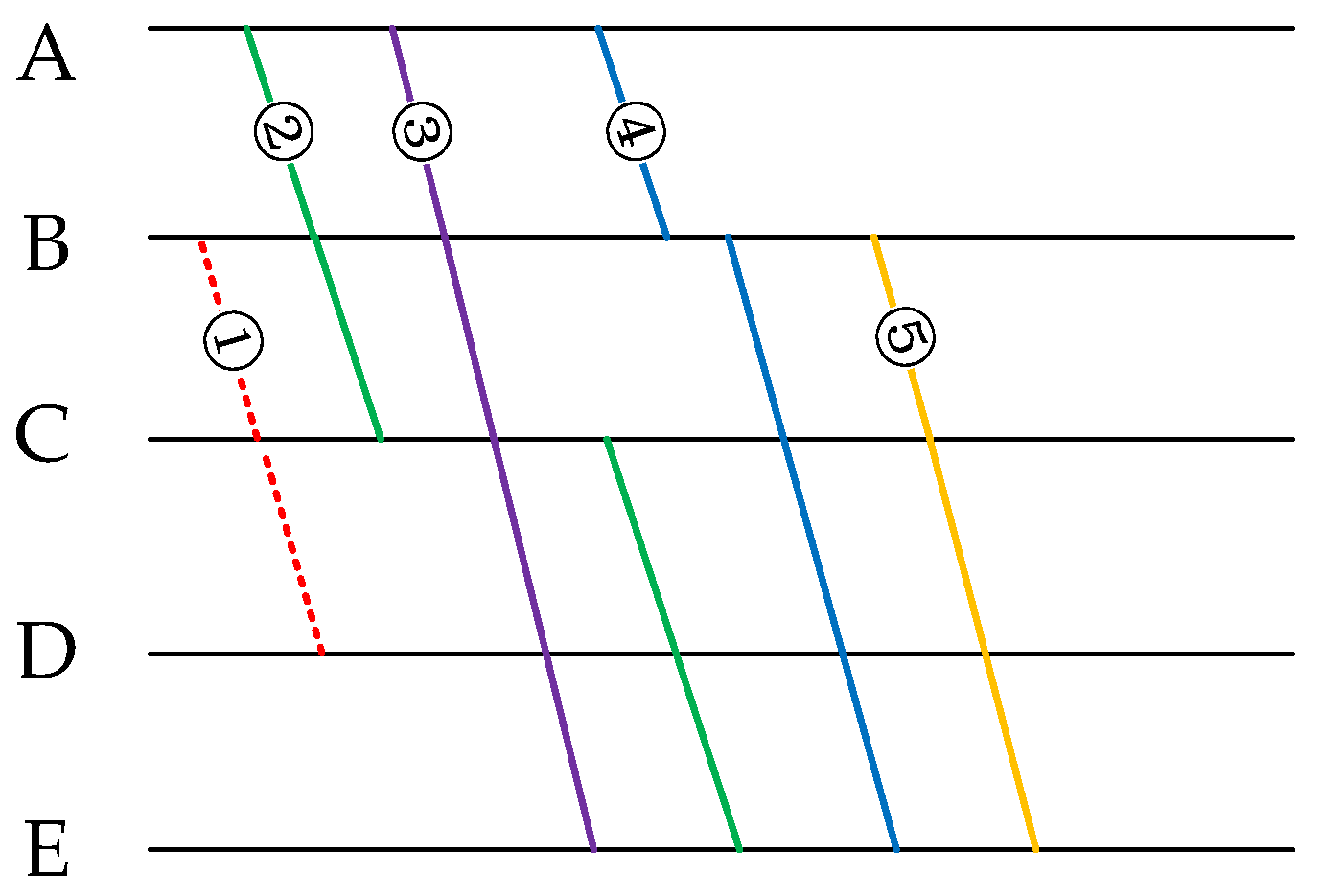
4.5.2. Generating Train Operation Sequence
- In the common operational section of train and train after the overtaking station, train and should swap the operation sequence, as shown in (27).
- The trains whose following train is train should adjust their following trains to train , as shown in (28).
- The trains whose preceding train is train should adjust their following trains to train , as shown in (29).
4.5.3. Calculating Train Timetable
4.5.4. Generating Assignment Plan for Passengers
4.6. Fitness Functions
4.7. Genetic Operators
4.7.1. Selection Process
4.7.2. Crossover Process
4.7.3. Mutation Process
4.8. Termination Conditions
4.9. Parallel Computation
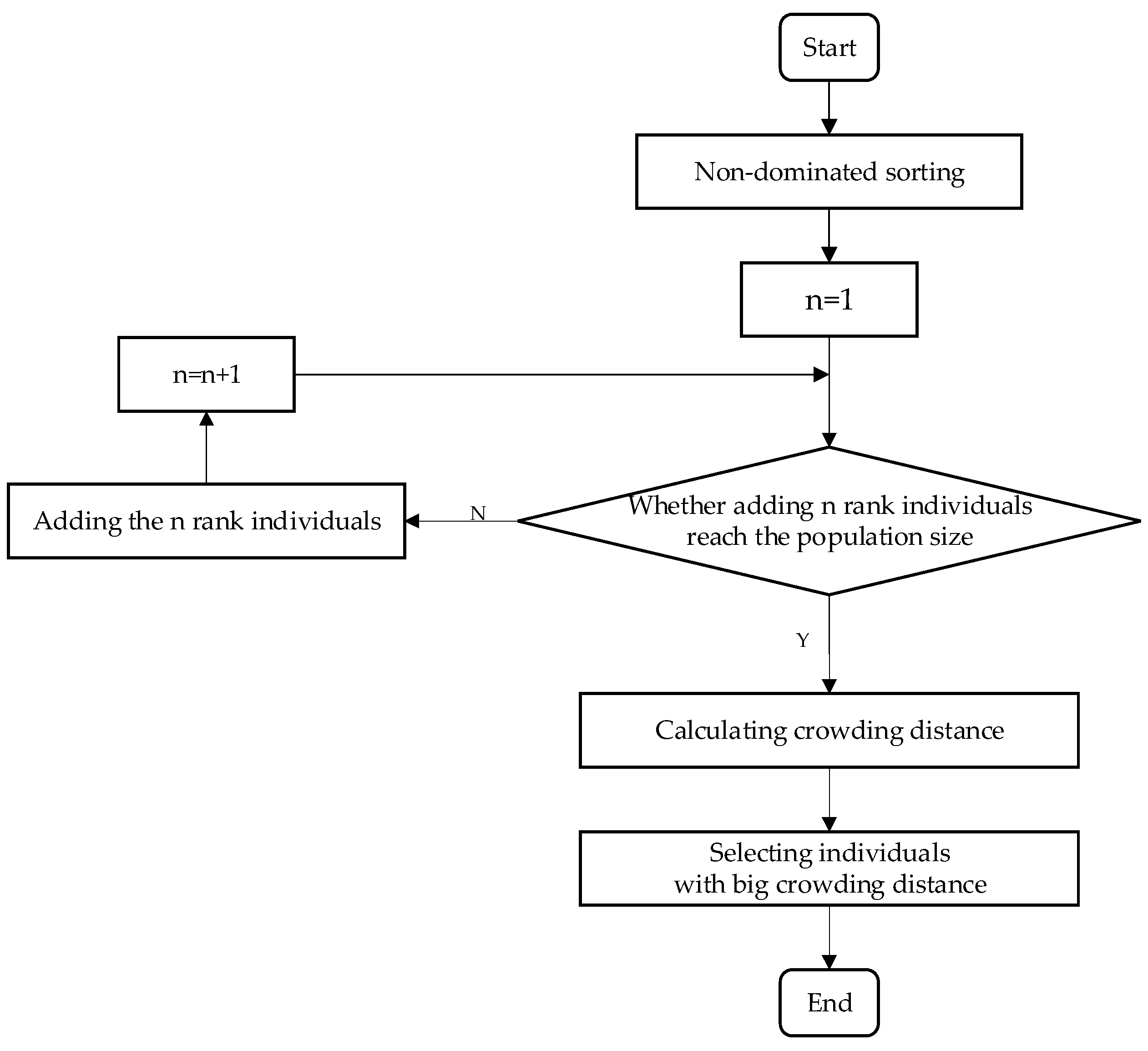
4.10. Algorithm Procedure
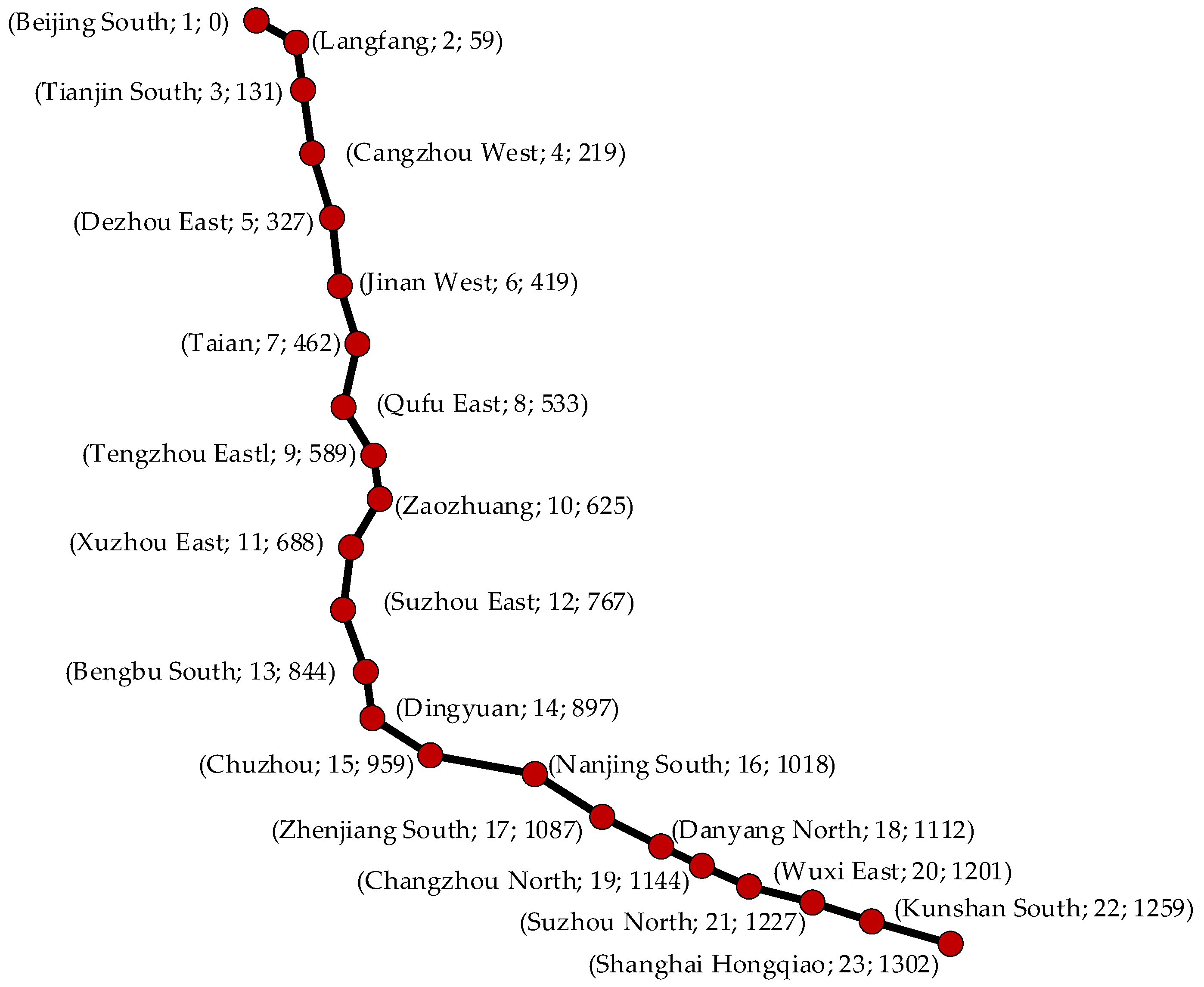
5. Case Study
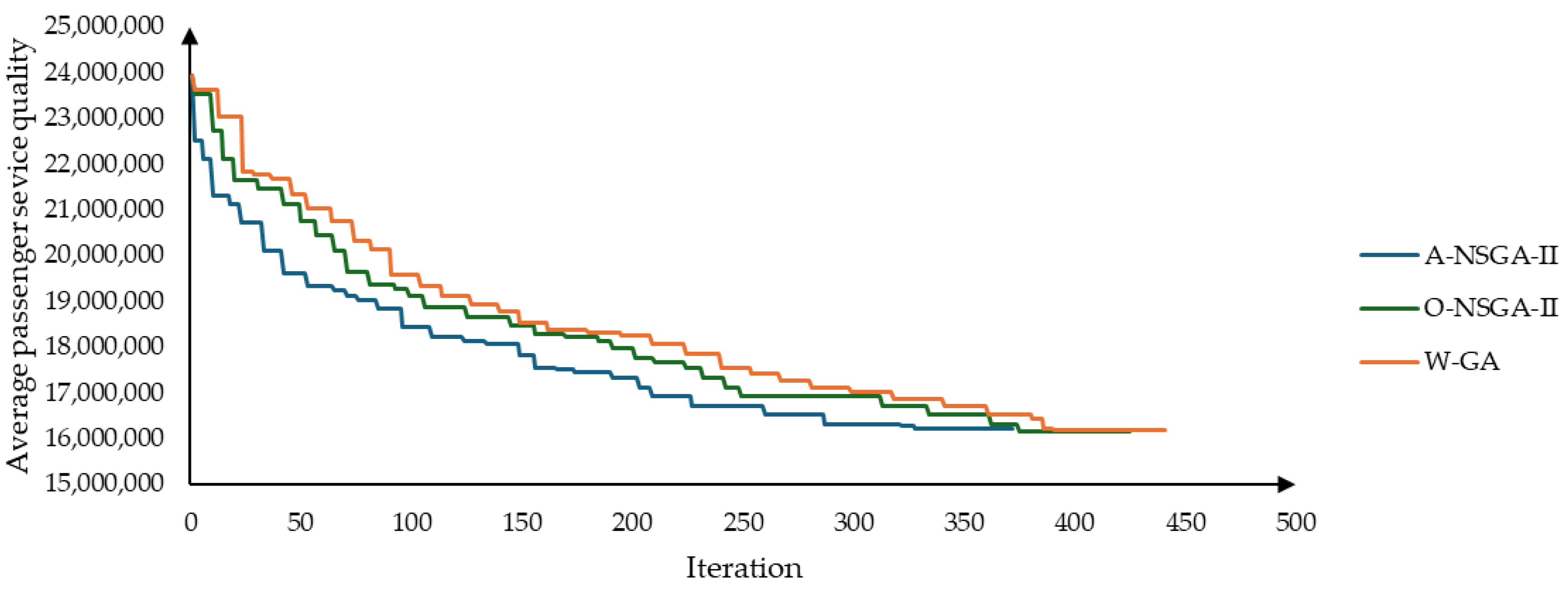
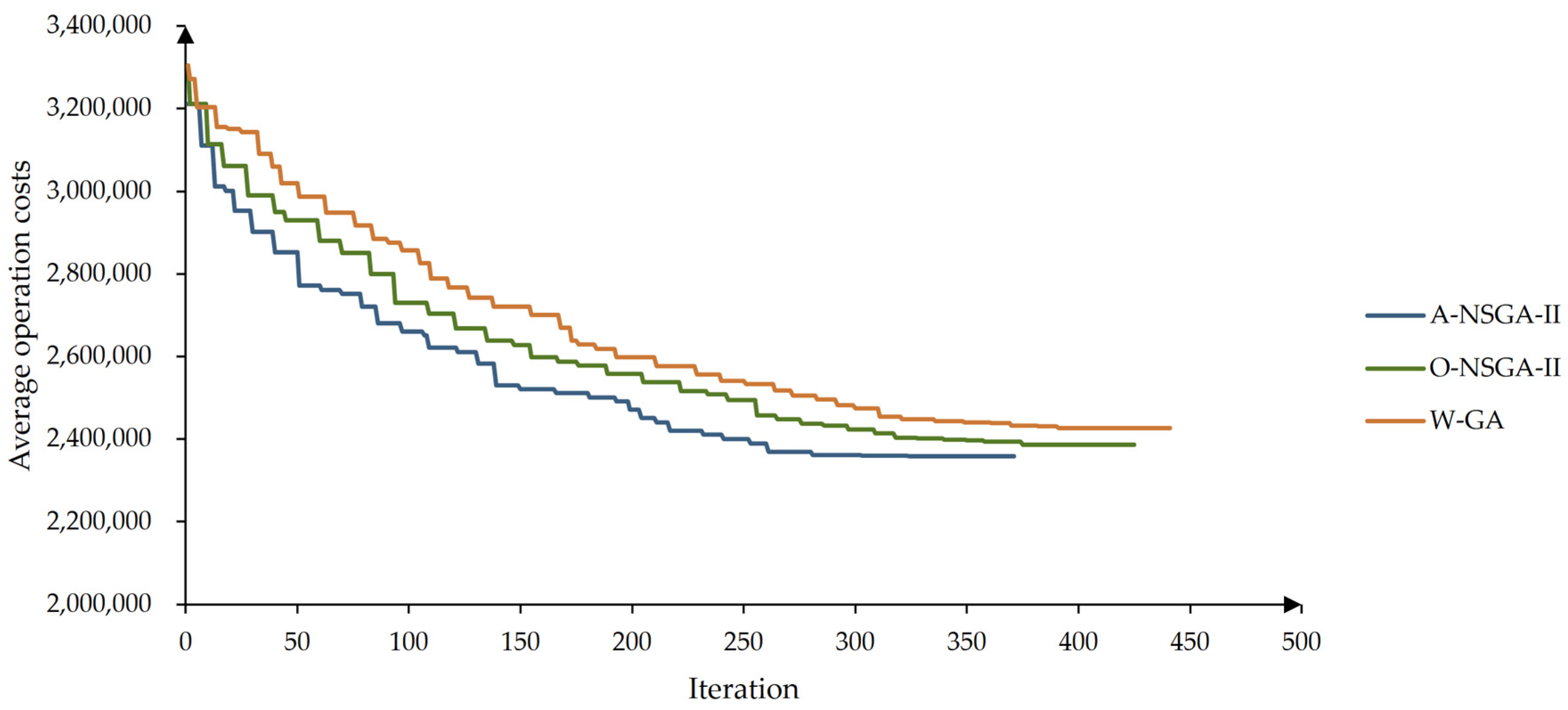
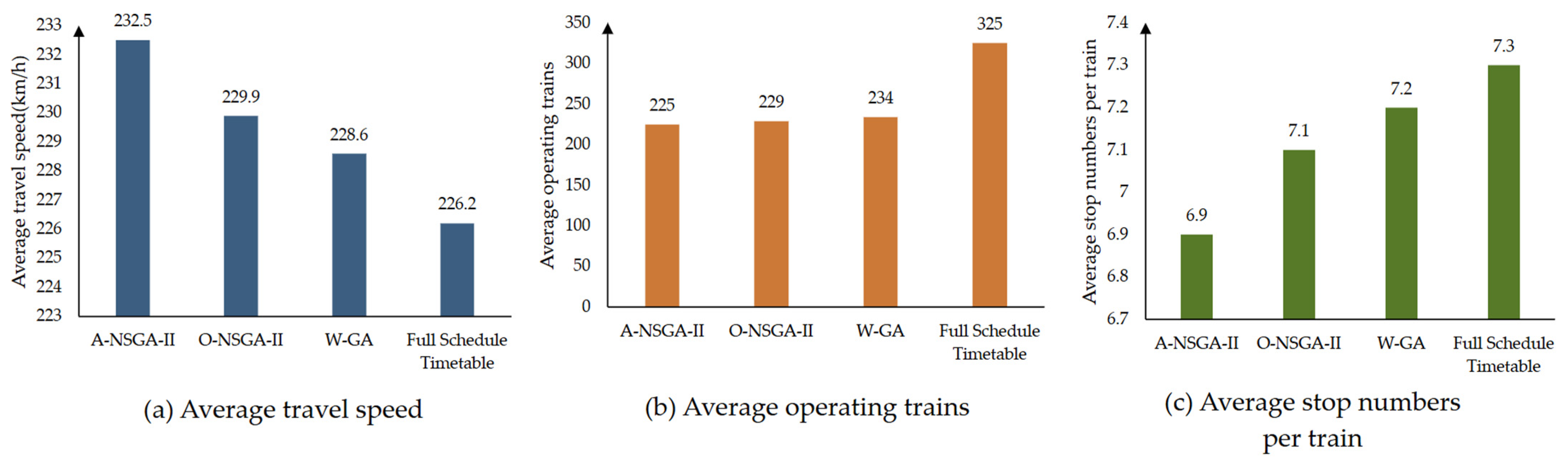
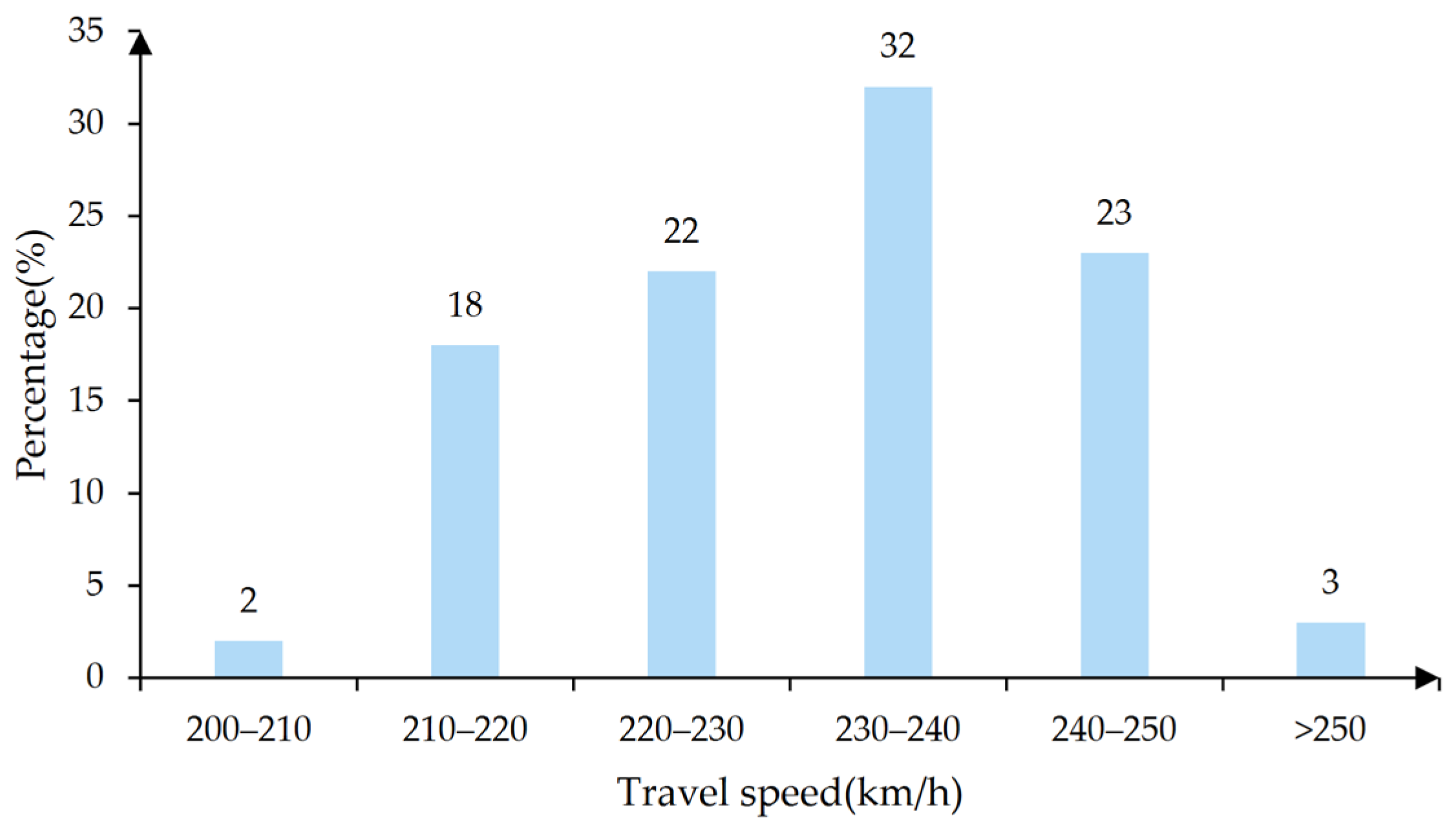
5.1. Results with Different Algorithms
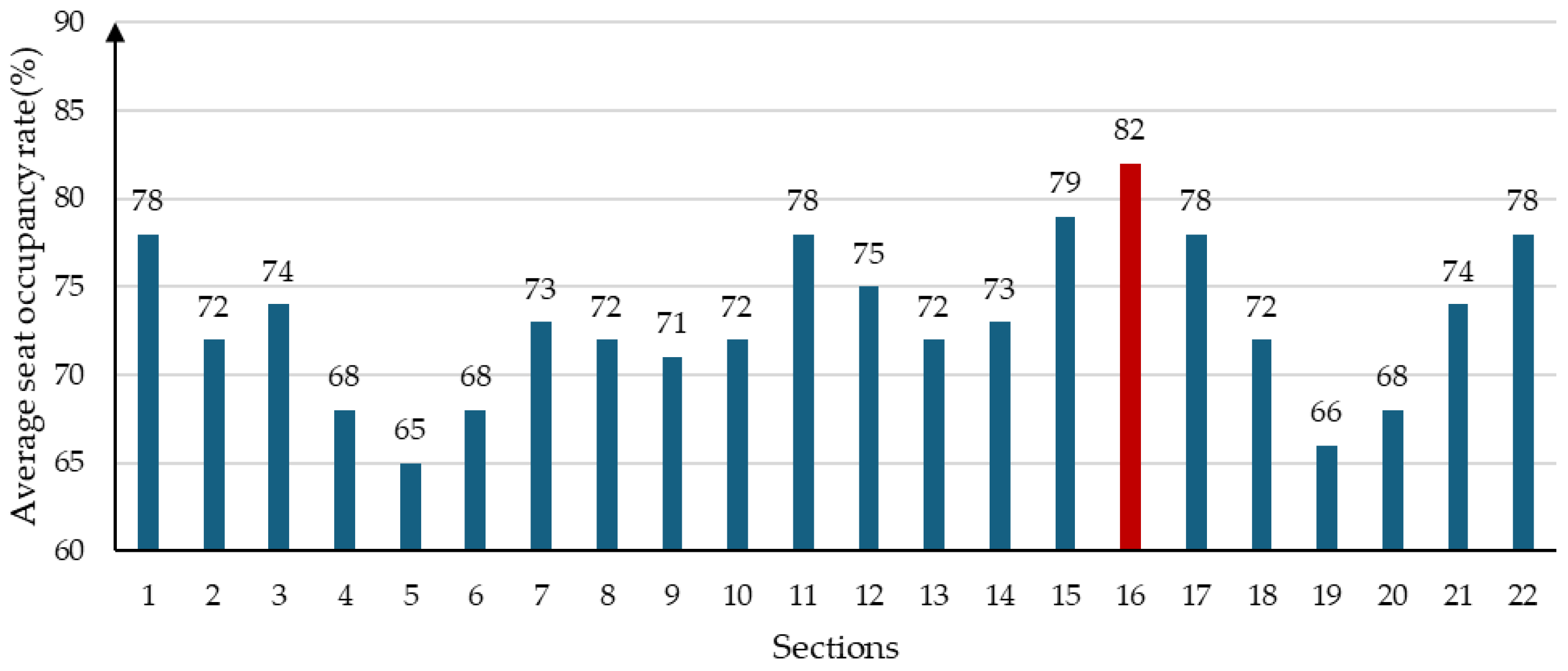
5.2. Results of Average Seat Occupancy Rates
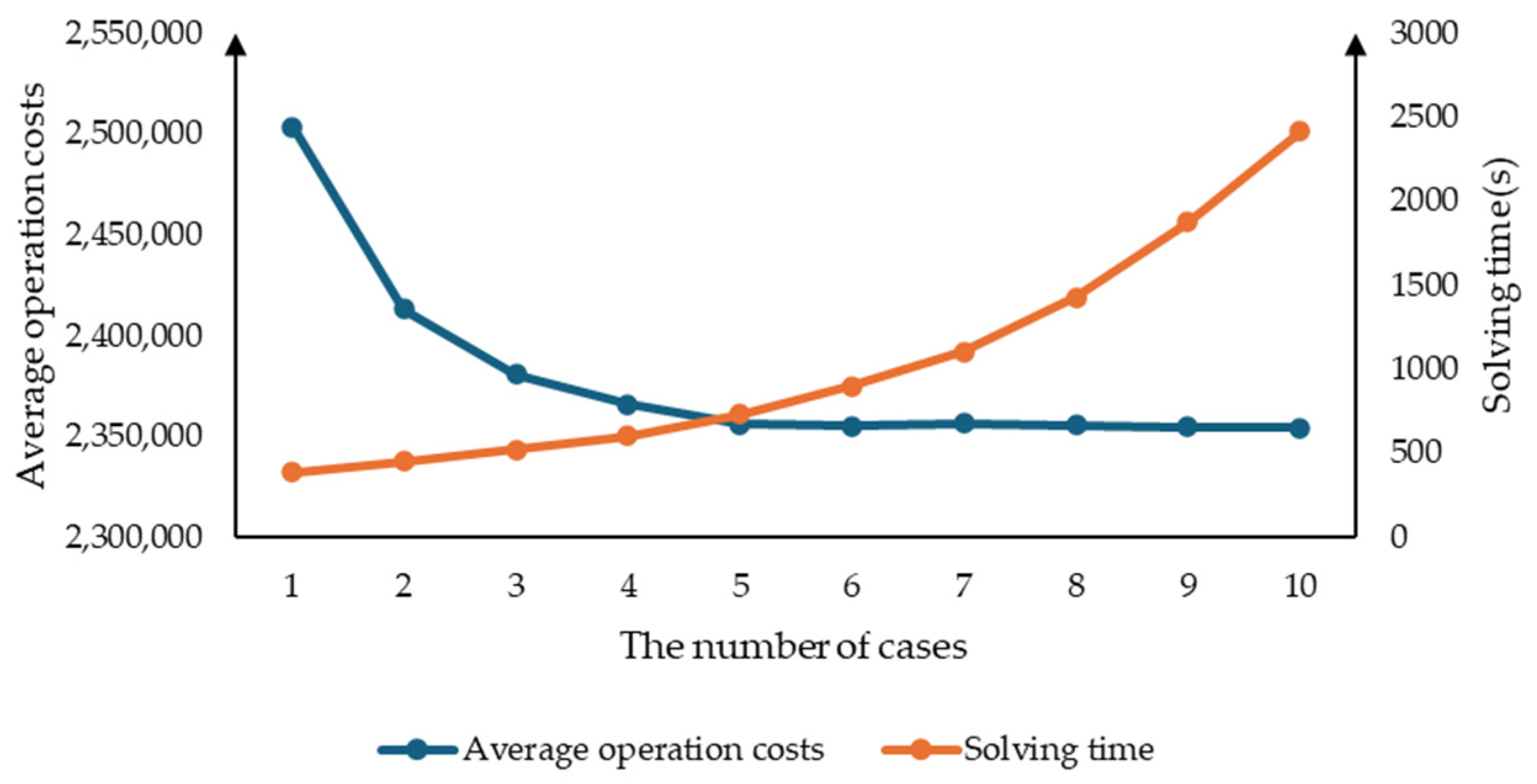
5.3. Results of Population Sizes
5.4. Results of Individuals in Pareto Fronts
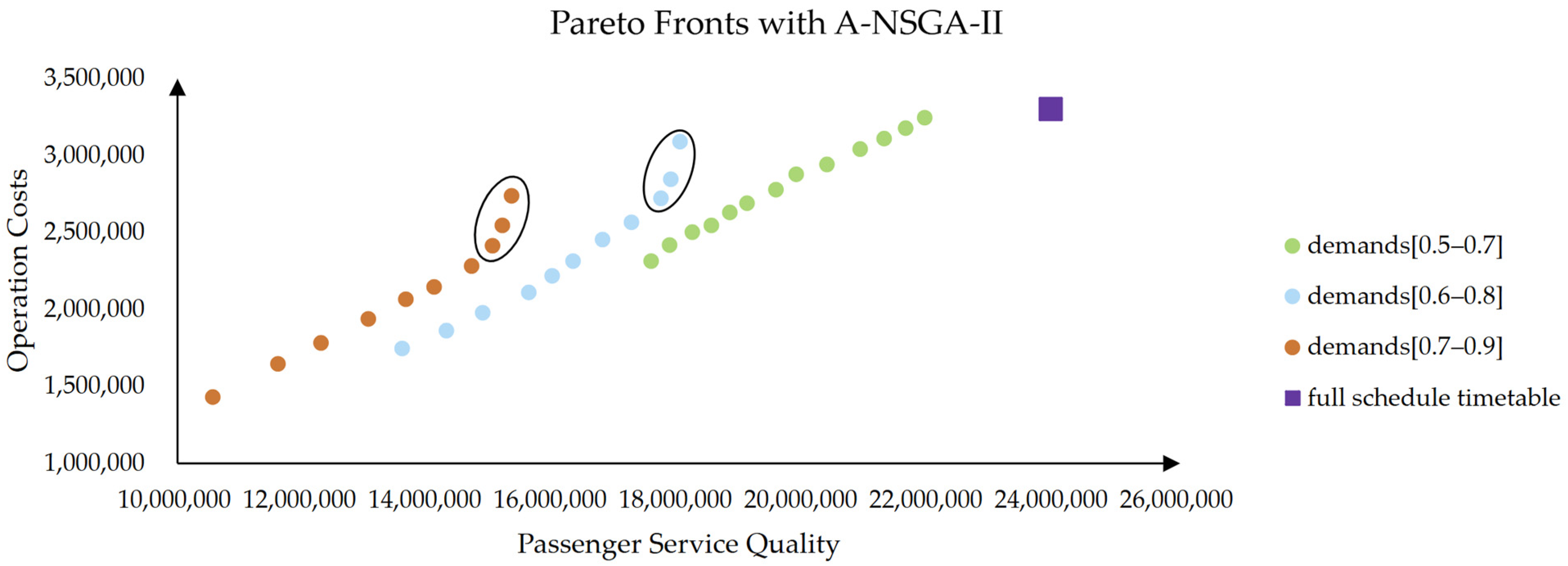
- As the passenger demands grow, the Pareto front is distributed more rightward, suggesting that when the passenger demands increase, a greater number of trains need to be operated to offer a superior passenger service quality, thereby satisfying the passenger demand.
- According to the individuals in the Pareto fronts of demands [0.5–0.7] and [0.6–0.8], we can see that when the operation cost is relatively high, with the increase in operation costs, the growth of passenger service quality slows down, as shown by the black circle in the two Pareto fronts. Since the passenger demands are relatively low and as the operation costs increase, most of the demands have already been satisfied by high-quality services (such as direct services without intermediate stops). Thus, further increasing operational costs can only provide a limited improvement in service quality. However, when the passenger demands are relatively high, the phenomena does not emerge at the Pareto front of demands [0.7–0.9]. We think it is restricted by the total number of trains in the full-schedule timetable. Although a substantial number of passengers need to be served, the passenger service quality that the full-schedule timetable can offer is limited, making it impossible for all passengers to choose high-quality travel patterns (such as direct services without intermediate stops), which reduces the maximum passenger service quality.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Headway Determination Method
Appendix A.2. Crowding Distance
Appendix A.3. Crossover Probability
Appendix A.4. The Multi-Objective Weighting Method
References
- Azzouz, L.; Jack, A. Benchmarking the sustainability reporting of high-speed railways (HSRs): Towards a state-of-the-art benchmarking and reporting framework for HSRs. J. Clean. Prod. 2019, 250, 119505. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, L.; Guo, B.; Chen, X.; Zhou, H. An Efficient Hybrid Approach for Scheduling the Train Timetable for the Longer Distance High-Speed Railway. Sustainability 2021, 13, 2538. [Google Scholar] [CrossRef]
- Yadav, V.; Kaswan, M.S.; Gahlot, P.; Duhan, R.K.; Garza-Reyes, J.A.; Rathi, R.; Chaudhary, R.; Yadav, G. Green Lean Six Sigma for sustainability improvement: A systematic review and future research agenda. Int. J. Lean Six Sigma 2023, 14, 759–790. [Google Scholar] [CrossRef]
- Yaser, A.H.; Komarudin. Integration of Lean Manufacturing and Industry 4.0: A Conceptual Framework. In Proceedings of the APCORISE 2020: 3rd Asia Pacific Conference on Research in Industrial and Systems Engineering 2020, Depok, Indonesia, 16–17 June 2020. [Google Scholar]
- Wu, S.C.; Tong, L. Research on Passenger Flow Distribution Based on High-Speed Railway Train Scheme. In Proceedings of the 23rd COTA International Conference of Transportation Professionals (CICTP)—Innovation-Empowered Technology for Sustainable, Intelligent, Decarbonized, and Connected Transportation, Beijing, China, 14–17 July 2023; pp. 2169–2178. [Google Scholar]
- Liu, P.; Han, B.M.; Zhang, Q. Optimization Model of Passenger Train Service Plan Based on the Degree of Passenger Satisfaction. In Proceedings of the 3rd International Conference on Civil Engineering and Transportation (ICCET 2013), Kunming, China, 14–15 December 2013; pp. 577–582. [Google Scholar]
- Nie, B.W.; Nie, L.; Fu, H.L.; Wu, X. Weekly line planning to improve the match between rail supply and passenger demand. Comput.-Aided Civ. Infrastruct. Eng. 2023, 38, 1810–1833. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, H.X.; Xu, Y.; Zhou, Y.; Wei, Y.G. Integrated optimization of train stop planning and ticket pricing with equity concerns of passengers for high-speed railways. Meas. Control 2023, 56, 792–812. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Q.; Fang, B.; Wei, Y.G. An optimisation and adjustment model of train line planning for EMU trains under multiple formation. Int. J. Syst. Sci.-Oper. Logist. 2024, 11, 2398568. [Google Scholar] [CrossRef]
- Qi, X.; Xiong, J. Optimization Method of Passenger Train Plan based on Stop Schedule Plan for Passenger Dedicated Line. In Proceedings of the 2nd International Conference on Uncertainty Reasoning and Knowledge Engineering (URKE), Jakarta, Indonesia, 14–15 August 2012; pp. 204–207. [Google Scholar]
- Zhi, L. A Common Model for Railway Train Timetable Optimization. In Proceedings of the 2019 11th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Qiqihar, China, 28–29 April 2019; pp. 115–119. [Google Scholar]
- Higgins, A.; Kozan, E.; Ferreira, L. Optimal scheduling of trains on a single line track. Transp. Res. Part B Methodol. 1996, 30, 147–161. [Google Scholar] [CrossRef]
- Ghoseiri, K.; Szidarovszky, F.; Asgharpour, M.J. A multi-objective train scheduling model and solution. Transp. Res. Part B Methodol. 2004, 38, 927–952. [Google Scholar] [CrossRef]
- Zhou, X.; Zhong, M. Single-track train timetabling with guaranteed optimality: Branch-and-bound algorithms with enhanced lower bounds. Transp. Res. Part B Methodol. 2007, 41, 320–341. [Google Scholar] [CrossRef]
- Liao, Z.W.; Miao, J.R.; Meng, L.Y.; Li, H.Y. A resource-oriented decomposition approach for train timetabling problem with variant running time and minimum headway. Transp. Lett.-Int. J. Transp. Res. 2022, 14, 129–142. [Google Scholar] [CrossRef]
- Wu, Y.; Ying, Z.; Wang, H.; Wang, X. A stochastic multi-objective optimization method for railways for Mixed Passenger and Freight Railway Transportation under the Prohibiting Meeting Requirement in the Section. In Proceedings of the 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Bilbao, Spain, 24–28 September 2023; pp. 2200–2205. [Google Scholar]
- Li, W.; Ni, S. Train timetabling with the general learning environment and multi-agent deep reinforcement learning. Transp. Res. Part B Methodol. 2022, 157, 230–251. [Google Scholar] [CrossRef]
- Meng, X.; Jia, L.; Xiang, W. Complex network model for railway timetable stability optimisation. IET Intell. Transp. Syst. 2018, 12, 1369–1377. [Google Scholar] [CrossRef]
- Chen, D.; Ni, S.; Xu, C.a.; Jiang, X. Optimizing the draft passenger train timetable based on node importance in a railway network. Transp. Lett. 2017, 11, 20–32. [Google Scholar] [CrossRef]
- Qi, J.G.; Li, S.K.; Gao, Y.; Yang, K.; Liu, P. Joint optimization model for train scheduling and train stop planning with passengers distribution on railway corridors. J. Oper. Res. Soc. 2018, 69, 556–570. [Google Scholar] [CrossRef]
- Qi, J.G.; Yang, L.X.; Gao, Y.; Li, S.K. Robust Train Timetabling Problem with Optimized Train Stop Plan. In Proceedings of the 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiaiie, China, 15–17 August 2015; pp. 936–940. [Google Scholar]
- Odijk, M.A. A constraint generation algorithm for the construction of periodic railway timetables. Transp. Res. Part B Methodol. 1996, 30, 455–464. [Google Scholar] [CrossRef]
- Eaton, J.; Yang, S.; Mavrovouniotis, M. Ant colony optimization with immigrants schemes for the dynamic railway junction rescheduling problem with multiple delays. Soft Comput. 2015, 20, 2951–2966. [Google Scholar] [CrossRef]
- Ren, X.Y.; Huang, Y.N.; Zhang, M. Train Timetable Optimization Research Based on PSO Energy-Efficient Operation Strategy. In Proceedings of the 2014 International Conference on Informative and Cybernetics for Computational Social Systems (ICCSS), Qingdao, China, 9–10 October 2014; pp. 134–138. [Google Scholar]
- Wu, Q.; Cole, C.; McSweeney, T. Applications of particle swarm optimization in the railway domain. Int. J. Rail Transp. 2016, 4, 167–190. [Google Scholar] [CrossRef]
- Cacchiani, V.; Caprara, A.; Toth, P. A column generation approach to train timetabling on a corridor. 4OR-Q. J. Oper. Res. 2008, 6, 125–142. [Google Scholar] [CrossRef]
- Brännlund, U.; Lindberg, P.O.; Nõu, A.; Nilsson, J. Railway Timetabling using Lagrangian Relaxation. Transp. Sci. 1998, 32, 358–369. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, M.; Dong, H.; Wu, X.; Li, Y.; Wang, F.-Y. ADMM-based joint rescheduling method for high-speed railway timetabling and platforming in case of uncertain perturbation. Transp. Res. Part C Emerg. Technol. 2023, 152, 104150. [Google Scholar] [CrossRef]
- Zhong, M.; Yue, Y.; Zhou, L.; Zhu, J. Parallel optimization method of train scheduling and shunting at complex high-speed railway stations. Comput.-Aided Civ. Inf. 2023, 39, 731–755. [Google Scholar] [CrossRef]
- Kokubo, T.; Fukuyama, Y. Practical Train Crew Scheduling Problems Using Parallel Tabu Search. In Proceedings of the 57th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Nara, Japan, 11–14 September 2018; pp. 1673–1678. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Martínez-Salazar, I.A.; Molina, J.; Ángel-Bello, F.; Gómez, T.; Caballero, R. Solving a bi-objective Transportation Location Routing Problem by metaheuristic algorithms. Eur. J. Oper. Res. 2014, 234, 25–36. [Google Scholar] [CrossRef]
- Seifpour, M.; Asghari, S.A.; Ghobaei-Arani, M. A stochastic multi-objective optimization method for railways scheduling: A NSGA-II-based hybrid approach. J. Supercomput. 2023, 80, 2128–2163. [Google Scholar] [CrossRef]
- Chen, X.; Li, K.; Zhang, L.; Tian, Z. Robust Optimization of Energy-Saving Train Trajectories Under Passenger Load Uncertainty Based on p-NSGA-II. IEEE Trans. Transp. Electrif. 2023, 9, 1826–1844. [Google Scholar] [CrossRef]
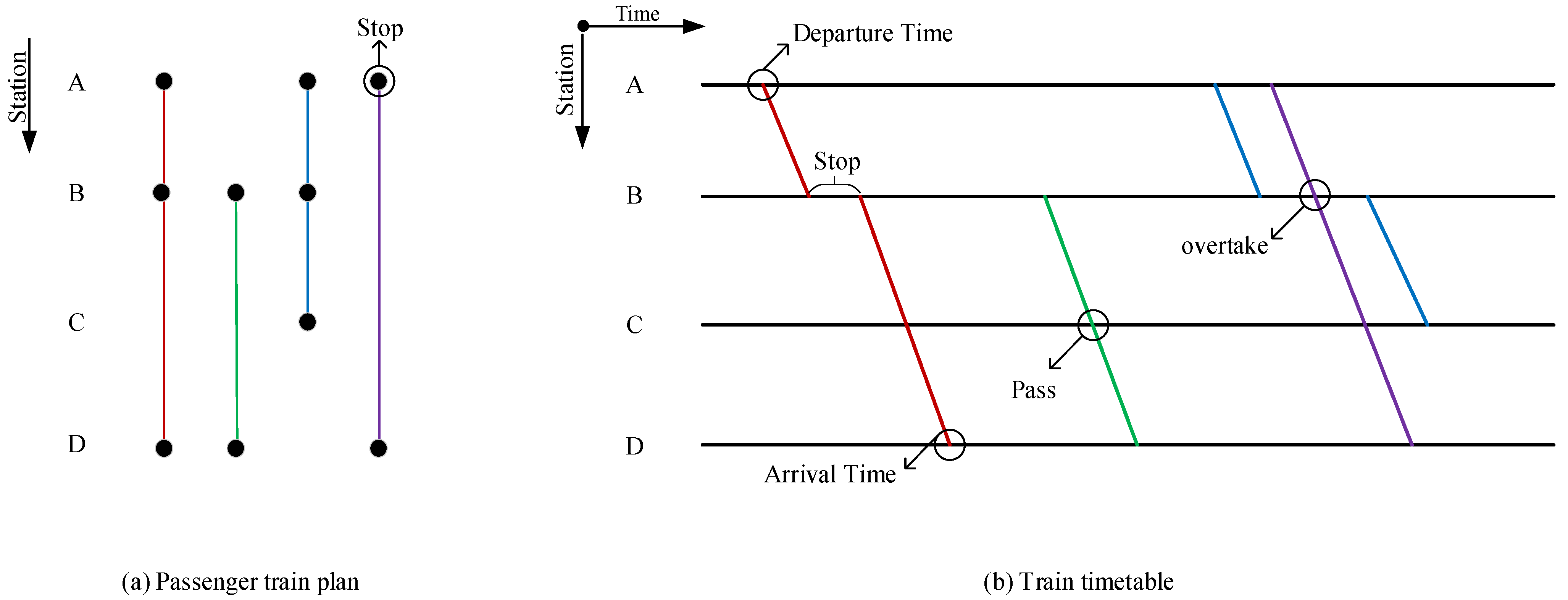
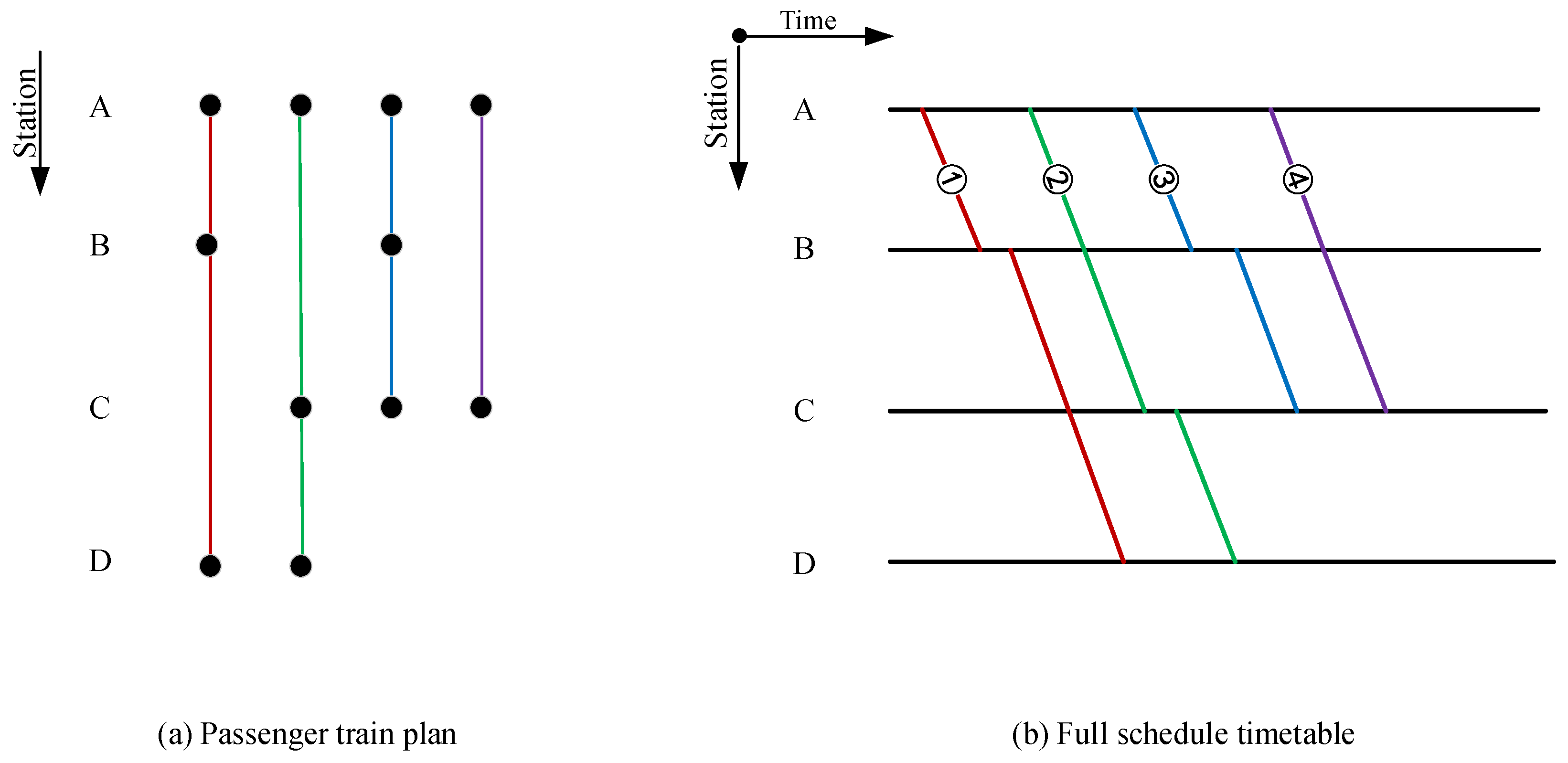
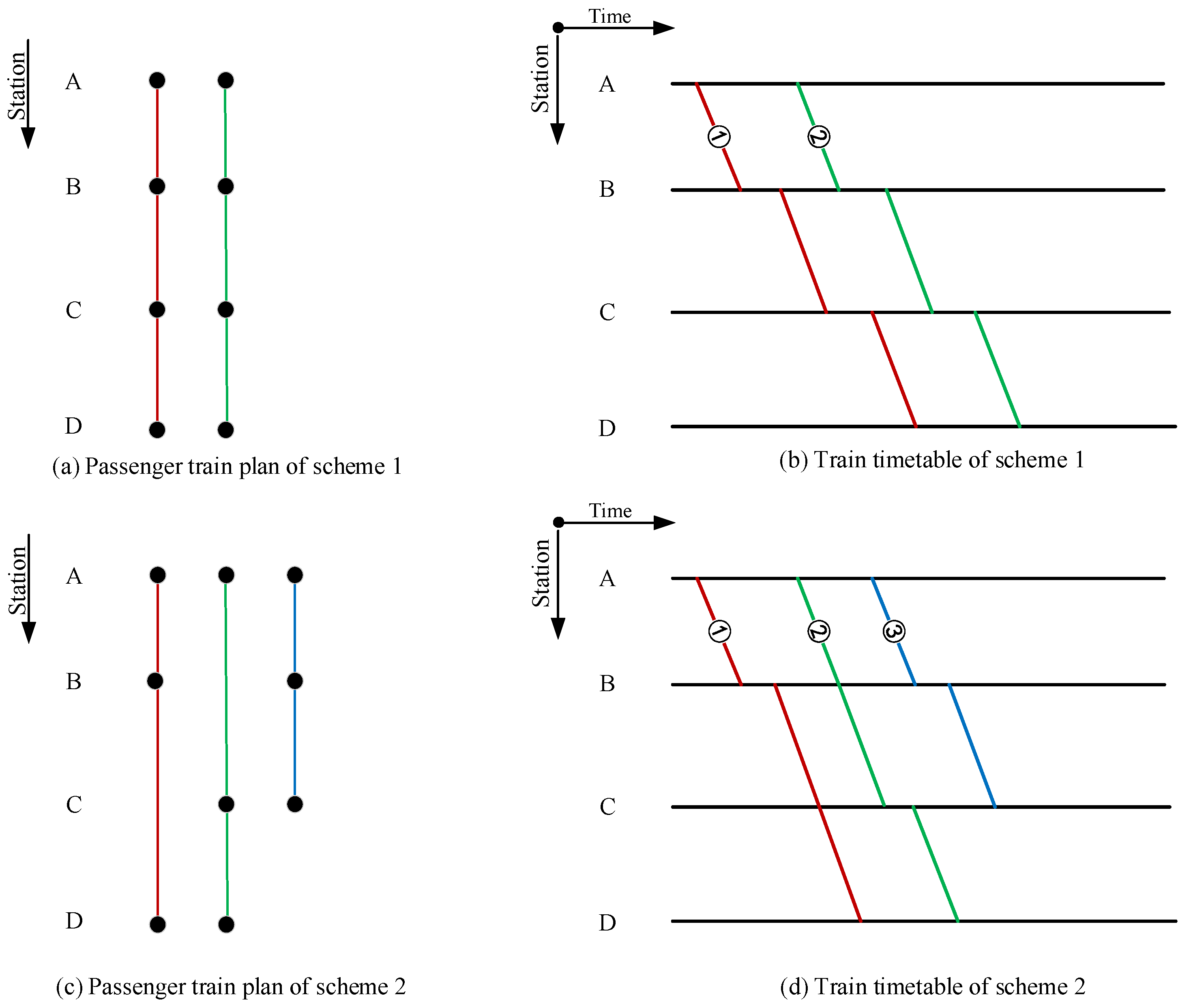
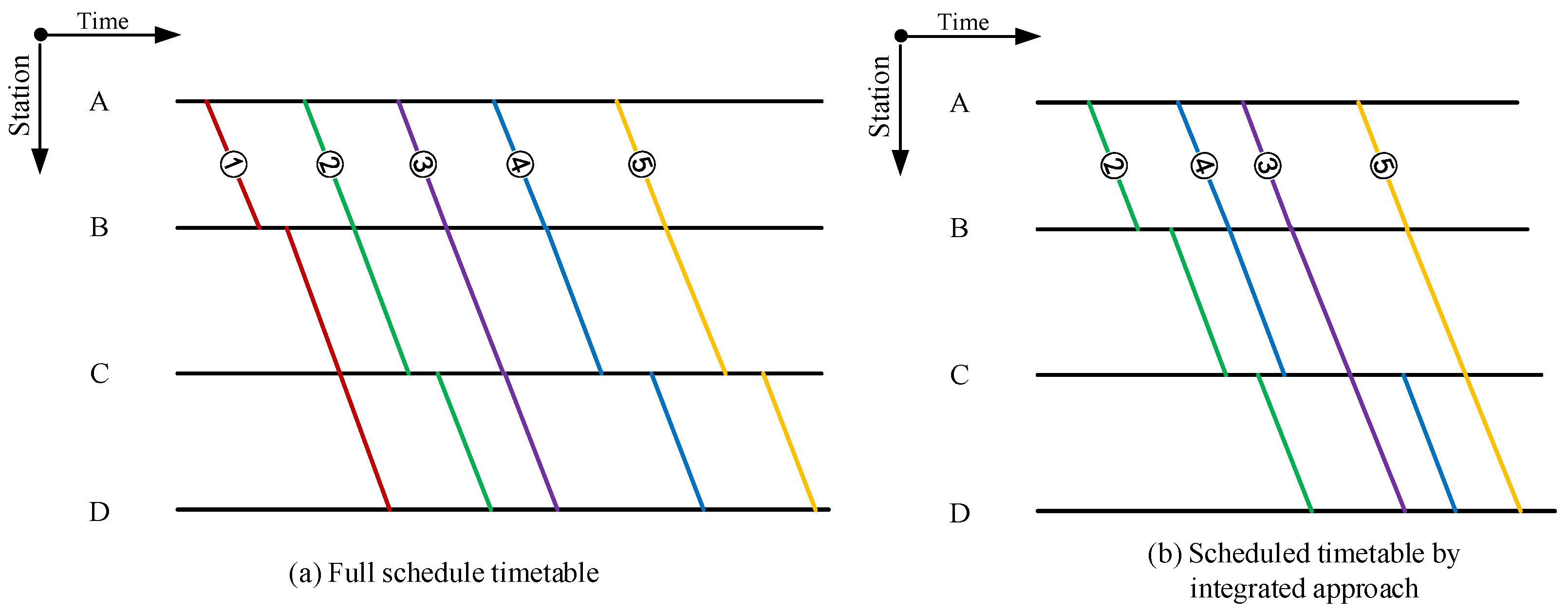
| Literature | Research Scope | Objective | Multi-Objective Processing |
|---|---|---|---|
| Wu [5] | Passenger train plan | Maximizing board seat rate | - |
| Liu [6] | Passenger train plan | Minimizing the total passenger train stop times and minimizing extra passenger transportation costs | Weighting multiple objectives |
| Xia [8] | Passenger train plan | Maximizing the total ticket revenue | - |
| Qi [10] | Passenger train plan | Maximizing the income of passenger transport and minimizing stopping and running cost | Weighting multiple objectives |
| Ghoseiri [13] | Train timetable | Minimizing fuel consumption and travel time | Weighting multiple objectives in different ways |
| Zhou [14] | Train timetable | Minimizing train total travel time | - |
| Wu [16] | Train timetable | Minimizing the average passenger expectation and the total number of train operation cycles | Pareto front |
| Meng [18] | Train timetable | Maximizing train timetable stability | - |
| Qi [20] | Passenger train plan and train timetable | Minimizing the travel time of all trains and passengers | - |
| Qi [21] | Passenger train plan and train timetable | Minimizing the travel time and variance | Weighting multiple objectives |
| Notations | Definition |
|---|---|
| Set of operation stations of train | |
| Set of operation sections of train | |
| Notations | Definition |
|---|---|
| The arrival time of train at station in the full-schedule timetable | |
| The departure time of train at station in the full-schedule timetable | |
| If train stops at station | |
| The origin station for train | |
| The destination station for train | |
| The origin station for section | |
| The destination station for section | |
| The origin station for demand | |
| The destination station for demand | |
| The capacity of train | |
| The quantity of passengers of demand | |
| Whether the range of demand contains section | |
| Travel time for train in section | |
| Extra operation time for arrival | |
| Extra operation time for departure | |
| The minimum dwelling time at station for train | |
| The maximum dwelling at station time for train | |
| The arrival headway between two trains | |
| The minimum arrival headway between passing train and stopping train | |
| The minimum arrival headway between two passing trains | |
| The minimum arrival headway between two stopping trains | |
| The minimum arrival headway between stopping train and passing train | |
| The departure headway between two trains | |
| The minimum departure headway between passing train and stopping train | |
| The minimum departure headway between two passing trains | |
| The minimum departure headway between two stopping trains | |
| The minimum departure headway between stopping train and passing train | |
| The earliest departure time of train at origin station | |
| The latest departure time of train at origin station | |
| The maximum times that train is allowed to be overtaken | |
| The maximum times that train is allowed to stop | |
| Whether train must stop at station | |
| The operation costs of operating train | |
| The operation costs of adding a stop | |
| The basic quality of train serving one passenger from demand | |
| The running time required for train to serve demand without extra stops | |
| The loss of service quality for one passenger of demand due to 1 min extra travel time | |
| The maximum deviation of departure and arrival time compared to the time in full-schedule timetable | |
| The number of individuals in the population | |
| A large integer |
| Notations | Definition |
|---|---|
| , train operates in optimized timetable | |
| The arrival time of train at station | |
| The departure time of train at station | |
| stops at station | |
| The number of passengers from demand allocated to train | |
| , train is the preceding train of train in section |
| Parameter | Value |
|---|---|
| The number of trains in full-schedule timetable | 325 |
| Time window allowing for train operating | [6:00–24:00] |
| Extra operation time for arrival | 3 min |
| Extra operation time for departure | 2 min |
| The minimum dwelling time at station for train | 2 min |
| The maximum dwelling at station time for train | 15 min |
| 4 min | |
| 3 min | |
| 4 min | |
| 2 min | |
| 6 min | |
| 3 min | |
| 3 min | |
| 7 min | |
| The maximum times for one train to be overtaken | 3 |
| The maximum times for one train to stop | 13 |
| NO. | Passenger Demands | Algorithm | Average Passenger Service Quality | Average Operation Costs | Solving Time (s) | Numberof Iterations |
|---|---|---|---|---|---|---|
| 1 | demands [0.5–0.7] | W-GA | 13,509,332 | 2,163,375 | 1177 | 395 |
| 2 | demands [0.5–0.7] | O-NSGA-II | 13,502,582 | 2,143,865 | 1109 | 388 |
| 3 | demands [0.5–0.7] | A-NSGA-II | 13,541,345 | 2,099,696 | 683 | 341 |
| 4 | demands [0.6–0.8] | W-GA | 16,161,044 | 2,426,758 | 1311 | 441 |
| 5 | demands [0.6–0.8] | O-NSGA-II | 16,159,024 | 2,386,110 | 1194 | 425 |
| 6 | demands [0.6–0.8] | A-NSGA-II | 16,201,046 | 2,356,076 | 732 | 372 |
| 7 | demands [0.7–0.9] | W-GA | 19,594,235 | 2,896,345 | 1405 | 473 |
| 8 | demands [0.7–0.9] | O-NSGA-II | 19,604,234 | 2,878,483 | 1300 | 466 |
| 9 | demands [0.7–0.9] | A-NSGA-II | 19,653,952 | 2,791,541 | 808 | 407 |
| 10 | full-schedule timetable | 23,934,921 | 3,304,947 | - | - | |
| NO. | Population Size | Number of Individuals in Pareto Front | Average Passenger Service Quality | Average Operation Costs | Solving Time (s) | Number of Iterations |
|---|---|---|---|---|---|---|
| 1 | 10 | 8 | 15,888,234 | 2,503,375 | 385 | 231 |
| 2 | 20 | 9 | 15,919,423 | 2,412,865 | 452 | 273 |
| 3 | 30 | 11 | 15,923,823 | 2,380,696 | 521 | 314 |
| 4 | 40 | 12 | 16,061,044 | 2,365,758 | 602 | 352 |
| 5 | 50 | 13 | 16,201,046 | 2,356,076 | 732 | 372 |
| 6 | 60 | 14 | 16,211,046 | 2,355,088 | 900 | 383 |
| 7 | 70 | 14 | 16,234,235 | 2,356,345 | 1101 | 398 |
| 8 | 80 | 13 | 16,233,234 | 2,355,483 | 1426 | 391 |
| 9 | 90 | 15 | 16,235,952 | 2,354,541 | 1877 | 404 |
| 10 | 100 | 14 | 16,236,921 | 2,354,147 | 2414 | 411 |
| Demands [0.5–0.7] | Demands [0.6–0.8] | Demands [0.7–0.9] | ||||||
|---|---|---|---|---|---|---|---|---|
| No. | Passenger Service Quality | Operation Costs | No. | Passenger Service Quality | Operation Costs | No. | Passenger Service Quality | Operation Costs |
| 1 | 15,326,831 | 2,738,265 | 1 | 18,013,125 | 3,092,910 | 1 | 21,918,731 | 3,247,053 |
| 2 | 15,176,346 | 2,547,886 | 2 | 17,869,752 | 2,849,031 | 2 | 21,616,714 | 3,179,914 |
| 3 | 15,025,849 | 2,413,496 | 3 | 17,707,415 | 2,721,178 | 3 | 21,271,266 | 3,110,030 |
| 4 | 14,685,707 | 2,282,060 | 4 | 17,240,425 | 2,567,312 | 4 | 20,894,309 | 3,044,312 |
| 5 | 14,085,304 | 2,145,387 | 5 | 16,773,621 | 2,456,574 | 5 | 20,356,795 | 2,944,076 |
| 6 | 13,641,601 | 2,067,602 | 6 | 16,306,818 | 2,315,738 | 6 | 19,872,791 | 2,879,075 |
| 7 | 13,034,598 | 1,939,432 | 7 | 15,976,765 | 2,217,473 | 7 | 19,545,160 | 2,779,322 |
| 8 | 12,284,095 | 1,783,404 | 8 | 15,595,478 | 2,110,440 | 8 | 19,083,834 | 2,692,131 |
| 9 | 11,598,066 | 1,648,248 | 9 | 14,861,125 | 1,978,573 | 9 | 18,806,574 | 2,630,000 |
| 10 | 10,555,054 | 1,431,188 | 10 | 14,287,241 | 1,861,918 | 10 | 18,516,809 | 2,548,421 |
| 11 | 13,579,745 | 1,745,696 | 11 | 18,213,863 | 2,502,417 | |||
| 12 | 17,852,238 | 2,420,236 | ||||||
| 13 | 17,552,287 | 2,313,043 | ||||||
| Average | 13,541,345 | 2,099,696 | - | 16,201,046 | 2,356,076 | - | 19,653,952 | 2,791,541 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C.; Zhou, L.; Bai, Z.; Zhao, W.; Yang, L. An Integrated Approach to Schedule Passenger Train Plans and Train Timetables Economically Under Fluctuating Passenger Demands. Sustainability 2025, 17, 2703. https://doi.org/10.3390/su17062703
Han C, Zhou L, Bai Z, Zhao W, Yang L. An Integrated Approach to Schedule Passenger Train Plans and Train Timetables Economically Under Fluctuating Passenger Demands. Sustainability. 2025; 17(6):2703. https://doi.org/10.3390/su17062703
Chicago/Turabian StyleHan, Chang, Leishan Zhou, Zixi Bai, Wenqiang Zhao, and Lu Yang. 2025. "An Integrated Approach to Schedule Passenger Train Plans and Train Timetables Economically Under Fluctuating Passenger Demands" Sustainability 17, no. 6: 2703. https://doi.org/10.3390/su17062703
APA StyleHan, C., Zhou, L., Bai, Z., Zhao, W., & Yang, L. (2025). An Integrated Approach to Schedule Passenger Train Plans and Train Timetables Economically Under Fluctuating Passenger Demands. Sustainability, 17(6), 2703. https://doi.org/10.3390/su17062703





