A Hybrid Optimization Approach Combining Rolling Horizon with Deep-Learning-Embedded NSGA-II Algorithm for High-Speed Railway Train Rescheduling Under Interruption Conditions
Abstract
1. Introduction
2. Literature Review
- Train timetable adjustment methods can be categorized into simulation-based, operations-research-based, and artificial-intelligence-based approaches. Simulation and optimization research techniques, such as mixed-integer programming and heuristic algorithms, have been widely used to adjust train schedules and minimize delays. More recently, deep reinforcement learning (DRL) has shown potential for optimizing timetables in real time, outperforming traditional methods in terms of reducing delays. However, few researchers concentrate on the integration between deep learning techniques and heuristic algorithms, which may further enhance optimization efficiency.
- Handling interference in train schedules involves both fixed-duration and uncertain-duration approaches. Fixed-duration models simplify interruption scenarios, allowing for efficient rescheduling. For unpredictable disruptions, rolling optimization strategies are widely used to adjust schedules dynamically in real time. These methods have proven effective in reducing delays and restoring operational order, especially under complex and busy conditions, and are also being applied in other transportation systems.
- Hybrid optimization algorithm integrating deep learning: This paper proposes a hybrid optimization algorithm that combines rolling horizon optimization with a deep-learning-embedded NSGA-II algorithm. This approach leverages deep learning to model the uncertainty in train operation adjustments and integrates the advantages of the NSGA-II algorithm, effectively solving multi-objective optimization problems. This innovative algorithm design better addresses the complexities and uncertainties of high-speed rail operation, improving decision quality and efficiency in train schedule adjustments.
- Fast computational speed, particularly for large-scale cases, requiring less resource consumption and making transportation greener and more sustainable: Traditional rolling horizon optimization algorithms have limitations when handling large-scale complex problems. To overcome this shortcoming, this paper uses a deep-learning-embedded NSGA-II algorithm to solve the train operation scheduling problem. Deep learning, by learning from large amounts of historical data, can predict potential delays and disruptions, thus optimizing the decision-making process. The integration of the NSGA-II algorithm’s multi-objective optimization capability enables faster solution times while handling large-scale complex problems, significantly improving the performance of rolling horizon optimization, particularly in real-world scenarios with large-scale and high-complexity problems. This measure can use less resources in the process of the calculation and reduce emissions indirectly, which contributes to low-carbon and sustainable transportation.
- The application of the NSGA-II algorithm provides decision makers with different choices: The paper employs the non-dominated sorting genetic algorithm II (NSGA-II) to solve the multi-objective optimization problem and generate a set of Pareto-optimal solutions. This approach allows decision makers to choose from a range of feasible alternatives, balancing multiple conflicting objectives, such as minimizing passenger service degradation and operational costs. The NSGA-II algorithm’s ability to produce a diverse set of solutions, each representing a trade-off between the objectives, provides decision makers with valuable insights into the potential outcomes of different scheduling strategies. This flexibility is particularly important in scenarios where decision makers need to consider multiple objectives simultaneously and make informed choices based on real-time, uncertain conditions.
3. Model
3.1. Model Description
3.2. Model Assumptions
- All trains adjust their passing sequence and station stop plans without changing the length of the original train operation lines.
- Prior to the occurrence of disruptions, all trains operate according to the scheduled train timetable.
- After adjustments to their passing sequence and stop plans, the trains or passenger flows that still fail to meet the constraints will be canceled.
3.3. Model Formulation
- (1)
- Minimum decline in passenger service quality
- (2)
- Minimum total operating cost
3.4. Constraints
- (1)
- Constraints of time range
- (2)
- Constraints of station stop time
- (3)
- Constraint of station tracking interval
- (4)
- Constraints of train operation time
- (5)
- Allocation constraints of passenger flow
- (6)
- Train overtaking constraint
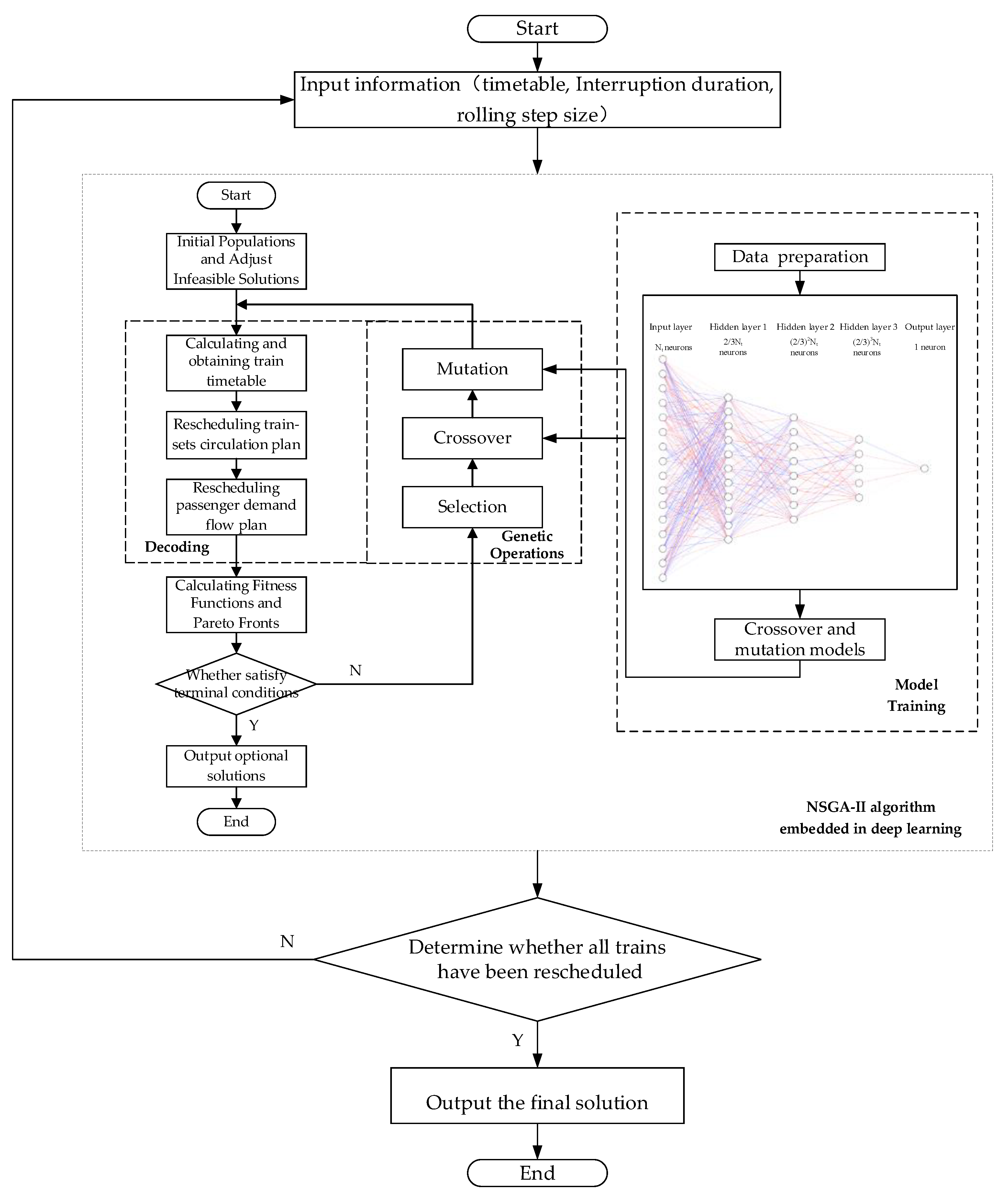
4. A Hybrid Solving Algorithm for the Rescheduling Problem
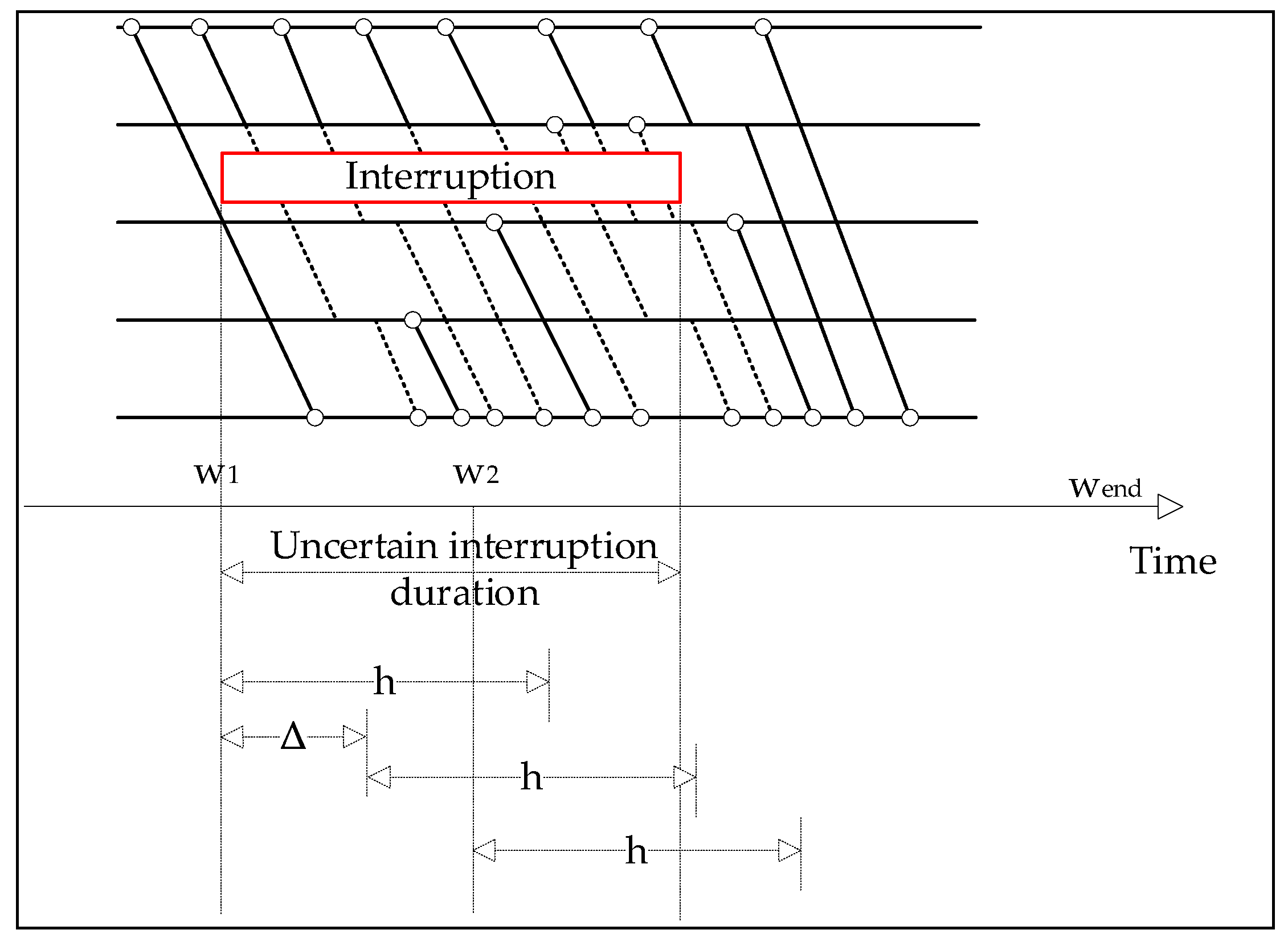
4.1. Rolling Horizon Algorithm
4.2. The Introduction of the NSGA-II Algorithm
4.3. Deep Learning Model Data Preparation and Training
4.3.1. Obtain Training Data for Deep Learning Models
4.3.2. Train the Deep Learning Models
4.4. The Process of the NSGA-II Algorithm Embedded in Deep Learning
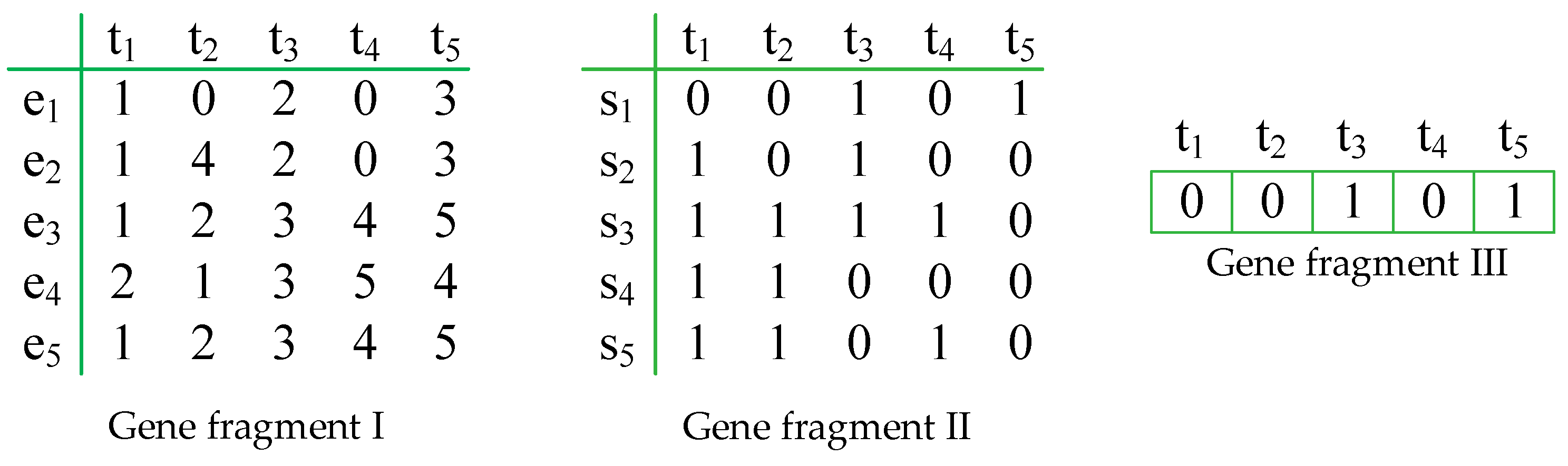
4.4.1. Gene Fragments
4.4.2. Initialize the Population
- The cancelled trains will not serve any passengers. The sequence values in its gene segment I and the station-stop values in its gene segment II will be 0 in all sections.
| Algorithm 1. Handle the cancelled trains. |
| Step 1. Determine the value of each variable based on gene fragment I. Determine the value of each variable based on gene fragment II. Determine the value of each variable based on gene fragment III. Step 2. Create set and add all the train to . Create set and add all the section to . Create set and add all the station to , |
| Step 3. Determine the values of variables and of the cancelled trains. For each train : If For each section : If Let If Continue For each station : If Let If Continue If Continue |
- 2.
- After the initialization of the solutions, there may be some infeasible sequence of the trains, such as 6,1,3,0,4,5,7, which should be adjusted to 5,1,2,0,3,4,6.
| Algorithm 2. Find the infeasible sequence and adjust gene fragment I. |
| Step 1. Obtain the value of each variable from the result of Algorithm 1. Step 2. Create set and add all the train to . Create set and add all the section to . Step 3. Get the feasible sequence of the trains in each section. Create set . For each section : For each train : Add to set . Check whether all the nonzero in is continuous, and begin with value 1. If not, Adjust all nonzero in to consecutive integers in their original order |
| If yes, Clear set . Continue. |
4.4.3. Chromosome Decoding
- Obtain train timetable
- 2.
- Distribution of affected passenger flow
| Algorithm 3. Allocate affected passenger flow |
| Step 1. Create affected passenger set and add all affected passenger demands to it. Create affected trains set and add all affected trains to it. Step 2. Allocate passenger flow to trains. For each passenger demand : For each train : Judge whether the total number of passengers does not exceed train ’s seating capacity after adding passenger demand . If yes, Judge whether the departure time of the passenger demand is later than the departure time of train at the origin station of the passenger demand . If yes, Judge whether train stops at the departure and arrival stations of passenger demand . If yes, Let train serve passenger demand and remove passenger demand from set . If not, Continue; If not, Continue; If not, Continue; |
| Step 3. Cancel the remaining passenger demands in set . |
4.4.4. Fitness Calculation
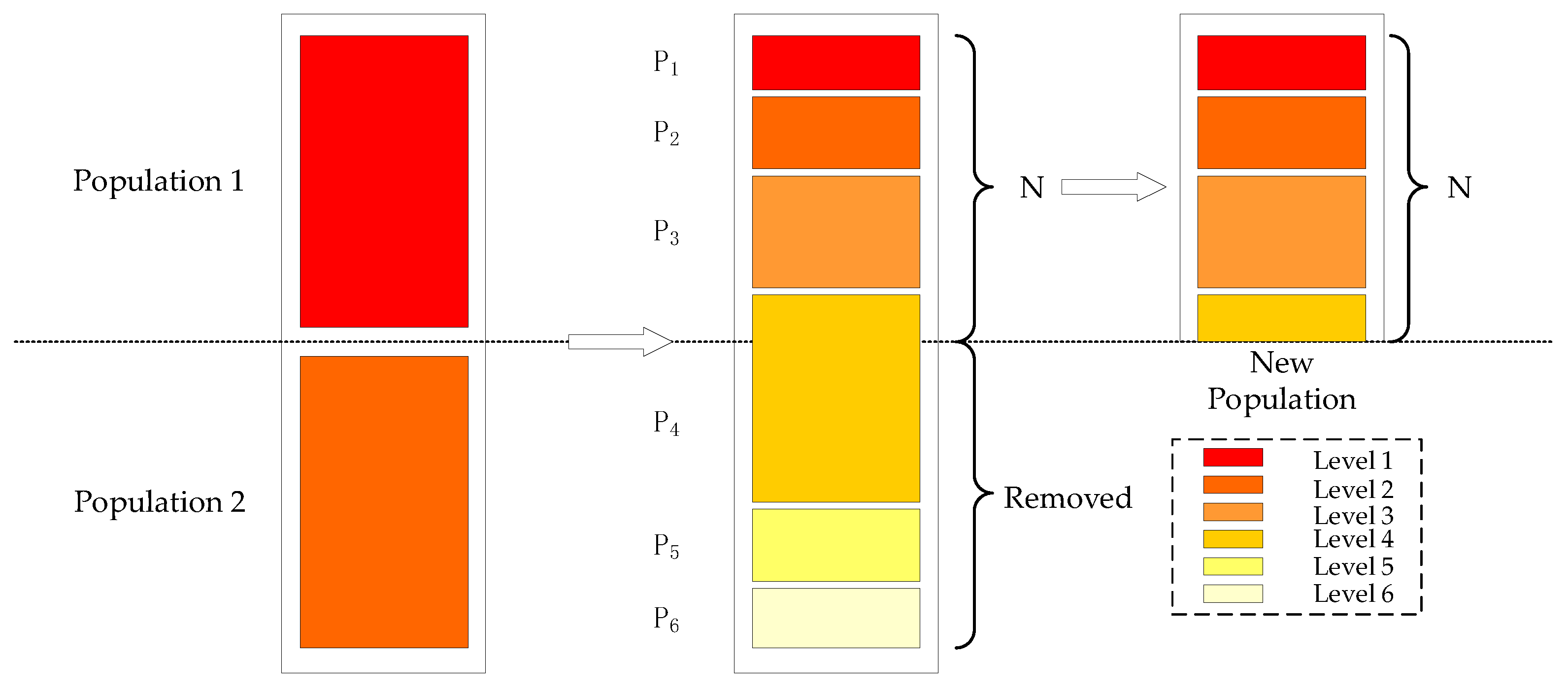
4.4.5. Selection
4.4.6. Crossover and Mutation
- Crossover
- 2.
- Mutation
4.4.7. Update Weights of MLP Model
4.4.8. Check Termination Conditions
4.5. The Process of the Hybrid Algorithm
5. Case Study
5.1. Basic Data
5.2. Effectiveness Analysis of the Model and Algorithm
5.2.1. The Comparison Before and After Iteration
5.2.2. The Converging Trend of the Objectives
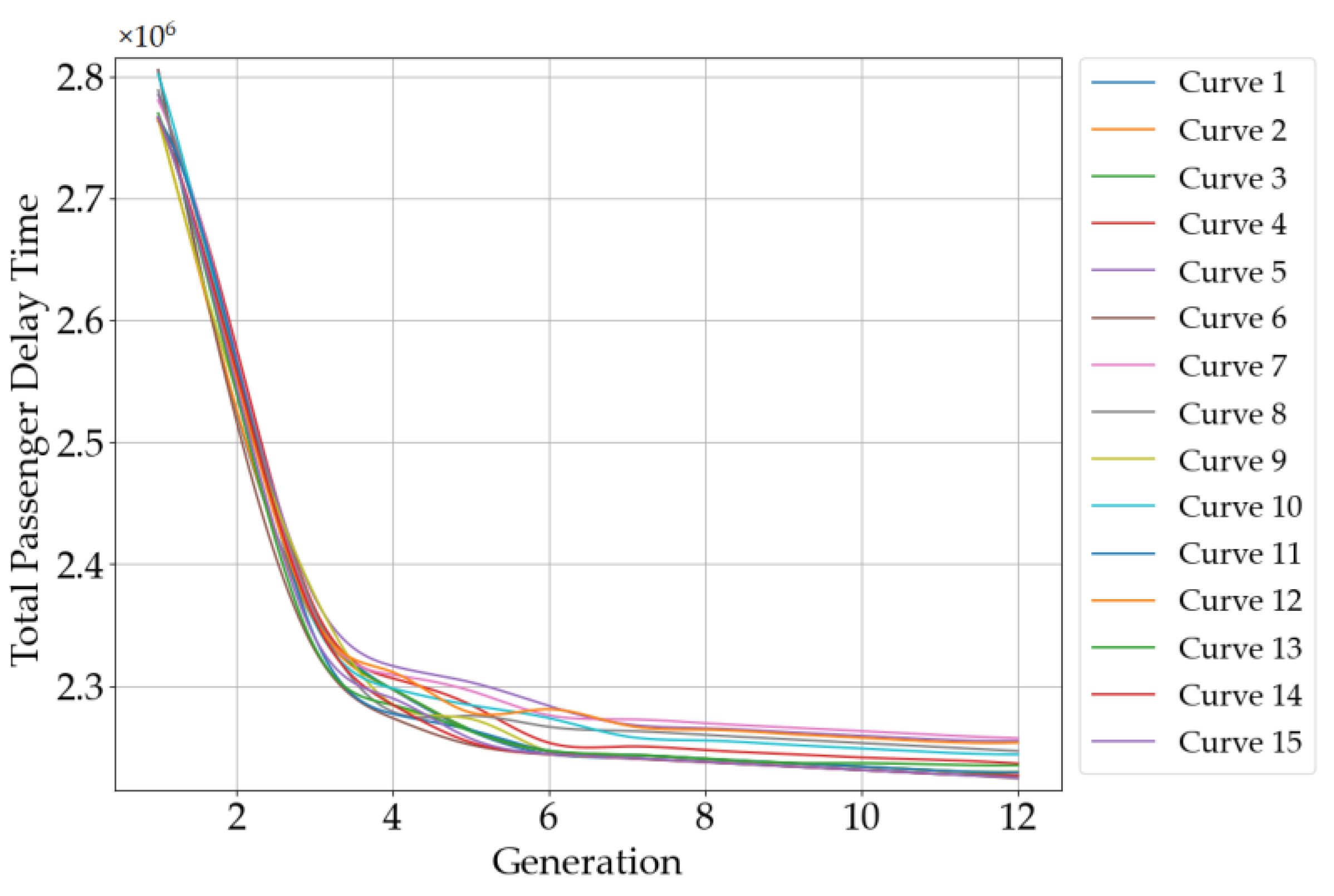
5.2.3. Stability Analysis of the Algorithms
5.3. Comparative Analysis of Hybrid Algorithm and Single Algorithm
5.3.1. Optimization Performance
- (1)
- Objective 1: average decline in passengers service quality
- (2)
- Objective 2: average total operating cost
5.3.2. Convergence and Computational Efficiency
- (1)
- Convergence generation
- (2)
- Calculation time
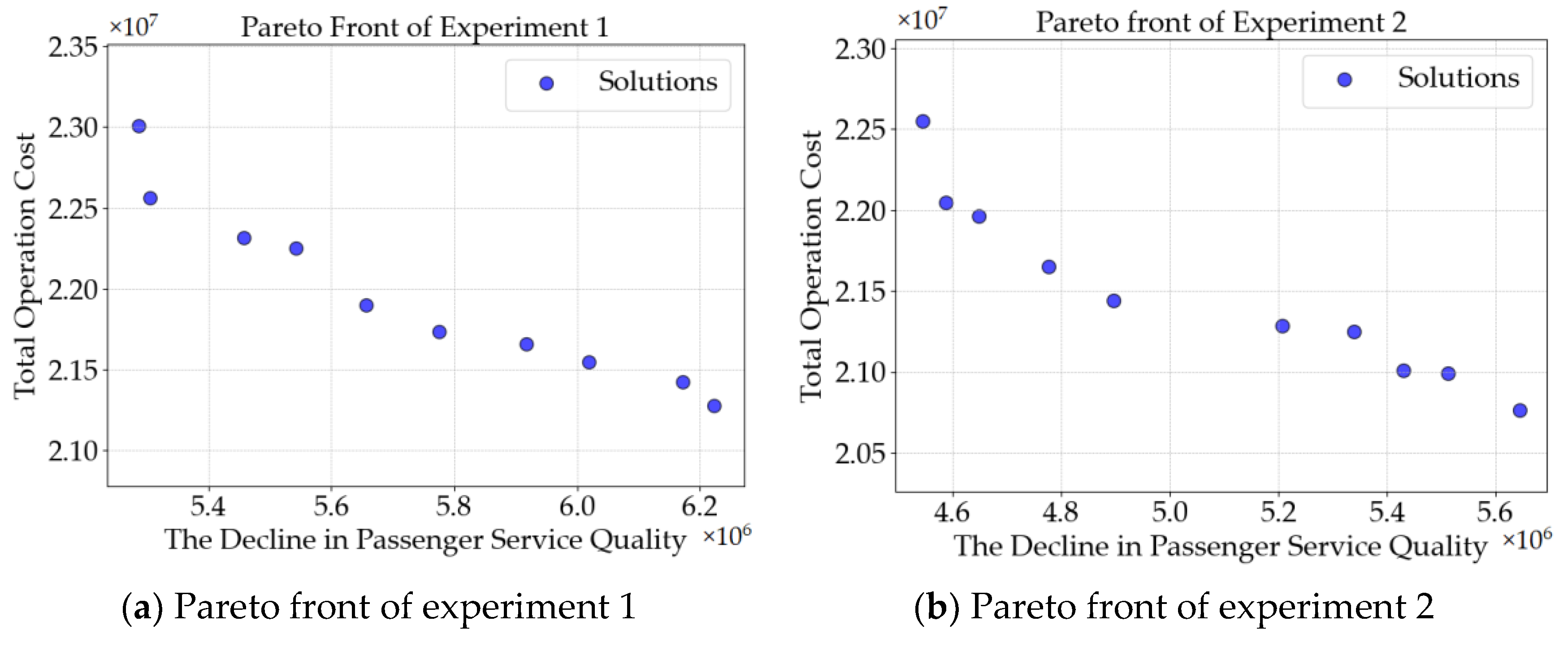
5.4. Pareto Front Analysis
5.4.1. Analysis of a Single Pareto Front Scatter Plot
5.4.2. Comparative Analysis Between Two Pareto Front Scatter Plots
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, Y. Hybrid simulation for resolving resource conflicts in train traffic rescheduling. Comput. Ind. 1998, 35, 233–246. [Google Scholar] [CrossRef]
- Sahin, I. Railway traffic control and train scheduling based on inter-train conflict management. Transp. Res. Part B-Methodol. 1999, 33, 511–534. [Google Scholar] [CrossRef]
- Norio, T.; Yoshiaki, T.; Noriyuki, T.; Chikara, H.; Kunimitsu, M. Train rescheduling algorithm which minimizes passengers’ dissatisfaction. Innov. Appl. Artif. Intell. 2005, 3533, 829–838. [Google Scholar]
- Yang, L.; Zhou, X.; Gao, Z. Rescheduling trains with scenario-based fuzzy recovery time representation on two-way double-track railways. Soft Comput. 2013, 17, 605–616. [Google Scholar] [CrossRef]
- Cavone, G.; Dotoli, M.; Epicoco, N.; Seatzu, C. A decision making procedure for robust train rescheduling based on mixed integer linear programming and Data Envelopment Analysis. Appl. Math. Model. 2017, 52, 255–273. [Google Scholar] [CrossRef]
- Zhou, M.; Dong, H.; Liu, X.; Zhang, H.; Wang, F.-Y. Integrated Timetable Rescheduling for Multidispatching Sections of High-Speed Railways During Large-Scale Disruptions. IEEE Trans. Comput. Soc. Syst. 2022, 9, 366–375. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, W.; Long, Y.; Qian, L.; Han, B. Train Rescheduling of Urban Rail Transit Under Bi-Direction Disruptions in Operation Section. Transp. Res. Rec. 2024, 2678, 635–650. [Google Scholar] [CrossRef]
- Nie, L.; Zhang, X.; Zhao, P.; Yang, H.; Hu, A. Study on the strategy of train operation adjustment on high speed railway. J. China Railw. Soc. 2001, 23, 12–16. [Google Scholar]
- Jones, W.; Gun, P. Train timetabling and destination selection in mining freight rail networks: A hybrid simulation methodology incorporating heuristics. J. Simul. 2024, 18, 1–14. [Google Scholar] [CrossRef]
- Hoegdahl, J.; Bohlin, M. A combined simulation-optimization approach for robust timetabling on main railway lines. Transp. Sci. 2023, 57, 52–81. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, L.; Chen, R. Optimization of high-speed railway timetabling based on maximum utilization of railway capacity. J. Railw. Sci. Eng. 2018, 15, 2746–2754. [Google Scholar]
- Zhou, H. Research on Calculation Method of High-Speed Railway Capacity Based on Abstract Train Timetable. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Yuan, Y.; Li, S.; Liu, R.; Yang, L.; Gao, Z. Decomposition and approximate dynamic programming approach to optimization of train timetable and skip-stop plan for metro networks. Transp. Res. Part C Emerg. Technol. 2023, 157, 104393. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, M.; Dong, H.; Wu, X.; Li, Y.; Wang, F.-Y. ADMM-based joint rescheduling method for high-speed railway timetabling and platforming in case of uncertain perturbation. Transp. Res. Part C Emerg. Technol. 2023, 152, 104150. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, Y.; Yang, Z.; Chen, C.; Zhang, S. Timetable Rescheduling Using Skip-Stop Strategy for Sustainable Urban Rail Transit. Sustainability 2023, 15, 14511. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, X.; Qu, L.; Li, P. Optimization of intercity railway train schedule based on passengers equilibrium analysis. J. Railw. Sci. Eng. 2019, 16, 231–238. [Google Scholar]
- Xu, C.; Li, S.; Chen, D.; Ni, S. Segmentation and connection optimization technique for maintenance window in the train timetable. Comput. Simul. 2021, 38, 68–72+102. [Google Scholar]
- Bao, X.; Li, Y.; Li, J.; Shi, R.; Ding, X.; Li, L. Prediction of Train Arrival Delay Using Hybrid ELM-PSO Approach. J. Adv. Transp. 2021, 2021, 7763126. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, J.; Yang, L.; Chen, F.; Li, S.; Gao, Z. Physics Guided Deep Learning-Based Model for Short-Term Origin-Destination Demand Prediction in Urban Rail Transit Systems Under Pandemic. Engineering 2024, 41, 276–296. [Google Scholar] [CrossRef]
- Zhang, J.; Mao, S.; Yang, L.; Ma, W.; Li, S.; Gao, Z. Physics-informed deep learning for traffic state estimation based on the traffic flow model and computational graph method. Inf. Fusion 2024, 101, 101971. [Google Scholar] [CrossRef]
- Ning, L.; Li, Y.; Zhou, M.; Song, H.; Dong, H. A Deep Reinforcement Learning Approach to High-speed Train Timetable Rescheduling under Disturbances. In Proceedings of the IEEE Intelligent Transportation Systems Conference (IEEE-ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar]
- Li, W.; Ni, S. Train timetabling with the general learning environment and multi-agent deep reinforcement learning. Transp. Res. Part B Methodol. 2022, 157, 230–251. [Google Scholar] [CrossRef]
- Sun, L.; Jin, J.G.; Lee, D.H.; Axhausen, K.W.; Erath, A. Demand-driven timetable design for metro services. Transp. Res. Part C Emerg. Technol. 2014, 46, 284–299. [Google Scholar] [CrossRef]
- Zhang, J.; Mao, S.; Zhang, S.; Yin, J.; Yang, L.; Gao, Z. EF-former for short-term passenger flow prediction during large-scale events in urban rail transit systems. Inf. Fusion 2025, 117, 102916. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Remeseiro, B. Feature selection in image analysis: A survey. Artif. Intell. Rev. 2020, 53, 2905–2931. [Google Scholar] [CrossRef]
- Kabir, H.; Garg, N. Machine learning enabled orthogonal camera goniometry for accurate and robust contact angle measurements. Sci. Rep. 2023, 13, 1497. [Google Scholar] [CrossRef]
- Yalçınkaya, Ö.; Mirac Bayhan, G. A feasible timetable generator simulation modelling framework for train scheduling problem. Simul. Model. Pract. Theory 2012, 20, 124–141. [Google Scholar] [CrossRef]
- Liao, Z. Research on Real-Time High-Speed Railway Rescheduling Under Station Disturbance and Interval Disturbance Scenarios. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Gkiotsalitis, K.; Cats, O. Timetable Recovery After Disturbances in Metro Operations: An Exact and Efficient Solution. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4075–4085. [Google Scholar] [CrossRef]
- Krasemann, J.T. Design of an effective algorithm for fast response to the re-scheduling of railway traffic during disturbances. Transp. Res. Part C Emerg. Technol. 2012, 20, 62–78. [Google Scholar] [CrossRef]
- Shakibayifar, M.; Sheikholeslami, A.; Corman, F.; Hassannayebi, E. An integrated rescheduling model for minimizing train delays in the case of line blockage. Oper. Res. 2020, 20, 59–87. [Google Scholar] [CrossRef]
- Zhan, S.; Kroon, L.G.; Zhao, J.; Peng, Q. A rolling horizon approach to the high speed train rescheduling problem in case of a partial segment blockage. Transp. Res. Part E Logist. Transp. Rev. 2016, 95, 32–61. [Google Scholar] [CrossRef]
- Tornquist, J. Railway traffic disturbance management: An experimental analysis of disturbance complexity, management objectives and limitations in planning horizon. Transp. Res. Part A-Policy Pract. 2007, 41, 249–266. [Google Scholar] [CrossRef]
- Peng, S.; Yang, X.; Ding, S.; Wu, J.; Sun, H. A dynamic rescheduling and speed management approach for high-speed trains with uncertain time-delay. Inf. Sci. 2023, 632, 201–220. [Google Scholar] [CrossRef]
- Pellegrini, P.; Marliere, G.; Rodriguez, J. Optimal train routing and scheduling for managing traffic perturbations in complex junctions. Transp. Res. Part B Methodol. 2014, 59, 58–80. [Google Scholar] [CrossRef]
- Zhu, Y.; Goverde, R.M.P. Dynamic railway timetable rescheduling for multiple connected disruptions. Transp. Res. Part C Emerg. Technol. 2021, 125, 103080. [Google Scholar] [CrossRef]
- Sama, M.; D’Ariano, A.; Pacciarelli, D. Rolling horizon approach for aircraft scheduling in the terminal control area of busy airports. Transp. Res. Part E Logist. Transp. Rev. 2013, 60, 140–155. [Google Scholar] [CrossRef]
- Zheng, H.; Xu, W.; Ma, D.; Qu, F. Dynamic Rolling Horizon Scheduling of Waterborne AGVs for Inter Terminal Transportation: Mathematical Modeling and Heuristic Solution. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3853–3865. [Google Scholar] [CrossRef]
- Pasqui, M.; Becchi, L.; Bindi, M.; Intravaia, M.; Grasso, F.; Fioriti, G.; Carcasci, C. Community Battery for Collective Self-Consumption and Energy Arbitrage: Independence Growth vs. Investment Cost-Effectiveness. Sustainability 2024, 16, 3111. [Google Scholar] [CrossRef]
- Zhang, J.; Zhai, Y.; Han, Z.; Lu, J. Improved Particle Swarm Optimization Based on Entropy and Its Application in Implicit Generalized Predictive Control. Entropy 2022, 24, 48. [Google Scholar] [CrossRef]
- Wang, J.; Mei, S.; Liu, C.; Peng, H.; Wu, Z. A decomposition-based multi-objective evolutionary algorithm using infinitesimal method. Appl. Soft Comput. 2024, 167, 112272. [Google Scholar] [CrossRef]
- Ma, H.; Ning, J.; Zheng, J.; Zhang, C. A Decomposition-Based Evolutionary Algorithm with Neighborhood Region Domination. Biomimetics 2025, 10, 19. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Farahani, A.A.; Sadeghi, S.H.H. Use of NSGA-II for Optimal Placement and Management of Renewable Energy Sources Considering Network Uncertainty and Fault Current Limiters. In Proceedings of the 29th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 18–20 May 2021. [Google Scholar]
- Liu, W.; Zhang, J.; Liu, C.; Qu, C. A bi-objective optimization for finance-based and resource-constrained robust project scheduling. Expert Syst. Appl. 2023, 231, 120623. [Google Scholar] [CrossRef]
- Elarbi, M.; Bechikh, S.; Gupta, A.; Ben Said, L.; Ong, Y.-S. A New Decomposition-Based NSGA-II for Many-Objective Optimization. IEEE Trans. Syst. Man Cybern.-Syst. 2018, 48, 1191–1210. [Google Scholar] [CrossRef]
- Noruzi, M.; Naderan, A.; Zakeri, J.A.; Rahimov, K. A Robust Optimization Model for Multi-Period Railway Network Design Problem Considering Economic Aspects and Environmental Impact. Sustainability 2023, 15, 5022. [Google Scholar] [CrossRef]

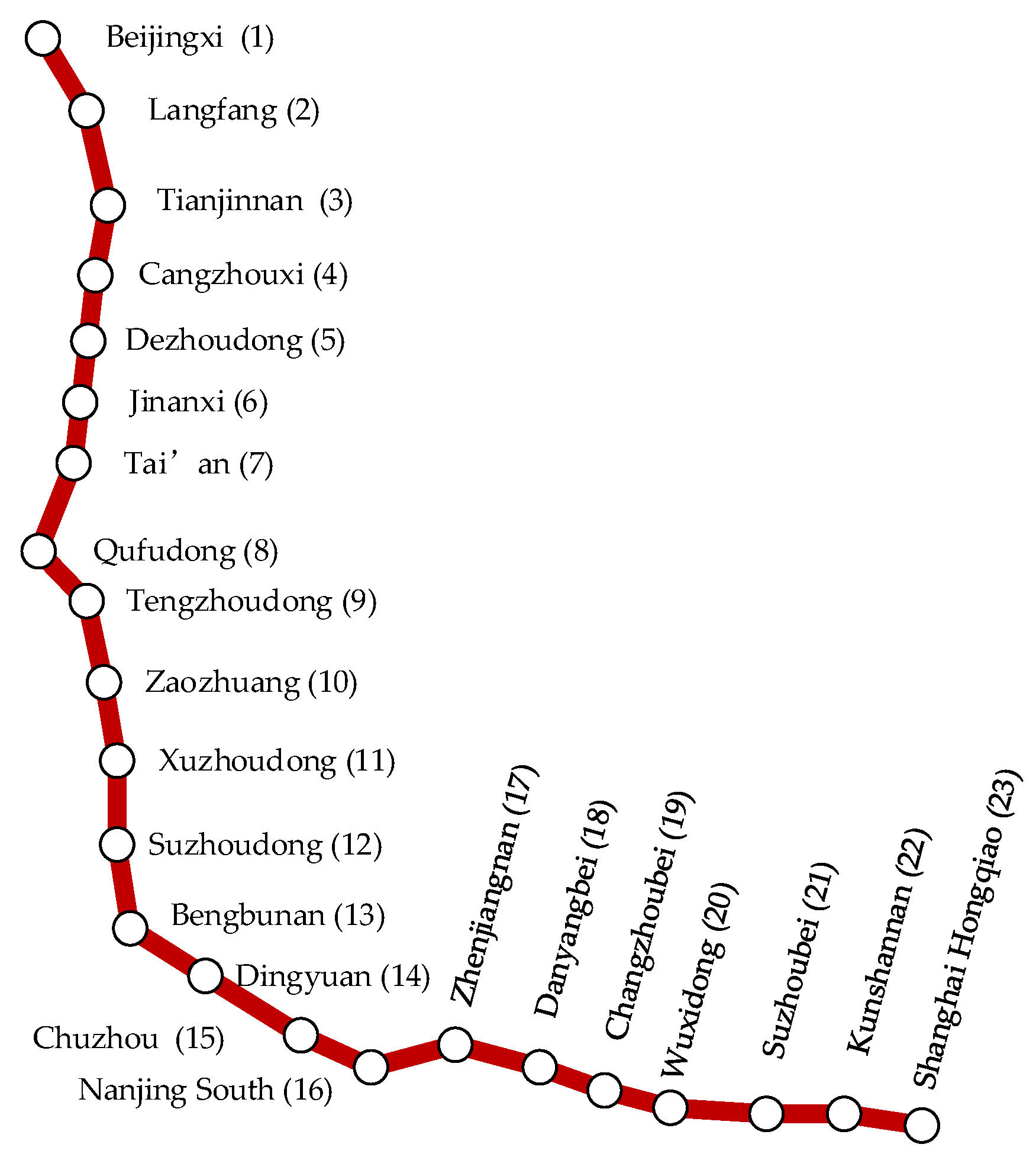


| Symbol | Definition |
|---|---|
| The set of trains in the train timetable, indexed with and | |
| The set of affected trains, | |
| The set of stations, indexed with and | |
| The set of passenger demands | |
| The set of affected passenger demands | |
| The set of sections, indexed with and —if the stations at both ends of the interval are and , respectively, then the interval can be represented as | |
| The set of rolling step |
| Parameters | Definition |
|---|---|
| The start time of the period for solving the timetable | |
| The end time of the period for solving the timetable | |
| The scheduled departure time of train at station | |
| The scheduled arrival time of train at station | |
| The end station of train | |
| The start station of train | |
| The end station of passenger flow in train | |
| The start station of passenger flow in train | |
| Penalty value for the cancellation of a passenger flow | |
| The start time of the interruption | |
| The predicted interruption duration in rolling step | |
| The start time of rolling step , ; m is the number of rolling steps | |
| The end time of rolling step , ; m is the number of rolling steps | |
| The section where the interruption occurs | |
| The start station of the section where the interruption occurs | |
| The end station of the section where the interruption occurs | |
| The latest arrival time of passenger flow at station | |
| The stop time of the train at station | |
| The extra starting time of the train at station | |
| The extra stopping time of the train at station | |
| The running time of train in section | |
| The distance of the section | |
| The operation cost per kilometer for each train | |
| The cost per kilometer for each passenger | |
| The maximum allowable additional dwell time | |
| The time interval between two consecutive trains passing through the same station. | |
| Whether train is scheduled to stop at station —if it stops, the value is 1; otherwise, the value is 0 | |
| Whether train passes through section —if train passes through section , its value is 1; otherwise, its value is 0 | |
| The planned number of passengers in train | |
| The number of passengers in passenger flow in train | |
| The passenger carrying capacity of train | |
| The coefficients inside objective function 1 | |
| A real number that is large enough |
| Symbol | Definition |
|---|---|
| The actual departure time of train in station | |
| The actual arrival time of train in station | |
| 0–1 variable, whether train is cancelled—if train is cancelled, its value is 1; otherwise, its value is 0 | |
| 0–1 variable, whether passenger flow in train is cancelled—if passenger flow in train is cancelled, its value is 1; otherwise, its value is 0 | |
| The sequence in which train passes through section , = 1, 2, …, K, where K is the total number of trains | |
| 0–1 variable, whether train stops at station —if train stops at station , its value is 1; otherwise, its value is 0 | |
| 0–1 variable, the order in which train and train pass through the section —if train passes through the section before train , its value is 1; otherwise, its value is 0 | |
| The number of affected passenger flow in train served by train | |
| 0–1 variable, whether the passenger flow on train is served by train —if the passenger flow on train is served by train , its value is 1; otherwise, its value is 0 |
| Parameter | Value |
|---|---|
| The extra starting time | 2 min |
| The extra stopping time | 3 min |
| Train stopping time at the station | 3 min |
| The cost per kilometer for each train | 330 yuan |
| The cost per kilometer for each passenger | 0.114 yuan |
| The passenger carrying capacity | 1200 people |
| Penalty time for the passenger flow cancellation | 720 min |
| Train tracking intervals | 4 min |
| The maximum allowable additional dwell time | 20 min |
| Section | Distance (km) | Time (min) | Section | Distance (km) | Time (min) |
|---|---|---|---|---|---|
| 1–2 | 59.5 | 18 | 12–13 | 88.0 | 20 |
| 2–3 | 62.6 | 14 | 13–14 | 54.3 | 12 |
| 3–4 | 87.9 | 20 | 14–15 | 62.0 | 14 |
| 4–5 | 103.8 | 23 | 15–16 | 59.0 | 14 |
| 5–6 | 92.2 | 21 | 16–17 | 65.4 | 15 |
| 6–7 | 58.7 | 14 | 17–18 | 28.6 | 7 |
| 7–8 | 70.4 | 15 | 18–19 | 32.4 | 8 |
| 8–9 | 56 | 12 | 19–20 | 57.4 | 13 |
| 9–10 | 36.1 | 8 | 20–21 | 26.8 | 6 |
| 10–11 | 64.4 | 14 | 21–22 | 31.4 | 7 |
| 11–12 | 67.2 | 15 | 22–23 | 44 | 13 |
| Average Decline in Passenger Service Quality | Average Total Operating Cost | ||
|---|---|---|---|
| Small-scale experiment (65 min) | Before iteration | 6,991,740.03 | 26,270,525.87 |
| After iteration | 5,854,112.53 | 22,178,020.07 | |
| Optimization rate | 16.27% | 15.58% | |
| Medium-scale experiment (123 min) | Before iteration | 11,787,649.67 | 30,745,108.43 |
| After iteration | 9,913,618.23 | 26,389,165.17 | |
| Optimization rate | 15.90% | 14.17% | |
| Large-scale experiment (225 min) | Before iteration | 15,193,746.93 | 43,718,573.23 |
| After iteration | 13,222,301.74 | 37,931,957.07 | |
| Optimization rate | 12.98% | 13.23% |
| Average Decline in Passenger Service Quality | Average Total Operating Cost | Time | |
|---|---|---|---|
| 1 | 17,981,400.10 | 37,675,865.81 | 2628 |
| 2 | 17,663,376.74 | 38,050,094.80 | 2636 |
| 3 | 18,428,048.81 | 36,580,427.13 | 2619 |
| 4 | 17,703,014.19 | 38,463,797.62 | 2676 |
| 5 | 17,179,913.87 | 38,607,104.42 | 2634 |
| 6 | 18,697,415.43 | 36,444,626.11 | 2632 |
| 7 | 17,499,388.73 | 39,016,232.10 | 2605 |
| 8 | 17,729,263.70 | 38,077,359.00 | 2598 |
| 9 | 17,962,408.54 | 37,110,804.84 | 2670 |
| 10 | 17,840,205.92 | 36,307,839.33 | 2642 |
| 11 | 18,480,678.37 | 37,285,517.82 | 2621 |
| 12 | 17,546,266.63 | 38,494,872.35 | 2615 |
| 13 | 17,155,270.56 | 38,054,814.79 | 2662 |
| 14 | 17,330,109.37 | 37,879,640.83 | 2635 |
| 15 | 17,134,583.91 | 38,944,548.68 | 2683 |
| Mean value | 17,755,422.99 | 37,799,569.71 | 2637.07 |
| Std | 472,285.04 | 851,699.54 | 24.64 |
| Proportion of std | 2.66% | 2.25% | 0.93% |
| Experiment | Algorithm | Interruption Duration/Predicted Duration (min) | Objective 1 | Objective 2 | Convergent Generation | Calculation Time (s) |
|---|---|---|---|---|---|---|
| 1 | NSGA-II | 60 | 6,735,122 | 24,624,726 | 130 | 2301 |
| 2 | RHA + NSGA-II | 82, 75, 66, 60 | 6,473,291 | 23,894,763 | - | 2015 |
| 3 | NSGA-II + DL | 60 | 5,983,373 | 23,595,738 | 91 | 2268 |
| 4 | RHA + NSGA-II + DL | 82, 75, 66, 60 | 5,729,385 | 22,985,716 | - | 1698 |
| 5 | NSGA-II | 120 | 12,350,174 | 46,592,385 | 139 | 4583 |
| 6 | RHA + NSGA-II | 152, 146, 138, 132, 124, 118, 120 | 11,641,787 | 43,206,595 | - | 3673 |
| 7 | NSGA-II + DL | 120 | 11,556,720 | 39,902,857 | 112 | 4489 |
| 8 | RHA + NSGA-II + DL | 152, 146, 138, 132, 124, 118, 120 | 10,427,757 | 39,038,572 | - | 2689 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Zhou, L.; Han, C. A Hybrid Optimization Approach Combining Rolling Horizon with Deep-Learning-Embedded NSGA-II Algorithm for High-Speed Railway Train Rescheduling Under Interruption Conditions. Sustainability 2025, 17, 2375. https://doi.org/10.3390/su17062375
Zhao W, Zhou L, Han C. A Hybrid Optimization Approach Combining Rolling Horizon with Deep-Learning-Embedded NSGA-II Algorithm for High-Speed Railway Train Rescheduling Under Interruption Conditions. Sustainability. 2025; 17(6):2375. https://doi.org/10.3390/su17062375
Chicago/Turabian StyleZhao, Wenqiang, Leishan Zhou, and Chang Han. 2025. "A Hybrid Optimization Approach Combining Rolling Horizon with Deep-Learning-Embedded NSGA-II Algorithm for High-Speed Railway Train Rescheduling Under Interruption Conditions" Sustainability 17, no. 6: 2375. https://doi.org/10.3390/su17062375
APA StyleZhao, W., Zhou, L., & Han, C. (2025). A Hybrid Optimization Approach Combining Rolling Horizon with Deep-Learning-Embedded NSGA-II Algorithm for High-Speed Railway Train Rescheduling Under Interruption Conditions. Sustainability, 17(6), 2375. https://doi.org/10.3390/su17062375





