Modular Scheduling Optimization of Multi-Scenario Intelligent Connected Buses Under Reservation-Based Travel
Abstract
1. Introduction
- (1)
- This study, based on actual bus card-swiping data, quantitatively analyzes the potential characteristics of users with reservation-based travel in order to address the issue of demand for reserved bus travel. Consequently, it is possible to extract data related to the demands of passengers with reservations, such as origin–destination pairs, expected travel time, and number of travelers.
- (2)
- Considering the demand for reserved travel and the spatiotemporal dynamics of passenger flows, this study is driven by data on reserved passenger demand and investigates various scenarios, including fixed-capacity scheduled buses, reserved buses with dwell-stop scheduling, reserved buses with skip-stop scheduling, and modular reserved bus combination scheduling. It comprehensively evaluates the performance of different scheduling strategies in these scenarios.
- (3)
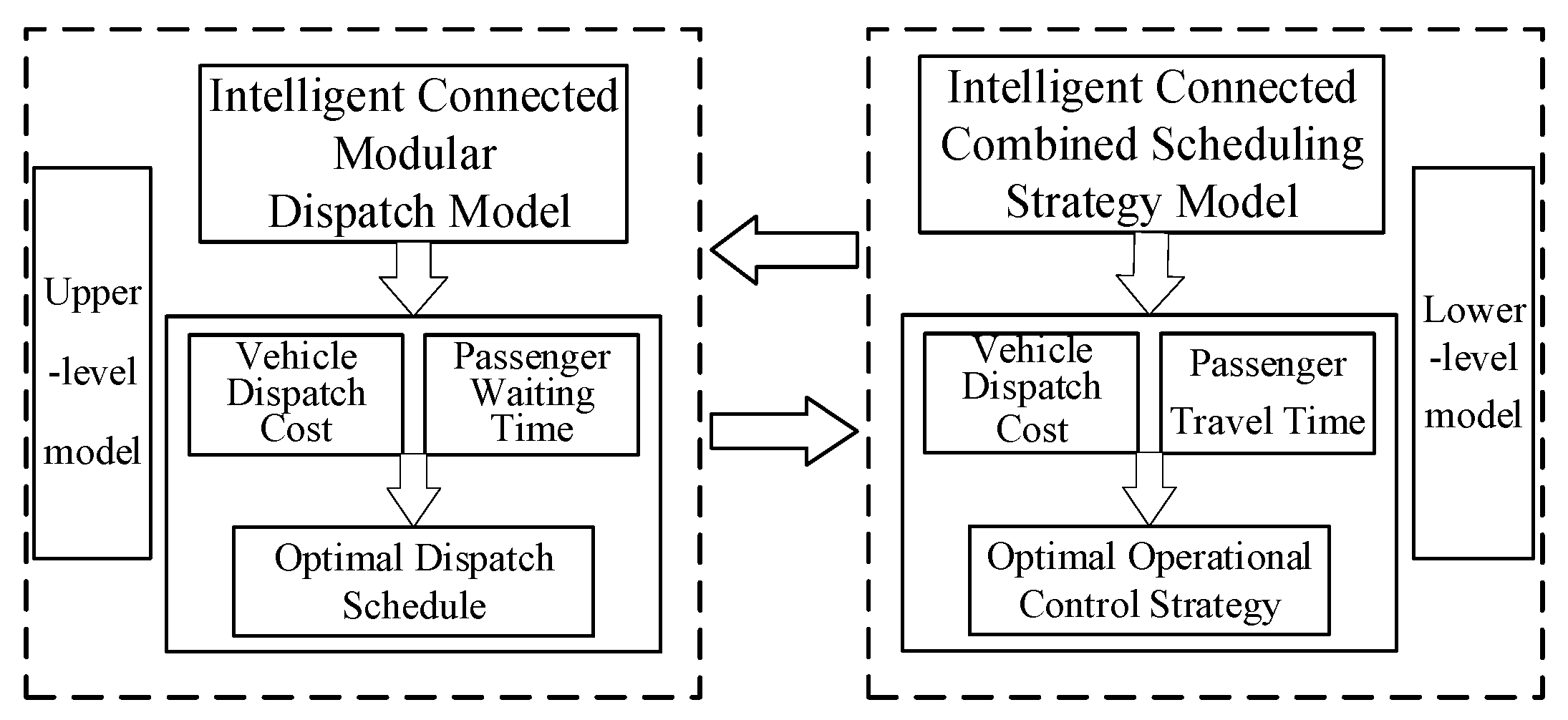
- A T-DLPSO-TOPSIS algorithm featuring adaptive parameter grids and solution-space pruning is designed to eliminate manual intervention, coupled with a bi-level public transit scheduling model. The model resolves dwell-stop/skip-stop coordination in reservation-based systems through hierarchical optimization: the upper layer governs vehicle grouping and departure plans, while the lower layer dynamically adjusts station-specific stopping strategies via real-time data exchange.
2. Problem Description
3. Model Formulation
3.1. Notation
3.2. Passenger Boarding and Alighting Process State
- (1)
- Passengers stranded due to station skipping
- (2)
- Passengers stranded due to bus capacity limitations
- (a)
- Overloading occurs during the service time
- (b) Overloading occurs during the dwell-stop time
3.3. Constraints
3.4. Objective Function
- (1)
- Upper-level model
- (2)
- Lower-level model
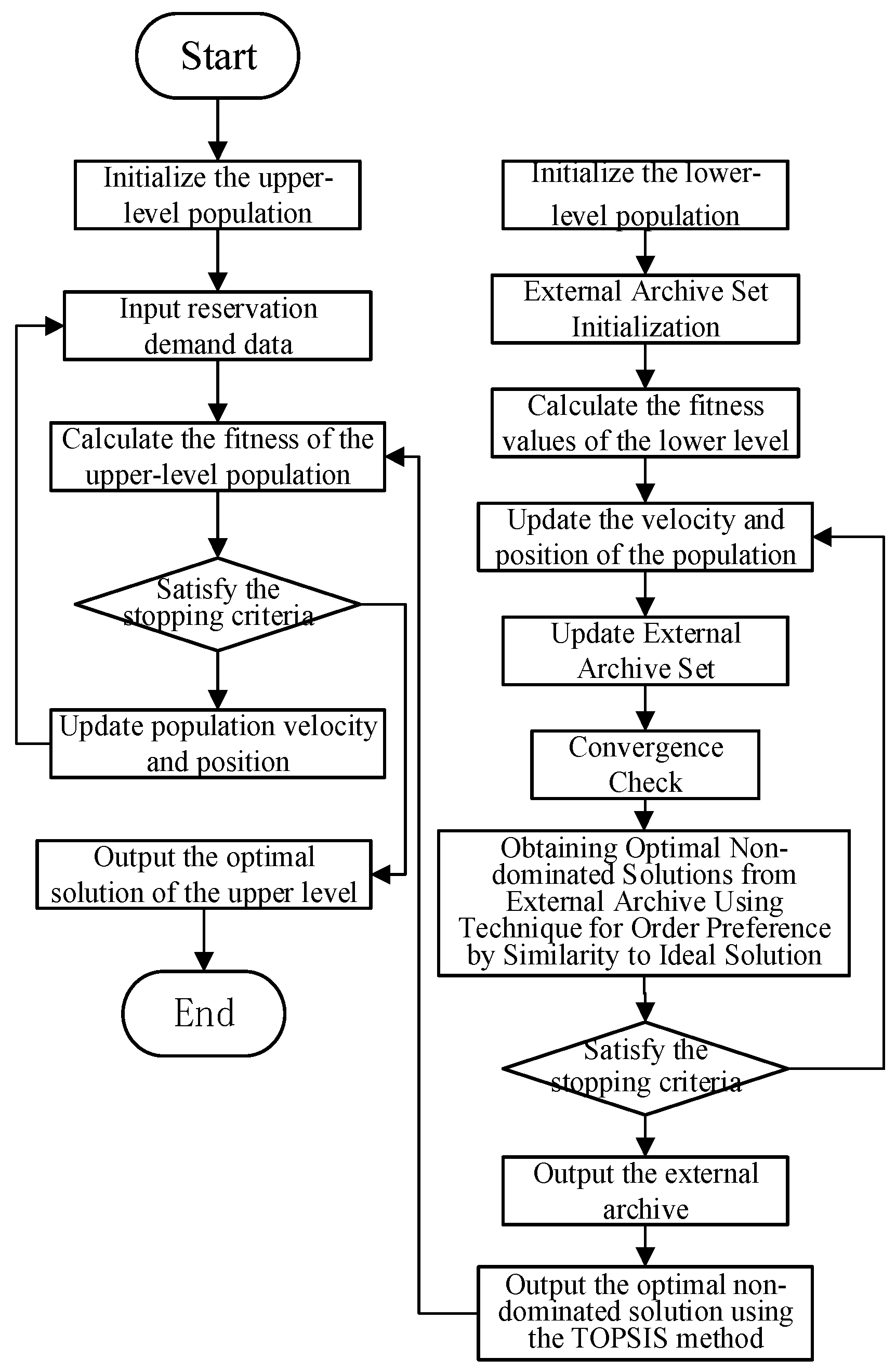
4. Solution Algorithm
- (1)
- Population particle velocity and position component update.
- (2)
- Parameter and adaptive adjustment
- (3)
- External repository grid update
- (a)
- Remove the examples that exceed the extremes of their respective objective functions.
- (b)
- If a grid contains only one particle, it is retained directly.
- (c)
- If a grid contains the extreme values of objective K, all other particles in this grid are removed, and only the extreme points are retained.
- (d)
- If a grid contains multiple particles and no extreme points, the distances D(n) between each particle and the grid vector are compared, and the particle with the minimum distance is retained, as expressed in Equation (41).
- (e)
- Selection of and
5. Numerical Experiments
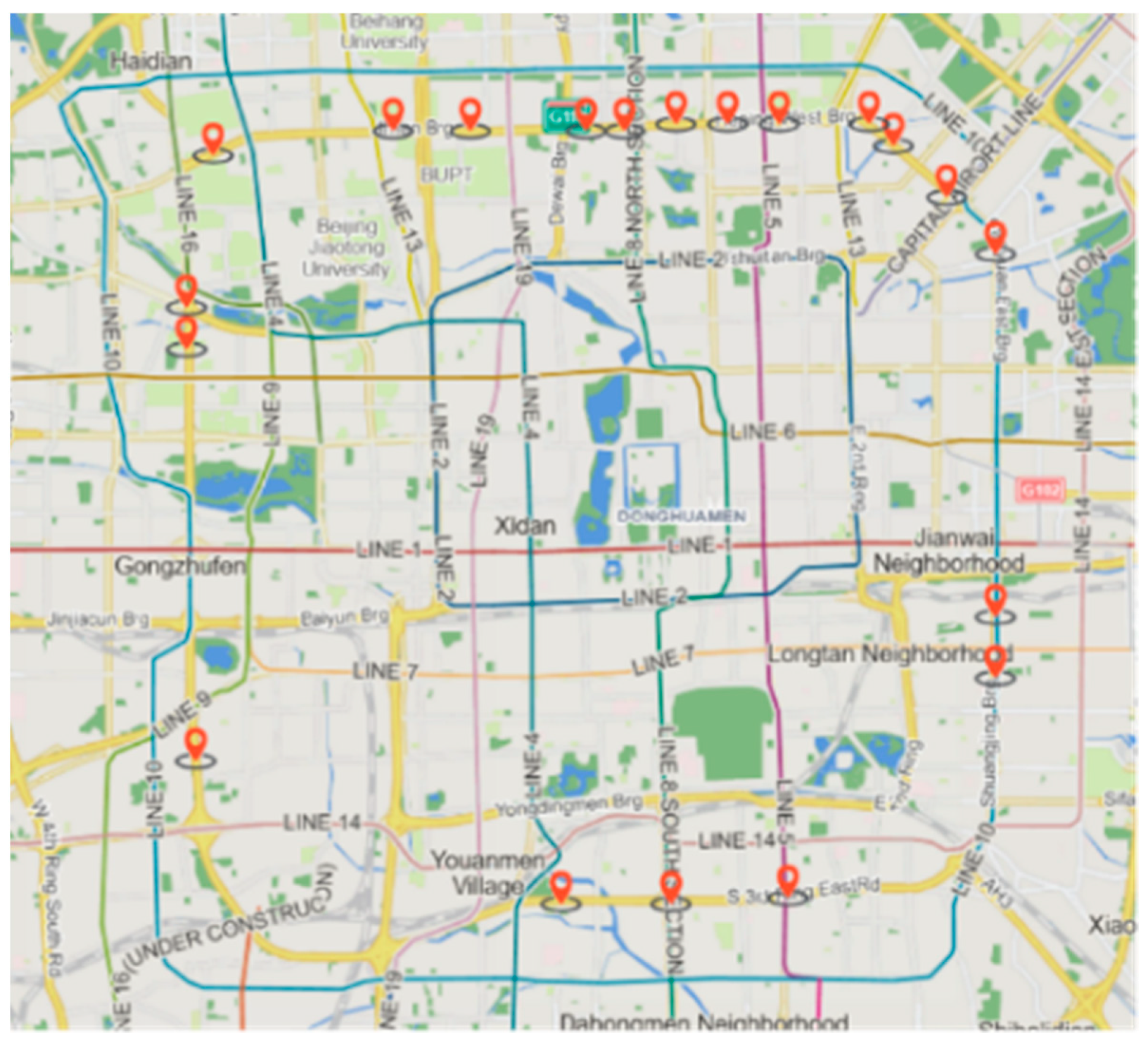
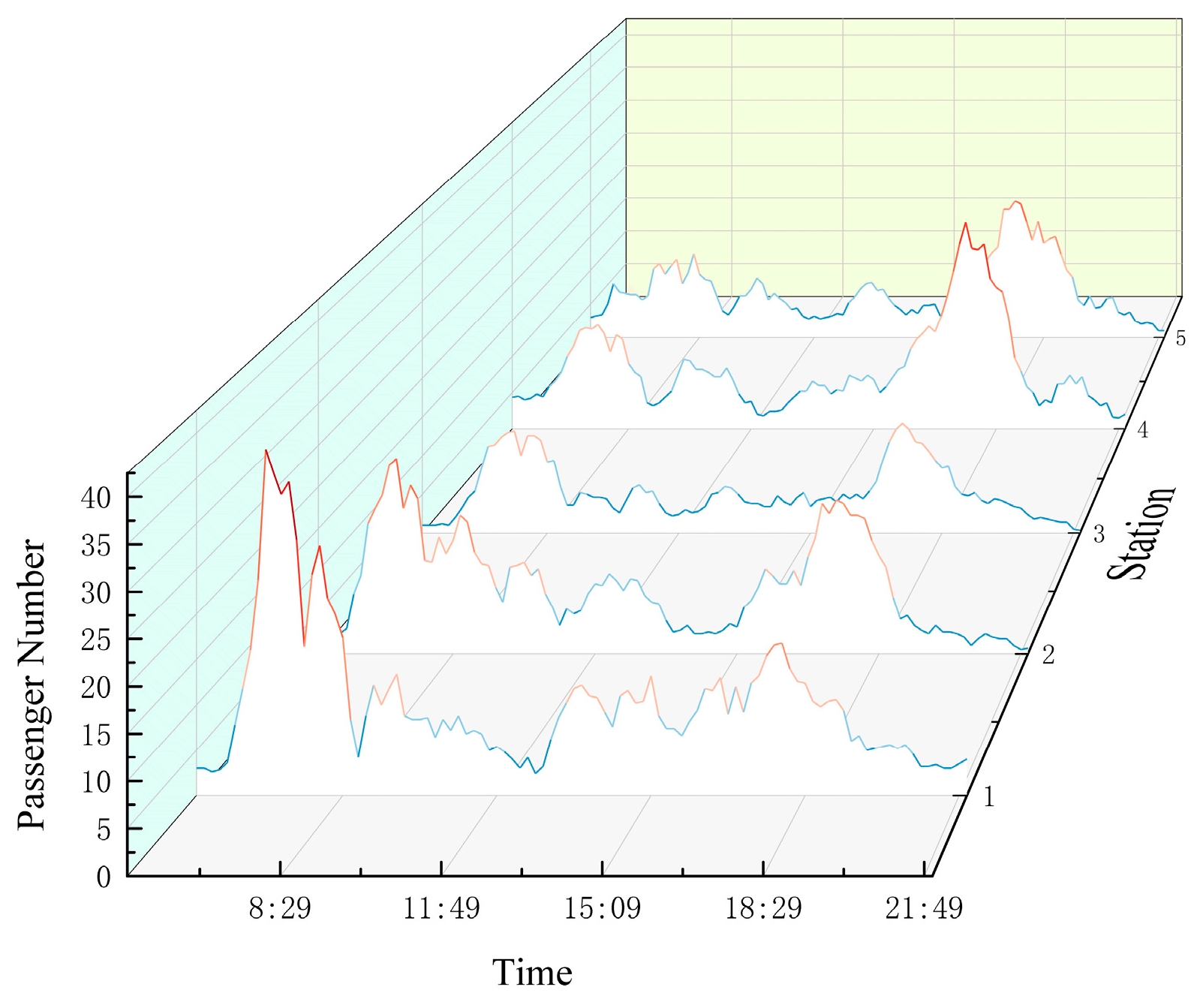
5.1. Data Analysis
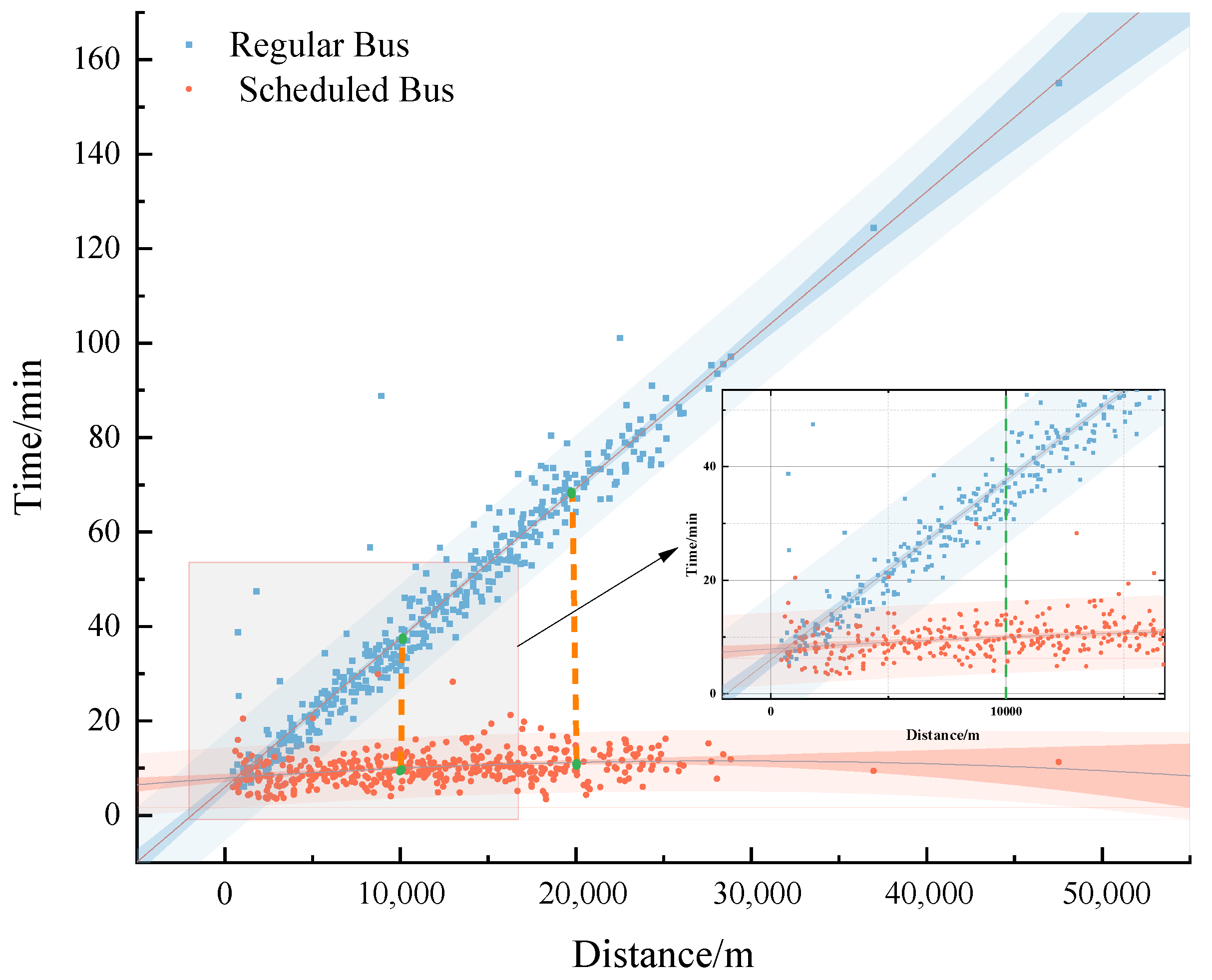
5.2. Model Validation
5.3. Results and Discussion
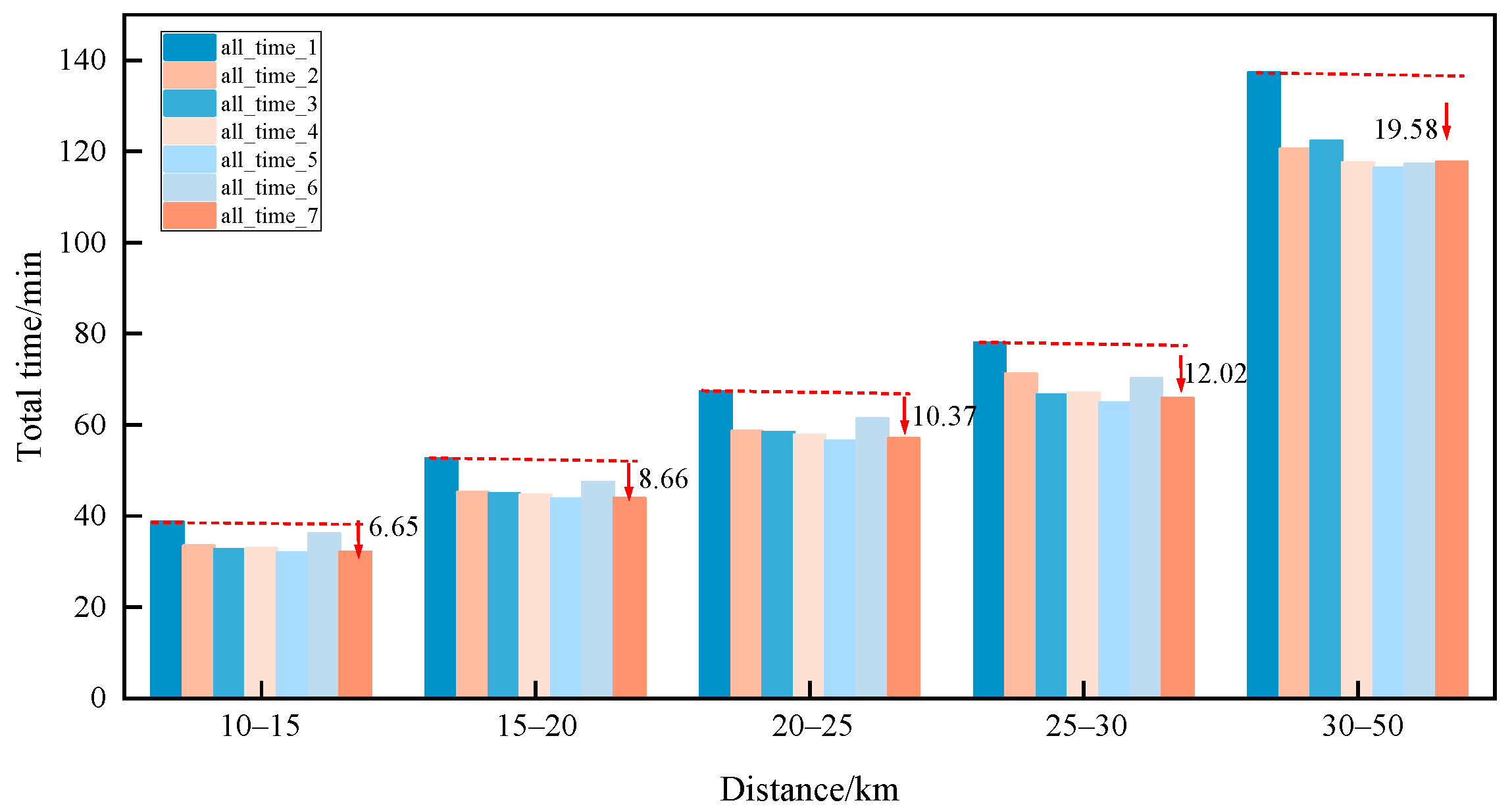
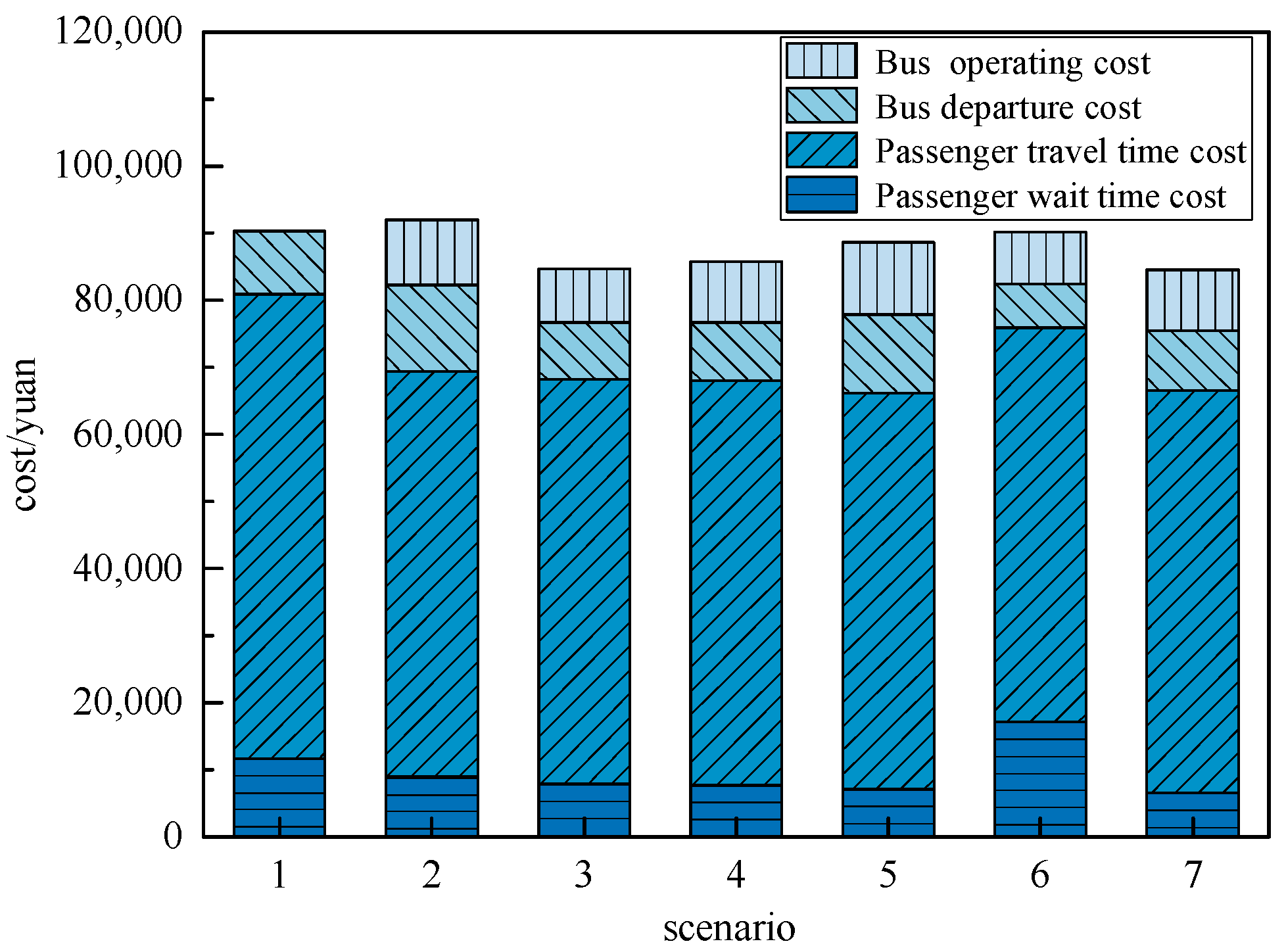
5.3.1. Cost and Time Characteristics of the Use of Various Scenarios
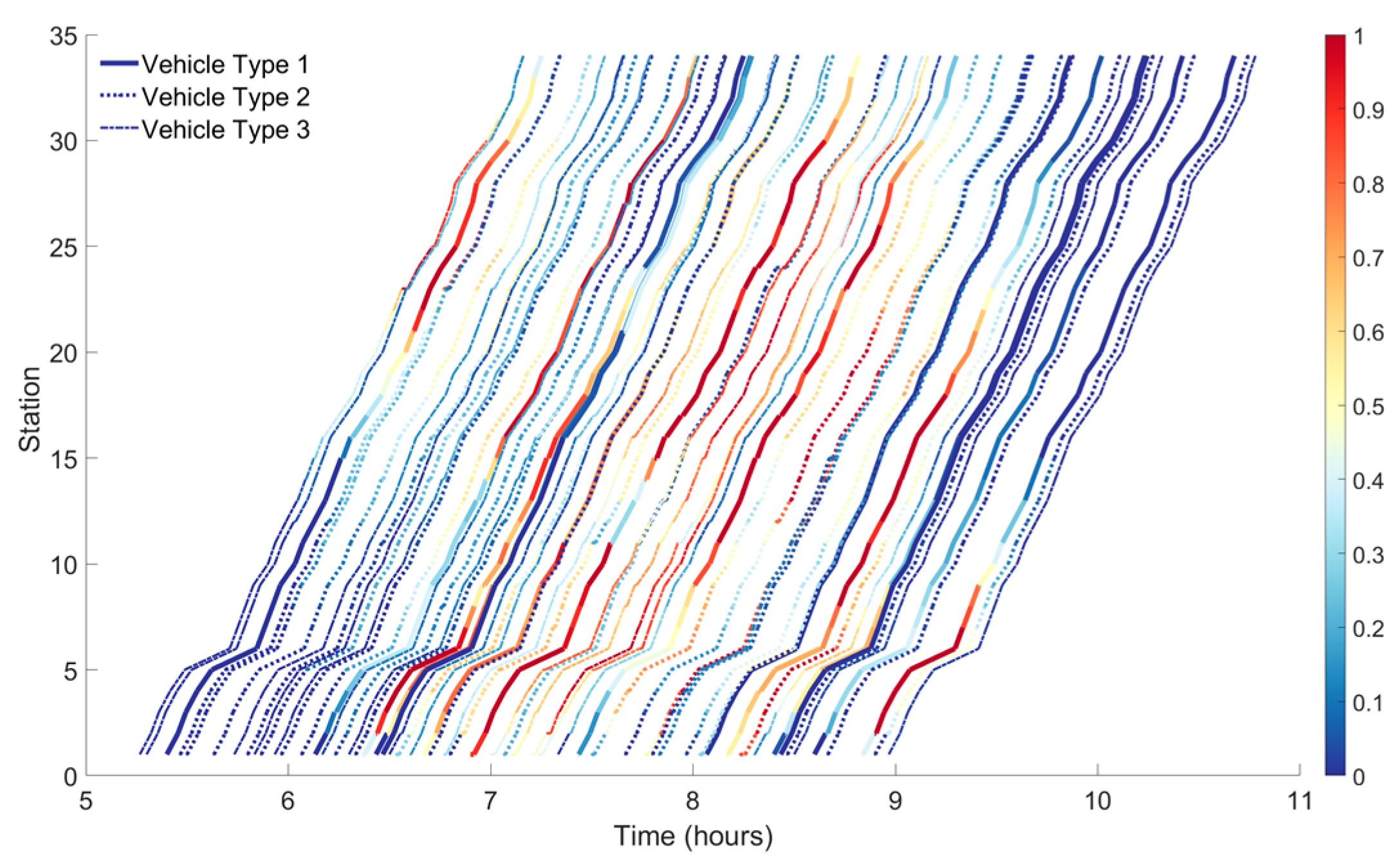
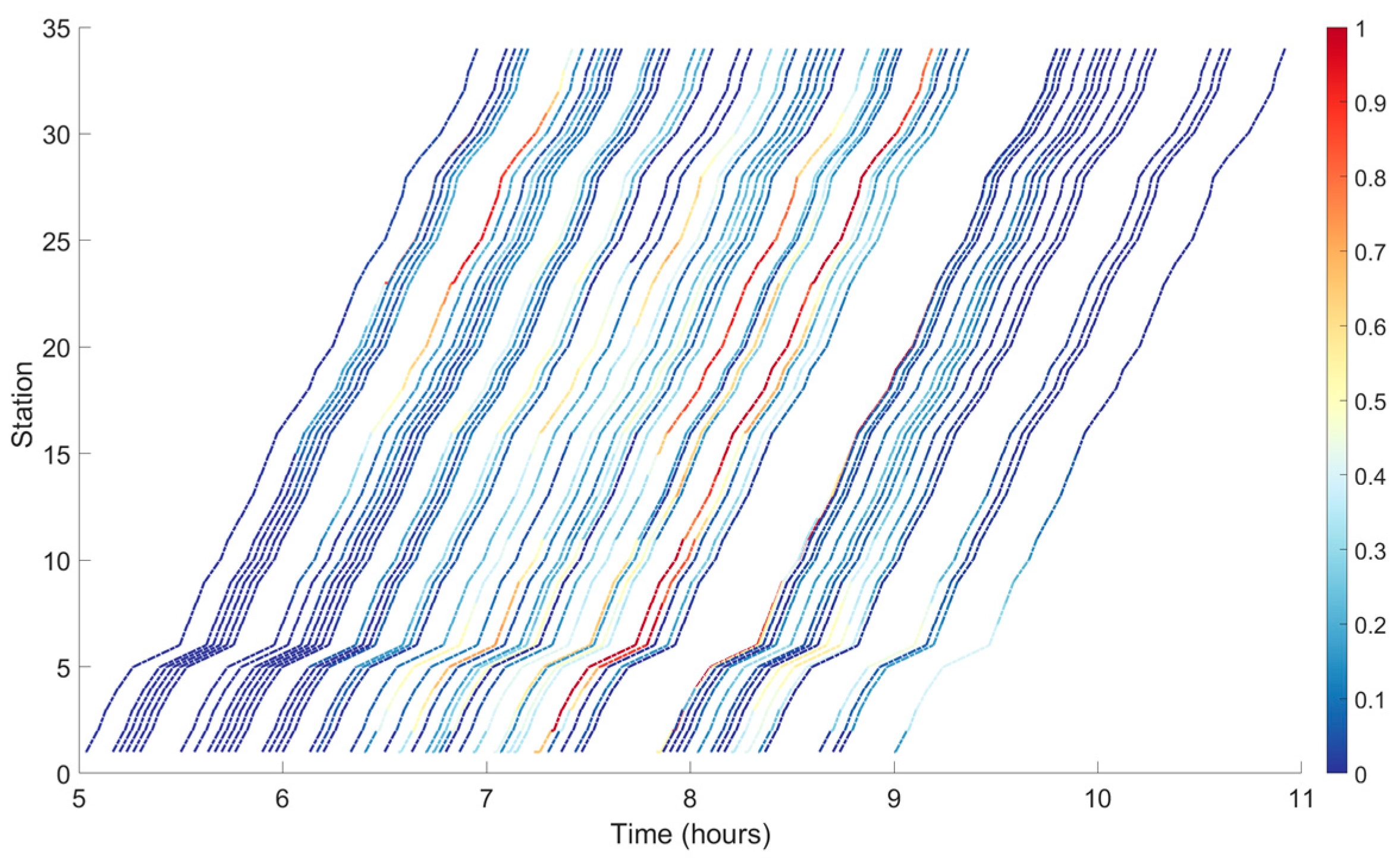
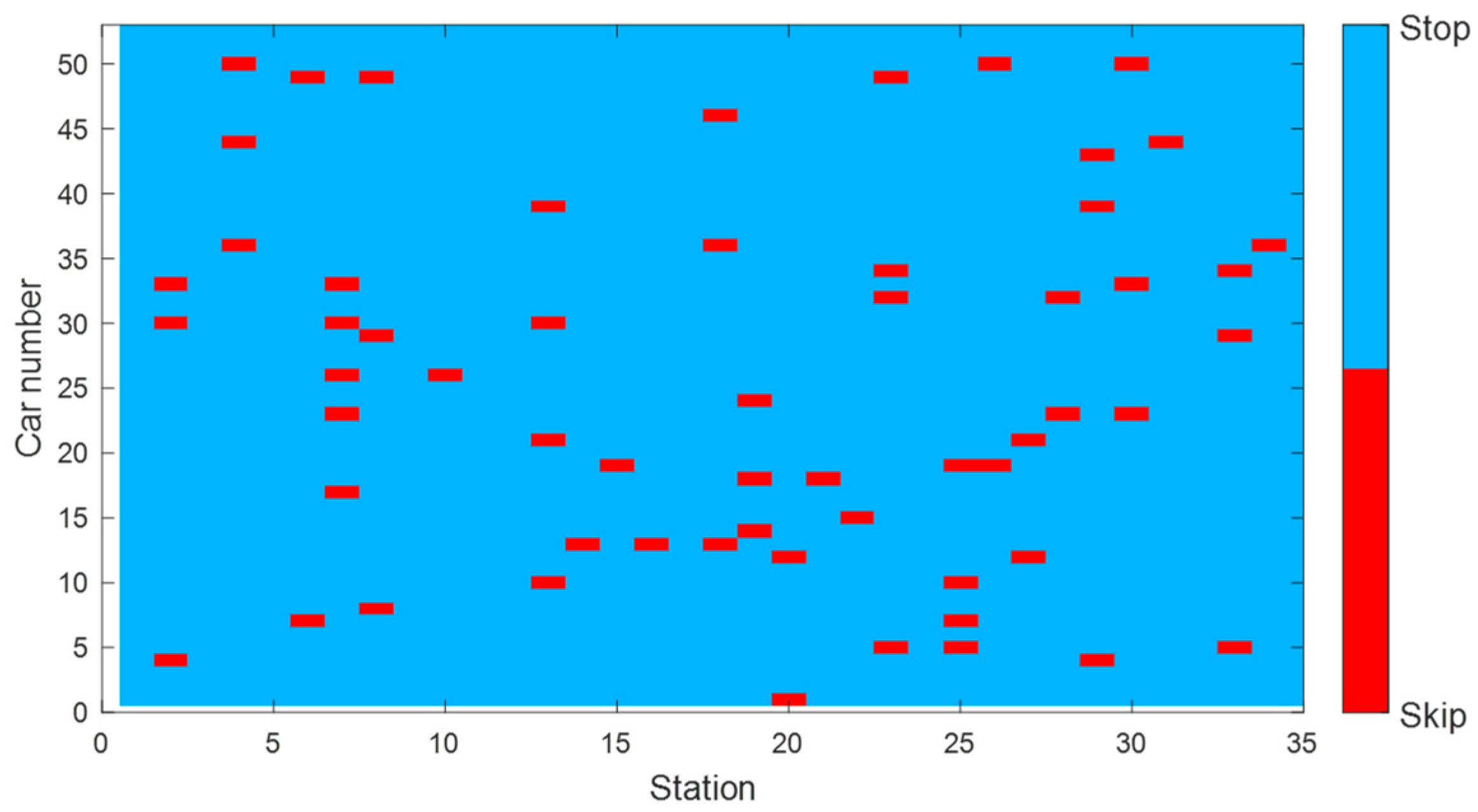
5.3.2. Scheduling Decisions
6. Conclusions
- (1)
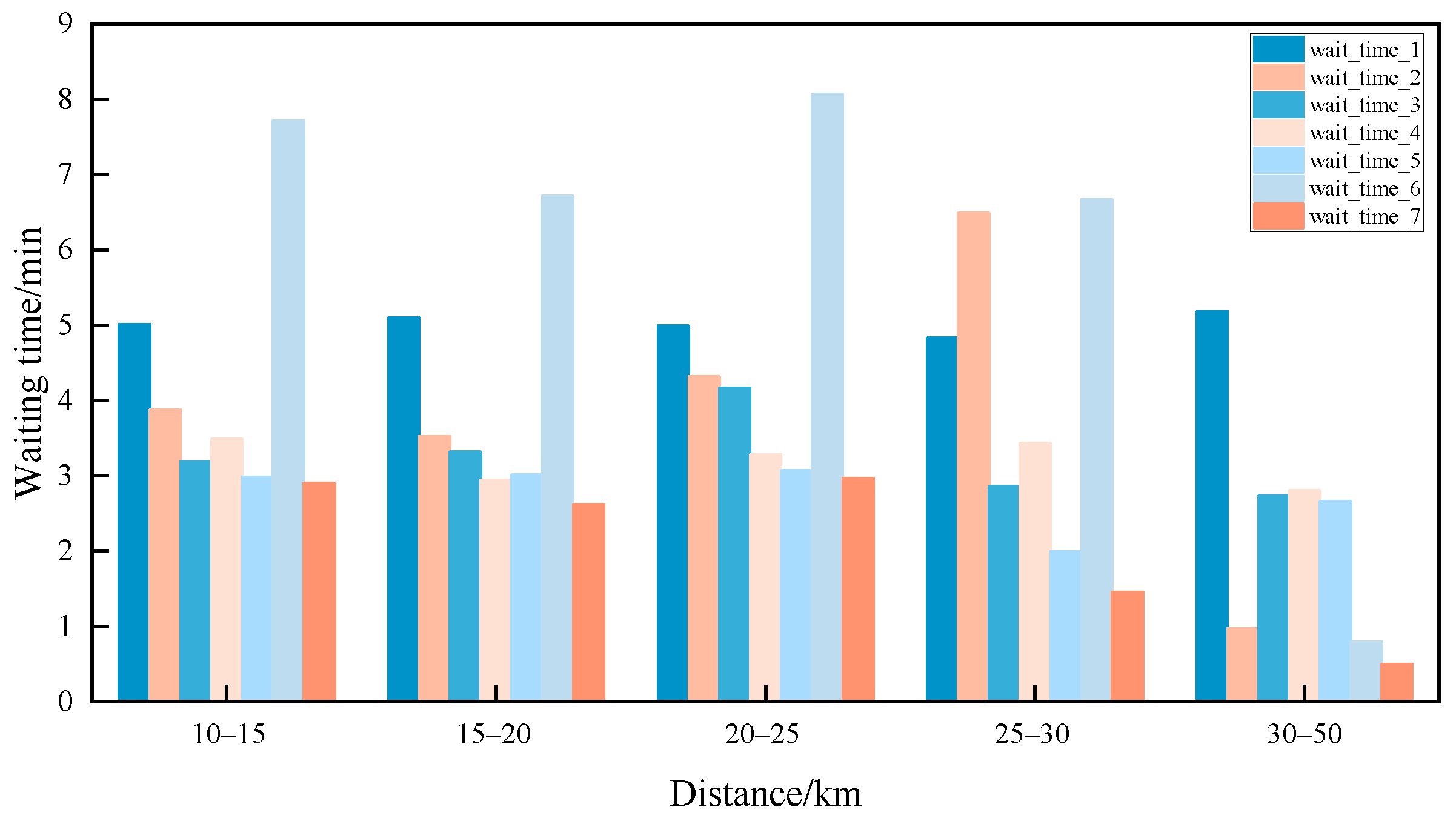
- By calculating multi-scale passenger waiting times based on non-homogeneous Poisson distribution using conventional bus data, this paper effectively obtained the passenger arrival intensity at each bus station. Combined with bus departure times, the average passenger waiting time expectation at each time and spatial scale was obtained. This provides a data foundation for comparing and analyzing passenger waiting times and travel times between conventional buses and reservation-based buses.
- (2)
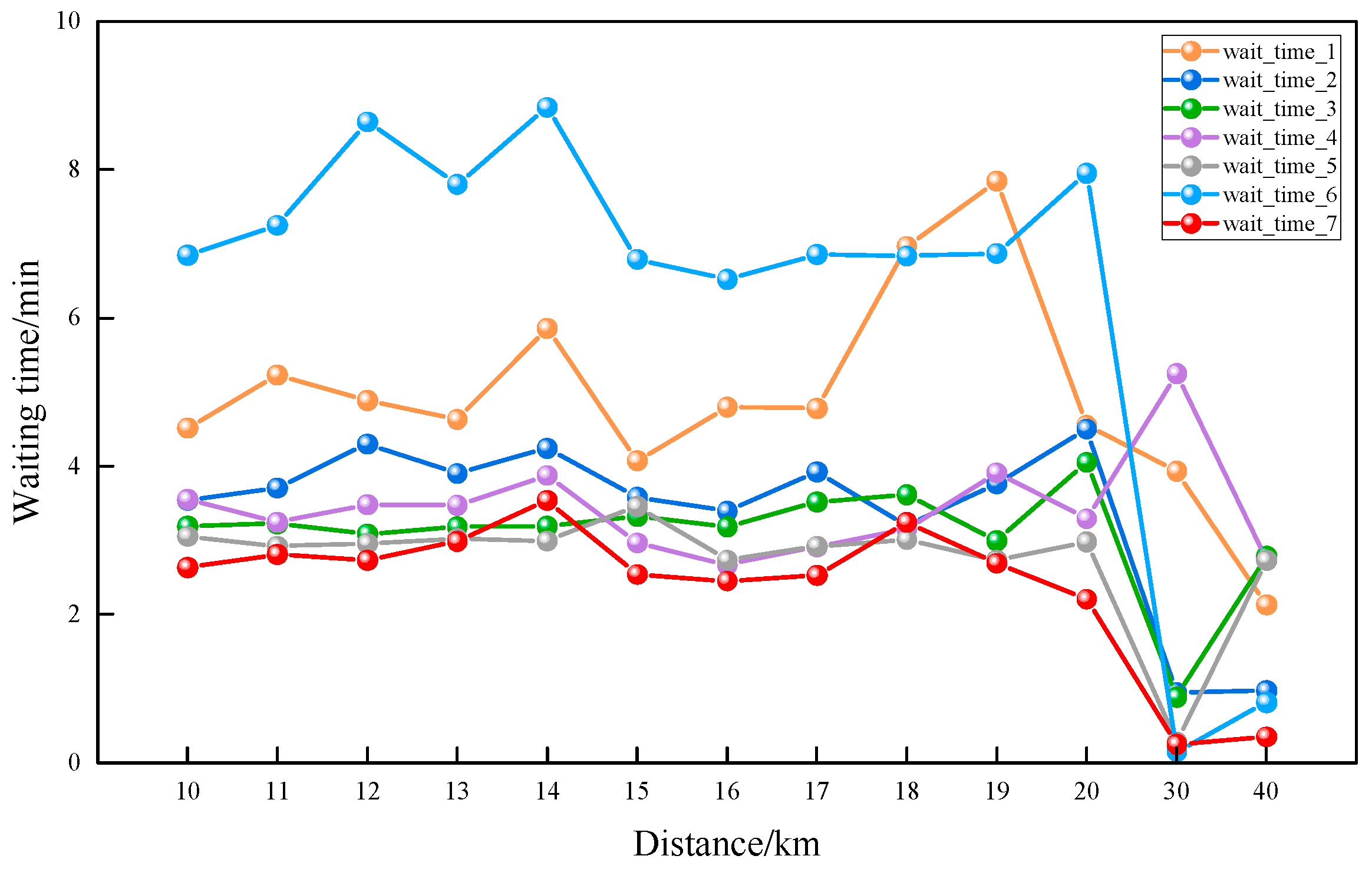
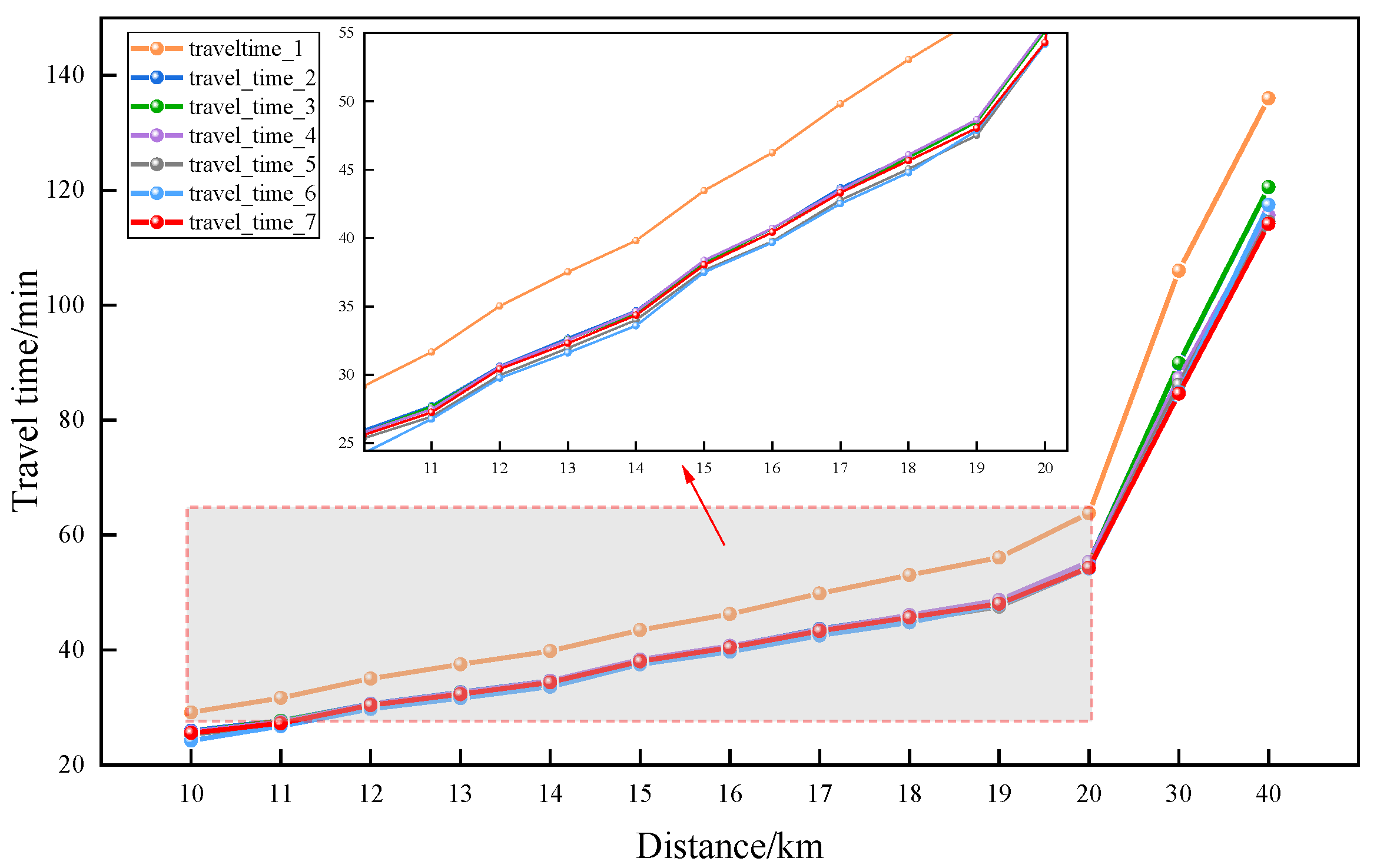
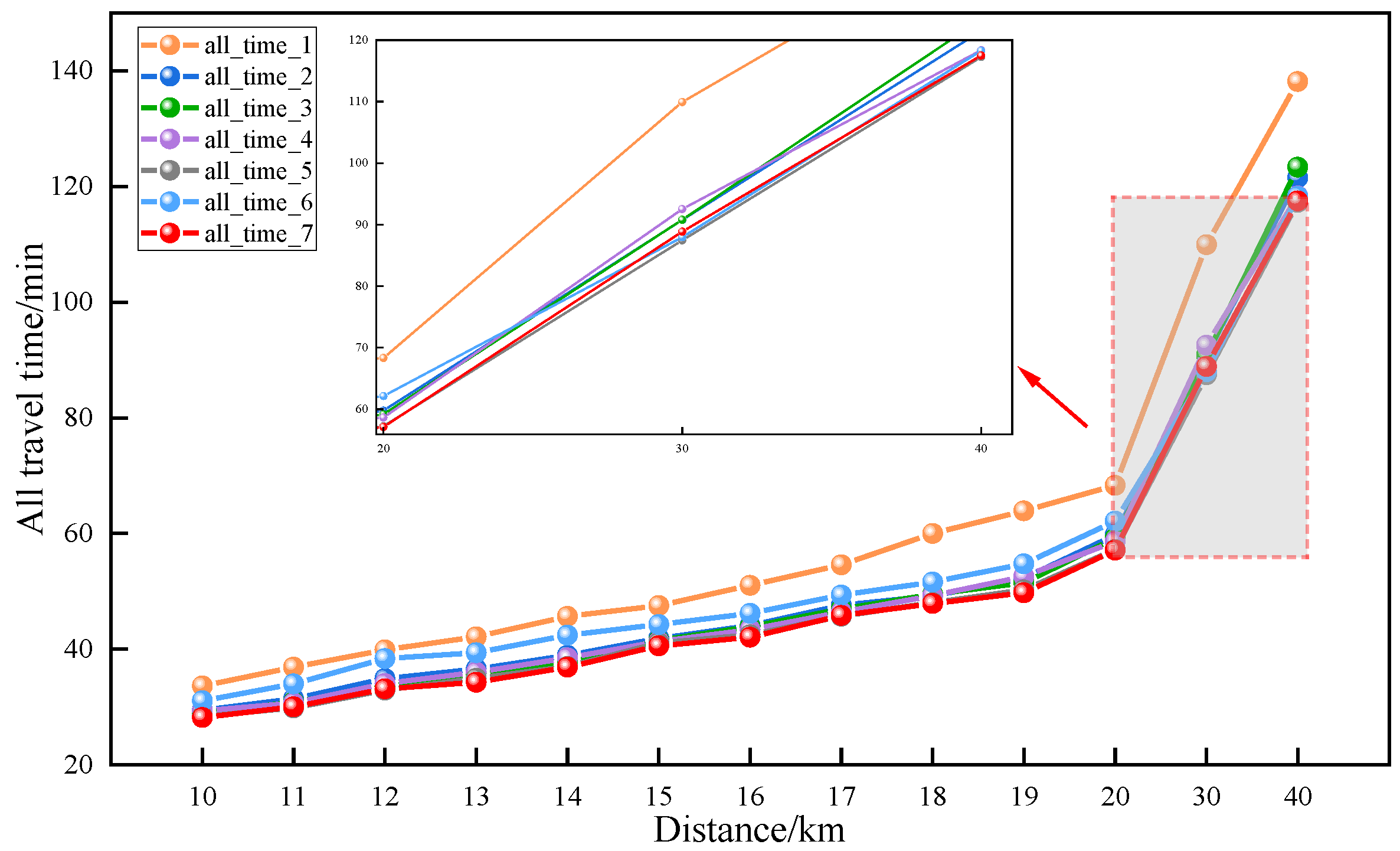
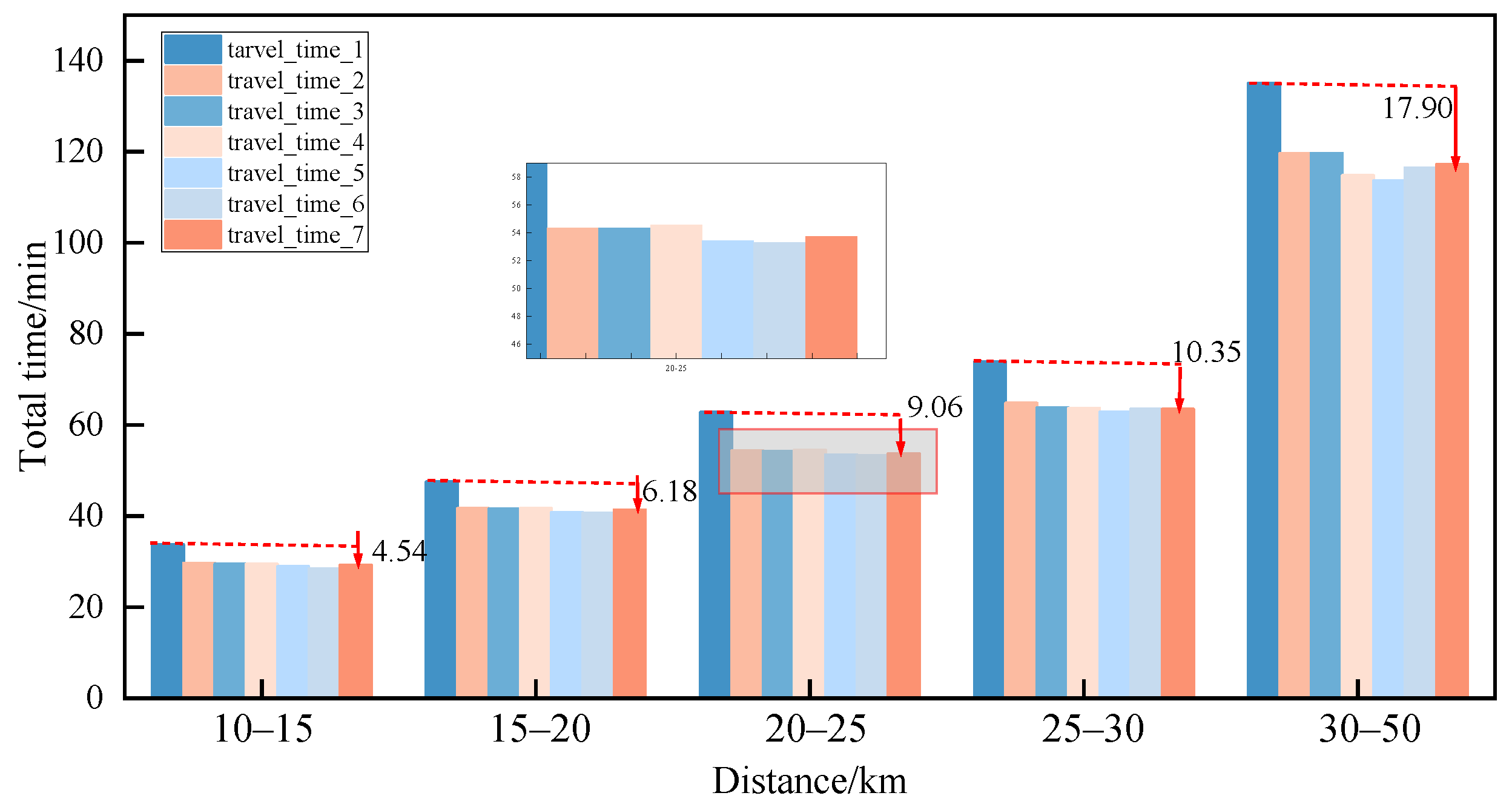
- The reservation-based public transport scheduling system proposed optimizes bus schedules, resulting in significantly lower passenger waiting times compared to conventional bus services. Furthermore, the system ensures that passenger waiting times remain consistently below 4 min. Additionally, the system demonstrates notable improvements in passenger travel times. Compared to conventional fixed-capacity buses, the introduction of intelligent connected vehicle technology with dynamic grouping reduces bus operating costs by 29.7%, while simultaneously decreasing passenger waiting time by 44.15%. This enhanced flexibility in bus operations allows for dynamic adjustments based on actual demand, avoiding unnecessary empty or overloaded situations and thereby improving the overall efficiency of the public transport system.
- (3)
- The introduced bus operation control strategy, combining skip-stop and dwell-time control in the model, significantly enhances the passenger travel experience. Specifically, the skip-stop strategy reduces passenger waiting time by 9.5%, and passenger travel time is shortened by 2.03%. With the inclusion of the dwell-time control strategy, passenger waiting time is reduced by 1.5%. When implementing both the skip-stop and dwell-time control strategies simultaneously, passenger waiting time is reduced by 15.99%, and there is also a certain improvement in passenger travel time. It is particularly noteworthy that, although the advantages of the skip-stop and dwell-time strategies are not pronounced in short-distance travel, these advantages gradually manifest with increased travel distance. This indicates that, through the judicious application of skip-stop and dwell-time control strategies, the bus system can respond more flexibly to real-time demands, avoiding unnecessary stops and waiting, successfully reducing passenger waiting time, and optimizing the overall travel experience.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bi, H.; Zhang, S.; Lu, F. Analysis of Decoupling Effects and Influence Factors in Transportation: Evidence from Guangdong Province, China. ISPRS Int. J. Geo-Inf. 2024, 13, 404. [Google Scholar] [CrossRef]
- Daganzo, C.F. Checkpoint dial-a-ride systems. Transp. Res. Part B Methodol. 1984, 18, 315–327. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Zhou, X. Operational design for shuttle systems with modular vehicles under oversaturated traffic: Discrete modeling method. Transp. Res. Part B Methodol. 2019, 122, 1–19. [Google Scholar] [CrossRef]
- Wang, T.; Guo, J.; Zhang, W.; Wang, K.; Qu, X. On the planning of zone-based electric on-demand minibus. Transp. Res. Part. E Logist. Transp. Rev. 2024, 186, 103566. [Google Scholar] [CrossRef]
- Lee, E.; Lo, H.K.; Li, M. Optimal zonal design for flexible bus service under spatial and temporal demand uncertainty. IEEE Trans. Intell. Transp. Syst. 2024, 25, 251–262. [Google Scholar] [CrossRef]
- He, P.; Jin, J.G.; Schulte, F. The flexible airport bus and last-mile ride-sharing problem: Math-heuristic and metaheuristic approaches. Transp. Res. Part E Logist. Transp. Rev. 2024, 184, 103489. [Google Scholar] [CrossRef]
- Liang, J.; Ren, M.; Huang, K.; Gao, Z. Data-driven timetable design and passenger flow control optimization in metro lines. Transp. Res. Part C Emerg. Technol. 2024, 166, 104761. [Google Scholar] [CrossRef]
- Su, Y.; Yang, H. Enhancing feeder bus service coverage with multi-agent reinforcement learning: A case study in hong kong. Transp. Res. Part E Logist. Transp. Rev. 2025, 196, 103997. [Google Scholar] [CrossRef]
- Ma, X.; Shen, X.; Zhang, Z.; Luan, S.; Chen, X. Optimization of autonomous bus scheduling based on lagrangian relaxation. China J. Highw. Transp. 2019, 32, 10–24. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, H.; Li, W.; Song, X.; Shibasaki, R. Mobile phone GPS data in urban customized bus: Dynamic line design and emission reduction potentials analysis. J. Clean. Prod. 2020, 272, 122471. [Google Scholar] [CrossRef]
- Papanikolaou, A.; Basbas, S. Analytical models for comparing demand responsive transport with bus services in low demand interurban areas. Transp. Lett. 2021, 13, 255–262. [Google Scholar] [CrossRef]
- Lee, E.; Cen, X.; Lo, H.K. Scheduling zonal-based flexible bus service under dynamic stochastic demand and time-dependent travel time. Transp. Res. Part E Logist. Transp. Rev. 2022, 168, 102931. [Google Scholar] [CrossRef]
- Ma, W.; Zeng, L.; An, K. Dynamic vehicle routing problem for flexible buses considering stochastic requests. Transp. Res. Part C Emerg. Technol. 2023, 148, 104030. [Google Scholar] [CrossRef]
- Liu, X.; Qu, X.; Ma, X. Improving flex-route transit services with modular autonomous vehicles. Transp. Res. Part E Logist. Transp. Rev. 2021, 149, 102331. [Google Scholar] [CrossRef]
- Guo, R.; Guan, W.; Vallati, M.; Zhang, W. Modular Autonomous Electric Vehicle Scheduling for Customized On-Demand Bus Services. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1–12. [Google Scholar] [CrossRef]
- Tian, Q.; Lin, Y.H.; Wang, D.Z.W. Joint scheduling and formation design for modular-vehicle transit service with time-dependent demand. Transp. Res. Part C Emerg. Technol. 2023, 147, 103986. [Google Scholar] [CrossRef]
- Dai, Z.; Liu, X.C.; Li, H.; Wang, M.; Ma, X. Semi-autonomous bus platooning service optimization with surrogate modeling. Comput. Ind. Eng. 2023, 175, 108838. [Google Scholar] [CrossRef]
- Wu, M.; Yu, C.; Ma, W.; An, K.; Zhong, Z. Joint optimization of timetabling, vehicle scheduling, and ride-matching in a flexible multi-type shuttle bus system. Transp. Res. Part C Emerg. Technol. 2022, 139, 103657. [Google Scholar] [CrossRef]
- Dai, Z.; Liu, X.C.; Chen, Z.; Guo, R.; Ma, X. A predictive headway-based bus-holding strategy with dynamic control point selection: A cooperative game theory approach. Transp. Res. Part B Methodol. 2019, 125, 29–51. [Google Scholar] [CrossRef]
- Vismara, L.; Chew, L.Y.; Saw, V. Optimal assignment of buses to bus stops in a loop by reinforcement learning. Phys. A 2021, 583, 126268. [Google Scholar] [CrossRef]
- Tang, C.; Shi, H.; Liu, T. Optimization of single-line electric bus scheduling with skip-stop operation. Transp. Res. Part D-Transp. Environ. 2023, 117, 103652. [Google Scholar] [CrossRef]
- Wu, W.; Zhu, Y.; Liu, R. Dynamic scheduling of flexible bus services with hybrid requests and fairness: Heuristics-guided multi-agent reinforcement learning with imitation learning. Transp. Res. Part B Methodol. 2024, 190, 103069. [Google Scholar] [CrossRef]
- Ma, H.; Yang, M.J.; Li, X. Integrated optimization of customized bus routes and timetables with consideration of holding control. Comput. Ind. Eng. 2022, 175, 108886. [Google Scholar] [CrossRef]
- Rodriguez, J.; Koutsopoulos, H.N.; Wang, S.; Zhao, J. Cooperative bus holding and stop-skipping: A deep reinforcement learning framework. Transp. Res. Part C Emerg. Technol. 2023, 155, 104308. [Google Scholar] [CrossRef]
- Bajada, J.; Grech, J.; Bajada, T. Deep reinforcement learning of autonomous control actions to improve bus-service regularity. In Proceedings of the Artificial Intelligence. ECAI 2023 International Workshops, Kraków, Poland, 30 September–4 October 2023; Springer Nature: Cham, Switzerland, 2024. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, P.; Li, J. Distribution network planning of distributed power sources and generalized energy storage considering operational characteristics. Electr. Power Autom. Equip. 2023, 43, 72–79. [Google Scholar] [CrossRef]
- Xiao-Chun, Z.; Yong, G.; Zhuang, Y.U.; Yu-Huan, W.; Jian, A.N. Passenger average waiting time estimation based on bus GPS and IC card data. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 236–241. Available online: http://www.tseit.org.cn/EN/abstract/abstract19930.shtml (accessed on 10 March 2025).
- Lu, H.; Burge, P.; Heywood, C.; Sheldon, R.; Lee, P.; Barber, K.; Phillips, A. The impact of real-time information on passengers’ value of bus waiting time. Transp. Res. Procedia 2018, 31, 18–34. [Google Scholar] [CrossRef]
- Gong, H.; Chen, X.; Yu, L.; Wu, L. An application-oriented model of passenger waiting time based on bus departure time intervals. Transp. Plan. Technol. 2016, 39, 424–437. [Google Scholar] [CrossRef]
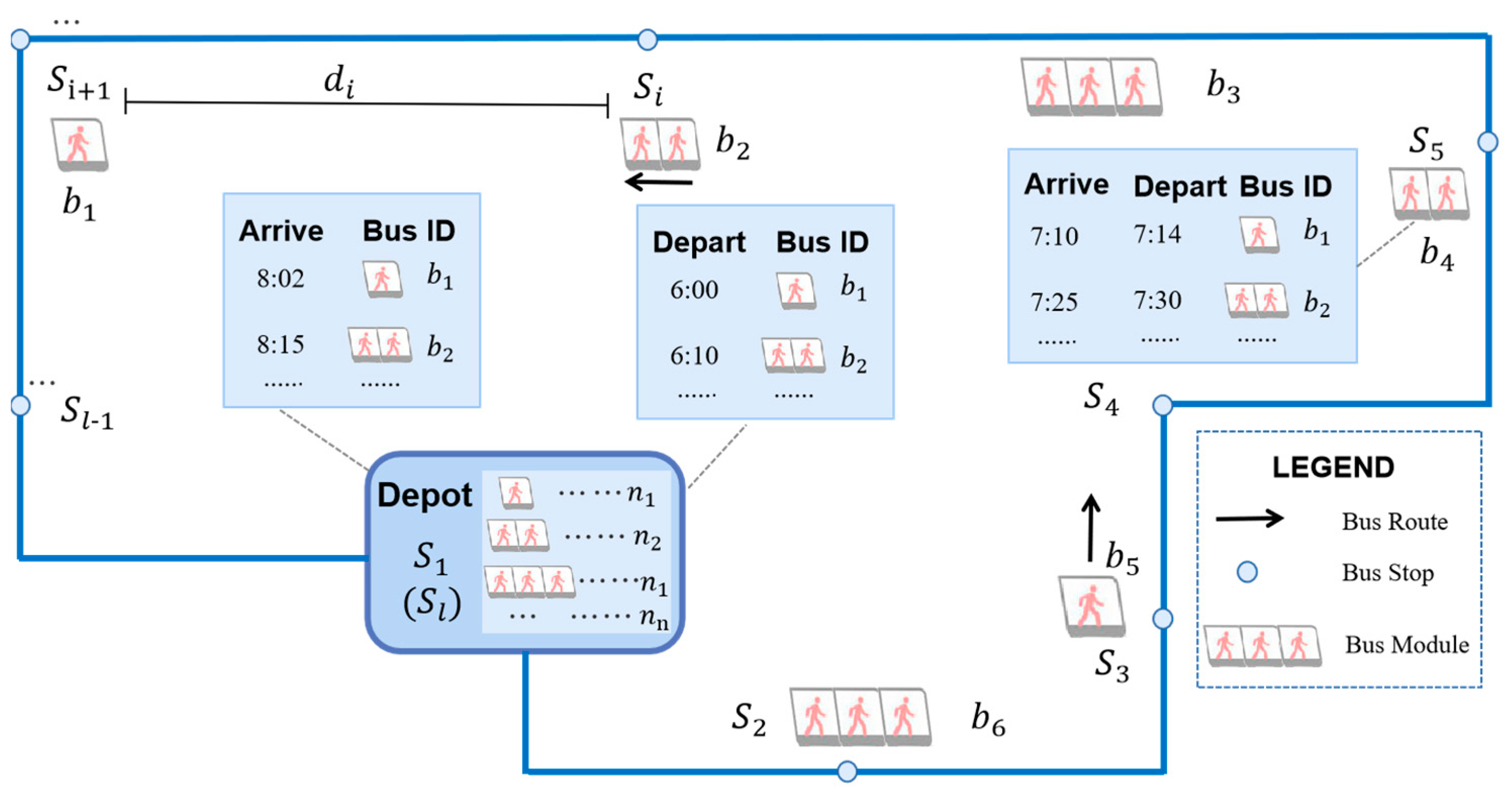
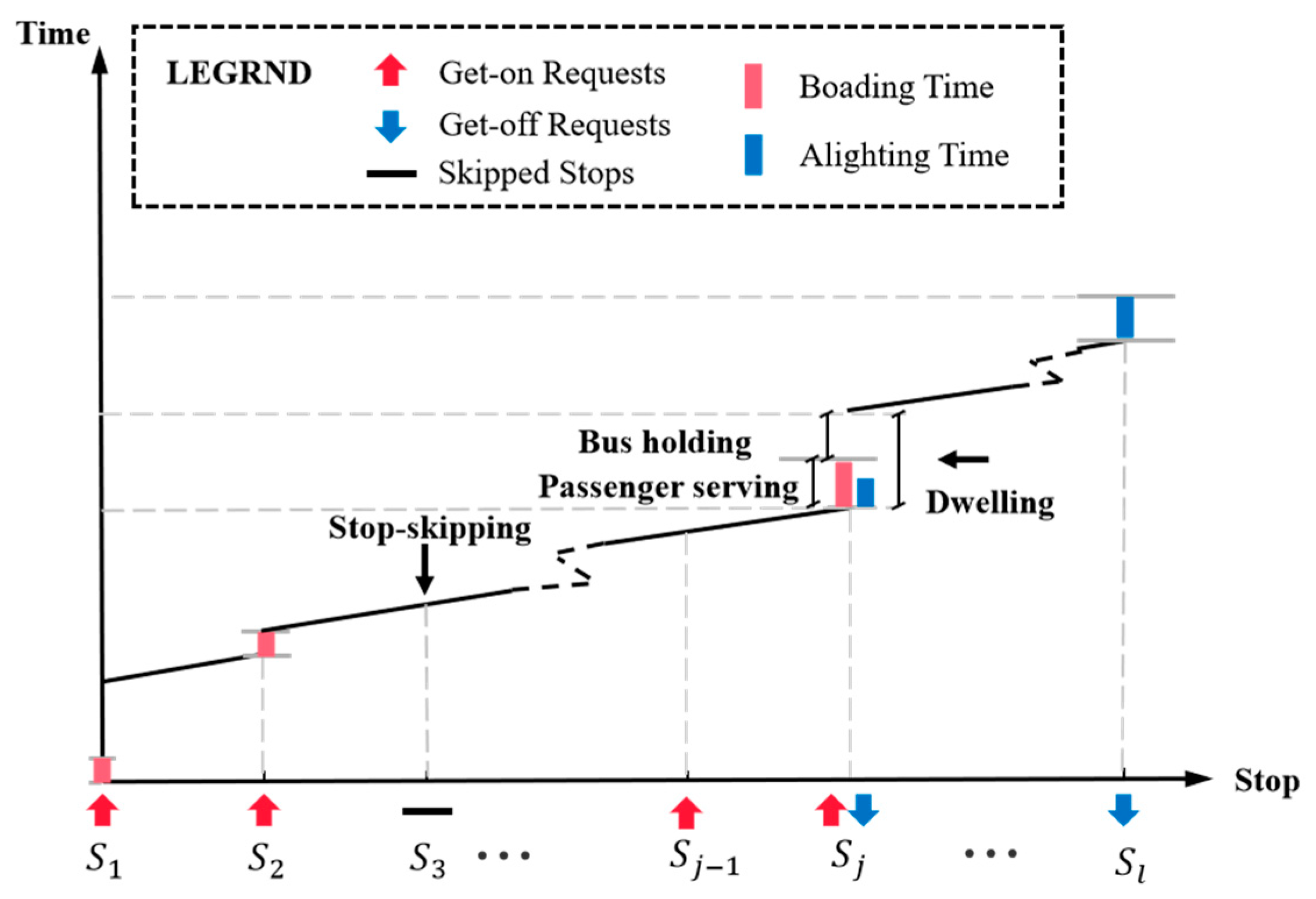
| Symbol | Description |
|---|---|
| Decision variable | |
| decision variable: vehicle type m for departure at time k | |
| decision variable: if vehicle i stops at station j, , and 0 otherwise | |
| Set | description |
| discretize the scheduling period into K uniformly distributed time intervals, and the discrete time nodes are given by | |
| bus stops | |
| fleet types of public buses | |
| bus ID | |
| bus stop ID | |
| passenger requests at stop | |
| Parameters | |
| travel time between stations | |
| capacity of the -th bus | |
| operational value of the vehicle | |
| time spent by a passenger boarding the bus/min | |
| time spent by a passenger disembarking/min | |
| fixed operating costs of smart connected buses, including maintenance costs, per trip in CNY | |
| capacity of the smart connected bus module | |
| operational cost of the smart connected bus during operation, measured in CNY per trip | |
| acceleration and deceleration time for vehicles entering and exiting the station | |
| the time for vehicle i to arrive at station j | |
| the time for vehicle i to depart at station | |
| the service time of vehicle i at station | |
| the headway between vehicle and i at station | |
| minimum headway | |
| the number of passengers alighting from bus i at station | |
| passengers waiting at station for bus i bound for station | |
| passengers successfully boarding bus i heading to k in request p at station j | |
| passengers alighting from bus i at station j | |
| dwell time of bus i at station j | |
| the expected time for request p from station to | |
| passengers waiting for bus i at station j during time period h | |
| passengers detained by bus i from station j to k for request p | |
| passengers from station j to k for request p | |
| the last time i car was served before reaching j | |
| passengers on i car going from j to k | |
| the actual number of passengers boarding i car at station j | |
| the number of passengers successfully boarding i car at station j who requested travel within the interval | |
| the beginning of the planning horizon | |
| discrete departure time nodes for vehicle i | |
| vehicle types | |
| passenger reservation request p is assigned to be served by vehicle i | |
| indicates that the origin of passenger p is | |
| indicates that the destination of passenger p is | |
| the index of the station where vehicle i is currently located or is about to arrive | |
| passengers delayed due to skip-stop | |
| the waiting time of passengers delayed because vehicle i skipped stop j | |
| overloaded passengers delayed within the service time | |
| Wait_n1 | passengers delayed due to bus capacity constraints arriving within the time range |
| part of the passengers arriving within the dwell-stop time during the dwell time are delayed | |
| Wait_n2 | passengers arriving within the time range are delayed due to bus capacity constraints |
| Scenarios | Passenger Waiting Time | Passenger Travel Time | Operation Cost | Bus Operating Cost | Passengers’ Travel Cost | Total Cost | ||
|---|---|---|---|---|---|---|---|---|
| Value/min | Variation/% | Value/min | Variation/% | Value/CNY | Value/CNY | Value/CNY | Value/CNY | |
| 1 | 9386.94 | ─ | 82,292.00 | ─ | 9408 | ─ | 80,858.96 | ─ |
| 2 | 7096.33 | 24.40 | 72,067.33 | 12.42 | 12,768 | 9789.40 | 69,406.97 | 91,964.37 |
| 3 | 6257.40 | 33.34 | 71,863.29 | 12.55 | 8383 | 8072.78 | 68,186.91 | 84,642.69 |
| 4 | 6163.82 | 34.34 | 71,789.22 | 12.76 | 8651 | 9083.9 | 68,007.72 | 85,742.62 |
| 5 | 5662.77 | 39.67 | 70,405.73 | 14.44 | 11,635 | 10,772 | 66,219.27 | 88,626.27 |
| 6 | 13,701.22 | −45.96 | 69,956.08 | 14.99 | 6534 | 7592.6 | 75,889.64 | 90,016.24 |
| 7 | 5257.12 | 44.00 | 71,304.80 | 13.35 | 8976 | 9050.8 | 66,467.43 | 84,494.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, W.; Cao, H.; Zhao, J. Modular Scheduling Optimization of Multi-Scenario Intelligent Connected Buses Under Reservation-Based Travel. Sustainability 2025, 17, 2645. https://doi.org/10.3390/su17062645
Shen W, Cao H, Zhao J. Modular Scheduling Optimization of Multi-Scenario Intelligent Connected Buses Under Reservation-Based Travel. Sustainability. 2025; 17(6):2645. https://doi.org/10.3390/su17062645
Chicago/Turabian StyleShen, Wei, Honglu Cao, and Jiandong Zhao. 2025. "Modular Scheduling Optimization of Multi-Scenario Intelligent Connected Buses Under Reservation-Based Travel" Sustainability 17, no. 6: 2645. https://doi.org/10.3390/su17062645
APA StyleShen, W., Cao, H., & Zhao, J. (2025). Modular Scheduling Optimization of Multi-Scenario Intelligent Connected Buses Under Reservation-Based Travel. Sustainability, 17(6), 2645. https://doi.org/10.3390/su17062645






