Response of the Evolution of Basin Hydrometeorological Drought to ENSO: A Case Study of the Jiaojiang River Basin in Southeast China
Abstract
:1. Introduction
2. Study Area and Data
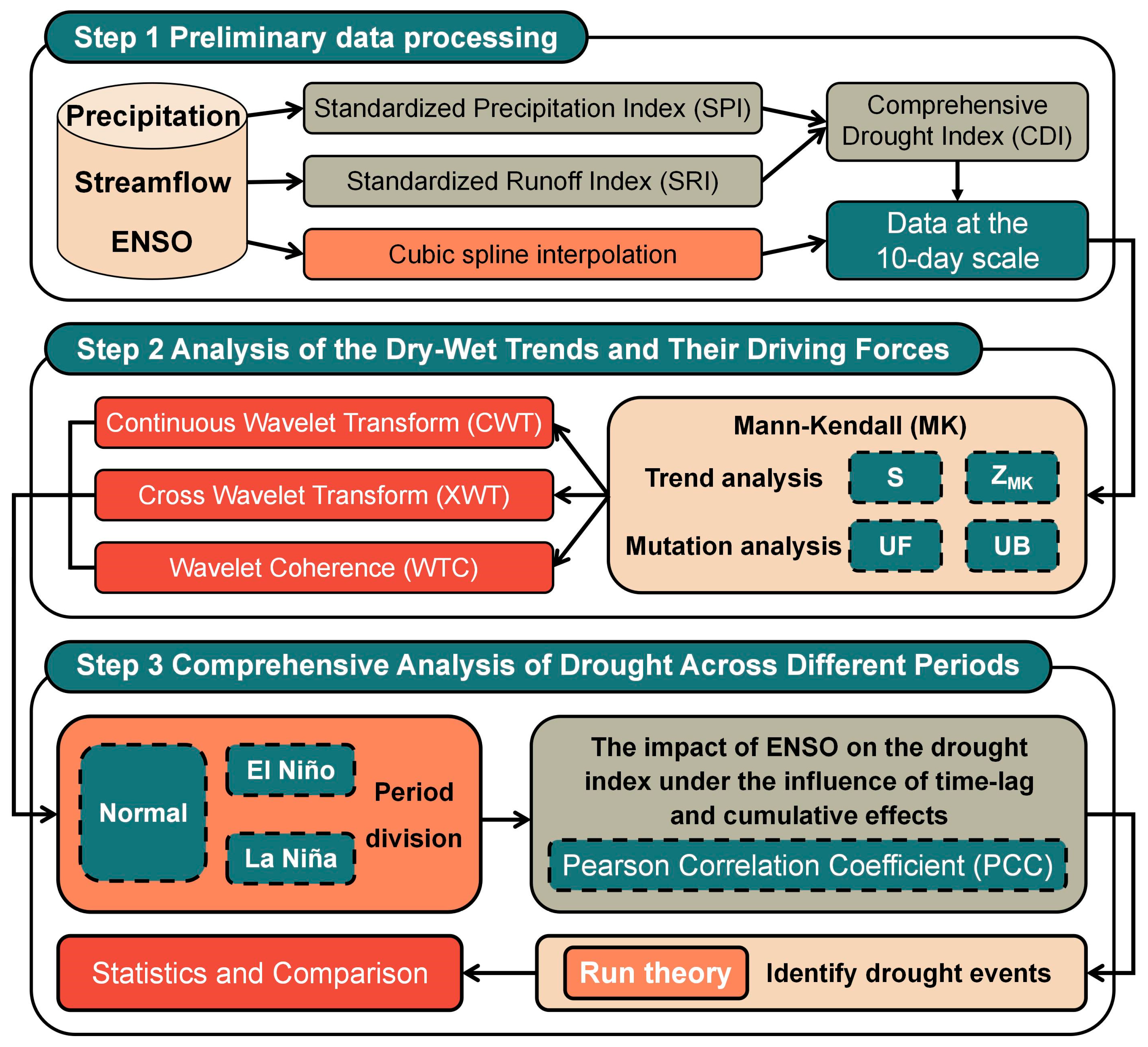
3. Methodology
3.1. Drought Index
3.1.1. Standardized Precipitation Index (SPI) and Standardized Runoff Index (SRI)
3.1.2. Comprehensive Drought Index (CDI)
3.2. Cubic Spline Interpolation
3.3. Trend and Mutation Test
3.3.1. Mann–Kendall (MK) Trend Test
3.3.2. Mann–Kendall (MK) Mutation Test
3.4. Wavelet Analysis
3.4.1. Continuous Wavelet Transform (CWT)
3.4.2. Cross Wavelet Transform (XWT)
3.4.3. Wavelet Coherence (WTC)
3.5. Analysis of Time Lag and Cumulative Effects
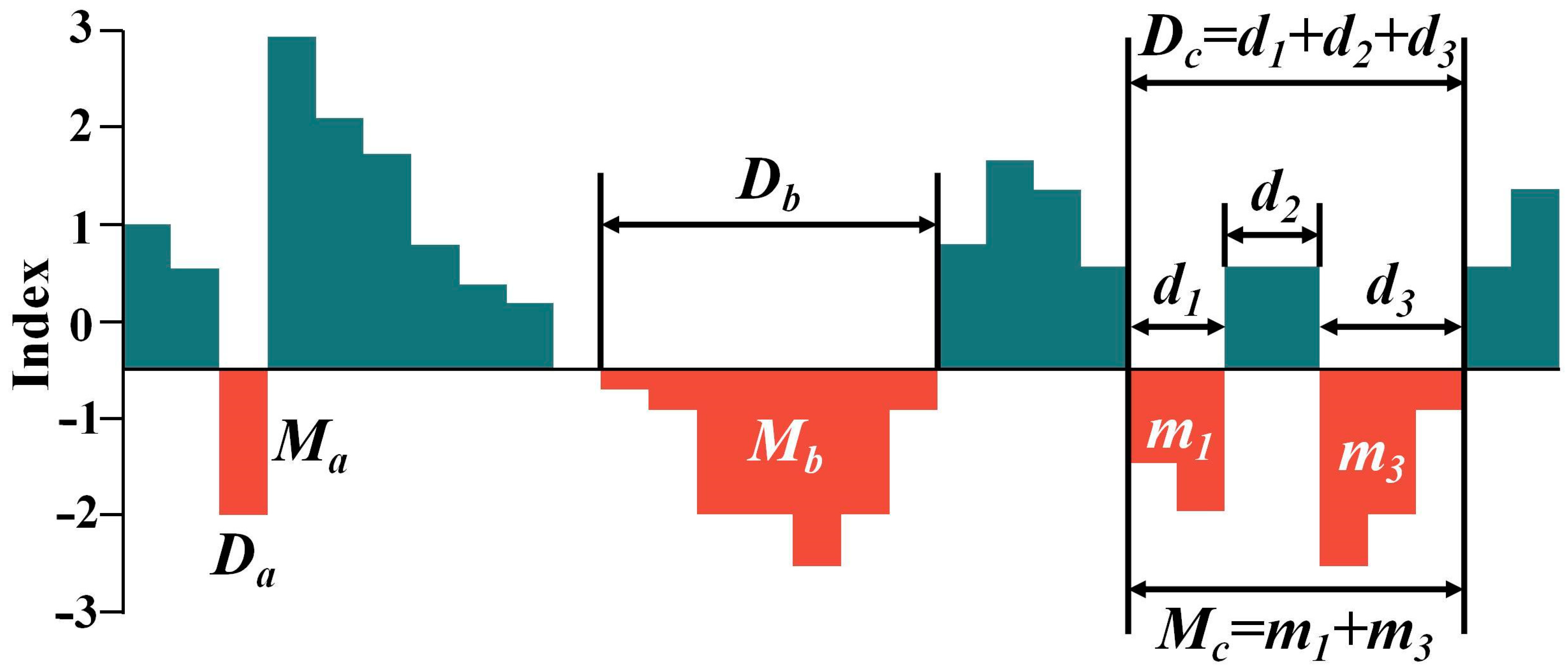
3.6. Run Theory
4. Results and Discussions
4.1. Analysis of the Dry-Wet Trends and Their Driving Forces
4.1.1. Establishment of Comprehensive Drought Index (CDI)
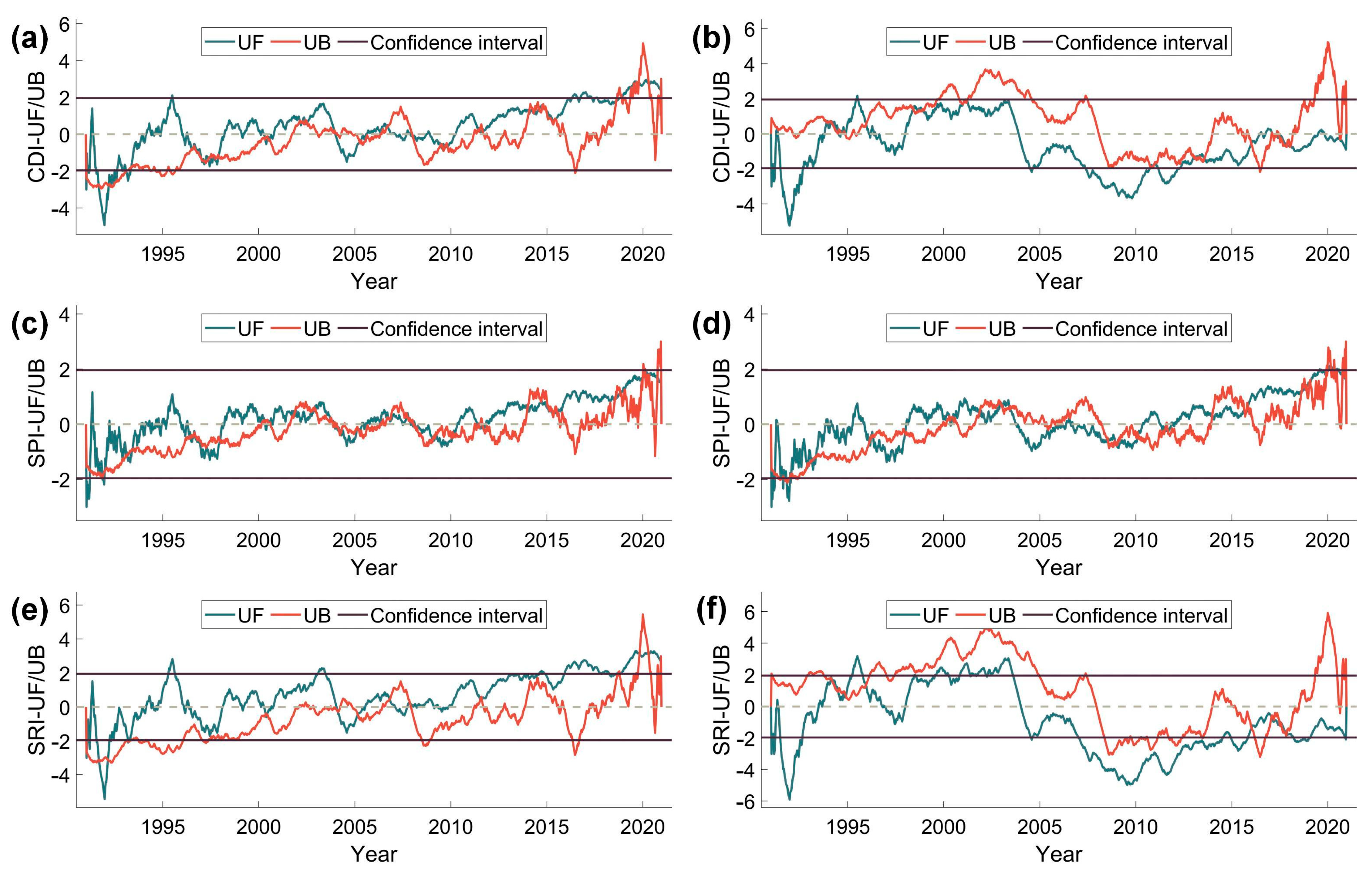
4.1.2. Trends and Mutation in Drought Index
4.1.3. Correlation Analysis Based on Wavelet Analysis
4.2. Comprehensive Analysis of Drought Across Different Periods
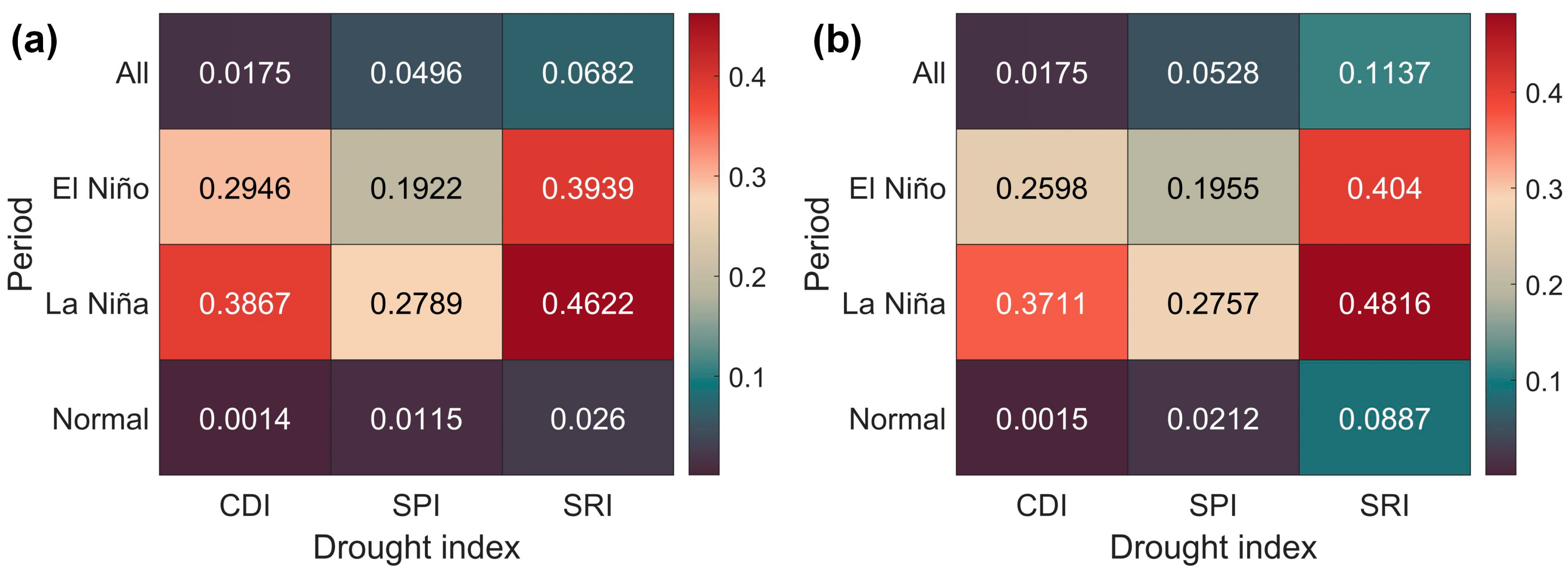
4.2.1. Differences in Drought Indices Across Different Periods
4.2.2. Time Lag and Cumulative Effects
4.2.3. Identification of Drought Events Across Different Periods
4.3. The Application Prospects and Limitations of the Research
- (1)
- This study focuses solely on the Jiaojiang River Basin in southeastern China as the research area. Although the Jiaojiang River Basin is representative, coastal basins differ in geographical environment, climatic conditions, and underlying surface characteristics. In the future, multiple coastal basins in different geographical locations will be selected for research to compare the similarities and differences in drought evolution responses to ENSO across regions.
- (2)
- The data used in this study span from 1991 to 2020, which is relatively short. In the future, meteorological and hydrological data over a longer period will be collected to explore the long-term trends in the relationship between ENSO and drought evolution, providing a more robust data foundation for predicting future drought trends.
- (3)
- Although the constructed CDI has advantages, it only considers two indicators, SPI and SRI, and does not include other factors that may influence droughts, such as temperature changes, soil moisture, and vegetation coverage. In the future, more variables affecting droughts will be incorporated to optimize the composite drought index model, enabling a more comprehensive and accurate characterization of drought features.
5. Conclusions
- (1)
- The CDI constructed using 10-day scale data effectively integrates the advantages of SPI and SRI, accurately reflecting the combined characteristics of meteorological and hydrological droughts in the basin. This demonstrates that 10-day scale data can finely capture short-term variations in drought features, providing more precise information for drought monitoring and assessment.
- (2)
- Wavelet analysis based on 10-day scale data reveals a high degree of alignment between the significant cycles of the drought indices in the Jiaojiang River Basin and ENSO events, indicating a strong response relationship. Moreover, this influence varies across different time scales. This highlights the ability of 10-day scale data to more precisely characterize the dynamic associations between drought indices and ENSO events at various time scales.
- (3)
- Analysis using 10-day scale data shows significant differences in drought characteristics of the Jiaojiang River Basin during different ENSO periods. The influence of ENSO on wet-dry variations in the basin is particularly strong during El Niño and La Niña periods. This underscores the advantage of 10-day scale data in revealing short-term changes and extreme conditions of drought events.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rezaei, A. Ocean-Atmosphere Circulation Controls on Integrated Meteorological and Agricultural Drought over Iran. J. Hydrol. 2021, 603, 126928. [Google Scholar] [CrossRef]
- Gan, R.; Li, D.; Chen, C.; Yang, F.; Ma, X. Impacts of Climate Change on Extreme Precipitation in the Upstream of Chushandian Reservoir, China. Hydrol. Res. 2022, 53, 504–518. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S.; Du, M.; Chen, Q.; He, C.; Zhang, J.; Zhu, Y.; Gong, Y. The Influence of ENSO and MJO on Drought in Different Ecological Geographic Regions in China. Remote Sens. 2021, 13, 875. [Google Scholar] [CrossRef]
- Yang, B.; Kong, L.; Lai, C.; Huang, D.; Cheng, X. A Framework on Analyzing Long-Term Drought Changes and Its Influential Factors Based on the PDSI. Atmosphere 2022, 13, 1151. [Google Scholar] [CrossRef]
- Yan, Y.; Mao, K.; Shen, X.; Cao, M.; Xu, T.; Guo, Z.; Bao, Q. Evaluation of the Influence of ENSO on Tropical Vegetation in Long Time Series Using a New Indicator. Ecol. Indic. 2021, 129, 107872. [Google Scholar] [CrossRef]
- Sun, B.; Wang, H.; Li, H.; Zhou, B.; Duan, M.; Li, H. A Long-Lasting Precipitation Deficit in South China During Autumn-Winter 2020/2021: Combined Effect of ENSO and Arctic Sea Ice. J. Geophys. Res. Atmos. 2022, 127, e2021JD035584. [Google Scholar] [CrossRef]
- Xing, Z.; Wei, J.; Li, Y.; Zhang, X.; Ma, M.; Yi, P.; Ju, Q.; Laux, P.; Kunstmann, H. Disentangling the Spatially Combined and Temporally Lagged Influences of Climate Oscillations on Seasonal Droughts in the East Asian Monsoon Influenced Poyang Lake Basin. Atmos. Res. 2024, 310, 107603. [Google Scholar] [CrossRef]
- Wongchuig, S.; Kitambo, B.; Papa, F.; Paris, A.; Fleischmann, A.S.; Gal, L.; Boucharel, J.; Paiva, R.; Oliveira, R.J.; Tshimanga, R.M.; et al. Improved Modeling of Congo’s Hydrology for Floods and Droughts Analysis and ENSO Teleconnections. J. Hydrol. Reg. Stud. 2023, 50, 101563. [Google Scholar] [CrossRef]
- Nurdiati, S.; Sopaheluwakan, A.; Septiawan, P. Joint Pattern Analysis of Forest Fire and Drought Indicators in Southeast Asia Associated with ENSO and IOD. Atmosphere 2022, 13, 1198. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, J.; Zhou, L.; Xie, B.; Zhou, J.; Li, C. Comparative Evaluation of Drought Indices for Monitoring Drought Based on Remote Sensing Data. Environ. Sci. Pollut. Res. 2021, 28, 20408–20425. [Google Scholar] [CrossRef]
- Zhu, Z.; Duan, W.; Zou, S.; Zeng, Z.; Chen, Y.; Feng, M.; Qin, J.; Liu, Y. Spatiotemporal Characteristics of Meteorological Drought Events in 34 Major Global River Basins during 1901–2021. Sci. Total Environ. 2024, 921, 170913. [Google Scholar] [CrossRef] [PubMed]
- Uddin, M.J.; Hu, J.; Islam, A.R.M.T.; Eibek, K.U.; Nasrin, Z.M. A Comprehensive Statistical Assessment of Drought Indices to Monitor Drought Status in Bangladesh. Arab. J. Geosci. 2020, 13, 323. [Google Scholar] [CrossRef]
- Vilanova, R.S.; Delgado, R.C.; Frossard De Andrade, C.; Lopes Dos Santos, G.; Magistrali, I.C.; Moreira De Oliveira, C.M.; Teodoro, P.E.; Capristo Silva, G.F.; Silva Junior, C.A.D.; De Ávila Rodrigues, R. Vegetation Degradation in ENSO Events: Drought Assessment, Soil Use and Vegetation Evapotranspiration in the Western Brazilian Amazon. Remote Sens. Appl. Soc. Environ. 2021, 23, 100531. [Google Scholar] [CrossRef]
- Ullah, I.; Ma, X.; Ren, G.; Yin, J.; Iyakaremye, V.; Syed, S.; Lu, K.; Xing, Y.; Singh, V.P. Recent Changes in Drought Events over South Asia and Their Possible Linkages with Climatic and Dynamic Factors. Remote Sens. 2022, 14, 3219. [Google Scholar] [CrossRef]
- Toledo, N.; Moulatlet, G.; Gaona, G.; Valencia, B.; Hirata, R.; Conicelli, B. Dynamics of Meteorological and Hydrological Drought: The Impact of Groundwater and El Niño Events on Forest Fires in the Amazon. Sci. Total Environ. 2024, 954, 176612. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Li, H.; Fan, Y.; Meng, Z.; Liu, D.; Pan, S. Optimization of Water Quantity Allocation in Multi-Source Urban Water Supply Systems Using Graph Theory. Water 2025, 17, 61. [Google Scholar] [CrossRef]
- Sun, H.; Liu, X.; Mao, X.; Jia, W.; Herzschuh, U. Centennial-Scale Variability of the Indian Summer Monsoon during the Middle to Late Holocene and Its Links with ENSO Activity. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2023, 612, 111380. [Google Scholar] [CrossRef]
- Abdelkader, M.; Yerdelen, C. Hydrological Drought Variability and Its Teleconnections with Climate Indices. J. Hydrol. 2022, 605, 127290. [Google Scholar] [CrossRef]
- Suhana, L.; Tan, M.L.; Luhaim, Z.; Ramli, M.H.P.; Subki, N.S.; Tangang, F.; Ishak, A.M. Spatiotemporal Characteristics of Hydrometeorological Droughts and Their Connections to Large-Scale Atmospheric Circulations in the Kelantan River Basin, Malaysia. Water Supply 2023, 23, 2283–2298. [Google Scholar] [CrossRef]
- Gimenez, B.O.; Souza, D.C.; Higuchi, N.; Negrón-Juárez, R.I.; Sampaio-Filho, I.D.J.; Araújo, A.C.; Lima, A.J.N.; Fontes, C.G.; Jardine, K.J.; Koven, C.D.; et al. Hysteresis Area at the Canopy Level during and after a Drought Event in the Central Amazon. Agric. For. Meteorol. 2024, 353, 110052. [Google Scholar] [CrossRef]
- Dixit, S.; Jayakumar, K.V. A Study on Copula-Based Bivariate and Trivariate Drought Assessment in Godavari River Basin and the Teleconnection of Drought with Large-Scale Climate Indices. Theor. Appl. Climatol. 2021, 146, 1335–1353. [Google Scholar] [CrossRef]
- Restrepo-Coupe, N.; O’Donnell Christoffersen, B.; Longo, M.; Alves, L.F.; Campos, K.S.; Da Araujo, A.C.; De Oliveira, R.C.; Prohaska, N.; Da Silva, R.; Tapajos, R.; et al. Asymmetric Response of Amazon Forest Water and Energy Fluxes to Wet and Dry Hydrological Extremes Reveals Onset of a Local Drought-Induced Tipping Point. Glob. Change Biol. 2023, 29, 6077–6092. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Wei, S.; Liu, D.; Qin, T.; Xu, F.; Wu, C.; Liu, G.; Cheng, Y. Impact of ENSO Events on Meteorological Drought in the Weihe River Basin, China. Front. Earth Sci. 2023, 11, 1093632. [Google Scholar] [CrossRef]
- Najib, M.K.; Nurdiati, S.; Sopaheluwakan, A. Copula-Based Joint Distribution Analysis of the ENSO Effect on the Drought Indicators over Borneo Fire-Prone Areas. Model. Earth Syst. Environ. 2022, 8, 2817–2826. [Google Scholar] [CrossRef]
- Huang, C.; Durán, S.M.; Hu, K.; Li, H.; Swenson, N.G.; Enquist, B.J. Remotely Sensed Assessment of Increasing Chronic and Episodic Drought Effects on a Costa Rican Tropical Dry Forest. Ecosphere 2021, 12, e03824. [Google Scholar] [CrossRef]
- Nguyen, T.-T.-H.; Li, M.-H.; Vu, T.M.; Chen, P.-Y. Multiple Drought Indices and Their Teleconnections with ENSO in Various Spatiotemporal Scales over the Mekong River Basin. Sci. Total Environ. 2023, 854, 158589. [Google Scholar] [CrossRef]
- Alemaw, B.F. The Recent Droughts of 2019/20 in Southern Africa and Its Teleconnection with ENSO Events. Atmos. Clim. Sci. 2022, 12, 246–263. [Google Scholar] [CrossRef]
- Hernández-López, J.A.; Puerta-Cortés, D.X.; Andrade, H.J. Predictive Analysis of Adaptation to Drought of Farmers in the Central Zone of Colombia. Sustainability 2024, 16, 7210. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Xu, Y.-P.; Teegavarapu, R.S.V.; Guo, Y.; Nie, H.; Xie, H.; Zhang, L. River Ecological Flow Early Warning Forecasting Using Baseflow Separation and Machine Learning in the Jiaojiang River Basin, Southeast China. Sci. Total Environ. 2023, 882, 163571. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, H.; Liu, Y.; Liu, W.; Wei, F.; Yang, C.; Ding, F.; Ye, J.; Nie, H.; Du, Y.; et al. Assessment of Hydrological and Meteorological Composite Drought Characteristics Based on Baseflow and Precipitation. Water 2024, 16, 1466. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, Y.; Zhao, Y.; Hu, H. Analysis of Drought and Flood Variations on a 200-Year Scale Based on Historical Environmental Information in Western China. Int. J. Environ. Res. Public Health 2022, 19, 2771. [Google Scholar] [CrossRef] [PubMed]
- Delcroix, T.; Michel, S.L.L.; Swingedouw, D.; Malaizé, B.; Daniau, A.-L.; Abarca-del-Rio, R.; Caley, T.; Sémah, A.-M. Clarifying the Role of ENSO on Easter Island Precipitation Changes: Potential Environmental Implications for the Last Millennium. Paleoceanogr. Paleoclimatology 2022, 37, e2022PA004514. [Google Scholar] [CrossRef]
- Gutierrez-Villarreal, R.A.; Espinoza, J.-C.; Lavado-Casimiro, W.; Junquas, C.; Molina-Carpio, J.; Condom, T.; Marengo, J.A. The 2022-23 Drought in the South American Altiplano: ENSO Effects on Moisture Flux in the Western Amazon during the Pre-Wet Season. Weather Clim. Extrem. 2024, 45, 100710. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, K.; Li, Z.; Liu, Y.; Yao, Y. A Novel ENSO Monitoring Index and Its Potential for Drought Application. J. Atmos. Sol. Terr. Phys. 2021, 225, 105762. [Google Scholar] [CrossRef]
- Afshar, M.H.; Bulut, B.; Duzenli, E.; Amjad, M.; Yilmaz, M.T. Global Spatiotemporal Consistency between Meteorological and Soil Moisture Drought Indices. Agric. For. Meteorol. 2022, 316, 108848. [Google Scholar] [CrossRef]
- Salimi, H.; Asadi, E.; Darbandi, S. Meteorological and Hydrological Drought Monitoring Using Several Drought Indices. Appl. Water Sci. 2021, 11, 11. [Google Scholar] [CrossRef]
- Muthuvel, D.; Amai, M. Multivariate Analysis of Concurrent Droughts and Their Effects on Kharif Crops-A Copula-Based Approach. Int. J. Climatol. 2022, 42, 2773–2794. [Google Scholar] [CrossRef]
- Perez Arango, J.D.; Lintner, B.R.; Carvalho, L.M.V.; Lyon, B. Spatial Extents of Tropical Droughts During El Niño in Current and Future Climate in Observations, Reanalysis, and CMIP5 Models. Geophys. Res. Lett. 2021, 48, e2021GL093701. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Qiu, H.; Huang, S.; Teegavarapu, R.S.V.; Xu, Y.-P.; Guo, Y.; Nie, H.; Xie, H. Adaptive assessment of reservoir scheduling to hydrometeorological comprehensive dry and wet condition evolution in a multi-reservoir region of southeastern China. J. Hydrol. 2025, 648, 132392. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, X.; Cheng, X.; Gun, Z.; Lin, J.; Zhao, J.; Yao, L.; Zhou, C. Drought Assessment of China in 2002–2017 Based on a Comprehensive Drought Index. Agric. For. Meteorol. 2022, 319, 108922. [Google Scholar] [CrossRef]
- Ma, Y.; Sun, J.; Dong, T.; Yu, W.; Dong, W. More Profound Impact of CP ENSO on Australian Spring Rainfall in Recent Decades. Clim. Dyn. 2023, 60, 3065–3079. [Google Scholar] [CrossRef]
- Coughlan De Perez, E.; Anderson, W.; Han, E.; Masukwedza, G.I.T.; Mphonyane, N. Detectable Use of ENSO Information on Crop Production in Southern Africa. Clim. Serv. 2024, 36, 100514. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, P.; Min, S.; Kim, Y. Combined Impacts of the El Niño-Southern Oscillation and Pacific Decadal Oscillation on Global Droughts Assessed Using the Standardized Precipitation Evapotranspiration Index. Int. J. Climatol. 2021, 41, E1645–E1662. [Google Scholar] [CrossRef]
- Henchiri, M.; Igbawua, T.; Javed, T.; Bai, Y.; Zhang, S.; Essifi, B.; Ujoh, F.; Zhang, J. Meteorological Drought Analysis and Return Periods over North and West Africa and Linkage with El Niño–Southern Oscillation (ENSO). Remote Sens. 2021, 13, 4730. [Google Scholar] [CrossRef]
- Chen, H.; Huang, S.; Xu, Y.-P.; Teegavarapu, R.S.V.; Guo, Y.; Nie, H.; Xie, H. Using Baseflow Ensembles for Hydrologic Hysteresis Characterization in Humid Basins of Southeastern China. Water Resour. Res. 2024, 60, e2023WR036195. [Google Scholar] [CrossRef]
- Singh, J.; Ashfaq, M.; Skinner, C.B.; Anderson, W.B.; Mishra, V.; Singh, D. Enhanced Risk of Concurrent Regional Droughts with Increased ENSO Variability and Warming. Nat. Clim. Change 2022, 12, 163–170. [Google Scholar] [CrossRef]
- Higgins, P.A.; Palmer, J.G.; Andersen, M.S.; Turney, C.S.M.; Johnson, F. Extreme Events in the Multi-Proxy South Pacific Drought Atlas. Clim. Change 2023, 176, 105. [Google Scholar] [CrossRef]
- Faiz, M.A.; Zhang, Y.; Zhang, X.; Ma, N.; Aryal, S.K.; Ha, T.T.V.; Baig, F.; Naz, F. A Composite Drought Index Developed for Detecting Large-Scale Drought Characteristics. J. Hydrol. 2022, 605, 127308. [Google Scholar] [CrossRef]
- Waseem, M.; Ajmal, M.; Kim, T.-W. Development of a New Composite Drought Index for Multivariate Drought Assessment. J. Hydrol. 2015, 527, 30–37. [Google Scholar] [CrossRef]
- Villatoro-Sánchez, M.; Le Bissonnais, Y.; Moussa, R.; Rapidel, B. Temporal Dynamics of Runoff and Soil Loss on a Plot Scale under a Coffee Plantation on Steep Soil (Ultisol), Costa Rica. J. Hydrol. 2015, 523, 409–426. [Google Scholar] [CrossRef]
- Zhu, M.; Yu, D.; Yu, Y.; Zheng, Y.; Li, S.; Cai, X.; Chen, N. ENSO Enhances Seasonal River Discharge Instability and Water Resource Allocation Pressure. Water Resour. Res. 2025, 61, e2023WR036965. [Google Scholar] [CrossRef]
- Wang, M.; Chen, Y.; Li, J.; Zhao, Y. Spatiotemporal Evolution and Driving Force Analysis of Drought Characteristics in the Yellow River Basin. Ecol. Indic. 2025, 170, 113007. [Google Scholar] [CrossRef]
- Fan, F.; Lin, R.; Fang, X.; Xue, F.; Zheng, F.; Zhu, J. Influence of the Eastern Pacific and Central Pacific Types of ENSO on the South Asian Summer Monsoon. Adv. Atmos. Sci. 2021, 38, 12–28. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Zhao, W.; Liu, Y. The Increasing Contribution of Potential Evapotranspiration to Severe Droughts in the Yellow River Basin. J. Hydrol. 2022, 605, 127310. [Google Scholar] [CrossRef]
- Piao, J.; Chen, W.; Chen, S.; Gong, H.; Chen, X.; Liu, B. The Intensified Impact of El Niño on Late-Summer Precipitation over East Asia since the Early 1990s. Clim. Dyn. 2020, 54, 4793–4809. [Google Scholar] [CrossRef]
- Yue, Y.; Liu, H.; Mu, X.; Qin, M.; Wang, T.; Wang, Q.; Yan, Y. Spatial and Temporal Characteristics of Drought and Its Correlation with Climate Indices in Northeast China. PLoS ONE 2021, 16, e0259774. [Google Scholar] [CrossRef]
- Tozer, C.R.; Risbey, J.S.; Monselesan, D.P.; Pook, M.J.; Irving, D.; Ramesh, N.; Reddy, J.; Squire, D.T. Impacts of ENSO on Australian Rainfall: What Not to Expect. J. South. Hemisph. Earth Syst. Sci. 2023, 73, 77–81. [Google Scholar] [CrossRef]
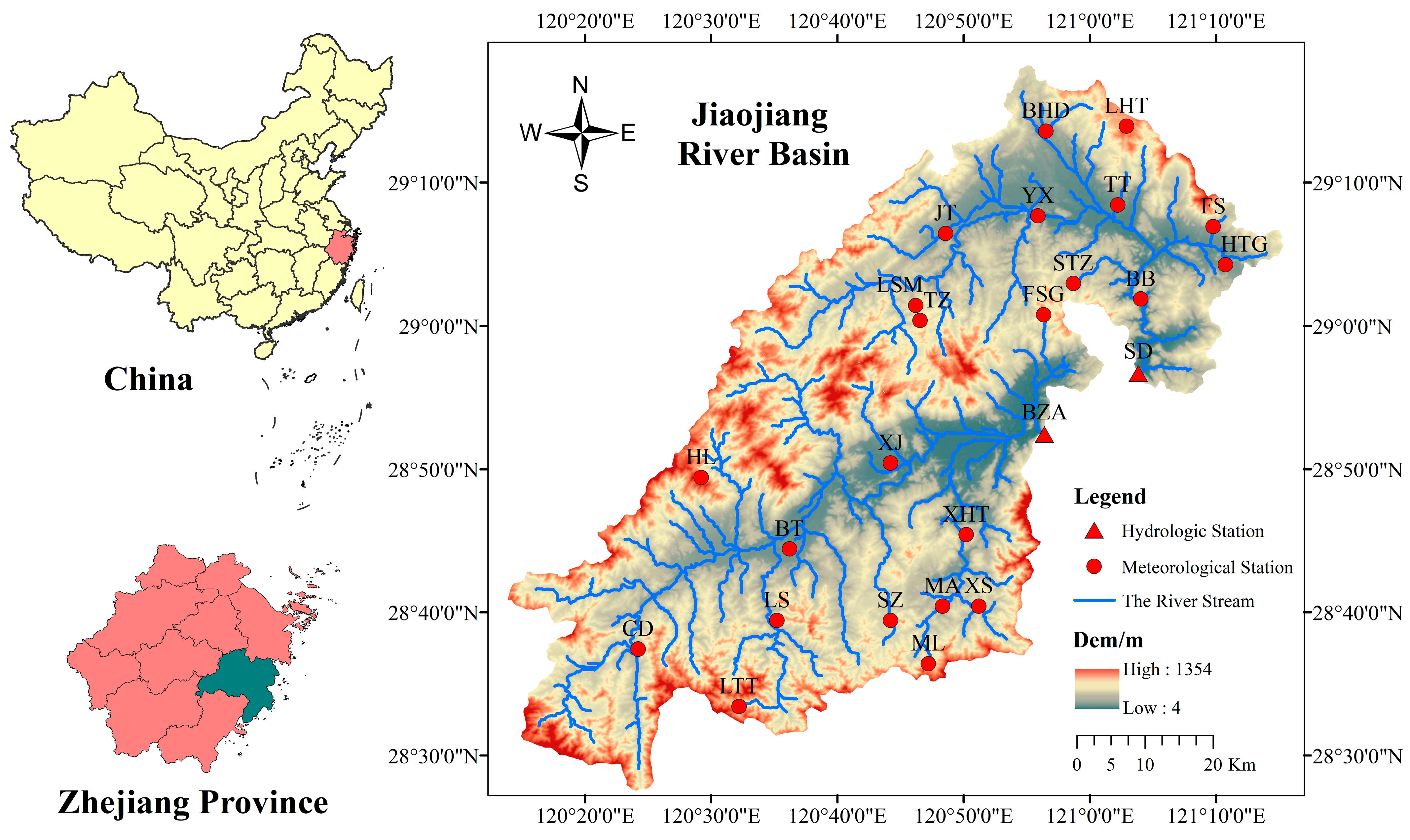





| Sub -Basin | Stations | Longitude (°E) | Latitude (°N) | Sub -Basin | Stations | Longitude (°E) | Latitude (°N) |
|---|---|---|---|---|---|---|---|
| Shifeng-xi | Shaduan (SD) | 121.06 | 28.95 | Yong’an -xi | Baizhiao(BZA) | 120.94 | 28.88 |
| Caodian (CD) | 120.40 | 28.63 | Fengshugang (FSG) | 120.94 | 29.02 | ||
| Hengliao (HL) | 120.48 | 28.83 | Jietou (JT) | 120.81 | 29.12 | ||
| Linshan (LS) | 120.58 | 28.67 | Lishimen (LSM) | 120.77 | 29.03 | ||
| Longtantou (LTT) | 120.53 | 28.57 | Tiantai Yanxia (YX) | 120.93 | 29.14 | ||
| Baita (BT) | 120.60 | 28.75 | Tianzhu (TZ) | 120.77 | 29.02 | ||
| Shangzhang (SZ) | 120.73 | 28.67 | Baihedian (BHD) | 120.94 | 29.24 | ||
| Xianju (XJ) | 120.73 | 28.85 | Feishu (FS) | 121.16 | 29.12 | ||
| Xianju Mei’ao (MA) | 120.80 | 28.68 | Hutanggang (HTG) | 121.18 | 29.08 | ||
| Xiahuitou (XHT) | 120.83 | 28.77 | Longhuangtang (LHT) | 121.05 | 29.24 | ||
| Xishang (XS) | 120.85 | 28.68 | Shantouzheng (STZ) | 120.97 | 29.06 | ||
| Miaoliao (ML) | 120.78 | 28.62 |
| El Niño | La Niña | ||||||
|---|---|---|---|---|---|---|---|
| Serial Number | Start Time | End Time | Intensity | Serial Number | Start Time | End Time | Intensity |
| 1 | 1991.5 | 1992.6 | strong | 1 | 1995.9 | 1996.3 | weak |
| 2 | 1994.9 | 1995.3 | weak | 2 | 1998.7 | 2000.6 | medium |
| 3 | 1997.5 | 1998.5 | superstrong | 3 | 2000.10 | 2001.2 | weak |
| 4 | 2002.6 | 2003.2 | medium | 4 | 2007.8 | 2008.5 | medium |
| 5 | 2004.7 | 2005.2 | weak | 5 | 2010.6 | 2011.5 | medium |
| 6 | 2006.9 | 2007.1 | weak | 6 | 2011.8 | 2012.3 | weak |
| 7 | 2009.7 | 2010.3 | medium | 7 | 2017.10 | 2018.4 | weak |
| 8 | 2014.10 | 2016.4 | superstrong | 8 | 2020.8 | 2020.12 | medium |
| 9 | 2018.9 | 2019.6 | weak | ||||
| Value | Drought Level |
|---|---|
| Light drought | |
| Moderate drought | |
| Severe drought | |
| Extreme drought |
| Station | SPI-CDI | SRI-CDI | SPI-SRI |
|---|---|---|---|
| BZA | 0.8966 | 0.8597 | 0.5988 |
| SD | 0.8764 | 0.8586 | 0.5619 |
| Station | Drought Index | Trend | ||
|---|---|---|---|---|
| BZA | CDI | 1 | 2.4093 | Significantly becoming moist |
| SPI | 0 | 1.6285 | No significant changes | |
| SRI | 0 | 2.6856 | No significant changes | |
| SD | CDI | 0 | −0.8835 | No significant changes |
| SPI | 1 | 1.7365 | Slightly becoming moist | |
| SRI | −1 | −2.0789 | Significantly becoming drought |
| Index | Station | Period | Mean | Median | Maximum | Minimum | Standard Deviation | Variance |
|---|---|---|---|---|---|---|---|---|
| CDI | BZA | El Niño | −0.388 | −0.526 | 2.296 | −2.937 | 1.019 | 1.038 |
| La Niña | −0.601 | −0.760 | 2.980 | −3.058 | 0.954 | 0.910 | ||
| Normal | −0.583 | −0.650 | 2.470 | −3.376 | 0.959 | 0.920 | ||
| SD | El Niño | −0.388 | −0.414 | 2.400 | −3.995 | 1.025 | 1.050 | |
| La Niña | −0.623 | −0.701 | 3.009 | −2.821 | 0.978 | 0.957 | ||
| Normal | −0.600 | −0.669 | 2.582 | −3.309 | 0.965 | 0.931 | ||
| SPI | BZA | El Niño | 0.120 | 0.171 | 2.380 | −2.666 | 1.007 | 1.014 |
| La Niña | −0.009 | −0.050 | 3.690 | −2.462 | 0.978 | 0.956 | ||
| Normal | −0.028 | 0.004 | 3.175 | −2.999 | 0.974 | 0.948 | ||
| SD | El Niño | 0.144 | 0.198 | 2.481 | −3.840 | 1.004 | 1.008 | |
| La Niña | −0.026 | 0.042 | 3.641 | −2.675 | 0.991 | 0.982 | ||
| Normal | −0.019 | 0.022 | 3.259 | −3.054 | 0.966 | 0.932 | ||
| SRI | BZA | El Niño | 0.173 | 0.025 | 3.279 | −1.770 | 1.062 | 1.128 |
| La Niña | −0.091 | −0.317 | 3.057 | −2.060 | 1.000 | 0.999 | ||
| Normal | −0.084 | −0.257 | 3.077 | −1.831 | 0.941 | 0.885 | ||
| SD | El Niño | 0.176 | 0.026 | 3.502 | −2.281 | 1.056 | 1.116 | |
| La Niña | −0.089 | −0.191 | 3.041 | −2.565 | 0.973 | 0.946 | ||
| Normal | −0.072 | −0.136 | 3.168 | −2.268 | 0.963 | 0.926 |
| Period | Time Effect | BZA | SD | ||||
|---|---|---|---|---|---|---|---|
| CDI | SPI | SRI | CDI | SPI | SRI | ||
| El Niño | No | 0 | 0 | 1 | 0 | 0 | 1 |
| Lag | 0 | 1 | 0 | 0 | 1 | 1 | |
| Accumulation | 0 | 0 | 0 | 0 | 0 | 0 | |
| Lag and accumulation | 9 | 8 | 8 | 9 | 8 | 7 | |
| La Niña | No | 0 | 0 | 0 | 0 | 0 | 0 |
| Lag | 0 | 0 | 0 | 0 | 0 | 1 | |
| Accumulation | 1 | 1 | 1 | 1 | 0 | 1 | |
| Lag and accumulation | 7 | 7 | 7 | 7 | 8 | 6 | |
| Normal | No | 0 | 0 | 0 | 0 | 0 | 0 |
| Lag | 0 | 0 | 1 | 0 | 0 | 1 | |
| Accumulation | 0 | 1 | 0 | 0 | 0 | 1 | |
| Lag and accumulation | 10 | 9 | 9 | 10 | 10 | 8 | |
| Period | Time Effect | Statistical Indicator | BZA | SD | ||||
|---|---|---|---|---|---|---|---|---|
| CDI | SPI | SRI | CDI | SPI | SRI | |||
| El Niño | Lag | Mean | 19 | 21 | 17 | 21 | 20 | 17 |
| Standard deviation | 9 | 9 | 12 | 11 | 11 | 11 | ||
| Accumulation | Mean | 16 | 13 | 16 | 15 | 13 | 16 | |
| Standard deviation | 10 | 11 | 8 | 13 | 11 | 7 | ||
| La Niña | Lag | Mean | 9 | 12 | 11 | 13 | 10 | 12 |
| Standard deviation | 10 | 7 | 12 | 13 | 8 | 12 | ||
| Accumulation | Mean | 12 | 14 | 12 | 11 | 8 | 11 | |
| Standard deviation | 10 | 10 | 10 | 10 | 7 | 8 | ||
| Normal | Lag | Mean | 16 | 18 | 15 | 11 | 14 | 12 |
| Standard deviation | 9 | 8 | 11 | 10 | 8 | 9 | ||
| Accumulation | Mean | 10 | 10 | 12 | 12 | 11 | 15 | |
| Standard deviation | 10 | 9 | 11 | 9 | 7 | 10 | ||
| Station | Period | Index | The Frequency of Different Types of Droughts | The Frequency of Different Levels of Droughts | Average Drought Intensity | Average Drought Duration | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Independent Drought | Subordinate Drought | Light Drought | Moderate Drought | Severe Drought | Extreme Drought | |||||
| BZA | El Niño | CDI | 13 | 9 | 18 | 1 | 2 | 1 | −0.91 | 8.36 |
| SPI | 12 | 21 | 18 | 7 | 5 | 3 | −1.41 | 3.36 | ||
| SRI | 5 | 16 | 10 | 6 | 2 | 3 | −1.64 | 5.24 | ||
| La Niña | CDI | 7 | 4 | 10 | 1 | 0 | 4 | −1.77 | 17.18 | |
| SPI | 13 | 13 | 14 | 5 | 2 | 5 | −1.59 | 4.50 | ||
| SRI | 8 | 11 | 12 | 2 | 3 | 4 | −1.96 | 6.32 | ||
| Normal | CDI | 26 | 9 | 30 | 3 | 2 | 0 | −0.72 | 11.86 | |
| SPI | 34 | 26 | 41 | 11 | 5 | 3 | −0.84 | 4.10 | ||
| SRI | 18 | 31 | 27 | 12 | 3 | 7 | −0.92 | 5.29 | ||
| SD | El Niño | CDI | 13 | 5 | 15 | 1 | 2 | 0 | −0.93 | 10.22 |
| SPI | 14 | 18 | 17 | 6 | 7 | 2 | −0.89 | 3.00 | ||
| SRI | 5 | 10 | 8 | 4 | 1 | 2 | −0.99 | 6.33 | ||
| La Niña | CDI | 11 | 5 | 9 | 2 | 2 | 3 | −1.19 | 13.25 | |
| SPI | 13 | 13 | 13 | 5 | 4 | 4 | −1.17 | 4.62 | ||
| SRI | 6 | 7 | 7 | 2 | 3 | 1 | −1.29 | 8.23 | ||
| Normal | CDI | 22 | 10 | 27 | 4 | 1 | 0 | −0.86 | 10.88 | |
| SPI | 34 | 22 | 40 | 8 | 4 | 4 | −0.83 | 4.59 | ||
| SRI | 18 | 25 | 22 | 13 | 5 | 3 | −1.02 | 5.65 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, H.; Chen, H.; Chen, Y.; Xu, C.; Guo, Y.; Huang, S.; Nie, H.; Xie, H. Response of the Evolution of Basin Hydrometeorological Drought to ENSO: A Case Study of the Jiaojiang River Basin in Southeast China. Sustainability 2025, 17, 2616. https://doi.org/10.3390/su17062616
Qiu H, Chen H, Chen Y, Xu C, Guo Y, Huang S, Nie H, Xie H. Response of the Evolution of Basin Hydrometeorological Drought to ENSO: A Case Study of the Jiaojiang River Basin in Southeast China. Sustainability. 2025; 17(6):2616. https://doi.org/10.3390/su17062616
Chicago/Turabian StyleQiu, He, Hao Chen, Yijing Chen, Chuyu Xu, Yuxue Guo, Saihua Huang, Hui Nie, and Huawei Xie. 2025. "Response of the Evolution of Basin Hydrometeorological Drought to ENSO: A Case Study of the Jiaojiang River Basin in Southeast China" Sustainability 17, no. 6: 2616. https://doi.org/10.3390/su17062616
APA StyleQiu, H., Chen, H., Chen, Y., Xu, C., Guo, Y., Huang, S., Nie, H., & Xie, H. (2025). Response of the Evolution of Basin Hydrometeorological Drought to ENSO: A Case Study of the Jiaojiang River Basin in Southeast China. Sustainability, 17(6), 2616. https://doi.org/10.3390/su17062616







