A Novel Sensitivity Analysis Framework for Quantifying Permafrost Impacts on Runoff Variability in the Yangtze River Source Region
Abstract
1. Introduction
2. Materials and Methods
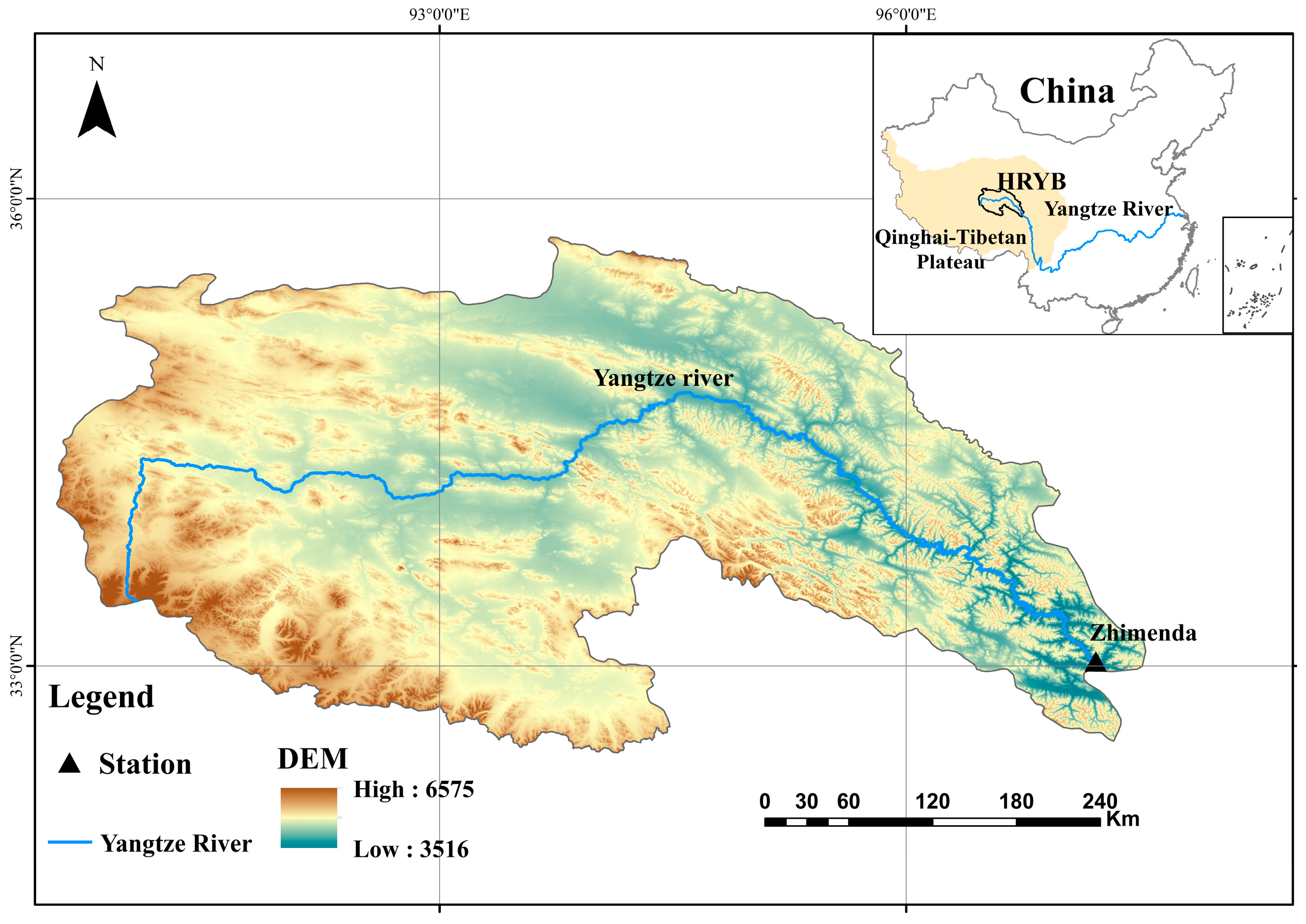
2.1. Study Area
2.2. Data
2.3. Methodology
2.3.1. Trend Analysis and Breakpoint Test
- TFPW-MK
- 2.
- Sliding t-Test method
2.3.2. Elasticity of Runoff Derived from the Budyko Function
- Yang’s function:
- Fu’s function:
2.3.3. Quantitative Contribution of Variables to Changes in Runoff
2.3.4. Sensitivity Analysis of Runoff Changes to Permafrost Characteristic Variation
3. Results
3.1. Analysis of Variable Trends
3.1.1. Hydrometeorological Variables
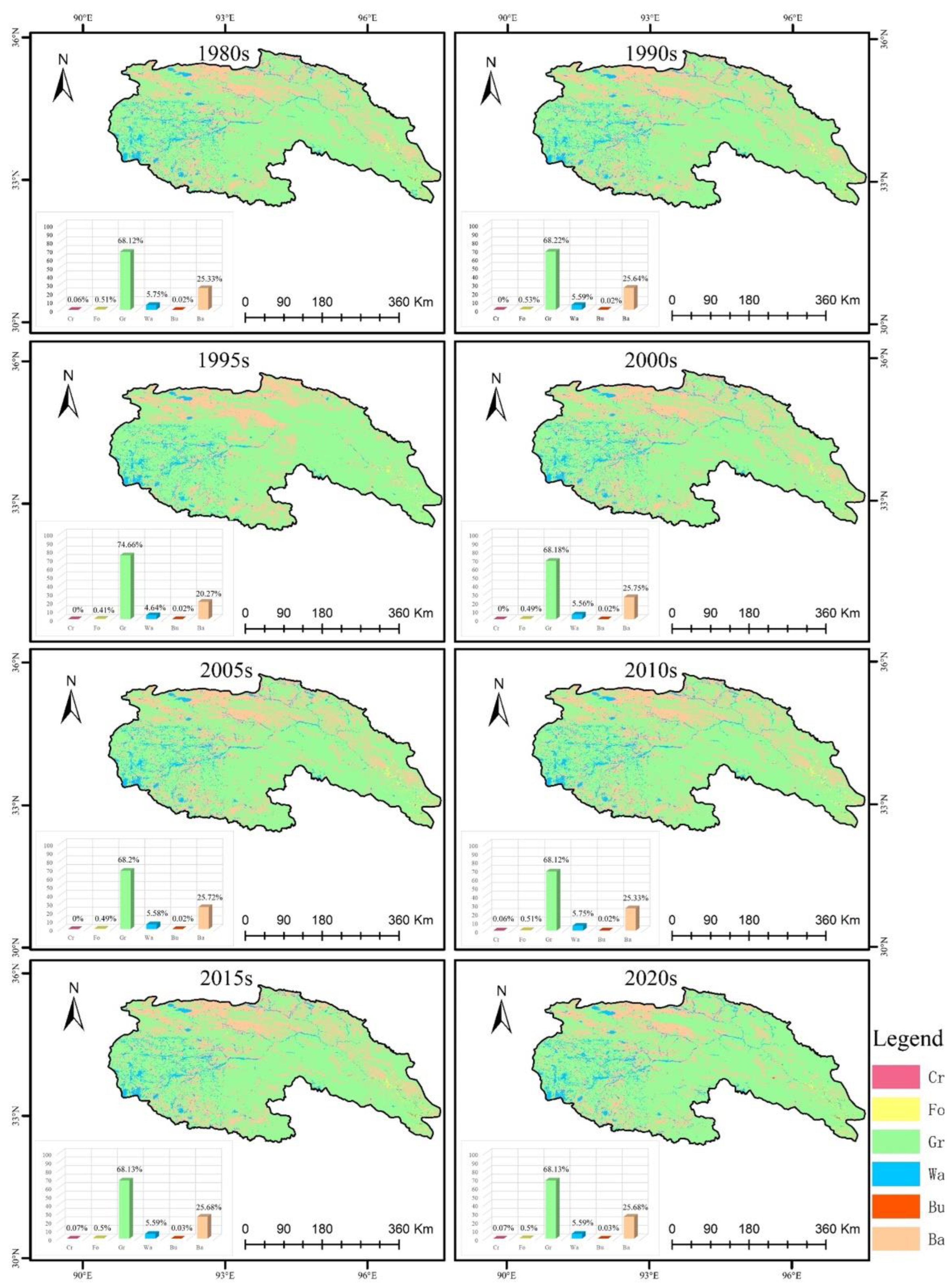
3.1.2. Land Use and Land Cover Changes
3.2. Breakpoint Detection and Water–Energy Balance Analysis
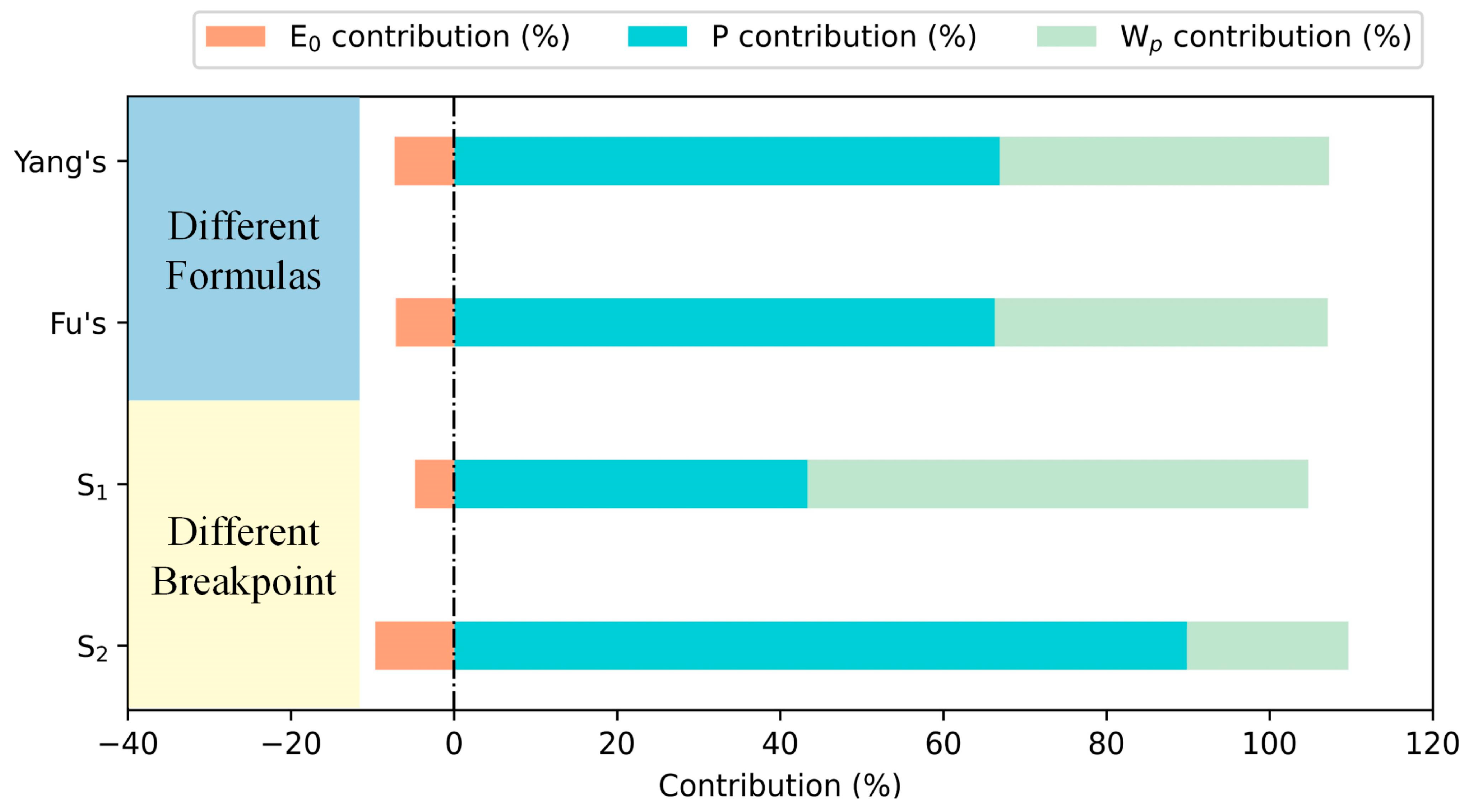
3.3. The Runoff Difference Resulting from Climate and Catchment Changes for Each Sub-Period
3.4. Relationship Between RWp and Permafrost Characteristic Changes
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Duan, A.; Xiao, Z. Does the climate warming hiatus exist over the Tibetan Plateau? Sci. Rep. 2015, 5, 13711. [Google Scholar] [CrossRef] [PubMed]
- Yao, T.; Liu, X.; Wang, N.; Shi, Y. Amplitude of climatic changes in Qinghai-Tibetan Plateau. Chin. Sci. Bull. 2000, 45, 1236–1243. [Google Scholar] [CrossRef]
- Hu, J.; Wu, Y.; Sun, P.; Zhao, F.; Sun, K.; Li, T.; Sivakumar, B.; Qiu, L.; Sun, Y.; Jin, Z. Predicting long-term hydrological change caused by climate shifting in the 21st century in the headwater area of the Yellow River Basin. Stoch. Environ. Res. Risk Assess. 2022, 36, 1651–1668. [Google Scholar] [CrossRef]
- Yang, J.; Wang, T.; Yang, D.; Yang, Y. Insights into runoff changes in the source region of Yellow River under frozen ground degradation. J. Hydrol. 2023, 617, 128892. [Google Scholar] [CrossRef]
- Jin, H.; Huang, Y.; Bense, V.F.; Ma, Q.; Marchenko, S.S.; Shepelev, V.V.; Hu, Y.; Liang, S.; Spektor, V.V.; Jin, X.; et al. Permafrost Degradation and Its Hydrogeological Impacts. Water 2022, 14, 372. [Google Scholar] [CrossRef]
- Jin, H.; Ma, Q. Impacts of Permafrost Degradation on Carbon Stocks and Emissions under a Warming Climate: A Review. Atmosphere 2021, 12, 1425. [Google Scholar] [CrossRef]
- Schuur, E.A.G.; McGuire, A.D.; Schädel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M.; et al. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. Simulation of permafrost and seasonally frozen ground conditions on the Tibetan Plateau, 1981–2010. J. Geophys. Res. Atmos. 2013, 118, 5216–5230. [Google Scholar] [CrossRef]
- Luo, D.; Wu, Q.; Jin, H.; Marchenko, S.S.; Lü, L.; Gao, S. Recent changes in the active layer thickness across the northern hemisphere. Environ. Earth Sci. 2016, 75, 555. [Google Scholar] [CrossRef]
- Zdanowicz, C.; Karlsson, P.; Beckholmen, I.; Roach, P.; Poulain, A.; Yumvihoze, E.; Martma, T.; Ryjkov, A.; Dastoor, A. Snowmelt, glacial and atmospheric sources of mercury to a subarctic mountain lake catchment, Yukon, Canada. Geochim. Cosmochim. Acta 2018, 238, 374–393. [Google Scholar] [CrossRef]
- Zipper, S.C.; Lamontagne-Hallé, P.; McKenzie, J.M.; Rocha, A.V. Groundwater Controls on Postfire Permafrost Thaw: Water and Energy Balance Effects. J. Geophys. Res. Earth Surf. 2018, 123, 2677–2694. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, J.; Wang, G.; Fu, G.; He, R.; Yan, X.; Jin, J.; Liu, Y.; Zhang, A. Attribution for decreasing streamflow of the Haihe River basin, northern China: Climate variability or human activities? J. Hydrol. 2012, 460–461, 117–129. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Separating the impacts of climate change and land surface alteration on runoff reduction in the Jing River catchment of China. Catena 2016, 147, 80–86. [Google Scholar] [CrossRef]
- Sinha, J.; Das, J.; Jha, S.; Goyal, M.K. Analysing model disparity in diagnosing the climatic and human stresses on runoff variability over India. J. Hydrol. 2020, 581, 124407. [Google Scholar] [CrossRef]
- Zhou, L.; Yang, Y.; Zhang, D.; Yao, H. Recent advances in hydrology studies under changing permafrost on the Qinghai-Xizang Plateau. Res. Cold Arid Reg. 2024, 16, 159–169. [Google Scholar] [CrossRef]
- Sun, X.; Dong, Q.; Zhang, X. Attribution analysis of runoff change based on Budyko-type model with time-varying parameters for the Lhasa River Basin, Qinghai–Tibet Plateau. J. Hydrol. Reg. Stud. 2023, 48, 101469. [Google Scholar] [CrossRef]
- Wang, W.; Shao, Q.; Yang, T.; Peng, S.; Xing, W.; Sun, F.; Luo, Y. Quantitative assessment of the impact of climate variability and human activities on runoff changes: A case study in four catchments of the Haihe River basin, China. Hydrol. Process. 2013, 27, 1158–1174. [Google Scholar] [CrossRef]
- Li, H.; Shi, C.; Zhang, Y.; Ning, T.; Sun, P.; Liu, X.; Ma, X.; Liu, W.; Collins, A.L. Using the Budyko hypothesis for detecting and attributing changes in runoff to climate and vegetation change in the soft sandstone area of the middle Yellow River basin, China. Sci. Total Environ. 2020, 703, 135588. [Google Scholar] [CrossRef]
- Xue, D.; Zhou, J.; Zhao, X.; Liu, C.; Wei, W.; Yang, X.; Li, Q.; Zhao, Y. Impacts of climate change and human activities on runoff change in a typical arid watershed, NW China. Ecol. Indic. 2021, 121, 107013. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Yong, B. Identification of dominant interactions between climatic seasonality, catchment characteristics and agricultural activities on Budyko-type equation parameter estimation. J. Hydrol. 2018, 556, 585–599. [Google Scholar] [CrossRef]
- Tan, X.; Jia, Y.; Yang, D.; Niu, C.; Hao, C. Impact ways and their contributions to vegetation-induced runoff changes in the Loess Plateau. J. Hydrol. Reg. Stud. 2024, 51, 101630. [Google Scholar] [CrossRef]
- Xu, X.; Liu, W.; Scanlon, B.R.; Zhang, L.; Pan, M. Local and global factors controlling water-energy balances within the Budyko framework. Geophys. Res. Lett. 2013, 40, 6123–6129. [Google Scholar] [CrossRef]
- Fu, B.P. On the calculation of the evaporation from land surface. Sci. Atmos. Sin. 1981, 5, 23. [Google Scholar]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. Res. 2008, 44, W03410. [Google Scholar] [CrossRef]
- Yang, Y.; Roderick, M.L.; Zhang, S.; McVicar, T.R.; Donohue, R.J. Hydrologic implications of vegetation response to elevated CO2 in climate projections. Nat. Clim. Change 2019, 9, 44–48. [Google Scholar] [CrossRef]
- Zhou, G.; Wei, X.; Chen, X.; Zhou, P.; Liu, X.; Xiao, Y.; Sun, G.; Scott, D.F.; Zhou, S.; Han, L.; et al. Global pattern for the effect of climate and land cover on water yield. Nat. Commun. 2015, 6, 5918. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Huang, Y.; Wang, G. The complementary relationship and generation of the Budyko functions. Geophys. Res. Lett. 2015, 42, 1781–1790. [Google Scholar] [CrossRef]
- Liang, W.; Bai, D.; Wang, F.; Fu, B.; Yan, J.; Wang, S.; Yang, Y.; Long, D.; Feng, M. Quantifying the impacts of climate change and ecological restoration on streamflow changes based on a Budyko hydrological model in China’s Loess Plateau. Water Resour. Res. 2015, 51, 6500–6519. [Google Scholar] [CrossRef]
- Wang, D.; Hejazi, M. Quantifying the relative contribution of the climate and direct human impacts on mean annual streamflow in the contiguous United States. Water Resour. Res. 2011, 47, W00J12. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, H.; Yang, D.; Jayawardena, A.W. Quantifying the effect of vegetation change on the regional water balance within the Budyko framework. Geophys. Res. Lett. 2016, 43, 1140–1148. [Google Scholar] [CrossRef]
- Mo, C.; Huang, K.; Ruan, Y.; Lai, S.; Lei, X. Quantifying uncertainty sources in runoff change attribution based on the Budyko framework. J. Hydrol. 2024, 630, 130790. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M.; Limbrunner, J.F. Climate elasticity of streamflow in the United States. Water Resour. Res. 2001, 37, 1771–1781. [Google Scholar] [CrossRef]
- Wang, W.; Zou, S.; Shao, Q.; Xing, W.; Chen, X.; Jiao, X.; Luo, Y.; Yong, B.; Yu, Z. The analytical derivation of multiple elasticities of runoff to climate change and catchment characteristics alteration. J. Hydrol. 2016, 541, 1042–1056. [Google Scholar] [CrossRef]
- Zheng, Y.; Huang, Y.; Zhou, S.; Wang, K.; Wang, G. Effect partition of climate and catchment changes on runoff variation at the headwater region of the Yellow River based on the Budyko complementary relationship. Sci. Total Environ. 2018, 643, 1166–1177. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, L.; Zhou, H.; Liu, S.; Liu, G.; Zou, D.; Du, E.; Hu, G.; Wang, C. Quantification of Water Released by Thawing Permafrost in the Source Region of the Yangtze River on the Tibetan Plateau by InSAR Monitoring. Water Resour. Res. 2023, 59, e2023WR034451. [Google Scholar] [CrossRef]
- Li, Z.; Liu, M.; Li, Z.; Feng, Q.; Song, L.; Xu, B.; Liu, X.; Gui, J. Where does the runoff come from in dry season in the source region of the Yangtze River? Agric. For. Meteorol. 2023, 330, 109314. [Google Scholar] [CrossRef]
- Mao, T.; Wang, G.; Zhang, T. Impacts of Climatic Change on Hydrological Regime in the Three-River Headwaters Region, China, 1960–2009. Water Resour Manag. 2016, 30, 115–131. [Google Scholar] [CrossRef]
- Ding, Y.; Peng, S. Spatiotemporal Trends and Attribution of Drought across China from 1901–2100. Sustainability 2020, 12, 477. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Liu, W.; Li, Z. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef]
- Peng, S.; Gang, C.; Cao, Y.; Chen, Y. Assessment of climate change trends over the Loess Plateau in China from 1901 to 2100. Int. J. Climatol. 2018, 38, 2250–2264. [Google Scholar] [CrossRef]
- Peng, S.; Ding, Y.; Wen, Z.; Chen, Y.; Cao, Y.; Ren, J. Spatiotemporal change and trend analysis of potential evapotranspiration over the Loess Plateau of China during 2011–2100. Agric. For. Meteorol. 2017, 233, 183–194. [Google Scholar] [CrossRef]
- Li, M.; Cao, S.; Zhu, Z.; Wang, Z.; Myneni, R.B.; Piao, S. Spatiotemporally consistent global dataset of the GIMMS Normalized Difference Vegetation Index (PKU GIMMS NDVI) from 1982 to 2022. Earth Syst. Sci. Data 2023, 15, 4181–4203. [Google Scholar] [CrossRef]
- Xu, X.; Liu, J.; Zhang, S.; Li, R.; Yan, C.; Wu, S. Remote Sensing Monitoring Data Set for Land Use and Cover in China. Data Registration and Publishing System of the Resource and Environmental Science Data Center of the Chinese Academy of Sciences. 2018. Available online: https://www.resdc.cn/DOI/DOI.aspx?DOIid=54 (accessed on 24 August 2024).
- Xu, N.; Lu, H.; Li, W.; Gong, P. Natural lakes dominate global water storage variability. Sci. Bull. 2024, 69, 1016–1019. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Zhao, Z.X.; Liang, S.; Kuang, X.; Feng, Y.; Hu, Z.; Feng, M. Frozen Ground Change Data Set in the Tibetan Plateau (1961–2020); National Tibetan Plateau Data Center: Tibet, China, 2024. [Google Scholar] [CrossRef]
- Peng, S. 1-km Monthly Potential Evapotranspiration Dataset for China (1901–2023); National Tibetan Plateau Data Center: Tibet, China, 2024. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Rank Correlation Methods; Griffin: Oxford, UK, 1948. [Google Scholar]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Yong, B.; Ren, L.; Hong, Y.; Gourley, J.J.; Chen, X.; Dong, J.; Wang, W.; Shen, Y.; Hardy, J. Spatial–Temporal Changes of Water Resources in a Typical Semiarid Basin of North China over the Past 50 Years and Assessment of Possible Natural and Socioeconomic Causes. J. Hydrometeorol. 2013, 14, 1009–1034. [Google Scholar] [CrossRef]
- Fu, G.; Chen, S.; Liu, C.; Shepard, D. Hydro-Climatic Trends of the Yellow River Basin for the Last 50 Years. Clim. Change 2004, 65, 149–178. [Google Scholar] [CrossRef]
- Zhai, L.; Feng, Q. Spatial and temporal pattern of precipitation and drought in Gansu Province, Northwest China. Nat. Hazards 2009, 49, 1–24. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Sonali, P.; Nagesh Kumar, D. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Liu, C.; Shao, Q.; Fukushima, Y. Changes in stream flow regime in headwater catchments of the Yellow River basin since the 1950s. Hydrol. Process. Int. J. 2007, 21, 886–893. [Google Scholar] [CrossRef]
- Budyko, M.I.; Miller, D.H. Climate and Life; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Choudhury, B.J. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. Roots, storms and soil pores: Incorporating key ecohydrological processes into Budyko’s hydrological model. J. Hydrol. 2012, 436–437, 35–50. [Google Scholar] [CrossRef]
- Wang, W.; Fu, J. Global assessment of predictability of water availability: A bivariate probabilistic Budyko analysis. J. Hydrol. 2018, 557, 643–650. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Zou, S.; Deng, C. Projection of future runoff change using climate elasticity method derived from Budyko framework in major basins across China. Glob. Planet. Change 2018, 162, 120–135. [Google Scholar] [CrossRef]
- Schaake, J.C. From Climate to Flow; John Wiley and Sons Inc.: New York, NY, USA, 1990. [Google Scholar]
- Yang, H.; Yang, D. Derivation of climate elasticity of runoff to assess the effects of climate change on annual runoff. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Xu, X.; Yang, D.; Yang, H.; Lei, H. Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; McVicar, T.R.; Guo, J.; Tang, Y.; Yao, A. Isolating the impacts of climate change and land use change on decadal streamflow variation: Assessing three complementary approaches. J. Hydrol. 2013, 507, 63–74. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, L.; Zhu, R.; Liu, C.; Sato, Y.; Fukushima, Y. Responses of streamflow to climate and land surface change in the headwaters of the Yellow River Basin. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Zou, F.; Li, H.; Hu, Q. Responses of vegetation greening and land surface temperature variations to global warming on the Qinghai-Tibetan Plateau, 2001–2016. Ecol. Indic. 2020, 119, 106867. [Google Scholar] [CrossRef]
- Fu, J.; Liu, B.; Wang, W.; Fei, E.X. Evaluating main drivers of runoff changes across China from 1956 to 2000 by using different budyko-based elasticity methods. J. Environ. Manag. 2023, 329, 117070. [Google Scholar] [CrossRef] [PubMed]
- Cheng, G.; Wu, T. Responses of permafrost to climate change and their environmental significance, Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surf. 2007, 112, F02S03. [Google Scholar] [CrossRef]
- Yang, M.; Nelson, F.E.; Shiklomanov, N.I.; Guo, D.; Wan, G. Permafrost degradation and its environmental effects on the Tibetan Plateau: A review of recent research. Earth-Sci. Rev. 2010, 103, 31–44. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Larsen, J.R.; van Emmerik, T.H.M.; Woods, R.A. A Global Assessment of Runoff Sensitivity to Changes in Precipitation, Potential Evaporation, and Other Factors. Water Resour. Res. 2017, 53, 8475–8486. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Li, Y.; Yan, D.; Peng, H.; Xiao, S. Evaluation of precipitation in CMIP6 over the Yangtze River Basin. Atmos. Res. 2021, 253, 105406. [Google Scholar] [CrossRef]
- Wu, H.; Lei, H.; Lu, W.; Liu, Z. Future changes in precipitation over the upper Yangtze River basin based on bias correction spatial downscaling of models from CMIP6. Environ. Res. Commun. 2022, 4, 045002. [Google Scholar] [CrossRef]
- Wan, H. Projection of Future Climate Change and Its Influence on Surface Runoff of the Upper Yangtze River Basin, China. Atmosphere 2023, 14, 1576. [Google Scholar] [CrossRef]
- He, S.; Chen, K.; Liu, Z.; Deng, L. Exploring the impacts of climate change and human activities on future runoff variations at the seasonal scale. J. Hydrol. 2023, 619, 129382. [Google Scholar] [CrossRef]
- Wang, T.; Yang, H.; Yang, D.; Qin, Y.; Wang, Y. Quantifying the streamflow response to frozen ground degradation in the source region of the Yellow River within the Budyko framework. J. Hydrol. 2018, 558, 301–313. [Google Scholar] [CrossRef]
- Woo, M.-K.; Kane, D.L.; Carey, S.K.; Yang, D. Progress in permafrost hydrology in the new millennium. Permafr. Periglac. Process. 2008, 19, 237–254. [Google Scholar] [CrossRef]










| Data | Time Span | Temporal Resolution | Data Source | Available Data |
|---|---|---|---|---|
| Precipitation | 1961–2020 | Monthly | [38,39,40,41] | https://doi.org/10.5281/zenodo.3114194 (accessed on 24 August 2024) |
| Temperature | 1961–2020 | Monthly | https://doi.org/10.11888/Meteoro.tpdc.270961 (accessed on 24 August 2024) | |
| Potential evapotranspiration | 1961–2020 | Monthly | [46] | https://doi.org/10.11866/db.loess.2021.001 (accessed on 24 August 2024) |
| Permafrost data | 1961–2020 | 5-Yearly | [45] | https://doi.org/10.11888/Cryos.tpdc.300955 (accessed on 24 August 2024) |
| LUCC | 1980, 1990, 1995, 2000, 2005, 2010, 2015, 2020 | Yearly | [43] | https://www.resdc.cn/ (accessed on 24 September 2024) |
| Runoff | 1961–2020 | Yearly | / | http://www.cjw.gov.cn/ (accessed on 24 February 2024) |
| NDVI | 1982–2020 | Half month | [42] | https://zenodo.org/records/8253971 (accessed on 24 October 2024) |
| Period | Average P (mm) | Change (%) | Average E0 (mm) | Change (%) | Average R (mm) | Change (%) | R/P | Change (%) | n | Change (%) | w | Change (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1961–2004 | 372.3 | N/A | 560 | N/A | 91.1 | N/A | 0.24 | N/A | 1.53 | N/A | 2.24 | N/A |
| 2005–2020 | 420.7 | 13% | 574.6 | 2.61% | 121.4 | 33.26% | 0.29 | 20.83% | 1.45 | −5.23% | 2.15 | −4.02% |
| 1961–2020 | 385.2 | 3.46% | 563.9 | 0.70% | 99.2 | 8.89% | 0.26 | 8.33% | 1.5 | −1.96% | 2.21 | −1.34% |
| Breakpoint | Budyko Function | Wp | Elasticity Coefficient | Runoff Change (mm) | Variable Contribution (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| εP | εE0 | εWp | ΔRP | ΔRE0 | ΔRWp | VCP | VCE0 | VCWp | |||
| 2004 | Yang’s | 1.45 | 1.96 | −0.96 | −1.14 | 27.34 | −2.96 | 5.92 | 90.23 | −9.77 | 19.54 |
| Fu’s | 2.15 | 1.94 | −0.94 | −1.71 | 27.11 | −2.89 | 6.08 | 89.47 | −9.54 | 20.07 | |
| Sub-Period | Year Range | Corresponding Runoff | E (mm) | P (mm) | R (mm) | Permafrost Area (104 km2) | ALT (m) | n | NDVI |
|---|---|---|---|---|---|---|---|---|---|
| T1 | 1961–1965 | R1 | 545.1 | 373.7 | 110.1 | 9.77 | 1.88 | 1.35 | / |
| T2 | 1966–1970 | R2 | 557.3 | 357 | 79.7 | 9.76 | 1.79 | 1.59 | / |
| T3 | 1971–1975 | R3 | 565.2 | 375 | 91.9 | 9.62 | 1.92 | 1.52 | / |
| T4 | 1976–1980 | R4 | 552.6 | 353.2 | 79 | 9.74 | 1.76 | 1.58 | / |
| T5 | 1981–1985 | R5 | 555.3 | 388 | 107.8 | 9.67 | 1.91 | 1.44 | 0.38 |
| T6 | 1986–1990 | R6 | 569.8 | 376.3 | 96.9 | 9.58 | 1.96 | 1.46 | 0.394 |
| T7 | 1991–1995 | R7 | 565.7 | 351.4 | 80.8 | 9.6 | 1.99 | 1.52 | 0.381 |
| T8 | 1996–2000 | R8 | 562.3 | 388.4 | 82 | 9.66 | 2.04 | 1.77 | 0.391 |
| T9 | 2001–2005 | R9 | 566 | 402.2 | 103.6 | 9.24 | 2.06 | 1.55 | 0.379 |
| T10 | 2006–2010 | R10 | 586.4 | 428.4 | 116.6 | 8.94 | 2.15 | 1.52 | 0.385 |
| T11 | 2011–2015 | R11 | 567.4 | 414.8 | 111.9 | 9.29 | 2.12 | 1.53 | 0.379 |
| T12 | 2016–2020 | R12 | 574 | 414.1 | 129.8 | 8.44 | 2.11 | 1.33 | 0.382 |
| Observed ∆R | ∆Rclimate | ∆RWp | |
|---|---|---|---|
| ∆R2 | −30.4 | −9.97 | −20.43 |
| ∆R3 | 12.2 | 7.84 | 4.36 |
| ∆R4 | −12.9 | −8.45 | −4.45 |
| ∆R5 | 28.8 | 18.63 | 10.17 |
| ∆R6 | −10.9 | −8.55 | −2.35 |
| ∆R7 | −16.1 | −11.3 | −4.8 |
| ∆R8 | 1.2 | 18.41 | −17.21 |
| ∆R9 | 21.6 | 6.57 | 15.03 |
| ∆R10 | 13 | 10.33 | 2.67 |
| ∆R11 | −4.7 | −3.68 | −1.02 |
| ∆R12 | 17.9 | −1.66 | 19.56 |
| ΔArea | ΔALT | EArea | EALT | |
|---|---|---|---|---|
| ∆R2 | −0.01 | −0.09 | 0.03 | −0.08 |
| ∆R3 | −0.14 | 0.13 | −0.04 | 0.05 |
| ∆R4 | 0.12 | −0.16 | −0.06 | 0.21 |
| ∆R5 | −0.07 | 0.15 | 0.28 | −0.38 |
| ∆R6 | −0.09 | 0.05 | −0.02 | 0.01 |
| ∆R7 | 0.02 | 0.03 | −0.04 | 0 |
| ∆R8 | 0.06 | 0.05 | 0.03 | 0.03 |
| ∆R9 | −0.42 | 0.02 | −0.02 | 0.06 |
| ∆R10 | −0.3 | 0.09 | 0.07 | −0.11 |
| ∆R11 | 0.35 | −0.03 | 0.01 | −0.07 |
| ∆R12 | −0.85 | −0.01 | −0.09 | 0.05 |
| median (E*) | −0.02 | 0.01 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, J.; Sang, X.; Zhang, Y.; Jia, Y.; Qu, J.; Zheng, Y.; Ding, H. A Novel Sensitivity Analysis Framework for Quantifying Permafrost Impacts on Runoff Variability in the Yangtze River Source Region. Sustainability 2025, 17, 1570. https://doi.org/10.3390/su17041570
Chang J, Sang X, Zhang Y, Jia Y, Qu J, Zheng Y, Ding H. A Novel Sensitivity Analysis Framework for Quantifying Permafrost Impacts on Runoff Variability in the Yangtze River Source Region. Sustainability. 2025; 17(4):1570. https://doi.org/10.3390/su17041570
Chicago/Turabian StyleChang, Jiaxuan, Xuefeng Sang, Yun Zhang, Yangwen Jia, Junlin Qu, Yang Zheng, and Haokai Ding. 2025. "A Novel Sensitivity Analysis Framework for Quantifying Permafrost Impacts on Runoff Variability in the Yangtze River Source Region" Sustainability 17, no. 4: 1570. https://doi.org/10.3390/su17041570
APA StyleChang, J., Sang, X., Zhang, Y., Jia, Y., Qu, J., Zheng, Y., & Ding, H. (2025). A Novel Sensitivity Analysis Framework for Quantifying Permafrost Impacts on Runoff Variability in the Yangtze River Source Region. Sustainability, 17(4), 1570. https://doi.org/10.3390/su17041570






