Considering the Sustainable Benefit Distribution in Agricultural Supply Chains from Sales Efforts: An Improved ‘Tripartite Synergy’ Model Based on Shapley–TOPSIS

Abstract

Balancing efficiency and equity within agricultural supply chains is crucial for rural revitalization and sustainable development. This study focuses on the three-tiered chain of ‘farmers–cooperatives–retailers’, constructing a joint decision-making model linking pricing, sales effort, and order volume. It compares the performance differences between decentralized and centralized decision-making structures. Methodologically, we introduce four corrective factors—risk-bearing capacity, cooperation level, capital investment, and information access—to the traditional Shapley value. By employing TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution) to calculate proximity, we derive an enhanced Shapley–TOPSIS allocation coefficient. Furthermore, we design a secondary distribution rule of ‘effort-based value-added distribution according to labor contribution,’ tightly binding the marginal returns of sales effort to input intensity, thereby reconciling structural fairness with incentive compatibility. Empirical findings indicate that, compared with decentralized approaches, centralized decision-making significantly enhances overall system revenue and reduces retail prices. The refined distribution scheme outperforms the baseline Shapley value in fairness and stability, effectively mitigating the misalignment where effort contributors receive disproportionately low returns. The optimal sales effort level is approximately 0.35. Under the ‘distribution according to labor’ approach, retailers (the primary effort providers) see a marked increase in their value-added share, whereas farmers and cooperatives also gain positive benefits, enhancing alliance stability. Unlike existing studies that rely mainly on revenue-sharing contracts or a single Shapley allocation, this study, on the one hand, explicitly endogenizes sales effort into demand and profit functions and systematically characterizes the joint mechanism between effort and profit allocation under both centralized and decentralized structures. On the other hand, an improved Shapley–TOPSIS modeling procedure and an ‘effort added-value allocation according to contribution’ rule are proposed. By adjusting demand parameters and the weights of the adjustment factors, the proposed framework can be readily extended to other agricultural products and green supply chain settings, providing a replicable tool and managerial implications for designing sustainable profit allocation schemes.

1. Introduction

1.1. Research Background

Agriculture is a pillar of China’s economic development and plays a pivotal role in rapid national growth and rural revitalization. In recent years, national policies have consistently supported ‘rural e-commerce,’ emphasizing the strengthening of supply chain infrastructure for agricultural products and proposing the optimization of benefit distribution to improve farmers’ livelihoods and logistics efficiency. With the rapid expansion of mobile internet and e-commerce, the supply chain for agricultural products has evolved into diverse new configurations; however, because this evolution is relatively recent and stakeholder interests are intricate, cooperation and conflict coexist within the chain [1,2]. Consequently, investigating the profit allocation mechanism among supply chain members is essential for enhancing distribution efficiency, lowering costs, and achieving sustainable development, thereby offering substantial academic value for rural revitalization and agricultural modernization. Within a three-tier ‘farmer–cooperative–retailer’ supply chain, this paper addresses how—while accounting for the retailer’s sales effort—to design a profit allocation mechanism that balances equity with incentives, maximizes system-wide profit, and ensures coalition stability.

Positioning agri-commerce linkage as an emerging, modern circulation model reveals substantial advantages. However, in practice, the distribution of benefits along the supply chain remains problematic [3,4]. With respect to the agri-commerce-integrated supply chain, such a linkage is a widely adopted model for agricultural product distribution in developed economies; mature systems in the United States, the Netherlands, and Japan offer successful precedents [5,6]. Scholars have noted that farmer–supermarket linkage supply chains are extensively applied in China’s agricultural product markets and are relatively compatible with national conditions; nevertheless, unstable supply, short-lived contractual relationships, and unequal bargaining power remain prominent, rendering production–marketing relationships under the farmer–supermarket model still unstable [7]. As a cooperative distribution arrangement between new-type agricultural business entities and agricultural product circulation enterprises, the agri-commerce linkage can mitigate mismatches and volatility between production and sales [8]; its efficient operation, however, hinges on effective coordination within the agri-commerce supply chain and an equitable distribution of benefits.

From the broader perspective of production networks, agricultural supply chains are not isolated ‘tripartite chains’ but rather subnetworks embedded within regional and even global value chains. Their coordination failure, misaligned benefits, and efficiency losses often stem from the highly interconnected structural attributes among economic entities. Research employing input–output data and complex network methodologies indicates that global value chains can be modeled as weighted directed networks. When critical industry or national nodes are disrupted, demand and supply shocks propagate through the network in cascading waves between upstream and downstream actors. Structural characteristics such as network concentration and betweenness centrality significantly influence systemic output losses and risk exposure [9]. Further trade network analysis reveals that international trade structures exhibit pronounced ‘geometric polarization’ and bipolar characteristics, with core nodes serving as both primary shock transmission points and the most vulnerable points susceptible to external shocks [10]. Against this backdrop, coordination issues within agricultural supply chains can be understood as localized responses by global or regional production networks to demand fluctuations, quality risks, and policy changes. Mismatches in decision-making authority allocation and benefit distribution mechanisms within the chain amplify structural shocks and exacerbate welfare losses. Consequently, it is theoretically necessary to compare the performance differences between centralized and decentralized decision-making within agricultural supply chains. Enhancing the stability and resilience of local subnetworks through contractual and distributional rules provides broader theoretical underpinnings for this study.

1.2. Literature Review

The rationalization of profit allocation mechanisms in supply chains is playing an increasingly pivotal role in coordinating relationships within supply chain integration, and many experts and researchers have consequently concentrated their efforts in this area. Focusing on issues specific to agricultural product supply chains, scholars—drawing on supply chain management theory, game theory, and the analytic network process (ANP) integrated with an improved Shapley value approach and related principles of profit allocation—have investigated how profits should be distributed among member firms in the supply chain.

In addressing profit allocation within agricultural product supply chains, the extant literature domestically and abroad can be grouped into several streams, among which (1) the Shapley value approach is prominent. The Shapley value method derives an allocation scheme on the basis of each member’s marginal contribution to the coalition as a whole; allocation mechanisms grounded in the Shapley value effectively avoid naive egalitarian averaging and sufficiently incentivize firms along the chain. Through an empirical analysis of Beijing’s agricultural wholesale markets, Wang, C.L. et al. (2023) developed an allocation model that is informative for profit-sharing problems requiring the joint consideration of dynamically varying, interdependent parameters [11]. Their results indicate that the revised allocation better aligns with the benefit demands of multiple stakeholders, is positively correlated with participants’ contribution levels, and can effectively enhance participating firms’ incentives to cooperate. (2) Evolutionary game theory: Game theory provides models for analyzing conflicts of interest and coordinated competition among independent, economically rational firms, and it likewise models the decision-making of interdependent members within a supply chain. Deng, Mingjun et al. [12] employed a transferable-utility cooperative game to examine the effectiveness of a green agricultural product model under multilateral coalitions. Kang, K. et al. (2019) used a Stackelberg game to address four low-carbon strategy combinations for retailers and manufacturers and then applied an evolutionary game framework to further evaluate these strategies and identify the evolutionarily stable strategy (ESS) [13]. Peng, X. et al. (2022) developed a tripartite evolutionary game model that captures the beneficial interactions among raw material suppliers, food manufacturers, and consumers [14]. Their study pinpoints key factors shaping each player’s decisions and leverages them to provide scientific guidance for the behavior of food supply chain members. Guo, L.B. et al. (2024) incorporated government subsidies and green-technology investment into a supply chain market model to assess their impacts on manufacturers, the government, and consumers [15]. They then constructed a three-party evolutionary game model for the government, manufacturers, and consumers; analyzed the equilibrium outcomes; and conducted sensitivity analyses on two parameters: government subsidies to manufacturers and subsidies to consumers purchasing green products. (3) Revenue-sharing contracts: Zheng Qi et al. [16], considering information asymmetry under the ‘farmer–supermarket direct-supply’ model, investigated profit allocation in a fresh agricultural product supply chain governed by a revenue-sharing contract, achieving Pareto-optimal profits for both parties. Chen Liuxin et al. [17] built a three-level agricultural product supply chain profit model and, combining shared freight costs with a revenue-sharing contract, analyzed retailers’ optimal decisions and members’ profits across the supply chain. (4) Integrated methods: Li Quanlin et al. [18] designed three simple and operational profit distribution mechanisms for agricultural product supply chains using the Shapley value, the weighted Shapley value, and the Owen value. Zhou Yefu [19] examined profit allocation among alliance entities along both vertical and horizontal dimensions by applying a Stackelberg game model and a Shapley value model. Anil Kumar Agrawal et al. [20], who treat firms as rational agents, proposed four distinct allocation schemes and argued that, on the basis of fairness and reasonableness, only long-term strategic cooperation maximizes firms’ profits. In addition, commonly used approaches include Nash equilibrium models, wholesale-price contracts under Stackelberg leadership, buy-back contracts under Nash bargaining, and wholesale-price contracts under Nash bargaining.

Recent international research in operations research, agricultural economics, and sustainable supply chain coordination has yielded new findings on centralized versus decentralized decision-making and contract design for perishable agricultural products and their associated green supply chains. Feng et al. [21] constructed a Stackelberg game model within a two-tier fresh produce supply chain, accounting for retailers’ risk aversion and preservation efforts. They analyzed optimal preservation efforts and pricing under centralized versus decentralized decision-making, designing a cost-sharing and compensation combination contract to achieve supply chain coordination. Wang et al. [22] introduced dynamic preservation efforts within a three-tier fresh produce supply chain. By comparing centralized and decentralized decision-making, they demonstrated centralized decision-making’s advantages in terms of system profitability and multiagent effort equilibrium, proposing a ‘preservation cost-sharing–two-part fee’ coordination contract; Liu et al. [23] examined a cross-border low-carbon agricultural supply chain, comparing optimal strategies and option-cost-sharing contracts under centralized versus decentralized decision structures while accounting for supply disruption risks and quality control constraints. They revealed coordination mechanisms when low-carbon constraints coexist with supply disruption risks. Mahato et al. [24] introduced carbon trading mechanisms and transport strategies within a two-tier sustainable supply chain. Through noncooperative and cooperative games, they characterized pricing and ordering decisions for perishable goods under carbon emission constraints, demonstrating that appropriate collaborative contracts in carbon market environments can simultaneously enhance economic returns and environmental performance. Such studies demonstrate, from diverse perspectives, that centralized decision-making and well-designed profit/cost-sharing contracts serve as crucial tools for mitigating efficiency losses and incentive misalignment within agricultural or perishable supply chains characterized by preservation efforts, carbon emission constraints, or disruption risks.

In summary, research on the agribusiness–retail supply chain model and profit distribution both domestically and internationally has focused predominantly on the impact of tools such as profit sharing, repurchase agreements, Nash bargaining, and traditional Shapley values on the fairness and efficiency of profit allocation. Even in recent international studies, while coordination issues concerning fresh produce preservation efforts, low-carbon constraints, and supply disruption risks have received relatively systematic discussion, insufficient attention has been given to the critical controllable variable of ‘sales effort’ and its integrated design with distribution rules. Concurrently, existing modified Shapley value approaches predominantly employ subjective weighting or single-dimensional adjustments, rarely integrating multidimensional factors such as risk-bearing capacity, cooperation levels, capital investment, and information access within a unified framework to systematically characterize structural fairness. Furthermore, the replicability and dissemination pathways for refining theoretical distribution models into reusable analytical templates and decision-making tools across diverse regional and agricultural product supply chains warrant further exploration. To address these research gaps, this paper constructs an enhanced Shapley–TOPSIS allocation model based on joint pricing–sales effort–order quantity decision-making. It incorporates a secondary distribution rule of ‘value-added distribution according to labor contribution’ to establish a clearer theoretical link between efficiency and equity.

2. Methodology

2.1. Shapley

The Shapley value method, proposed by L.S. Shapley in 1953, is a widely used approach for allocating payoffs among participants in cooperative games. It distributes the aggregate payoff according to each participant’s contribution to the outcome, as captured by marginal contributions [25]. The Shapley value has also been broadly applied to profit sharing among member firms within supply chains, offering strong practical applicability and sound theoretical justification [26].

Assume that n member enterprises jointly engage in economic activities, where their economic benefits depend on the cooperative arrangements among the member enterprises. If the cooperative inclination among enterprises outweighs competition, an increase in the number of members within the supply chain will not reduce profits but rather enhance overall profitability. This optimization allows the supply chain alliance to function at its best, thereby achieving a reasonable profit distribution plan. Therefore, in the Shapley value method, let $\mathrm{I}=(1,2,3,\dots ,\mathrm{n})$ represent the set of participants, and let $\mathsf{\phi }(\mathrm{v})$ denote the profit of each party under supply chain cooperation. Define $\mathsf{\phi }\left(\mathrm{v}\right)=({\mathsf{\phi }}_1\left(\mathrm{v}\right),{\mathsf{\phi }}_2\left(\mathrm{v}\right),\dots ,{\mathsf{\phi }}_{\mathrm{n}}\left(\mathrm{v}\right))$, and $\mathrm{v}(\mathrm{x})$ as the real-valued functions of cooperation I, where n represents the number of cooperative members in the supply chain and where ${\mathsf{\phi }}_{\mathrm{i}}\left(\mathrm{v}\right)$ denotes the profit distribution value for the i-th enterprise under cooperation I. The conditions for the Shapley value method to hold are as follows:

$$\mathrm{V}(\mathrm{N})\ge \sum \mathrm{v}\left(\mathrm{i}\right),\mathrm{i}=1,2,\dots ,\mathrm{n}$$

(1)

$${\mathsf{\phi }}_{\mathrm{i}}\left(\mathrm{v}\right)\ge \mathrm{v}\left(\mathrm{i}\right)$$

(2)

$$\mathrm{v}\left(\mathrm{N}\right)=\sum {\mathsf{\phi }}_{\mathrm{i}}\left(\mathrm{v}\right)$$

(3)

Specifically, Equation (1) states that the total payoff of the integrated supply chain with all members participating is no less than the sum of the members’ standalone payoffs and that the cooperative surplus from participation is nonnegative; Equation (2) requires that the payoff allocated to each member from the supply chain is not less than that of the member’s standalone payoff (individual rationality); and Equation (3) enforces efficiency, namely, that the total supply chain payoff equals the sum of the payoffs allocated to all members. The Shapley value method can then be formulated by the following mathematical model:

$$\mathrm{w}\left(\left|\mathrm{s}\right|\right)=\left(\left|\mathrm{s}\right|-1\right)!\left(\mathrm{n}-\left|\mathrm{s}\right|\right)!/\mathrm{n}!$$

(4)

$${\mathsf{\phi }}_{\mathrm{i}}\left(\mathrm{v}\right)={\sum }_{\mathrm{s}\in \mathrm{S}}\mathrm{w}(\left|\mathrm{s}\right|)\left[\mathrm{v}\left(\mathrm{s}\right)-\mathrm{v}\left(\mathrm{s}\setminus \mathrm{i}\right)\right]$$

(5)

where $\mathrm{w}\left(\left|\mathrm{s}\right|\right)$ is the weight factor, $\left|\mathrm{s}\right|$ is the number of elements in supply chain subset s, n is the number of cooperative members in the supply chain, $\mathrm{v}\left(\mathrm{s}\right)$ represents the benefit generated by supply chain subset s, and $\mathrm{v}\left(\mathrm{s}\setminus \mathrm{i}\right)$ denotes the benefit generated by supply chain subset s excluding member i.

2.2. Shapley Value Method Improvement

The Shapley value approach accounts for the expected marginal contributions of supply chain partners and thus avoids naive equal-split allocations; however, its factor set is narrow and overlooks how risk exposure and capital commitments affect benefit distribution [27,28]. In agri-food supply chain alliances, participants differ in capital input, risk bearing, and cooperation intensity [29,30,31]; moreover, information acquisition capability influences each member’s expected return [32]. Zheng Qi et al. [33] further show that the risk preferences of participating agents shape overall supply chain profits. Accordingly, this study revises the traditional Shapley value framework by incorporating four dimensions—risk bearing, cooperation intensity, capital investment, and information acquisition—and employs the TOPSIS method to determine the revenue-sharing coefficients.

TOPSIS-Based Computation of the Closeness Coefficient

To incorporate the four structural correction factors (risk bearing, cooperation level, capital investment, and information acquisition) into the allocation scheme, we apply the TOPSIS method to obtain a closeness coefficient for each member of the alliance. Let ${\mathrm{x}}_{\mathrm{i}\mathrm{j}}$ denote the performance of member i (i = 1, 2, 3) on factor j (j = 1, …, 4), and X = (${\mathrm{x}}_{\mathrm{i}\mathrm{j}}$) be the original decision matrix. All four indicators are treated as benefit-type criteria after the necessary direction checks.

(1)

Normalization. Each column is first normalized to eliminate the effects of different units:

$${\mathrm{r}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\mathrm{x}}_{\mathrm{i}\mathrm{j}}}{\sqrt{{\sum }_{\mathrm{i}=1}^3{\mathrm{x}}_{\mathrm{i}\mathrm{j}}^2}}}, \mathrm{I}=1,2,3; \mathrm{j}=1,\dots ,4.$$

(6)

(2)

Weighted normalized decision matrix. Using the weight vector $\mathsf{\omega }=({\mathsf{\omega }}_1,{\mathsf{\omega }}_2,{\mathsf{\omega }}_3,{\mathsf{\omega }}_4)$, we obtain

$${\mathsf{\upsilon }}_{\mathrm{i}\mathrm{j}}={\mathsf{\omega }}_{\mathrm{j}}{\mathrm{r}}_{\mathrm{i}\mathrm{j}}, \mathrm{I}=1,2,3; \mathrm{j}=1,\dots ,4.$$

(7)

(3)

Positive and negative ideal solutions. For benefit-type indicators, the positive ideal solution ${\mathsf{\nu }}^{+}$ and negative ideal solution ${\mathsf{\nu }}^{-}$ are defined as

$${\mathsf{\upsilon }}_{\mathrm{j}}^{+}=\underset{\mathrm{i}}{\max } {\mathsf{\upsilon }}_{\mathrm{i}\mathrm{j}}, {\mathsf{\upsilon }}_{\mathrm{j}}^{-}=\underset{\mathrm{i}}{\min } {\mathsf{\upsilon }}_{\mathrm{i}\mathrm{j}}, \mathrm{j}=1,\dots ,4.$$

(8)

(4)

Distances to ideal solutions. The Euclidean distances from member iii to the positive and negative ideal solutions are

$${\mathrm{S}}_{\mathrm{i}}^{+}=\sqrt{{\sum }_{\mathrm{j}=1}^4{({\mathsf{\upsilon }}_{\mathrm{i}\mathrm{j}}-{\mathsf{\upsilon }}_{\mathrm{j}}^{+})}^2}, {\mathrm{S}}_{\mathrm{i}}^{-}=\sqrt{{\sum }_{\mathrm{j}=1}^4{({\mathsf{\upsilon }}_{\mathrm{i}\mathrm{j}}-{\mathsf{\upsilon }}_{\mathrm{j}}^{-})}^2}$$

(9)

(5)

Closeness coefficient. The TOPSIS closeness coefficient of member iii is finally given by

$${\mathrm{C}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{S}}_{\mathrm{i}}^{-}}{{\mathrm{S}}_{\mathrm{i}}^{+}+{\mathrm{S}}_{\mathrm{i}}^{-}}}, \mathrm{I}=1,2,3.$$

(10)

Substituting the data in

Table 1. Raw data.

Collaborative Entity	Risk Bearing	Effort Level	Financial Investment	Information Acquisition
Farmers	0.7	0.4	0.4	0.3
Cooperatives	0.4	0.5	0.6	0.4
Retailers	0.5	0.3	0.4	0.5

into Equations (6)–(10) yields the following closeness coefficients for the farmer, cooperative, and e-commerce firm:

$$\mathrm{C}=(\mathrm{C}1,\mathrm{C}2,\mathrm{C}3)$$

(11)

2.3. Supply Chain Profit Allocation Model Under the ‘Farmer–Cooperative–Retailer’ Agribusiness Linkage Method Based on an Improved Shapley Value Method

2.3.1. Theoretical Definition of the Tripartite Synergy Model

Within the three-tier agricultural supply chain comprising farmers, cooperatives, and merchants, when all three parties collectively determine retail prices, sales effort levels, and order quantities through centralized decision-making and adopt a two-stage profit distribution mechanism combining an ‘enhanced Shapley–TOPSIS’ approach with effort-based value-added distribution, the following conditions are satisfied:

(1)

The expected profits for all parties under centralized decision-making are no lower than those under decentralized decision-making;

(2)

No single entity derives higher long-term expected returns by unilaterally deviating from the alliance (alliance stability);

(3)

The equilibrium level of sales effort is endogenously determined by overall profit maximization, with marginal returns matching marginal distribution weights (incentive compatibility);

Then the supply chain is deemed to operate under the ‘tripartite synergy model’.

2.3.2. Model Setup

This study examines a three-tier agri-food supply chain composed of farmers, a cooperative, and retailers. Farmers are the producers of agricultural products, the cooperative undertakes processing and transportation, and retailers engage in buying and selling.

(1)

This research focuses on a supply chain structured as ‘farmers–cooperative–retailers.’ All three parties are rational business entities, and the objective is to maximize collective (system-wide) profit.

(2)

The analysis considers only the distribution of supply chain benefits within a single cooperation period.

(3)

Within a cooperation period, retailers determine the order quantity q on the basis of market conditions. Farmers sell their output to the cooperative at price ${\mathrm{p}}_1$; after processing, the cooperative sells to retailers at price ${\mathrm{p}}_2$; and retailers then sell to consumers at retail price ${\mathrm{p}}_3$

(4)

The model incorporates retailers’ sales effort with level $\mathrm{y}\left(\mathrm{x}\right)=1-{\mathrm{e}}^{-\mathrm{x}}$, $\mathrm{y}\in \left[\mathrm{0,1})\right.$, where x is the incremental input coefficient for sales effort. Following Ref. [34], the relationship between sales effort input and cost is specified as ${\mathrm{c}}_5={\displaystyle \frac{1}{2}}\mathsf{\delta }{\mathrm{x}}^2$, where $\mathsf{\delta }$ denotes the sensitivity of retailers’ sales cost to sales effort.

(5)

The market demand for the agricultural product is represented in additive form [35] as $\mathrm{Q}=\mathsf{\alpha }-\mathsf{\beta }{\mathrm{p}}_3+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})$, Q = q, where $\mathsf{\alpha }$ is the initial market demand and where $\mathsf{\beta }$ and $\mathsf{\gamma }$ denote the sensitivities of market demand to price and to product production quality, respectively.

(6)

The cost parameters are defined as follows: farmer unit input cost, ${\mathrm{c}}_1$; cooperative unit processing cost, ${\mathrm{c}}_2$; unit transportation cost, ${\mathrm{c}}_3$; and retailer unit selling input cost, ${\mathrm{c}}_4$

2.3.3. Stakeholder Payoff Distribution Under Decentralized Decision-Making

Decentralized decision-making refers to a setting in which all parties act noncooperatively: farmers, cooperatives, and retailers each pursue their own profit maximization, thereby determining the price and order quantity of agricultural products. The profit functions of the three agents are formulated as follows:

$${\mathsf{\pi }}_1=({\mathrm{p}}_1-{\mathrm{c}}_1)\mathrm{q}$$

(12)

$${\mathsf{\pi }}_2=({\mathrm{p}}_2-{\mathrm{p}}_1-{\mathrm{c}}_2-{\mathrm{c}}_3)\mathrm{q}$$

(13)

$${\mathsf{\pi }}_3=({\mathrm{p}}_3-{\mathrm{p}}_2-{\mathrm{c}}_4-{\mathrm{c}}_5)\mathrm{q}=({\mathrm{p}}_3-{\mathrm{p}}_2-{\mathrm{c}}_4-{\displaystyle \frac{1}{2}}\mathsf{\delta }{\mathrm{x}}^2)\mathrm{q}$$

(14)

Substituting $\mathrm{Q}=\mathsf{\alpha }-\mathsf{\beta }{\mathrm{p}}_3+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})=\mathrm{q}$ into Equation (14) yields

$${\mathsf{\pi }}_3=({\mathrm{p}}_3-{\mathrm{p}}_2-{\mathrm{c}}_4-{\displaystyle \frac{1}{2}}\mathsf{\delta }{\mathrm{x}}^2)(\mathsf{\alpha }-\mathsf{\beta }{\mathrm{p}}_3+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}}))$$

(15)

Taking the second derivative of ${\mathsf{\pi }}_3$ with respect to ${\mathrm{p}}_3$ in Equation (15) yields ${\displaystyle \frac{\partial {\mathsf{\pi }}_3}{\partial {\mathrm{p}}_3}}=-2\mathsf{\beta }<0$. This indicates that the profit function ${\mathsf{\pi }}_3$ of the retailers under decentralized decision-making is a concave function of the price ${\mathrm{p}}_3$. Let ${\displaystyle \frac{\partial {\mathsf{\pi }}_3}{\partial {\mathrm{p}}_3}}=\mathsf{\alpha }-\mathsf{\beta }{\mathrm{p}}_3+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-({\mathrm{p}}_3-{\mathrm{p}}_2-{\mathrm{c}}_4-{\displaystyle \frac{1}{2}}\mathsf{\delta }{\mathrm{x}}^2)\mathsf{\beta }=0$, obtain the optimal retail price

$${\mathrm{p}}_3^{\mathrm{*}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})+\mathsf{\beta }({\mathrm{p}}_2+{\mathrm{c}}_4+\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2)}{2\mathsf{\beta }}}$$

(16)

and subsequently derive the optimal order quantity

$${\mathrm{q}}^{\mathrm{*}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }({\mathrm{p}}_2+{\mathrm{c}}_4+\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2)}{2}}$$

(17)

Substituting ${\mathrm{q}}^{\mathrm{*}}$ into Equation (13) yields

$${\mathsf{\pi }}_2={\displaystyle \frac{({\mathrm{p}}_2-{\mathrm{p}}_1-{\mathrm{c}}_2-{\mathrm{c}}_3)(\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }({\mathrm{p}}_2+{\mathrm{c}}_4+\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2))}{2}}$$

(18)

Taking the first derivative of Equation (18) with respect to ${\mathrm{p}}_2$ and setting it equal to zero, i.e., ${\displaystyle \frac{\partial {\mathsf{\pi }}_2}{\partial {\mathrm{p}}_2}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }({2\mathrm{p}}_2{-\mathrm{p}}_1-{\mathrm{c}}_2-{\mathrm{c}}_3+{\mathrm{c}}_4+\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2)}{2}}=0$, yields the optimal price

$${\mathrm{p}}_2^{\mathrm{*}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})+\mathsf{\beta }({\mathrm{p}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3-{\mathrm{c}}_4-\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2)}{2\mathsf{\beta }}}$$

(19)

for the cooperative to sell to the retailers. Substituting ${\mathrm{q}}^{\mathrm{*}}$ and ${\mathrm{p}}_2^{\mathrm{*}}$ into Equation (12) results in

$${\mathsf{\pi }}_1=({\mathrm{p}}_1-{\mathrm{c}}_1){\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }({\mathrm{p}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4+\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2)}{4}}$$

(20)

Taking the first derivative of Equation (20) with respect to ${\mathrm{p}}_1$ and setting it equal to zero, i.e., ${\displaystyle \frac{\partial {\mathsf{\pi }}_1}{\partial {\mathrm{p}}_1}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(2{\mathrm{p}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4+\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2-{\mathrm{c}}_1)}{4}}=0$, yields the optimal price for the farmers as follows:

$${\mathrm{p}}_1^{\mathrm{*}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4-{\mathrm{c}}_1)}{2\mathsf{\beta }}}$$

(21)

Substituting ${\mathrm{p}}_1^{\mathrm{*}}$, ${\mathrm{p}}_2^{\mathrm{*}}$, and ${\mathrm{p}}_3^{\mathrm{*}}$ into Equations (15), (18) and (20), respectively, yields the optimal expected returns for the farmers, cooperatives, and retailers as follows:

$${\mathsf{\pi }}_1^{\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{16\mathsf{\beta }}}$$

(22)

$${\mathsf{\pi }}_2^{\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{32\mathsf{\beta }}}$$

(23)

$${\mathsf{\pi }}_3^{\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{64\mathsf{\beta }}}$$

(24)

Taking the first derivative of Equation (24) with respect to x and setting it equal to zero yields the optimal value of the sales effort level x for the retailers as follows:

$${\mathrm{x}}^{\mathrm{*}}=\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{w}({\displaystyle \frac{\mathsf{\gamma }}{\mathsf{\delta }\mathsf{\beta }}})$$

(25)

2.3.4. Benefits Accrued to Multiple Parties Under Centralized Decision-Making

Once farmers, cooperatives, and retailers form an alliance, each party’s decisions no longer seek to maximize its own payoff; rather, choices are made from the perspective of maximizing the overall supply chain surplus. Under the foregoing assumption, the aggregate supply chain profit in the farmer + cooperative + retailer farmer–business linkage model can be computed as

$$\mathsf{\pi }=({\mathrm{p}}_3-{\displaystyle \frac{1}{2}}\mathsf{\delta }{\mathrm{x}}^2-{\mathrm{c}}_1-{\mathrm{c}}_2-{\mathrm{c}}_3-{\mathrm{c}}_4)(\mathsf{\alpha }-\mathsf{\beta }{\mathrm{p}}_3+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}}))$$

(26)

By differentiating Equation (26), the optimal selling price for the retailers under centralized decision-making among the three parties can be derived as

$${\mathrm{p}}_3^{\mathrm{*}\mathrm{*}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})+\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)}{2\mathsf{\beta }}}$$

(27)

The optimal order quantity is as follows:

$${\mathrm{q}}^{\mathrm{*}\mathrm{*}}={\displaystyle \frac{\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)}{2}}$$

(28)

Substituting ${\mathrm{p}}_3^{\mathrm{*}\mathrm{*}}$ into Equation (26) yields the overall optimal profit of the supply chain as follows:

$${\mathsf{\pi }}^{\mathrm{*}\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{4\mathsf{\beta }}}$$

(29)

By taking the first derivative of Equation (29) with respect to x and setting it equal to zero, the optimal value of the additional investment coefficient for product quality in the supply chain is obtained as

$${\mathrm{x}}^{\mathrm{*}\mathrm{*}}=\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{w}({\displaystyle \frac{\mathsf{\gamma }}{\mathsf{\delta }\mathsf{\beta }}})$$

(30)

2.3.5. Allocation of Stakeholder Payoffs Based on the Shapley Value Method

Let farm households, cooperatives, and retailers be coded as 1, 2, and 3, respectively. The coalition contains three members, and the corresponding set includes 8 subsets. In this work, we employ only the Shapley value method to compute the payoff allocated to each participant when the three parties form a coalition under centralized decision-making. Under the tripartite coalition agreement with centralized decision-making, the supply chain’s overall optimal profit is as follows:

$$\mathrm{v}(\mathrm{1,2},3)={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{4\mathsf{\beta }}}$$

(31)

We compute, under four distinct modes of cooperation, the benefits accruing to each stakeholder; applying the Shapley value principle yields the following postcoalition payoffs for farmers, cooperatives, and retailers:

$${\mathsf{\phi }}_1(\mathrm{v})={\displaystyle \frac{{7\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{64\mathsf{\beta }}}$$

(32)

$${\mathsf{\phi }}_2(\mathrm{v})={\displaystyle \frac{{11\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{128\mathsf{\beta }}}$$

(33)

$${\mathsf{\phi }}_3(\mathrm{v})={\displaystyle \frac{{7\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{128\mathsf{\beta }}}$$

(34)

2.3.6. Benefit Allocation via an Improved Shapley Value Method

Building on the baseline Shapley value method, we incorporate a comprehensive influence factor into the payoff allocation model as a corrective term. The improved Shapley value-based model is formulated as follows:

$${\mathsf{\phi }}_{\mathrm{i}}^{\mathrm{\prime }}\left(\mathrm{v}\right)={\mathsf{\phi }}_{\mathrm{i}}\left(\mathrm{v}\right)+\mathrm{v}(\mathrm{I})∆{\mathsf{\lambda }}_{\mathrm{i}}$$

(35)

$$∆{\mathsf{\lambda }}_{\mathrm{i}}={\mathsf{\lambda }}_{\mathrm{i}}-{\displaystyle \frac{1}{\mathrm{n}}}$$

(36)

$${\mathsf{\lambda }}_{\mathrm{i}}={\mathrm{C}}_{\mathrm{i}}/{\sum }_{\mathrm{t}=1}^{\mathrm{n}}{\mathrm{C}}_{\mathrm{i}}$$

(37)

Here, ${\mathsf{\phi }}_{\mathrm{i}}^{\mathrm{\prime }}\left(\mathrm{v}\right)$ represents the expected profit distribution scheme for the i-th member in the supply chain after modification. Equation (36) indicates the difference between the comprehensive evaluation value of the i-th member and the average level value, where ${\sum }_{\mathrm{t}=1}^{\mathrm{n}}∆{\mathsf{\lambda }}_{\mathrm{i}}=0$. Equation (37) represents the comprehensive evaluation value of the influencing factors for the i-th member, where ${\sum }_{\mathrm{t}=1}^{\mathrm{n}}{\mathsf{\lambda }}_{\mathrm{i}}=1$ and where ${\mathrm{C}}_{\mathrm{i}}$ is the closeness coefficient calculated via the TOPSIS method.

3. Results

References [30,31] assume that the relationship between the market demand Q and a certain agricultural product is related to its sales price and sales effort level, satisfying $\mathrm{Q}({\mathrm{p}}_3,\mathrm{x})=\mathrm{10,000}-200{\mathrm{p}}_3+800\mathrm{x}$, where $\mathsf{\alpha }=\mathrm{10,000}$, $\mathsf{\beta }=200$, and $\mathsf{\gamma }=800$. The cost of sales effort investment by the retailers is ${\mathrm{c}}_5={\displaystyle \frac{1}{2}}\mathsf{\delta }{\mathrm{x}}^2={4\mathrm{x}}^2$, with $\mathsf{\delta }$ = 8. The farmer’s unit input cost is ${\mathrm{c}}_1$ = 8 CNY/kg, the cooperative’s unit processing cost is ${\mathrm{c}}_2=2$ CNY/kg, the unit transportation cost is ${\mathrm{c}}_3=1$ CNY/kg, and the retailer’s unit sales input cost is ${\mathrm{c}}_4=3$ CNY/kg. Assume that over a given period, the risk bearing, effort level, financial investment, and information acquisition of the three members are as shown in Table 1.

The comprehensive weights of the four correction factors—risk-bearing capacity, cooperation (effort) level, capital input, and information acquisition—were obtained by combining the Delphi expert consultation method with gray relational analysis. First, several domain experts were invited to score the relative importance of each factor. After two rounds of Delphi consultation, the experts’ opinions converged, and the mean importance scores for the four factors were obtained. Second, taking the vector composed of the maximum mean scores as the reference sequence, the original data were normalized, and the gray relational coefficients and relational degrees of each factor were calculated (distinguishing coefficient $\mathsf{\xi }=0.5$). Finally, the relational degrees are normalized to yield the comprehensive weights ${\mathsf{\omega }}_{\mathrm{i}}=(0.27, 0.24, 0.23, 0.26)$.

Equation (30) shows that the optimal value of the additional investment coefficient for product quality is ${\mathrm{x}}^{\mathrm{*}\mathrm{*}}=\mathrm{l}\mathrm{a}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{w}({\displaystyle \frac{\mathsf{\gamma }}{\mathsf{\delta }\mathsf{\beta }}})=$ 0.3517. Substituting this value into the preceding formulas yields the following:

(1)

Under decentralized decision-making, the payoffs of the respective stakeholders are as follows:

Optimal Revenue of Farmers:

${\mathsf{\pi }}_1^{\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{16\mathsf{\beta }}}=\mathrm{16,828}$ CNY, ${\mathrm{p}}_1^{\mathrm{*}}=26.3456$ CNY/kg

Optimal Revenue of Cooperatives:

${\mathsf{\pi }}_2^{\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{32\mathsf{\beta }}}=8414.1$ CNY, ${\mathrm{p}}_2^{\mathrm{*}}=38.5184$ CNY/kg

Optimal Revenues of Retailers:

${\mathsf{\pi }}_3^{\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }(1-{\mathrm{e}}^{-\mathrm{x}})-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{64\mathsf{\beta }}}=4207$ CNY, ${\mathrm{p}}_3^{\mathrm{*}}=46.5996$ CNY/kg

${\mathrm{q}}^{\mathrm{*}}=917.2816$ kg

(2)

The system-wide optimal profit of the supply chain under centralized decision-making is as follows:

${\mathsf{\pi }}^{\mathrm{*}\mathrm{*}}={\displaystyle \frac{{\left[\mathsf{\alpha }+\mathsf{\gamma }\left(1-{\mathrm{e}}^{-\mathrm{x}}\right)-\mathsf{\beta }(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4)\right]}^2}{4\mathsf{\beta }}}=\mathrm{67,312}$ CNY

${\mathrm{q}}^{\mathrm{*}\mathrm{*}}=3669.1$ kg, ${\mathrm{p}}_3^{\mathrm{*}\mathrm{*}}=32.8404$ CNY/kg

(3)

Benefit allocation among the players under the traditional Shapley value method:

Revenue of Farmers:

${\mathsf{\phi }}_1\left(\mathrm{v}\right)={\displaystyle \frac{{7\left[\mathsf{\alpha }+\mathsf{\gamma }\left(1-{\mathrm{e}}^{-\mathrm{x}}\right)-\mathsf{\beta }\left(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4\right)\right]}^2}{64\mathsf{\beta }}}=\mathrm{29,449}$ CNY

Revenue of Cooperatives:

${\mathsf{\phi }}_2\left(\mathrm{v}\right)={\displaystyle \frac{{11\left[\mathsf{\alpha }+\mathsf{\gamma }\left(1-{\mathrm{e}}^{-\mathrm{x}}\right)-\mathsf{\beta }\left(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4\right)\right]}^2}{128\mathsf{\beta }}}=\mathrm{23,139}$ CNY

Revenue of Retailers:

${\mathsf{\phi }}_3\left(\mathrm{v}\right)={\displaystyle \frac{{7\left[\mathsf{\alpha }+\mathsf{\gamma }\left(1-{\mathrm{e}}^{-\mathrm{x}}\right)-\mathsf{\beta }\left(\frac{1}{2}\mathsf{\delta }{\mathrm{x}}^2+{\mathrm{c}}_1+{\mathrm{c}}_2+{\mathrm{c}}_3+{\mathrm{c}}_4\right)\right]}^2}{128\mathsf{\beta }}}=\mathrm{14,725}$ CNY

(4)

Distribution of benefits among parties under the improved Shapley value method:

According to the TOPSIS method, the proximity values calculated from Equations (6)–(10) are $\mathrm{C}=(0.5349, 0.4563, 0.4062)$. According to Equations (36) and (37), the adjustment coefficient $∆\mathsf{\lambda }=(0.0494, -0.0068, -0.0426)$. Substituting these values into Equation (35), the profit distribution among the stakeholders is obtained as follows:

Revenue of Farmers:

${\mathsf{\phi }}_1^{\mathrm{\prime }}\left(\mathrm{v}\right)={\mathsf{\phi }}_1\left(\mathrm{v}\right)+\mathrm{v}\left(\mathrm{I}\right)∆{\mathsf{\lambda }}_1=\mathrm{32,774}$ CNY

Revenue of Cooperatives:

${\mathsf{\phi }}_2^{\mathrm{\prime }}\left(\mathrm{v}\right)={\mathsf{\phi }}_2\left(\mathrm{v}\right)+\mathrm{v}\left(\mathrm{I}\right)∆{\mathsf{\lambda }}_2=\mathrm{22,681}$ CNY

Revenue of Retailers:

${\mathsf{\phi }}_3^{\mathrm{\prime }}\left(\mathrm{v}\right)={\mathsf{\phi }}_3\left(\mathrm{v}\right)+\mathrm{v}\left(\mathrm{I}\right)∆{\mathsf{\lambda }}_3=\mathrm{11,857}$ CNY

(5)

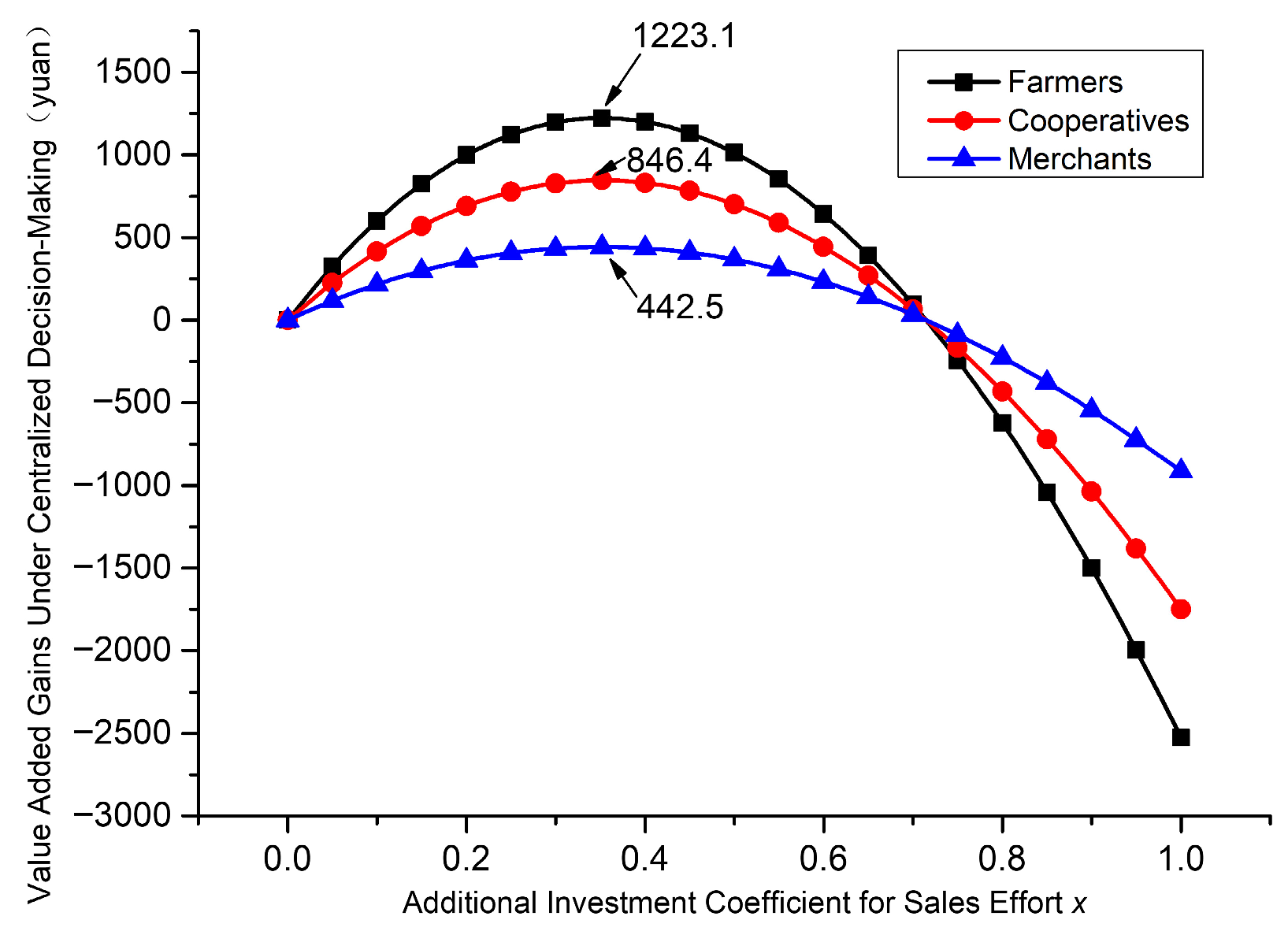
Effect of the additional investment coefficient of sales effort on the payoffs of all parties:

Figure 1 illustrates how the coefficient of additional investment in sales effort affects each party’s payoff under decentralized decision-making, whereas Figure 2 shows the corresponding effect under centralized decision-making. As indicated by Figure 1 and Figure 2, regardless of the decision regime, the relationship between the additional investment coefficient of sales effort (denoted xxx) and the stakeholders’ payoffs is convex, with a maximum at x = 0.3517. When x > 0.3517, the incremental payoff decreases as x increases and may even become negative. Under both decentralized and centralized decision-making, the value created (or the loss incurred) by sales effort is allocated predominantly to farmers and least to retailers, even though retailers are the primary contributors to sales effort—an allocation that is neither efficient nor equitable. Moreover, when the additional sales effort investment yields a negative incremental value, assigning the majority of the loss to farmers is likewise inappropriate.

Table 2. Incremental value allocation from additional investment in product quality.

Coefficient x	Decentralized Decision-Making			Centralized Decision-Making with Improved Shapley Value Method
	Farmers	Cooperatives	Retailers	Farmers	Cooperatives	Retailers
0.00	0	0	0	0.0	0.0	0.0
0.05	167	83.5	41.8	325.0	224.8	117.6
0.10	308	154	77	599.9	415.1	217.0
0.15	423	211.6	105.8	824.7	570.7	298.4
0.20	513	256.3	128.1	998.3	690.8	361.2
0.25	576	288.2	144.1	1122.9	777.1	406.3
0.30	615	307.4	153.7	1197.5	828.7	433.3
0.3517	628	314.1	157	1223.1	846.4	442.5
0.40	617	308.3	154.2	1200.8	831.0	434.5
0.45	581	290.3	145.2	1130.8	782.4	409.1
0.50	521	260.3	130.2	1013.9	701.6	366.8
0.55	437	218.4	109.2	851.4	589.1	308.1
0.60	330	165	82.5	642.2	444.3	232.3
0.65	200	100.1	50.1	389.6	269.5	140.9
0.70	48	24.2	12.1	94.6	65.4	34.3
0.75	−125	−62.6	−31.3	−243.7	−168.7	−88.1
0.80	−320	−160	−80	−623.2	−431.3	−225.5
0.85	−535	−267.6	−133.8	−1042.7	−721.7	−377.3
0.90	−770	−385.1	−192.6	−1500.2	−1038.2	−542.7
0.95	−1025	−512.3	−256.1	−1995.4	−1381.0	−721.9
1.00	−1297	−648.6	−324.3	−2526.3	−1748.3	−913.9

presents the allocation of the incremental value generated by additional investment in product sales effort under decentralized and centralized decision-making. The incremental value realized under decentralization is lower than that under centralization. Under decentralized decision-making, the value added is apportioned among farmers, cooperatives, and retailers at a 4:2:1 ratio, whereas under centralized decision-making, the corresponding ratio is 2.76:1.91:1.

4. Discussion

The preceding empirical results clearly show that the total payoff under centralized decision-making (CNY 67,312) is markedly greater than that under decentralized decision-making (CNY 29,449.1), as reported in

Table 3. Revenue values under different decision-making scenarios.

Collaborative Entity	Decentralized Decision-Making		Centralized Decision-Making
		Total	Traditional Shapley Value Method	Improved Shapley Value Method	Modified Value	Total
Farmers	16,828	29,449.1	29,449	32,774	3325	67,312
Cooperatives	8414.1		23,139	22,681	−458
Retailers	4207		14,725	11,857	−2868

. This aligns with prior findings [36], indicating that the research design adopted here is valid and further underscoring the value and advantages of the Shapley value method in allocating supply chain profits. In the ‘farmer–commerce docking’ supply chain, decentralized decisions trigger rent-seeking among members, which erodes the total supply chain profit; in contrast, under centralized decision-making, key actors—farmers, cooperatives, and retailers—generate sufficient premium surplus through continuous innovation in product quality, production methods, industrial organization, and market development [37,38]. Moreover, the unit retail price of agricultural products is lower under centralized decision-making than under decentralized decision-making—specifically, ${\mathrm{p}}_3^{\mathrm{*}\mathrm{*}}=32.8404$ CNY/kg < ${\mathrm{p}}_3^{\mathrm{*}}=46.5996$ CNY/kg/kg—implying that consumers can purchase agricultural goods at lower prices, thereby achieving a win–win outcome for both consumers and the farmer–commerce supply chain.

To ensure that the tripartite total profit of farmers, cooperatives, and retailers is maximized under the ‘farm–retail linkage’ model, it is also essential to guarantee fair and reasonable profit allocation among the three parties; otherwise, the supply chain alliance will be unsustainable [39]. The traditional Shapley value method, when applied in practice, overlooks the sources of incremental benefits after the supply chain is formed—namely, that participants differ in risk bearing, effort levels, capital investment, and information acquisition—so that each party’s contribution to alliance stability is not the same. In contrast, the improved Shapley value method incorporates these factors and adjusts the allocation results accordingly, yielding a more equitable and reasonable distribution. As shown in Table 3, under the improved Shapley value method, the profits accruing to farmers, cooperatives, and retailers increase from CNY 16,828, CNY 8414.1, and CNY 4207 under decentralized decision-making to CNY 32,774, CNY 22,681, and CNY 11,857, respectively. All three parties experience profit growth after forming the alliance, and such increases in their individual payoffs help stabilize the agri-retail supply chain.

The rationality of allocating the incremental value generated by additional sales effort directly affects retailers’ incentives to increase sales effort and, in turn, the supply chain’s overall profit. Reference [40] examines how supermarket effort intensity influences market demand for agricultural products and proposes a profit-sharing contract based on effort-cost sharing to achieve win–win outcomes for all supply chain members. Reference [41] constructs a consumer utility function that includes farmers’ production-effort levels and uses a profit-sharing contract to coordinate the supply chain. While these studies use contractual mechanisms to secure the effort provider’s payoff and thereby sustain incentives, the reasonableness of such contracts can be difficult to guarantee in practice. As shown in Table 2, the allocation ratio of the incremental value from additional sales effort under decentralized decision-making is farmer–cooperative–retailer = 4:2:1, and that under centralized decision-making is 2.76:1.91:1. In both cases, the retailer receives the smallest share; allocating the least profit to the party that supplies the sales effort is clearly unreasonable. Since retailers are the primary providers of sales effort, they should receive the largest share to effectively motivate them. Moreover, when allocating the incremental value generated by additional sales effort, the interests of farmers and cooperatives should also be considered to maintain supply chain stability. On this basis, this paper proposes an effort-based (‘more effort, more return’) allocation rule: the extra income attributable to sales effort is allocated such that farmers and cooperatives receive only the profit stemming from sales-volume growth induced by that effort, whereas the residual accrues to the effort-providing retailer. The specific allocation is as follows:

$${\mathsf{\phi }}_1^{\mathrm{\prime }}\left(\mathrm{x}\right)={\mathsf{\phi }}_1\left(0\right)+∆\mathrm{q}(\mathrm{x}){\displaystyle \raisebox{1ex}{${\mathsf{\phi }}_1\left(0\right)$}\!\left/ \!\raisebox{-1ex}{$\mathrm{q}(0)$}\right.}$$

(38)

$${\mathsf{\phi }}_2^{\mathrm{\prime }}\left(\mathrm{x}\right)={\mathsf{\phi }}_2\left(0\right)+∆\mathrm{q}(\mathrm{x}){\displaystyle \raisebox{1ex}{${\mathsf{\phi }}_2\left(0\right)$}\!\left/ \!\raisebox{-1ex}{$\mathrm{q}(0)$}\right.}$$

(39)

$${\mathsf{\phi }}_3^{\mathrm{\prime }}\left(\mathrm{x}\right)=∆\mathsf{\phi }(\mathrm{x})-{\mathsf{\phi }}_2^{\mathrm{\prime }}\left(\mathrm{x}\right)-{\mathsf{\phi }}_1^{\mathrm{\prime }}\left(\mathrm{x}\right)$$

(40)

The value-added allocation of sales effort proposed in this study is presented in

Table 4. Incremental revenue allocation for additional sales effort (performance-based distribution).

Coefficient x	Centralized Decision-Making
	Improved Shapley Value Method			Value Redistribution (Performance-Based Distribution)
	Farmers	Cooperatives	Retailers	Farmers	Cooperatives	Retailers
0.00	0.0	0.0	0.0	0.0	0.0	0.0
0.05	325.0	224.8	117.6	162.1	112.2	393.7
0.10	599.9	415.1	217.0	298.9	206.8	726.3
0.15	824.7	570.7	298.4	409.3	283.2	1000.5
0.20	998.3	690.8	361.2	495.2	342.7	1212.1
0.25	1122.9	777.1	406.3	556.5	385.1	1363.3
0.30	1197.5	828.7	433.3	593.3	410.6	1455.1
0.3517	1223.1	846.4	442.5	605.6	419.1	1487.3
0.40	1200.8	831.0	434.5	595.1	411.8	1459.1
0.45	1130.8	782.4	409.1	560.0	387.6	1375.4
0.50	1013.9	701.6	366.8	503.1	348.1	1230.8
0.55	851.4	589.1	308.1	422.4	292.3	1033.2
0.60	642.2	444.3	232.3	319.9	221.4	778.7
0.65	389.6	269.5	140.9	194.6	134.6	471.8
0.70	94.6	65.4	34.3	47.3	32.8	112.9
0.75	−243.7	−168.7	−88.1	−121.8	−84.3	−294.9
0.80	−623.2	−431.3	−225.5	−312.9	−216.5	−750.6
0.85	−1042.7	−721.7	−377.3	−525.9	−363.9	−1251.2
0.90	−1500.2	−1038.2	−542.7	−759.0	−525.2	−1796.8
0.95	−1995.4	−1381.0	−721.9	−1014.0	−701.7	−2382.2
1.00	−2526.3	−1748.3	−913.9	−1290.1	−892.8	−3006.1

. Under centralized decision-making, the allocation ratio shifts from farmers–cooperatives–retailers = 2.76:1.91:1 to 1.45:1:3.5. The retailer’s allocated share of value added increases markedly, safeguarding retailers’ returns and incentives while still ensuring value-added gains for farmers and cooperatives and thereby sustaining the stability of the supply chain.

Figure 3 depicts a contribution-based (‘more work, more pay’) allocation scheme. The retailer receives the largest share of the value-added returns so that the majority of gains or losses arising from sales effort are borne by the retailers, thereby incentivizing adequate investment in sales effort. Moreover, a portion of the value-added returns is allocated to farmers and cooperatives to increase their willingness to collaborate.

5. Conclusions

5.1. Main Conclusions

This paper centers on ‘sales effort’ and establishes a three-tier chain—farmers–cooperatives–retailers—within a simultaneous pricing–effort–order quantity model, comparing decentralized and centralized decision structures. Building on the traditional Shapley value, we introduce a composite adjustment factor set (risk bearing, degree of cooperation, capital investment, and information acquisition) and compute closeness coefficients via TOPSIS to obtain improved Shapley-based allocation coefficients. We further propose a secondary allocation rule—‘effort value added distributed according to labor’—to ensure adequate marginal incentives for the parties that undertake sales effort. The main findings are as follows:

Initially, under centralized decision-making, the total supply chain profit is significantly greater than that under decentralized decision-making, indicating that centralization improves supply chain efficiency. Moreover, the retail price per unit of agricultural product is lower under centralization than under decentralization, enabling customers to purchase at lower prices and thereby promoting a win–win outcome for consumers and the agri-retail supply chain.

Second, by incorporating adjustment factors such as risk bearing, effort intensity, capital investment, and information acquisition capability and improving the traditional Shapley value method through the Delphi–gray relational analysis approach and the TOPSIS method, profit allocation among supply chain alliance members becomes fairer and more reasonable. Although the benefits accruing to cooperatives and retailers decrease relative to the initial (unadjusted) Shapley allocation, they remain substantially higher than the payoffs in the noncooperative baseline. Centralized decision-making and refined distribution schemes can provide quantitative grounds for government departments, cooperatives, and e-commerce platforms to design profit-sharing rules and subsidy policies within ‘agriculture–commerce integration’ and ‘agricultural produce uplift’ projects. This approach helps prevent alliance instability arising from egalitarianism or unilateral dominant bargaining power.

Third, in both decentralized and centralized regimes, the coefficient of additional investment in sales effort directly affects each party’s payoff, with payoffs exhibiting a convex relationship. Moreover, a comparative analysis of allocation shares under decentralized and centralized decisions shows that retailers—the primary contributors to sales effort—receive the smallest share, which undermines their incentives.

Finally, to increase both efficiency and equity in the supply chain, the allocation mechanism should be optimized to avoid adverse effects on sales effort providers and other members arising from unreasonable benefit distributions. We propose a ‘more effort, larger share’ scheme whereby the party bearing the main sales effort burden receives a higher allocation while still accommodating the interests of the other parties. In this way, retailer incentives are strengthened, and supply chain stability and sustained returns are preserved. Refining the Shapley–TOPSIS model and the secondary distribution mechanism of ‘more work, more gain’ can serve as a parameter calibration tool for local cooperatives and e-commerce enterprises during contract negotiations. This facilitates the assessment of equitable profit-sharing ratios under varying scenarios of risk-sharing arrangements, capital investment levels, and information asymmetry.

5.2. Contributions and Limitations

Contributions. From the perspective of agricultural supply chain management and policy, the research findings indicate that within the three-tiered chain of ‘farmers–cooperatives–retailers’, centralized decision-making and improved profit-sharing mechanisms can enhance overall returns while simultaneously addressing structural equity and incentive compatibility. This finding offers guidance for government departments seeking to refine agricultural supply chain governance systems: first, encouraging farmers, cooperatives, and new business entities such as e-commerce platforms to form stable alliances through contract farming, long-term cooperation agreements and joint investment; second, utilizing fiscal subsidies, tax relief, and interest-subsidized loans to guide stakeholders toward increased investment in critical areas such as quality enhancement, cold chain logistics, and digital marketing; and finally, advancing the establishment of agricultural product quality standards, traceability systems, and information-sharing platforms on a broader scale. This would reduce information asymmetry and market access barriers for farmers and small cooperatives, thereby creating an institutional foundation for equitable and reasonable profit distribution. In managing supply chain members, cooperatives and merchants should comprehensively consider multidimensional factors such as risk-bearing capacity, capital investment, and sales efforts when designing profit-sharing schemes, avoiding reliance on quantity or price as the sole basis. On the basis of the proposed ‘enhanced Shapley–TOPSIS+ merit-based distribution’ mechanism, managers can make intangible contributions such as sales efforts, brand investment, and channel expansion explicit. These become crucial references for adjusting profit-sharing ratios, performance evaluations, and incentive mechanisms. Concurrently, by integrating local policies such as ‘Digital Village’ and ‘agricultural produce uplift initiatives,’ complementary schemes that link government subsidies and platform commission reductions to supply chain performance can be explored. This approach enhances the sustainable operational capacity of agribusiness–consumer-interconnected supply chains within the context of rural revitalization.

Limitations. First, the model relies primarily on simplified assumptions of a single cycle, deterministic demand, and a single-interface mode, failing to adequately capture more complex real-world scenarios, such as multicycle dynamic games, random fluctuations in demand, and the coexistence of multiple platforms. Second, the level of sales effort and related parameters are mainly based on the literature and hypothetical settings and lack systematic empirical data support from different regions and multiple agricultural product categories. Future research may advance in the following directions: first, within a multiperiod or rolling decision framework, factors such as random demand disturbances, platform commissions, and return rates should be incorporated to examine the long-term effects of different policy variables on alliance stability and profit distribution; second, questionnaire surveys, operational data, and experimental simulations should be combined to conduct empirical estimation and sensitivity analysis of key parameters such as sales effort and risk preference; and third, sustainability metrics such as green production and carbon emission constraints should be integrated into revenue distribution models to establish multiobjective economic–environmental coordination mechanisms for agricultural supply chains, thereby enriching theoretical frameworks and enhancing the practical applicability of research conclusions.