Developing a Model for Determining the Charging Station Location for Electric Vehicles
Abstract
1. Introduction
2. Flow Capturing Location Model and Flow Refueling Location Model
3. Prepare Initial Solution
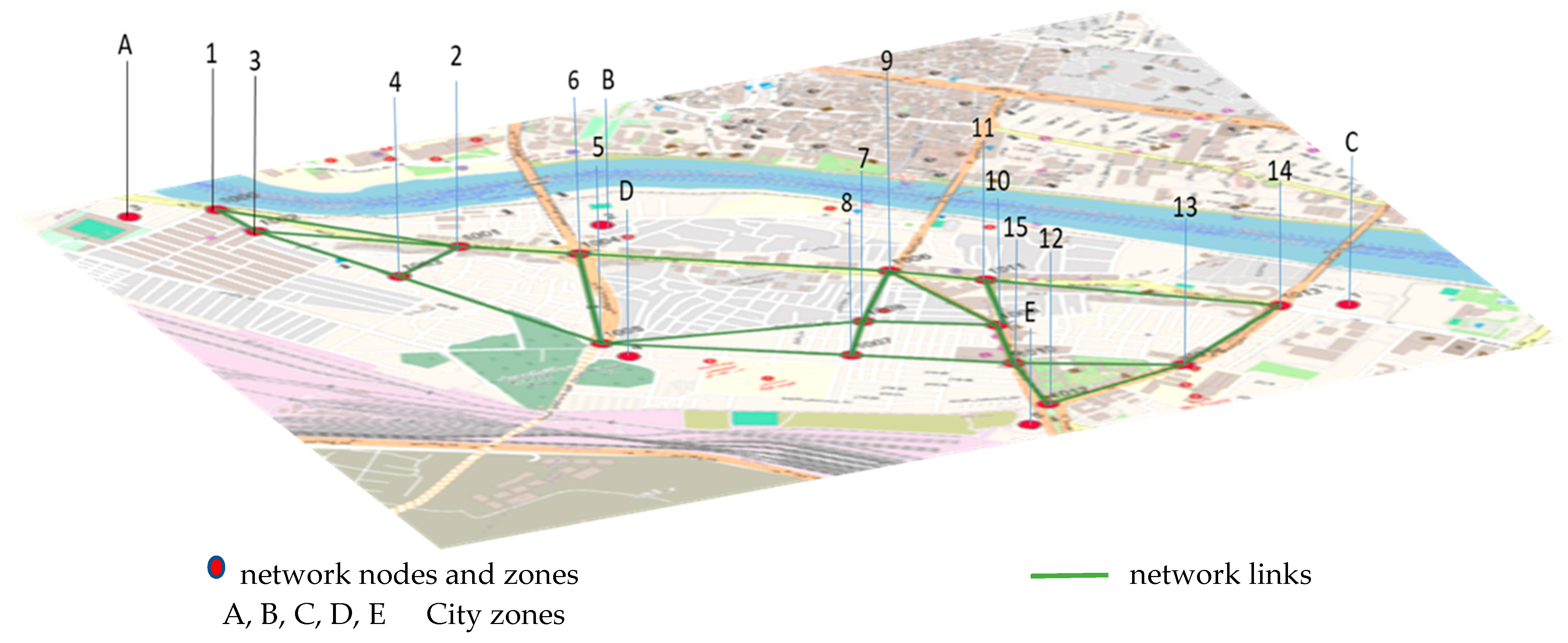
- Identify the Traffic Flow Network
- 2.
- Calculate Path Requirements
- 3.
- Connect Nodes and Determine Station Numbers
Case Study and Solution Procedures
- The location experiences exceptionally high traffic volumes on two approaches.
- The location is located along an expressway that intersects with two secondary streets.
- A concentration of locations for commercial or other socio-economic activities are situated in proximity to the intersection [33].
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raihan, A.; Rashid, M.; Voumik, L.C.; Akter, S.; Esquivias, M.A. The dynamic impacts of economic growth, financial globalization, fossil fuel, renewable energy, and urbanization on load capacity factor in Mexico. Sustainability 2023, 15, 13462. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, S.; Liu, J.; Sun, H. Network of tourism–industrial complex in cities: Typologies and implications through a critical literature review. Int. J. Environ. Res. Public Health 2022, 19, 4934. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, Å.L.; Lindberg, K.B.; Sartori, I.; Andresen, I. Analysis of residential EV energy flexibility potential based on real-world charging reports and smart meter data. Energy Build. 2021, 241, 110923. [Google Scholar] [CrossRef]
- Davidov, S.; Pantoš, M. Optimization model for charging infrastructure planning with electric power system reliability check. Energy 2019, 166, 886–894. [Google Scholar] [CrossRef]
- Hamwi, H.; Rushby, T.; Mahdy, M.; Bahaj, A.S. Effects of high ambient temperature on electric vehicle efficiency and range: Case study of Kuwait. Energies 2022, 15, 3178. [Google Scholar] [CrossRef]
- Shen, Z.-J.M.; Feng, B.; Mao, C.; Ran, L. Optimization models for electric vehicle service operations: A literature review. Transp. Res. Part B Methodol. 2019, 128, 462–477. [Google Scholar] [CrossRef]
- Yuvaraj, T.; Devabalaji, R.K.; Kumar, J.A.; Thanikanti, S.B.; Nwulu, N.I. A comprehensive review and analysis of the allocation of electric vehicle charging stations in distribution networks. IEEE Access 2024, 12, 5404–5461. [Google Scholar] [CrossRef]
- Lin, W.; Hua, G. The flow capturing location model and algorithm of electric vehicle charging stations. In Proceedings of the 2015 International Conference on Logistics, Informatics and Service Sciences (LISS), Barcelona, Spain, 27–29 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Hopkins, E.; Potoglou, D.; Orford, S.; Cipcigan, L. Can the equitable roll out of electric vehicle charging infrastructure be achieved? Renew. Sustain. Energy Rev. 2023, 182, 113398. [Google Scholar] [CrossRef]
- Capar, I.; Kuby, M.; Leon, V.J.; Tsai, Y.-J. An arc cover–path-cover formulation and strategic analysis of alternative-fuel station locations. Eur. J. Oper. Res. 2013, 227, 142–151. [Google Scholar] [CrossRef]
- Daşcıoğlu, B.G.; Tuzkaya, G.; Kılıç, H.S. A model for determining the locations of electric vehicles’ charging stations in Istanbul. Pamukkale Üniver. Mühendis. Bilim. Derg. 2019, 25, 1056–1061. [Google Scholar] [CrossRef]
- Hodgson, M.J. A flow-capturing location-allocation model. Geogr. Anal. 1990, 22, 270–279. [Google Scholar] [CrossRef]
- Xiao, S.; Lei, X.; Huang, T.; Wang, X. Coordinated planning for fast charging stations and distribution networks based on an improved flow capture location model. CSEE J. Power Energy Syst. 2022, 9, 1505–1516. [Google Scholar] [CrossRef]
- Saksuriya, P.; Likasiri, C. Balancing Staff Finishing Times vs. Minimizing Total Travel Distance in Home Healthcare Scheduling. Appl. Sci. 2024, 14, 7381. [Google Scholar] [CrossRef]
- Sugishita, N.; Carvalho, M.; Atallah, R. The Strength of Fuel Refueling Location Problem Formulations. arXiv 2024, arXiv:2409.04554. [Google Scholar] [CrossRef]
- Abbaas, O.; Ventura, J.A. An edge scanning method for the continuous deviation-flow refueling station location problem on a general network. Networks 2022, 79, 264–291. [Google Scholar] [CrossRef]
- Isaac, N.; Saha, A.K. A review of the optimization strategies and methods used to locate hydrogen fuel refueling stations. Energies 2023, 16, 2171. [Google Scholar] [CrossRef]
- Hernández, B.; Alkayas, A.; Azar, E.; Mayyas, A.T. Mathematical model for the placement of hydrogen refueling stations to support future fuel cell trucks. IEEE Access 2021, 9, 148118–148131. [Google Scholar] [CrossRef]
- Lin, C.-C.; Lin, C.-C. The p-center flow-refueling facility location problem. Transp. Res. Part B Methodol. 2018, 118, 124–142. [Google Scholar] [CrossRef]
- Scheiper, B. Strategic Planning of Charging Infrastructure for Battery Electric Vehicles Considering Interactions with the Energy Sector. Ph.D. Dissertation, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 2021. [Google Scholar]
- Kchaou-Boujelben, M. Charging station location problem: A comprehensive review on models and solution approaches. Transp. Res. Part C Emerg. Technol. 2021, 132, 103376. [Google Scholar] [CrossRef]
- Spencer, R.L.; Ware, M. Introduction to MATLAB; Brigham Young University: Provo, UT, USA, 2008; Volume 7, p. 2008. [Google Scholar]
- Capar, I.; Kuby, M. An efficient formulation of the flow refueling location model for alternative-fuel stations. IIE Trans. 2012, 44, 622–636. [Google Scholar] [CrossRef]
- Hodgson, M.J.; Rosing, K.E.; Leontien, A.; Storrier, G. Applying the flow-capturing location-allocation model to an authentic network: Edmonton, Canada. Eur. J. Oper. Res. 1996, 90, 427–443. [Google Scholar] [CrossRef]
- Hwang, S.W.; Kweon, S.J.; Ventura, J.A. An alternative fuel refueling station location model considering detour traffic flows on a highway road system. J. Adv. Transp. 2020, 2020, 9473831. [Google Scholar] [CrossRef]
- Park, T. A heuristic approach to the location of the refueling stations for the alternative fuel vehicles. ICIC Express Lett. Part B Appl. 2017, 8, 519–524. [Google Scholar]
- Kuby, M.; Lim, S. The flow-refueling location problem for alternative-fuel vehicles. Socio-Econ. Plan. Sci. 2005, 39, 125–145. [Google Scholar] [CrossRef]
- Hodgson, M.J. Developments in flow-based location-allocation models. In Econometric Advances in Spatial Modelling and Methodology: Essays in Honour of Jean Paelinck; Springer: Boston, MA, USA, 1998; pp. 119–132. [Google Scholar]
- Tong, D.; Murray, A.T. Location analysis: Developments on the horizon. In Regional Research Frontiers-Vol. 2: Methodological Advances, Regional Systems Modeling and Open Sciences; Springer: Cham, Switzerland, 2017; pp. 193–208. [Google Scholar]
- Mohamedmeki, M.Z.; Al-Mumaiz, M. Improving the transportation system in Baghdad city. In IOP Conference Series: Materials Science and Engineering, Proceeding of the 4th International Conference on Engineering Sciences (ICES 2020), Kerbala, Iraq, 5–6 December 2020; IOP Publishing: Bristol, UK, 2021; Volume 1067, p. 012087. [Google Scholar]
- Ali, S.M.; Al-hemiary, E. Baghdad Vehicle Traffic Congestion: Case Study. Avrupa Bilim Teknol. Derg. 2023, 48, 34–39. [Google Scholar]
- Alkaissi, Z.A. Capacity Estimation of Urban Road in Baghdad City: A Case Study of Palestine Arterial Road. ARPN J. Eng. Appl. Sci. 2018, 13, 8456–8484. [Google Scholar]
- Abdulkareem, M.; Mohammed, A.; Khudair, M. Evaluation and improvement of traffic operation for al-furat signalized intersection in Baghdad city. Int. J. Eng. Res. Ind. Appl. 2016, 9, 15–25. [Google Scholar]
| Model | Equation | Mathematical Formulation | Detailed Explanation | EV Interpretation |
|---|---|---|---|---|
| FCLM (Flow Capture Location Model) | (1) | Objective function: maximize the total weighted flow covered by stations. Each flow Z has a weight fq (e.g., number of vehicles). | Ensures that the placement of stations captures the maximum traffic flow of EVs on major roads. | |
| (2) | Coverage constraint: a flow Z is covered if there is at least one station along its candidate path Nq. | An EV trip is considered feasible if at least one charging station lies on the route. | ||
| (3) | Station budget: exactly P stations must be located among all candidate sites Nq. | Limits the number of charging stations due to budget or infrastructure constraints. | ||
| (4) | Binary variables: xk = 1 if a station is built at site i; yq = 1 if flow k is covered. | Indicates yes/no decision: whether to build a station or whether a trip is covered. | ||
| FRLM (Flow Refueling Location Model) | (5) | Objective: maximize the total demand (flows) that can be fully refueled across complete routes. Each route Z has weight fq. | Focuses on ensuring entire trips (not just parts) are possible for EVs. | |
| (6) | Feasibility constraint: for each route q, and for each sub segment h, there must be at least one station in the feasible interval yq. | Guarantees EVs can refuel/charge within driving range limits on all trip segments. | ||
| (7) | A facility combination h is “open” (uh = 1) only if all its required stations are sited (xi = 1) | ahi: equals 1 if facility i belongs to combination h. | ||
| (8) | Station budget: at most, p stations can be built. | Models real-world financial/policy limitations in charging station rollout. | ||
| (9) | Binary variables: xi = 1 if a station is built at site i; yq = 1 if route p is fully covered. | Ensures a binary outcome: a route is either feasible for EVs or not. |
| Symbol | Definition |
|---|---|
| Z | Objective function: total flow volume captured at least once |
| p | Number of facilities to be located |
| Q | Set of all O–D pairs |
| H | Set of all potential facility combinations |
| Nq | set of potential facility locations capable of capturing q |
| q | Index of origin–destination (O–D) pairs (and their shortest paths) |
| h | Index of facility combinations |
| i | Index of potential facility locations |
| f₍q₎ | Flow volume on the shortest path between O–D pair q |
| b₍qh₎ | Coefficient = 1 if facility combination h can refuel O–D pair q; 0 otherwise |
| a₍hi₎ | Coefficient = 1 if facility iii is included in combination h; 0 otherwise |
| y₍q₎ | Binary variable = 1 if flow fq is captured, 0 otherwise |
| u₍h₎ | Binary variable = 1 if all facilities in combination h are open, 0 otherwise |
| x₍i₎ | Binary variable = 1 if a facility is located at site k, 0 otherwise |
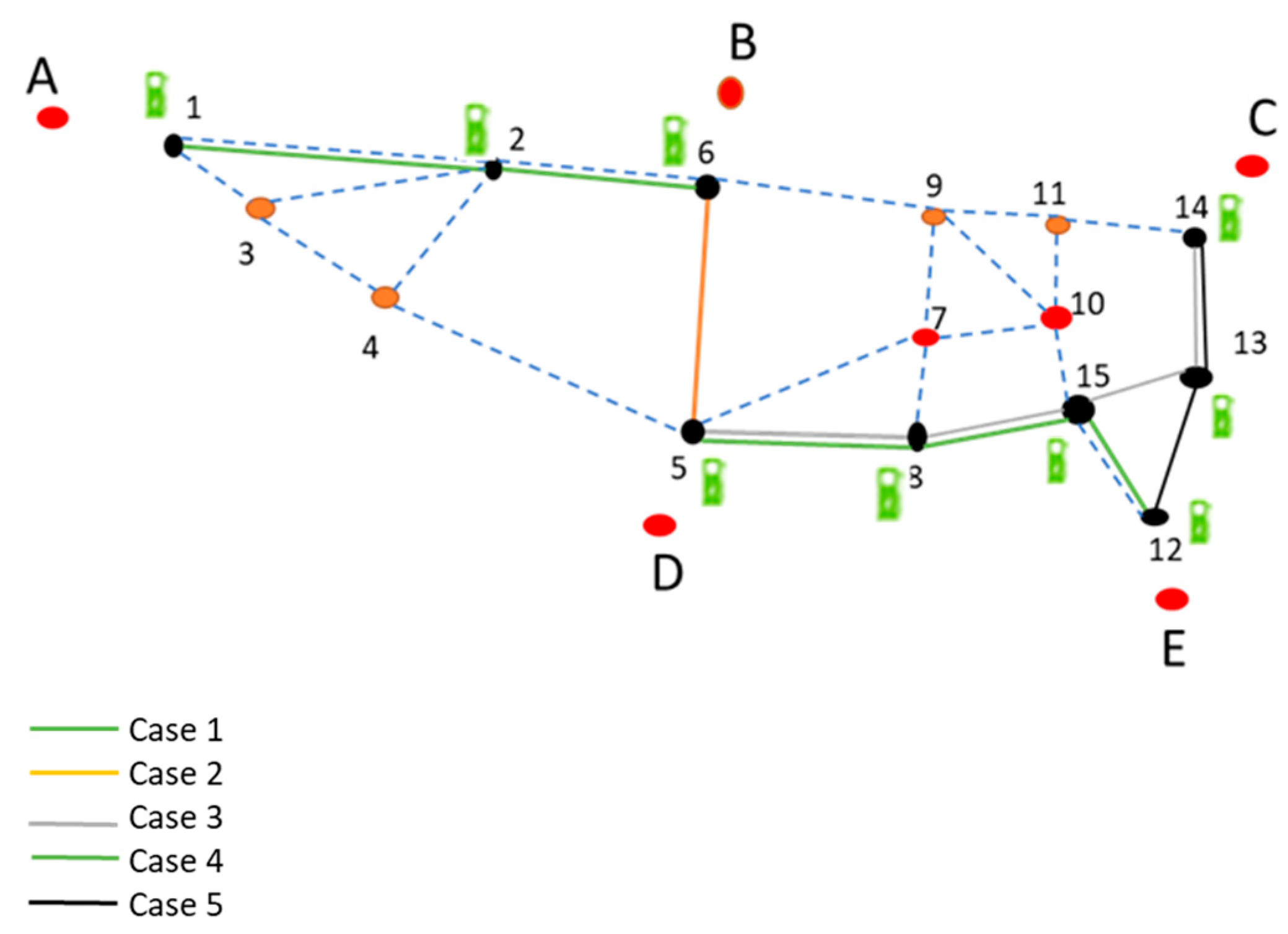
| First Node (Origin) | A | B | D | E | C | 1 | 1 | 3 | 4 | 2 | 5 | 11 | 15 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Second Node (destination) | 1 | 6 | 5 | 12 | 14 | 2 | 3 | 4 | 5 | 6 | 6 | 9 | 10 | 11 |
| Mileage | connector | connector | connector | connector | connector | 59 | 15 | 61 | 61 | 27 | 56 | 22 | 23 | 70 |
| First Node (origin) | 6 | 9 | 9 | 7 | 8 | 8 | 10 | 8 | 12 | 15 | 11 | 14 | 12 | |
| Second Node (destination) | 9 | 7 | 10 | 5 | 5 | 7 | 7 | 15 | 15 | 13 | 10 | 13 | 13 | |
| Mileage | 72 | 30 | 40 | 62 | 57 | 20 | 30 | 37 | 25 | 40 | 25 | 42 | 39 |
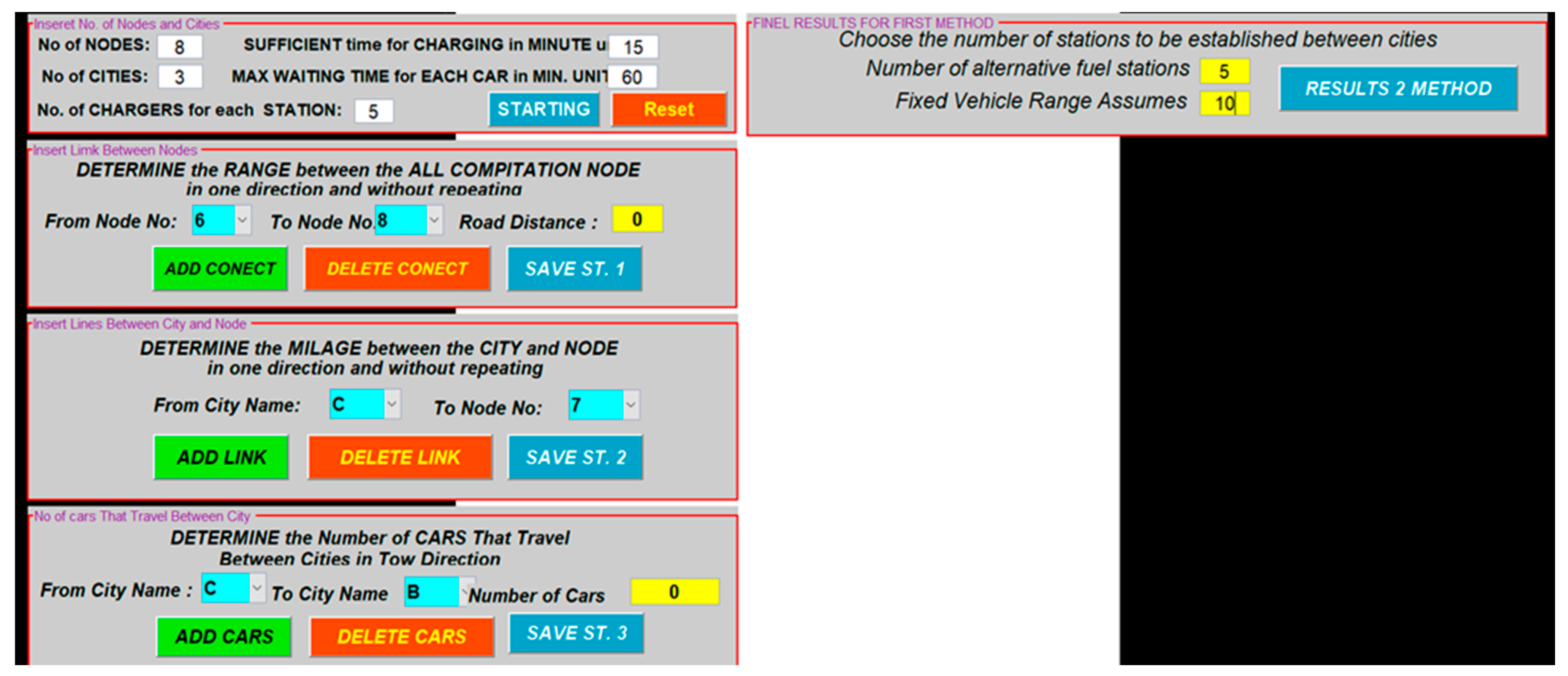
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of nodes | 15 | Distance between O–D | Table 1 |
| Number of cities | 5 | Connection between every city with nodes | Table 1 |
| Sufficient time to charge in min | 30 | Traffic flow between each city | 23,702 |
| Maximum time for each vehicle in min. | 60 | Number of alternative stations | 5 |
| Number of chargers in each station | 5 | Fixed vehicle range assumed | 60 |
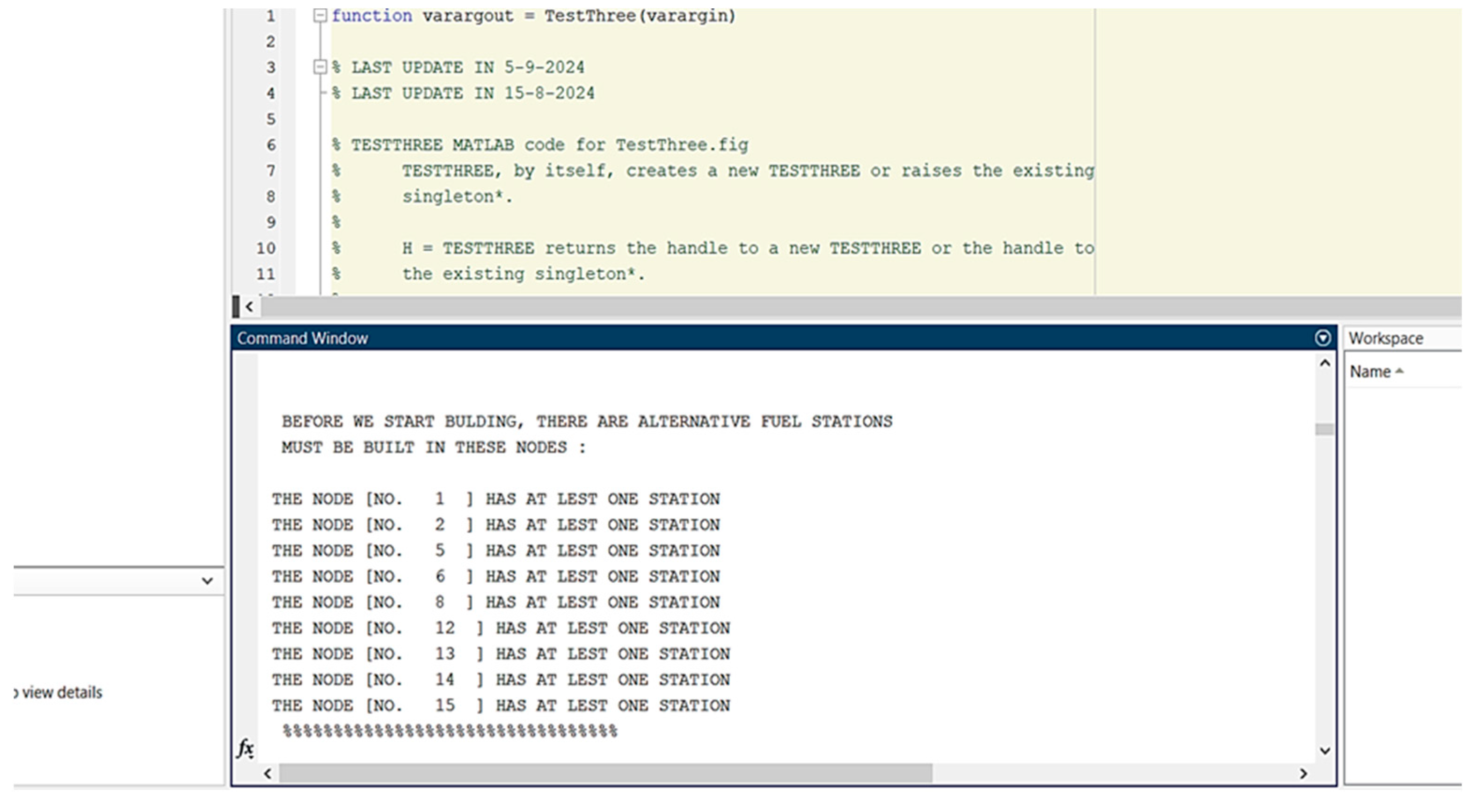
| No | Fifth Panel—Mark the Station Exits in Each Node |
|---|---|
| 1 | Nodeic = Nodeic + 1; % (3 Times in our Example, A, B and C) |
| 2 | for idm = 1: NONode |
| 3 | if(id~ = idm) % JUST when ‘A’ != ‘A’ and ‘B’ != ‘B’ and so means (1 != 1) and(2 != 2) and so |
| 4 | if(isempty(str2num(G.Nodes.Name{idm}))) % JUST if (id) is CHAR ‘A’ ‘B’ ‘C’ |
| 5 | % just for [6 Times] in our Example (3 cites * tow way) |
| 6 | [P,d] = shortestpath(G,G.Nodes.Name{id},G.Nodes.Name{idm}); |
| 7 | NewP = “”; |
| 8 | namesToInteger= []; |
| 9 | for i = 1: size(P, 2) |
| 10 | NewP = strcat(NewP, string (P(i))); |
| 11 | End |
| 12 | TZN= [TZN; NewP]; |
| 13 | for i = 1: size(P,2) % for each [P] covert it to integer |
| 14 | if i == 1 |
| 15 | namesToInteger(i) = id; |
| 16 | elseif i == size(P,2) |
| namesToInteger(i) = idm; | |
| Else | |
| if isletter(string(P(i))) | |
| [Ro Col]= find (CityNodeLink == string(P(i))); | |
| namesToInteger(i) = CityNodeLink(Ro, 2); | |
| Else | |
| . | |
| . | |
| . | |
| . | |
| ss = 0; | |
| comb = []; | |
| comb2 = []; | |
| for k =1: size(nam,1) | |
| h = nam(k, :); | |
| if A1(h(1,1), h(1,2)) >= 1 | |
| if (ps (1) == char(CarsInPath(k,1))) && (ps(end) == char(CarsInPath(k,2))) | |
| NoCAR= CarsInPath(k,3); % TO BRING NO OF CARS FOR ALL PATHES | |
| kk = 0; | |
| for j = 1: length(ps) | |
| for m = 1: length(NodeName) | |
| if (ps(j) == char(NodeName(m))) | |
| 1622 | End |
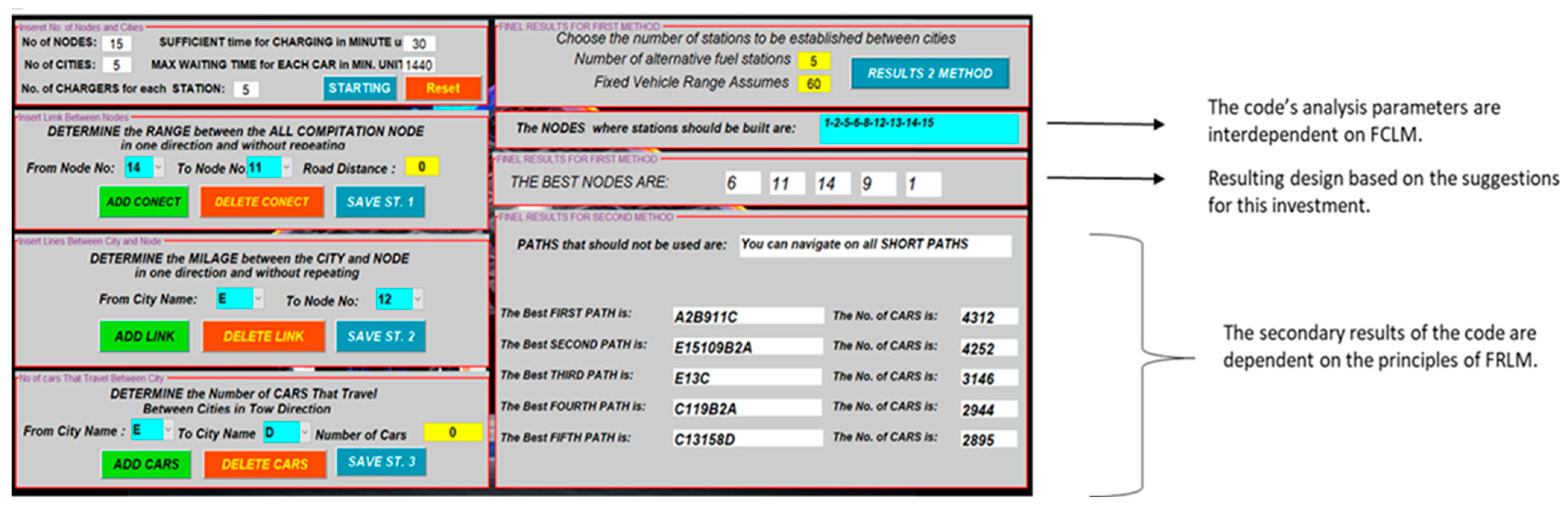
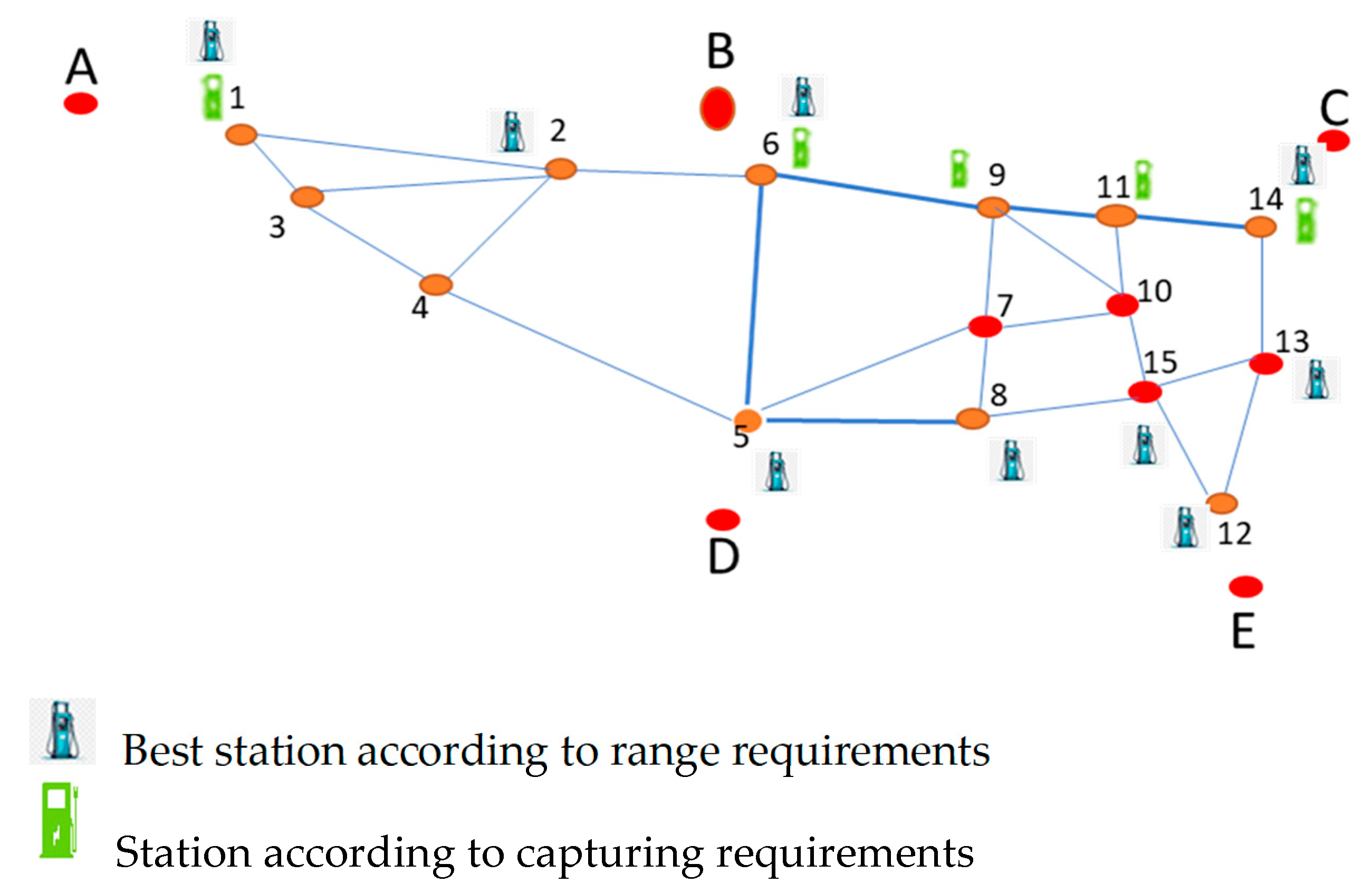
| Selected Stations | Potential Stations | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No | 1 | 2 | 3 | 4 | 5 | No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Suggestion of optimal node locations | 11 | 6 | 1 | 14 | 9 | Nodes where stations should be located | 1 | 2 | 5 | 6 | 8 | 12 | 13 | 14 | 15 |
| No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nodes that are best for station-location | 11 | 6 | 5 | 14 | 9 | 12 | 1 | 3 | 2 | 8 | 4 |
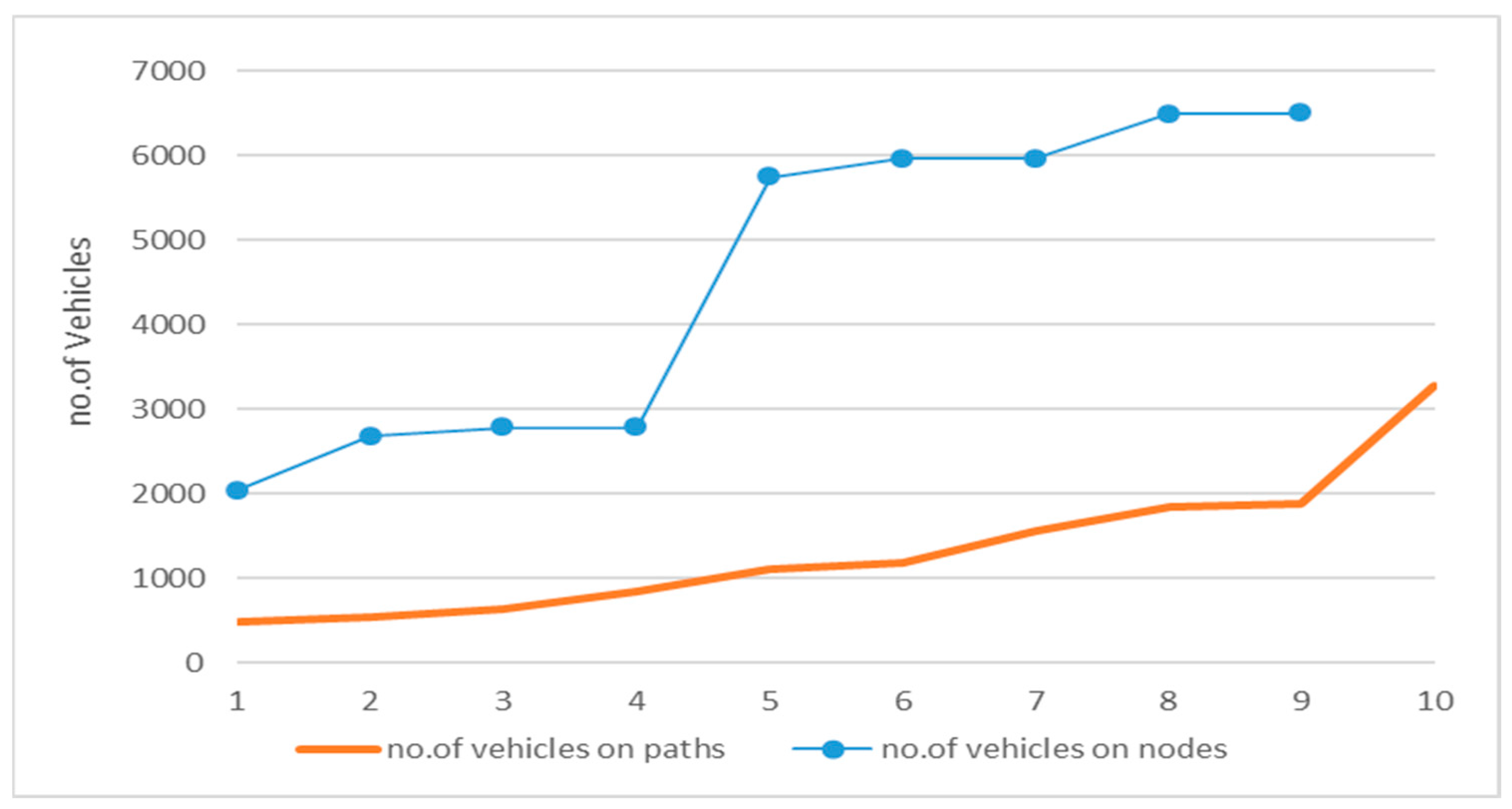
| No. of vehicles | 15,986 | 15,233 | 10,677 | 10,017 | 9551 | 7629 | 7442 | 5780 | 5408 | 4775 | 2034 |
| Case | Path | No. Vehicles | Case | Path | No. Vehicles |
|---|---|---|---|---|---|
| 1 | E → C 12-13-14 [E13C] | 3278 | 11 | E → B 12-15-10-9-6 [E15109B] | [996] |
| 2 | C → B 14-11-9-6 [C119B] | [1995] | 12 | A → D 1-3-4-5 [A34D] | [925] |
| 3 | B → C 6-9-11-14 [B911C] | [1873] | 13 | B → D 6-5 [BD] | [856] |
| 4 | D → B 5-6 [DB] | [1833] | 14 | B → A 6-2-1 [B2A] | [845] |
| 5 | C → E 14-13-12 [C13E] | [1558] | 15 | C → A 14-11-9-6-2-1 [C119B2A | [736] |
| 6 | D → A 5-4-3-1 [D43A] | [1234] | 16 | E → A 12-10-9-6-2-1 [E15109B2A] | [725] |
| 7 | A → B 1-2-6 [A2B] | [1189] | 17 | A → E 1-2-6-9-10-15-12 [A2B91015E] | [710] |
| 8 | D → E 5-8-15-12 [D815E] | [1114] | 18 | C → D 14-13-15-8-5 [C13158D] | [632] |
| 9 | B → E 6-9-10-15-12 [B91015E] | [1090] | 19 | E → D 12-15-8-5 [E158D] | [546] |
| 10 | A → C 1-2-6-9-11-14 [A2B911C] | [1078] | 20 | D → C 5-8-15-13-14 [D81513C] | [489] |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| The path | A34D | A2B91015E | A2B911C | D43A | B91015E | B911C | E15109B2A | E15109B | C119B2A | C119B |
| Case | O-D | No of Vehicles | Station p | Node | No of Vehicles | Frequency | Frequency % |
|---|---|---|---|---|---|---|---|
| 1 | A2B | 1189 | 2 | A1 | 2034 | 2 | 5% |
| B2A | 845 | 2 | 2678 | 2 | 7% | ||
| 2 | BD | 1873 | 2 | B6 | 5740 | 4 | 14% |
| DB | 1833 | D5 | 6487 | 6 | 16% | ||
| 3 | D81513C | 489 | 4 | 8 | 2781 | 2 | 7% |
| C13158D | 632 | 15 | 2781 | 2 | 7% | ||
| 4 | D815E | 1114 | 1 | E12 | 6496 | 6 | 16% |
| E158D | 546 | 13 | 5957 | 4 | 15% | ||
| 5 | E13C | 3278 | 0 | C14 | 5957 | 4 | 15% |
| C13E | 1558 | total | 40,911 | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mijdim AL_HAMEEDAWI, S.H.; Ozen, H. Developing a Model for Determining the Charging Station Location for Electric Vehicles. Sustainability 2025, 17, 10562. https://doi.org/10.3390/su172310562
Mijdim AL_HAMEEDAWI SH, Ozen H. Developing a Model for Determining the Charging Station Location for Electric Vehicles. Sustainability. 2025; 17(23):10562. https://doi.org/10.3390/su172310562
Chicago/Turabian StyleMijdim AL_HAMEEDAWI, Sura Hussein, and Halit Ozen. 2025. "Developing a Model for Determining the Charging Station Location for Electric Vehicles" Sustainability 17, no. 23: 10562. https://doi.org/10.3390/su172310562
APA StyleMijdim AL_HAMEEDAWI, S. H., & Ozen, H. (2025). Developing a Model for Determining the Charging Station Location for Electric Vehicles. Sustainability, 17(23), 10562. https://doi.org/10.3390/su172310562






