Comparative Analysis of Parametric and Neural Network Models for Rural Highway Traffic Volume Prediction
Abstract
1. Introduction
- The identification of NAR network as a highly accurate and data-efficient model for long-term rural traffic prediction, achieving an average MAPE of 2%, demonstrating that accurate forecasts can be achieved primarily using past traffic data with minimal reliance on extensive exogenous inputs.
- The finding that traditional parametric models (ARIMA, SARIMA) can compete with, and in some cases outperform, complex neural network architectures (specifically ANN-SCG and ANN-LM in this study), challenging the common assumption that nonparametric methods are universally superior for this task.
- A practical benchmark and guidance for transportation planners, comparing six diverse models on real-world data and highlighting the trade-offs between accuracy, model complexity, and computational cost for rural highway applications.
- This study serves as the first comprehensive evaluation for long-term rural traffic forecasting in Saudi Arabia and establishes a foundational reference for the Saudi Ministry of Transport and future researchers in the region, guiding model selection based on accuracy, complexity and cost.
- The results from this research can aid highway network management by applying and expanding intelligent transportation systems.
2. Literature Review
2.1. Traffic Prediction Modeling
2.2. Key Factors of Traffic Volume Prediction
2.3. Prediction Methods Groups
2.4. Traffic Prediction Methods
2.4.1. Short-Term Traffic Prediction
2.4.2. Long-Term Traffic Prediction
2.5. Findings of the Literature Review
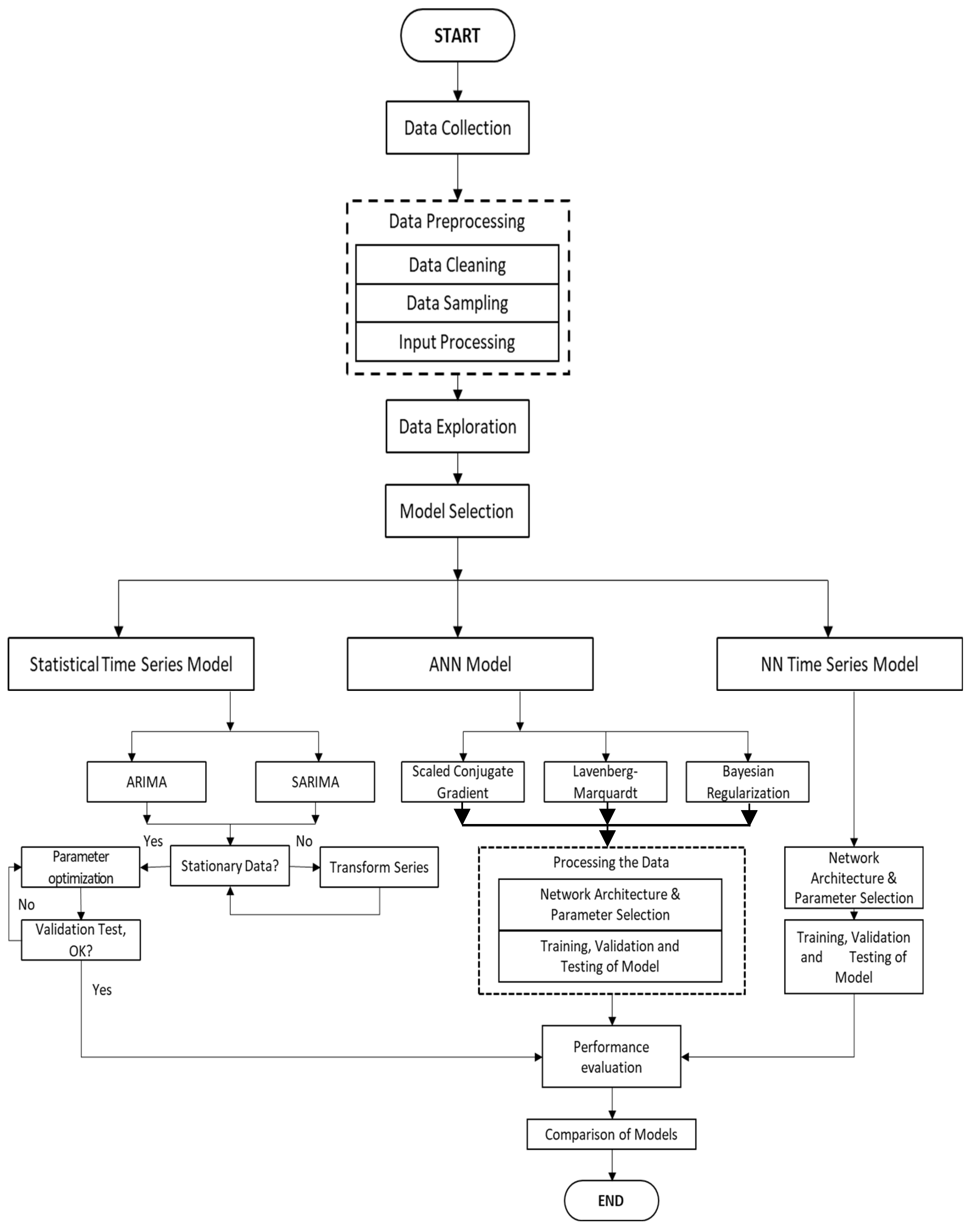
3. Materials and Methods
3.1. Data Collection
3.2. Selection of the Highways Sample
3.3. Inputs Processing
- ×1: the day of the month (1–31),
- ×2: the month (1 January to 12 December),
- ×3: the year (1 for 2013 up to 7 for 2019),
- ×4: the day of the week (1–Sunday to 7–Saturday).
| Date (×1) | Month (×2) | Year (×3) | Day of the Week (×4) | Fuel Price (×5) (Saudi Riyals) | Total Daily Volume (y) (No. of Vehicles) |
|---|---|---|---|---|---|
| 13 | 1 | 1 | 2 | 0.45 | 13,378 |
| 14 | 1 | 1 | 3 | 0.45 | 14,322 |
| 15 | 1 | 1 | 4 | 0.45 | 15,704 |
3.4. Data Exploration
3.5. Selection of the Prediction Models
3.6. Statistical Time Series Models
3.7. Artificial Neural Networks (ANNs)
3.7.1. Scaled Conjugate Gradient (SCG)
3.7.2. Levenberg–Marquardt (LM)
3.7.3. Bayesian Regularization (BR)
3.8. Neural Network Time Series
3.9. Model Evaluation
4. Results and Discussion
4.1. Results of the Statistical Time Series Models
4.2. Results of the Artificial Neural Networks
4.3. Results of the Neural Network Time Series
| Delay Numbers | RTD | RTQ | QTR | Average |
|---|---|---|---|---|
| 1 | 15.221 | 10.371 | 13.970 | 13.130 |
| 2 | 9.623 | 9.281 | 10.936 | 9.990 |
| 3 | 7.605 | 8.710 | 8.036 | 8.100 |
| 4 | 6.309 | 8.416 | 7.614 | 7.430 |
| 5 | 5.602 | 7.768 | 6.886 | 6.700 |
| 6 | 4.509 | 7.038 | 6.577 | 6.000 |
| 7 | 3.801 | 5.558 | 5.384 | 4.866 |
| 8 | 3.704 | 5.531 | 5.012 | 4.733 |
| 9 | 3.607 | 5.265 | 4.795 | 4.500 |
| 15 | 3.408 | 5.649 | 5.040 | 4.666 |
| 25 | 2.801 | 4.330 | 4.233 | 3.766 |
| 50 | 1.952 | 3.778 | 3.558 | 3.300 |
| 100 | 1.702 | 4.243 | 2.428 | 2.766 |
| 200 | 1.648 | 1.695 | 2.566 | 2.000 |
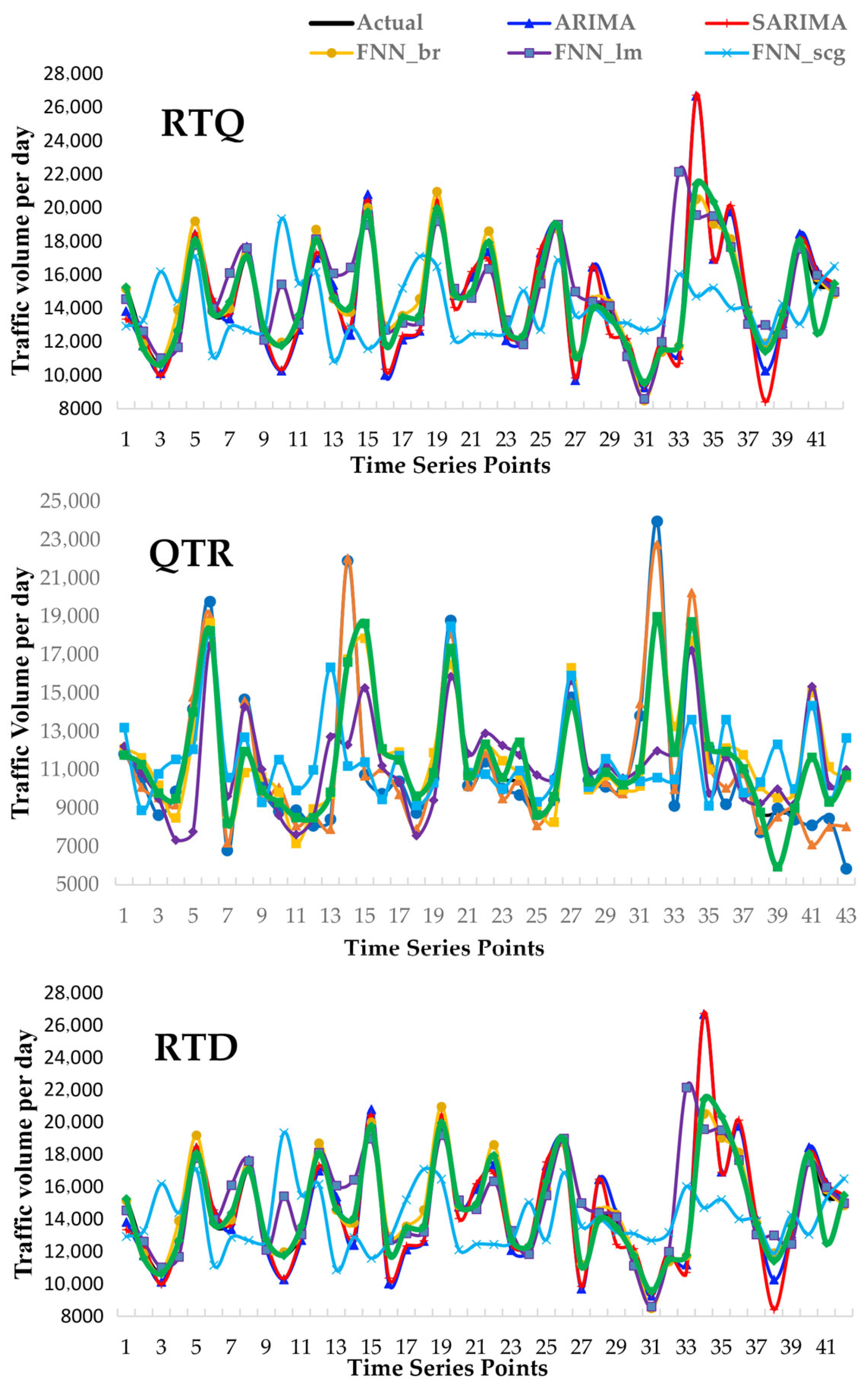
4.4. Comparisons of the Applied Prediction Models
- The NAR model is the most accurate predictor. It consistently achieved the lowest prediction error across all datasets, with an average MAPE of 2%. Its design, which relies solely on past traffic volumes to forecast future values, proved exceptionally effective at capturing the underlying temporal dynamics of rural highway traffic, making it a highly recommended model for applications where forecasting precision is paramount.
- The superiority of neural networks is not universal. While the ANN trained with Bayesian Regularization (ANN-BR) was a strong performer (Average MAPE: 4.5%), the results challenge the assumption that nonparametric methods always outperform classical ones. The ANN-SCG model performed poorly, and the ANN-LM model showed accuracy comparable to the much simpler and more interpretable ARIMA and SARIMA models. This indicates that well-specified parametric models remain competitive for this specific task.
- Model design and configuration are critical to performance. The significant performance gap between ANN-BR and the other ANN training algorithms underscores the importance of the training method and inherent regularization. Furthermore, the systematic search for optimal hyperparameters, such as the number of hidden neurons in ANNs and the feedback delays in the NAR model, was proven to be a necessary step, as these choices profoundly influenced predictive accuracy.
- A clear trade-off exists between accuracy and computational cost. The NAR model’s superior accuracy came at the cost of significantly longer training times (up to 19 h for 200 delays) compared to the near-instantaneous training of ARIMA/SARIMA and the relatively fast training of other ANNs. This highlights a critical practical consideration: the choice of model often involves balancing the need for high accuracy against available computational resources and time constraints for model development.
4.5. Implications for Sustainable Transportation
5. Conclusions and Recommendations
- Highly accurate long-term traffic prediction for rural highways is achievable. The evaluated models effectively captured the complex, nonlinear patterns in the data.
- Model choice significantly impacts accuracy. The NAR model was the most accurate (avg. MAPE: 2%), followed by the ANN-BR (avg. MAPE: 4.5%). The ARIMA, SARIMA, and ANN-LM models formed a third tier of performance (avg. MAPE: ~7.5%).
- The superiority of neural networks is not universal. The poor performance of ANN-SCG and the comparable performance of ANN-LM to traditional ARIMA/SARIMA models demonstrate that well-specified parametric models remain competitive and can outperform certain neural network approaches.
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIC | Akaike Information Criterion |
| ANN | Artificial Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| ASTAM | Adaptive Spatio-Temporal Attention-Based Multi-Model |
| AST-DGCN | Adaptive Spatiotemporal Dynamic Graph Convolutional Network |
| BR | Bayesian Regularization |
| BS | Background Subtraction |
| CB | CatBoost |
| CNN | Convolutional Neural Network |
| DAT-STAN | Dual-module Adaptive Transformer and Spatio-Temporal Attention Network |
| DBN | Deep Belief Network |
| DNN | Deep Neural Network |
| DOF | Deep Optical Flow |
| EEMD | Ensemble Empirical Mode Decomposition |
| EN | Energy |
| FCM | Fuzzy C-Means |
| FNM | Fuzzy Neural Model |
| GA | Genetic Algorithm |
| GDP | Gross Domestic Product |
| GM | Graph Mining |
| GPS | Global Positioning System |
| ITS | Intelligent Transportation System |
| k-NN | k-Nearest Neighbor |
| LASSO | Least Absolute Shrinkage and Selection Operator |
| LM | Levenberg–Marquardt |
| LSSVM | Least Squares Support Vector Machine |
| LSTM | Long Short-Term Memory |
| LSTAR | Localized Space-Time Autoregressive |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MASTGCNet | Multi-scale Attention-Based Spatio-Temporal Graph Convolution Recurrent Network |
| MetaSTC | Metapopulation Spatio-Temporal Clustering |
| MLP | Multilayer Perceptron |
| MOT | Ministry of Transport |
| MSE | Mean Square Error |
| MSTFLN | Multiscale Spatiotemporal Feature Learning Network |
| NAR | Nonlinear Autoregressive |
| PI | Performance Index |
| PSPJSTGCN | Parallel Self-learned and Predefined Joint Spatial–Temporal Graph Convolutional Network |
| QTR | Qassim—Riyadh (Highway code) |
| RBF | Radial Basis Function |
| RBANN | Radial Basis Function Artificial Neural Network |
| RF | Random Forest |
| RFE | Recursive Feature Elimination |
| RNN | Recurrent Neural Network |
| RTD | Riyadh-Dammam (Highway code) |
| RTQ | Riyadh—Qassim (Highway code) |
| SAR | Saudi Riyal |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| SAE | Stacked Auto-Encoder |
| SCG | Scaled Conjugate Gradient |
| SHAP | Shapley Additive Explanations |
| STCNN | Spatio-Temporal Convolutional Neural Network |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| T2F-LSTM | Type-2 Fuzzy Long Short-Term Memory |
| UAV | Unmanned Aerial Vehicle |
| VAPE | Variance of Absolute Percentage Error |
| XAI | Explainable Artificial Intelligence |
| XGB | Extreme Gradient Boosting |
References
- Kashifi, M.T.; Al-Turki, M.; Sharify, A.W. Deep Hybrid Learning Framework for Spatiotemporal Crash Prediction Using Big Traffic Data. Int. J. Transp. Sci. Technol. 2023, 12, 793–808. [Google Scholar] [CrossRef]
- Taheri, A.; Moghadasi, R.; Rasaizadi, A. The Short-Term Prediction of Traffic Parameters: A Review of Parametric and Nonparametric Approaches. AUT J. Civ. Eng. 2022, 6, 369–386. [Google Scholar]
- Le, L.-V.; Sinh, D.; Tung, L.-P.; Lin, B.-S.P. A Practical Model for Traffic Forecasting Based on Big Data, Machine-Learning, and Network KPIs. In 15th IEEE Annual Consumer Communications & Networking Conference (CCNC); IEEE: Las Vegas, NV, USA, 2018; pp. 1–4. [Google Scholar]
- Gao, Y.; Zhu, J. Characteristics, Impacts and Trends of Urban Transportation. Encyclopedia 2022, 2, 1168–1182. [Google Scholar] [CrossRef]
- Sayed, S.A.; Abdel-Hamid, Y.; Hefny, H.A. Intelligent Traffic Flow Prediction Using Deep Learning Techniques: A Comparative Study. SN Comput. Sci. 2025, 6, 60. [Google Scholar] [CrossRef]
- Doğan, G.; Ergen, B. A New Mobile Convolutional Neural Network-Based Approach for Pixel-Wise Road Surface Crack Detection. Measurement 2022, 195, 111119. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y. A Comparative Study of Three Multivariate Short-Term Freeway Flow Forecasting Methods with Missing Data. J. Intell. Transp. Syst. 2016, 20, 205–218. [Google Scholar] [CrossRef]
- Cheng, Z.; Pang, M.-S.; Pavlou, P.A. Mitigating Traffic Congestion: The Role of Intelligent Transportation Systems. Inf. Syst. Res. 2020, 31, 653–674. [Google Scholar] [CrossRef]
- Shepelev, V.; Slobodin, I.; Gritsenko, A.; Fadina, O. Forecasting the Amount of Traffic-Related Pollutant Emissions by Neural Networks. Front. Built Env. 2022, 8, 945615. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Golias, I. Effects of Road Geometry and Traffic Volumes on Rural Roadway Accident Rates. Accid. Anal. Prev. 2002, 34, 357–365. [Google Scholar] [CrossRef]
- Do, V.M.; Tran, Q.H.; Le, K.G.; Vuong, X.C.; Vu, V.T. Enhanced Deep Neural Networks for Traffic Speed Forecasting Regarding Sustainable Traffic Management Using Probe Data from Registered Transport Vehicles on Multilane Roads. Sustainability 2024, 16, 2453. [Google Scholar] [CrossRef]
- Chen, Y.; Guizani, M.; Zhang, Y.; Wang, L.; Crespi, N.; Lee, G.M. When Traffic Flow Prediction Meets Wireless Big Data Analytics meet. IEEE Network 2017, 33, 161–167. [Google Scholar] [CrossRef]
- Chen, J.; Li, D.; Zhang, G.; Zhang, X. Localized Space-Time Autoregressive Parameters Estimation for traffic Flow Prediction in Urban Road Networks. Appl. Sci. 2018, 8, 277. [Google Scholar] [CrossRef]
- Smith, B.L. Forecasting Freeway Traffic Flow for Intelligent Transportation Application. Transp. Res. Part. A 1997, 123, 261–266. [Google Scholar]
- Lin, L.; Wang, Q.; Sadek, A. Short-Term Forecasting of Traffic Volume: Evaluating Models Based on Multiple Data Sets and Data Diagnosis Measures. Transp. Res. Rec. J. Transp. Res. Board. 2013, 2392, 40–47. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef]
- Alajali, W.; Zhou, W.; Wen, S. Traffic Flow Prediction for Road Intersection Safety. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018; IEEE: New York, NY, USA, 2018; pp. 812–820. [Google Scholar]
- Hou, Z.; Li, X. Repeatability and Similarity of Freeway Traffic Flow and Long-Term under Big Data. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1786–1796. [Google Scholar] [CrossRef]
- Su, F.; Dong, H.; Jia, L.; Qin, Y.; Tian, Z. Long-Term Forecasting Oriented to Urban Expressway Traffic Situation. Adv. Mech. Eng. 2016, 8, 1687814016628397. [Google Scholar] [CrossRef]
- Li, L.; He, S.; Zhang, J.; Ran, B. Short-Term Highway Traffic Flow Prediction Based on a Hybrid Considering Temporal-Spatial Information. J. Adv. Transp. 2016, 50, 2029–2040. [Google Scholar] [CrossRef]
- Narayanan, S.; Emmanouil, C.; Constantinos, A. Factors Affecting Traffic Flow Efficiency Implications of Connected and Autonomous Vehicles: A Review and Policy Recommendations. Adv. Transp. Policy Plan. 2020, 5, 1–50. [Google Scholar]
- Topić, J.; Škugor, B.; Deur, J. Neural Network-Based Prediction of Vehicle Fuel Consumption Based on Driving Cycle Data. Sustainability 2022, 14, 744. [Google Scholar] [CrossRef]
- Rakhmanto, G.B. Short-Term Traffic Flow Prediction with Support Vector Machine to Reduce Congestion on Toll Roads in Jakarta. Eduvest J. Univers. Stud. 2025, 5, 6433–6444. [Google Scholar] [CrossRef]
- Chen, M.; Chen, R.; Cai, F.; Li, W.; Guo, N.; Li, G. Short-Term Traffic Flow Prediction with Recurrent Mixture Density Network. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Qu, L.; Ma, D.; Wang, Y. Daily Long-Term Traffic Flow Forecasting Based on a Deep Neural. Expert. Syst. Appl. 2019, 121, 304–312. [Google Scholar] [CrossRef]
- Brownlee, J. Master Machine Learning Algorithms: Discover How They Work and implement Them from Scratch. Machine Learning Mastery; Guiding Tech Media: San Juan, Puerto Rico, 2016. [Google Scholar]
- Lee, S.; Fambro, D.B. Application of Subset Autoregressive Integrated Moving Average for Short-Term Freeway Traffic Volume Forecasting. Transp. Res. Rec. 1999, 1678, 179–188. [Google Scholar] [CrossRef]
- Ahmed, A.; Gazder, U. Traffic Forecasting for King Fahd Causeway: Comparison of Parametric Technique with Artificial Neural Networks. Int. J. Adv. Civ. Struct. Environ. Eng. IJACSE 2013, 1, 75–79. [Google Scholar]
- Siddiquee, M.S.A.; Hoque, S. Predicting the Daily Traffic Volume from Hourly Traffic Data Using Neural Network. Neural Netw. World 2017, 27, 283–294. [Google Scholar] [CrossRef]
- Yin, K.; Wu, J.; Wang, W.; Lee, D.-H.; Wei, Y. An Integrated Resilience Assessment Model of Urban Transportation Network: A Case Study of 40 Cities in China. Transp. Res. Part. A Policy Pr. 2023, 173, 103687. [Google Scholar] [CrossRef]
- Sporkmann, J.; Liu, Y.; Spinler, S. Carbon Emissions from European Land Transportation: A Comprehensive Analysis. Transp. Res. D Transp. Env. 2023, 121, 103851. [Google Scholar] [CrossRef]
- Momin, K.A.; Barua, S.; Jamil, M.S.; Hamim, O.F. Short Duration Traffic Flow Prediction Using Kalman Filtering. In Proceedings of the 6th International Conference on Civil Engineering for Sustainable Development (Iccesd 2022), Khulna, Bangladesh, 10–12 February 2022; AIP Publishing LLC: Melville, NY, USA, 2023; p. 040011. [Google Scholar]
- Zheng, Z.; Su, D. Short-Term Traffic Volume Forecasting: A k-Nearest Neighbor Enhanced by Constrained Linearly Sewing Principle Algorithm. Transp. Res. Part. C Emerg. Technol. 2014, 43, 143–157. [Google Scholar] [CrossRef]
- Wang, J.; Boukerche, A. Non-Parametric Models with Optimized Training Strategy for Vehicles Traffic Flow Prediction. Comput. Netw. 2021, 187, 107791. [Google Scholar] [CrossRef]
- Mladenović, D.; Janković, S.; Zdravković, S.; Mladenović, S.; Uzelac, A. Night Traffic Flow Prediction Using K-Nearest Neighbors Algorithm. Oper. Res. Eng. Sci. Theory Appl. 2022, 5, 152–168. [Google Scholar] [CrossRef]
- Alam, M.S.; Deb, J.B.; Al Amin, A.; Chowdhury, S. An Artificial Neural Network for Predicting Air Traffic Demand Based on Socio-Economic Parameters. Decis. Anal. J. 2024, 10, 100382. [Google Scholar] [CrossRef]
- Chen, J. Characterization and Implementation of Neural Network Time Series Models for Traffic Volume Forecasting; The University of Toledo: Toledo, OH, USA, 1997. [Google Scholar]
- Zhang, Q.; Lu, J.; Kuang, W.; Wu, L.; Wang, Z. Short-Term Charging Load Prediction of Electric Vehicles with Dynamic Traffic Information Based on a Support Vector Machine. World Electr. Veh. J. 2024, 15, 189. [Google Scholar] [CrossRef]
- Kumar, S. V Traffic Flow Prediction Using Kalman Filtering Technique. Procedia Eng. 2017, 187, 582–587. [Google Scholar] [CrossRef]
- Wang, C.; Huang, S.; Zhang, C. Short-Term Traffic Flow Prediction Considering Weather Factors Based on Optimized Deep Learning Neural Networks: Bo-GRA-CNN-BiLSTM. Sustainability 2025, 17, 2576. [Google Scholar] [CrossRef]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O.; Severino, A. Comparative Traffic Flow Prediction of a Heuristic ANN Model and a Hybrid ANN-PSO Model in the Traffic Flow Modelling of Vehicles at a Four-Way Signalized Road Intersection. Sustainability 2021, 13, 10704. [Google Scholar] [CrossRef]
- Olayode, I.O.; Tartibu, L.K.; Okwu, M.O. Traffic Flow Prediction at Signalized Road Intersections: A Case of Markov Chain and Artificial Neural Network Model. In Proceedings of the 2021 IEEE 12th International Conference on Mechanical and Intelligent Manufacturing Technologies (ICMIMT), Cape Town, South Africa, 13–15 May 2021; IEEE: New York, NY, USA, 2021; pp. 287–292. [Google Scholar]
- Xu, K.; Yu, Z.; Gao, Y.; Zhang, S.; Fang, J.; Gao, X.; Chen, G. MetaSTC: A Backbone Agnostic Spatio-Temporal Framework for Traffic Forecasting. In Proceedings of the 2024 IEEE International Conference on Data Mining (ICDM), Abu Dhabi, United Arab Emirates, 9–12 December 2024; IEEE: New York, NY, USA, 2024; pp. 899–904. [Google Scholar]
- Yang, X.; Li, Q.; Xu, P.; He, D.; Tan, H. Parallel Self-Learned and Predefined Joint Spatial–Temporal Graph Convolutional Networks for Traffic Flow Prediction. IEEE Internet Things J. 2025, 12, 11698–11707. [Google Scholar] [CrossRef]
- Xiao, Z.; Shen, Q.; Li, C.; Li, D.; Liu, Q. An Adaptive Spatiotemporal Dynamic Graph Convolutional Network for Traffic Prediction. Sci. Rep. 2025, 15, 27098. [Google Scholar] [CrossRef]
- Zhou, B.; Liu, J.; Cui, S.; Zhao, Y. A Large-Scale Spatio-Temporal Multimodal Fusion Framework for Traffic Prediction. Big Data Min. Anal. 2024, 7, 621–636. [Google Scholar] [CrossRef]
- Lee, E.H. Traffic Speed Prediction of Urban Road Network Based on High Importance Links Using XGB and SHAP. IEEE Access 2023, 11, 113217–113226. [Google Scholar] [CrossRef]
- Min, J.H.; Ham, S.W.; Kim, D.-K.; Lee, E.H. Deep Multimodal Learning for Traffic Speed Estimation Combining Dedicated Short-Range Communication and Vehicle Detection System Data. Transp. Res. Rec. J. Transp. Res. Board. 2023, 2677, 247–259. [Google Scholar] [CrossRef]
- Shen, Z. Long-Time Traffic Speed Prediction Model Based on XGBoost 2023. preprint 2023, 1–11. [Google Scholar] [CrossRef]
- Nesa, M.; Yoon, Y. Speed Prediction and Nearby Road Impact Analysis Using Machine Learning and Ensemble of Explainable AI Techniques. Sci. Rep. 2024, 14, 25208. [Google Scholar] [CrossRef] [PubMed]
- Wieczorek, G.; un din Tahir, S.B.; Akhter, I.; Kurek, J. Vehicle Detection and Recognition Approach in Multi-Scale Traffic Monitoring System via Graph-Based Data Optimization. Sensors 2023, 23, 1731. [Google Scholar] [CrossRef] [PubMed]
- Satyanarayana, G.S.R.; Deshmukh, P.; Das, S.K. Vehicle Detection and Classification with Spatio-Temporal Information Obtained from CNN. Displays 2022, 75, 102294. [Google Scholar] [CrossRef]
- Singh, A.; Rahma, M.Z.U.; Rani, P.; Agrawal, N.K.; Sharma, R.; Kariri, E.; Aray, D.G. Smart Traffic Monitoring Through Real-Time Moving Vehicle Detection Using Deep Learning via Aerial Images for Consumer Application. IEEE Trans. Consum. Electron. 2024, 70, 7302–7309. [Google Scholar] [CrossRef]
- Bakirci, M. Enhancing Vehicle Detection in Intelligent Transportation Systems via Autonomous UAV Platform and YOLOv8 Integration. Appl. Soft Comput. 2024, 164, 112015. [Google Scholar] [CrossRef]
- Guo, F.; Polak, J.W.; Krishnan, R. Comparison of Modelling Approaches for Short Term Traffic Prediction under Normal and Abnormal Conditions. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; IEEE: New York, NY, USA, 2010; pp. 1209–1214. [Google Scholar]
- Hsueh, Y.-L.; Yang, Y.-R. A Short-Term Traffic Speed Prediction Model Based on LSTM Networks. Int. J. Intell. Transp. Syst. Res. 2021, 19, 510–524. [Google Scholar] [CrossRef]
- Wisconsin Department of Transportation. Transportation Planning Manual; Wisconsin Department of Transportation: Madison, WI, USA, 2008.
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.-Y. Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Al-Masaeid, H.R.; Al-Omoush, N.J. Traffic Volume Forecasting for Rural Roads in Jordan. Jordan J. Civ. Eng. 2014, 159, 1–13. [Google Scholar]
- Hong, W.-C.; Dong, Y.; Zheng, F.; Lai, C.-Y. Forecasting Urban Traffic Flow by SVR with Continuous ACO. Appl. Math. Model. 2011, 35, 1282–1291. [Google Scholar] [CrossRef]
- Altikat, S. Prediction of CO2 Emission from Greenhouse to Atmosphere with Artificial Neural Networks and Deep Learning Neural Networks. Int. J. Environ. Sci. Technol. 2021, 18, 3169–3178. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, Q.; Chen, D. Nonparametric Method for Optimizing the Start Time of Short-Term Road Maintenance Operations Using Real-Time Traffic Map Data. Adv. Transp. Stud. 2023, 59, 51–70. [Google Scholar]
- Mor, A.; Kumar, M. Multivariate Short-Term Traffic Flow Prediction Based on Real-Time Expressway Toll Plaza Data Using Non-Parametric Techniques. Int. J. Veh. Inf. Commun. Syst. 2022, 7, 32. [Google Scholar] [CrossRef]
- Alrumaidhi, M.; Farag, M.M.G.; Rakha, H.A. Comparative Analysis of Parametric and Non-Parametric Data-Driven Models to Predict Road Crash Severity among Elderly Drivers Using Synthetic Resampling Techniques. Sustainability 2023, 15, 9878. [Google Scholar] [CrossRef]
- Park, B. Hybrid Neuro-Fuzzy Application in Short-Term Freeway Traffic Forecasting. Transp. Res. Rec. 2002, 1802, 190–196. [Google Scholar] [CrossRef]
- Kumar, K.; Parida, M.; Katiyar, V.K. Short Term Traffic Flow Prediction for a Non Urban Highway Using Neural Network. Procedia Soc. Behav. Sci. 2013, 104, 755–764. [Google Scholar] [CrossRef]
- Alsehaimi, B.; Alzamzami, O.; Alowidi, N.; Ali, M. An Adaptive Spatio-Temporal Traffic Flow Prediction Using Self-Attention and Multi-Graph Networks. Sensors 2025, 25, 282. [Google Scholar] [CrossRef]
- Yin, K.; Niu, X.; Zhu, J.; Jiang, Y.; Min, F. DAT-STAN: Dual-Module Adaptive Transformer and Spatio-Temporal Attention Network for Large-Scale Traffic Flow Prediction. Tsinghua Sci. Technol. 2025. [Google Scholar] [CrossRef]
- Ali, A.; Ullah, I.; Singh, S.K.; Sharafian, A.; Jiang, W.; Sherazi, H.I.; Bai, X. Energy-Efficient Resource Allocation for Urban Traffic Flow Prediction in Edge-Cloud Computing. Int. J. Intell. Syst. 2025, 2025, 1863025. [Google Scholar] [CrossRef]
- Yasdi, R. Prediction of Road Traffic Using a Neural Network Approach. Neural Comput. Appl. 1999, 8, 135–142. [Google Scholar] [CrossRef]
- Stutz, C.; Runkler, T.A. Classification and Prediction of Road Traffic Using-Specific Fuzzy Clustering. IEEE Trans. Fuzzy Syst. 2002, 10, 297–308. [Google Scholar] [CrossRef]
- Yin, H.; Wong, S.; Xu, J.; Wong, C. Urban Traffic Flow Prediction Using a Fuzzy-Neural Approach. Transp. Res. Part. C Emerg. Technol. 2002, 10, 85–98. [Google Scholar] [CrossRef]
- Ratrout, N.T.; Gazder, U. Factors Affecting Performance of Parametric and Non-Parametric for Daily Traffic Forecasting. Procedia Comput. Sci. 2014, 32, 285–292. [Google Scholar] [CrossRef]
- Khalifa, A.; Idsouguou, Y.; Benabbou, L.; Zirari, M. Case Study of the Moroccan Highway Network. arXiv 2017, arXiv:1711.06779. [Google Scholar] [CrossRef]
- Zang, D.; Fang, Y.; Wang, D.; Wei, Z.; Tang, K.; Li, X. Long Term Traffic Flow Prediction Using Residual Net and deconvolutional Neural Network. In Chinese Conference on Pattern Recognition and Computer Vision (PRCV); Springer: Berlin/Heidelberg, Germany, 2018; pp. 62–74. [Google Scholar]
- Zang, D.; Ling, J.; Wei, Z.; Tang, K.; Cheng, J. Long-Term Traffic Speed Prediction Based on Multiscale-Temporal Feature Learning Network. IEEE Trans. Intell. Transp. Syst. 2018, 20, 3700–3709. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Qin, L.; Ran, B.; Jiang, Z. A Hybrid Deep Learning Based Traffic Flow Prediction Method and its Understanding. Transp. Res. Part. C Emerg. Technol. 2018, 90, 166–180. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, Y.; Lu, H.; Fujita, H. Parallel Computing Method of Deep Belief Networks and Its to Traffic Flow Prediction. Knowl. Based Syst. 2019, 163, 972–987. [Google Scholar] [CrossRef]
- Li, R.; Huang, Y.; Wang, J. Long-Term Traffic Volume Prediction Based on K-Means Gaussian Type-2 Fuzzy Sets. IEEE/CAA J. Autom. Sin. 2019, 6, 1344–1351. [Google Scholar] [CrossRef]
- Tang, J.; Chen, X.; Hu, Z.; Zong, F.; Han, C.; Li, L. Traffic Flow Prediction Based on Combination of Support Vector and Data Denoising Schemes. Phys. A Stat. Mech. Its Appl. 2019, 534, 120642. [Google Scholar] [CrossRef]
- He, Z.; Chow, C.-Y.; Zhang, J.-D. STCNN: A Spatio-Temporal Convolutional Neural Network for long-Term Traffic Prediction. In 20th IEEE International Conference on Mobile Data Management (MDM); IEEE: Hong Kong, China, 2019; pp. 226–233. [Google Scholar]
- Li, R.; Hu, Y.; Liang, Q. T2F-LSTM Method for Long-Term Traffic Volume Prediction. IEEE Trans. Fuzzy Syst. 2020, 28, 3256–3264. [Google Scholar] [CrossRef]
- Li, Y.; Chai, S.; Ma, Z.; Wang, G. A Hybrid Deep Learning Framework for Long-Term Traffic Flow Prediction. IEEE Access 2021, 9, 11264–11271. [Google Scholar] [CrossRef]
- Park, S.; Kim, M.; Kim, J. Hourly Long-Term Traffic Volume Prediction with Meteorological Information Using Graph Convolutional Networks. Appl. Sci. 2024, 14, 2285. [Google Scholar] [CrossRef]
- Toba, A.-L.; Kulkarni, S.; Khallouli, W.; Pennington, T. Long-Term Traffic Prediction Using Deep Learning Long Short-Term Memory. Smart Cities 2025, 8, 126. [Google Scholar] [CrossRef]
- Smeeton, N.; Neil, H.S.; Peter, S. Applied Nonparametric Statistical Methods, 5th ed.; CRC Press: Boca Raton, FL, USA, 2025. [Google Scholar]
- Sayed, S.A.; Abdel-Hamid, Y.; Hefny, H.A. Artificial Intelligence-Based Traffic Flow Prediction: A Comprehensive Review. J. Electr. Syst. Inf. Technol. 2023, 10, 13. [Google Scholar] [CrossRef]
- Duraku, R.K.; Ramadani, R. Development of Traffic Volume Forecasting Using Multiple Regression Analysis and Artificial Neural Network. Civ. Eng. J. 2019, 5, 1698–1713. [Google Scholar] [CrossRef]
- Ariyo, A.A.; Adewumi, A.O.; Ayo, C.K. Stock Price Prediction Using the ARIMA Model. In UKSim-AMSS 16th International Conference on Computer Modelling and Simulation; IEEE: Cambridge, UK, 2014; pp. 106–112. [Google Scholar]
- Tantekin, A. Heating Degree Days (HDD) Forecasting and Heating Degree Days Factor (HDDF) Assessment in Selected European Countries. Energy 2025, 332, 137277. [Google Scholar] [CrossRef]
- Farinango, P.; Estrada, R.; Vera, N. Evaluation of Indoor Positioning System Design Based on Empirical Propagation Models versus Optimizable Regression Models. Procedia Comput. Sci. 2025, 265, 301–309. [Google Scholar] [CrossRef]
- Møller, M.F. A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning. Neural Netw. 1993, 6, 525–533. [Google Scholar] [CrossRef]
- Baghirli, O. Comparison of Lavenberg-Marquardt, Scaled Conjugate Gradient and Bayesian Regularization Backpropagation Algorithms for Multistep Wind Speed Forecasting Using Multilayer Perceptron Neural Network. Master’s Thesis, Uppsala University, Disciplinary Domain of Science and Technology, Earth Sciences, Department of Earth Sciences, Uppsala, Sweden, 2015. [Google Scholar]
- Mohamad, N.; Zaini, F.; Johari, A.; Yassin, I.; Zabidi, A. Comparison between Levenberg-Marquardt and Scaled Conjugate Training Algorithms for Breast Cancer Diagnosis Using. In 6th International Colloquium on Signal Processing & Its Applications; IEEE: Malacca City, Malaysia, 2010; pp. 1–7. [Google Scholar]
- Fischer, A.; Izmailov, A.F.; Solodov, M.V. The Levenberg–Marquardt Method: An Overview of Modern Convergence Theories and More. Comput. Optim. Appl. 2024, 89, 33–67. [Google Scholar] [CrossRef]
- Demuth, H.; Beale, M.; Hagan, M. MATLAB User’s Guide, Version 4.0: Neural Network Toolbox; MathWorks Inc: Natick, MA, USA, 2005. [Google Scholar]
- Fiorentini, N.; Pellegrini, D.; Losa, M. Overfitting Prevention in Accident Prediction Models: Bayesian Regularization of Artificial Neural Networks. Transp. Res. Rec. J. Transp. Res. Board. 2023, 2677, 1455–1470. [Google Scholar] [CrossRef]
- Wang, K.W.; Deng, C.; Li, J.P.; Zhang, Y.Y.; Li, X.Y.; Wu, M.C. Hybrid Methodology for Tuberculosis Incidence Time-Series Based on ARIMA and a NAR Neural Network. Epidemiol. Infect. 2017, 145, 1118–1129. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Kim, H. A New Metric of Absolute Percentage Error for Intermittent Demand Forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Khoshvaght, H.; Permala, R.R.; Razmjou, A.; Khiadani, M. A Critical Review on Selecting Performance Evaluation Metrics for Supervised Machine Learning Models in Wastewater Quality Prediction. J. Env. Chem. Eng. 2025, 13, 119675. [Google Scholar] [CrossRef]
- Alali, Y.; Harrou, F.; Sun, Y. Unlocking the Potential of Wastewater Treatment: Machine Learning Based Energy Consumption Prediction. Water 2023, 15, 2349. [Google Scholar] [CrossRef]
- Khan, F.M.; Gupta, R. Arima and Nar Based Prediction Model for Time Series Analysis Of-19 Cases in India. J. Saf. Sci. Resil. 2020, 1, 12–18. [Google Scholar] [CrossRef]
| Authors | Prediction Methods | Main Findings |
|---|---|---|
| Yasdi [70] | Recurrent neural networks with backpropagation | The model showed good results for traffic prediction |
| Stutz and Runkler [71] | Fuzzy clustering method | The method showed promising results for traffic prediction |
| Yin [72] | Fuzzy neural model (FNM); ANN with backpropagation | FNM provided more accurate predictions compared to Backpropagation networks |
| Ahmed and Gazder [28] | ANNs with Multi-layer perceptron (MLP); Linear regression | The MLP has better accuracy than the linear regression technique |
| Al-MASAEID AND Al-Omoush [59] | Aggregate regression; Disaggregate trend; Empirical Bayesian | Aggregate regression and empirical Bayesian analysis provided similar results. Trend method was not efficient. |
| Ratrout and Gazder [73] | ANN with (MLP); ANN with radial basis function neural network (RBANN); Linear regression analysis | ANNs have better accuracy than linear regression technique |
| Su et al. [19] | Nonparametric kernel regression; SARIMA; Back propagation NN; Least Squares Support Vector Machine (LSSVM) | Nonparametric kernel regression is more accurate and effective than all of the compared models |
| Khalifa et al. [74] | Holt-Winters; ARIMA; Random Forest; MLP; AdaBoost; Long Short-Term Memory networks (LSTM); Extra Trees | Holt-Winters and ARIMA showed unsatisfactory performance. The MLP and LSTM gave a better performance than the others. |
| Zang et at. [75] | Residual net and Deconvolutional Neural Network | The model performed better than any other existing model for traffic long-term flow prediction. |
| Zang et al. [76] | Multiscale Spatiotemporal Feature Learning Network (MSTFLN) | The model could effectively predict the long-term traffic Information. |
| Wu et al. [77] | Denoising schemes and support vector machine | Ensemble Empirical Mode Detection (EEMD) outperforms other denoising algorithms in prediction accuracy. |
| Zhao et al. [78] | Deep belief networks (DBNs) | Parallel DBN learning reduces pre-training and fine-tuning times, enhancing efficiency and effectiveness. |
| Li et al. [79] | Gaussian interval type-2 fuzzy set | Forecasted traffic range fully encompassed the actual traffic volume within upper and lower bounds. |
| Tang et al. [80] | DNN based traffic flow model | The DNN-BTF model, using CNN and RNN to extract spatial-temporal features, outperformed all models. |
| He et al. [81] | Spatio-Temporal Convolutional Neural Network (STCNN) model | STCNN model showed significantly better performance than any other predictive model |
| Li et al. [82] | T2F-LSTM neural network model | The introduction of interval sets of T2F provided a better LSTM model performance for Long-term traffic volume prediction. |
| Li et al. [83] | Wavelet-Decomposed Convolutional Neural Network-Long Short-Term Memory (W-CNN-LSTM) | W-CNN-LSTM combines wavelet, CNN, and LSTM for improved long-term traffic flow prediction. |
| Park et al. [84] | Graph Convolutional Network | This model predicts traffic better, incorporating weather data and outperforming traditional methods. |
| Toba et al. [85] | Combination of K-means clustering, LSTM and Fourier transform | This method accurately predicts long-term traffic trends, capturing periodicity and variations effectively. |
| Highway Name | Highway Code | No of Lanes | Highway Distance (km) | Data Period | No of Available Days |
|---|---|---|---|---|---|
| Riyadh—Dammam | RTD | 3 | 383 | (13 January 2014)–(10 July 2019) | 1685 |
| Riyadh—Qassim | RTQ | 3 | 317 | (25 February 2013)–(22 May 2019) | 1748 |
| Qassim—Riyadh | QTR | 3 | 317 | (26 February 2013)–(02 October 2019) | 1905 |
| Highway Code | Time Series Model | |
|---|---|---|
| ARIMA | SARIMA | |
| RTD | MAPE = 7.098% (p, D, q) = (7, 1, 2) AIC = 2.983 × 104 | MAPE = 6.599% AIC = 3.114 × 104 (p, D, q) × (ps, Ds, qs) = (7, 1, 2) × (7, 1, 2) |
| RTQ | MAPE = 7.218% (p, D, q) = (7, 1, 2) AIC = 2.814 × 104 | MAPE = 6.836% AIC = 2.858 × 104 (p, D, q) × (ps, Ds, qs) = (7, 1, 2) × (7, 1, 3) |
| QTR | MAPE = 7.926% (p, D, q) = (7, 1, 2) AIC = 3.324 × 104 | MAPE = 7.574% AIC = 3.429 × 104 (p, D, q) × (ps, Ds, qs) = (7, 1, 2) × (7, 1, 2) |
| Average MAPE | 7.400 | 7.000 |
| No. of Hidden Neurons | 5 | 25 | 50 | 75 | 100 | 125 | 150 | 200 | 500 | 600 |
| MAPE (%) | 13.2 | 6.37 | 4.92 | 3.95 | 3.56 | 3.22 | 3.25 | 3.48 | 3.82 | 3.70 |
| ANN Training Method/Highway Code | RTD | RTQ | QTR | Average |
|---|---|---|---|---|
| Bayesian Regularization (BR) | 3.222 | 4.432 | 5.869 | 4.466 |
| Scaled Conjugate Gradient (SCG) | 14.618 | 12.409 | 14.459 | 13.800 |
| Levenberg–Marquardt (LM) | 7.484 | 6.936 | 9.598 | 8.000 |
| Prediction Model Name | RTD | RTQ | QTR | Average |
|---|---|---|---|---|
| ARIMA | 7.098 | 7.218 | 7.926 | 7.420 |
| SARIMA | 6.599 | 6.836 | 7.574 | 7.000 |
| ANN with Bayesian Regularization (BR) | 3.222 | 4.432 | 5.869 | 4.500 |
| ANN with Scaled Conjugate Gradient (SCG) | 14.618 | 12.409 | 14.459 | 13.830 |
| ANN with Levenberg–Marquardt (LM) | 7.484 | 6.936 | 9.598 | 8.100 |
| NN time series with Nonlinear Autoregressive model (NAR) | 1.647 | 1.695 | 2.566 | 2.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Turki, M. Comparative Analysis of Parametric and Neural Network Models for Rural Highway Traffic Volume Prediction. Sustainability 2025, 17, 10526. https://doi.org/10.3390/su172310526
Al-Turki M. Comparative Analysis of Parametric and Neural Network Models for Rural Highway Traffic Volume Prediction. Sustainability. 2025; 17(23):10526. https://doi.org/10.3390/su172310526
Chicago/Turabian StyleAl-Turki, Mohammed. 2025. "Comparative Analysis of Parametric and Neural Network Models for Rural Highway Traffic Volume Prediction" Sustainability 17, no. 23: 10526. https://doi.org/10.3390/su172310526
APA StyleAl-Turki, M. (2025). Comparative Analysis of Parametric and Neural Network Models for Rural Highway Traffic Volume Prediction. Sustainability, 17(23), 10526. https://doi.org/10.3390/su172310526