Empowering Sustainability in Power Grids: A Multi-Scale Adaptive Load Forecasting Framework with Expert Collaboration
Abstract
1. Introduction
- We introduce a pioneering prediction head that integrates a Kolmogorov–Arnold network based mixture-of-experts architecture. This design is specifically engineered to adaptively capture the heterogeneous and often complex distribution and fluctuation patterns inherent in real-world time-series power load data. Unlike traditional linear layers or single-model approaches that assume uniform data characteristics, our MoE-KAN framework leverages the intrinsic flexibility of KANs, which learn univariate functions on their edges—to allow multiple specialized experts to collectively model distinct data sub-patterns. This significantly enhances the model’s capacity to precisely fit diverse non-linear dynamics, thereby leading to superior predictive accuracy and robustness, especially in dynamic and unpredictable power grid environments.
- We propose an innovative iterative auto-regressive learning mechanism, coupled with multi-scale representation extraction, to enable highly flexible, variable-length prediction generation without the need for arduous retraining. By transforming the prediction process into an iterative loop that progressively refines time-series representations from coarse to fine granularities, our model can dynamically adapt to varying forecasting horizons. This design contrasts sharply with conventional deep learning models that typically predefine a fixed-length prediction head, severely limiting their real-world applicability. Our approach ensures operational efficiency and resource optimization by supporting dynamic forecasting scenarios, a critical requirement for modern, sustainable power grid management.
- Extensive evaluations conducted on three real-world benchmark datasets, Electricity, NSG-2020, and NSG-2023, consistently demonstrate that MAFMC achieves state-of-the-art performance in power load forecasting. Across various future prediction lengths, our model significantly outperforms six leading baseline methods, evidenced by substantial reductions in MSE and MAE. This empirical superiority underscores the effectiveness of MAFMC’s integrated architecture in addressing the inherent complexities and challenges of power load forecasting, establishing a new benchmark for predictive accuracy and adaptability in this domain.
2. Related Work
2.1. Power Load Forecasting
2.2. Kolmogorov–Arnold Networks
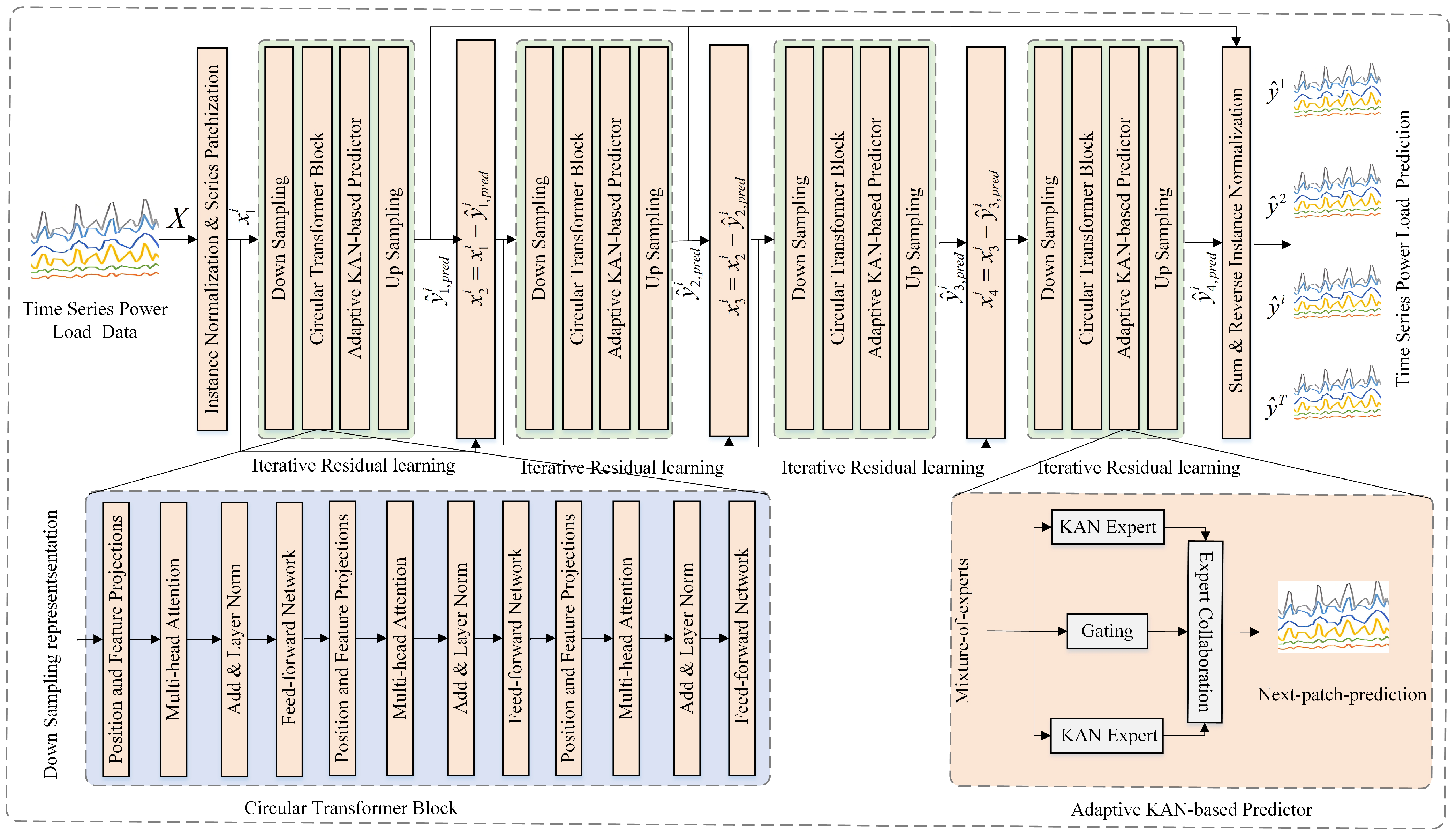
3. The Proposed Method
3.1. Input Series Patchization
3.2. Multi-Expert Adaptive Prediction
3.3. Iterative Auto-Regressive Learning
3.4. Theoretical Analysis of MAFMC
3.4.1. Optimization of Expected Loss on Heterogeneous Distributions
3.4.2. Generalization Under Covariate Shift via Normalization
3.4.3. Optimization Simplification via Iterative Residual Decomposition
- Stage 1:
- Stage s:
4. Experiment
4.1. Setup
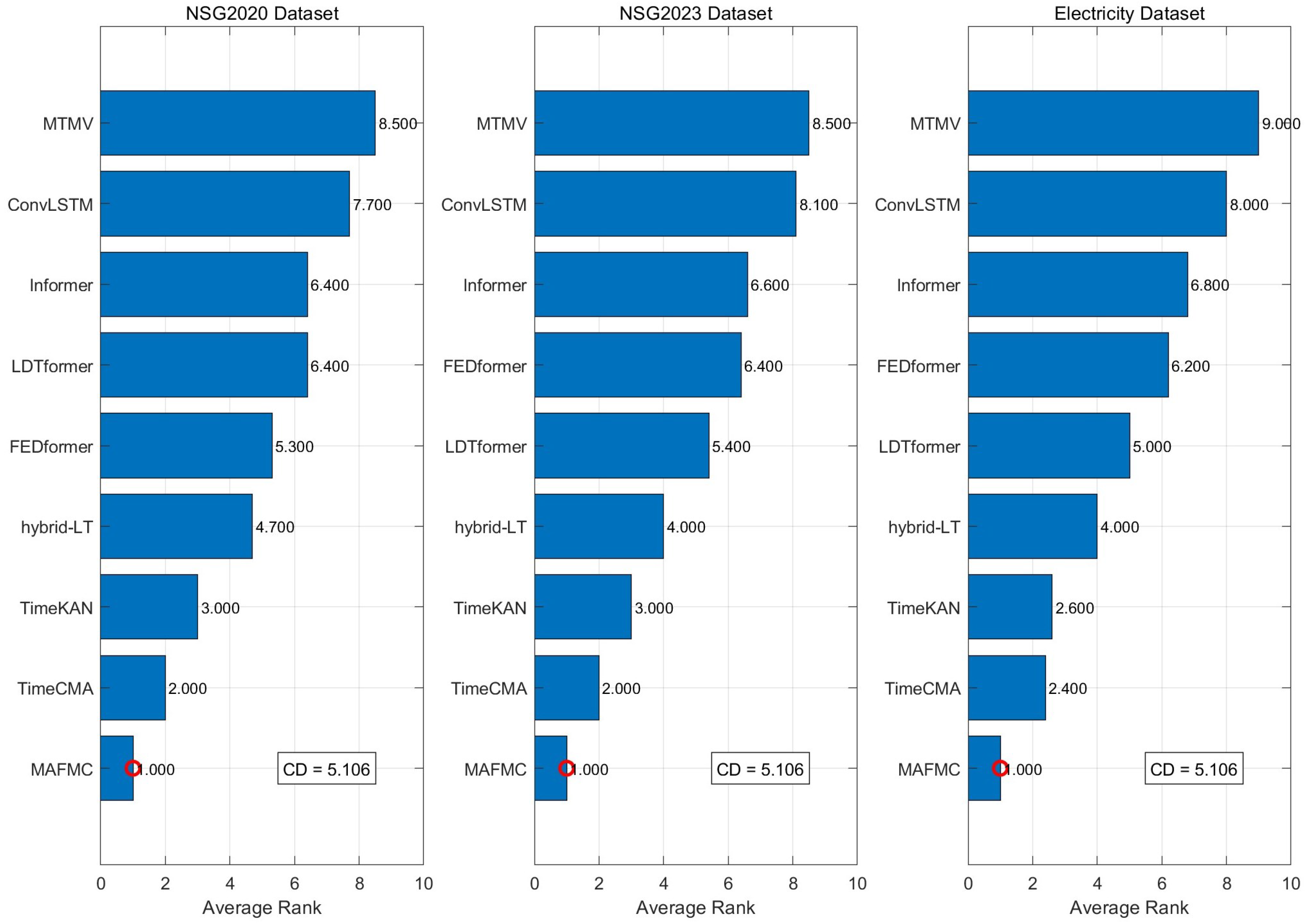
4.2. Performance Comparison
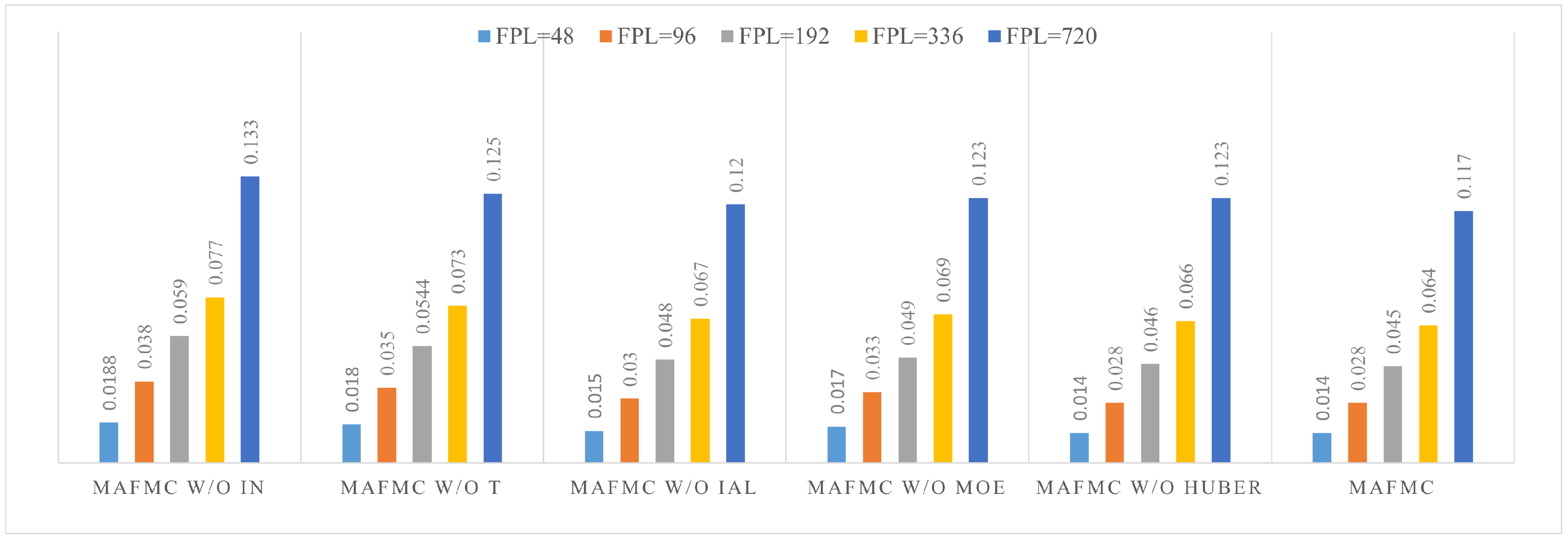
4.3. Ablation Study
- MAFMC w/o IN denotes the excision of the instance normalization.
- MAFMC w/o T denotes the excision of Transformer. This variant directly uses KAN-based mixture-of-experts to generation prediction results.
- MAFMC w/o IAL denotes the excision of the iterative auto-regressive learning.
- MAFMC w/o MOE denotes the excision of KAN-based mixture-of-experts. This variant uses traditional linear layer as the predictor.
- MAFMC w/o Huber denotes the excision of the Huber loss. This variant uses traditional MSE as the optimization loss.
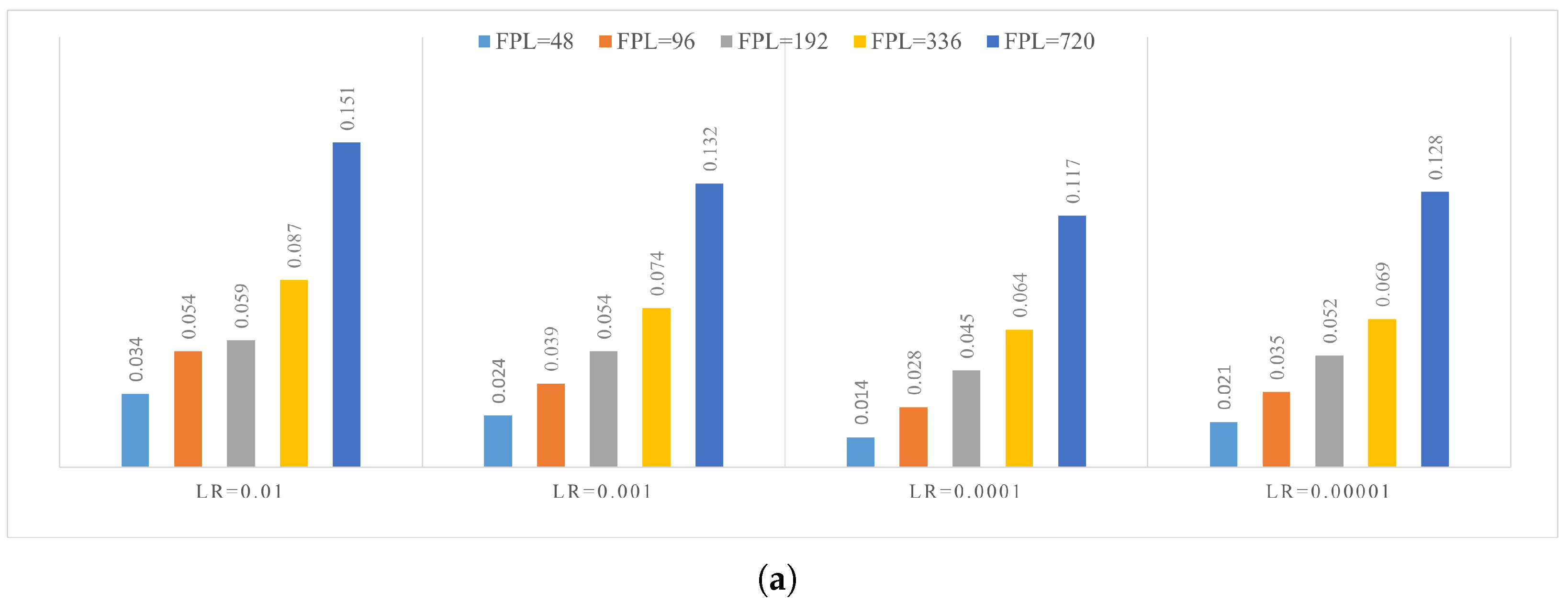
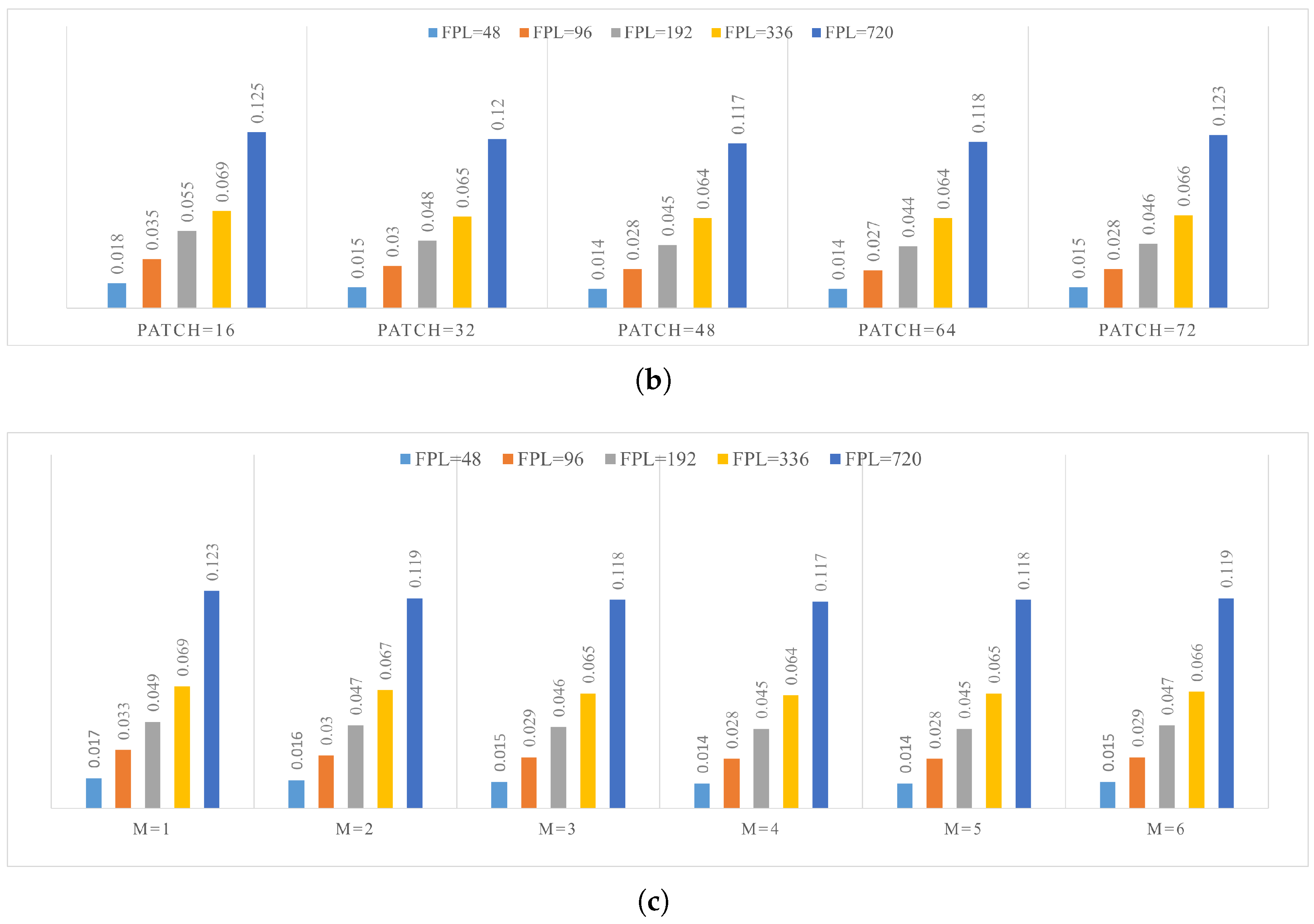
4.4. Parameter Study
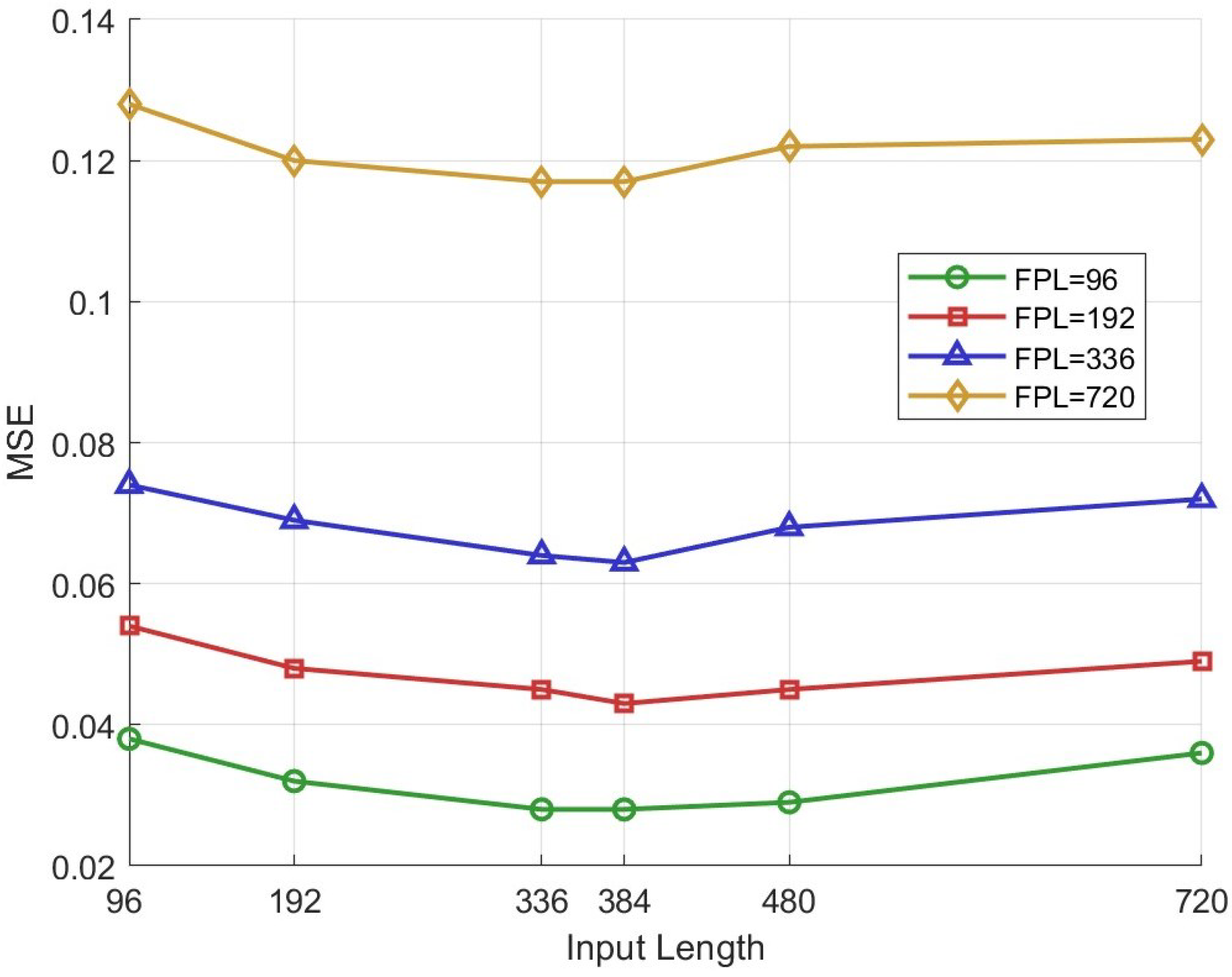
4.5. Input Length Study
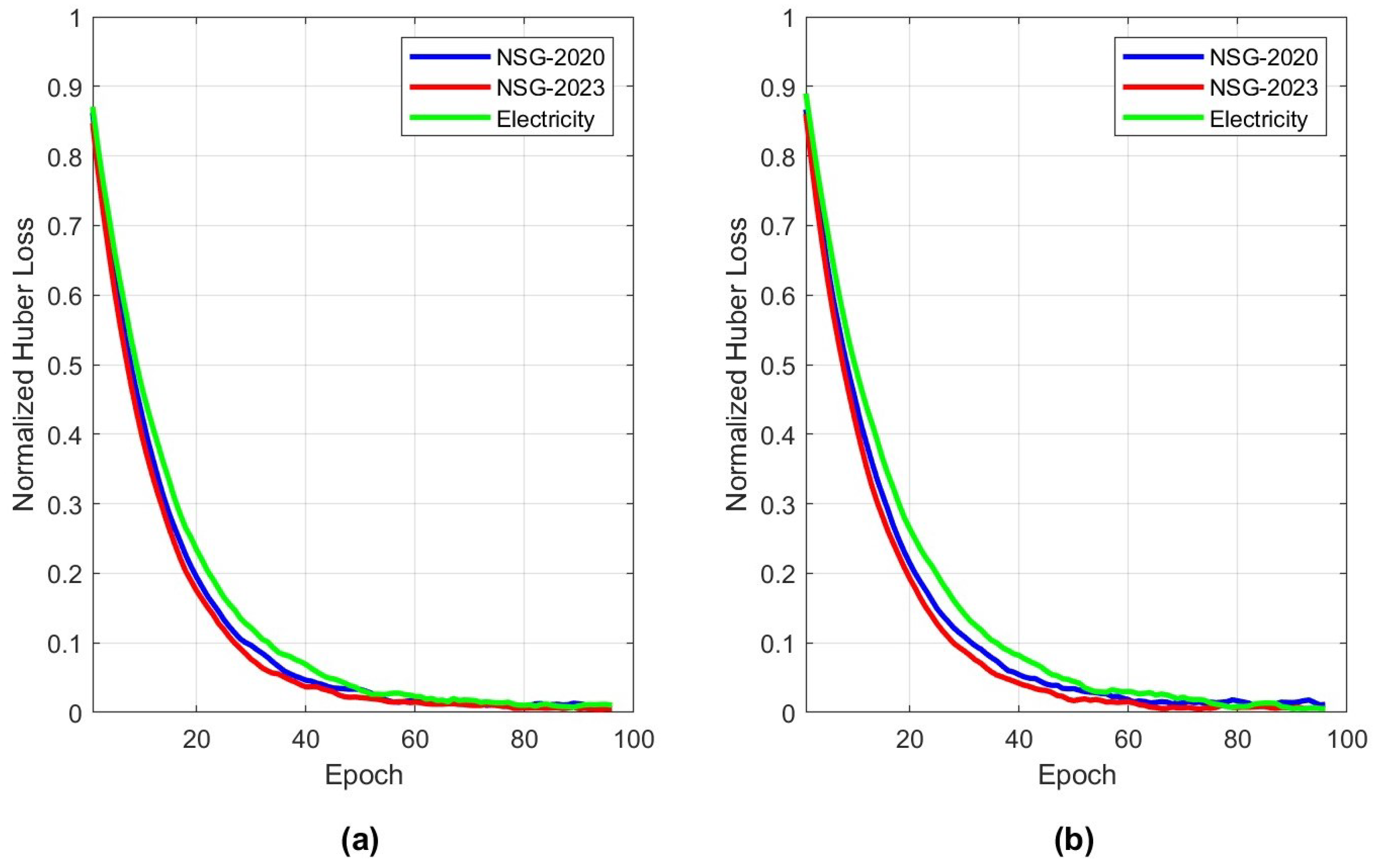
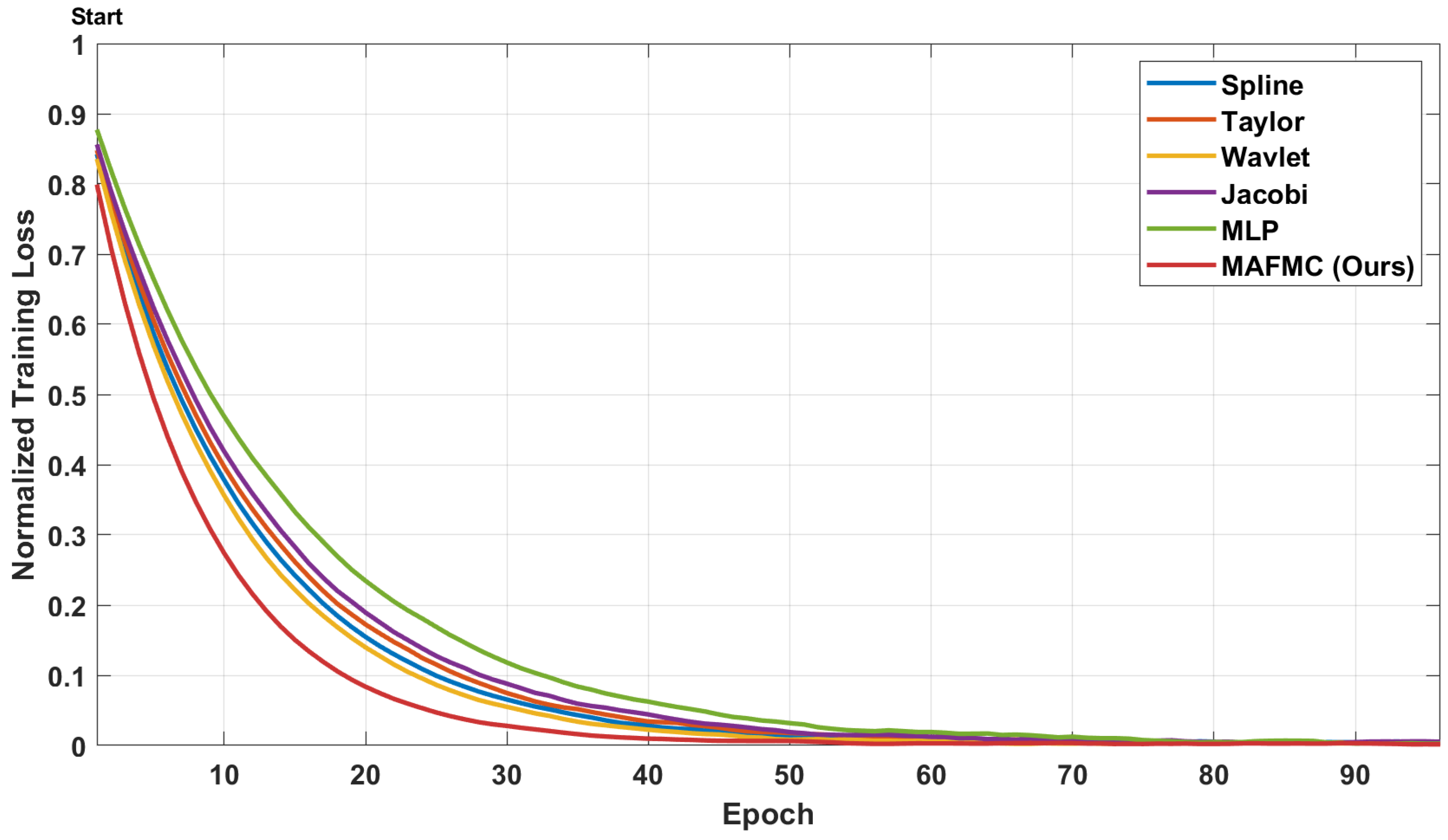
4.6. Convergence Study
4.7. Zero-Shot Study
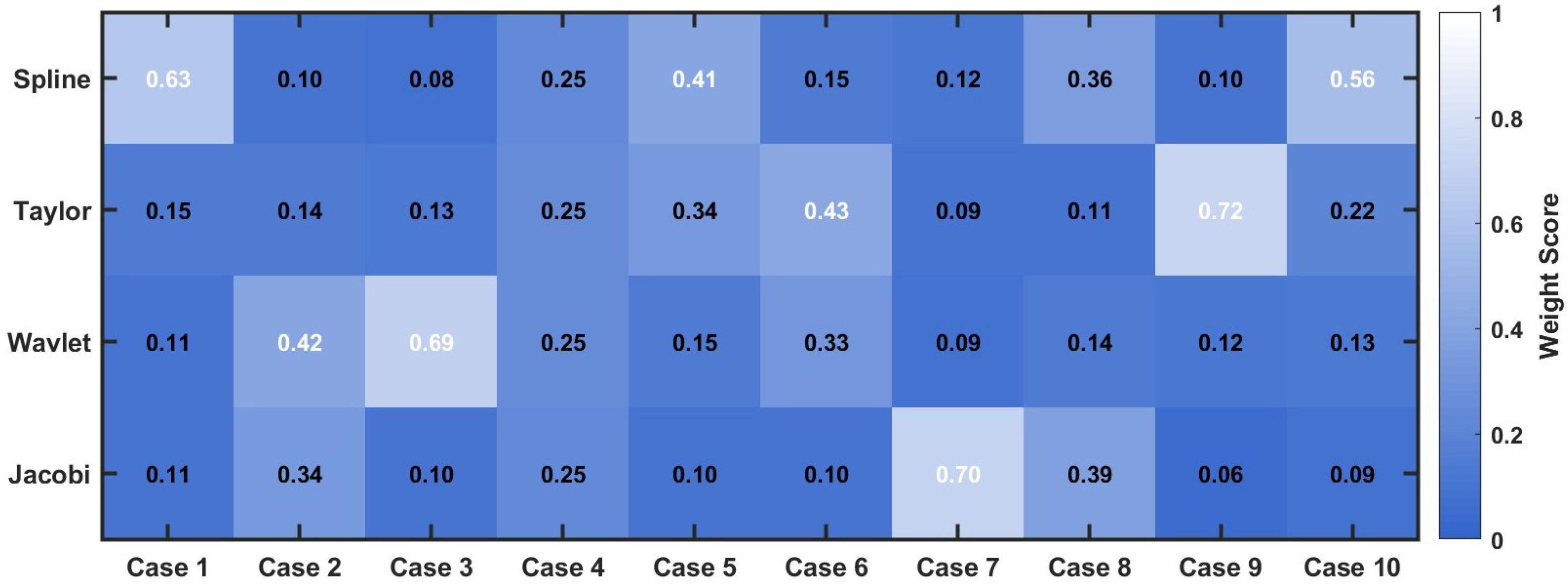
4.8. Case Study
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pentsos, V.; Tragoudas, S.; Wibbenmeyer, J.; Khdeer, N. A hybrid LSTM-Transformer model for power load forecasting. IEEE Trans. Smart Grid 2025, 16, 2624–2634. [Google Scholar] [CrossRef]
- Jalalifar, R.; Delavar, M.R.; Ghaderi, S.F. A novel approach for photovoltaic plant site selection in megacities utilizing power load forecasting and fuzzy inference system. Renew. Energy 2025, 243, 122527. [Google Scholar] [CrossRef]
- Peng, X.; Yang, X. Short-and medium-term power load forecasting model based on a hybrid attention mechanism in the time and frequency domains. Expert Syst. Appl. 2025, 278, 127329. [Google Scholar] [CrossRef]
- Gao, J.; Liu, M.; Li, P.; Zhang, J.; Chen, Z. Deep Multiview Adaptive Clustering With Semantic Invariance. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 12965–12978. [Google Scholar] [CrossRef]
- Gao, J.; Liu, M.; Li, P.; Laghari, A.A.; Javed, A.R.; Victor, N.; Gadekallu, T.R. Deep incomplete multiview clustering via information bottleneck for pattern mining of data in extreme-environment IoT. IEEE Internet Things J. 2024, 11, 26700–26712. [Google Scholar] [CrossRef]
- Fan, G.-F.; Han, Y.-Y.; Li, J.-W.; Peng, L.-L.; Yeh, Y.-H.; Hong, W.-C. A hybrid model for deep learning short-term power load forecasting based on feature extraction statistics techniques. Expert Syst. Appl. 2024, 238, 122012. [Google Scholar] [CrossRef]
- Jalalifar, R.; Delavar, M.R.; Ghaderi, S.F. SAC-ConvLSTM: A novel spatio-temporal deep learning-based approach for a short term power load forecasting. Expert Syst. Appl. 2024, 237, 121487. [Google Scholar] [CrossRef]
- Yang, F.; Fu, X.; Yang, Q.; Chu, Z. Decomposition strategy and attention-based long short-term memory network for multi-step ultra-short-term agricultural power load forecasting. Expert Syst. Appl. 2024, 238, 122226. [Google Scholar] [CrossRef]
- Mao, Q.; Wang, L.; Long, Y.; Han, L.; Wang, Z.; Chen, K. A blockchain-based framework for federated learning with privacy preservation in power load forecasting. Knowl.-Based Syst. 2024, 284, 111338. [Google Scholar] [CrossRef]
- Dong, J.; Luo, L.; Lu, Y.; Zhang, Q. A parallel short-term power load forecasting method considering high-level elastic loads. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Nahid, J.; Ongsakul, W.; Singh, J.G.; Roy, J. Short-term customer-centric electric load forecasting for low carbon microgrids using a hybrid model. Energy Syst. 2024. [Google Scholar] [CrossRef]
- Wang, Y.; Hao, Y.; Zhao, K.; Yao, Y. Stochastic configuration networks for short-term power load forecasting. Inf. Sci. 2025, 689, 121489. [Google Scholar] [CrossRef]
- Guo, W.; Liu, S.; Weng, L.; Liang, X. Power grid load forecasting using a CNN-LSTM network based on a multi-modal attention mechanism. Appl. Sci. 2025, 15, 2435. [Google Scholar] [CrossRef]
- Zhu, L.; Gao, J.; Zhu, C.; Deng, F. Short-term power load forecasting based on spatial-temporal dynamic graph and multi-scale Transformer. J. Comput. Des. Eng. 2025, 12, 92–111. [Google Scholar] [CrossRef]
- Hu, X.; Li, H.; Si, C. Improved composite model using metaheuristic optimization algorithm for short-term power load forecasting. Electr. Power Syst. Res. 2025, 241, 111330. [Google Scholar] [CrossRef]
- Somvanshi, S.; Javed, S.A.; Islam, M.M.; Pandit, D.; Das, S. A survey on Kolmogorov-Arnold network. ACM Comput. Surv. 2025, 58, 55. [Google Scholar] [CrossRef]
- Gbadega, P.A.; Sun, Y. Enhancing medium-term electric load forecasting accuracy leveraging swarm intelligence and neural networks optimization. In Proceedings of the 2024 18th International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Auckland, New Zealand, 24–26 June 2024; pp. 1–6. [Google Scholar]
- Lv, Z.; Wang, L.; Guan, Z.; Wu, J.; Du, X.; Zhao, H.; Guizani, M. An optimizing and differentially private clustering algorithm for mixed data in SDN-based smart grid. IEEE Access 2019, 7, 45773–45782. [Google Scholar] [CrossRef]
- Tsai, J.-L.; Lo, N.-W. Secure anonymous key distribution scheme for smart grid. IEEE Trans. Smart Grid 2015, 7, 906–914. [Google Scholar] [CrossRef]
- Chalmers, C.; Fergus, P.; Montanez, C.A.C.; Sikdar, S.; Ball, F.; Kendall, B. Detecting activities of daily living and routine behaviours in dementia patients living alone using smart meter load disaggregation. IEEE Trans. Emerg. Top. Comput. 2020, 10, 157–169. [Google Scholar] [CrossRef]
- Weber, M.; Turowski, M.; Çakmak, H.K.; Mikut, R.; Kühnapfel, U.; Hagenmeyer, V. Data-driven copy-paste imputation for energy time series. IEEE Trans. Smart Grid 2021, 12, 5409–5419. [Google Scholar] [CrossRef]
- Ullah, A.; Javaid, N.; Javed, M.U.; Pamir; Kim, B.-S.; Bahaj, S.A. Adaptive data balancing method using stacking ensemble model and its application to non-technical loss detection in smart grids. IEEE Access 2022, 10, 133244–133255. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, R.; Cao, J.; Tan, J. A CNN and LSTM-based multi-task learning architecture for short and medium-term electricity load forecasting. Electr. Power Syst. Res. 2023, 222, 109507. [Google Scholar] [CrossRef]
- Hua, H.; Liu, M.; Li, Y.; Deng, S.; Wang, Q. An ensemble framework for short-term load forecasting based on parallel CNN and GRU with improved ResNet. Electr. Power Syst. Res. 2023, 216, 109057. [Google Scholar] [CrossRef]
- Gong, J.; Qu, Z.; Zhu, Z.; Xu, H.; Yang, Q. Ensemble models of TCN-LSTM-LightGBM based on ensemble learning methods for short-term electrical load forecasting. Energy 2025, 318, 134757. [Google Scholar] [CrossRef]
- Ma, W.; Wu, W.; Ahmed, S.F.; Liu, G. Techno-economic feasibility of utilizing electrical load forecasting in microgrid optimization planning. Sustain. Energy Technol. Assess. 2025, 73, 104135. [Google Scholar] [CrossRef]
- Liu, M.; Xia, C.; Xia, Y.; Deng, S.; Wang, Y. TDCN: A novel temporal depthwise convolutional network for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2025, 165, 110512. [Google Scholar] [CrossRef]
- Sidharth, S.S.; Keerthana, A.R.; Gokul, R.; Anas, K.P. Chebyshev polynomial-based Kolmogorov-Arnold networks: An efficient architecture for nonlinear function approximation. arXiv 2024, arXiv:2405.07200. [Google Scholar]
- Li, Z. Kolmogorov-Arnold networks are radial basis function networks. arXiv 2024, arXiv:2405.06721. [Google Scholar] [CrossRef]
- Abd Elaziz, M.; Fares, I.A.; Aseeri, A.O. CKAN: Convolutional Kolmogorov–Arnold networks model for intrusion detection in IoT environment. IEEE Access 2024, 12, 134837–134851. [Google Scholar] [CrossRef]
- Li, C.; Liu, X.; Li, W.; Wang, C.; Liu, H.; Liu, Y.; Chen, Z.; Yuan, Y. U-KAN makes strong backbone for medical image segmentation and generation. In Proceedings of the Thirty-Ninth AAAI Conference on Artificial Intelligence (AAAI’25), Philadelphia, PA, USA, 25 February–4 March 2025; pp. 4652–4660. [Google Scholar]
- Shukla, K.; Toscano, J.D.; Wang, Z.; Zou, Z.; Karniadakis, G.E. A comprehensive and fair comparison between MLP and KAN representations for differential equations and operator networks. Comput. Methods Appl. Mech. Eng. 2024, 431, 117290. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, J.; Bai, J.; Anitescu, C.; Eshaghi, M.S.; Zhuang, X.; Rabczuk, T.; Liu, Y. Kolmogorov Arnold Informed neural network: A physics-informed deep learning framework for solving forward and inverse problems based on Kolmogorov Arnold Networks. arXiv 2024, arXiv:2406.11045. [Google Scholar] [CrossRef]
- Liu, C.; Xu, Q.; Miao, H.; Yang, S.; Zhang, L.; Long, C.; Li, Z.; Zhao, R. TimeCMA: Towards llm-empowered multivariate time series forecasting via cross-modality alignment. In Proceedings of the Thirty-Ninth AAAI Conference on Artificial Intelligence (AAAI’25), Philadelphia, PA, USA, 25 February–4 March 2025; pp. 18780–18788. [Google Scholar]
- Huang, S.; Zhao, Z.; Li, C.; Bai, L. TimeKAN: KAN-based Frequency Decomposition Learning Architecture for Long-term Time Series Forecasting. arXiv 2025, arXiv:2502.06910. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI 2021), Virtually, 2–9 February 2021; pp. 11106–11115. [Google Scholar]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. FEDformer: Frequency Enhanced Decomposed Transformer for Long-term Series Forecasting. In Proceedings of the 39th International Conference on Machine Learning (ICML), Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar]
| Name | Variables | Frequency | Length | Train/Valid/Test |
|---|---|---|---|---|
| Electricity | 321 | 1 h | 26,304 | 60%/10%/30% |
| NSG-2020 | 5 | 15 min | 35,136 | 60%/10%/30% |
| NSG-2023 | 5 | 15 min | 35,136 | 60%/10%/30% |
| Dataset | FPL | MAFMC | TimeCMA | TimeKAN | Hybrid-LT | LDTformer | ConvLSTM | MTMV | Informer | FEDformer | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MAE | MSE | MAE | MSE | ||
| NSG2020 | 48 | 0.014 | 0.042 | 0.015 | 0.045 | 0.017 | 0.048 | 0.019 | 0.051 | 0.020 | 0.052 | 0.022 | 0.054 | 0.025 | 0.057 | 0.021 | 0.050 | 0.019 | 0.049 |
| 96 | 0.028 | 0.119 | 0.032 | 0.125 | 0.035 | 0.129 | 0.038 | 0.134 | 0.040 | 0.137 | 0.042 | 0.140 | 0.045 | 0.145 | 0.039 | 0.138 | 0.037 | 0.135 | |
| 192 | 0.045 | 0.154 | 0.052 | 0.162 | 0.058 | 0.168 | 0.064 | 0.174 | 0.067 | 0.177 | 0.070 | 0.180 | 0.075 | 0.185 | 0.065 | 0.169 | 0.066 | 0.167 | |
| 336 | 0.064 | 0.186 | 0.088 | 0.198 | 0.095 | 0.205 | 0.103 | 0.212 | 0.108 | 0.217 | 0.114 | 0.222 | 0.121 | 0.227 | 0.109 | 0.212 | 0.105 | 0.197 | |
| 720 | 0.117 | 0.255 | 0.134 | 0.268 | 0.145 | 0.275 | 0.156 | 0.285 | 0.162 | 0.290 | 0.169 | 0.295 | 0.178 | 0.303 | 0.162 | 0.280 | 0.158 | 0.284 | |
| Avg | 0.053 | 0.151 | 0.064 | 0.161 | 0.071 | 0.169 | 0.079 | 0.177 | 0.083 | 0.181 | 0.088 | 0.186 | 0.097 | 0.194 | 0.079 | 0.169 | 0.077 | 0.164 | |
| NSG2023 | 48 | 0.012 | 0.097 | 0.013 | 0.102 | 0.014 | 0.105 | 0.016 | 0.110 | 0.018 | 0.115 | 0.020 | 0.120 | 0.022 | 0.125 | 0.019 | 0.117 | 0.019 | 0.118 |
| 96 | 0.049 | 0.152 | 0.053 | 0.160 | 0.058 | 0.165 | 0.063 | 0.170 | 0.068 | 0.175 | 0.073 | 0.180 | 0.078 | 0.185 | 0.070 | 0.175 | 0.069 | 0.173 | |
| 192 | 0.082 | 0.202 | 0.088 | 0.210 | 0.095 | 0.215 | 0.103 | 0.220 | 0.111 | 0.225 | 0.119 | 0.230 | 0.127 | 0.235 | 0.116 | 0.224 | 0.112 | 0.222 | |
| 336 | 0.126 | 0.257 | 0.135 | 0.265 | 0.145 | 0.270 | 0.156 | 0.275 | 0.168 | 0.280 | 0.180 | 0.285 | 0.193 | 0.290 | 0.173 | 0.277 | 0.175 | 0.278 | |
| 720 | 0.274 | 0.387 | 0.295 | 0.400 | 0.317 | 0.410 | 0.341 | 0.420 | 0.366 | 0.430 | 0.392 | 0.440 | 0.420 | 0.450 | 0.372 | 0.421 | 0.366 | 0.414 | |
| Avg | 0.109 | 0.219 | 0.117 | 0.227 | 0.126 | 0.233 | 0.136 | 0.239 | 0.146 | 0.245 | 0.157 | 0.251 | 0.168 | 0.257 | 0.150 | 0.242 | 0.148 | 0.241 | |
| Electricity | 48 | 0.122 | 0.223 | 0.130 | 0.230 | 0.138 | 0.237 | 0.145 | 0.244 | 0.155 | 0.250 | 0.165 | 0.257 | 0.175 | 0.263 | 0.162 | 0.252 | 0.163 | 0.253 |
| 96 | 0.155 | 0.237 | 0.165 | 0.245 | 0.174 | 0.266 | 0.185 | 0.261 | 0.195 | 0.269 | 0.205 | 0.277 | 0.215 | 0.285 | 0.200 | 0.272 | 0.198 | 0.267 | |
| 192 | 0.162 | 0.254 | 0.173 | 0.263 | 0.182 | 0.272 | 0.195 | 0.281 | 0.207 | 0.290 | 0.219 | 0.299 | 0.231 | 0.308 | 0.214 | 0.293 | 0.208 | 0.288 | |
| 336 | 0.187 | 0.274 | 0.198 | 0.283 | 0.197 | 0.286 | 0.223 | 0.301 | 0.237 | 0.310 | 0.252 | 0.319 | 0.268 | 0.328 | 0.247 | 0.310 | 0.242 | 0.308 | |
| 720 | 0.225 | 0.319 | 0.238 | 0.328 | 0.236 | 0.320 | 0.267 | 0.346 | 0.284 | 0.355 | 0.302 | 0.364 | 0.321 | 0.373 | 0.300 | 0.360 | 0.293 | 0.357 | |
| Avg | 0.170 | 0.261 | 0.180 | 0.270 | 0.185 | 0.258 | 0.183 | 0.286 | 0.215 | 0.294 | 0.228 | 0.295 | 0.235 | 0.310 | 0.224 | 0.297 | 0.220 | 0.294 | |
| Dataset | FPL | MAFMC | TimeCMA | TimeKAN | Hybrid-LT | LDTformer | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | ||
| NSG2020 | 48 | 0.022 | 0.058 | 0.026 | 0.067 | 0.029 | 0.072 | 0.034 | 0.075 | 0.048 | 0.082 |
| 96 | 0.039 | 0.133 | 0.047 | 0.145 | 0.052 | 0.149 | 0.055 | 0.162 | 0.062 | 0.177 | |
| 192 | 0.057 | 0.171 | 0.068 | 0.187 | 0.072 | 0.192 | 0.075 | 0.200 | 0.082 | 0.217 | |
| 336 | 0.077 | 0.198 | 0.097 | 0.213 | 0.099 | 0.215 | 0.113 | 0.227 | 0.128 | 0.227 | |
| 720 | 0.128 | 0.281 | 0.147 | 0.292 | 0.151 | 0.295 | 0.176 | 0.305 | 0.182 | 0.313 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.; Deng, W.; Liu, M.; Lv, L.; Chen, Z. Empowering Sustainability in Power Grids: A Multi-Scale Adaptive Load Forecasting Framework with Expert Collaboration. Sustainability 2025, 17, 10434. https://doi.org/10.3390/su172310434
Tian Z, Deng W, Liu M, Lv L, Chen Z. Empowering Sustainability in Power Grids: A Multi-Scale Adaptive Load Forecasting Framework with Expert Collaboration. Sustainability. 2025; 17(23):10434. https://doi.org/10.3390/su172310434
Chicago/Turabian StyleTian, Zengyao, Wenchen Deng, Meng Liu, Li Lv, and Zhikui Chen. 2025. "Empowering Sustainability in Power Grids: A Multi-Scale Adaptive Load Forecasting Framework with Expert Collaboration" Sustainability 17, no. 23: 10434. https://doi.org/10.3390/su172310434
APA StyleTian, Z., Deng, W., Liu, M., Lv, L., & Chen, Z. (2025). Empowering Sustainability in Power Grids: A Multi-Scale Adaptive Load Forecasting Framework with Expert Collaboration. Sustainability, 17(23), 10434. https://doi.org/10.3390/su172310434







