A Universal Urban Flood Risk Model Based on Particle-Swarm-Optimization-Enhanced Spiking Graph Convolutional Networks
Abstract
1. Introduction
2. Materials and Methods
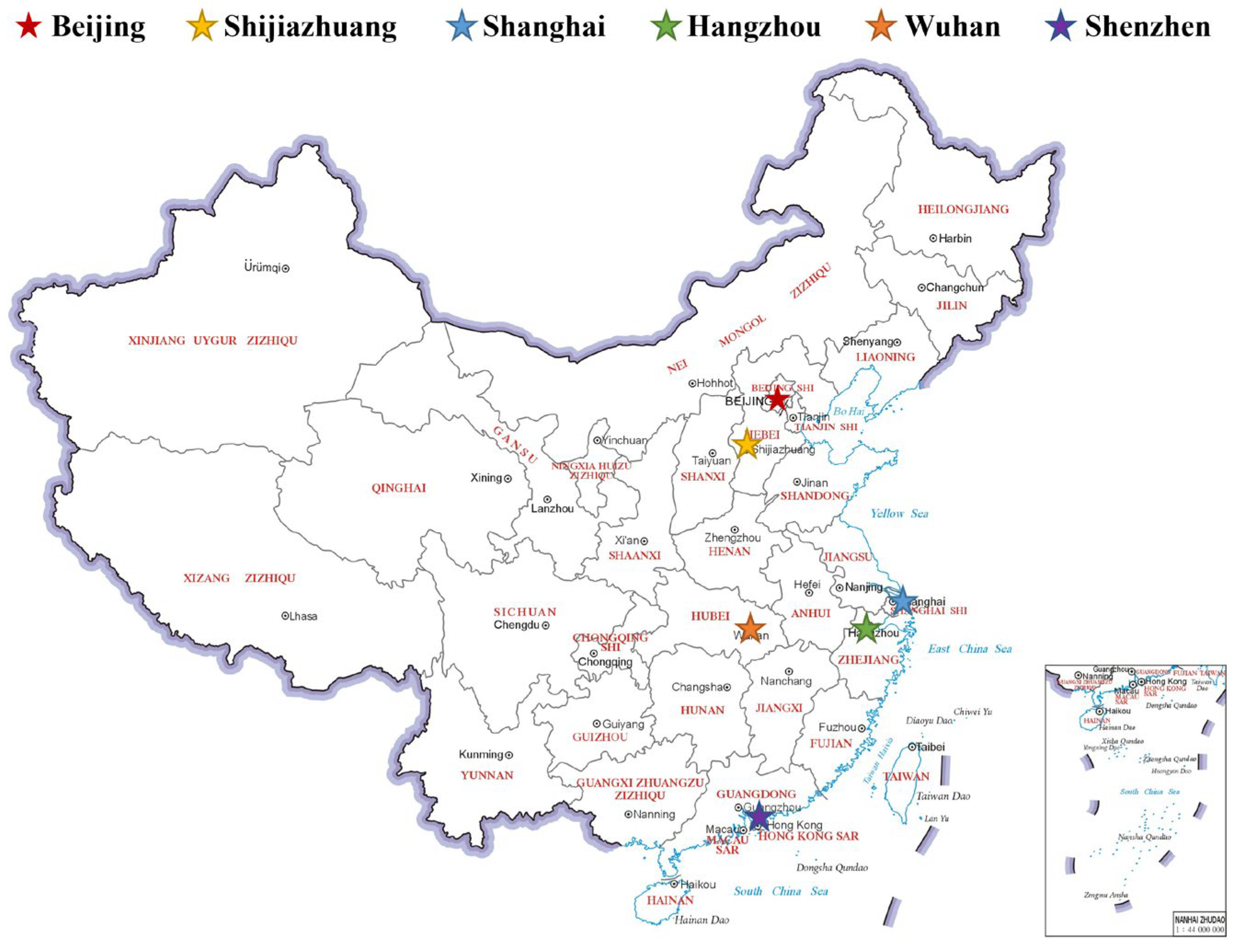
2.1. Study Area
2.2. Mixed-City Flood Risk Dataset
3. Methodology
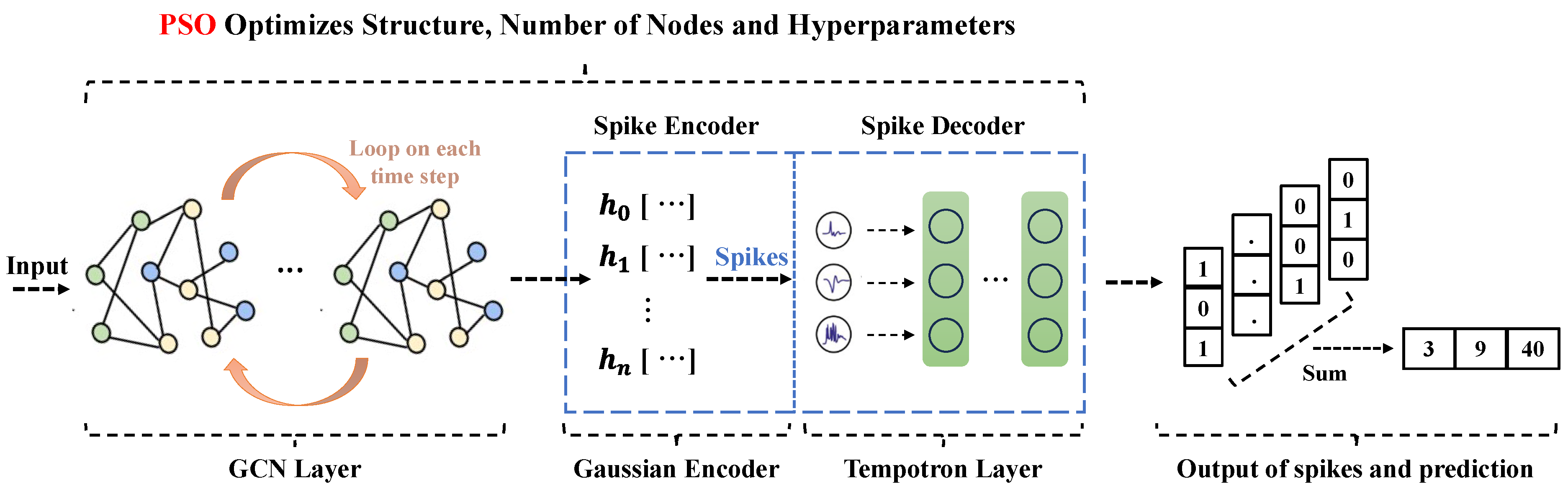
3.1. Graph Convolutional Network
3.2. Spiking Neural Network
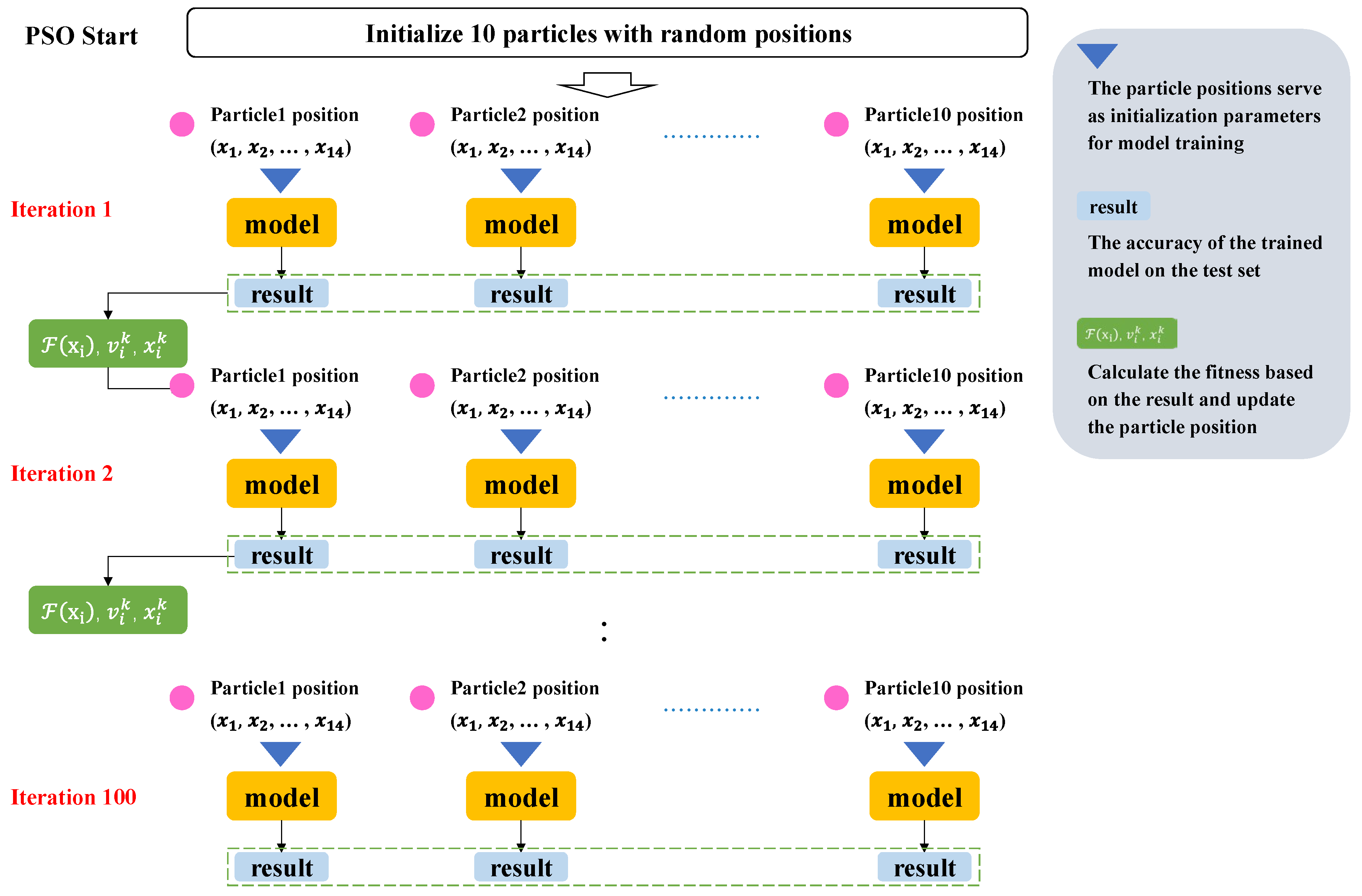
3.3. Particle Swarm Optimization
3.4. Experimental Setup
4. Results and Discussion
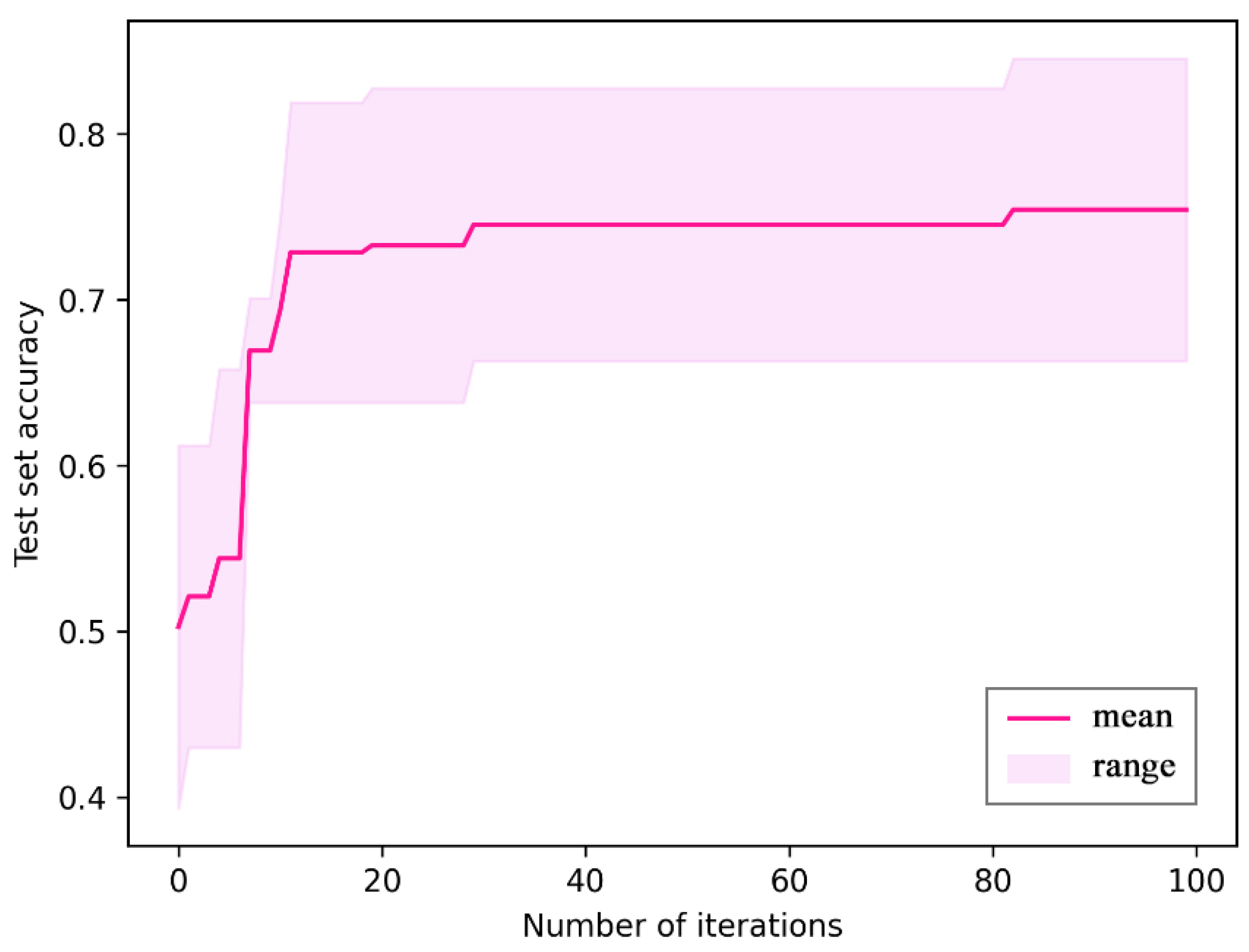
4.1. Parameter Optimization with P-SGCN Model Performance
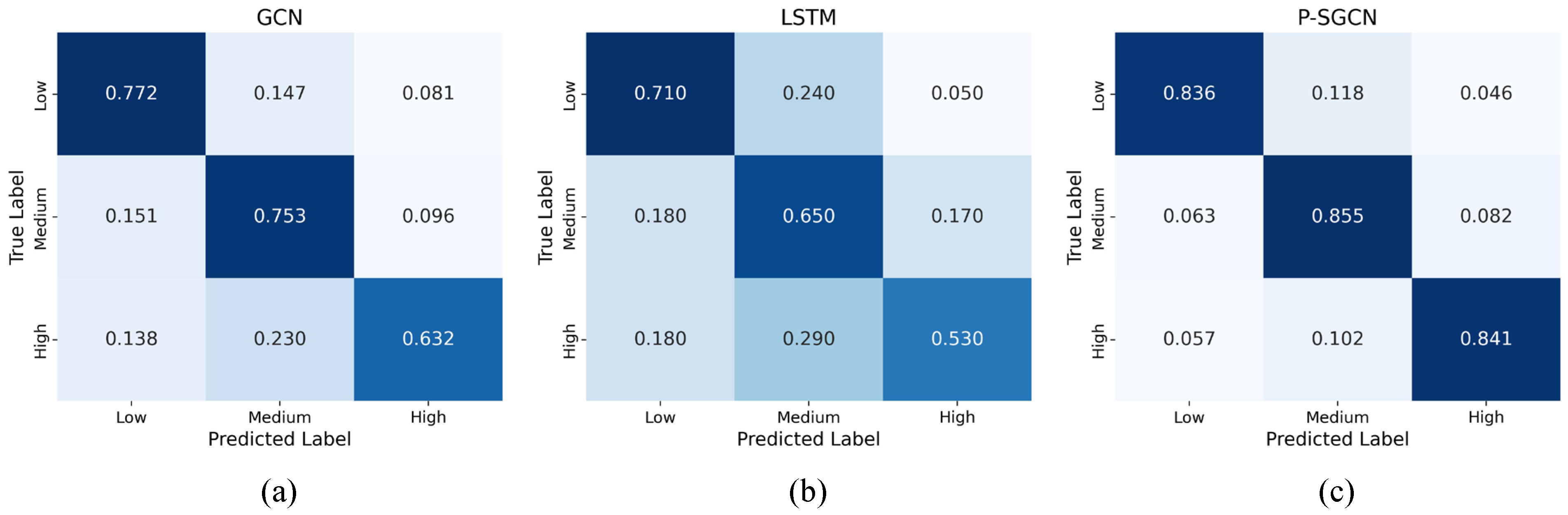
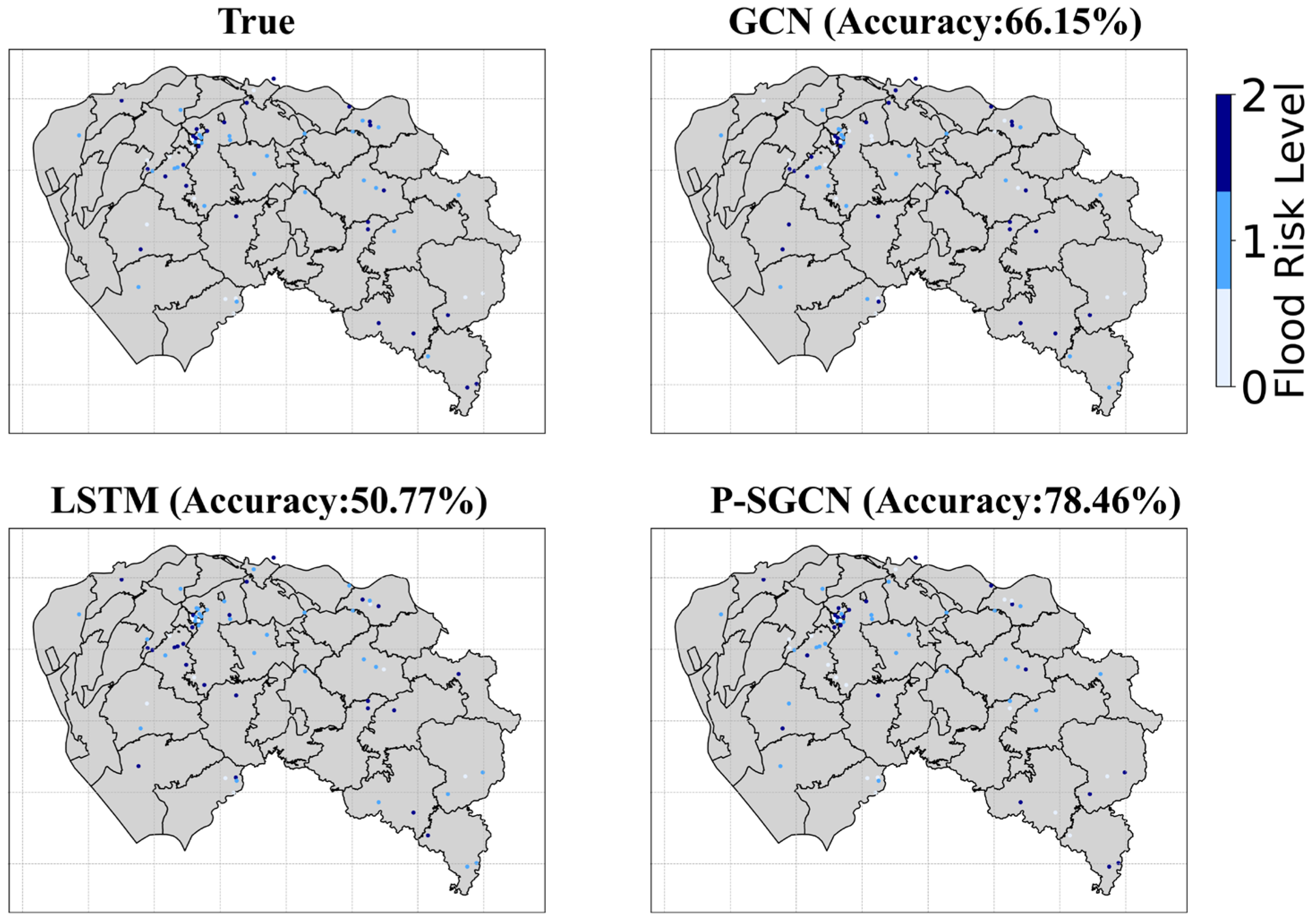
4.2. Performance Results of Different Models
4.3. Energy Consumption and Parameters of Different Models
4.4. P-SGCN Model Adaptation via Transfer Learning
5. Discussion
5.1. Impact of PSO on Model Stability and Optimization Efficiency
5.2. Interpretation of Cross-Model Performance Differences
5.3. Energy Efficiency and Lightweight Architecture Advantages
5.4. Transfer Learning and Model Adaptability Across Cities
5.5. Practical Implications, Data Reliability, and Future Research Directions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jongman, B.; Hochrainer-Stigler, S.; Feyen, L.; Aerts, J.C.; Mechler, R.; Botzen, W.W.; Bouwer, L.M.; Pflug, G.; Rojas, R.; Ward, P.J. Increasing Stress on Disaster-Risk Finance Due to Large Floods. Nat. Clim. Change 2014, 4, 264–268. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Gayen, A.; Panahi, M.; Rezaie, F.; Blaschke, T. Multi-Hazard Probability Assessment and Mapping in Iran. Sci. Total Environ. 2019, 692, 556–571. [Google Scholar] [CrossRef]
- Rahmati, O.; Darabi, H.; Panahi, M.; Kalantari, Z.; Naghibi, S.A.; Ferreira, C.S.S.; Kornejady, A.; Karimidastenaei, Z.; Mohammadi, F.; Stefanidis, S. Development of Novel Hybridized Models for Urban Flood Susceptibility Mapping. Sci. Rep. 2020, 10, 12937. [Google Scholar] [CrossRef]
- Rusk, J.; Maharjan, A.; Tiwari, P.; Chen, T.-H.K.; Shneiderman, S.; Turin, M.; Seto, K.C. Multi-Hazard Susceptibility and Exposure Assessment of the Hindu Kush Himalaya. Sci. Total Environ. 2022, 804, 150039. [Google Scholar] [CrossRef]
- Yousefi, S.; Pourghasemi, H.R.; Rahmati, O.; Keesstra, S.; Emami, S.N.; Hooke, J. Geomorphological Change Detection of an Urban Meander Loop Caused by an Extreme Flood Using Remote Sensing and Bathymetry Measurements (a Case Study of Karoon River, Iran). J. Hydrol. 2021, 597, 125712. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, X.; Liang, S.; Zhu, B.; Yao, Y.; Meng, S.; Lu, C. Quantifying the Response of Potential Flooding Risk to Urban Growth in Beijing. Sci. Total Environ. 2020, 705, 135868. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Y.; Guo, Y.; Wu, Z.; Yan, D. Urban Flood Forecasting Based on the Coupling of Numerical Weather Model and Stormwater Model: A Case Study of Zhengzhou City. J. Hydrol. Reg. Stud. 2022, 39, 100985. [Google Scholar] [CrossRef]
- Ziegler, A.D.; She, L.H.; Tantasarin, C.; Jachowski, N.R.; Wasson, R. Floods, False Hope, and the Future. Hydrol. Process. 2012, 26, 1748–1750. [Google Scholar] [CrossRef]
- Wang, M.; Fu, X.; Zhang, D.; Chen, F.; Liu, M.; Zhou, S.; Su, J.; Tan, S.K. Assessing Urban Flooding Risk in Response to Climate Change and Urbanization Based on Shared Socio-Economic Pathways. Sci. Total Environ. 2023, 880, 163470. [Google Scholar] [CrossRef]
- Chen, Z.; Fang, X.; Li, J.; Wang, M.; Chen, A.; Yin, L. An Overview of Application of Machine Learning Models in Urban Flood Simulation and Forecasting. Pearl River 2025, 46, 9–22. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, Z.; Chen, X.; Lai, C. Fast Simulation and Prediction of Urban Pluvial Floods Using a Deep Convolutional Neural Network Model. J. Hydrol. 2023, 624, 129945. [Google Scholar] [CrossRef]
- Mignot, E.; Dewals, B. Hydraulic Modelling of Inland Urban Flooding: Recent Advances. J. Hydrol. 2022, 609, 127763. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Lin, K.; Liu, Z.; Liang, Y.; Liu, Y.; Li, C. A Novel Framework for Urban Flood Risk Assessment: Multiple Perspectives and Causal Analysis. Water Res. 2024, 256, 121591. [Google Scholar] [CrossRef]
- Mukerji, A.; Chatterjee, C.; Raghuwanshi, N.S. Flood Forecasting Using ANN, Neuro-Fuzzy, and Neuro-GA Models. J. Hydrol. Eng. 2009, 14, 647–652. [Google Scholar] [CrossRef]
- Mudashiru, R.B.; Sabtu, N.; Abustan, I.; Balogun, W. Flood Hazard Mapping Methods: A Review. J. Hydrol. 2021, 603, 126846. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Zhang, J.; Lin, K. Impact of 2D and 3D Factors on Urban Flooding: Spatial Characteristics and Interpretable Analysis of Drivers. Water Res. 2025, 280, 123537. [Google Scholar] [CrossRef]
- Jodar-Abellan, A.; Valdes-Abellan, J.; Pla, C.; Gomariz-Castillo, F. Impact of Land Use Changes on Flash Flood Prediction Using a Sub-Daily SWAT Model in Five Mediterranean Ungauged Watersheds (SE Spain). Sci. Total Environ. 2019, 657, 1578–1591. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A New Applications Manual for the Storm Water Management Model (SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q.; Ming, X. A Full-Scale Fluvial Flood Modelling Framework Based on a High-Performance Integrated Hydrodynamic Modelling System (HiPIMS). Adv. Water Resour. 2019, 132, 103392. [Google Scholar] [CrossRef]
- Mesa-Mingorance, J.L.; Ariza-López, F.J. Accuracy Assessment of Digital Elevation Models (DEMs): A Critical Review of Practices of the Past Three Decades. Remote Sens. 2020, 12, 2630. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S. Flood Inundation Modelling: A Review of Methods, Recent Advances and Uncertainty Analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Yatsalo, B.; Radaev, A.; Martínez, L. From MCDA to Fuzzy MCDA: Presumption of Model Adequacy or Is Every Fuzzification of an mCDA Method Justified? Inf. Sci. 2022, 587, 371–392. [Google Scholar] [CrossRef]
- Bączkiewicz, A.; Wątróbski, J.; Kizielewicz, B.; Sałabun, W. Towards Objectification of Multi-Criteria Assessments: A Comparative Study on MCDA Methods. In Proceedings of the 2021 16th Conference on Computer Science and Intelligence Systems (FedCSIS), Sofia, Bulgaria, 2–5 September 2021; pp. 417–425. [Google Scholar]
- Lin, L.; Tang, C.; Liang, Q.; Wu, Z.; Wang, X.; Zhao, S. Rapid Urban Flood Risk Mapping for Data-Scarce Environments Using Social Sensing and Region-Stable Deep Neural Network. J. Hydrol. 2023, 617, 128758. [Google Scholar] [CrossRef]
- Fu, G.; Jin, Y.; Sun, S.; Yuan, Z.; Butler, D. The Role of Deep Learning in Urban Water Management: A Critical Review. Water Res. 2022, 223, 118973. [Google Scholar] [CrossRef]
- Li, C.; Sun, N.; Lu, Y.; Guo, B.; Wang, Y.; Sun, X.; Yao, Y. Review on Urban Flood Risk Assessment. Sustainability 2022, 15, 765. [Google Scholar] [CrossRef]
- Farahmand, H.; Xu, Y.; Mostafavi, A. A Spatial–Temporal Graph Deep Learning Model for Urban Flood Nowcasting Leveraging Heterogeneous Community Features. Sci. Rep. 2023, 13, 6768. [Google Scholar] [CrossRef]
- Guo, K.; Guan, M.; Yu, D. Urban Surface Water Flood Modelling–a Comprehensive Review of Current Models and Future Challenges. Hydrol. Earth Syst. Sci. 2021, 25, 2843–2860. [Google Scholar] [CrossRef]
- Karmegam, D.; Ramamoorthy, S.; Mappillairaju, B. Near Real Time Flood Inundation Mapping Using Social Media Data as an Information Source: A Case Study of 2015 Chennai Flood. Geoenviron. Disasters 2021, 8, 25. [Google Scholar] [CrossRef]
- Young, J.C.; Arthur, R.; Spruce, M.; Williams, H.T. Social Sensing of Flood Impacts in India: A Case Study of Kerala 2018. Int. J. Disaster Risk Reduct. 2022, 74, 102908. [Google Scholar] [CrossRef]
- Wang, Y. Medieval Chinese Autobiographical Writing: The Self-Written Epitaph. Mediev. Hist. J. 2015, 18, 305–345. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 5th International Conference on Learning Representations (ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph Convolutional Networks: A Comprehensive Review. Comput. Soc. Netw. 2019, 6, 11. [Google Scholar] [CrossRef] [PubMed]
- Tavanaei, A.; Ghodrati, M.; Kheradpisheh, S.R.; Masquelier, T.; Maida, A. Deep Learning in Spiking Neural Networks. Neural Netw. 2019, 111, 47–63. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Khemani, B.; Patil, S.; Kotecha, K.; Tanwar, S. A Review of Graph Neural Networks: Concepts, Architectures, Techniques, Challenges, Datasets, Applications, and Future Directions. J. Big Data 2024, 11, 18. [Google Scholar] [CrossRef]
- Taherkhani, A.; Belatreche, A.; Li, Y.; Cosma, G.; Maguire, L.P.; McGinnity, T.M. A Review of Learning in Biologically Plausible Spiking Neural Networks. Neural Netw. 2020, 122, 253–272. [Google Scholar] [CrossRef]
- Lorenzo, P.R.; Nalepa, J.; Kawulok, M.; Ramos, L.S.; Pastor, J.R. Particle Swarm Optimization for Hyper-Parameter Selection in Deep Neural Networks. In Proceedings of the Genetic and Evolutionary Computation Conference, Berlin, Germany, 15–19 July 2017; ACM: Berlin, Germany, 2017; pp. 481–488. [Google Scholar]
- Boyarskikh, K.A.; Khishchenko, K.V. Algorithm for Finding Parameters of Equations of State by Particle Swarm Optimization. Bull. Russ. Acad. Sci. Phys. 2024, 88, 1446–1451. [Google Scholar] [CrossRef]
- Yin, K.; Ma, J.; Mostafavi, A. Unsupervised Graph Deep Learning Reveals Emergent Flood Risk Profile of Urban Areas. arXiv 2023, arXiv:2309.14610. [Google Scholar] [CrossRef]
- Zhang, L.; Qin, H.; Mao, J.; Cao, X.; Fu, G. High Temporal Resolution Urban Flood Prediction Using Attention-Based LSTM Models. J. Hydrol. 2023, 620, 129499. [Google Scholar] [CrossRef]
- Zhao, Z.; Alzubaidi, L.; Zhang, J.; Duan, Y.; Gu, Y. A Comparison Review of Transfer Learning and Self-Supervised Learning: Definitions, Applications, Advantages and Limitations. Expert. Syst. Appl. 2023, 242, 122807. [Google Scholar] [CrossRef]
- Qin, D.; Tao, S.; Dong, S.; Luo, Y. Climate, Environmental, and Socioeconomic Characteristics of China. In Climate and Environmental Change in China: 1951–2012; Qin, D., Ding, Y., Mu, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–27. ISBN 978-3-662-48480-7. [Google Scholar]
- Hou, H.; Shen, L.; Jia, J.; Xu, Z. An Integrated Framework for Flood Disaster Information Extraction and Analysis Leveraging Social Media Data: A Case Study of the Shouguang Flood in China. Sci. Total Environ. 2024, 949, 174948. [Google Scholar] [CrossRef]
- Zeng, Z.; Lan, J.; Hamidi, A.R.; Zou, S. Integrating Internet Media into Urban Flooding Susceptibility Assessment: A Case Study in China. Cities 2020, 101, 102697. [Google Scholar] [CrossRef]
- Li, C.; Liu, M.; Hu, Y.; Wang, H.; Zhou, R.; Wu, W.; Wang, Y. Spatial Distribution Patterns and Potential Exposure Risks of Urban Floods in Chinese Megacities. J. Hydrol. 2022, 610, 127838. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, S. Floods losses and hazards in China from 2001 to 2020. Clim. Change Res. 2022, 18, 154. [Google Scholar] [CrossRef]
- Song, J.; Chang, Z.; Li, W.; Feng, Z.; Wu, J.; Cao, Q.; Liu, J. Resilience-Vulnerability Balance to Urban Flooding: A Case Study in a Densely Populated Coastal City in China. Cities 2019, 95, 102381. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA Global Precipitation Measurement (GPM) Integrated Multi-Satellite Retrievals for GPM (IMERG); National Aeronautics and Space Administration: Washington, DC, USA, 2015; Volume 4, p. 30. [Google Scholar]
- Yan, Z.; Guo, X.; Zhao, Z.; Tang, L. Achieving Fine-Grained Urban Flood Perception and Spatio-Temporal Evolution Analysis Based on Social Media. Sustain. Cities Soc. 2024, 101, 105077. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montréal, QC, Canada, 8–13 December 2014; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 27, pp. 2672–2680. [Google Scholar]
- Lobo, J.L.; Del Ser, J.; Bifet, A.; Kasabov, N. Spiking Neural Networks and Online Learning: An Overview and Perspectives. Neural Netw. 2020, 121, 88–100. [Google Scholar] [CrossRef]
- Zhu, R.-J.; Zhang, M.; Zhao, Q.; Deng, H.; Duan, Y.; Deng, L.-J. Tcja-Snn: Temporal-Channel Joint Attention for Spiking Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 5112–5125. [Google Scholar] [CrossRef] [PubMed]
- Sboev, A.; Serenko, A.; Rybka, R.; Vlasov, D. Solving a Classification Task by Spiking Neural Network with STDP Based on Rate and Temporal Input Encoding. Math. Methods Appl. Sci. 2020, 43, 7802–7814. [Google Scholar] [CrossRef]
- Gütig, R.; Sompolinsky, H. The Tempotron: A Neuron That Learns Spike Timing–Based Decisions. Nat. Neurosci. 2006, 9, 420–428. [Google Scholar] [CrossRef]
- Beni, G. Swarm Intelligence. In Complex Social and Behavioral Systems; Sotomayor, M., Pérez-Castrillo, D., Castiglione, F., Eds.; Springer: New York, NY, USA, 2020; pp. 791–818. ISBN 978-1-07-160367-3. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., D'Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; Volume 32, pp. 8024–8035. [Google Scholar]
- Fang, W.; Chen, Y.; Ding, J.; Yu, Z.; Masquelier, T.; Chen, D.; Huang, L.; Zhou, H.; Li, G.; Tian, Y. SpikingJelly: An Open-Source Machine Learning Infrastructure Platform for Spike-Based Intelligence. Sci. Adv. 2023, 9, eadi1480. [Google Scholar] [CrossRef]
- Jeddi, A.; Shafiee, M.J.; Karg, M.; Scharfenberger, C.; Wong, A. Learn2perturb: An End-to-End Feature Perturbation Learning to Improve Adversarial Robustness. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Online, 14–19 June 2020; pp. 1241–1250. [Google Scholar]
- Li, C.; Zhang, D.; Huang, W.; Zhang, J. Cross Contrasting Feature Perturbation for Domain Generalization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 1327–1337. [Google Scholar]
- Fakhouri, H.N.; Alawadi, S.; Awaysheh, F.M.; Hamad, F. Novel Hybrid Success History Intelligent Optimizer with Gaussian Transformation: Application in CNN Hyperparameter Tuning. Clust. Comput. 2024, 27, 3717–3739. [Google Scholar] [CrossRef]
- Huang, Y.; Wei, X. Improved BP Neural Network Prediction Model Based on Particle Swarm Algorithm. Acad. J. Comput. Inf. Sci. 2024, 7, 143–151. [Google Scholar] [CrossRef]
- Omar, M.; Yakub, F.; Abdullah, S.S.; Abd Rahim, M.S.; Zuhairi, A.H.; Govindan, N. One-Step vs Horizon-Step Training Strategies for Multi-Step Traffic Flow Forecasting with Direct Particle Swarm Optimization Grid Search Support Vector Regression and Long Short-Term Memory. Expert. Syst. Appl. 2024, 252, 124154. [Google Scholar] [CrossRef]
- Guo, K.; Guan, M.; Yan, H. Utilising Social Media Data to Evaluate Urban Flood Impact in Data Scarce Cities. Int. J. Disaster Risk Reduct. 2023, 93, 103780. [Google Scholar] [CrossRef]




| Data | Resolution | Year | Source |
|---|---|---|---|
| Urban flood | Point data | 2015–2024 | Sina Weibo |
| Precipitation | 0.1° × 0.1° | 2015–2024 | GPM [50] |
| DEM | 30 m × 30 m | 2015–2020 | Zhongke Chaotu Geographic Data Cloud Platform |
| Population Density | 30 m × 30 m | 2015–2020 | Local statistical bureaus of various cities |
| Building Density | 30 m × 30 m | 2015–2020 |
| Risk Level | Description | Water Depth (cm) |
|---|---|---|
| Low risk (0 level) | Incidents where no visible flooding is observed, or water submerges less than half of a car’s tire | 30 |
| Medium risk (1 level) | Incidents where water rises above the sidewalk curb or submerges half of a car’s wheel but does not reach the car’s engine hood | 30 50 |
| High risk (2 level) | Incidents where water submerges a car’s engine hood or reaches above pedestrians’ knees, potentially completely submerging vehicles | 50 |
| SGCN Component | Parameter | Type | Annotation |
|---|---|---|---|
| Graph dataset | Int | Number of nodes in the model’s input graph | |
| Float | Distance-related coefficient | ||
| Float | Elevation difference coefficient | ||
| Float | City relationship coefficient | ||
| GCN architecture | Int | Number of GCN layers | |
| Int | Number of hidden units in GCN | ||
| SNN architecture | Int | Number of SNN layers | |
| Int | Number of neurons in the SNN | ||
| Float | Total time for the simulation (SNN) | ||
| Float | Decay constant for synaptic current | ||
| Float | Time constant for neuronal integration | ||
| Hyperparameters | Int | Number of training epochs | |
| Int | Batch size for training | ||
| Float | Learning rate for model training |
| SGCN Component | Parameter | Optimized Value | Value Range |
|---|---|---|---|
| Graph dataset | 5 | 2 to 10 | |
| 0.334 | 0 to 10 | ||
| 0.016 | 0 to 10 | ||
| 0.025 | 0 to 10 | ||
| GCN architecture | 4 | 1 to 8 | |
| 205 | 8 to 256 | ||
| SNN architecture | 3 | 1 to 8 | |
| 24 | 8 to 256 | ||
| 14 | 10 to 200 | ||
| 232.77 | 20 to 400 | ||
| 74.43 | 5 to 100 | ||
| Hyperparameters | 87 | 20 to 200 | |
| 8 | 2 to 64 | ||
| 0.035 | 1 × 10−5 to 1 × 10−1 |
| Model | Precision | Recall | F1 Score | Accuracy | PR-AUC | ROC-AUC |
|---|---|---|---|---|---|---|
| GCN | 0.7280 | 0.7084 | 0.7101 | 0.7084 | 0.7451 | 0.7623 |
| LSTM | 0.6372 | 0.6147 | 0.6150 | 0.6141 | 0.6580 | 0.6752 |
| P-SGCN | 0.8474 | 0.8456 | 0.8458 | 0.8456 | 0.8784 | 0.8921 |
| Model | Precipitation | Population Density | Building Density | Elevation Relationship | Proximity Relationship |
|---|---|---|---|---|---|
| GCN | 1.2 | 0.3 | 0.4 | 1.8 | 2.3 |
| LSTM | 2.1 | 0.8 | 0.6 | N/A | N/A |
| P-SGCN | 1.7 | 0.2 | 0.3 | 1.5 | 2.5 |
| Model | Parameters (Million) | RAM Power (kWh) | CPU Power (kWh) | GPU Power (kWh) | Total Energy (J) |
|---|---|---|---|---|---|
| GCN | 2.06 | 5.4 × 10−6 | 9 × 10−6 | 5.4 × 10−6 | 53.5 |
| LSTM | 2.37 | 1.8 × 10−6 | 1.8 × 10−6 | 2.7 × 10−6 | 20.4 |
| P-SGCN | 1.31 | 3.6 × 10−6 | 9 × 10−6 | 9 × 10−6 | 11.9 |
| Model/Dataset | BJ | SH | SZ | HZ | SJZ | WH |
|---|---|---|---|---|---|---|
| Universal model | 0.865 | 0.853 | 0.869 | 0.809 | 0.861 | 0.817 |
| Universal model transfer to each city | 0.904 | 0.892 | 0.870 | 0.864 | 0.861 | 0.878 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, X.; Li, J.; Wang, M.; Chen, A.; Shao, S.; Liu, Q. A Universal Urban Flood Risk Model Based on Particle-Swarm-Optimization-Enhanced Spiking Graph Convolutional Networks. Sustainability 2025, 17, 9973. https://doi.org/10.3390/su17229973
Fang X, Li J, Wang M, Chen A, Shao S, Liu Q. A Universal Urban Flood Risk Model Based on Particle-Swarm-Optimization-Enhanced Spiking Graph Convolutional Networks. Sustainability. 2025; 17(22):9973. https://doi.org/10.3390/su17229973
Chicago/Turabian StyleFang, Xuhong, Jiaye Li, Mengyao Wang, Aifang Chen, Songdong Shao, and Qunfeng Liu. 2025. "A Universal Urban Flood Risk Model Based on Particle-Swarm-Optimization-Enhanced Spiking Graph Convolutional Networks" Sustainability 17, no. 22: 9973. https://doi.org/10.3390/su17229973
APA StyleFang, X., Li, J., Wang, M., Chen, A., Shao, S., & Liu, Q. (2025). A Universal Urban Flood Risk Model Based on Particle-Swarm-Optimization-Enhanced Spiking Graph Convolutional Networks. Sustainability, 17(22), 9973. https://doi.org/10.3390/su17229973







