From an implementation perspective, prioritizing wheelchair users and other mobility-impaired individuals in evacuation protocols represents a sustainability investment in equitable urban systems. By developing AI-augmented optimization methods that can efficiently handle accessibility constraints, we enable city planners and building managers to design truly inclusive infrastructure without sacrificing evacuation speed or safety. This computational capability removes a primary barrier to sustainable, accessible building design.
3.1. Methodological Framework Overview
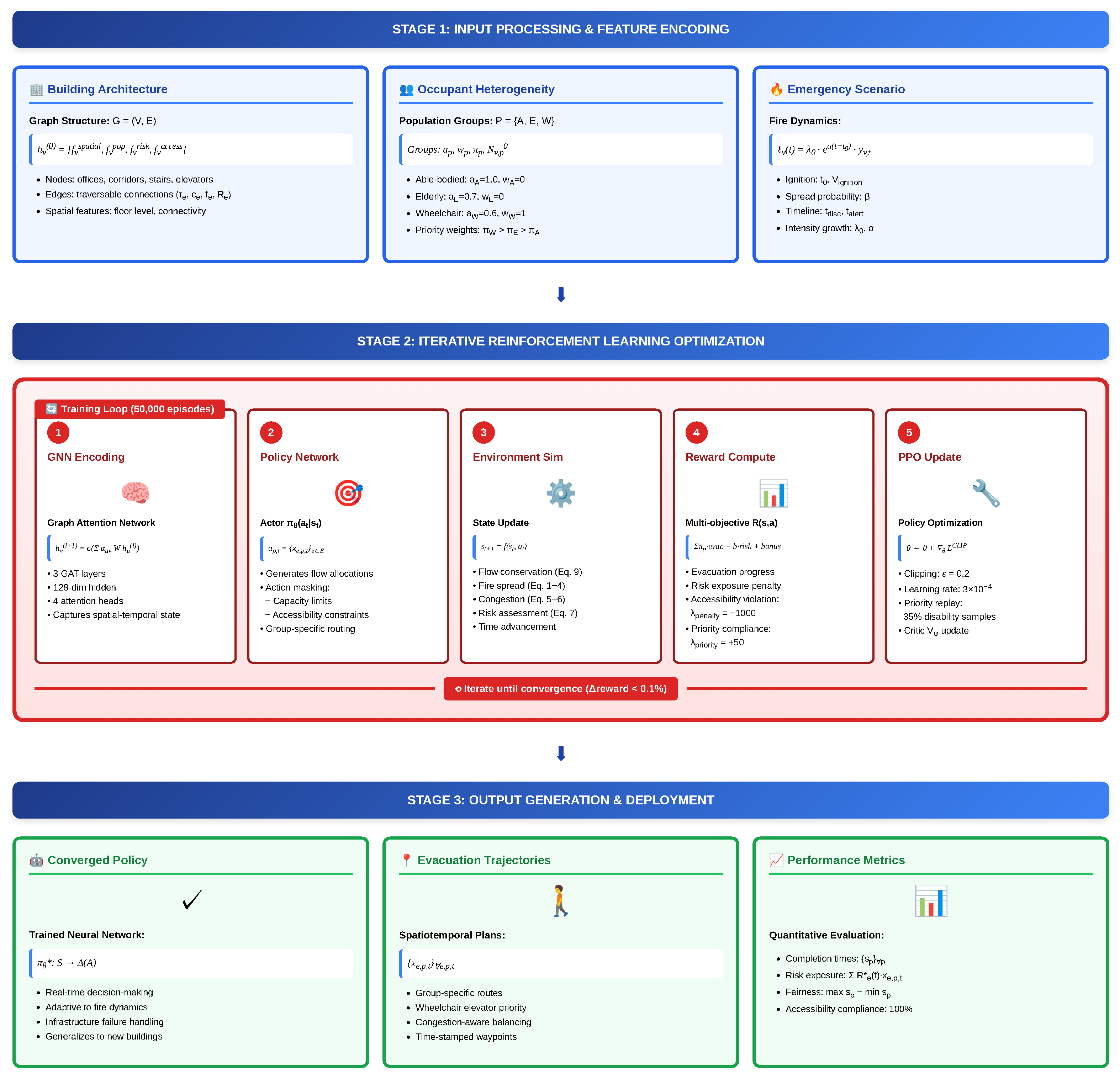
To enhance accessibility and provide a high-level understanding before detailed technical exposition, we present a comprehensive visual overview of the proposed GNN-PPO framework architecture.
Figure 1 illustrates the complete solution pipeline, showing how mathematical modeling components (
Section 2), neural network architectures, and reinforcement learning procedures integrate to generate adaptive evacuation policies.
The flowchart reveals the complete information flow from raw building data to actionable evacuation strategies:
(1) Stage 1—Input Encoding (Top): Building Architecture: Floor plans converted to directed graph with node features capturing spatial geometry, current occupancy, hazard levels, and infrastructure accessibility.
Occupant Heterogeneity: Population groups characterized by mobility coefficients , accessibility requirements , and priority weights , with initial distributions specifying starting locations.
Emergency Scenario: Fire ignition parameters (, ignition nodes , intensity , growth rate , spread probability ) and information dissemination timeline (, ) define the evolving threat landscape.
(2) Stage 2—Iterative Optimization (Center): State Representation: At each timestep
t, GNN processes graph structure through multi-layer attention mechanism (Equations (
29) and (30)) to produce node embeddings that capture both local occupancy and global building context.
Policy Evaluation: Actor network
generates probability distribution over feasible actions (flow allocations) for each population group, with action masking enforcing hard constraints (Equations (
20)–(
23)) ensuring accessibility compliance and capacity limits.
Environment Dynamics: Simulator advances system state by one timestep using flow conservation (Equation (
9)), fire spread (Equations (
1)–(
4)), congestion evolution (Equations (5) and (6)), and risk assessment (Equation (
7)), producing next state
.
Reward Computation: Multi-objective reward (Equation (
36)) evaluates action quality considering evacuation progress (prioritizing vulnerable groups), risk exposure minimization, accessibility constraint satisfaction (heavy penalty
for violations), and elevator priority compliance (bonus
for wheelchair users).
Policy Update: PPO algorithm updates actor and critic networks using collected trajectories, with prioritized replay oversampling disability-related transitions to accelerate learning of inclusive strategies.
(3) Stage 3—Output and Deployment (Bottom): Converged Policy: Trained neural network policy provides real-time evacuation decisions adaptable to any building state, handling dynamic fire conditions, infrastructure failures, and varying occupant distributions.
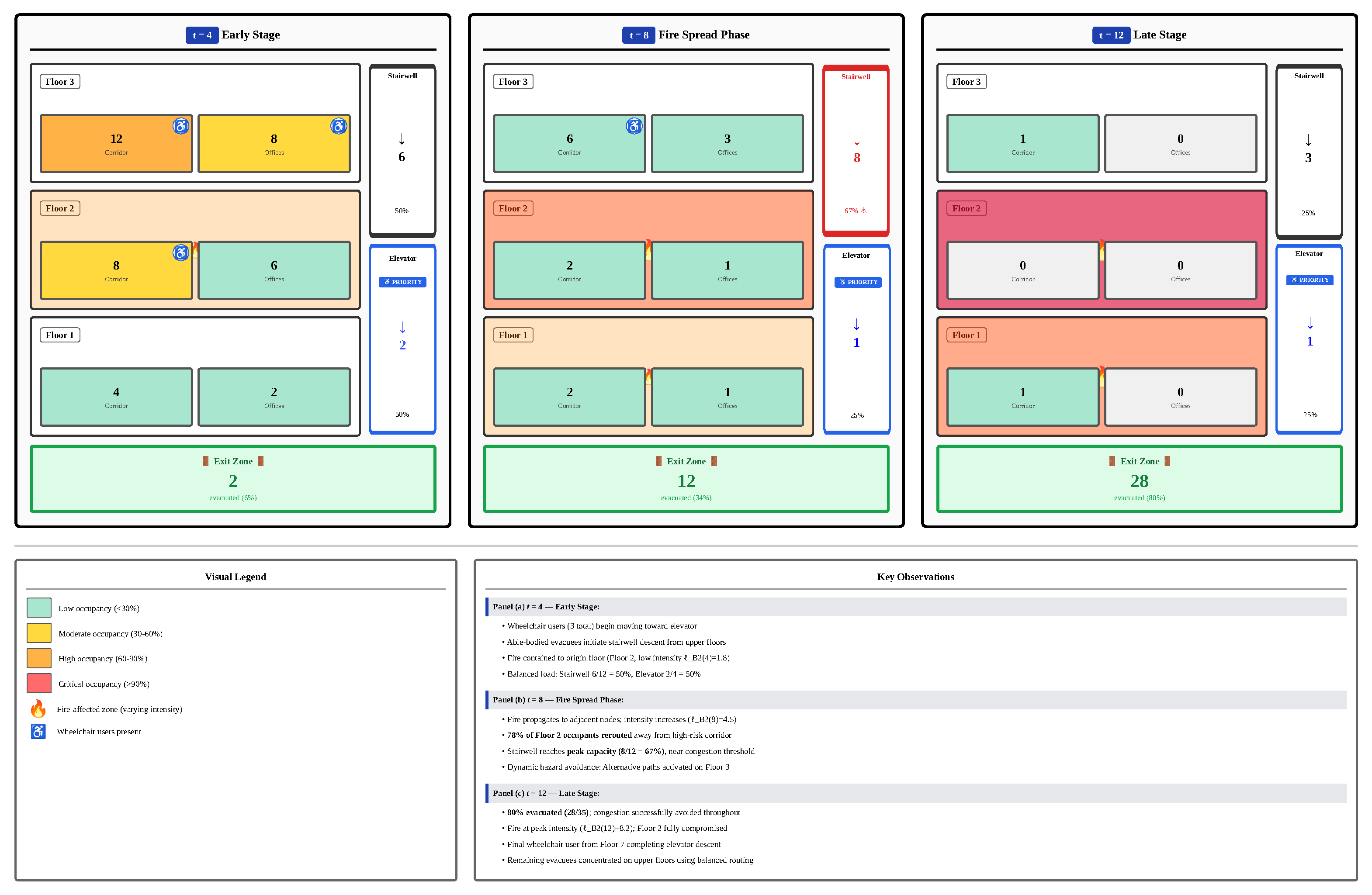
Evacuation Trajectories: Complete spatiotemporal plans specify which population groups should use which routes at each timestep, with explicit elevator prioritization for wheelchair users and congestion-aware load balancing.
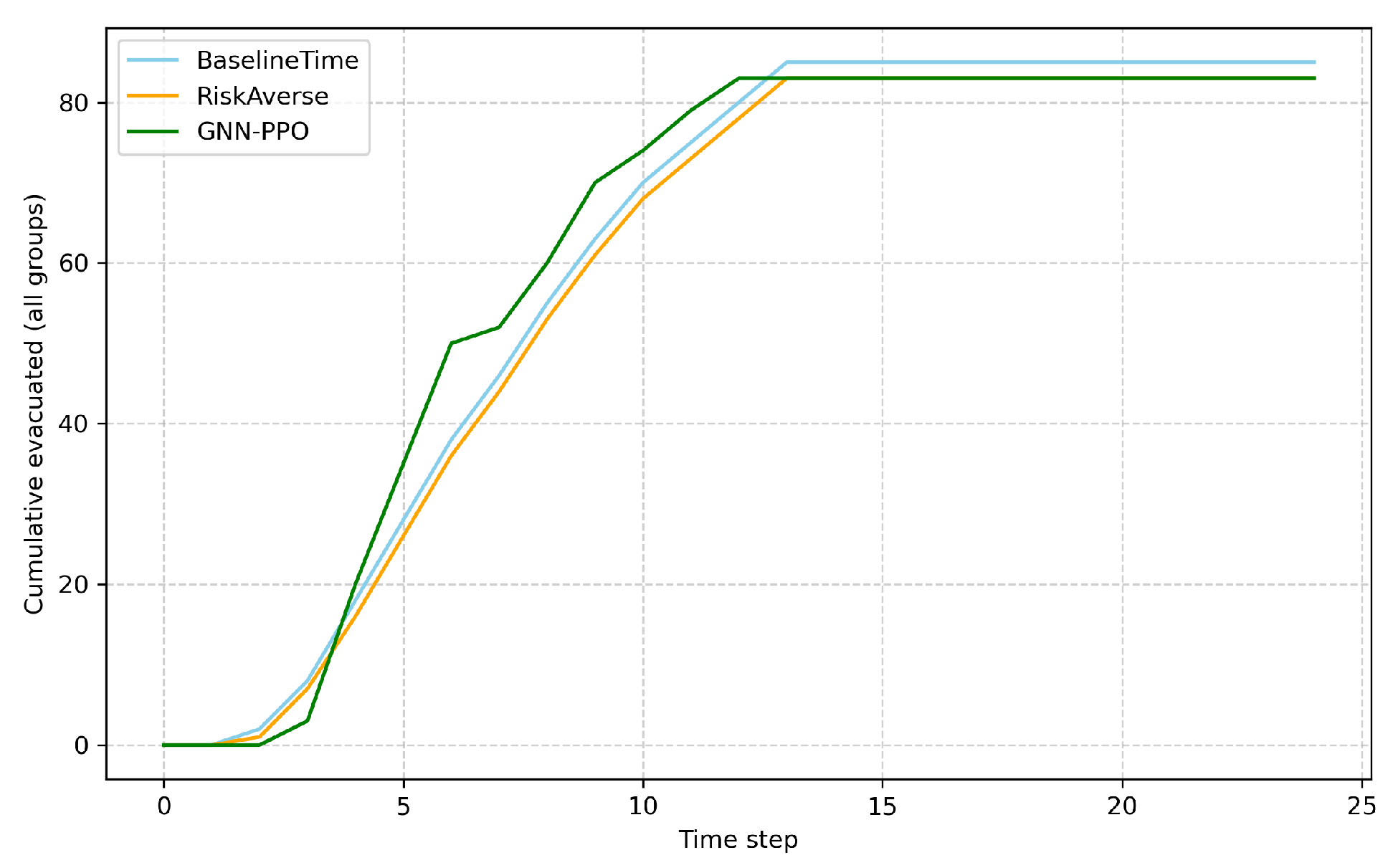
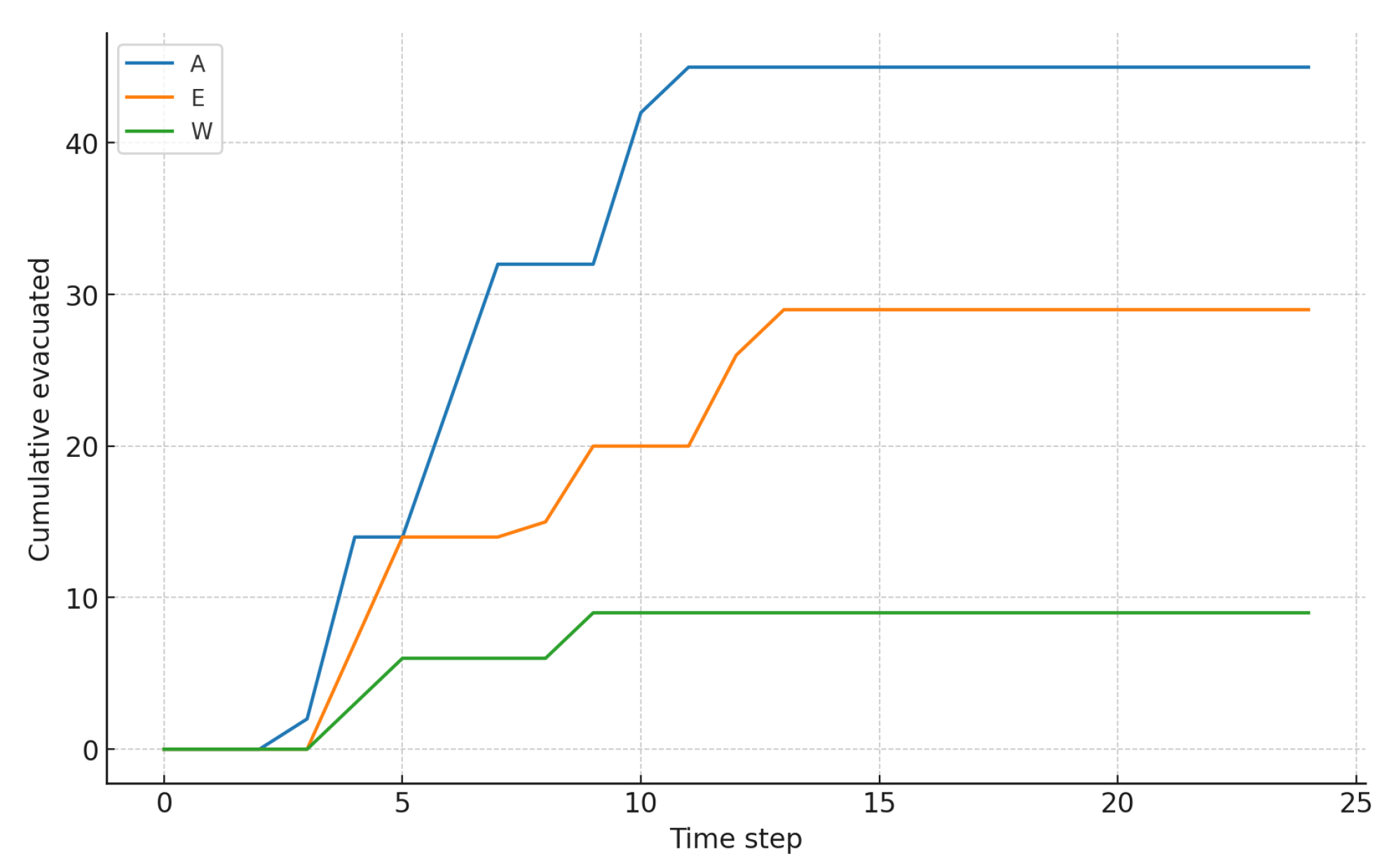
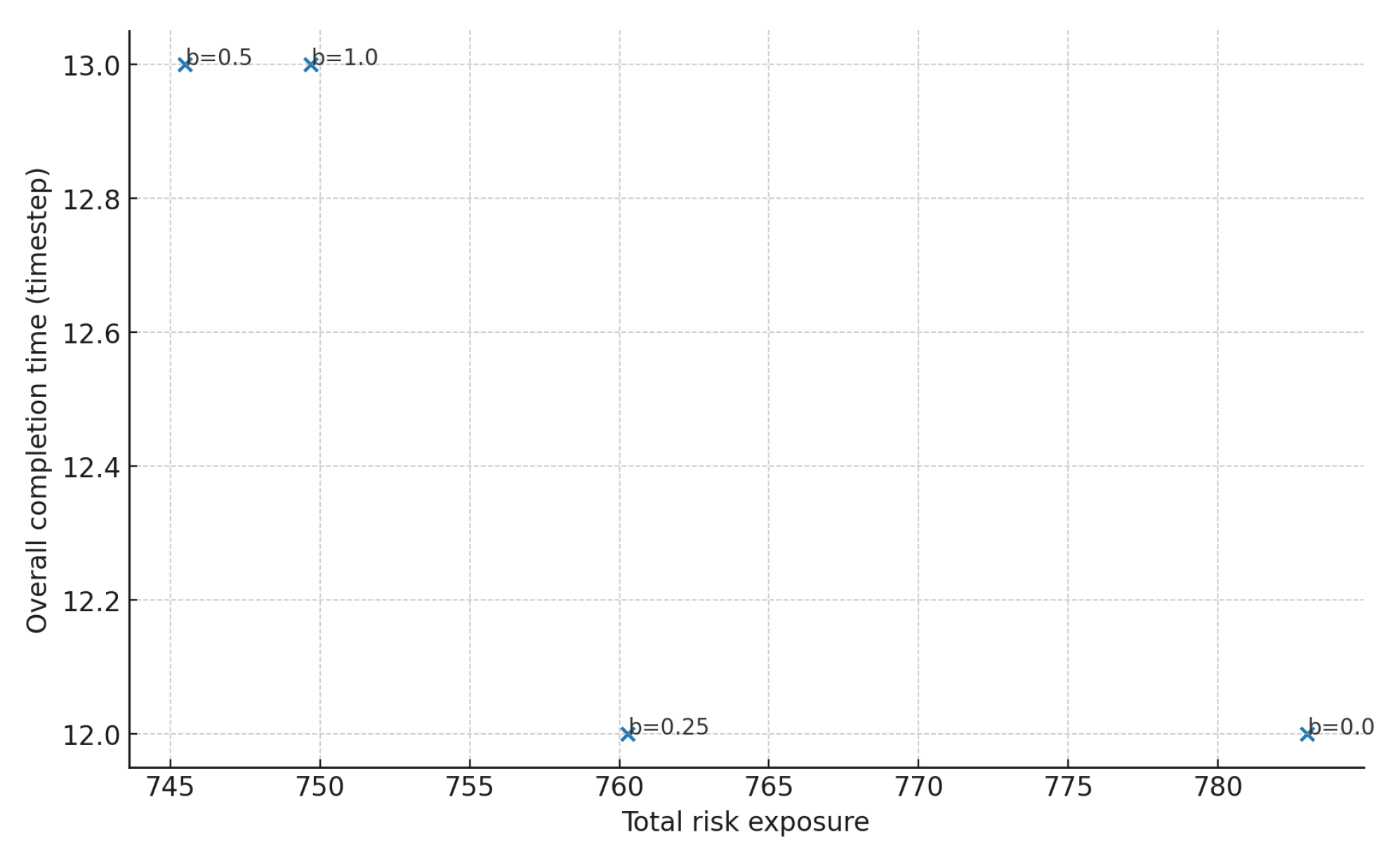
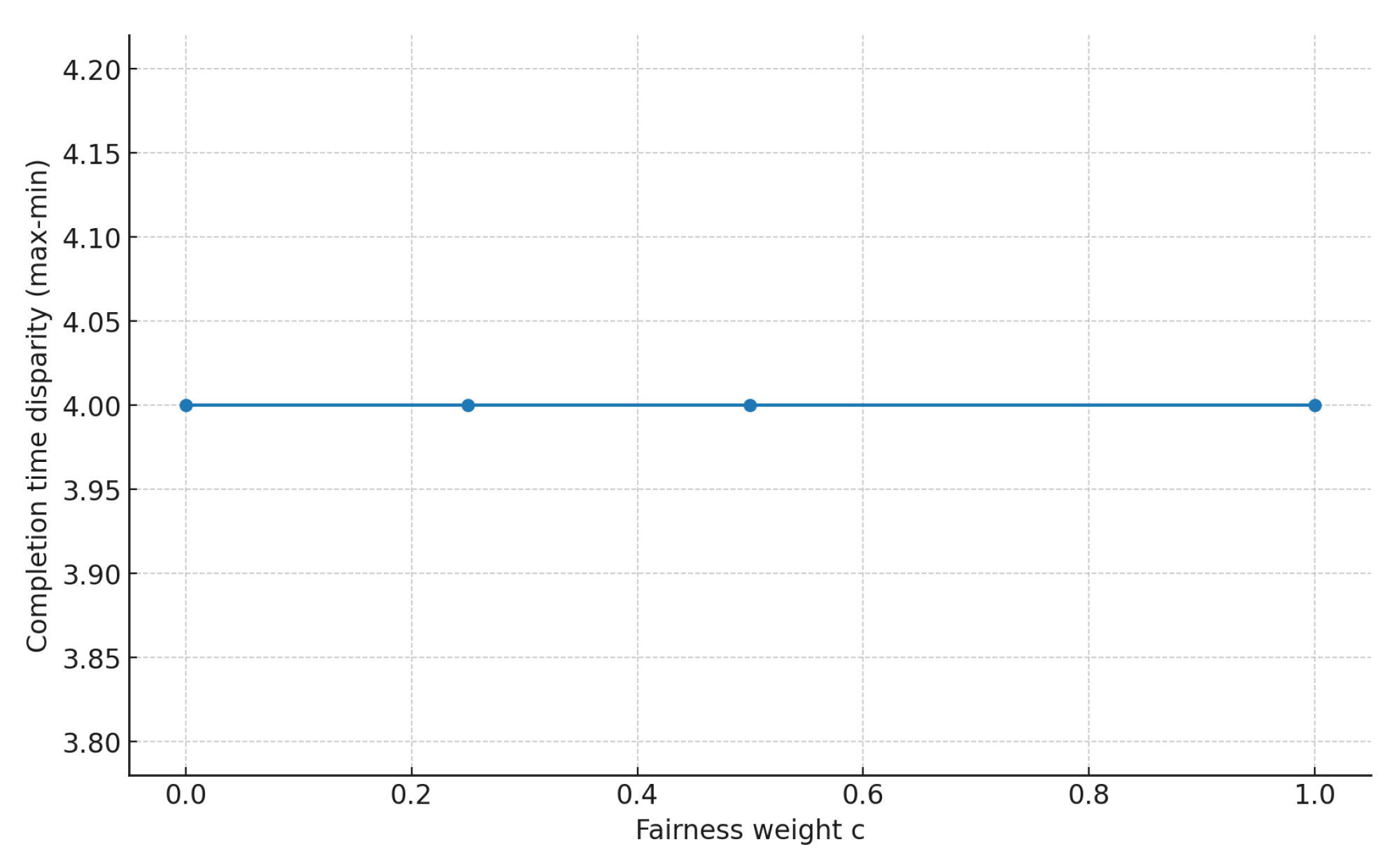
Performance Metrics: Quantitative evaluation of completion times , total risk exposure , and inter-group fairness validates solution quality.
This integrated framework addresses three critical challenges simultaneously: (1) Computational Scalability—GNN-PPO handles 100+ node buildings in real-time versus hours for exact MINLP solvers; (2) Accessibility Compliance—Hard constraint enforcement and priority-aware training ensure wheelchair users receive appropriate resources; (3) Dynamic Adaptability—Learned policy responds to real-time fire evolution and congestion patterns rather than relying on predetermined static plans.
3.2. Computational Complexity Analysis
The evacuation optimization problem exhibits exponential complexity growth with respect to problem dimensions. For a building with nodes, edges, population groups, and time horizon , the total number of decision variables scales as for flow variables and for occupancy variables . The constraint system includes the following:
Flow conservation constraints:
Capacity and accessibility constraints:
Risk-based routing constraints:
Fire spread dynamics:
For realistic high-rise buildings with 50–100 floors, 500–2000 nodes, and planning horizons of 30–60 time periods, the resulting MINLP contains to variables and constraints, making exact solution approaches computationally intractable within practical time limits required for emergency response planning.
Standard approaches such as branch-and-bound, Lagrangian relaxation, and metaheuristics exhibit the following limitations:
Exponential time complexity: Solution time grows exponentially with problem size
Poor scalability: Cannot handle buildings with more than 200–300 nodes
Limited real-time capability: Require hours or days for solution, unsuitable for emergency response
Accessibility constraints handling: Struggle with the logical constraints for persons with disabilities
Figure 1.
Comprehensive methodology flowchart of the GNN-PPO framework.
Figure 1.
Comprehensive methodology flowchart of the GNN-PPO framework.
3.3. AI-Enhanced Solution Framework
3.3.1. Graph Neural Network for Spatial-Temporal Feature Learning
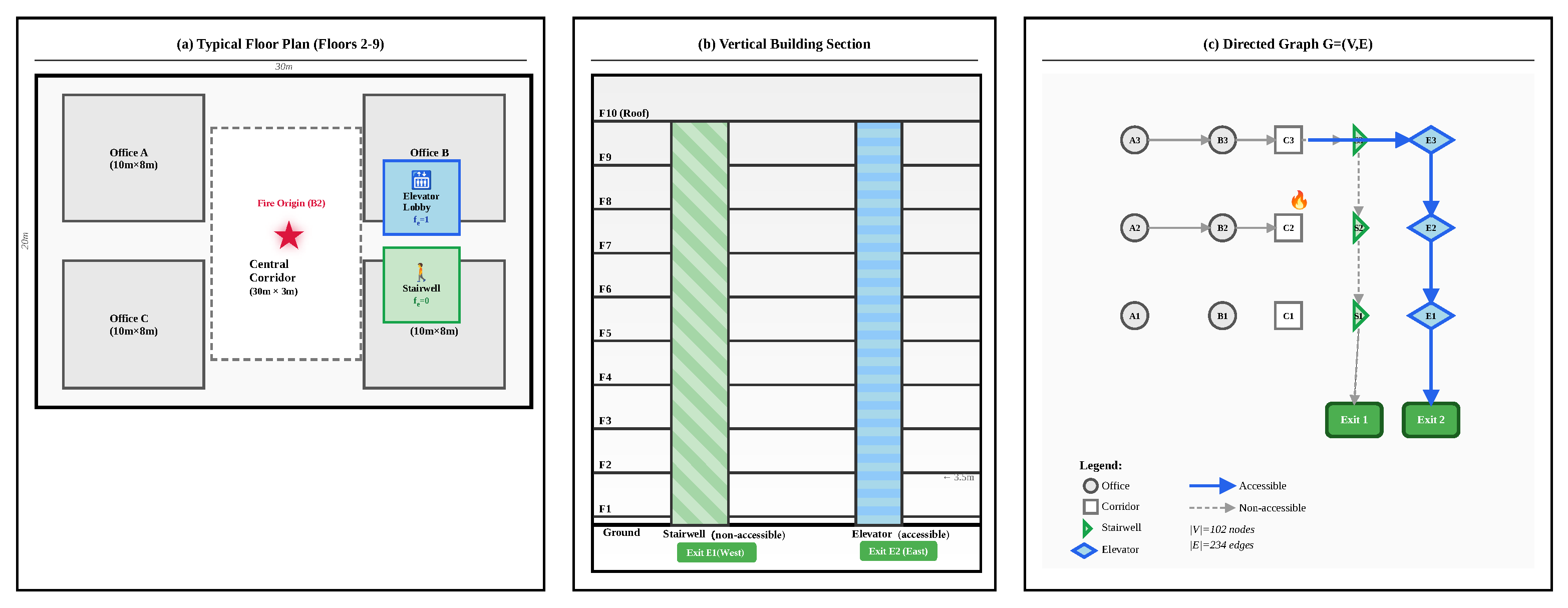
The high-rise building evacuation problem is naturally formulated as a dynamic graph where nodes represent spatial locations and edges represent traversable connections. We employ a Graph Attention Network (GAT) architecture to capture the complex spatial relationships and temporal dependencies in evacuation dynamics:
where
represents the feature vector of node
v at layer
,
is the learnable weight matrix,
is the attention mechanism parameter vector, and
denotes concatenation. The attention mechanism
learns to focus on the most relevant neighboring nodes for each evacuation decision.
The initial node features
integrate multiple information modalities critical for evacuation planning:
where:
: geometric features (floor level, room type, distance to exits, connectivity degree)
: current occupancy characteristics for each population group p
: fire hazard indicators, smoke density, temperature, and structural risk levels
: disability infrastructure availability (elevator access, ramp availability, door widths)
The concatenated feature vector enables the GNN to learn comprehensive spatial representations that account for all relevant evacuation factors simultaneously.
3.3.2. Reinforcement Learning for Dynamic Route Planning
The evacuation planning problem is formulated as a multi-agent MDP where each population group constitutes an agent seeking to minimize evacuation time while respecting safety and accessibility constraints. The MDP tuple is defined as follows:
At time
t, the global state
aggregates all relevant system information:
This state representation captures the complete building occupancy distribution, fire spread status, edge-level risks, and infrastructure operational status.
For each population group
p and time step
t, the action
specifies the flow allocation vector across all edges:
subject to the feasibility constraints:
The immediate reward at time
t balances multiple evacuation objectives while enforcing accessibility compliance:
The reward function components serve distinct purposes:
First term: Promotes faster evacuation with priority weighting for vulnerable groups
Second term: Penalizes high-risk route usage with weight parameter b
Third term: Heavily penalizes accessibility violations to ensure feasible solutions
Fourth term: Provides positive reinforcement for elevator priority allocation to persons with disabilities
3.3.3. Hybrid Deep Reinforcement Learning Architecture
We propose a novel architecture that combines graph neural networks with the Proximal Policy Optimization (PPO) algorithm for stable policy learning in the complex evacuation environment:
where:
and are graph neural networks with parameters and respectively
MLP represents multi-layer perceptrons for final action/value prediction
GlobalPool aggregates node-level representations using attention-weighted global pooling:
To accelerate learning for disability-inclusive scenarios, we implement a priority replay buffer that oversamples transitions involving persons with disabilities:
where:
is the temporal difference error for transition i
prevents zero probabilities
controls prioritization strength
This prioritization mechanism ensures that the learning algorithm gives special attention to scenarios involving persons with disabilities, leading to more robust and inclusive evacuation policies.
3.3.4. Implementation Details and Hyperparameters
The GNN-PPO architecture comprises the following components with specific configurations:
Graph Neural Network Architecture:
Number of GAT layers:
Hidden dimension:
Number of attention heads:
Activation function: LeakyReLU with negative slope
Dropout rate: applied after each GAT layer
Initial feature dimensions: (spatial), (population), (risk), (accessibility)
PPO Algorithm Configuration:
Learning rate: with linear decay
Discount factor:
GAE parameter:
Clipping parameter:
Value function coefficient:
Entropy coefficient:
Mini-batch size: 64
Number of epochs per update: 10
Horizon length: steps
Training Protocol:
Total training episodes:
Prioritized replay buffer size: transitions
Priority exponent:
Importance sampling exponent: annealed from to
Optimizer: Adam with ,
Gradient clipping: max norm
Convergence criterion: Average reward improvement over 1000 consecutive episodes
The priority weight ranges from 1.0 (transitions involving only able-bodied evacuees) to 2.0 (transitions involving wheelchair users). Combined with the TD-error term , this ensures that learning episodes featuring wheelchair users and high-stake decisions receive 1.5–2× higher sampling probability. During training, approximately 35% of mini-batch samples involve disability-related decisions despite these scenarios comprising only 12% of total environment transitions, accelerating policy convergence for inclusive evacuation strategies.