AI-Driven Prediction of Ecological Footprint Using an Optimized Extreme Learning Machine Framework

Abstract

Accurate forecasting of the ecological footprint (EF) is critical for advancing the Sustainable Development Goals, particularly those related to climate action, responsible consumption and production, and sustainable cities. To address the limitations of conventional machine learning models, such as instability due to random weight initialization and poor generalization, this study proposes a novel hybrid model that integrates the Chinese Pangolin Optimizer (CPO) with the Extreme Learning Machine (ELM). Inspired by the foraging behavior of pangolins, the CPO efficiently optimizes the ELM’s input weights and biases, significantly enhancing prediction accuracy and robustness. Using comprehensive monthly United States data from 1991 to 2020, the model forecasts EF based on key socioeconomic and environmental indicators, including GDP per capita, human capital, financial development, urbanization, globalization, and foreign direct investment. The CPO–ELM model outperforms benchmark models, achieving an R² of 0.9880 and the lowest error metrics across multiple validation schemes. Furthermore, SHAP (Shapley Additive Explanations) analysis reveals that GDP per capita, human capital, and financial development are the most influential drivers of EF, offering policymakers actionable insights. This study demonstrates how interpretable AI-driven forecasting can support evidence-based environmental governance and contribute directly to sustainability targets under the SDG framework.

1. Introduction

Sustaining human well-being within planetary boundaries requires reliable, policy-relevant indicators that translate complex resource demands into actionable insights for governments. The Ecological Footprint (EF) remains one of the most widely used, consumption-based indicators of human pressure on ecosystems, summarizing competing demands on bioproductive land and sea, including cropland, grazing land, fishing grounds, forest, built-up land, and carbon uptake land. Its long, harmonized time series have underpinned national and international sustainability assessments and overshoot diagnostics for decades, with the most recent national footprint and biocapacity accounts updating country-level trajectories for decades and documenting persistent ecological deficits in most nations [1,2]. Against the backdrop of accelerating globalization and capital mobility, accurately forecasting EF has direct implications for designing green growth strategies, aligning investment with decarbonization, and targeting interventions that reduce resource overuse without undermining development gains. Yet the EF’s responsiveness to macro-financial conditions, demographic pressures, and cross-border integration renders its dynamics highly nonlinear and time-varying, features that challenge classical econometric tools and motivate robust machine learning (ML) approaches. Beyond its headline appeal, EF accounting rests on a well-specified and continuously refined methodology that reconciles demand for ecosystem services with the biosphere’s regenerative capacity. Methodological updates since the early 2010s have clarified yield and equivalence factor calculations, improved carbon uptake land estimates, and strengthened the use of United Nations-based statistical sources, thereby supporting cross-country comparability and temporal consistency [2]. These methodological advances justify EF’s use as a dependent variable in forecasting frameworks that integrate socio-economic and financial covariates, provided models can capture structural breaks and complex interactions among drivers. A rapidly expanding empirical literature has examined EF’s macro-determinants, typically within panel frameworks spanning diverse income groups. A recent systematic review synthesizing several decades of work identifies GDP per capita, urbanization, energy structure, biocapacity, human capital, financial development, trade openness, and foreign direct investment as recurrent and significant correlates, though their signs and magnitudes vary across contexts, time horizons, and estimation strategies [3]. Studies focusing on globalization suggest heterogeneous effects: while some panels report that broader integration amplifies EF in developing regions, others find regime-dependent or statistically insignificant relationships once cross-sectional dependence and slope heterogeneity are addressed [4,5]. These inconsistencies underscore the need for predictive models that can (i) flexibly represent nonlinearities and thresholds and (ii) quantify the relative importance of overlapping drivers. Financial development has emerged as a particularly influential, yet ambiguous, factor. Multidimensional measures (depth, access, efficiency) often exhibit an inverted-U relationship with EF for financial institutions, whereas the contribution of financial markets appears less consistently benign, suggesting channel-specific scale, composition, and technology effects [6]. Complementary evidence from developed economies confirms that finance can either worsen or improve environmental quality, depending on structural conditions and time scales, again arguing for context-aware, data-driven methods [7]. Because financial cycles and investment booms propagate through energy use, urban expansion, and capital deepening, an EF prediction framework based on macro-financial indicators could offer early signals of sustainability risks, provided the models are accurate and interpretable. Concurrently, Earth and environmental sciences are witnessing a methodological shift: hybrid ML systems and data-driven models are increasingly used to emulate complex dynamics, from sub-grid climate processes to ecosystem fluxes [8,9]. While these advances demonstrate the feasibility of ML for high-dimensional environmental prediction, their translation to national-scale EF forecasting has been comparatively limited, with many EF studies still anchored in linear cointegration or vector autoregression (VAR) frameworks that can struggle with nonstationarity, interaction effects, and regime changes [3,10]. The opportunity, therefore, is to leverage modern learning algorithms that reconcile speed, accuracy, and interpretability for policy-relevant EF horizons.

Extreme Learning Machines (ELMs) offer an attractive base learner for such tasks. ELMs are single-hidden-layer feedforward networks with randomly assigned input weights and biases and analytically solved output weights, enabling exceptionally fast training and competitive generalization across regression and classification tasks [11]. However, the very features that make ELMs fast, random hidden-layer initialization and one-shot output estimation, introduce variance and sensitivity to hyperparameters, leading to inconsistent performance, especially under noise, heteroskedasticity, or nonstationarity [12,13]. Addressing these sources of instability without sacrificing computational efficiency is thus central to positioning ELMs as reliable EF forecasters. In response, a rich strand of research has coupled ELMs with metaheuristic optimizers to tune input weights, hidden biases, and structural hyperparameters. Swarm and physics-inspired algorithms such as the Grey Wolf Optimizer (GWO) [14], the Sine Cosine Algorithm (SCA) [15], and the Arithmetic Optimization Algorithm (AOA) [16] have been widely used to enhance exploration–exploitation balance, escape local minima, and improve convergence profiles. In energy and industrial forecasting, GWO-ELM variants have improved short-term wind power prediction, while other metaheuristic–ELM hybrids have reported consistent gains over standalone ELM in both accuracy and stability [17,18,19]. These studies suggest that lightweight random-feature learners can be robust via biologically inspired search, opening a pathway for fast, accurate EF prediction at national scales.

Despite this progress, three gaps persist in the EF prediction literature. First, relative to energy and emissions forecasting, there are few studies that tailor metaheuristic-tuned ELMs to EF specifically, even though EF aggregates multiple pressures and is likely to exhibit stronger nonlinearities than single-pollutant targets [3,10]. Second, model interpretability is often treated as secondary to accuracy; many studies report error metrics without systematically decomposing feature contributions, limiting the policy insights that can be drawn from black-box predictors. Third, ELM’s stochasticity is rarely addressed with rigorous stability assessments, making it difficult to separate genuine model superiority from favorable random initializations. Together, these gaps motivate the development of an EF optimizer-based predictive model that combines (i) principled stochastic optimization for consistent training, (ii) post hoc explanation techniques for transparent inference, and (iii) robust experimental comparison. Model interpretability is essential for environmental governance, where decisions must balance economic and social objectives under uncertainty. Shapley Additive Explanations (SHAP) provide a theoretically grounded framework for local and global attribution that is model-agnostic and consistent, enabling decomposition of predictions into additive feature contributions and interaction effects [20,21]. Integrating SHAP into EF prediction can reveal, for instance, whether increases in financial development amplify EF via scale effects or mitigate it via composition and technology effects, and how these effects vary with investment intensity or globalization. Such transparency is particularly valuable when ML models inform industrial policies that incorporate environmental constraints.

Our approach builds on this agenda by introducing a new nature-inspired optimizer, the Chinese Pangolin Optimizer (CPO), and coupling it with ELMs to form a hybrid CPO–ELM predictor. The Chinese pangolin (Manis pentadactyla) is a nocturnal, myrmecophagous mammal whose foraging ecology combines targeted excavation of prey-rich patches with adaptive movement across heterogeneous terrain; empirical studies describe how burrow site selection depends on slope, canopy cover, and proximity to ant nests, and how activity rhythms and home ranges adjust to resource density [22,23]. Abstracted into an optimizer, these behaviors naturally map onto intensification (localized exploitation of promising regions), diversification (movement across patches under uncertainty), and parsimonious step selection (energy-aware exploration). By mathematically encoding pangolin-inspired operators for patch identification, depth-adaptive probing, and guided relocation, the CPO seeks a principled exploration–exploitation trade-off suited to the rugged error landscapes often encountered when tuning ELMs’ hidden-layer parameters. The proposed model was tested on monthly ecological footprint and macro indicators from 1991 to 2020 from the United States, which supports robust model training and validation. The United States exhibits substantial variation in the drivers considered in this study, including GDP per capita, human capital, financial development, globalization, urbanization, and foreign direct investment, enabling a stringent stress test of the learning algorithm. The country’s policy relevance for climate and sustainability agendas makes interpretability especially valuable for decision makers. This study addresses the aforementioned gaps by developing and evaluating a Chinese Pangolin Optimizer–Extreme Learning Machine (CPO–ELM) framework for sustainable ecological forecasting. Below are the contributions of this study:

• Improved EF prediction: We introduce the CPO–ELM model, which leverages pangolin-inspired foraging intelligence to optimize ELM parameters, achieving higher accuracy and stability than baseline ELMs and established metaheuristic–ELM hybrids.
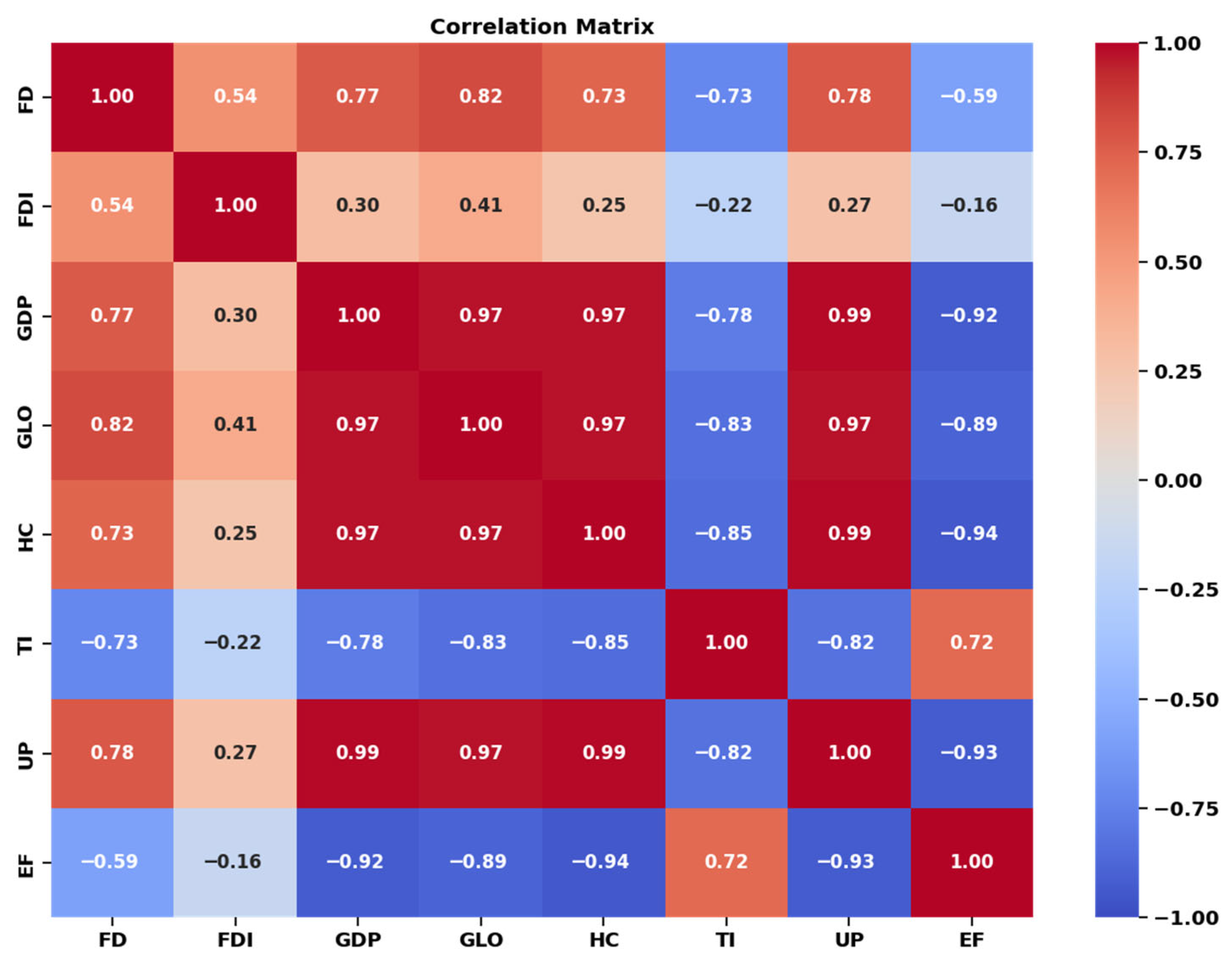
• Interpretable insights: Using SHAP, we quantify the individual and interactive effects of socio-economic drivers, GDP per capita, human capital, financial development, total investment, urban population, globalization, and foreign direct investment on EF predictions, enabling transparent, policy-relevant interpretation.
• Robust validation: We provide comprehensive metrics on accuracy, error dispersion, and bias, mitigating stochastic variability.

The remainder of this manuscript is organized as follows. Section 2 provides a critical review of the literature. Section 3 details the theoretical foundations of ELM, formalizes the mathematical operators of the Chinese Pangolin Optimizer (CPO), and describes the dataset and input variables. Section 4 presents the empirical results, including predictive performance metrics and SHAP-based interpretability analyses. Section 5 offers concluding remarks and provides directions for future research.

2. Literature Review

Advancements in machine learning and metaheuristic optimization have transformed the forecasting of environmental degradation and associated environmental metrics, enabling more precise assessments of sustainability pressures amid global resource constraints. Moayedi et al. [24] explored hybrid metaheuristic–ANN frameworks to forecast energy-related CO₂ emissions. Their model incorporated GDP and multiple energy-source variables as predictors, optimizing multilayer perceptrons (MLPs) using five distinct algorithms. Results showed that Teaching–Learning-Based Optimization (TLBO) delivered superior generalization, achieving the lowest testing MSE values, thus outperforming other hybrids in both convergence and stability. Ghorbal et al. [25] addressed the problem of accurately forecasting global CO₂ emissions by combining a Dual-Path Recurrent Neural Network (DPRNN) with the novel Ninja Optimization Algorithm (NiOA). They first applied Principal Component Analysis (PCA) and Blind Source Separation (BSS) for feature-cleaning and then trained the DPRNN and tuned it using NiOA. The resulting hybrid achieved lower error metrics and superior performance relative to competing metaheuristics. Janković et al. [26] developed and rigorously compared four distinct hybrid machine learning models to forecast the total ecological footprint of consumption, using energy-related macroeconomic indicators as primary inputs. Their methodology centered on Bayesian-optimized ensemble techniques to handle the inherent nonlinearity in the data. The study demonstrated that the hybrid models significantly outperformed their standalone counterparts. Almsallti et al. [27] introduced a novel hybrid framework, the RBMO-ELM, which integrates a metaheuristic optimizer with an Extreme Learning Machine to predict CO₂ emissions, a key component of the broader ecological footprint. The research applied this model to a rich, multidimensional Indonesian dataset encompassing economic and technological variables. Empirical validation showed that the RBMO-ELM model surpassed several state-of-the-art hybrid competitors.

A recent study, focused on India, by Mukherjee et al. [28] evaluated a suite of conventional machine learning algorithms to predict the country’s national ecological footprint, leveraging a set of eleven socio-economic and trade-related predictors. The research found that Random Forests provided the most robust and accurate forecasts for this complex, developing economy. Meng and Noman [29] designed an artificial intelligence system based on machine learning to project future CO₂ emission trajectories for major global economies. Their work emphasized the model’s ability to capture long-term, nonlinear trends in emission data, providing policymakers with a powerful tool for scenario analysis and long-range environmental planning. The proposed model exhibited high predictive fidelity. Feda et al. [30] systematically investigated the impact of harmonizing various established metaheuristic algorithms, including the ELM, for carbon emission prediction. Their comparative analysis revealed that integrating these optimizers consistently improved the ELM’s stability and accuracy by effectively mitigating its random initialization issue. Khajavi and Rastgoo [31] introduced a hybrid approach that employed six metaheuristic algorithms to fine-tune the hyperparameters of a Random Forest model for forecasting carbon dioxide emissions from road transport. Their results indicated that the RF model optimized by the Slime Mould Algorithm (SMA) achieved the lowest prediction error, demonstrating the value of metaheuristic-driven hyperparameter optimization in this domain. Arık et al. [32] applied five distinct metaheuristic algorithms to forecast Turkey’s national carbon dioxide emissions. The study’s objective was to identify the most efficient and accurate algorithm for this specific national context, using historical emission data as the primary input. The comparative results indicated that the metaheuristic-tuned optimizer demonstrated superior accuracy. Moros-Ochoa et al. [33] extended the application of machine learning to the joint forecasting of both biocapacity and ecological footprint.

Their work built upon earlier hybrid modeling successes, demonstrating that advanced ML techniques could effectively model the dynamic balance between a nation’s ecological demand and its regenerative supply. Priya et al. [34] independently developed machine learning and deep learning systems to monitor and predict India’s carbon footprint, motivated by the country’s status as a top global emitter. Their models, which included both classical ML and neural network architectures, were trained on national greenhouse gas inventories and aimed to provide a real-time monitoring framework. Alhussan and Metwally [35] systematically investigated the efficacy of machine learning models optimized with the metaheuristic optimizer for CO₂ emissions prediction using a detailed fuel consumption dataset. Their work provided a granular analysis of model performance on high-resolution data, finding that ensemble methods again demonstrated superior predictive power. Jin and Sharifi [36] performed a comprehensive review of 75 studies that applied machine learning to forecast urban greenhouse gas emissions, a critical sub-component of the national ecological footprint. Their analysis mapped the evolution of methodological approaches and identified a clear trend toward the adoption of hybrid and ensemble models, which consistently delivered higher accuracy and reliability for urban-scale environmental prediction.

3. Methodology

3.1. Chinese Pangolin Optimizer (CPO)

The CPO is a recently developed bio-inspired metaheuristic algorithm that simulates the dual foraging mechanisms of the Manis pentadactyla, namely luring and predation, to balance exploration and exploitation during optimization. Unlike conventional swarm or evolutionary frameworks [37], the CPO models its behavioral intelligence through aroma-based search dynamics, where individuals navigate the search space using an adaptive Gaussian plume model to represent olfactory diffusion, followed by behavioral transitions that simulate attraction, capture, pursuit, and feeding stages. The pangolin’s foraging process is driven by its olfactory sensing, which is mathematically modeled through Gaussian plume diffusion. Assuming the aroma source lies at the origin O(0,0,0) and the average wind direction aligns with the x-axis, the aroma concentration at a point M(x,y,z) can be expressed as given in Equation (1):

$$M(x,y,z)=R\left(x\right)e^{-a{y}^2}{e}^{-b{z}^2}$$

(1)

where $R(x)={\displaystyle \frac{Q}{2\pi u{\sigma }_y{\sigma }_z}}$ represents the distribution term dependent on the source emission rate Q, mean wind velocity u, and the dispersion coefficients ${\sigma }_y$ and ${\sigma }_z$ in the lateral (y) and vertical directions (z), respectively. The dispersion parameters are defined through second-moment integrals of the concentration field according to Equation (2):

$${\sigma }_y^2={\displaystyle \frac{{\int }_0^{\mathrm{\infty }} y^{2}M(x,y,z)dy}{{\int }_0^{\mathrm{\infty }} M(x,y,z)dy}},{\sigma }_z^2={\displaystyle \frac{{\int }_0^{\mathrm{\infty }} z^{2}M(x,y,z)dz}{{\int }_0^{\mathrm{\infty }} M(x,y,z)dz}}$$

(2)

and the source strength at the origin O is given in Equation (3):

$$Q={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }} {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }} uM(x,y,z)dydz$$

(3)

Combining Equations (1)–(3) yields the Gaussian distribution of aroma concentration in Equation (4):

$$M(x,y,z)={\displaystyle \frac{Q}{2\pi u{\sigma }_y{\sigma }_z}}\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{y^2}{{\sigma }_y^2}}+{\displaystyle \frac{z^2}{{\sigma }_z^2}}\right)\right]$$

(4)

Since the pangolin and ants interact near the ground, a bounded diffusion model is used by invoking the image-source principle to account for reflection at the Earth’s surface. The ground-level aroma concentration is therefore as follows in Equation (5):

$$M(x,\mathrm{0,0})={\displaystyle \frac{Q}{\pi u{\sigma }_y{\sigma }_z}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{H^2}{2{\sigma }_z^2}}\right)$$

(5)

where H is the effective release height of the aroma (typically 0−0.5 m). Q is the constant source strength, set to 100, $u=2+r_1\in \left[\mathrm{2,3}\right]\mathrm{m}/\mathrm{s}$ is the mean wind speed modulated by a uniform random variable $r_1\in \left[\mathrm{0,1}\right]$, $H=r_2/2\in \left[\mathrm{0,0.5}\right]\mathrm{m}$ is the effective emission height, and ${\sigma }_y$ and ${\sigma }_z$ are horizontal and vertical diffusion parameters, respectively, given in Equation (6). The diffusion parameters vary dynamically with iteration t.

$${\sigma }_y=50-10{\displaystyle \frac{t}{T}},{\sigma }_z=\mathrm{s}\mathrm{i}\mathrm{n}\left(\pi {\displaystyle \frac{t}{T}}\right)+40e^{-t/T}-10\mathrm{l}\mathrm{n}\left(\pi {\displaystyle \frac{t}{T}}\right)$$

(6)

The normalized aroma intensity controlling the behavioral switch is obtained as given in Equation (7):

$$C_M(t)={\displaystyle \frac{M\left(t\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(M\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\left(M\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(M\right)}}$$

(7)

Here, $C_M\left(t\right)\in \left[\mathrm{0,1}\right]$ denotes the olfactory field intensity, dynamically guiding exploration (C_M < 0.2) and exploitation (C_M > 0.7) transitions. M(t) denotes the aroma concentration over iterations. Each pangolin represents a candidate solution X_i = [x_i,1,x_i,2,…,x_i,d] in a d-dimensional space. The matrix in Equation (8) defines the initial population.

$$X=\left[\begin{array}{ccc}{x}_{\mathrm{1,1}}& \dots & x_{1,d}\\ ⋮& \ddots & ⋮\\ x_{n,1}& \dots & x_{n,d}\end{array}\right]$$

(8)

Each dimension is initialized within the search boundary defined in Equation (9)

x_i,j = rand × (UB_j −LB_j) + LB_j

(9)

where rand $\in \left[\mathrm{0,1}\right]$, and UB_j, LB_j denote the upper and lower bounds of the j^th decision variable. When aroma intensity is sufficient (C_M ≥ 0.2, r₁ ≤ 0.5), pangolins employ luring to attract prey through the Attraction–Capture and Movement–Feeding stages. The distance between the pangolin and ant at iteration t is defined as expressed in Equation (10):

$$D_A\left(t\right)=‖a\cdot X_A\left(t\right)-X_M\left(t\right)‖$$

(10)

and the ant’s updated position is as follows in Equation (11):

X_A(t+1) = X(t)+X_A(t)−A₁⋅D_A(t)

(11)

Here, a denotes the aroma trajectory vector, combining Brownian motion and diffusion perturbation; its mathematical formulation is given in Equations (12)–(15):

$$a=\sqrt{a_x^2+a_y^2+a_z^2}$$

(12)

$$a_x=x\left(t\right)+r_2\sqrt{2D_c/T}$$

(13)

$$a_y=y\left(t\right)+r_2\sqrt{2D_c/T}$$

(14)

$$a_z=z\left(t\right)+r_2\sqrt{2D_c/T}$$

(15)

where D_c = 0.6 is the diffusion coefficient, r₂ ∼ N(0,1), and T is the total iteration count. The energy fluctuation factor A₁ and energy consumption E describes fatigue and metabolic variation given in Equations (16) and (17):

A₁ = 2E × rand() − E

(16)

$$E=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\eta V_{O_2}t(1+\mathrm{Fatigue})\right]$$

(17)

where $\eta =0.1\times \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(\right)$ is the energy correction factor, $V_{O_2}=0.2\times \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\left(\right)$ models oxygen intake, and the fatigue index evolves as follows in Equation (18).

$$\mathrm{Fatigue} =\mathrm{l}\mathrm{o}\mathrm{g}\left({\displaystyle \frac{t\times \pi +T}{T}}\right)$$

(18)

After attraction, the pangolin moves toward the optimal site for feeding as follows in Equations (19) and (20):

$$D_M(t)=‖C_1\cdot D_A\left(t\right)-X_M\left(t\right)‖+L_{\mathrm{Levy} }\left(1-{\displaystyle \frac{t}{T}}\right)$$

(19)

X_M(t+1) = X(t) + X_M(t) − A₁⋅D_M(t)

(20)

where C₁ = 2−2t/T is the rapid descent factor, and L_Levy denotes the Lévy flight step length, defined in Equations (21) and (22).

$$L_{levy}=s\times {\displaystyle \frac{u\times \sigma }{|v{|}^{\frac{1}{\beta }}}}$$

(21)

$$\sigma =\left({\displaystyle \frac{\mathsf{\Gamma }(1+\beta )\times \mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{\pi \beta }{2}\right)}{\mathsf{\Gamma }\left(\frac{1+\beta }{2}\right)\times \beta \times 2^{\frac{\beta -1}{2}}}}\right)$$

(22)

β = 1.5, s = 0.01, and u, v∼u (0,1). The updated position in this stage integrates attraction and oscillatory movement as defined in Equation (23):

$$X(t+1)={\displaystyle \frac{X_M\left(t\right)+X_A\left(t\right)}{2}}+{\displaystyle \frac{\frac{r_3}{2}\sin \left(X_A\left(t\right)e^{\frac{t}{T}}\right)}{4\pi \mathrm{t}\mathrm{a}\mathrm{n}\left(X_M\left(t\right)e^{4{\pi }^{2}t/T}\right)}}$$

(23)

When aroma intensity is low (C_M < 0.7 or r₁ > 0.5), pangolins engage in predation, consisting of search localization, rapid approach, and digging-feeding phases. The pangolin wanders via Lévy flights until it detects aroma, according to Equations (24) and (25)

$$D_M\left(t\right)=‖L_{\mathrm{L}\mathrm{e}\mathrm{v}\mathrm{y}}\cdot X_M\left(t\right)-X\left(t\right)‖$$

(24)

$$X_M(t+1)=\mathrm{s}\mathrm{i}\mathrm{n}\left[C_{1}X\left(t\right)+A_1‖X_M\left(t\right)-L_{\mathrm{L}\mathrm{e}\mathrm{v}\mathrm{y}}{D}_M\left(t\right)‖\right]$$

(25)

Upon detecting prey, it accelerates toward the best location following aroma gradients as defined in Equations (26) and (27):

$$D_M\left(t\right)=‖a\cdot X_M\left(t\right)-X\left(t\right)‖$$

(26)

$$X_M(t+1)=X\left(t\right)-A_1‖X_M\left(t\right)-e^{-a}\mathrm{s}\mathrm{i}\mathrm{n}(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}\times \pi )D_M\left(t\right)‖$$

(27)

Finally, it performs local exploitation by adjusting its position around the best-known solution as defined in Equations (28)–(30):

$$D_M\left(t\right)=‖C_1\cdot X_M\left(t\right)-X\left(t\right)‖$$

(28)

$$X(t+1)=X\left(t\right)+A_1‖X_M\left(t\right)-D_M\left(t\right)‖$$

(29)

X(t+1) = C₁⋅X_M(t)

(30)

3.2. Extreme Learning Machine

The Extreme Learning Machine (ELM), originally introduced by Huang et al. [11], represents an efficient single-hidden-layer feedforward neural network (SLFN) designed to achieve rapid learning with strong generalization capability. Unlike traditional gradient-based networks that require iterative weight updates, the ELM assigns random input weights and biases while analytically determining output weights through the Moore–Penrose pseudoinverse. This method substantially reduces computational complexity and eliminates local minima issues common in backpropagation networks. Consider a dataset $\mathcal{D}=\left\{\left(X_j,t_j\right)\mid j=\mathrm{1,2},\dots ,N\right\}$, where $X_j\in {\mathbb{R}}^n$ represents the input vector with n features, and $t_j\in {\mathbb{R}}^m$ denotes the corresponding target output. The ELM architecture consists of an input layer with n neurons, a hidden layer with L neurons, and an output layer with m neurons [38]. The forward mapping from input to output in an ELM can be expressed as defined in Equation (31):

$$o_j={\sum }_{i=1}^L {\beta }_{i}g\left(W_i\cdot X_j+b_i\right),j=\mathrm{1,2},\dots ,N$$

(31)

where W_i is the input weight vector of the i^th hidden neuron, b_i represent the bias term associated with the i^th hidden neuron, ${\beta }_i$ is the output weight vector connecting the i^th hidden neuron to the output layer, g(⋅) represents the activation function, and o_j is the predicted network output for the j^th sample. The training objective of the ELM is to minimize the total output error across all samples, expressed in Equation (32):

$${\sum }_{j=1}^N {‖o_j-t_j‖}^2={\sum }_{j=1}^N {‖{\sum }_{i=1}^L {\beta }_{i}g\left(W_i\cdot X_j+b_i\right)-t_j‖}^2$$

(32)

The ideal parameter configuration satisfies the following condition:

$${\sum }_{i=1}^L {\beta }_{i}g\left(W_i\cdot X_j+b_i\right)=t_j,j=\mathrm{1,2},\dots ,N$$

(33)

Equation (33) represents the ideal learning scenario with optimal weight, where the model output equals the target. To compactly express the ELM network in matrix form, the mathematical expression is given in Equation (34):

$$H\beta =T$$

(34)

where H, $\beta ,$ and T are given in Equations (35)–(37).

$$H={\left[\begin{array}{ccc}g\left(W_1\cdot X_1+b_1\right)& \dots & g\left(W_L\cdot X_1+b_L\right)\\ ⋮& \ddots & ⋮\\ g\left(W_1\cdot X_N+b_1\right)& \dots & g\left(W_L\cdot X_N+b_L\right)\end{array}\right]}_{N\times L}$$

(35)

$$T={\left[\begin{array}{c}{t}_1^T\\ t_2^T\\ ⋮\\ t_N^T\end{array}\right]}_{N\times m}$$

(36)

$$\beta ={\left[\begin{array}{c}{\beta }_1^T\\ {\beta }_2^T\\ ⋮\\ {\beta }_L^T\end{array}\right]}_{L\times m}$$

(37)

Here, H denotes the hidden-layer output matrix, capturing the nonlinear transformation of all inputs through the activation function. Each column of H represents the response of a single hidden neuron across all input samples, and each row corresponds to the hidden-layer representation of one sample.

3.3. Proposed CPO-ELM Model

The flowchart in Figure 1 depicts the architecture of the CPO–ELM model, a hybrid predictive framework developed to enhance the accuracy and stability of ecological footprint forecasting. The model integrates the adaptive exploration–exploitation balance of the CPO with the computational efficiency of the ELM. The process starts with the initialization of a population of pangolins, where each pangolin represents a potential solution consisting of the input weights and biases of the ELM network as defined in Equation (8). Each decision variable is randomly generated within a bounded search space according to Equation (9), ensuring diverse population initialization. The ELM computes the hidden-layer output matrix based on the nonlinear activation function, as described in Equation (35), and generates the predicted output for each sample following the relationship defined in Equation (31). The fitness of each pangolin is then evaluated using the root mean squared error (RMSE) between the actual and predicted ecological footprint values, which serves as the optimization criterion.

The optimization process in the CPO is inspired by the dual foraging behaviors of the Chinese pangolin, luring and predation, both governed by the olfactory diffusion mechanism. The aroma concentration that drives the behavioral transitions is computed using the Gaussian plume diffusion model as described in Equations (1)–(5), while the horizontal and vertical diffusion parameters that influence the aroma distribution are defined in Equation (6). The normalized aroma concentration, which determines whether the pangolin performs local exploitation or global exploration, is obtained from Equation (7). When the normalized concentration is high, the pangolin engages in luring behavior, exploiting promising areas of the search space. In this phase, the distance between the pangolin and its prey is computed according to Equation (10), and the prey’s updated position is determined using Equation (11). The aroma trajectory influencing this interaction follows the formulations in Equations (12)–(15), while the energy fluctuation, energy consumption, and fatigue effects guiding movement are modeled using Equations (16)–(18). After attracting prey, the pangolin transitions to the movement and feeding phase, updating its position based on the distance function in Equation (19) and the movement rule defined in Equation (20). The rapid descent factor and Lévy flight step length that control the pangolin’s movement are given in Equations (21) and (22). The final position adjustment, incorporating oscillatory and sinusoidal refinements to enhance local search performance, is given by Equation (23). When the aroma concentration is low, the pangolin switches to predation behavior to broaden its exploration. In this mode, the search and localization, rapid approach, and digging–feeding processes are modeled sequentially using Equations (24)–(30), ensuring that the optimizer adaptively navigates between exploration and exploitation to achieve global optimization. The updated solutions are re-evaluated through the ELM during each iteration, and the best-performing configuration is preserved using an elitist strategy. The optimization continues until the maximum iteration threshold is reached, at which point the optimal weights and biases obtained through the CPO become the final parameters of the ELM model. Although ELM offers rapid learning through analytical computation of output weights using the Moore–Penrose pseudoinverse in Equation (34), it remains limited by its sensitivity to random initialization, a lack of a self-correcting mechanism for parameter refinement, and inconsistent convergence in nonlinear or noisy datasets. The integration of the CPO effectively mitigates these weaknesses by introducing a dynamic and biologically inspired search process that adaptively adjusts ELM’s parameters. Figure 1 illustrates the CPO-ELM model.

3.4. Data

The dataset contains monthly data from 1991 to 2020 for the United States, encompassing key macroeconomic, environmental, and socio-developmental indicators that contribute to assessing ecological sustainability. The target variable in the modeling framework is the ecological footprint (EF), which quantifies the aggregate demand placed on environmental resources by human activities. The EF is an essential metric for evaluating ecological balance, resource efficiency, and environmental sustainability within an economy. The predictive attributes utilized for modeling EF include total investment(TI), human capital(HC), financial development(FD), globalization(GLO), urban population (UP), Gross Domestic Product (GDP) per capita, and foreign direct investment (FDI). These indicators were selected based on theoretical and empirical evidence linking economic growth, financial systems, demographic dynamics, and global integration to environmental pressure and resource consumption [39,40,41,42]. All variables were obtained from reputable international databases. The ecological footprint (EF) data were obtained from the Global Footprint Network (GFN) [40], which provides harmonized, methodologically consistent measures of national ecological performance. The macroeconomic and financial variables (TI, FD, GDP, and FDI) were sourced from the World Bank’s database [43], ensuring data reliability and comparability across time. The Human Capital Index (HC) data were extracted from the World Bank Database [44], which offers a standardized measure of human capital. The Globalization Index (GLO) was obtained from the KOF Swiss Economic Institute [45], while the urban population (UP) was obtained from the World Development Indicators dataset [46].

Since the variables exhibit different measurement scales and magnitudes, preprocessing was performed to normalize the data before model training. To ensure uniformity and improve the convergence efficiency of the CPO-ELM framework, all predictor variables were scaled using min–max normalization, which linearly transforms the original data to the range [0, 1]. This scaling method preserves the relative relationships among variables while preventing those with larger numeric ranges from dominating the learning process. The transformation for each variable X was applied as follows in Equation (38):

$$X^{\prime }={\displaystyle \frac{X-X_{min}}{X_{max}-X_{min}}}$$

(38)

where X_min and X_max represent the minimum and maximum observed values of the respective variable. This preprocessing step ensures that all input features contribute proportionately to the CPO–ELM model’s optimization and prediction. The dataset’s descriptive statistics are summarized in

Table 1. Characteristics of the dataset.

	Mean	Std. Dev.	Min	Q1 (25%)	Median	Q3 (75%)	iqr	Max
EF	3.7024	0.2052	3.3952	3.5256	3.6746	3.8796	0.354	4.1081
FD	0.8657	0.0882	0.5687	0.8846	0.9037	0.9085	0.0239	0.9165
FDI	1.6059	0.7068	0.4649	1.0827	1.5406	2.1008	1.0181	3.4058
GDP	50,940.16	6159.172	38,739.8	46,538.11	52,681.02	55,253.09	8714.971	60,698.01
GLO	78.6426	3.2157	71.1255	77.1783	79.9714	81.3171	4.1388	82.3054
HC	3.6354	0.0899	3.4523	3.5615	3.6423	3.7202	0.1587	3.7493
TI	17.8528	1.3924	14.62	17.0103	17.8055	18.7438	1.7335	23.359
UP	79.8525	1.9111	75.701	78.5595	80.099	81.391	2.8315	82.664

. The distributions of each feature are shown in Figure 2, and the pairwise correlations among all variables are presented in the heatmap in Figure 3. Although energy variables such as CO₂ emissions and renewable energy consumption are commonly used in ecological footprint modeling, they were excluded in this study to prevent redundancy with the dependent variable. The ecological footprint already aggregates the environmental effects of energy use, production, and consumption. Including direct energy indicators would therefore introduce high multicollinearity and obscure the contribution of macroeconomic drivers such as GDP per capita and financial development.

4. Experiment and Discussion

In this section, a comprehensive experimental analysis was conducted to evaluate the predictive performance and robustness of the proposed CPO–ELM model in comparison with other ELM-based hybrid optimizers. The assessment was carried out in two distinct validation phases to ensure the models’ stability and generalization capability. A 5-fold cross-validation procedure was implemented in the first phase to assess the model’s consistency across different data partitions. The complete dataset was divided into five equal subsets, with four used for training and one for testing in each iteration. This process was repeated five times, ensuring that each subset served once as the test set while the remaining four were used for model training. The average performance across all folds was then computed to provide an unbiased estimation of the model’s generalization accuracy.

In the second phase, an independent simulation experiment consisting of 20 separate runs was performed for each algorithm under identical experimental conditions. This procedure was adopted to mitigate the influence of stochastic variability inherent to population-based optimization algorithms and to confirm the results’ statistical reliability. The mean and standard deviation of performance metrics across the 20 runs were used to evaluate model stability and convergence consistency. The optimization parameters utilized for all comparative algorithms are summarized in

Table 2. Algorithm parameters.

Optimizer	Hyperparameter
AO	µ = 0.00565, $\omega =0.005,$ $\alpha = \delta =0.1$
CPO	Q = 100, Dc = 0.6, β = 1.5
EDO	Switch Parameter = 0.5
GWO	a0 = 2
SCA	a = 2

. These include the specific control parameters. The hidden-layer neuron size for both the proposed CPO–ELM model and all comparative ELM-based models was fixed at 10 to maintain uniform model complexity across experiments. The search bounds for the weights and biases optimized by each metaheuristic were constrained to –10 to 10, ensuring feasible parameter exploration while preventing numerical instability during training. All optimizers used a population size of 20 and 50 iterations. To ensure a fair and systematic comparison, the performance of the proposed CPO–ELM model was benchmarked against widely recognized metaheuristic-based ELM optimizers: the Aquila Optimizer (AO) [47], Exponential Distribution Optimizer (EDO) [48], Grey Wolf Optimizer (GWO) [14], and Sine Cosine Algorithm (SCA) [15]. These algorithms were selected for their established performance in nonlinear optimization and proven ability to balance exploration and exploitation in complex search spaces. To ensure a comprehensive and objective comparison of model performance, all experiments were evaluated using a consistent set of statistical performance indicators. The selected metrics evaluate the models’ predictive accuracy, reliability, and error characteristics. Specifically, the evaluation criteria included the Coefficient of Determination (R²), root mean squared error (RMSE), mean squared error(MSE), Mean Error (ME), and Relative Absolute Error (RAE). All experiments were conducted in Python 3.10 using Windows 11. Core libraries included NumPy for numerical operations, pandas for data handling, scikit-learn for model evaluation and preprocessing, and Matplotlib 3.0.7 for visualization. The optimization and ELM procedures were implemented in native Python, and SHAP was used for interpretability analysis. Computations were performed on an Intel Core i7 processor with 16 GB RAM.

The application of the proposed model United States data shows consistent accuracy and stability of the model across folds and repetitions. The performance results of the proposed CPO-ELM model and the comparative hybrid algorithms obtained from the 5-fold cross-validation experiments are presented in

Table 3. Training result of 5-fold cross validation.

		AO-ELM	CPO-ELM	EDO-ELM	GWO-ELM	SCA-ELM	ELM
R2	AVG	0.9747	0.9828	0.9738	0.9756	0.9774	0.9324
	STD	4.384 × 10−3	1.612 × 10−3	2.337 × 10−3	2.349 × 10−3	1.947 × 10−3	4.185 × 10−3
RMSE	AVG	3.243 × 10−2	2.688 × 10−2	3.311 × 10−2	3.196 × 10−2	3.079 × 10−2	5.324 × 10−2
	STD	2.030 × 10−3	1.455 × 10−3	1.622 × 10−3	1.471 × 10−3	1.176 × 10−3	1.571 × 10−3
MSE	AVG	1.056 × 10−3	7.246 × 10−4	1.099 × 10−3	1.024 × 10−3	9.496 × 10−4	2.837 × 10−3
	STD	1.372 × 10−4	7.713 × 10−5	1.074 × 10−4	9.294 × 10−5	7.228 × 10−5	1.638 × 10−4
ME	AVG	1.225 × 10−1	9.792 × 10−2	1.248 × 10−1	1.108 × 10−1	1.147 × 10−1	1.744 × 10−1
	STD	1.624 × 10−2	1.421 × 10−2	2.776 × 10−2	1.600 × 10−2	1.697 × 10−2	6.023 × 10−3
RAE	AVG	8.746 × 10−3	7.249 × 10−3	8.930 × 10−3	8.620 × 10−3	8.304 × 10−3	1.436 × 10−2
	STD	5.560 × 10−4	3.963 × 10−4	4.435 × 10−4	3.998 × 10−4	3.131 × 10−4	4.221 × 10−4

and

Table 4. Heldout result of 5-fold cross validation.

		AO-ELM	CPO-ELM	EDO-ELM	GWO-ELM	SCA-ELM	ELM
R2	AVG	0.9694	0.9793	0.9721	0.9704	0.9739	0.9271
	STD	4.630 × 10−3	5.868 × 10−3	7.288 × 10−3	3.740 × 10−3	5.565 × 10−3	1.443 × 10−2
RMSE	AVG	3.541 × 10−2	2.890 × 10−2	3.360 × 10−2	3.492 × 10−2	3.264 × 10−2	5.452 × 10−2
	STD	3.093 × 10−3	3.512 × 10−3	3.545 × 10−3	2.282 × 10−3	2.879 × 10−3	5.597 × 10−3
MSE	AVG	1.264 × 10−3	8.476 × 10−4	1.141 × 10−3	1.225 × 10−3	1.074 × 10−3	3.004 × 10−3
	STD	2.243 × 10−4	2.092 × 10−4	2.398 × 10−4	1.576 × 10−4	1.949 × 10−4	6.526 × 10−4
ME	AVG	1.120 × 10−1	8.882 × 10−2	1.039 × 10−1	1.103 × 10−1	1.078 × 10−1	1.528 × 10−1
	STD	2.023 × 10−2	2.273 × 10−2	1.867 × 10−2	1.877 × 10−2	1.197 × 10−2	2.032 × 10−2
RAE	AVG	9.549 × 10−3	7.798 × 10−3	9.062 × 10−3	9.421 × 10−3	8.807 × 10−3	1.470 × 10−2
	STD	8.208 × 10−4	9.738 × 10−4	9.725 × 10−4	6.585 × 10−4	8.188 × 10−4	1.500 × 10−3

, respectively, for the training and held-out validation phases. These results comprehensively evaluate each model’s predictive performance, generalization, and convergence stability in forecasting the ecological footprint. As shown in Table 3, the proposed CPO-ELM model achieved the best overall performance across all evaluation metrics, outperforming both the standalone ELM and the other optimized variants. Specifically, CPO-ELM achieved the highest R² of 0.9828, indicating that it explained approximately 98.3% of the variance in the ecological footprint data during training. This value was superior to the AO-ELM (0.9747), EDO-ELM (0.9738), GWO-ELM (0.9756), SCA-ELM (0.9774), and conventional ELM (0.9324), clearly demonstrating the improved fitting accuracy achieved through CPO-based optimization. Furthermore, the CPO-ELM exhibited the lowest RMSE and MSE values of 2.688 × 10⁻² and 7.246 × 10⁻⁴, respectively, which reflect its superior precision and reduced residual variance compared to other models. The ME and RAE also highlight the robustness of the proposed approach. The CPO-ELM recorded the smallest ME (9.792 × 10⁻²) and RAE (7.249 × 10⁻³), indicating that its predictions were more consistent and closer to the actual ecological footprint values. The relatively low standard deviations (STDs) across all performance metrics for the CPO-ELM confirm the algorithm’s high convergence stability and reduced sensitivity to stochastic variations across folds. In contrast, the conventional ELM demonstrated the weakest performance, with a higher RMSE (5.324 × 10⁻²), MSE (2.837 × 10⁻³), and the lowest R² (0.9324), suggesting that its random weight and bias initialization led to suboptimal convergence and higher predictive uncertainty. Among the other optimizers, the SCA-ELM and GWO-ELM performed relatively well, with R² values of 0.9774 and 0.9756, respectively, but their accuracy metrics remained inferior to those of the CPO-ELM. The AO-ELM and EDE-ELM variants also achieved competitive results, though their higher RMSE and MSE values indicate less efficient exploitation during training. The superior results of the CPO-ELM model in the training phase can be attributed to the pangolin’s adaptive foraging dynamics, which effectively balance exploration and exploitation to identify optimal weight–bias configurations for the ELM network.

The predictive performance of the models on the unseen validation folds reported in Table 4 further substantiates the generalization advantage of the proposed CPO-ELM model. During the held-out phase, the CPO-ELM maintained the highest R² value of 0.9793, closely followed by the SCA-ELM (0.9739) and EDO-ELM (0.9721), while the baseline ELM again recorded the lowest R² of 0.9271. This result confirms that the proposed model fits the training data effectively and generalizes well to unseen samples without overfitting. Similarly, the CPO-ELM achieved the lowest RMSE (2.890 × 10⁻²) and MSE (8.476 × 10⁻⁴) among all competing models, reflecting its superior prediction accuracy and reduced error dispersion on the validation sets. The ME and RAE values for the CPO-ELM, recorded at 8.882 × 10⁻² and 7.798 × 10⁻³, respectively, were also the smallest among all compared models, reinforcing its consistent predictive precision and minimal bias. The relatively small standard deviations across all metrics indicate stable convergence across the five folds, validating the algorithm’s reliability across different training–test partitions. In contrast, the conventional ELM model exhibited a clear degradation in generalization performance, with the highest RMSE (5.452 × 10⁻²), MSE (3.004 × 10⁻³), and the lowest R² (0.9271), confirming its instability due to random initialization. Among the hybrid competitors, the SCA-ELM and GWO-ELM maintained moderately good validation accuracy, though their slightly higher errors and greater variability suggest less consistent convergence than the CPO-ELM.

To further verify the proposed CPO-ELM model’s robustness, stability, and convergence reliability, an extensive set of 20 independent experimental runs was conducted for each algorithm under identical conditions. The evaluation metrics’ averaged and standard deviation values across the 20 runs are summarized in

Table 5. Train result of 20 independent runs.

		AO-ELM	CPO-ELM	EDO-ELM	GWO-ELM	SCA-ELM	ELM
R2	AVG	0.9764	0.9855	0.9739	0.9706	0.9721	0.9335
	STD	4.117 × 10−3	3.796 × 10−3	5.401 × 10−3	6.071 × 10−3	4.705 × 10−3	4.441 × 10−16
RMSE	AVG	3.198 × 10−2	2.396 × 10−2	3.219 × 10−2	3.419 × 10−2	3.332 × 10−2	5.390 × 10−2
	STD	2.721 × 10−3	3.118 × 10−3	3.349 × 10−3	3.528 × 10−3	2.880 × 10−3	1.388 × 10−17
MSE	AVG	1.030 × 10−3	5.837 × 10−4	1.048 × 10−3	1.181 × 10−3	1.119 × 10−3	2.905 × 10−3
	STD	1.799 × 10−4	1.523 × 10−4	2.167 × 10−4	2.437 × 10−4	1.888 × 10−4	8.674 × 10−19
ME	AVG	1.125 × 10−1	8.426 × 10−2	1.118 × 10−1	1.251 × 10−1	1.269 × 10−1	1.883 × 10−1
	STD	1.352 × 10−2	1.598 × 10−2	2.124 × 10−2	1.940 × 10−2	2.439 × 10−2	5.551 × 10−17
RAE	AVG	8.612 × 10−3	6.479 × 10−3	8.707 × 10−3	9.246 × 10−3	9.012 × 10−3	1.452 × 10−2
	STD	7.328 × 10−4	8.432 × 10−4	9.057 × 10−4	9.542 × 10−4	7.788 × 10−4	0

and

Table 6. Test result of 20 independent runs.

		AO-ELM	CPO-ELM	EDO-ELM	GWO-ELM	SCA-ELM	ELM
R2	AVG	0.9734	0.9880	0.9760	0.9739	0.9742	0.9249
	STD	5.831 × 10−3	3.048 × 10−3	6.674 × 10−3	7.347 × 10−3	5.859 × 10−3	0
RMSE	AVG	3.157 × 10−2	2.322 × 10−2	3.275 × 10−2	3.415 × 10−2	3.404 × 10−2	5.334 × 10−2
	STD	3.343 × 10−3	2.951 × 10−3	4.575 × 10−3	4.815 × 10−3	4.100 × 10−3	1.388 × 10−17
MSE	AVG	1.008 × 10−3	5.479 × 10−4	1.093 × 10−3	1.189 × 10−3	1.176 × 10−3	2.845 × 10−3
	STD	2.209 × 10−4	1.388 × 10−4	3.038 × 10−4	3.346 × 10−4	2.668 × 10−4	0
ME	AVG	1.006 × 10−1	7.516 × 10−2	9.763 × 10−2	1.071 × 10−1	1.121 × 10−1	1.720 × 10−1
	STD	1.605 × 10−2	1.197 × 10−2	2.074 × 10−2	2.125 × 10−2	2.159 × 10−2	8.327 × 10−17
RAE	AVG	8.543 × 10−3	6.221 × 10−3	8.775 × 10−3	9.150 × 10−3	9.121 × 10−3	1.443 × 10−2
	STD	9.048 × 10−4	7.906 × 10−4	1.226 × 10−3	1.290 × 10−3	1.099 × 10−3	3.469 × 10−18

, respectively. As shown in Table 5, the CPO-ELM model consistently achieved superior predictive accuracy and convergence stability across all evaluation metrics compared to the other ELM-based hybrid models and the standalone ELM. The proposed model attained the highest R² of 0.9855, indicating that it captured approximately 98.5% of the variance in the training data, outperforming the AO-ELM (0.9764), EDO-ELM (0.9739), GWO-ELM (0.9706), SCA-ELM (0.9721), and ELM (0.9335). Correspondingly, the CPO-ELM recorded the lowest RMSE and MSE values of 2.396 × 10⁻² and 5.837 × 10⁻⁴, respectively, demonstrating its superior accuracy and minimized residual error. In addition, the ME and RAE values for the CPO-ELM were the smallest among all models, indicating that its predictions closely aligned with the observed ecological footprint values. The low standard deviations across all metrics reflect consistent convergence and robustness against random initialization effects. By contrast, the standalone ELM model exhibited the poorest performance R² of 0.9335 R² and RMSE of 5.390 × 10⁻², reaffirming its limitation due to random parameter initialization and a lack of adaptive tuning. The AO-ELM and EDO-ELM achieved moderately strong performance among the comparative hybrid models, with R² values of 0.9764 and 0.9739, respectively, but both fell short of the precision achieved by the CPO-ELM. The GWO-ELM and SCA-ELM models also demonstrated satisfactory performance but showed higher RMSE and MSE values, suggesting weaker convergence. The results from this phase clearly indicate that the CPO-ELM model’s olfactory-guided adaptive mechanism provides a more efficient balance between exploration and exploitation, thereby identifying near-optimal weight–bias configurations for the ELM network.

The robustness of these findings was further confirmed in the test experiment, as summarized in Table 6, which yielded consistent performance trends. The CPO-ELM model maintained its dominance, achieving the highest R² of 0.9880 and the lowest RMSE and MSE values of 2.322 × 10⁻² and 5.479 × 10⁻⁴, respectively. These results emphasize that the proposed model fits the data accurately and demonstrates strong generalization capability and repeatability across multiple random trials. In terms of error measures, the CPO-ELM again outperformed all competitors, achieving the lowest ME (7.516 × 10⁻²) and RAE (6.221 × 10⁻³), indicating minimal bias and consistently reliable predictions. The low standard deviation across all metrics confirms the algorithm’s high stability and resistance to stochastic fluctuations, a key advantage of the pangolin-inspired dynamic learning mechanism. When compared to the alternative hybrid models, the AO-ELM and EDO-ELM achieved R² values of 0.9734 and 0.9760, respectively, but with higher RMSE and MSE, indicating less efficient convergence toward optimal solutions. The GWO-ELM and SCA-ELM variants also produced acceptable results but were less precise and displayed greater variability. The conventional ELM again recorded the lowest performance, with R² of 0.9249, a RMSE of 5.334 × 10⁻², and a MSE of 2.845 × 10⁻³, confirming its inadequacy in nonlinear and high-dimensional learning tasks without optimization support. The results from both sets of independent runs conclusively demonstrate the superior reliability and performance of the CPO-ELM model. The minimal variation between the two experimental trials indicates strong reproducibility and convergence consistency, validating the model’s capacity to achieve near-optimal solutions under diverse initialization conditions. The enhanced performance of the CPO-ELM can be attributed to its dual-phase optimization strategy, in which the luring phase fine-tunes around promising solutions and the predation phase maintains sufficient exploration to avoid local minima. This adaptive, energy-driven mechanism enables the CPO-ELM to achieve a better trade-off between accuracy and stability than other metaheuristic-based ELM variants. The CPO–ELM framework can be adapted to countries with varying economic and environmental structures. Because the CPO dynamically balances exploration and exploitation, it can tune ELM parameters even under different data distributions or nonlinear relationships.

The predictive performance of the developed models was further examined through the visual comparison of the predicted versus actual ecological footprint values, as presented in Figure 4. These scatter plots illustrate the alignment between the observed and estimated outputs for both the training and testing datasets across all hybrid ELM-based models, and the standalone ELM. The plotted results show that the proposed CPO–ELM model exhibits the highest degree of agreement between predicted and actual ecological footprint values, with data points clustering closely along the ideal line. This strong linear correspondence indicates that the CPO–ELM model effectively captured the underlying functional relationships among the predictors, such as total investment, human capital, globalization, financial development, and GDP per capita, and the target ecological footprint variable. The minimal deviation between predicted and actual values reflects the model’s exceptional fitting accuracy and low generalization error. By contrast, the comparative models, particularly the conventional ELM, exhibit greater dispersion of data points around the reference line, suggesting less consistent approximation and greater prediction bias. Among the other hybrid models, the SCA–ELM and GWO–ELM show moderate alignment, while the AO–ELM and EDO–ELM exhibit slightly higher variance, indicative of less stable convergence patterns. The CPO–ELM model not only demonstrates superior predictive precision but also maintains stable performance across both training and test sets, confirming its robustness and reliability in modeling complex nonlinear ecological footprint dynamics. The close alignment between actual and predicted outputs further validates the efficacy of the CPO’s adaptive search mechanism in optimizing the ELM’s parameters for improved generalization and accuracy.

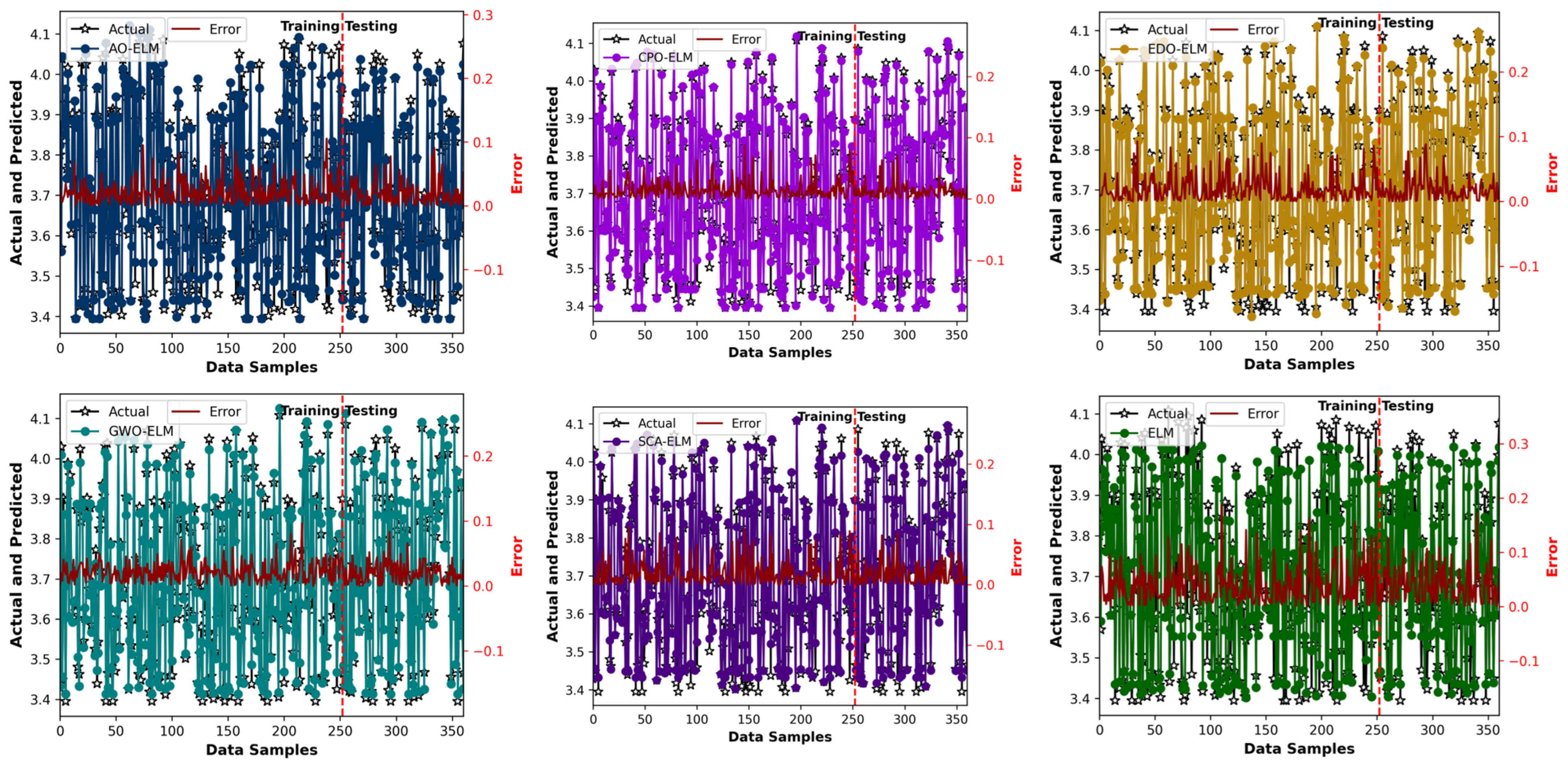
The prediction error plots presented in Figure 5 provide a visual depiction of the models’ performance in approximating the ecological footprint over the full dataset. Each subplot corresponds to a distinct ELM-based model: the AO-ELM, CPO-ELM, EDO-ELM, GWO-ELM, SCA-ELM, and standalone ELM. The black star markers represent the actual ecological footprint values, while the colored lines denote the predicted outputs of each model. The red line, plotted along the secondary y-axis, indicates the absolute prediction error distribution, capturing the magnitude and variability of deviations between predicted and actual values. The vertical dashed line separates the training and testing regions, allowing for a clear visual distinction of model performance in both learning and generalization phases. Across all models, the fluctuations of the red error curves around the zero baseline indicate the presence and magnitude of residual prediction differences. However, the CPO-ELM model demonstrates the most desirable error characteristics. Its error curve remains tightly concentrated near zero across both training and testing samples, reflecting minimal bias and excellent prediction stability. The amplitude of the error fluctuations is consistently lower than that observed in the other models, signifying superior learning consistency and a more accurate approximation of the ecological footprint dynamics. The predicted line of the CPO-ELM closely follows the actual data trajectory, illustrating the optimizer’s ability to effectively tune the ELM parameters for precise mapping of complex nonlinear relationships.

In contrast, the other hybrid models—the AO-ELM, EDO-ELM, GWO-ELM, and SCA-ELM—exhibit relatively wider deviations. Although these models maintain moderate accuracy, the presence of larger oscillations and sporadic spikes indicates less consistent error control. Among them, the SCA-ELM and GWO-ELM perform comparatively better than the AO-ELM and EDO-ELM, yet both still show regions with slightly higher error amplitudes, suggesting weaker generalization in certain data intervals. The AO-ELM and EDO-ELM models display noticeable irregularities, implying that their convergence was occasionally trapped in suboptimal local solutions during training. The standalone ELM model presents the largest and most irregular error variations, especially in the testing phase. The red error line deviates significantly from the zero baseline, confirming the model’s high sensitivity to random initialization and its inability to maintain stable predictive performance without parameter optimization. The misalignment between its predicted and actual curves further highlights ELM’s lack of adaptive learning control. The plots confirm that the CPO-ELM model achieves the best predictive balance, producing the smallest and most stable error distribution across all data samples. The compact clustering of its predicted values around the actual observations and the near-zero mean of the error curve demonstrate both strong fitting and excellent generalization. This result aligns with the statistical outcomes from the cross-validation and independent-run analyses, reinforcing the conclusion that the CPO-ELM is the most robust and reliable approach for ecological footprint prediction among the tested models.

Figure 6 compares the average runtime of all examined models. The proposed CPO–ELM model exhibits the shortest execution time among the hybrid models, which demonstrates its computational efficiency relative to other hybrid approaches. The EDO–ELM and AO–ELM required moderate processing time, while the SCA–ELM and GWO–ELM consumed more resources. The conventional ELM exhibited the least runtime due to its lack of adaptive parameter search. The superior efficiency of the CPO–ELM among the hybrids confirms that its adaptive exploration–exploitation mechanism not only enhances convergence accuracy but also reduces computational cost, making it suitable for large-scale ecological forecasting tasks.

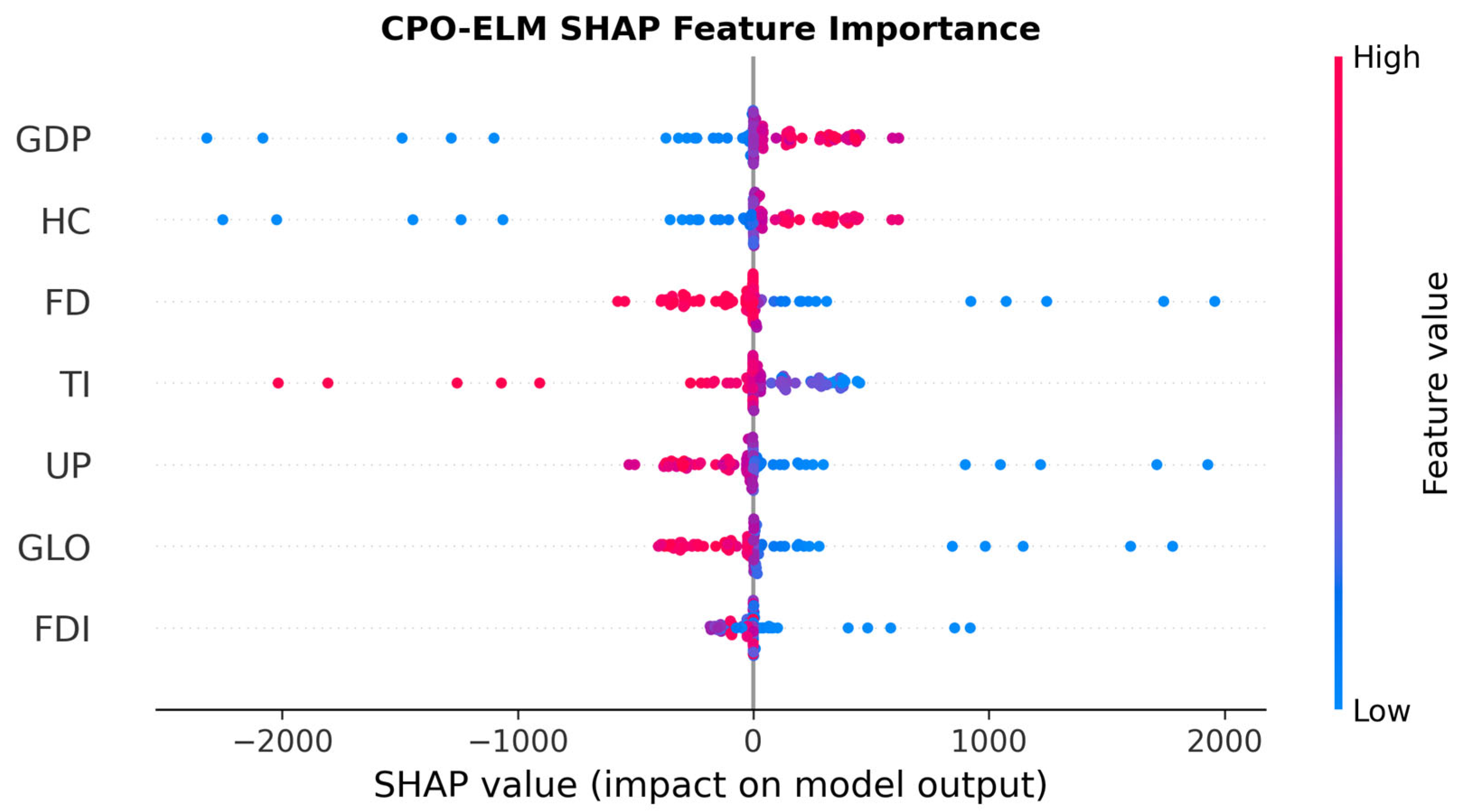
To further interpret the internal learning behavior of the proposed CPO–ELM model and to identify the most influential determinants of the ecological footprint, a SHAP analysis was conducted. The SHAP framework provides a theoretically grounded approach to quantifying the marginal contribution of each predictor variable to the model’s output, thereby enabling a transparent and interpretable assessment of feature importance across the entire prediction space. As depicted in Figure 7, the SHAP summary plot organizes features vertically by their overall impact magnitude, with the horizontal axis representing the SHAP value, the directional and quantitative influence of each feature on the predicted ecological footprint, and the color gradient indicating the underlying feature value, ranging from low (blue) to high (red). GDP does demonstrate a clear trend wherein higher values (red dots) correlate with positive SHAP values, implying increased ecological pressure. Its distribution also includes substantial negative SHAP values at lower GDP levels, suggesting contextual heterogeneity. This pattern is consistent with the Environmental Kuznets Curve hypothesis, which posits that environmental degradation initially rises with income but may plateau or decline at very high levels of development, contingent on institutional quality, and technological adoption. Similarly, HC exhibits mixed effects: while some high-HC observations yield positive SHAP values, others yield negative values, indicating that human capital alone does not linearly drive ecological burden. Rather, its effect appears to be moderated by other socioeconomic conditions; for instance, education may enhance environmental awareness in advanced economies but stimulate consumption-driven footprints in developing contexts.

Financial development (FD) and total investment (TI) emerge as the next most potent mitigating forces. High FD values (red dots) are strongly associated with large negative SHAP values, indicating that robust financial systems, particularly those that facilitate green finance, sustainable lending, or equity markets aligned with environmental, social, and governance (ESG) criteria, exert a significant downward pressure on the ecological footprint. Likewise, TI shows an unequivocally negative relationship: higher investment levels consistently correspond to lower ecological impact, likely reflecting capital allocation toward energy-efficient infrastructure, renewable energy deployment, and circular-economy initiatives. These findings underscore the critical role of institutional and financial architecture in decoupling economic activity from environmental degradation. Urban population (UP) and globalization (GLO) exhibit moderate yet discernible influences. UP shows a tendency for high population density to correlate with positive SHAP values, reinforcing the notion that urbanization intensifies resource demand and emissions, particularly in rapidly industrializing regions lacking sustainable urban planning. GLO, while less dominant than GDP or FD, demonstrates a net positive association with ecological footprint, consistent with the literature highlighting that trade-induced production externalities, transport emissions, and pollution have an effect, whereby global supply chains relocate environmentally intensive activities to jurisdictions with weaker regulations. The interpretation of foreign direct investment (FDI) requires particular nuance; the plot suggests that high FDI (red dots) is associated with small or slightly negative SHAP values, while low FDI (blue dots) corresponds to more variable and occasionally positive impacts. This implies that FDI, when present at scale, may contribute modestly to footprint reduction, perhaps through technology transfer or adherence to international environmental standards. Rather, the ecological consequences of FDI appear contingent on sectoral composition, host-country governance, and investor intent.

Collectively, these results suggest that while macroeconomic indicators such as GDP remain central to ecological footprint dynamics, their influence is neither uniform nor deterministic. Instead, the model reveals that structural factors, including financial system maturity, investment orientation, and global integration play, decisive roles in modulating environmental outcomes. Policy implications therefore extend beyond growth management to encompass institutional design: fostering inclusive financial development, directing public and private investment toward sustainability, and embedding environmental safeguards within globalization frameworks may prove more effective than targeting GDP or human capital alone. The results align with several UN Sustainable Development Goals. The positive association between GDP per capita and ecological footprint highlights the tension between decent work and economic growth and climate action, suggesting that growth-oriented policies must integrate low-carbon strategies. The influence of financial development supports responsible consumption and production by indicating that sustainable investment channels can mitigate environmental pressure. The significant impact of human capital highlights the crucial role of education and innovation in promoting affordable and clean energy, sustainable cities, and communities through behavioral and technological adaptation. These relationships demonstrate how the CPO–ELM framework can help policymakers balance economic and environmental objectives in line with the UN Agenda.

5. Conclusions

This study proposed a hybrid Chinese Pangolin Optimizer–Extreme Learning Machine (CPO–ELM) model for predicting the ecological footprint based on key macroeconomic and developmental indicators, including GDP per capita, human capital, financial development, total investment, urban population, globalization, and foreign direct investment. The CPO algorithm was employed to optimize the input weights and biases of the ELM, addressing its inherent limitations such as random initialization, unstable convergence, and susceptibility to local minima. By leveraging the adaptive dual foraging strategy of the Chinese pangolin, comprising aroma-guided exploration and energy-regulated exploitation, the CPO effectively enhanced the global search capability of the ELM, achieving a superior balance between accuracy and generalization. Comprehensive experimental validation was conducted using monthly data from 1991 to 2020, where the proposed model’s performance was benchmarked against other metaheuristic-optimized ELM variants. Results consistently demonstrated that the CPO–ELM model outperformed all comparative methods in both training and testing phases, yielding the highest R² and the lowest error metrics.

Despite its demonstrated effectiveness, the proposed CPO–ELM model is not without limitations. The ELM’s structural simplicity, while computationally efficient, restricts its ability to capture deep temporal dependencies or complex hierarchical representations inherent in high-dimensional ecological systems. Moreover, the optimization process remains computationally demanding for large datasets, as metaheuristic-based training incurs additional iterations and evaluations. Another limitation is the model’s dependence on the chosen hyperparameter configurations of both the CPO and ELM, which may affect transferability across datasets with differing statistical properties. The present analysis relies exclusively on the United States dataset, which benefits from consistent and high-quality monthly indicators. Although the proposed CPO–ELM framework demonstrates strong predictive accuracy, its performance may vary across countries with limited data continuity, different economic structures, or inconsistent environmental reporting. Further studies should test the model in emerging economies with multi-country data to evaluate its transferability and adapt the parameter bounds accordingly.

For future research, several promising directions can be explored. First, integrating ensemble or deep hybrid architectures may further enhance dynamic modeling capability. Second, the inclusion of spatial and climatic variables could provide richer contextual information, enabling regionalized ecological footprint forecasting. Third, adaptive or multi-objective variants of CPO could be developed to simultaneously optimize accuracy and model interpretability. Future work will also explore dynamic weighting, alternative scaling methods, and broader variable integration to strengthen cross-country applicability.