Developing a Capacity Model for Roundabouts Using SIDRA Calibrated via Simulation-Based Optimization
Abstract
1. Introduction
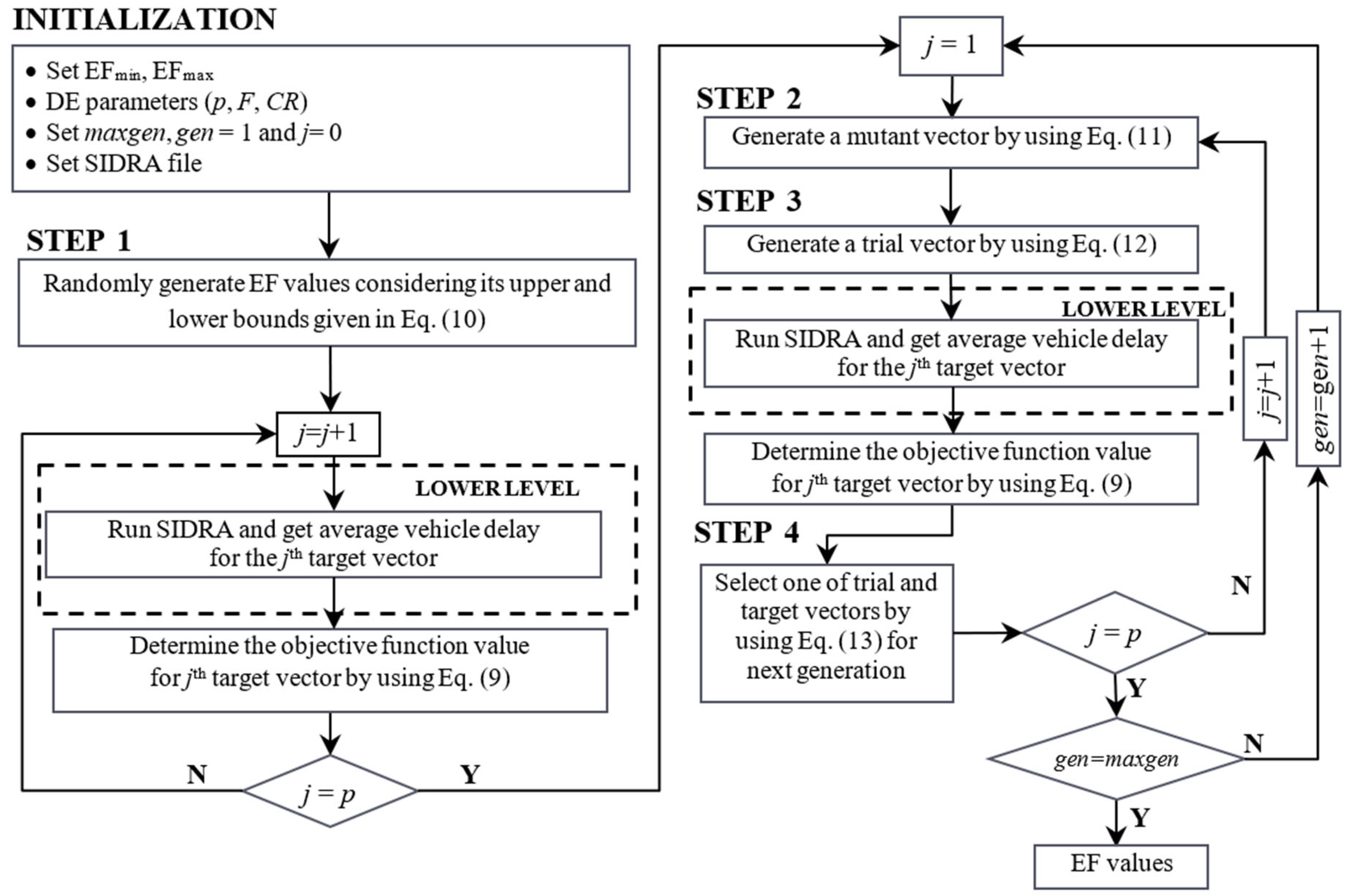
2. Bi-Level Calibration Model
2.1. Differential Evolution (DE) Algorithm
2.2. DEBCAM
3. Study Area
4. Development of Capacity Estimation Model
4.1. SIDRA Analyses
4.2. DEBCAM Analyses
4.3. Capacity Estimation Model
5. Conclusions and Future Studies
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sisiopiku, V.; Oh, H. Evaluation of roundabout performance using SIDRA. J. Transp. Eng. 2001, 127, 143–150. [Google Scholar] [CrossRef]
- Erol, D. Kent İçi Işıklı ve Dönel Kavşak Uygulamalarının Performans Kriterlerine Etkisi: Denizli Örneği. Master’s Thesis, Pamukkale University, Denizli, Turkey, 2018. [Google Scholar]
- Ahmad, A.; Rastogi, R. Calibrating HCM model for roundabout entry capacity under heterogeneous traffic. J. Mod. Transp. 2019, 27, 293–305. [Google Scholar] [CrossRef]
- Tanyel, S. Türkiye’deki Dönel Kavşaklar Için Kapasite Hesap Yöntemi. Ph.D. Thesis, İstanbul Teknik University, İstanbul, Turkey, 2001. [Google Scholar]
- Silva, A.B.; Santos, S.; Vasconcelos, L.; Seco, A.; Silva, J.P. Driver behavior characterization in roundabout crossings. In Proceedings of the 17th Meeting of the EURO Working Group on Transportation (EWGT 2014), Seville, Spain, 2–4 July 2014. [Google Scholar]
- Yap, Y.H.; Gibson, M.H.; Waterson, B.J. An International Review of Roundabout Capacity Modelling. Transp. Rev. 2013, 33, 593–616. [Google Scholar] [CrossRef]
- Liu, W.W.; Qin, Y.; Dong, H.H.; Yang, Y.F. Driving behavior parameter sensitivity analysis based on VISSIM. Appl. Mech. Mater. 2014, 668, 1453–1457. [Google Scholar] [CrossRef]
- Erol, D.; Başkan, Ö.; Ozan, C. Dönel Kavşak Uygulamalarında Merkez Ada Yarıçapının Gecikme ve Hız Parametrelerine Etkisinin İncelenmesi. In proceeding of the International Congress on Engineering and Arhitecture (ENAR), Alanya, Turkey, 14–18 November 2018. [Google Scholar]
- Al-Masaeid, H.R.; Faddah, M.Z. Capacity of roundabouts in Jordan. Transp. Res. Rec. 1997, 1572, 76–85. [Google Scholar] [CrossRef]
- Hagring, O.; Rouphail, N.M.; Sørensen, H.A. Comparison of capacity models for two-lane roundabouts. Transp. Res. Rec. 2003, 1852, 114–123. [Google Scholar] [CrossRef]
- Tanyel, S. Yuvarlakada Kavşaklarda Anaakımdaki Ağır Araç Yüzdesinin Yanyol Kapasitesi Üzerindeki Etkisi. Deü Mühendislik Fakültesi Fen Ve Mühendislik Derg. 2005, 7, 19–30. [Google Scholar]
- Cheng, J.; Yang, X.; Deng, W.; Huang, X. Driver’s critical gap calibration at urban roundabouts: A case study in China. Tsinghua Sci. Technol. 2008, 13, 237–242. [Google Scholar] [CrossRef]
- Tanyel, S.; Yayla, N. Yuvarlakada kavşakların kapasiteleri üzerine bir tartışma. İMO Tek. Dergi 2010, 21, 4935–4958. [Google Scholar]
- Yin, D.; Qiu, T.Z. Comparison of Macroscopic and Microscopic Simulation Models in Modern Roundabout Analysis. Transp. Res. Rec. J. Transp. Res. Board 2011, 2265, 244–252. [Google Scholar] [CrossRef]
- Wang, W.; Yang, X. Research on Capacity of Roundabouts in Beijing. In Proceedings of the 8th International Conference on Traffic and Transportation Studies (ICTTS), Changsha, China, 1–4 August 2012. [Google Scholar]
- Shi, J.; Wang, W.; Yang, X. Model of Capacity Estimation of Roundabout in Beijing. In Proceedings of the IEEE 17th International Conference on Intelligent Transportation Systems (ITSC 2014), Qingdao, China, 8–11 October 2014; IEEE: Piscataway, NJ, USA. [Google Scholar]
- Chen, X.; Lee, M.S. A case study on multi-lane roundabouts under congestion: Comparing software capacity and delay estimates with field data. J. Traffic Transp. Eng. (Engl. Ed.) 2016, 3, 154–165. [Google Scholar] [CrossRef]
- Macioszek, E.; Akçelik, R. A comparison of two roundabout capacity models. In Proceedings of the 5th International Roundabout Conference, Transportation Research Board, Green Bay, WI, USA, 8–10 May 2017. [Google Scholar]
- Fang, C.F.; Castaneda, H. Computer Simulation Modeling of Driver Behavior at Roundabouts. Int. J. Intell. Transp. Syst. Res. 2018, 16, 66–77. [Google Scholar]
- Stanimirovic, D.; Bogdanović, V.; Davidović, S.; Zavadskas, E.K.; Stević, Ž. The Influence of the Participation of Non-Resident Drivers on Roundabout Capacity. Sustainability 2019, 11, 3896. [Google Scholar] [CrossRef]
- Karunarathne, H.K.D.T.; Sandaruwan, M.A.K.; Madushani, U.K.A.H.; Wickramasinghe, W.M.V.S.K. Capacity Analysis for Urban Roundabouts in Sri Lanka Using Modified SIDRA Model. In Proceedings of the 10th International Conference on Structural Engineering and Construction Management (ICSECM), Kandy, Sri Lanka, 13–15 December 2019. [Google Scholar]
- Macioszek, E. Roundabout Entry Capacity Calculation—A Case Study Based on Roundabouts in Tokyo, Japan, and Tokyo Surroundings. Sustainability 2020, 12, 1533. [Google Scholar] [CrossRef]
- Shaaban, K.; Hamad, H. Critical Gap Comparison between One-, Two-, and Three-Lane Roundabouts in Qatar. Sustainability 2020, 12, 4232. [Google Scholar] [CrossRef]
- Anagnostopoulos, A.; Kehagia, F.; Damaskou, E.; Mouratidis, A.; Aretoulis, G. Predicting Roundabout Lane Capacity using Artificial Neural Networks. J. Eng. Sci. Technol. Rev. 2021, 14, 210–215. [Google Scholar] [CrossRef]
- Pratellia, A.; Brocchini, L. Two Geometry Roundabouts: Estimation of Capacity. Transp. Res. Procedia 2022, 64, 232–239. [Google Scholar] [CrossRef]
- Assolie, A.A.; Sukor NS, A.; Khliefat, I.; Abd Manan, T.S.B. Modeling of Queue Detector Location at Signalized Roundabouts via VISSIM Micro-Simulation Software in Amman City, Jordan. Sustainability 2023, 15, 8451. [Google Scholar] [CrossRef]
- Chen, S.; Piao, L.; Zang, X.; Luo, Q.; Li, J.; Yang, J.; Rong, J. Analyzing differences of highway lane-changing behavior using vehicle trajectory data. Phys. A Stat. Mech. Its Appl. 2023, 624, 128980. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, D.; Han, Y.; Fu, A.; Zhang, H.; Tian, Y.; Yue, L.; Wang, D.; Sun, J. Parallel-Computing-Based Calibration for Microscopic Traffic Simulation Model. Transp. Res. Rec. 2024, 2678, 279–294. [Google Scholar] [CrossRef]
- Guerrieri, M. Total capacity and LOS estimation of innovative and conventional roundabouts through macroscopic fundamental diagrams. Transp. Res. Interdiscip. Perspect. 2024, 27, 101232. [Google Scholar] [CrossRef]
- Afshari, A.; Lee, J.; Besenski, D.; Dimitrijevic, B.; Spasovic, L. Calibrating Microscopic Traffic Simulation Model Using Connected Vehicle Data and Genetic Algorithm. Appl. Sci. 2025, 15, 1496. [Google Scholar] [CrossRef]
- Avsar, Ö.Y.; Yıldırım, Z.B.; Politi, R.R.; Tanyel, S. Investigation of the effect of geometric irregularities on capacity of traffic circles by using partial least squares regression method. Can. J. Civ. Eng. 2024, 51, 1388–1408. [Google Scholar] [CrossRef]
- Algherbal, E.A.; Ratrout, N.T. A Comparative Analysis of Currently Used Microscopic, Macroscopic, and Mesoscopic Traffic Simulation Software. In Proceedings of the 1st International Conference on Smart Mobility and Logistics Ecosystems (SMiLE), Dhahran, Saudi Arabia, 17–19 September 2024. [Google Scholar]
- Akcelik & Associates Pty Ltd. SIDRA Intersection 8.0 User Guide; Akcelik & Associates PTY Ltd.: Greythorn, Australia, 2016. [Google Scholar]
- Gedizlioğlu, E. Denetimsiz Kavşaklarda Yanyol Sürücülerinin Davranışlarına Göre Pratik Kapasite Saptanması Için bir Yöntem. Ph.D. Thesis, İstanbul Teknik University, İstanbul, Turkey, 1979. [Google Scholar]
- Colson, B.; Marcotte, P.; Savard, G. An overview of bilevel optimization. Ann. Oper. Res. 2007, 153, 235–256. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Y.; Qi, X.; Wang, M.; Wang, X. A Bi-Level Optimization Model for Virtual Power Plant Membership Selection Considering Load Time Series. Sustainability 2023, 15, 2138. [Google Scholar] [CrossRef]
- Başkan, Ö. Karınca Kolonisi Optimizasyonu ile Ulaşım ağ Tasarımı. Ph.D. Thesis, Pamukkale University, Denizli, Turkey, 2009. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report TR-95-012; International Computer Science Institute: Berkeley, CA, USA, 1995. [Google Scholar]
- Başkan, Ö. Birleştirilmiş Ulaşım Ağ Tasarım Probleminin Diferansiyel Gelişim Algoritması ile Çözümü. In Proceedings of the 10. Ulaştırma Kongresi, İzmir, Turkey, 24–27 September 2013. [Google Scholar]
- Başkan, Ö.; Ceylan, H. Ulaşım Ağ Tasarımı Problemlerinin Çözümünde Diferansiyel Gelişim Algoritması Tabanlı Çözüm Yaklaşımları. Pamukkale Üniversitesi Mühendislik Bilim. Derg. 2014, 20, 324–331. [Google Scholar] [CrossRef][Green Version]
- Baskan, O.; Ceylan, H.; Ozan, C. A Simultaneous Solution for Reserve Capacity Maximization and Delay Minimization Problems in Signalized Road Networks. J. Adv. Transp. 2019, 6203137. [Google Scholar] [CrossRef]
- Karaboğa, D. Yapay Zekâ Optimizasyon Algoritmaları; Nobel Publication: İstanbul, Turkey, 2004. [Google Scholar]
- Karaboga, D.; Basturk, B. Image Segmentation Using Differential Evolution Algorithm. In Proceedings of the 13th IEEE Signal Processing and Communications Applications Conference (SIU 2005), Kayseri, Turkey, 16–18 May 2005. [Google Scholar]
- Gürarslan, G. Yeraltı Suyu Kirletici Kaynak Yerlerinin ve Boşalım Geçmişlerinin Diferansiyel Gelişim Algoritması Kullanılarak Belirlenmesi. Ph.D. Thesis, Pamukkale University, Denizli, Turkey, 2011. [Google Scholar]
- Liu, H.; Cai, Z.; Wang, Y. Hybridizing Particle Swarm Optimization with Differential Evolution for Constrained Numerical and Engineering Optimization. Appl. Soft Comput. 2010, 10, 629–640. [Google Scholar] [CrossRef]
- Keskintürk, T. Diferansiyel Gelişim Algoritması. İstanbul Ticaret Üniversitesi Fen Bilim. Derg. 2006, 5, 85–99. [Google Scholar]
- Baskan, O. A Multiobjective Bilevel Programming Model for Environmentally Friendly Traffic Signal Timings. Adv. Civ. Eng. 2019, 2019, 1638618. [Google Scholar] [CrossRef]
- Abadi, A.; Rajabioun, T.; Ioannou, P.A. Traffic flow prediction for road transportation networks with limited traffic data. IEEE Trans. Intell. Transp. Syst. 2014, 16, 653–662. [Google Scholar] [CrossRef]
- Kang, N.; Kanbe, N.; Nakamura, H.; Odaka, S. Development and validation of a roundabout entry capacity model considering pedestrians under Japanese conditions. Asian Transp. Stud. 2016, 4, 350–365. [Google Scholar]
- Politi, R.R.; Tanyel, S. Minimizing Delay at Closely Spaced Signalized Intersections Through Green Time Ratio Optimization: A Hybrid Approach With K-Means Clustering and Genetic Algorithms. IEEE Veh. Technol. Soc. Sect. 2025, 13, 43981–43999. [Google Scholar] [CrossRef]
- An, H.K.; Javeed, M.A.; Bae, G.; Zubair, N.; Metwally, A.S.M.; Bocchetta, P.; Na, F.; Javed, M.S. Optimized Intersection Signal Timing: An Intelligent Approach-Based Study for Sustainable Models. Sustainability 2022, 14, 11422. [Google Scholar] [CrossRef]
- Gürünlü Alma, Ö.; Vupa, Ö. Regresyon Analizinde Kullanılan En Küçük Kareler ve En Küçük Medyan Kareler Yöntemlerinin Karşılaştırılması. SDÜ Fen Edeb. Fakültesi Fen Derg. E-Dergi 2008, 3, 219–229. [Google Scholar]
- Birkes, D.; Dodge, Y. Alternative Methods of Regression; John Wiley & Sons: New York, NY, USA, 1993; pp. 80–140. [Google Scholar]
- Ümit, A.Ö.; Bulut, E. Türkiye’de işsizliği etkileyen faktörlerin kısmi en küçük kareler regresyon yöntemi ile analizi: 2005–2010 dönemi. Dumlupınar Üniversitesi Sos. Bilim. Derg. 2013, 37, 131–141. [Google Scholar]
- Bulut, E.; Alın, A. Kısmi En Küçük Kareler Regresyon Yöntemi Algoritmalarından Nipals ve PLS-Kernel Algoritmalarının Karşılaştırılması ve Bir Uygulama. Dokuz Eylül Üniversitesi İktisadi Ve İdari Bilim. Fakültesi Derg. 2009, 24, 127–138. [Google Scholar]
- Lu, J.; Chen, S.; Wang, W.; Van Zuylen, H.J. A hybrid model of partial least squares and neural network for traffic incident detection. Expert Syst. Appl. 2012, 39, 4775–4784. [Google Scholar] [CrossRef]
- Wang, W.; Chen, S.; Qu, G. Incident Detection Algorithm Based on Partial Least Squares Regression. Transp. Res. Part C Emerg. Technol. 2008, 16, 54–70. [Google Scholar] [CrossRef]
- Skrivanek, S. The Use of Dummy Variables in Regression Analysis; More Steam, LLC.: Powell, OH, USA, 2009. [Google Scholar]
- Garavaglia, S.; Sharma, A. A Smart Guide to Dummy Variables: Four Applications and a Macro. In Proceedings of the Northeast SAS Users Group Conference, Pittsburgh, PA, USA, 4–6 October 1998. [Google Scholar]
- Chen, F.; Song, M.; Ma, X. Investigation on the injury severity of drivers in rear-end collisions between cars using a random parameters bivariate ordered probit model. Int. J. Environ. Res. Public Health 2019, 16, 2632. [Google Scholar] [CrossRef]
- Alomari, A.H.; Khedaywi, T.S.; Marian AR, O.; Jadah, A.A. Traffic speed prediction techniques in urban environments. Heliyon 2022, 8, e11847. [Google Scholar] [CrossRef]
- Toledo, T.; Koutsopoulos, N.; Ben, M. Estimation of an Integrated Driving Behavior Model. Transp. Res. Part C Emerg. Technol. 2009, 17, 365–380. [Google Scholar] [CrossRef]
- Graffelman, J.; De Leeuw, J. Improved approximation and visualization of the correlation matrix. Am. Stat. 2023, 77, 432–442. [Google Scholar] [CrossRef]
- Yılmaz Sönmez, H. Kentiçi Demiryolunda Trafik Yükünün Ray Aşınmaları Üzerindeki Etkisinin Araştırılması. Ph.D. Thesis, İstanbul Teknik University, İstanbul, Turkey, 2021. [Google Scholar]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Jierula, A.; Wang, S.; Oh, T.-M.; Wang, P. Study on accuracy metrics for evaluating the predictions of damage locations in deep piles using artificial neural networks with acoustic emission data. Appl. Sci. 2021, 11, 2314. [Google Scholar] [CrossRef]
- Ünver, Ö.; Gamgam, H. Uygulamalı Temel Istatistik Yöntemler; Seçkin Publication: Ankara, Turkey, 2008. [Google Scholar]
- Han, S.; Li, Y.; Shen, D.; Wang, C. Comprehensive evaluation method of privacy-preserving record linkage technology based on the modified criteria importance through intercriteria correlation method. Mathematics 2024, 12, 3476. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge: New York, NY, USA, 1988. [Google Scholar]
- Cohen, J. A power primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef] [PubMed]
- Vos, J.; Farah, H.; Hagenzieker, M. How do Dutch drivers perceive horizontal curves on freeway interchanges and which cues influence their speed choice? IATSS Res. 2021, 45, 258–266. [Google Scholar] [CrossRef]
- Gardner, B.; Abraham, C. Psychological correlates of car use: A meta-analysis. Transp. Res. Part F Traffic Psychol. Behav. 2008, 11, 300–311. [Google Scholar] [CrossRef]
- Vatcheva, K.P.; Lee, M. Multicollinearity in Regression Analyses Conducted in Epidemiologic Studies. Epidemiology 2016, 6, 227. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
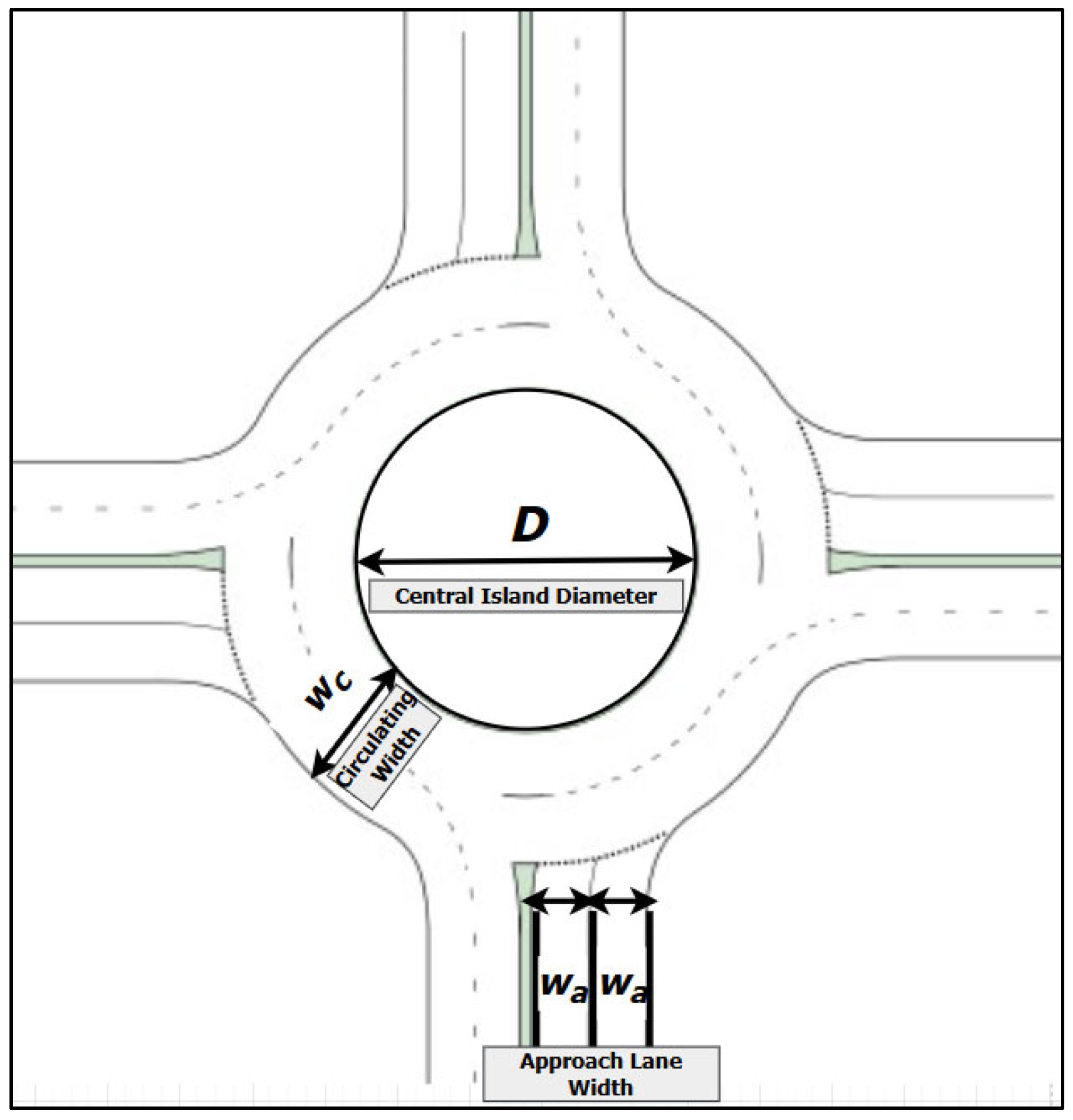
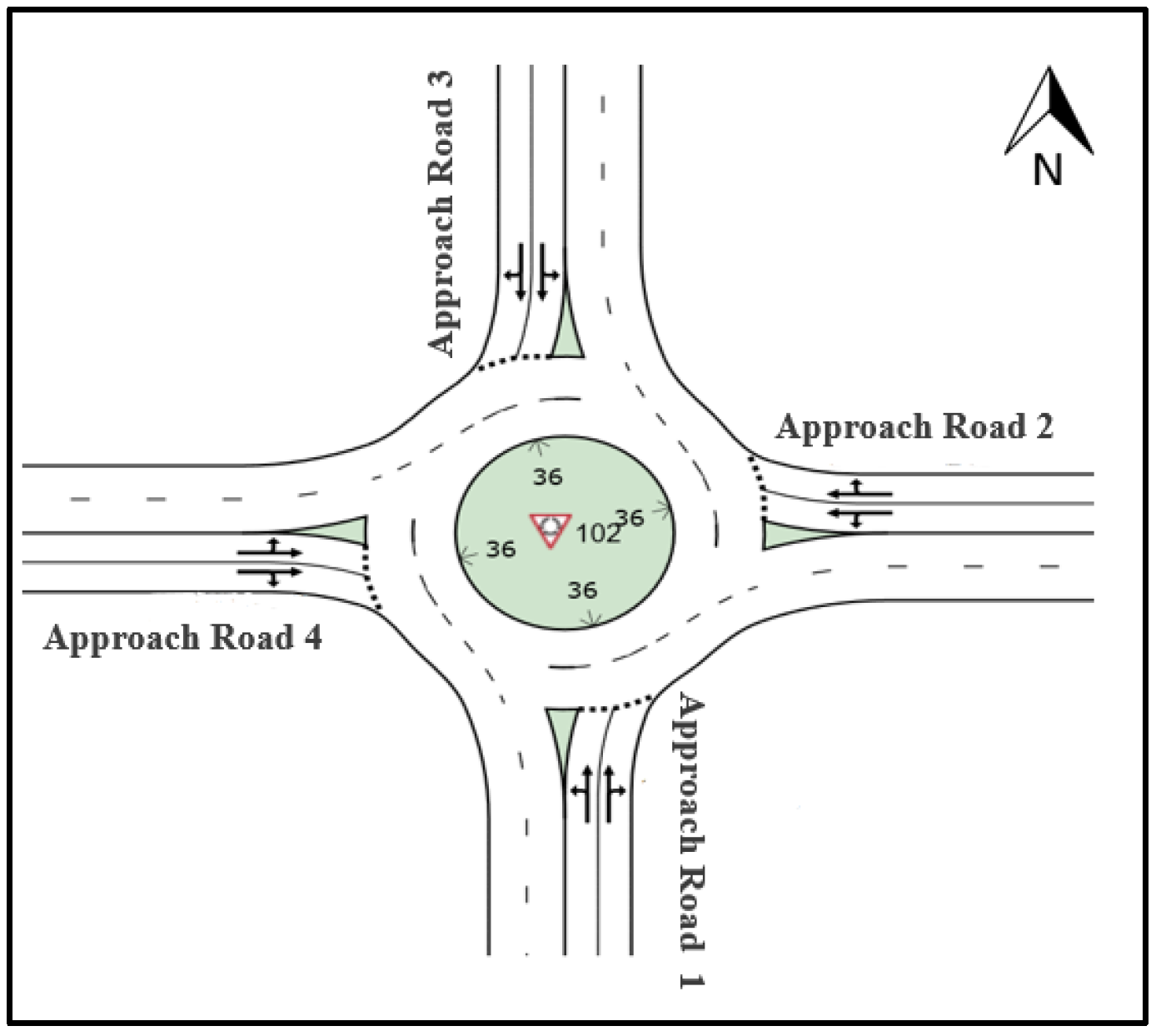
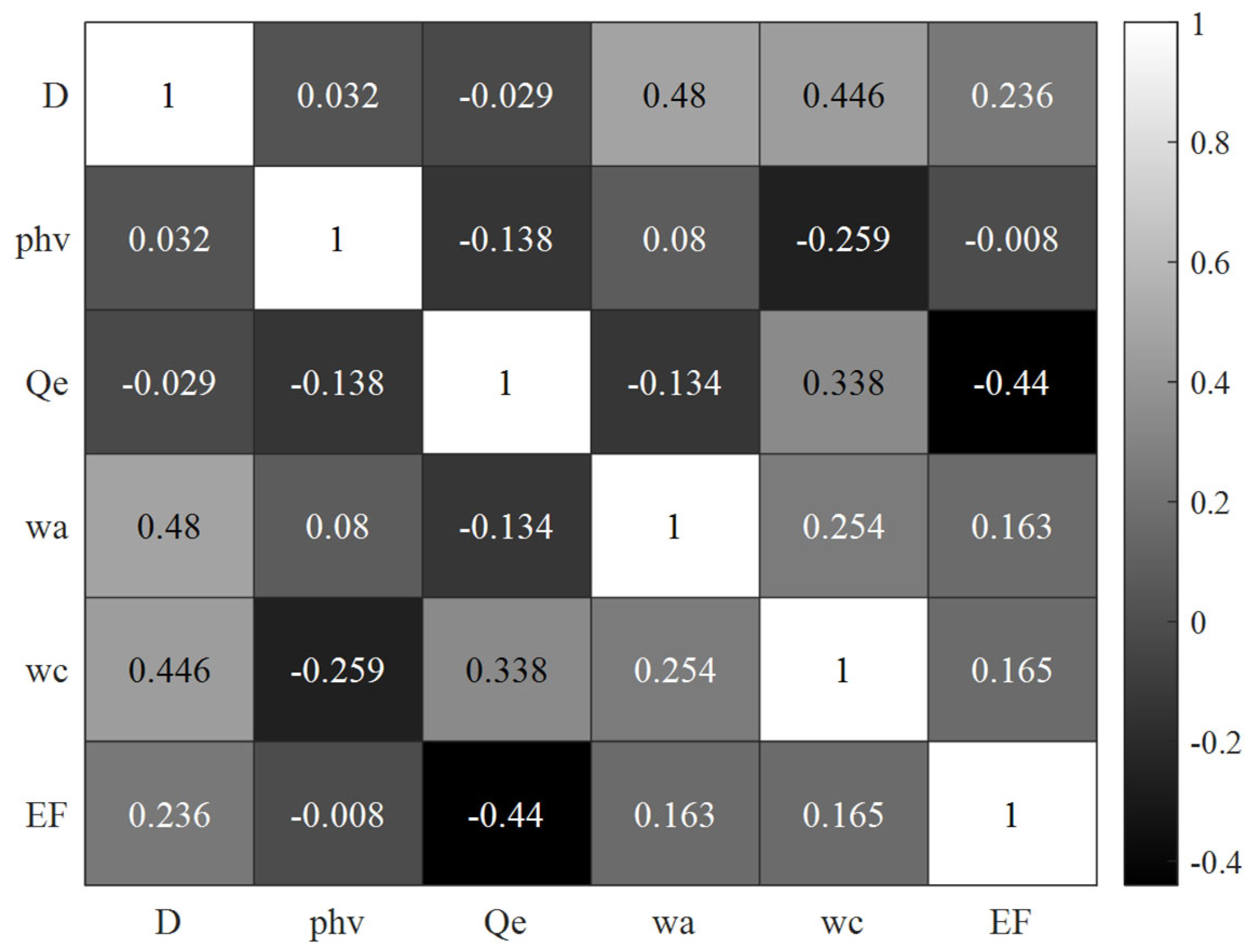
| Intersection No. | Approach Road No. | D (m) | q (veh/h) | ql (%) | qr (%) | qth (%) | phv (%) | wa (m) | wc (m) | d0 (s) | Qe (veh/h) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 36 | 600 | 16 | 10 | 74 | 4 | 3 | 8 | 13.72 | 493 |
| 2 | 36 | 672 | 34 | 12 | 54 | 0 | 2.4 | 8.5 | 18.98 | 707 | |
| 3 | 36 | 900 | 8 | 13 | 79 | 0 | 3.25 | 8 | 16.06 | 764 | |
| 4 | 36 | 540 | 22 | 27 | 51 | 0 | 3.25 | 8 | 17.79 | 1074 | |
| 2 | 1 | 79 | 1104 | 84 | 1 | 15 | 0 | 3.5 | 8 | 25.5 | 960 |
| 2 | 79 | 84 | 14 | 28 | 58 | 28 | 2.5 | 10 | 27.42 | 2002 | |
| 3 | 79 | 960 | 4 | 66 | 30 | 5 | 3.5 | 8 | 18.31 | 1042 | |
| 4 | 79 | 1704 | 46 | 50 | 4 | 7 | 3.5 | 8.5 | 22.56 | 373 | |
| 3 | 1 | 25 | 1116 | 19 | 14 | 67 | 10 | 3 | 7 | 22.61 | 1131 |
| 2 | 25 | 492 | 22 | 22 | 56 | 0 | 3.5 | 7 | 21.97 | 1547 | |
| 3 | 25 | 888 | 20 | 24 | 56 | 5 | 3 | 6 | 15.56 | 632 | |
| 4 | 25 | 1056 | 18 | 41 | 41 | 7 | 3 | 6 | 23.23 | 821 | |
| 4 | 1 | 80 | 1188 | 12 | 27 | 61 | 3 | 3.5 | 9 | 17.25 | 505 |
| 2 | 80 | 948 | 37 | 25 | 38 | 3 | 3.5 | 10 | 25.15 | 1061 | |
| 3 | 80 | 1008 | 19 | 18 | 63 | 4 | 3.5 | 9 | 20.86 | 916 | |
| 4 | 80 | 360 | 33 | 23 | 44 | 0 | 3.5 | 10 | 23.2 | 1263 | |
| 5 | 1 | 50 | 864 | 10 | 38 | 52 | 3 | 3.5 | 8.6 | 16.34 | 556 |
| 2 | 50 | 792 | 54 | 36 | 10 | 16 | 4.2 | 8 | 23.55 | 777 | |
| 3 | 50 | 708 | 14 | 10 | 76 | 5 | 3.5 | 8.5 | 19.57 | 657 | |
| 4 | 50 | 564 | 34 | 30 | 36 | 11 | 3.6 | 8.5 | 22.25 | 1194 | |
| 6 | 1 | 57 | 1056 | 22 | 25 | 53 | 1 | 3.5 | 9.5 | 19.25 | 796 |
| 2 | 57 | 756 | 41 | 25 | 34 | 2 | 3.6 | 9.8 | 24.8 | 966 | |
| 3 | 57 | 840 | 36 | 4 | 60 | 4 | 3.5 | 9.8 | 27.08 | 840 | |
| 4 | 57 | 600 | 20 | 26 | 54 | 6 | 3 | 10 | 25.58 | 1219 | |
| 7 | 1 | 75 | 1092 | 22 | 22 | 56 | 0 | 4.25 | 11 | 22.38 | 1149 |
| 2 | 75 | 1560 | 31 | 17 | 52 | 5 | 5.4 | 11 | 22.91 | 1162 | |
| 3 | 75 | 684 | 30 | 10 | 50 | 7 | 4.25 | 10 | 25.63 | 1649 | |
| 4 | 75 | 1008 | 23 | 13 | 64 | 2 | 4.5 | 11 | 18.61 | 1181 | |
| 8 | 1 | 75 | 108 | 56 | 10 | 34 | 11 | 4.5 | 7 | 32.37 | 783 |
| 2 | 75 | 264 | 18 | 22 | 60 | 9 | 4.5 | 7 | 24.72 | 524 | |
| 3 | 75 | 444 | 5 | 81 | 14 | 8 | 4.5 | 7 | 13.29 | 290 | |
| 4 | 75 | 672 | 57 | 5 | 38 | 14 | 4.5 | 7 | 18.21 | 139 |
| Intersection No. | Approach Road No. | SIDRA | Observation | Intersection No. | Approach Road No. | SIDRA | Observation |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 4.50 | 13.72 | 5 | 1 | 3.10 | 16.34 |
| 2 | 6.80 | 18.98 | 2 | 8.30 | 23.55 | ||
| 3 | 6.20 | 16.06 | 3 | 3.70 | 19.57 | ||
| 4 | 7.30 | 17.79 | 4 | 8.20 | 22.25 | ||
| 2 | 1 | 145.40 | 25.5 | 6 | 1 | 7.90 | 19.25 |
| 2 | 27.70 | 27.42 | 2 | 7.90 | 24.8 | ||
| 3 | 18.20 | 18.31 | 3 | 8.10 | 27.08 | ||
| 4 | 7.50 | 22.56 | 4 | 8.20 | 25.58 | ||
| 3 | 1 | 121.10 | 22.61 | 7 | 1 | 7.80 | 22.38 |
| 2 | 17.60 | 21.97 | 2 | 7.90 | 22.91 | ||
| 3 | 9.00 | 15.56 | 3 | 9.70 | 25.63 | ||
| 4 | 16.00 | 23.23 | 4 | 8.00 | 18.61 | ||
| 4 | 1 | 4.60 | 17.25 | 8 | 1 | 17.70 | 32.37 |
| 2 | 7.60 | 25.15 | 2 | 14.20 | 24.72 | ||
| 3 | 6.40 | 20.86 | 3 | 9.40 | 13.29 | ||
| 4 | 6.70 | 23.2 | 4 | 16.60 | 18.21 |
| Intersection No. | Approach Road No. | EF | Intersection No. | Approach Road No. | EF |
|---|---|---|---|---|---|
| 1 | 1 | 1.71 | 5 | 1 | 1.74 |
| 2 | 1.51 | 2 | 1.40 | ||
| 3 | 1.33 | 3 | 1.80 | ||
| 4 | 1.42 | 4 | 1.50 | ||
| 2 | 1 | 0.83 | 6 | 1 | 1.32 |
| 2 | 0.78 | 2 | 1.49 | ||
| 3 | 0.80 | 3 | 1.48 | ||
| 4 | 1.35 | 4 | 1.40 | ||
| 3 | 1 | 0.84 | 7 | 1 | 1.25 |
| 2 | 1.01 | 2 | 1.24 | ||
| 3 | 1.28 | 3 | 1.34 | ||
| 4 | 1.10 | 4 | 1.34 | ||
| 4 | 1 | 1.59 | 8 | 1 | 2.00 |
| 2 | 1.32 | 2 | 2.00 | ||
| 3 | 1.39 | 3 | 1.74 | ||
| 4 | 1.91 | 4 | 1.86 |
| Intersection No. | Approach Road No. | Intersection No. | Approach Road No. | ||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 13.72 | 13.70 | 5 | 1 | 16.34 | 16.30 |
| 2 | 18.98 | 19.00 | 2 | 23.55 | 23.60 | ||
| 3 | 16.06 | 16.10 | 3 | 19.57 | 19.80 | ||
| 4 | 17.79 | 17.80 | 4 | 22.25 | 22.30 | ||
| 2 | 1 | 25.50 | 25.50 | 6 | 1 | 19.25 | 19.30 |
| 2 | 27.42 | 27.40 | 2 | 24.80 | 24.80 | ||
| 3 | 18.31 | 18.30 | 3 | 27.08 | 27.10 | ||
| 4 | 22.56 | 22.60 | 4 | 25.58 | 25.60 | ||
| 3 | 1 | 22.61 | 22.60 | 7 | 1 | 22.38 | 22.40 |
| 2 | 21.97 | 22.00 | 2 | 22.91 | 22.90 | ||
| 3 | 15.56 | 15.60 | 3 | 25.63 | 25.60 | ||
| 4 | 23.23 | 23.20 | 4 | 18.61 | 18.60 | ||
| 4 | 1 | 17.25 | 14.90 | 8 | 1 | 32.37 | 24.10 |
| 2 | 25.15 | 21.10 | 2 | 24.72 | 19.00 | ||
| 3 | 20.86 | 18.20 | 3 | 13.29 | 13.30 | ||
| 4 | 23.20 | 21.10 | 4 | 18.21 | 18.60 |
| Intersection No. | Approach Road No. | GEH | Intersection No | Approach Road No. | GEH |
|---|---|---|---|---|---|
| 1 | 1 | 0.005 | 5 | 1 | 0.001 |
| 2 | 0.004 | 2 | 0.010 | ||
| 3 | 0.010 | 3 | 0.052 | ||
| 4 | 0.002 | 4 | 0.011 | ||
| 2 | 1 | 0.000 | 6 | 1 | 0.012 |
| 2 | 0.004 | 2 | 0.000 | ||
| 3 | 0.002 | 3 | 0.004 | ||
| 4 | 0.008 | 4 | 0.004 | ||
| 3 | 1 | 0.002 | 7 | 1 | 0.004 |
| 2 | 0.006 | 2 | 0.002 | ||
| 3 | 0.010 | 3 | 0.006 | ||
| 4 | 0.006 | 4 | 0.002 | ||
| 4 | 1 | 0.586 | 8 | 1 | 1.556 |
| 2 | 0.842 | 2 | 1.223 | ||
| 3 | 0.602 | 3 | 0.003 | ||
| 4 | 0.446 | 4 | 0.090 |
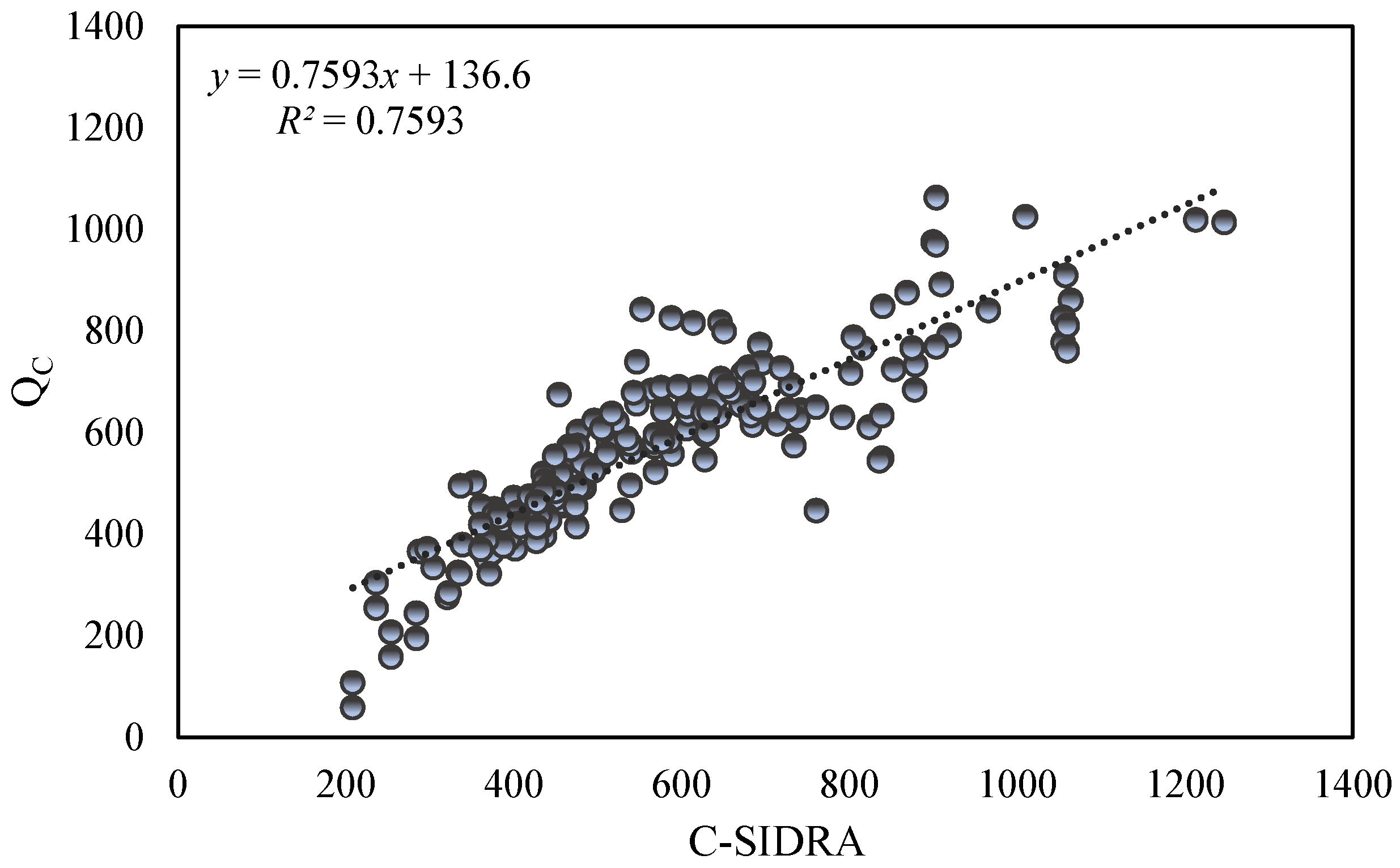
| Intersection No. | Model | Capacity (veh/h) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| South | East | North | West | ||||||
| Left Lane | Right Lane | Left Lane | Right Lane | Left Lane | Right Lane | Left Lane | Right Lane | ||
| 1 | SIDRAST | 1242 | 786 | 990 | 1273 | 1031 | 1411 | 1563 | 1183 |
| C-SIDRA | 371 | 297 | 431 | 436 | 454 | 678 | 761 | 686 | |
| 2 | SIDRAST | 836 | 641 | 231 | 231 | 544 | 789 | 1082 | 1354 |
| C-SIDRA | 1064 | 1058 | 236 | 236 | 588 | 869 | 919 | 966 | |
| 3 | SIDRAST | 535 | 539 | 453 | 527 | 855 | 1034 | 698 | 826 |
| C-SIDRA | 738 | 631 | 405 | 477 | 568 | 792 | 569 | 742 | |
| 4 | SIDRAST | 1091 | 1416 | 790 | 1123 | 813 | 1175 | 702 | 1032 |
| C-SIDRA | 727 | 730 | 535 | 608 | 577 | 644 | 284 | 284 | |
| 5 | SIDRAST | 1144 | 1445 | 876 | 851 | 1111 | 921 | 820 | 647 |
| C-SIDRA | 353 | 839 | 477 | 606 | 434 | 458 | 368 | 401 | |
| 6 | SIDRAST | 437 | 761 | 466 | 523 | 374 | 432 | 336 | 360 |
| C-SIDRA | 642 | 673 | 456 | 468 | 511 | 505 | 413 | 361 | |
| 7 | SIDRAST | 752 | 1070 | 1085 | 1085 | 534 | 763 | 769 | 1066 |
| C-SIDRA | 576 | 696 | 1055 | 1055 | 368 | 439 | 578 | 654 | |
| 8 | SIDRAST | 1242 | 786 | 990 | 1273 | 1031 | 1411 | 1563 | 1183 |
| C-SIDRA | 371 | 297 | 431 | 436 | 454 | 678 | 761 | 686 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erol, D.; Baskan, O. Developing a Capacity Model for Roundabouts Using SIDRA Calibrated via Simulation-Based Optimization. Sustainability 2025, 17, 10289. https://doi.org/10.3390/su172210289
Erol D, Baskan O. Developing a Capacity Model for Roundabouts Using SIDRA Calibrated via Simulation-Based Optimization. Sustainability. 2025; 17(22):10289. https://doi.org/10.3390/su172210289
Chicago/Turabian StyleErol, Duygu, and Ozgur Baskan. 2025. "Developing a Capacity Model for Roundabouts Using SIDRA Calibrated via Simulation-Based Optimization" Sustainability 17, no. 22: 10289. https://doi.org/10.3390/su172210289
APA StyleErol, D., & Baskan, O. (2025). Developing a Capacity Model for Roundabouts Using SIDRA Calibrated via Simulation-Based Optimization. Sustainability, 17(22), 10289. https://doi.org/10.3390/su172210289






