Mining-Induced Permeability Evolution of Inclined Floor Strata and In Situ Protection of Confined Aquifers
Abstract
1. Introduction
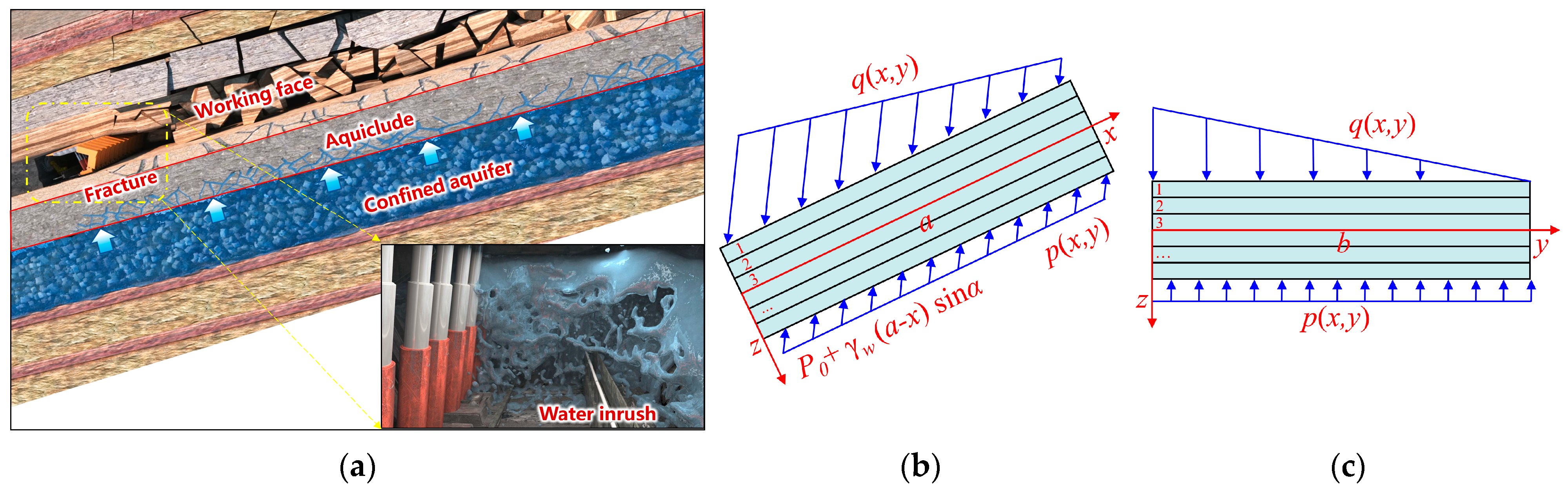
2. Mining-Induced Floor Permeability Evolution Based on Cooperative Deformation of the Aquiclude Assemblage
2.1. Mining-Induced Floor Permeability Model
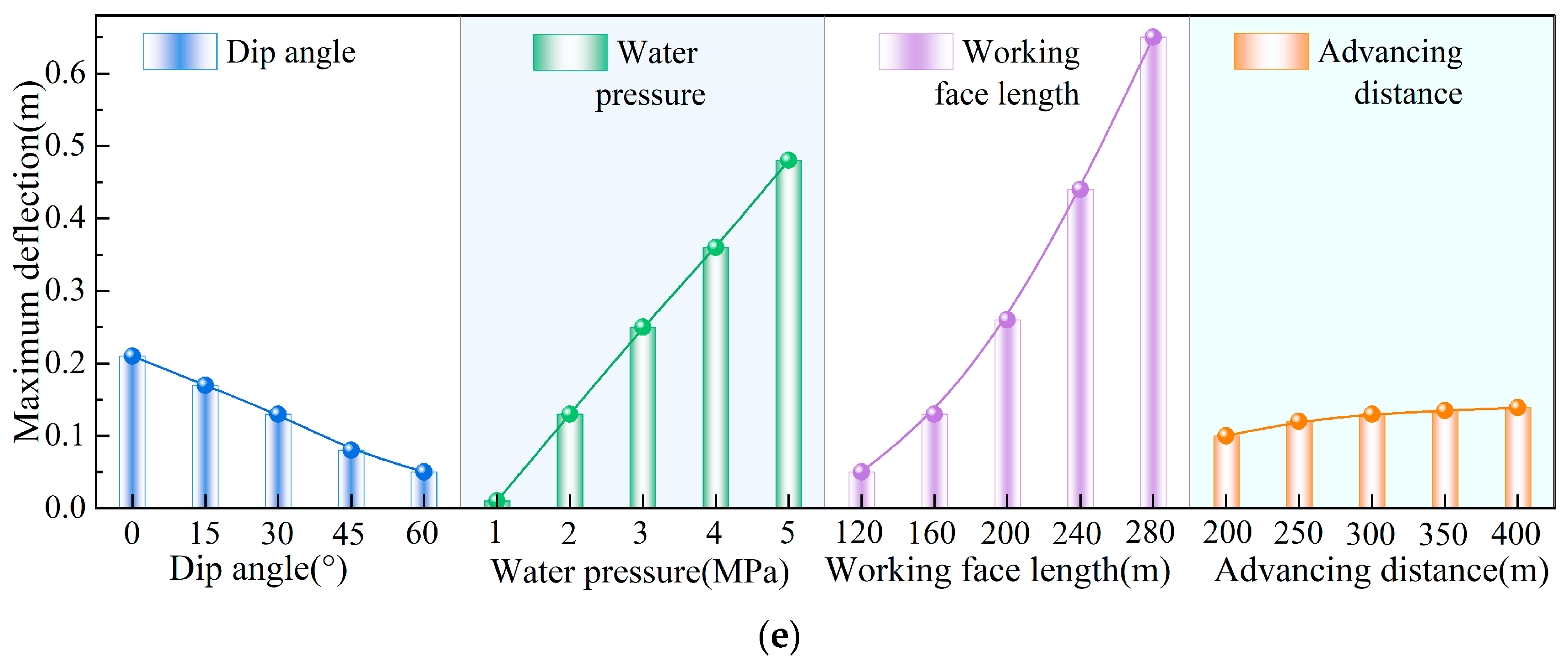
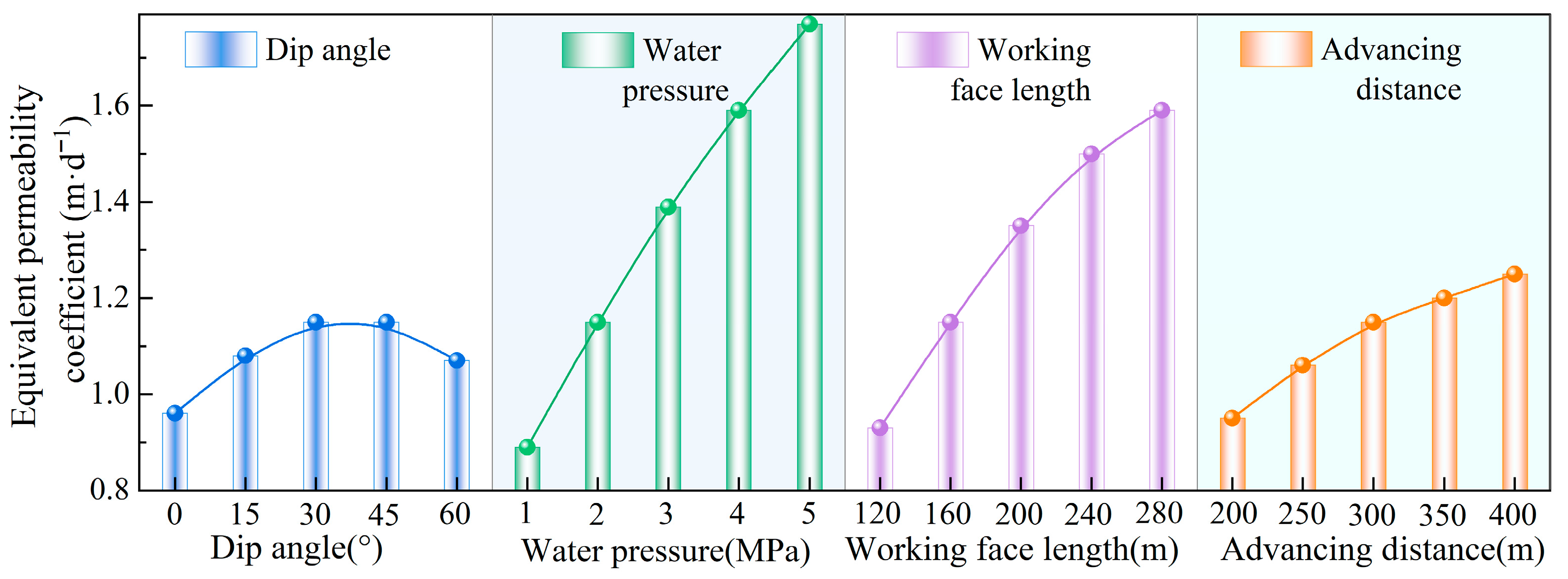
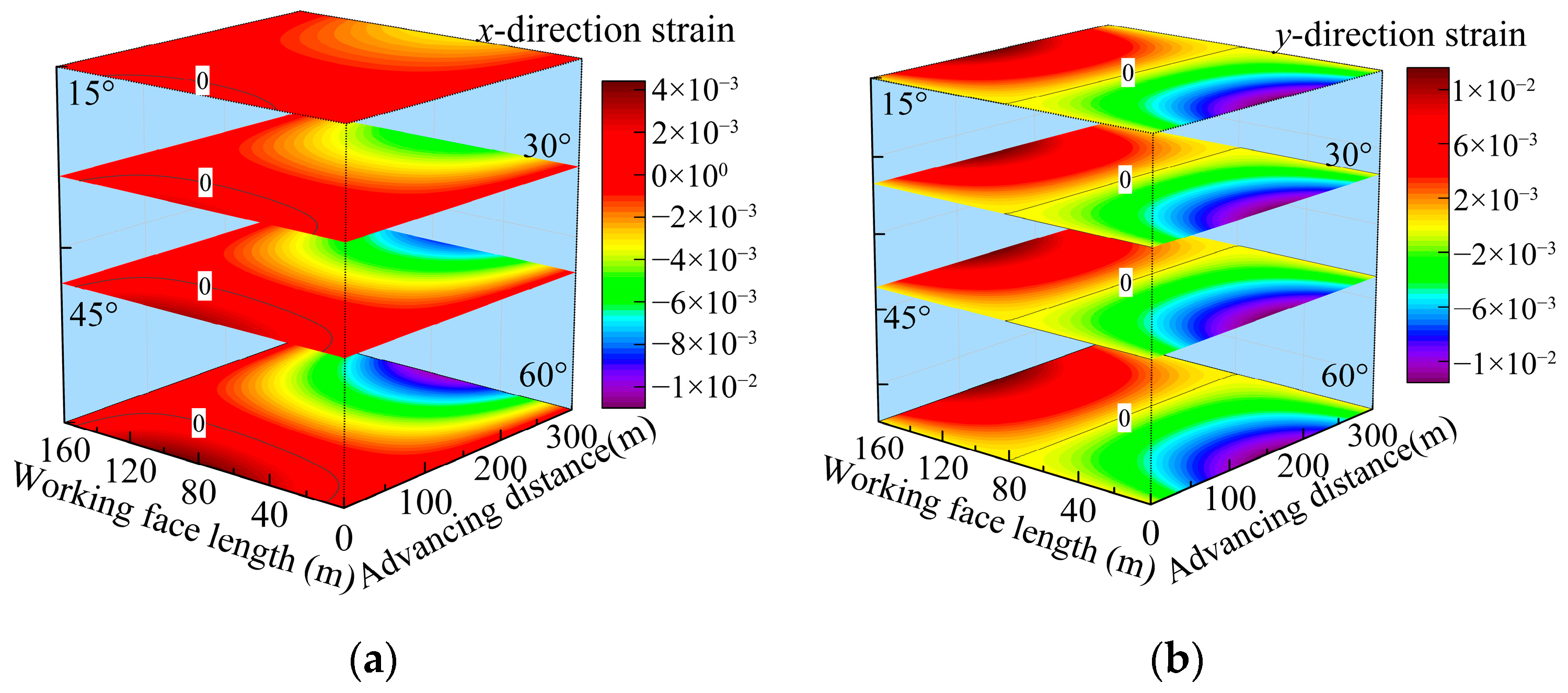
2.2. Influencing Factor Analysis of Equivalent Hydraulic Conductivity
2.3. Effect of Lithologic Assemblage on Equivalent Hydraulic Conductivity
3. Multi-Parameter Model for Equivalent Permeability and Feasibility Assessment of In Situ Protection of Confined Floor Water
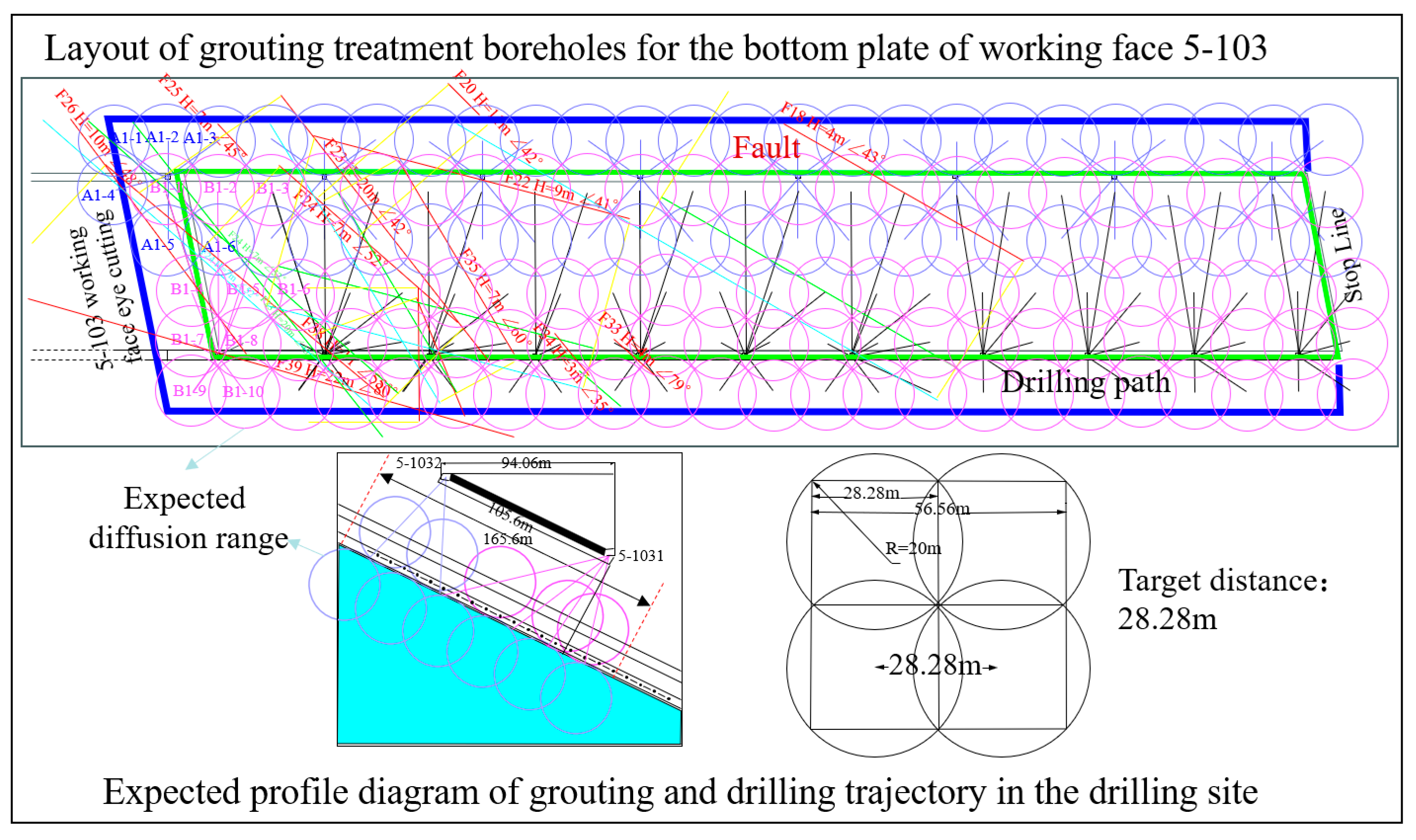
3.1. Engineering Background
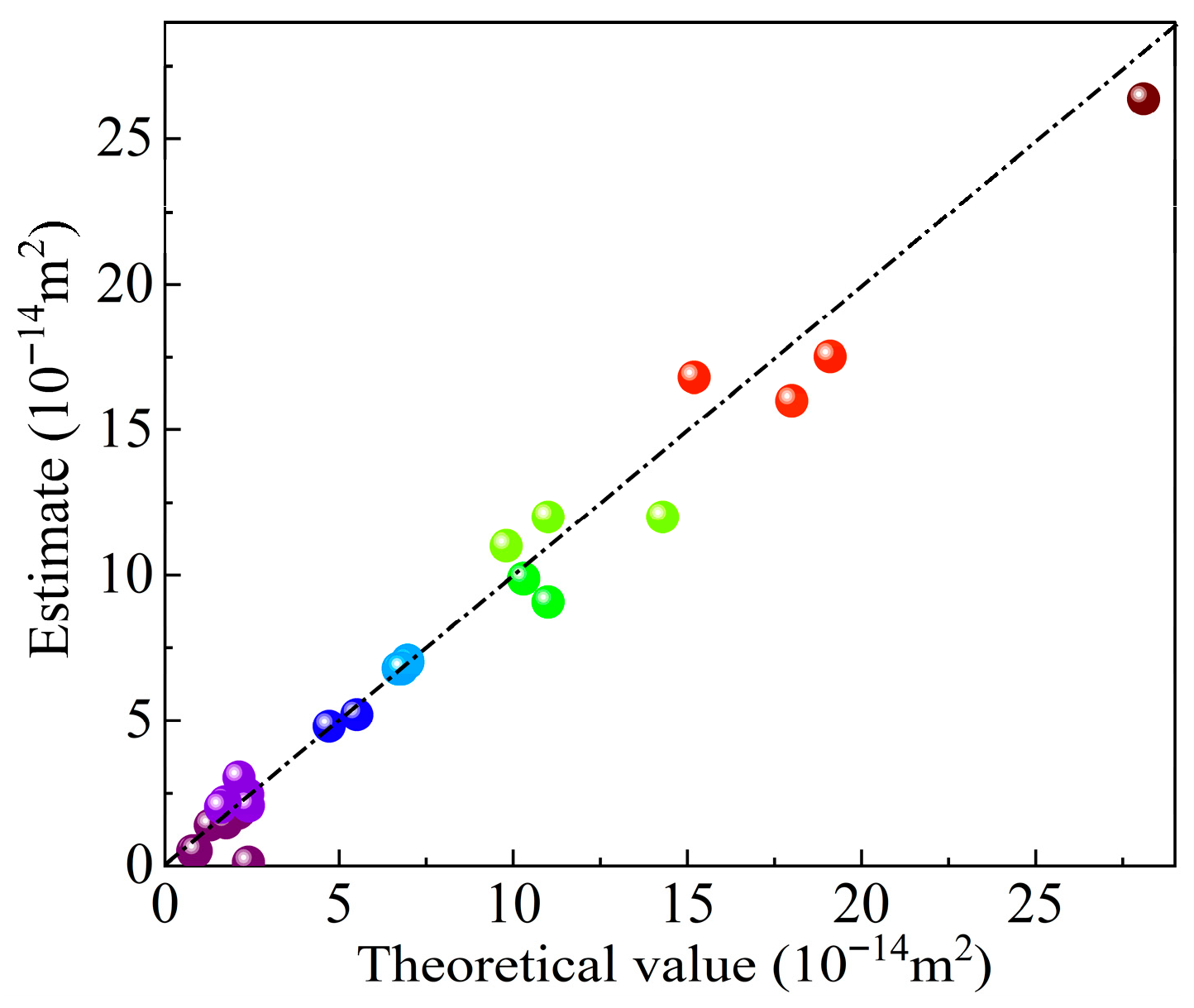
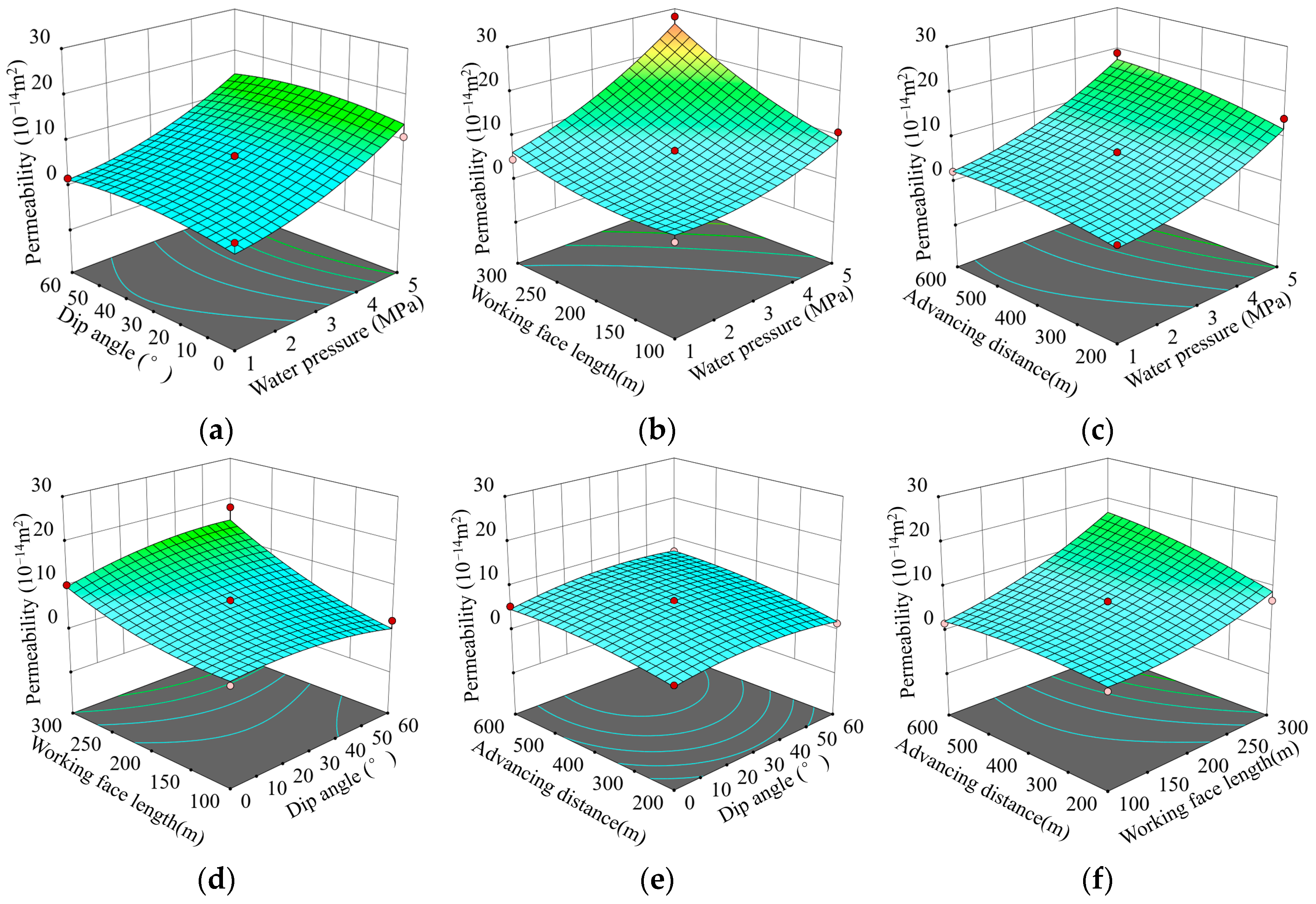
3.2. Response Surface Methodology (RSM)-Based Model for Floor Permeability
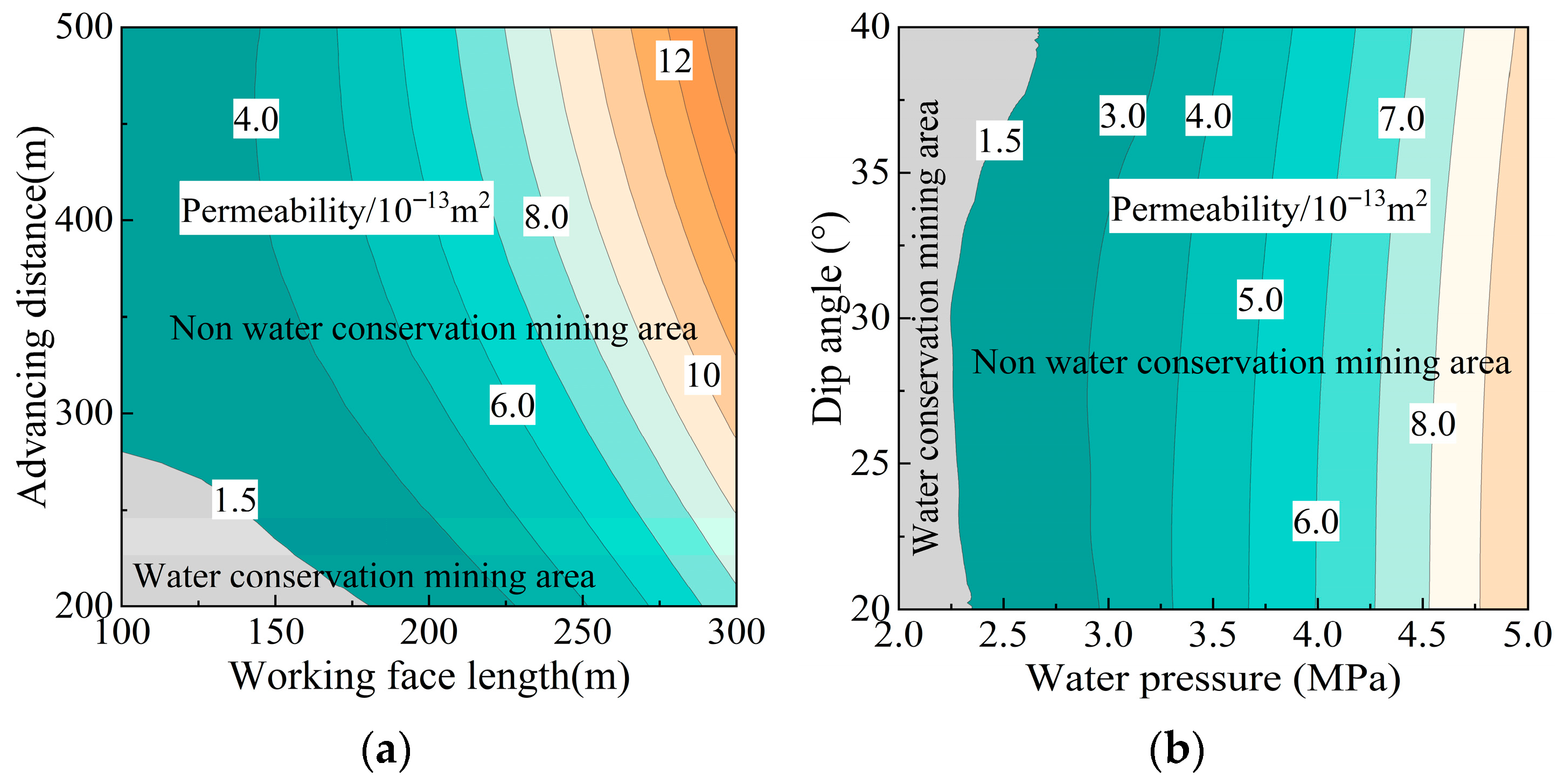
3.3. Multi-Factor Interaction Mechanism of Equivalent Permeability
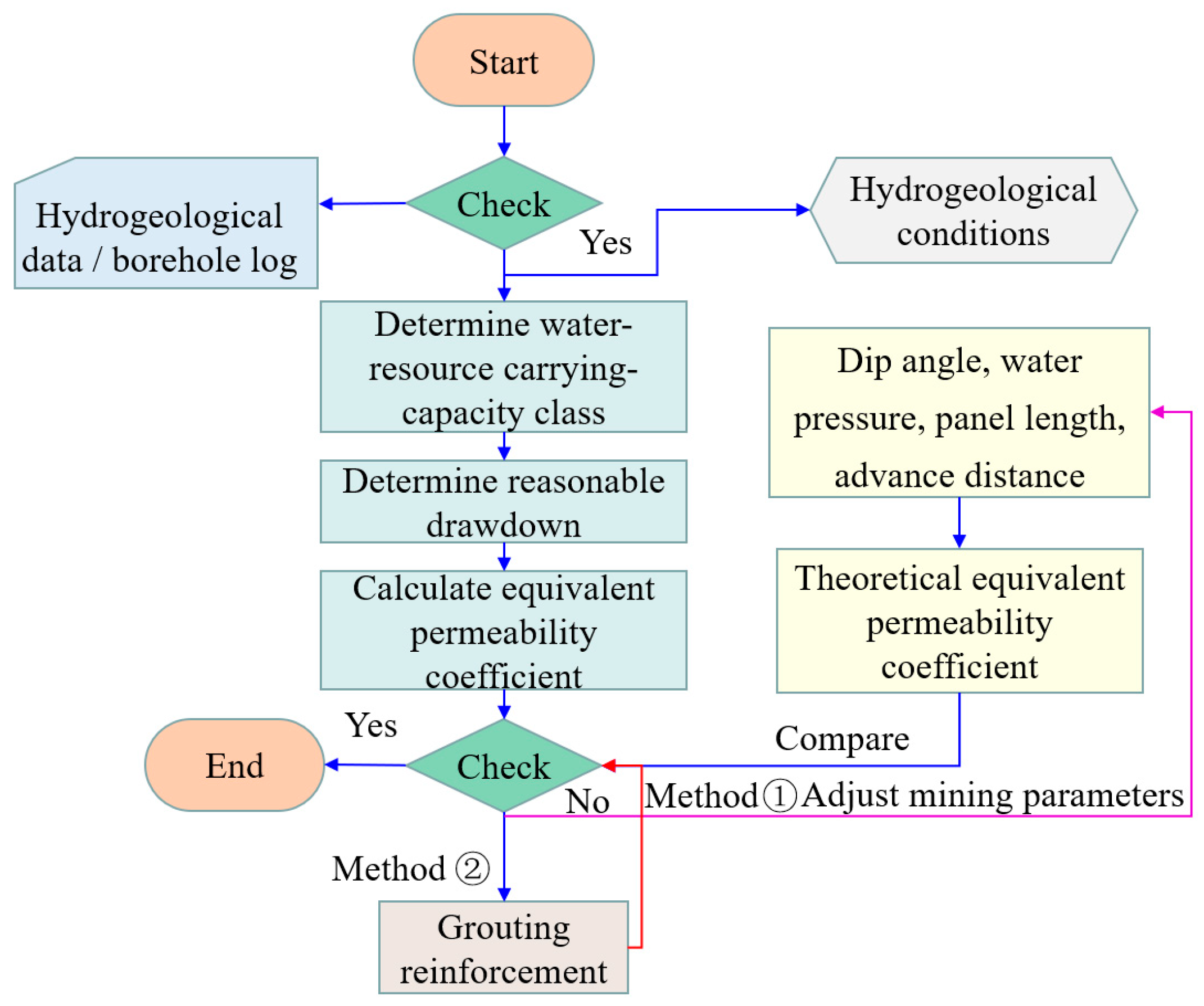
3.4. Decision Procedure for In Situ Protection of Floor Water
- (1)
- Scope and data collation. Target high-pressure confined aquifers. Compile hydrogeological data and borehole logs to judge both the protection value of the aquifer and the water-inrush risk during mining.
- (2)
- Carrying-capacity tiering. If the aquifer is worth protecting or the inrush risk is high, determine the mine’s allowable water-resource carrying-capacity class and the corresponding drawdown tier.
- (3)
- Permeability target. From the drawdown permeability relation, derive the required equivalent permeability ; alternatively, adopt a critical equivalent permeability as the threshold.
- (4)
- Theoretical . Using overburden conditions and hydrogeologic features, compute the theoretical equivalent permeability under its current dip angle, water pressure, panel length, and advance distance.
- (5)
- Gap analysis and control options. Compare the theory with the required . If theory required , apply one (or both) of the following: grouting reinforcement of the floor; design optimization (reduce panel length and/or adjust advance distance).
- (6)
- Iterate to compliance. Update parameters and recompute until both the equivalent permeability target and the carrying capacity requirement are satisfied; then proceed with normal panel extraction.
4. Control of Mining-Induced Permeability and Water-Preservation Performance
4.1. Scheme for Controlling Mining-Induced Floor Equivalent Permeability
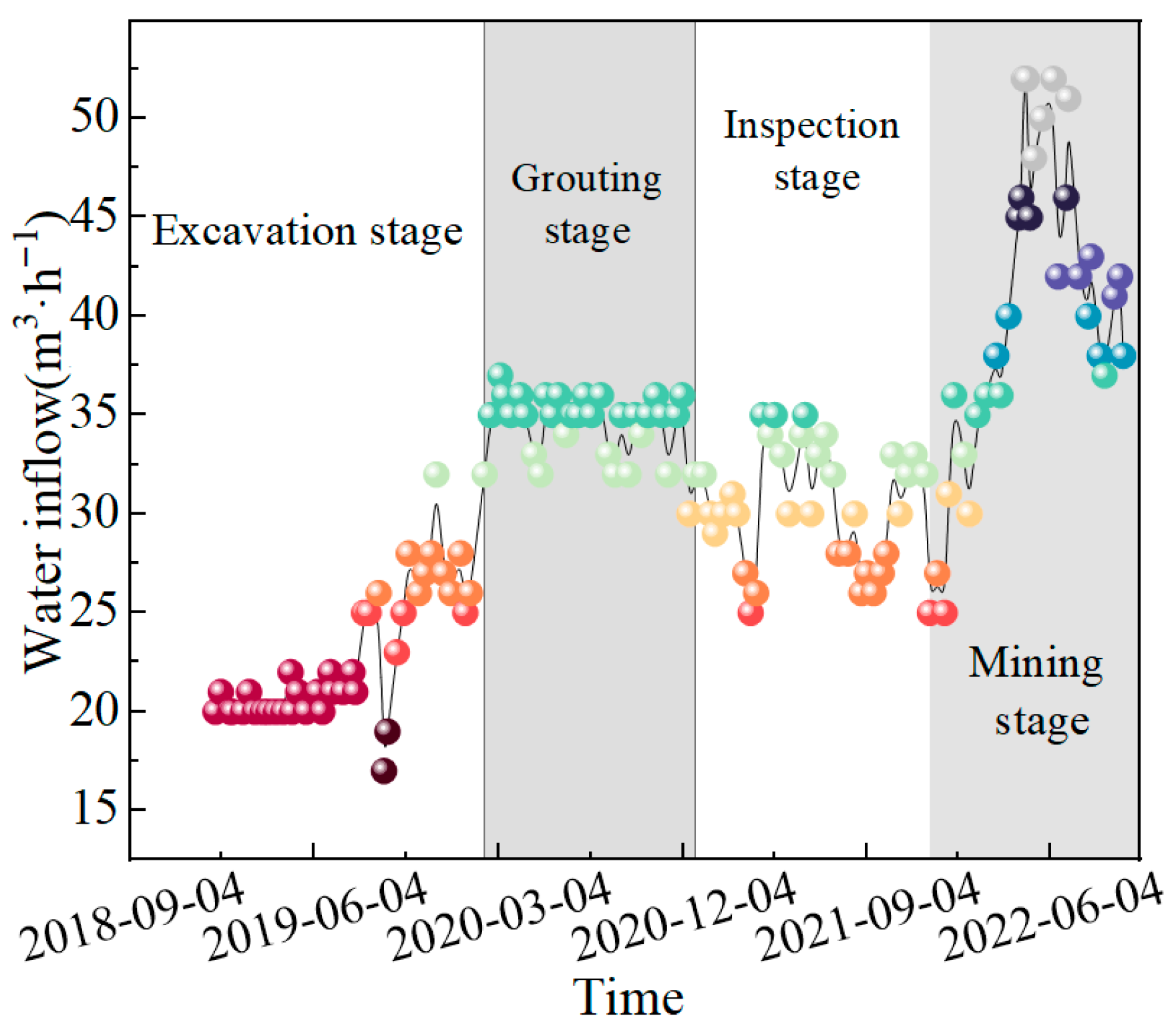
4.2. Working Face Inflow Variation Characteristics
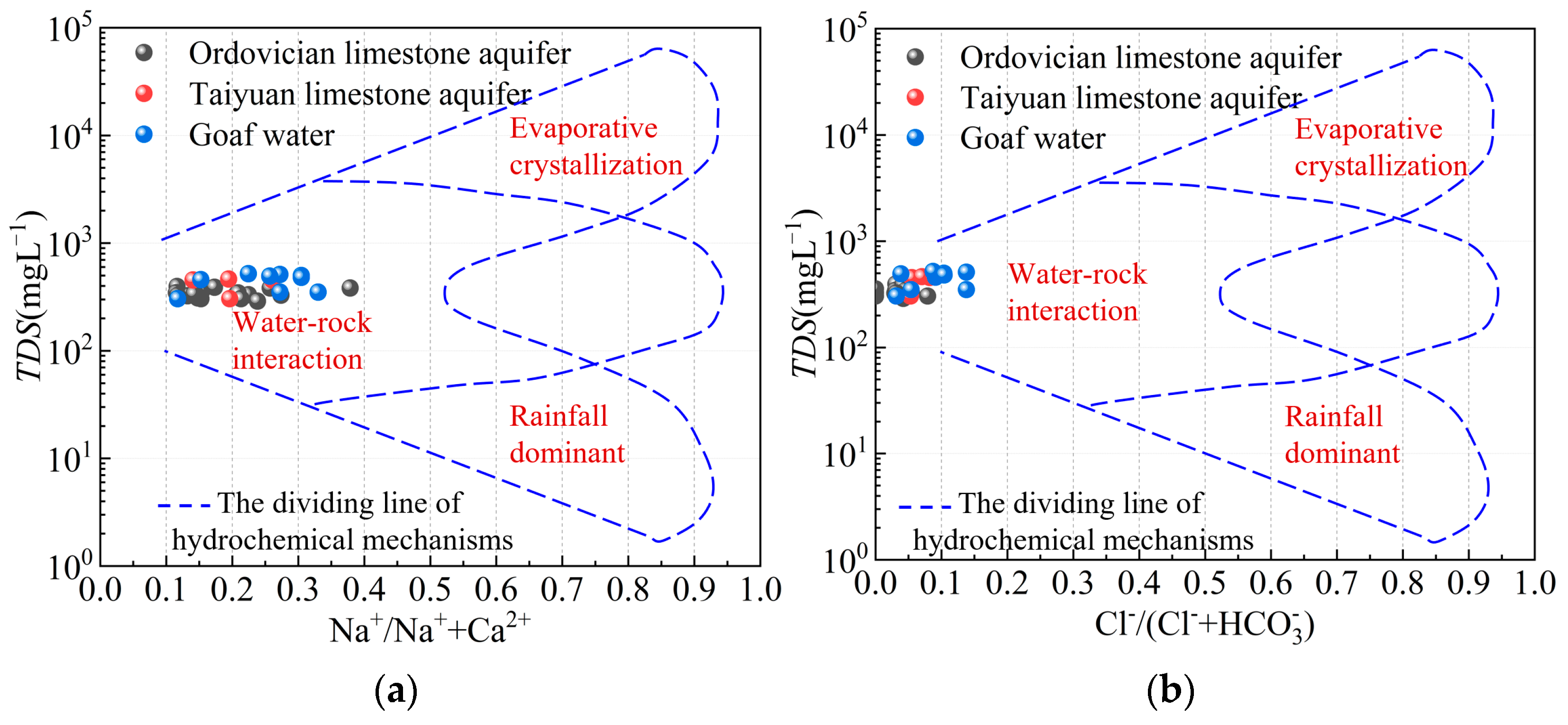
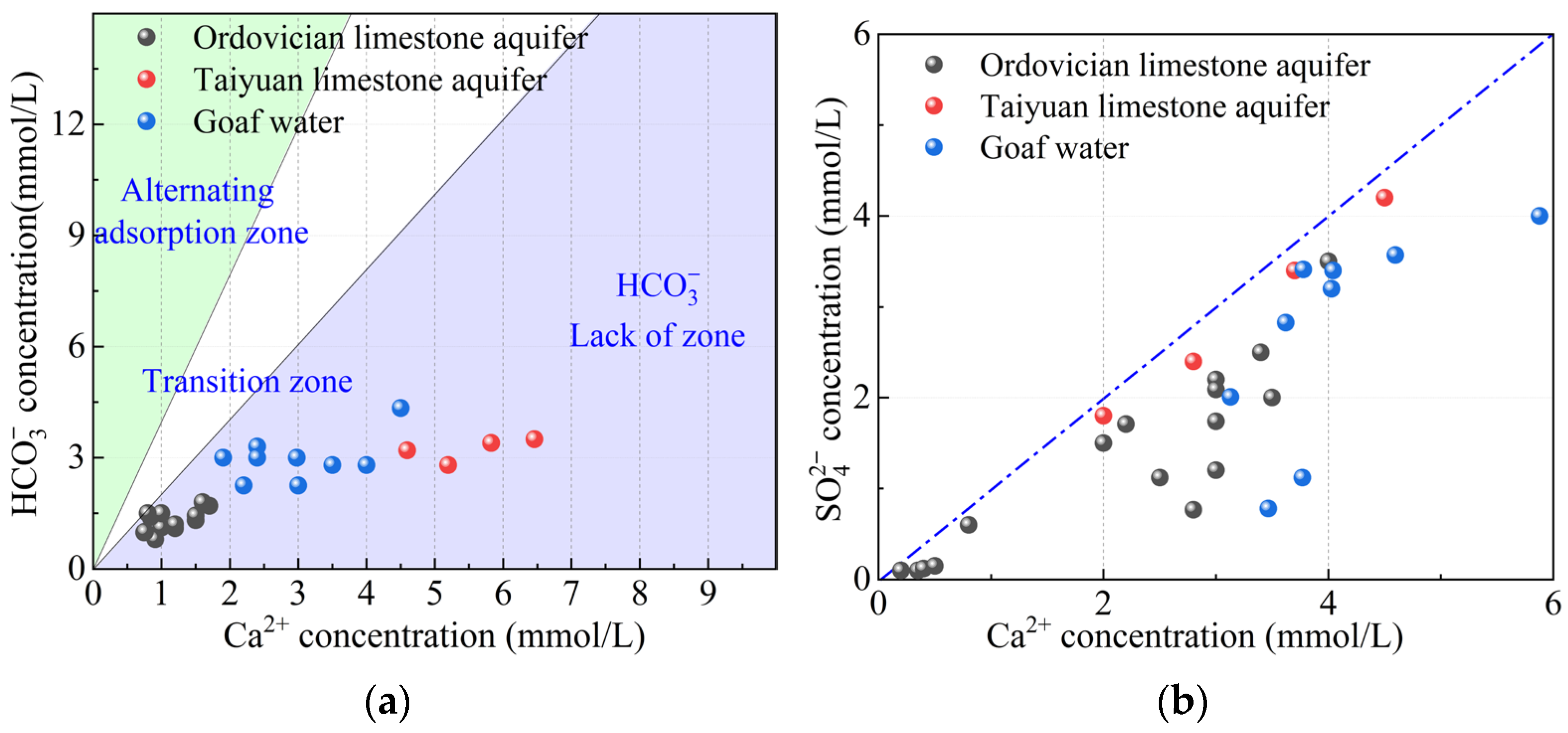
4.3. Water-Quality Characteristics and Inflow Sources
5. Discussion
6. Conclusions
- (1)
- The mining-induced floor equivalent permeability is inversely proportional to deflection and positively proportional to neutral plane strain. As the dip angle increases, the deflection of the floor aquiclude decreases approximately linearly, while the extreme value of neutral plane strain increases, revealing a shift in the dominant control on permeability between neutral plane strain and deflection with dip. The equivalent permeability first increases and then decreases with a turning point at 35°.
- (2)
- Lithologic assemblage affects the position of the neutral plane and the bending-stiffness matrix. A soft–hard interbedded floor effectively suppresses deformation and reduces equivalent permeability. Deflection at different locations contributes unevenly to equivalent permeability. For an inclined water-resistant key stratum, the hazard ranking of failure-prone zones for water inrush is as follows: lower end > upper end > coal wall position > rear of the goaf.
- (3)
- A quadratic multi-parameter coupling model of mining-induced floor equivalent permeability was constructed, identifying panel length and water pressure as the primary controls. The influence of dip angle on equivalent permeability becomes more pronounced when water pressure and panel length are larger.
- (4)
- Water–rock interaction is the main driver of hydrochemical ion evolution in the study area; dissolution/leaching dominates groundwater ion evolution. In the roof limestone aquifer, SO42− arises from gypsum dissolution and pyrite oxidation, and can serve, together with HCO3−, as a diagnostic ion for distinguishing aquifers.
- (5)
- The feasibility of in situ protection of floor water for Working Face 5-103 at the Fenyuan Coal Mine was determined: under the current mining parameters, the requirement is met only when water pressure < 2.2 MPa. After on-site grouting reinforcement to increase resistance, the working-face inflow stabilized at 40 m3/h, composed mainly of roof limestone water, indicating that the targeted high-pressure Ordovician floor aquifer was protected in situ.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| panel length (m) | advance distance (m) | ||
| coal seam dip angle (°) | extensional stiffness matrices (N/m) | ||
| undetermined coefficient | coupling stiffness matrices (N) | ||
| bending stiffness matrices (N·m) | isotropic bending stiffness (N·m) | ||
| the heights of the lower fractured zones (m) | the heights of upper fractured zones (m) | ||
| current permeability (m2) | initial permeability (m2) | ||
| volumetric strain | initial porosity | ||
| equivalent permeability of strata I (m2) | mining-induced equivalent permeability (m2) | ||
| deformation elements of length (m) | deformation elements of length i (m) | ||
| current permeabilities at an arbitrary point in the floor (m2) | initial permeabilities at an arbitrary point in the floor (m2) | ||
| mid-plane curvature in the x direction (m−1) | mid-plane curvature in the y direction (m−1) | ||
| mid-plane curvature in the xy direction (m−1) | the transformed reduced stiffness (Pa) | ||
| moment in the x direction (N·m) | moment in the y direction (N·m) | ||
| moment in the xy direction (N·m) | series orders | ||
| total thickness of the strata (m) | the thickness of a single layer | ||
| internal force per unit width in the x direction (N) | internal force per unit width in the y direction (N) | ||
| internal force per unit width in the xy direction (N) | series orders | ||
| water pressure at the upper end (Pa) | total number of floors | ||
| stress perpendicular to the laminate (Pa) | stress parallel to the laminate (Pa) | ||
| water pressure perpendicular to the laminate (Pa) | water pressure stress parallel to the laminate (Pa) | ||
| the unit weights of water (N/m3) | the unit weights of rock (N/m3) | ||
| Poisson’s ratio | total potential energy (J) | ||
| mid-surface strain in the x direction | mid-surface strain in the y direction | ||
| mid-surface strain in the xy direction | the deformation energy of the laminated plate | ||
| displacements in the x direction (m) | neutral plane displacements in the x direction (m) | ||
| displacements in the y direction (m) | neutral plane displacements in the y direction (m) | ||
| displacements in the z direction (m) | neutral plane displacements in the z direction (m) | ||
| work done by the transverse load (J) | work done by the longitudinal load (J) | ||
| layer k of the laminates | layer k-1 of the laminates | ||
| Acronyms | |||
| RSM | response surface method | ||
References
- Huang, L.; Xu, Y.; Liu, S.; Gai, Q.; Miao, W.; Li, Y.; Zhao, L. Research on the Development Law of Pre-Mining Microseisms and Risk Assessment of Floor Water Inrush: A Case Study of the Wutongzhuang Coal Mine in China. Sustainability 2022, 14, 9774. [Google Scholar] [CrossRef]
- Wang, P.; Jiang, Y.; Ren, Q. Roof Hydraulic Fracturing for Preventing Floor Water Inrush under Multi Aquifers and Mining Disturbance: A Case Study. Energies 2022, 15, 1187. [Google Scholar] [CrossRef]
- Li, Y.; Yin, H.; Dong, F.; Cheng, W.; Zhuang, N.; Xie, D.; Di, W. The key to green water-preserved mining: Prediction and integration of mining rock failure height by big data fusion simulation algorithm. Process. Saf. Environ. Prot. 2025, 193, 1015–1035. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, L.; Mu, W.; Liu, S.; Zhao, D. Water-inrush Risk through Fault Zones with Multiple Karst Aquifers Underlying the Coal Floor: A Case Study in the Liuzhuang Coal Mine, Southern China. Mine Water Environ. 2021, 40, 1037–1047. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, X.; Gai, Q.; Han, D.; He, M. An integrated method to prevent confined floor water inrush based on no pillar mining with pressure relief and grouting reinforcement. Geomech. Geophys. Geo-Energy Geo-Resour. 2025, 11, 85. [Google Scholar] [CrossRef]
- Li, Q.; Meng, X.; Liu, Y. Sensitivity analysis of water inrush evaluation model based on the theory of water resistant key strata: A case study in a coal mine, China. Earth Sci. Inform. 2022, 15, 2481–2494. [Google Scholar] [CrossRef]
- Liang, S.; Zhang, D.; Fan, G.; Kovalsky, E.; Fan, Z.; Zhang, L.; Han, X. Mechanical structure and seepage stability of confined floor response to longwall mining of inclined coal seam. J. Cent. South Univ. 2023, 30, 2948–2965. [Google Scholar] [CrossRef]
- Zhang, Y.; Cui, B.; Wang, Y.; Zhang, S.; Feng, G.; Zhang, Z. Evolution Law of Shallow Water in Multi-Face Mining Based on Partition Characteristics of Catastrophe Theory. Fractal Fract. 2023, 7, 779. [Google Scholar] [CrossRef]
- Dong, S.; Wang, H.; Guo, X.; Zhou, Z. Characteristics of Water Hazards in China’s Coal Mines: A Review. Mine Water Environ. 2021, 40, 325–333. [Google Scholar] [CrossRef]
- Cao, M.; Yin, S.; Lian, H.; Wang, X.; Wang, G.; Li, S.; Li, Q.; Xu, W. Failure Mechanism and Risk Evaluation of Water Inrush in Floor of Extra-Thick Coal Seam. Water 2025, 17, 743. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, S.; Wang, H.; Wang, X.; Nan, S.; Liu, D. Macroscopic and mesoscopic development characteristics of the top strata of Middle Ordovician limestone in the Hanxing mining area. Environ. Earth Sci. 2021, 80, 526. [Google Scholar] [CrossRef]
- Li, J.; Xu, Y. Estimation of Aperture and Stiffness of Fractures under High Water Pressure Using Hydrological Data and Slurry Consolidating Body. Geofluids 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, D.; Wu, Q.; Cui, Y.; Liu, Z. Mechanism of Instantaneous High-Strength Sand—Water Inrush in Steeply Inclined Mining of Soft Coal Seam under Disturbed Rock—Soil Overburden. Lithosphere 2024, 2024, 3. [Google Scholar] [CrossRef]
- Ran, Q.; Liang, Y.; Ye, C.; Ning, Y.; Ma, T.; Kong, F. Failure analysis of overlying strata during inclined coal seam mining: Insights from acoustic emission monitoring. Eng. Fail. Anal. 2025, 182, 110023. [Google Scholar] [CrossRef]
- Eremin, M.; Peryshkin, A.; Esterhuizen, G.; Pavlova, L.; Fryanov, V. Numerical Analysis of Pillar Stability in Longwall Mining of Two Adjacent Panels of an Inclined Coal Seam. Appl. Sci. 2022, 12, 11028. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, H.; Shu, C.; Chu, T. Study on the pressure relief effect in gob-side coal body during mining an inclined longwall panel. Energy Sci. Eng. 2021, 9, 1530–1542. [Google Scholar] [CrossRef]
- He, J.; Li, W.; Qiao, W. P-H-q evaluation system for risk assessment of water inrush in underground mining in North China coal field, based on rock-breaking theory and water-pressure transmission theory. Geomat. Nat. Hazards Risk 2018, 9, 524–543. [Google Scholar] [CrossRef]
- Wei, M.; Zhu, Y.; Wang, P.; Luo, Y.; Ren, H.; Li, P. Failure characteristics and stress field distribution law of roadway in downward mining of deep close distance coal seam. Sci. Rep. 2024, 14, 28735. [Google Scholar] [CrossRef]
- Liang, Z.; Song, W.; Liu, W. Theoretical models for simulating the failure range and stability of inclined floor strata induced by mining and water pressure. Int. J. Rock Mech. Min. Sci. 2020, 132, 104382. [Google Scholar] [CrossRef]
- Liang, Z.; Song, W. Theoretical and Numerical Investigations of the Failure Characteristics of a Faulted Coal Mine Floor Above a Confined Aquifer. Mine Water Environ. 2021, 40, 456–465. [Google Scholar] [CrossRef]
- Shang, Y.; Wang, Y.; Zhang, L.; Wu, G.; Kong, D.; Zhang, P.; Jia, T. Impact of Lower Protective Coal Seam Mining on Overlying Strata: Deformation, Pressure Relief, and Permeability Enhancement. Int. J. Geomech. 2024, 24, 9. [Google Scholar] [CrossRef]
- Zhang, D.; Fan, G.; Liu, Y.; Ma, L. Field trials of aquifer protection in longwall mining of shallow coal seams in China. Int. J. Rock Mech. Min. Sci. 2010, 47, 908–914. [Google Scholar] [CrossRef]
- Gong, X.; Xue, S.; Han, B.; Zheng, C.; Zhu, L.; Dong, Y.; Li, Y. Research Progress on Stress–Fracture–Seepage Characteristics for Hazard Prevention in Mine Goafs: A Review. Sustainability 2022, 14, 12107. [Google Scholar] [CrossRef]
- Zhang, C.; Tu, S.; Zhang, L. Field Measurements of Compaction Seepage Characteristics in Longwall Mining Goaf. Nat. Resour. Res. 2020, 29, 905–917. [Google Scholar] [CrossRef]
- Lu, S.; Li, M.; Ma, Y.; Wang, S.; Zhao, W. Permeability changes in mining-damaged coal: A review of mathematical models. J. Nat. Gas Sci. Eng. 2022, 106, 104739. [Google Scholar] [CrossRef]
- Zhou, H.W.; Zhao, J.W.; Su, T.; Zhang, L.; Zhong, J.C.; Liu, Z.L. Characterization of gas flow in backfill mining-induced coal seam using a fractional derivative-based permeability model. Int. J. Rock Mech. Min. Sci. 2021, 138, 104571. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, M. Characterization of water bursting and discharge into underground mines with multilayered groundwater flow systems in the North China coal basin. Hydrogeol. J. 2006, 14, 882–893. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, Y.; Li, J.; Li, K.; Cao, X. Water and Sand Inrush During Mining Under Thick Unconsolidated Layers and Thin Bedrock in the Zhaogu No. 1 Coal Mine, China. Mine Water Environ. 2018, 37, 336–345. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, X.; Jiang, N.; Yin, L.; Guo, W. Porosity zoning characteristics of fault floor under fluid-solid coupling. Bull. Eng. Geol. Environ. 2020, 79, 2529–2541. [Google Scholar] [CrossRef]
- Wu, Y.; Tang, Y.; Xie, P.; Hu, B.; Lang, D.; Wang, H. Stability analysis of ‘roof-coal pillar’ structure in longwall multi-section mining of steeply dipping coal seam. Geomat. Nat. Hazards Risk 2024, 15, 2359998. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.; Liu, X.; Sun, Y.; Yang, Z.; Zhong, Y. Rule Study on the Risk of Floor Water Inrush Based on the Plate Model Theory. Sustainability 2023, 15, 7844. [Google Scholar] [CrossRef]
- Li, Y.; Tai, Y.; Yu, B.; Kuang, T.; Gao, R.; Liu, J. Evolution and control technology of energy aggregation and dissipation of a high hard roof during breakage and destabilization. Int. J. Fract. 2024, 245, 1–23. [Google Scholar] [CrossRef]
- Sun, J.; Wang, L.; Zhao, G. Stress Distribution and Failure Characteristics for Workface Floor of a Tilted Coal Seam. KSCE J. Civ. Eng. 2019, 23, 3793–3806. [Google Scholar] [CrossRef]
- Zhao, D.; Wu, Q.; Cui, F.; Xu, H.; Zeng, Y.; Cao, Y.; Du, Y. Using random forest for the risk assessment of coal-floor water inrush in Panjiayao Coal Mine, northern China. Hydrogeol. J. 2018, 26, 2327–2340. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, Y.; Wang, A.; Chang, Z.; Zhang, J.; Wang, Z. Investigation of the mode-I delamination behavior of Double-Double laminate carbon fiber reinforced composite. Compos. Sci. Technol. 2024, 248, 110463. [Google Scholar] [CrossRef]
- Yang, S.; Song, G.; Yang, J. An analytical solution for the geometric broken characteristics of the overlying strata and its physical modeling study in longwall coal mining. Arab. J. Geosci. 2020, 13, 139. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, G.; Zhang, D.; Zhang, L.; Zhang, S.; Liang, S.; Yu, W. Optimal injection timing and gas mixture proportion for enhancing coalbed methane recovery. Energy 2021, 222, 119880. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, G.; Zhang, D. Permeability and Energy Evolution Characteristics of Heterogeneous Coal and Rock Mass. Nat. Resour. Res. 2021, 30, 4493–4514. [Google Scholar] [CrossRef]
- Peng, X.; Qi, L.; Wang, Z.; Zhou, X.; Hua, C. Study on Overburden Movement Deformation and Roof Breakage Law of Under-Protective Steeply Inclined Coal Seam Mining. Sustainability 2022, 14, 10068. [Google Scholar] [CrossRef]
- Cong, R.; Yang, R.; Gong, Y.; Li, G.; Huang, Z.; Zhang, B. Numerical investigation of mechanical responses and failure features of coal measure strata using combined finite-discrete element method. Comput. Geotech. 2024, 171, 106346. [Google Scholar] [CrossRef]
- Zhang, D.; Fan, G.; Zhang, S.; Ma, L.; Wang, X. Equivalent water-resisting overburden thickness forwater-conservation mining: Conception, method and application. J. China Coal Soc. 2022, 47, 128–136. [Google Scholar]
- Chi, M.; Zhang, D.; Zhao, Q.; Yu, W.; Liang, S. Determining the scale of coal mining in an ecologically fragile mining area under the constraint of water resources carrying capacity. J. Environ. Manag. 2021, 279, 111621. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Zhang, X.; Ke, F.; Liu, J.; Yao, Q.; Luo, H.; Li, X.; Xu, Y. Evolution of Overlying Strata Bed Separation and Water Inrush Hazard Assessment in Fully Mechanized Longwall Top-Coal Caving of an Ultra-Thick Coal Seam. Water 2025, 17, 850. [Google Scholar] [CrossRef]
- Zhou, K.; Dou, L.; Kan, J.; Yang, K.; Li, J.; Ma, X. Coal burst mechanism in large-scale panel under extra-thick key strata. Geomat. Nat. Hazards Risk 2024, 15, 2347420. [Google Scholar] [CrossRef]
- Fan, G.; Fan, Z.; Zhang, D.; Zhang, S. Rock strength and permeability under compression shear coupling corresponding to different loading angles. J. China Coal Soc. 2024, 49, 3090–3101. (In Chinese) [Google Scholar]

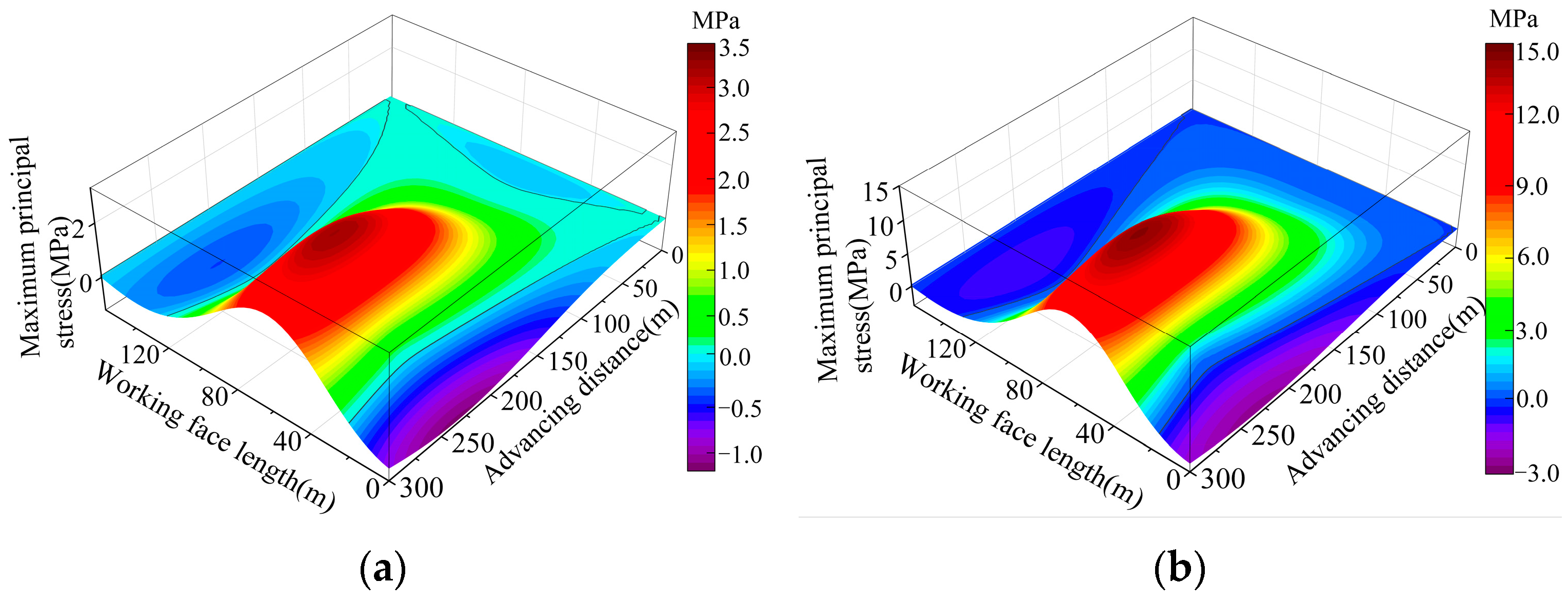
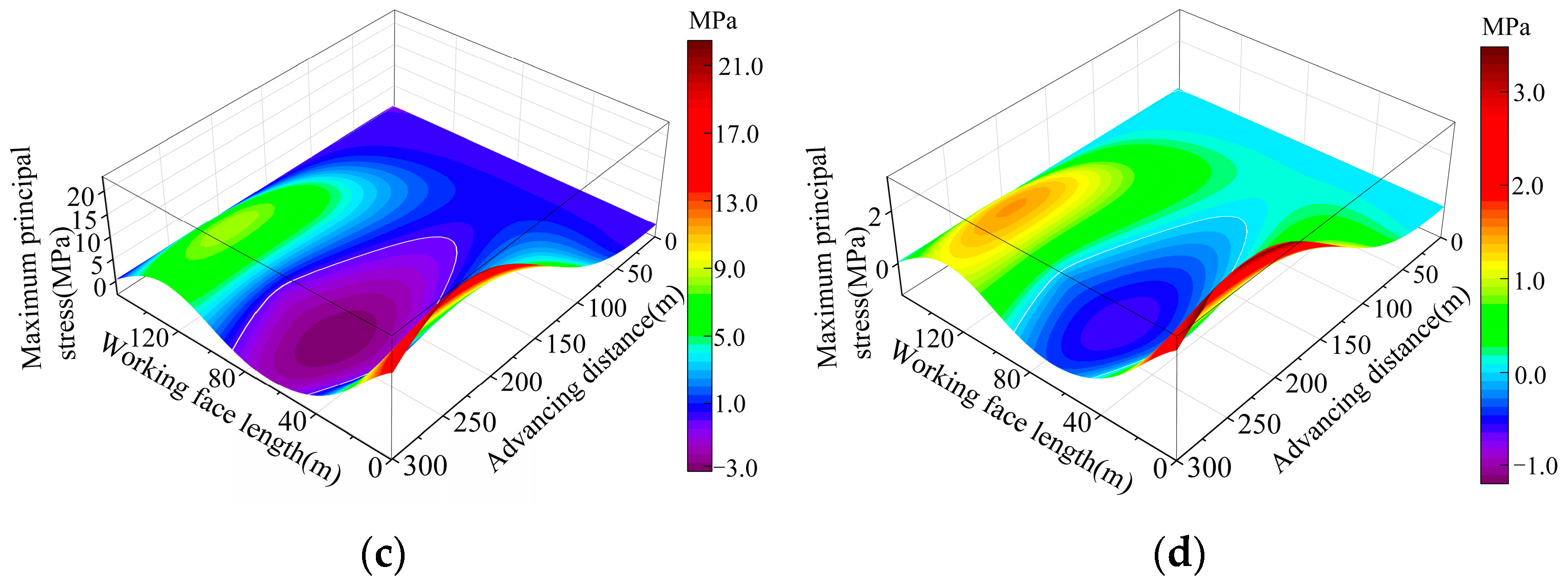
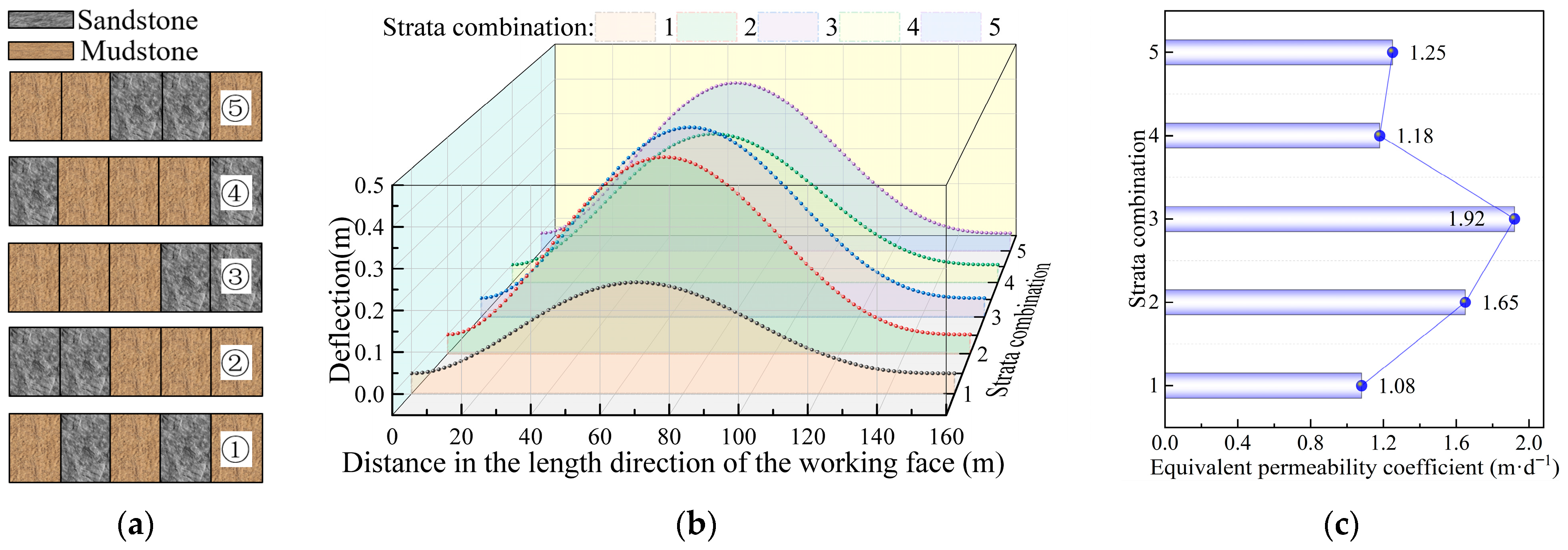
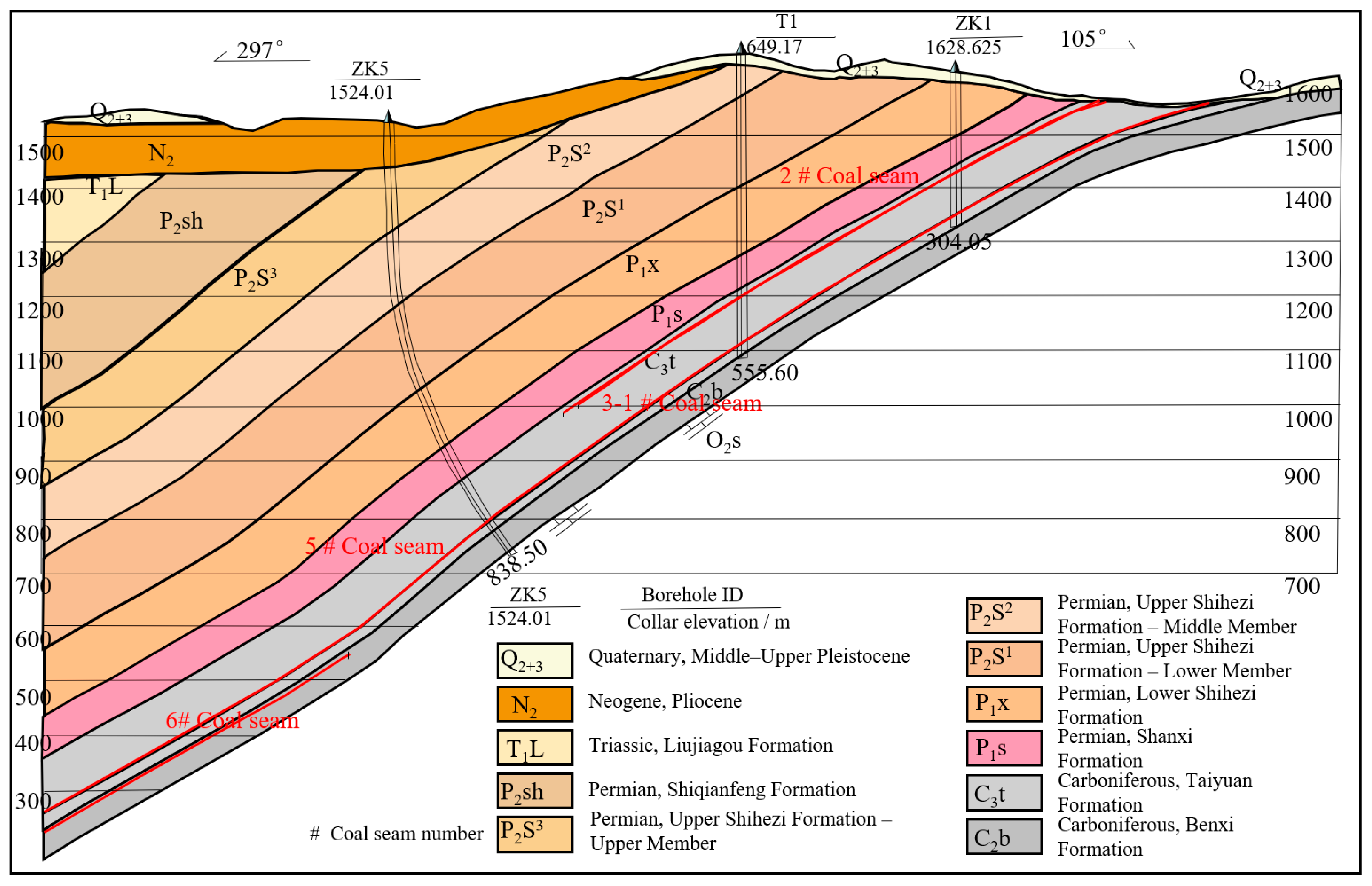

| Research Subjects | Theories | Assumption | Displacement Boundary Condition | Stress Boundary Condition | References |
|---|---|---|---|---|---|
| Horizontal coal seam | Elastic thin plate theory | Isotropic | Four-sided fixed | Uniform distribution of stress and water pressure | [2] |
| Inclined coal seam | Elastic thin plate theory | Isotropic | Four-sided fixed | Top stress uniform distribution; non-uniform water pressure distribution at the bottom | [6] |
| Inclined coal seam | Laminate theory | Isotropic | Four-sided fixed | Moving toward uniformity and tending toward non-uniformity; water pressure is perpendicular to the floor | [7] |
| Horizontal coal seam | Beam theory | Isotropic | Four-sided fixed | Uniform distribution of stress and water pressure | [17] |
| Horizontal coal seam | Elastic semi-infinite theory | Isotropic | / | Top stress uniform distribution | [18] |
| Inclined coal seam | Elastic half-space theory | Isotropic | / | Top stress uniform distribution; non-uniform water pressure distribution at the bottom | [19] |
| Horizontal coal seam | Limit equilibrium theory | Isotropic | / | Top stress uniform distribution | [20] |
| Inclined coal seam (proposed) | Laminate theory | Isotropic within the layer | Four-sided fixed | Uniform distribution of stress and water pressure | / |
| Thickness/m | Lithology | Elastic Modulus/GPa | Poisson’s Ratio | Porosity/% | Permeability /10−14 m2 |
|---|---|---|---|---|---|
| 3 | Mudstone | 1 | 0.25 | 1.5 | 2 |
| 5 | Sandstone | 2 | 0.20 | 2.5 | 10 |
| 11 | Mudstone | 1 | 0.25 | 1.5 | 2 |
| 3 | Sandstone | 2 | 0.20 | 2.5 | 10 |
| 2 | Mudstone | 1 | 0.25 | 1.5 | 2 |
| 3 | Limestone | 4 | 0.20 | 3.5 | 30 |
| 5 | Sandstone | 2 | 0.20 | 2.5 | 10 |
| 3 | Mudstone | 1 | 0.25 | 1.5 | 2 |
| 5 | Sandstone | 2 | 0.20 | 2.5 | 10 |
| 3 | Mudstone | 1 | 0.25 | 1.5 | 2 |
| 2 | Sandstone | 2 | 0.20 | 2.5 | 10 |
| 9 | Mudstone | 1 | 0.25 | 1.5 | 2 |
| Standard Order | Water Pressure/MPa | Dip Angle /° | Working Face Length/m | Advancing Distance/m | Permeability /10−14 m2 |
|---|---|---|---|---|---|
| 5 | 3 | 30 | 100 | 200 | 1.05 |
| 27 | 3 | 30 | 200 | 400 | 6.70 |
| 19 | 1 | 30 | 300 | 400 | 4.72 |
| 23 | 3 | 0 | 200 | 600 | 5.51 |
| 20 | 5 | 30 | 300 | 400 | 41.10 |
| 14 | 3 | 60 | 100 | 400 | 1.05 |
| 24 | 3 | 60 | 200 | 600 | 6.97 |
| 15 | 3 | 0 | 300 | 400 | 10.30 |
| 8 | 3 | 30 | 300 | 600 | 15.20 |
| 12 | 5 | 30 | 200 | 600 | 19.10 |
| 16 | 3 | 60 | 300 | 400 | 18.00 |
| 10 | 5 | 30 | 200 | 200 | 4.29 |
| 11 | 1 | 30 | 200 | 600 | 2.38 |
| 13 | 3 | 0 | 100 | 400 | 1.13 |
| 17 | 1 | 30 | 100 | 400 | 0.60 |
| 1 | 1 | 0 | 200 | 400 | 0.86 |
| 3 | 1 | 60 | 200 | 400 | 1.76 |
| 2 | 5 | 0 | 200 | 400 | 11.00 |
| 28 | 3 | 30 | 200 | 400 | 6.80 |
| 9 | 1 | 30 | 200 | 200 | 0.80 |
| 21 | 3 | 0 | 200 | 200 | 1.87 |
| 7 | 3 | 30 | 100 | 600 | 1.53 |
| 22 | 3 | 60 | 200 | 200 | 1.60 |
| 4 | 5 | 60 | 200 | 400 | 9.80 |
| 29 | 3 | 30 | 200 | 400 | 6.80 |
| 6 | 3 | 30 | 300 | 200 | 1.98 |
| 25 | 3 | 30 | 200 | 400 | 6.80 |
| 18 | 5 | 30 | 100 | 400 | 2.40 |
| 26 | 3 | 30 | 200 | 400 | 6.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Fan, G.; Zhang, D.; Luo, T.; Yang, C.; Gao, X.; Kong, Z. Mining-Induced Permeability Evolution of Inclined Floor Strata and In Situ Protection of Confined Aquifers. Sustainability 2025, 17, 10273. https://doi.org/10.3390/su172210273
Fan Z, Fan G, Zhang D, Luo T, Yang C, Gao X, Kong Z. Mining-Induced Permeability Evolution of Inclined Floor Strata and In Situ Protection of Confined Aquifers. Sustainability. 2025; 17(22):10273. https://doi.org/10.3390/su172210273
Chicago/Turabian StyleFan, Zhanglei, Gangwei Fan, Dongsheng Zhang, Tao Luo, Congxin Yang, Xinyao Gao, and Zihan Kong. 2025. "Mining-Induced Permeability Evolution of Inclined Floor Strata and In Situ Protection of Confined Aquifers" Sustainability 17, no. 22: 10273. https://doi.org/10.3390/su172210273
APA StyleFan, Z., Fan, G., Zhang, D., Luo, T., Yang, C., Gao, X., & Kong, Z. (2025). Mining-Induced Permeability Evolution of Inclined Floor Strata and In Situ Protection of Confined Aquifers. Sustainability, 17(22), 10273. https://doi.org/10.3390/su172210273








