A Novel Hybrid Framework for Short-Term Carbon Emissions Forecasting in China: Aggregate and Sectoral Perspectives

Abstract

Accurate forecasting of carbon emissions is not only essential for addressing the challenges of climate governance but also provides timely support for dynamic carbon quota adjustments and emergency emission reduction decisions. In this study, we take China’s daily carbon emission data from 2021 to 2024 as the research objects and propose a novel forecasting framework called STL-wLSTM-SVR based on seasonal-trend decomposition with Loess (STL), long short-term memory network (LSTM) and support vector regression (SVR). First, the original carbon emission sequence is decomposed via STL into seasonal, trend and residual components. Subsequently, LSTM is employed to predict the seasonal and trend components with hyper-parameters optimized by whale optimization algorithm (WOA), and SVR is used to predict the residual component with parameters optimized through grid search method. Then, the final results are obtained by accumulating the forecasted values of the three subsequences. The experimental results illustrate that the STL-wLSTM-SVR model achieved a high-precision forecast for China’s total daily carbon emissions (RMSE of 0.1129, MAPE of 0.28%, MAE of 0.0851) and demonstrated remarkable adaptability for five major sectors—from navigating the high volatility of ground transport (MAPE of 0.36%) to effectively handling the dramatic post-pandemic structural break in aviation (MAPE of 0.72%). These findings assess the effectiveness of the hybrid forecasting framework and provide a valuable methodological reference for similar prediction tasks, such as sector-specific pollutant emissions and regional energy consumption.

1. Introduction

Climate change has emerged as a central issue in the discourse surrounding global sustainability and future well-being, exerting profound impacts on ecosystems, climate systems, as well as socio-economic structures. Thomas et al. [1] estimated that by 2050, around 37% of species could be at risk of extinction under mid-range warming scenarios, which highlights the critical need to curb greenhouse gas emissions. As Solomon et al. [2] demonstrated, the effects of elevated atmospheric CO₂ are largely irreversible on a millennial scale, with persistent sea-level rise and long-term reductions in dry-season rainfall continuing for centuries, even if emissions cease. Economic studies, such as that by Tol [3], reveal that while the early climate change may yield marginal benefits, long-term impact will disproportionately harm vulnerable economies and ecosystems, underscoring the urgency of carbon emission management.

Many studies have explored the influencing factors behind carbon emissions across regions and sectors. In this direction, Gonz’alez and Mart’inez [4] utilized decomposition analysis to examine CO₂ drivers in Mexico’s industrial sector from 1965 to 2003, indicating that industrial activity, structure and fuel mix significantly contributed to emissions growth, while energy intensity mitigated it. Loo and Li [5] used trend analysis and decomposition to analyze carbon emissions from passenger transport in China, suggesting that road transportation is the primary emitter, with income growth as the dominant influencing factor. In addition, multiple linear regression has been used to examine energy-related carbon emissions in Turkey from 1971 to 2010, identifying population growth and fossil fuel consumption as the main driving forces [6].

Energy consumption forecasting has emerged as a critical topic in global sustainable development, serving an essential role in mitigating climate change, guiding policy decisions and optimizing energy systems. Traditional statistical forecasting approaches typically rely on historical data for model construction [7]. The advantages of such models lie in their simplicity and ease of implementation. Integrating regression models with artificial neural networks, Kialashaki and Reisel [8] developed a new method for predicting residential energy demand in the United States. Xie et al. [9] proposed an effective forecasting method for China’s energy production and consumption over the period 2006–2020 by combining a grey forecasting model with the Markov approach and optimization techniques. Yuan et al. [10] developed a hybrid forecasting framework for China’s primary energy consumption that combines the autoregressive integrated moving average (ARIMA) model with grey relational analysis, achieving superior performance compared with baseline models.

Although these statistical models offer high computational efficiency, their performance is limited when handling nonlinear complex data in practical applications; thus, many studies have explored various machine learning and hybrid approaches to forecast carbon emissions in different contexts [11,12,13]. Based on the least squares support vector machine (LSSVM), Sun et al. [14] conducted an analysis of carbon dioxide emissions from multiple sectors in China and developed a novel forecasting model. Acheampong et al. [15] applied artificial neural networks (ANN) to simulate carbon emission intensity for the USA, Brazil, China, Australia and India. Ma et al. [16] developed a new hybrid forecasting method by using association rule algorithm and optimized grey model, illustrating superior predictive performance and highlighting the challenges of China’s carbon emission reduction.

With the development of deep learning techniques, time series forecasting has achieved significant progresses. However, no single model is universally applicable for all scenarios. To address this, researchers have explored and developed a number of hybrid modeling approaches. Li et al. [17] proposed an EA-LSTM model that incorporates evolutionary algorithms and attention mechanisms into LSTM, effectively enhancing temporal feature learning and improving prediction accuracy. Qiao et al. [18] developed a hybrid method combining an improved lion swarm optimizer with traditional models, achieving better convergence and accuracy in carbon emission forecasting. Lin et al. [19] constructed an attention-based LSTM model for cross-country carbon emission forecasting, effectively modeling regional characteristics and economic variations. Han et al. [20] presented a coupled LSTM-CNN model for carbon emission prediction across 30 Chinese provinces, leveraging complementary strengths in sequence modeling and feature extraction. Based on quantile regression and attention-based bidirectional long short-term memory (BiLSTM) network, Zhou et al. [21] proposed an ensemble forecasting model for predicting daily carbon emissions of five major carbon-emitting countries. Xu et al. [22] developed a hybrid forecasting model for crude oil prices by integrating financial market factors, where commodity and foreign exchange were found to have significant impact on oil price volatility.

China, as the largest carbon emitter, has actively engaged in climate governance by unveiling its dual-carbon objectives in 2020, reaching a peak in carbon emissions by 2030 and achieving carbon neutrality by 2060 [23]. However, China still faces significant challenges, including delays in restructuring its energy system and the disparities in emission reduction capacities between regions [24]. Most existing studies rely on annual data, which fail to capture seasonal or quarterly fluctuations in emissions [25]. Moreover, these models cannot account for complex external factors including economic cycles and policy interventions, resulting in limited prediction accuracy and robustness.

The impact of climate risk on the financial system is becoming increasingly prominent. Accurate prediction of carbon emissions has become a crucial research issue connecting environmental governance with financial decision-making. Recent research shows that there exists a close relationship between climate policy risk and asset prices. Dietz et al. [26] introduced the concept of ’Value at Risk’ (VaR) to climate change by modifying the classic dynamic integrated climate-economy (DICE) model for probabilistic forecasting to assess the impact on economic output. Bolton et al. [27] investigated whether carbon emissions affect the cross-section of US stock returns and found that stocks of firms with higher carbon emissions earn higher returns, indicating investors are pricing in carbon emission risks. More recently, scholars have examined the impact of economic policy uncertainty on corporate decisions related to carbon emissions and renewable energy, finding that heightened uncertainty tends to increase carbon emissions, with renewable energy consumption serving as a mediating factor in this relationship [28].

The rest of this paper is organized as follows. Section 2 illustrates the proposed STL-wLSTM-SVR model in detail. Next, the experimental setup, including data source and evaluation metrics, is presented in Section 3. The experimental results for aggregate-level and sector-level carbon emission forecasts are presented in Section 4. Subsequently, the model’s rationality is verified through two sets of comparison experiments in Section 5. Some brief conclusions, limitations and future directions for this work are given in Section 6 and Section 7, respectively.

2. The Proposed STL-wLSTM-SVR Model

Carbon emission time series exhibit complex composite characteristics, which not only encompass long-term evolutionary trends such as economic cycles but also are influenced by policy interventions, seasonal variations and short-term demand shocks. Leveraging the capability of machine learning to process high-dimensional and complex data, an ensemble forecasting strategy that integrates multiple models can more effectively reduce the prediction errors inherent in single-model approaches.

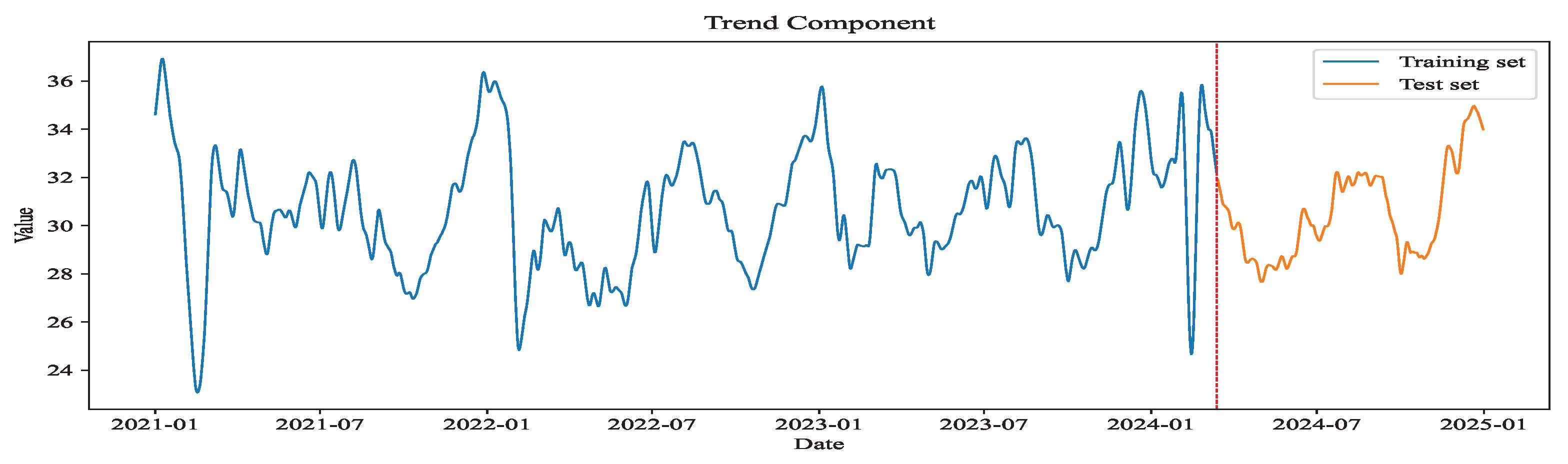
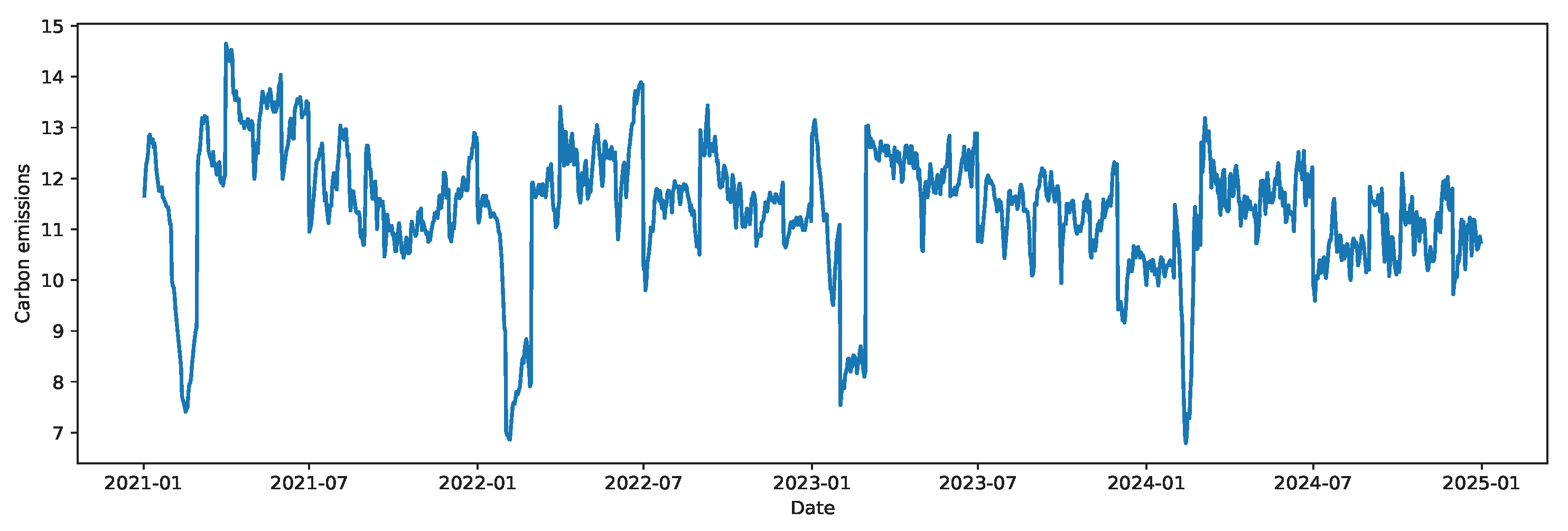
The proposed STL-wLSTM-SVR hybrid forecasting model is illustrated in Figure 1, which consists of four phases. (1) Data preprocessing. China’s daily carbon emission data during 2021–2024 comes from the Carbon Monitor platform via the China Carbon Emissions Database. The dataset is then normalized and split. (2) Model selection. Four data decomposition models and seven single forecasting models are evaluated. The analysis identifies the STL decomposition method, long short-term memory (LSTM) network and support vector regression (SVR) as the most suitable components for different modules of the hybrid forecasting framework. (3) Combined prediction. In this phase, the STL decomposition method is first applied to decompose the carbon emission time series data into trend, seasonal and residual components. The LSTM model is then used for forecasting the trend and seasonal components, while the SVR model is used for forecasting the residual component. To enhance prediction accuracy, the WOA is employed for hyperparameter tuning in the LSTM model, while traditional grid search is applied for hyperparameter selection in the SVR model. (4) Forecasting results. The final predicted values are obtained by performing inverse normalization and combining the forecasted values of the three subsequences. The first two phases will be introduced in Section 4, and the following focuses on the data decomposition and combined prediction modules.

2.1. Seasonal-Trend Decomposition Using Loess Method

The STL decomposition technique [29], which applies seasonal-trend decomposition with Loess, is a widely adopted method in time series prediction. It is also widely used in anomaly detection and data cleaning. The core idea is to decompose a given time series into trend, seasonal and residual components using the locally estimated scatterplot smoothing (LOESS) method. As a non-parametric regression technique, LOESS dynamically adjusts time weights to accurately capture the trend features.

Carbon emissions data are often influenced by seasonal fluctuations (such as climate change and policy implementation cycles) and long-term trends (such as industrial development and energy transition). Additionally, due to factors like economic activity, policy adjustments and fluctuations in energy demand, the carbon emission series exhibit significant nonlinear characteristics. The STL method employs local regression to perform smoothing for accurately capturing such nonlinear relationships, and it can handle time series data with varying periodic and trending characteristics, making it highly suitable for the study of complex carbon emissions data.

2.2. wLSTM-Based Trend and Seasonal Prediction Module

Recurrent neural networks (RNNs), which specialize in processing sequential data, effectively model temporal dependencies owing to their memory-based architecture. However, when processing long sequences, RNNs are constrained by gradient vanishing or exploding issues. In response to this challenge, Hochreiter and Schmidhuber innovatively designed the novel long short-term memory (LSTM) networks [30], depicted in Figure 2.

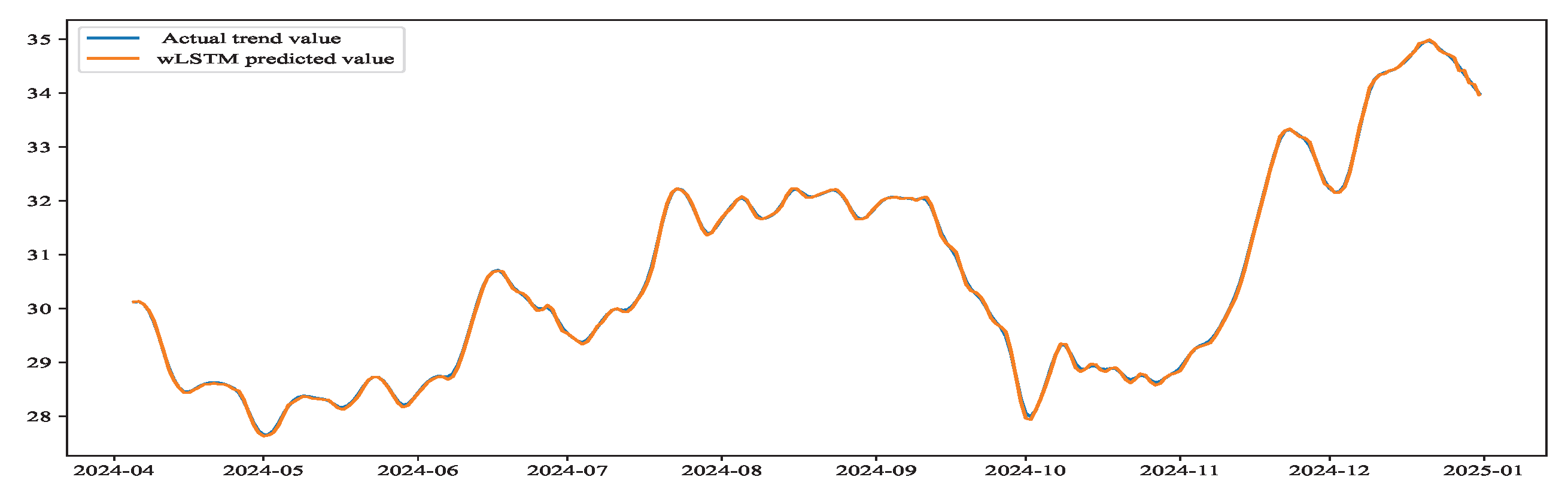
The advantage of LSTM lies in its strong ability for extracting long-term and short-term dependencies in time series data, which can memorize seasonal patterns that span multiple cycles and track the evolution of trend components. Comparing with traditional recurrent neural networks, it can better capture asymmetric and abrupt features in emission fluctuations, such as trend shifts caused by policy changes or external shocks [20].

The following equations define the forget gate $f_t$, input gate $i_t$, candidate cell state $\overline{C_t}$, updated cell state $C_t$, output gate $o_t$ and hidden state $h_t$ [30].

$$f_t=\sigma (W_f·[h_{t-1},s_t]+b_f)$$

(1)

$$\begin{array}{cc}\hfill i_t& =\sigma (W_i·[h_{t-1},s_t]+b_i),\hfill \\ \hfill {\tilde{C}}_t& =tanh(W_C·[h_{t-1},s_t]+b_C),\hfill \\ \hfill C_t& =f_t·C_{t-1}+i_t·{\tilde{C}}_t\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill o_t& =\sigma (W_o·[h_{t-1},s_t]+b_o),\hfill \\ \hfill h_t& =o_t·tanh\left(C_t\right).\hfill \end{array}$$

(3)

The complexity of LSTM originates from its unique network topology and diverse parameter configurations, with parameter settings crucial for performance and generalization [31]. To enhance the performance of LSTM models, it is necessary to optimize hyperparameters such as the number of hidden layer neurons, learning rate and the number of iterations. Traditional hyperparameter tuning relies on manual trial-and-error, which is not only time-consuming but also prone to getting stuck in local optima. Therefore, this study introduces the WOA for tuning hyperparameters automatically [32].

WOA is a nature-inspired intelligent optimization technique, whose core idea is to simulate the hunting behavior of humpback whales based on two mechanisms. One is encircling prey, which means that all candidate solutions gradually approach the current optimal solution, thus narrowing the search range. The other one is bubble-net feeding, which indicates that random walks and spiral movements are used to break free from local optima, expanding the parameter search space, thus balancing local search precision and global search breadth. Compared to manual tuning, WOA does not rely on experience-based preset parameter ranges. Through the iterative process, it automatically selects the optimal LSTM hyperparameter combination for the current forecasting task, reducing the subjective influence of human intervention and providing a reliable optimization path to improve the model’s predictive performance [33,34].

Specifically, the wLSTM algorithm consists of four steps as follows.

Step 1. Initializing the hyperparameters

For the seasonal and trend forecast in carbon emission series, the initial positions $X_0$ of the whale individuals are defined as the hyperparameter combinations of the LSTM model, including the input sequence length (time_step), the number of units in the LSTM layers (units1, units2), the number of training iterations (epochs), the batch size for each iteration (batch_size), the learning rate for weight updates (learning_rate) and the control parameters A and C.

Step 2. Training and evaluating model

The carbon emission series data are partitioned into training and test sets at an 8:2 ratio, where the training set is employed for model building and the test set is used to validate forecasting performance. For each set of hyperparameters, the training set is employed to train the LSTM model. Based on this, the fitness value is calculated to quantitatively evaluate the carbon emission prediction corresponding to the specific set of hyperparameters. The calculation formula is as follows:

$$f\left(X_i\right)=L_{\mathrm{LSTM}}={\displaystyle \frac{1}{N}}\sum _{j=1}^N{(s_j-{\widehat{s}}_j)}^2,$$

(4)

where $s_j$ and $\widehat{s_j}$ correspond to the actual and predicted values of the seasonal component, and N is the total data points. With the aid of (4), the performance of hyperparameter combination $X_i$ is evaluated.

Step 3. Updating optimal solution

Based on the current optimal solution $X^{*}$ and the position of $X_i$, the position of the hyperparameter in LSTM is updated as follows [32]:

$$\begin{array}{c}{X}_i(t+1)=X^{*}\left(t\right)-A·D·cos\left(2\pi \right),\hfill \\ D=|C·X^{*}\left(t\right)-X_i\left(t\right)|,\hfill \end{array}$$

(5)

where A and C represent search range and direction coefficients, respectively. Through the updating optimal solution, the current hyperparameter combination will gradually approach the optimal solution.

Step 4. Generating optimal LSTM hyperparameters

The optimization stops if the number of iterations reaches the maximum $T_{max}$ or if the error $L_{LSTM}$ is less than the predefined tolerance coefficient $ϵ$. If the termination condition is not satisfied, return to step 3. Otherwise, the optimal hyperparameters ${\mathbf{X}}_{\mathrm{opt}}$ with the smallest fitness value are obtained, which will be used to train the final LSTM model.

2.3. SVR-Based Residual Prediction Module

The support vector regression (SVR) [35] algorithm, as an extension of support vector machine (SVM), is a robust and effective supervised learning method. This algorithm focuses on determining the optimal hyperplane that separates the data points by maximizing the distance to the nearest ones. In the case of linearly separable data, it adopts a hard-margin approach for maximization, while for non-linearly separable data, it utilizes kernel functions to project the input into a higher-dimensional space and addresses the optimization problem using a soft-margin technique.

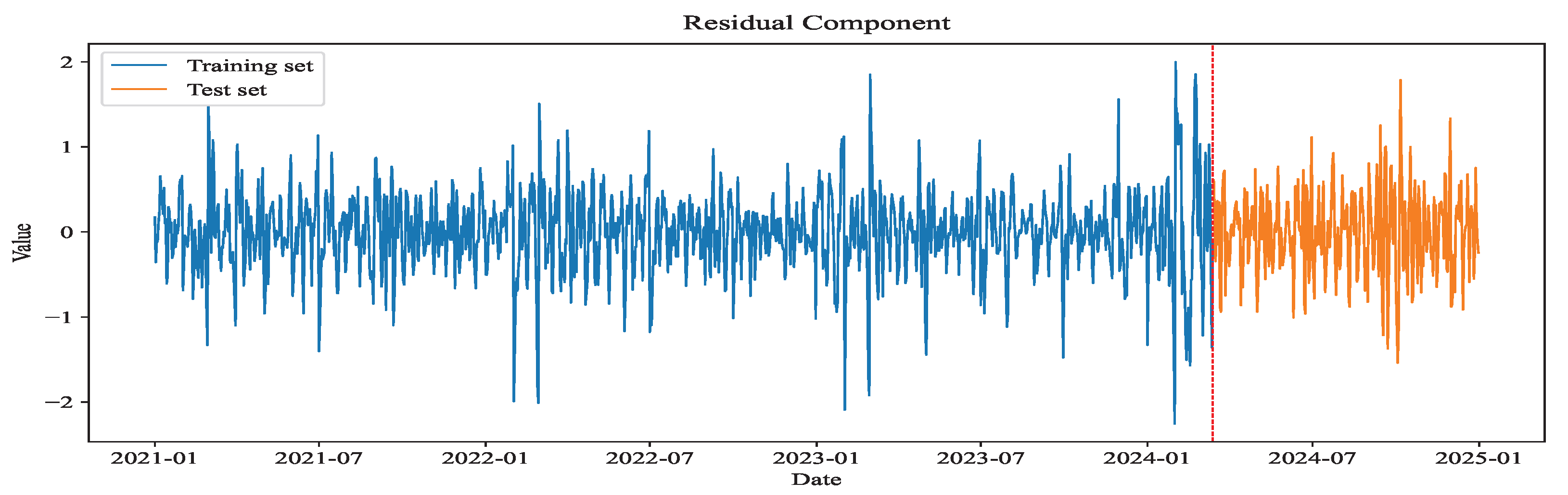
The residual component, after STL decomposition, represents the noise-like remainder from which trend and seasonal patterns have been removed. It lacks significant periodicity and trends, often containing random disturbances such as short-term policy adjustments and temporary fluctuations in energy demand. Compared to complex deep learning models, SVR is simpler and more suitable for residual data, which typically have lower dimensionality and weak regular patterns [36,37].

The SVR model is trained with the following objective function [35],

$$\begin{array}{cc}\hfill & \underset{w,b,{\xi }_i,{\xi }_i^{*}}{min}{\displaystyle \frac{1}{2}}{\parallel w\parallel }^2+C\sum _{i=1}^N({\xi }_i+{\xi }_i^{*}),\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.y_i-f\left(x_i\right)\le ϵ+{\xi }_i,\hfill \\ \hfill & f\left(x_i\right)-y_i\le ϵ+{\xi }_i^{*},\hfill \\ \hfill & {\xi }_i,{\xi }_i^{*}\ge 0,i=1,\cdots ,N\hfill \end{array}$$

(6)

where w refers to the weight vector, b denotes the bias, ${\xi }_i$ and ${\xi }_i^{*}$ are the slack variables, and $ϵ$ and C are the tolerance and penalty parameter, respectively.

When the data exhibit a nonlinear relationship, SVR uses the kernel function transformation to map the original data into a higher-dimensional feature space and then performs linear regression in that space. Several hyperparameters such as the kernel function, penalty coefficient C, kernel parameter $\gamma$ and insensitive loss parameter $\epsilon$ are set to their initial values. Through the classic grid search method, all possible combinations are traversed in the hyperparameter space, and the optimal hyperparameter combination with the minimized RMSE or other metrics can be derived.

2.4. Research Assumptions

In this study, four research assumptions are proposed to ensure the robustness and generalization performance of the STL-wLSTM-SVR model.

First, we assume that after data decomposition, the obtained trend, seasonal and residual components of carbon emission series remain stationary or quasi-stationary, enabling time-series models based on historical patterns.

Second, we assume that decomposing carbon emission series and applying proper predictive models to its components can effectively capture linear and nonlinear dynamics.

Third, the prediction errors of each model in the hybrid method are assumed to be independent, which forms the basis for combining different models’ predictions to improve predictive accuracy.

Finally, we assume that external factors such as macroeconomic conditions and energy policies remain stable over the short-term forecast horizon, without abrupt disruptions that could significantly alter emission patterns.

3. Experiment Setup

3.1. Data Source

In this study, we use China’s daily carbon emission data obtained from the Carbon Monitor platform via the China Carbon Emissions Database. Developed by the Department of Earth System Science at Tsinghua University in collaboration with international research partners, Carbon Monitor provides a high-resolution framework for estimating carbon emissions across major sectors, including electricity generation, industry, ground transportation, aviation, shipping and residential energy consumption.

Carbon Monitor platform offers global daily carbon emission data since 1 January 2019. As shown in Figure 3, we only focus on China’s carbon emissions covering 1461 days, examining both total and sector-specific trends. The data can be accessed through the China Carbon Emissions Database (CEADS) at https://www.ceads.net.cn/, which provides a link to the Carbon Monitor platform https://carbonmonitor.org.cn/.

3.2. Evaluation Metrics

This research utilizes three metrics to assess the model’s predictive accuracy: root mean squared error (RMSE) [38], mean absolute error (MAE) [39] and mean absolute percentage error (MAPE) [40]. Their mathematical expressions are as follows

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{(y_i-{\widehat{y}}_i)}^2}$$

(7)

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N|y_i-{\widehat{y}}_i|$$

(8)

$$\mathrm{MAPE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{|y_i-{\widehat{y}}_i|}{y_i}}$$

(9)

where N represents the total data points, $y_i$ and $\widehat{y_i}$ denote the actual and predicted values, and $\overline{y}$ means the average of the actual values. A smaller value of MAPE, MAE and RMSE indicates higher prediction accuracy.

FDP is employed to evaluate the directional prediction accuracy of a forecasting model [41], which can be calculated by

$$\mathrm{FDP}={\displaystyle \frac{1}{(N-1)}}\sum _{i=1}^{N-1}{\nu }_i$$

(10)

where

$${\nu }_i=\left\{\begin{array}{cc}1\hfill & \mathrm{if}{\displaystyle \frac{(y_{i+1}-y_i)}{({\widehat{y}}_{i+1}-{\widehat{y}}_i)}}>0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(11)

The closer the value of FDP is to 1, the stronger the model’s trend prediction ability.

4. China Daily Carbon Emission Forecasting: Aggregate and Sectoral Perspective

This section presents an empirical analysis using China’s daily carbon emission data to validate the effectiveness and generalizability of the proposed STL-wLSTM-SVR model. First, the model’s performance in forecasting China’s total carbon emissions is evaluated. Subsequently, its application is extended to predict carbon emissions across five sectors, thereby verifying its prediction accuracy and generalization ability.

4.1. Aggregate Level Carbon Emission Forecasting Using STL-wLSTM-SVR Model

To forecast total carbon emissions, we first perform a single data split on the carbon emission series to illustrate the details of the proposed model. Based on this, we further conduct a six-round rolling forecast experiment for testing the proposed model’s effectiveness and superiority in the short-term carbon emission forecasting for China.

4.1.1. The Predictive Workflow of the STL-wLSTM-SVR Model

Step 1. STL-based carbon emission decomposition

To extract trend, seasonality and residual features from the carbon emission series, this study adopts the STL decomposition method, where three parameters need to be optimized: period, seasonal and trend. Following the parameter constraints [29], and considering the time granularity and potential seasonality of carbon emissions (e.g., weekly, bi-weekly, monthly and annual fluctuations), the candidate values for the period parameter are set as $\{7, 14, 30, 365\}$. The seasonal parameter must be set as an odd number greater than 7, and the trend parameter is selected as the smallest odd number greater than $1.5\times$$period$$/(1-1.5/$$seasonal)$. Then, the four parameter combinations are shown in

Table 1. Comparison of parameter optimization in STL decomposition.

(Period, Seasonal, Trend)	Resid_Var	Resid_Ratio	acf_Mean_abs	DW
(7, 9, 13)	0.2327	4.05%	0.0901	1.1630
(14, 15, 25)	0.6276	11.44%	0.1396	0.5941
(30, 31, 45)	1.4084	26.77%	0.1944	0.2992
(365, 367, 551)	1.0632	17.16%	0.2159	0.1798

.

The optimal parameters are chosen based on the residual autocorrelation function (ACF) and Durbin–Watson (DW) statistic [42]: the smaller the mean ACF, the weaker the residual autocorrelation; the closer the DW value is to 2, the closer the residual is to white noise. The optimal parameter combination is obtained as period = 7, seasonal = 9, trend = 13. In this case, three decomposed sub-series of daily carbon emissions are displayed in Figure 4.

The basic statistical features of subsequences are shown in

Table 2. Descriptive statistics of the STL-decomposed carbon emission components.

	Mean	Max	Min	Std	Var	Pearson Correlation Coefficient
Trend	30.664	36.935	23.074	2.334	5.45	0.95
Season	0.000	1.250	−0.906	0.258	0.067	0.13
Residual	0.001	2.001	−2.255	0.482	0.23	0.38

. Among them, the trend component accounts for the highest proportion of the total carbon emissions, and it exhibits low-frequency fluctuations, the largest variance and the strongest correlation with the carbon emission series, making it the key focus for the forecasting model. The seasonal component exhibits high-frequency variations, with relatively low variability and clear periodic patterns. The residual component has a relatively high variance, indicating that it contains a higher level of noise, which requires a robust model to capture irregular changes.

Step 2. wLSTM-based trend prediction module

According to the STL-wLSTM-SVR model, the trend component obtained from STL decomposition will be predicted based on the LSTM. The visualization of this division is shown in Figure 5, where the first 80% of the data (containing 1168 data points) are used for model training, and the remaining 20% are used for testing.

It is important to note that the choice of hyperparameters in the LSTM model impacts its predictive accuracy. To further improve prediction performance, the WOA is used to optimize hyperparameters on the training set. With the optimal parameter combination, the LSTM model is applied to the test set for validation, with the fitting results between the predicted and actual values shown in Figure 6.

Step 3. wLSTM-based seasonal prediction module

The seasonal component generated by STL decomposition is also predicted using LSTM. The training and test set division for the seasonal component is shown in Figure 7, where the blue sample represents the training data, and the orange point denotes the test data. It is obvious that the fluctuations in the seasonal component exhibit significant regularity. This characteristic indicates a strong correlation between carbon emission changes and seasonal factors, providing a reasonable basis for using the LSTM model to capture its periodic variation patterns.

To improve prediction accuracy, WOA is also used to optimize the hyperparameters in the LSTM. With the optimized hyperparameters, the model’s performance is then validated on the test set. Figure 8 demonstrates that the optimized LSTM model effectively captures the periodic variations of the seasonal component, as evidenced by the close alignment between the predicted and actual values.

Step 4. SVR-based residual prediction module

The residual component exhibits significant high-frequency, short-term fluctuations and randomness; thus, the irregular variations and noise in the carbon emission data cannot be explained by the trend and seasonal components. The division of training and test sets for the residual component is shown in Figure 9. The red line denotes the boundary between the two datasets, which indicates that the fluctuations in the training set exhibit stronger stability, while the fluctuations in the test set are noticeably larger. This difference may reflect that the test set data contain more significant random disturbances.

The SVR model has strong fitting ability when handling small samples and nonlinear data, where proper kernel functions can effectively capture the random fluctuation patterns in the residual component, and its regularization mechanism helps reduce the interference of noise on the prediction results. A classic grid search is employed to obtain the optimal parameters: the kernel function (linear, polynomial or rbf), the penalty coefficient C (0.1, 0.5, 1 or 10), the kernel parameter $\gamma$ (scale, auto, 0.1 or 1) and the insensitive loss parameter $ϵ$ (0.01, 0.1 or 0.2). With the optimal parameter combination, the SVR model achieves improved predictive accuracy, as illustrated in Figure 10.

Step 5. Generating the predictive values

Performing Step 2 to Step 4, the predicted values for the trend, seasonal and residual components of carbon emission series can be obtained. By combining the predictions of these three components, the final forecast result can be generated. Figure 11 presents the fitting curve of the predicted values and the actual values on the testing dataset, clearly demonstrating the alignment in their variation trends.

4.1.2. Rolling Forecast and Performance Evaluation for China’s Daily Carbon Emissions

To comprehensively assess the performance of the STL–wLSTM–SVR model, a sliding-window cross-validation approach is adopted. This method mitigates the data partition bias inherent in a single training–testing split, ensures a more robust and stable evaluation and prevents the leakage of future information into the training process. The dataset is chronologically divided into several consecutive segments, where a fixed-length historical window serves as the training set and the immediately following short sequence is designated as the testing set. After each validation round, the window is advanced by one step, and the process is repeated until the entire dataset has been utilized. The detailed splitting scheme for each round is presented in

Table 3. Time window divisions for sliding window cross-validation.

Period	Training Set	Testing Set
1	1 January 2021–30 June 2023	1 July 2023–13 February 2024
2	2 March 2021–29 August 2023	30 August 2023–14 April 2024
3	1 May 2021–28 October 2023	29 October 2023–13 June 2024
4	30 June 2021–27 December 2023	28 December 2023–12 August 2024
5	29 August 2021–25 February 2024	26 February 2024–11 October 2024
6	28 October 2021–25 April 2024	26 April 2024–31 December 2024

. The model’s final performance metric is obtained by averaging the results over six validation rounds.

Through the sliding window cross-validation strategy (see Table 3), the prediction accuracy under different data splitting can be assessed, avoiding evaluation biases caused by a single data partition.

Table 4. Rolling forecast accuracy of the STL-wLSTM-SVR model for aggregate carbon emissions.

Period	RMSE	MAPE (%)	MAE	FDP (%)
1	0.0943	0.23	0.0710	93.56
2	0.1183	0.28	0.0864	95.59
3	0.1437	0.35	0.1079	92.79
4	0.1253	0.29	0.0891	94.37
5	0.1102	0.29	0.0879	93.93
6	0.0856	0.22	0.0683	94.02
Average	0.1129	0.28	0.0851	94.04

shows the model’s performance on forecasting China’s daily carbon emission in aggregate perspective.

Table 4 presents the results of the six-round rolling forecast experiment, which demonstrate the model’s exceptional effectiveness and stability. Across the six periods, the model maintains a consistently low prediction error. The key performance indicator, MAPE, averages an outstanding 0.28%, signifying that the model’s predictions deviate from the actual values by less than one-third of one percent on average. Even in the least accurate period (Period 3, MAPE of 0.35%), the performance remains at a very high standard, highlighting the model’s robustness against temporal variations in the data. In addition, the proposed model proves highly adept at capturing the underlying trend dynamics. The forecast directional precision (FDP) is consistently above 92%, averaging 94.04%. This suggests that the model can reliably predict whether carbon emissions will increase or decrease on a daily basis, a critical feature for policy-making and timely intervention.

In summary, the multi-round rolling validation confirms that the STL-wLSTM-SVR model is not only highly accurate (as shown by low RMSE, MAE and MAPE) but also robust and reliable over time (as shown by the stable performance across all six periods). This demonstrates its strong potential for deployment in other short-term carbon emission forecasting scenarios.

4.2. Sector-Level Carbon Emission Forecasting Using STL-wLSTM-SVR Model

Compared with aggregate forecasting, sector-level carbon emission predictions can uncover the heterogeneous contributions of different sectors to overall emissions and capture their unique dynamic patterns. At the same time, this enables us to evaluate the proposed model’s generalization ability across various carbon emission series.

4.2.1. Sector Carbon Emissions Description

In China Carbon Accounting Database, daily carbon emission can be further classified in terms of sectors, including power, industry, residential, ground transport, domestic aviation and international aviation. Considering that the carbon emissions from domestic and international aviation account for a relatively small proportion, these two sectors are combined in this study, and the subsequent forecasting analysis is conducted for five sectors. The annual carbon emissions of five sectors are displayed in Figure 12.

As shown in Figure 12, the power sector consistently exhibits the highest carbon emissions among the five sectors during 2021–2024, followed by industry. While emissions from the power sector exhibit a steady increase, those from industry declined gradually. Residential and ground transport emissions remain relatively stable with minor fluctuations, whereas aviation, though contributing the smallest share, displayed a marked increase after 2022.

Table 5. The statistical characteristics of China’s carbon emissions by sector during 2021–2024.

Statistical Data	Total	Power	Industry	Residential	Ground Transport	Aviation
mean	30.66	14.41	11.41	2.2	2.48	0.2
std	2.49	1.85	1.25	0.96	0.13	0.06
min	22.69	10.05	6.79	1.38	1.64	0.04
25%	28.95	13.03	10.87	1.38	2.45	0.15
50%	30.56	14.24	11.55	1.74	2.52	0.2
75%	32.27	15.77	12.16	2.99	2.57	0.24
max	37.93	19.39	14.65	5.05	2.67	0.3

indicates that China’s daily carbon emissions ranged from 28.95 Mt to 32.27 Mt in the period 2021–2024, with a peak of 37.93 Mt. The power sector reported the highest mean emissions (14.41 Mt), while aviation remained the lowest (0.20 Mt). Specifically, emissions ranged from 10.03 Mt to 15.77 Mt in the power sector, 10.87 Mt to 12.16 Mt in industry, 1.38 Mt to 3.00 Mt in the residential sector, and 2.45 Mt to 2.67 Mt in ground transport. Aviation emissions were consistently low, ranging only from 0.15 Mt to 0.24 Mt. These findings not only reveal the evolving trajectories across sectors but also underscore the importance of forecasting to capture future trends.

4.2.2. Empirical Analysis of Carbon Emission Forecasting Across Five Sectors

Carbon emissions in different sectors exhibit distinct trends and features. To further validate the model’s effectiveness, the sector-level forecast is conducted as follows.

(1) Carbon emission forecast for the power sector

First, we consider the power sector, the primary source of carbon emissions in China. As illustrated in Figure 13, its carbon emission series presents a significant forecasting challenge due to a combination of complex characteristics. The series is marked by a strong seasonal pattern, with peaks in winter and summer corresponding to heating and cooling demands. This underlying trend is further compounded by significant high-frequency fluctuations and volatility, complicating accurate prediction.

In the sector-level carbon emission forecasting, we also employ a sliding window cross-validation method, which divides the data into six consecutive intervals in chronological order as shown in Table 3.

Table 6. Rolling forecast accuracy of the STL-wLSTM-SVR Model for the power sector.

Period	RMSE	MAPE (%)	MAE	FDP (%)
1	0.1076	0.44	0.0671	86.14
2	0.0841	0.38	0.0568	91.63
3	0.0969	0.44	0.0655	89.16
4	0.0880	0.40	0.0599	93.10
5	0.0579	0.30	0.0444	94.09
6	0.0699	0.39	0.0567	93.30
Average	0.0841	0.39	0.0584	91.24

displays the rolling forecast results for the power sector. The STL-wLSTM-SVR model achieves an average RMSE of 0.0841, average MAPE of 0.39% and average MAE of 0.0584. The consistency of these metrics for six periods underscores the model’s robustness and its ability to maintain high accuracy regardless of the specific time window. Furthermore, the model excels at capturing the underlying trend dynamics, achieving an average FDP of 91.24%. Therefore, our model can effectively capture complex patterns of the power sector’s emissions and deliver highly accurate and reliable forecasts.

(2) Carbon emission forecast for the industry sector

The time-series data for industrial carbon emissions, shown in Figure 14, are characterized by high daily volatility and sharp, periodic downturns that align with major public holidays, most notably the Chinese New Year. These abrupt shifts in emission patterns require a model that is both sensitive to sudden changes and robust against random noise.

Despite the complexities in industrial carbon emissions data, the STL-wLSTM-SVR model demonstrates exceptional and stable performance, as displayed in

Table 7. Rolling forecast accuracy of the STL-wLSTM-SVR Model for the industry sector.

Period	RMSE	MAPE (%)	MAE	FDP (%)
1	0.0498	0.36	0.0384	92.52
2	0.0438	0.32	0.0335	91.63
3	0.0948	0.76	0.0837	95.07
4	0.0521	0.37	0.0386	92.82
5	0.0544	0.40	0.0536	93.47
6	0.0533	0.40	0.0447	94.48
Average	0.0580	0.44	0.0488	93.33

. The model achieves a remarkably low average MAPE of 0.44%, indicating that its predictions are highly precise. Furthermore, the model can capture the trend dynamics, achieving an average FDP of 93.33%. By effectively decoupling the underlying trend from volatile holiday effects and daily noise, the model achieves robust performance, as confirmed by a consistently low MAPE (under 0.76%) for six forecast periods.

(3) Carbon emission forecast for the residential sector

The carbon emissions from the residential sector, as depicted in Figure 15, are dominated by a pronounced and stable U-shaped annual cycle, driven by seasonal heating demands. However, superimposed on this predictable macro-pattern is significant high-frequency volatility, particularly during the peak winter months. This combination of a strong, regular seasonal component and chaotic daily fluctuations requires a model that can both capture the long-term trend and manage short-term noise.

The carbon emission series for the residential sector is characterized by a strong seasonal trend overlaid with high daily volatility. As shown in

Table 8. Rolling forecast accuracy of the STL-wLSTM-SVR Model for the residential sector.

Period	RMSE	MAPE (%)	MAE	FDP (%)
1	0.0232	0.60	0.0157	79.25
2	0.0251	0.68	0.0204	94.63
3	0.0354	0.80	0.0238	79.72
4	0.0249	0.69	0.0186	91.71
5	0.0164	0.76	0.0118	68.12
6	0.0243	1.14	0.0209	74.35
Average	0.0249	0.78	0.0185	81.30

, it achieves impressive accuracy (average RMSE of 0.0249, MAPE of 0.78%, MAE of 0.0185), confirming its ability in capturing the overall emission magnitude. However, the inherent daily noise makes directional forecasting more difficult, resulting in a more variable FDP of 81.30%. This indicates the proposed model’s robustness in providing reliable forecasts even for complex and volatile emission patterns.

(4) Carbon emission forecast for the ground transport sector

The ground transport sector, as illustrated in Figure 16, presents a significantly challenging forecasting. The carbon emissions series is characterized by strong nonlinearity and significant high-frequency fluctuations, reflecting the complex dynamics of daily commuting and logistics. Furthermore, the series is punctuated by sharp, deep downturns corresponding to the Spring Festival holiday, which introduces predictable but severe shocks. The presence of a structural break—the historic low in 2022 due to COVID-19 measures—adds another complexity for prediction.

Despite the data’s extreme volatility, the proposed model demonstrates excellent performance, as shown in

Table 9. Rolling forecast accuracy of the STL-wLSTM-SVR Model for the ground transport sector.

Period	RMSE	MAPE (%)	MAE	FDP (%)
1	0.0134	0.43	0.0108	73.93
2	0.0127	0.40	0.0098	81.11
3	0.0144	0.39	0.0095	76.96
4	0.0100	0.29	0.0073	80.49
5	0.0078	0.23	0.0059	76.44
6	0.0130	0.43	0.0109	73.21
Average	0.0119	0.36	0.0090	77.02

. It achieves a relatively low and stable average RMSE of 0.0119 (below 0.0144 for six periods), average MAPE of 0.36% (below 0.43 for six periods) and average MAE of 0.009 (below 0.44% for all periods). This highlights its robustness against daily noise and anomalies. In contrast, the intense daily stochasticity makes directional forecasting more difficult, resulting in average FDP of 77.02%.

(5) Carbon emission forecast for the aviation sector

The aviation sector’s carbon emissions, as illustrated in Figure 17, show their highly non-stationary and event-driven nature. The most prominent feature of the time series is a major structural break in early 2023, marking the transition from a period of suppressed travel to a post-pandemic rebound. Furthermore, the data are characterized by sharp, holiday-induced fluctuations and significant daily volatility, making it difficult to forecast.

The proposed model excels in forecasting aviation carbon emissions, successfully navigating the post-pandemic structural break (

Table 10. Rolling forecast accuracy of the STL-wLSTM-SVR Model for the aviation sector.

Period	RMSE	MAPE (%)	MAE	FDP (%)
1	0.0021	0.68	0.0017	64.53
2	0.0018	0.60	0.0015	66.34
3	0.0014	0.44	0.0011	64.25
4	0.0027	0.91	0.0024	57.64
5	0.0020	0.61	0.0016	58.62
6	0.0031	1.05	0.0027	57.59
Average	0.0022	0.72	0.0018	61.50

). However, its performance on directional accuracy is more moderate, with average FDP of 61.50%. This is attributed to the high-frequency noise that makes predicting daily direction more challenging. Nevertheless, its outstanding prediction accuracy validates the robustness of the STL-wLSTM-SVR model for forecasting complex, non-stationary time series.

In conclusion, the proposed STL-wLSTM-SVR model performs consistently well across sectors, with minor variations reflecting sector-specific characteristics. The rolling experiments validate the robustness and generalizability of the model, supporting its use for both aggregate-level and sector-level carbon emission prediction tasks.

5. Model and Decomposition Selection for the Hybrid Forecasting Framework

The proposed STL-wLSTM-SVR model employs an ensemble forecasting framework. Through two sets of experiments, this section evaluates the model’s rationality and advantages by comparing it with seven baseline models and by constructing hybrid models that combine four decomposition methods with the optimal baseline model.

5.1. Comparisons with Different Forecasting Methods

Using China’s daily total carbon emission data during 2021–2024 as the experimental sample, seven widely used prediction models are selected for comparative analysis, including ARIMA, SVR, XGBoost, RF, CNN, Transformer and LSTM. Their predictive accuracy and stability are evaluated by four metrics. Based on multidimensional evaluation, the model with the best suitability is identified as the baseline forecasting model. The performance of each model is summarized in

Table 11. Comparisons of baseline models for daily carbon emission forecasting.

Model	RMSE	MAPE (%)	MAE	FDP (%)
ARIMA	1.9157	5.22	1.6012	0.34
SVR	0.9397	2.76	0.8432	100
CNN	0.8167	2.06	0.6246	49.79
XGBoost	0.7015	7.25	0.5425	49.95
RF	0.7274	7.26	0.5618	49.95
Transformer	0.6959	1.77	0.5411	53.78
LSTM	0.6893	1.73	0.5246	53.24

.

Table 11 presents a comparative analysis of seven baseline models. The results indicate that the LSTM model achieves the lowest error with RMSE (0.6893), MAPE (1.73%) and MAE (0.5246). This demonstrates its superior capability in carbon emissions forecasting. In contrast, the SVR model exhibits a perfect FDP of 100%; its directional accuracy suggests an exceptional robustness in capturing the underlying trend evolution pattern, even if it sacrifices some precision in the absolute values.

The LSTM model, with its proven accuracy in capturing complex temporal dependencies, is logically selected to forecast the more structured trend and seasonal components. Meanwhile, the SVR model is utilized to simulate the residual component in carbon emission data. Its outstanding generalization ability makes it efficiently model the noisier, less predictable fluctuations remaining in the time series data.

5.2. Comparisons with Different Decomposition Techniques

With the optimal baseline model, four types of data decomposition techniques, namely, STL, EMD, VMD and CEEMDAN, are then combined to construct hybrid forecasting frameworks [43]. By comparing their predictive performance under the same experimental sample, the optimal hybrid framework configuration is finally verified and determined. The results are summarized in

Table 12. Comparisons of decomposition-based hybrid models for daily carbon emission forecasting.

Model	RMSE	MAPE (%)	MAE	FDP (%)
EMD-LSTM	0.4751	1.24	0.3784	64.97
CEEMDAN-LSTM	0.4370	1.13	0.3459	67.47
STL-LSTM	0.4258	1.10	0.3326	64.39
EMD-LSTM-SVR	0.4516	1.14	0.3507	64.79
CEEMDAN-LSTM-SVR	0.4194	1.07	0.3272	68.06
CEEMDAN-BiLSTM-GRU	0.4699	1.23	0.3735	73.94
VMD-Transformer	0.3810	0.93	0.2824	75.50
STL-BiLSTM-SVR	0.2890	0.78	0.2390	92.21
STL-LSTM-SVR	0.2124	0.56	0.1722	92.53

.

Table 12 shows the STL-LSTM-SVR model achieves the best overall performance, with the lowest values in RMSE (0.2124), MAPE (0.56%) and MAE (0.1722), as well as the highest FDP (92.53%), indicating both high prediction accuracy and strong generalization capability. Those hybrid models with EMD or CEEMDAN show relatively higher errors and lower FDP values, regardless of whether they are combined with LSTM, BiLSTM or Transformer. These findings suggest that STL decomposition is more suitable for the carbon emission forecasting, as it better separates the underlying trend, seasonality and residual components. The above analysis confirms the effectiveness of the STL-LSTM-SVR model and the suitability of the selected components.

6. Limitations and Future Directions

The proposed hybrid model achieved excellent performance in forecasting China’s total daily carbon emissions and sectoral emissions. This study is subject to several limitations, which, in turn, suggest promising future directions.

6.1. Limitations

(1) Model generalizability and regional heterogeneity

The proposed model achieves high prediction accuracy for forecasting China’s daily carbon emissions. However, its effectiveness is closely tied to the statistical properties of the studied data. When directly applied to other countries or regions, the model’s predictive accuracy may be restricted due to significant disparities in energy structures, industrial layouts and policy environments. Therefore, the model’s cross-regional generalization ability warrants further validation and refinement.

(2) Robustness to extreme events and structural breaks

A core challenge in time-series forecasting is maintaining model stability in the presence of outliers and sudden events. While the proposed model efficiently captures regular cyclical and trend components, its accuracy may fluctuate significantly when encountering public health crises (e.g., COVID-19), major policy shocks or extreme weather events. The model’s capacity to adapt to such structural breaks requires further enhancement.

(3) Spatiotemporal scale adaptability

This research focuses on China’s daily carbon emission forecasting at the aggregate and sectoral levels, without accounting for the multi-level characteristics of emissions across different spatiotemporal scales. For instance, local urban carbon emission hotspots exhibit significant spatiotemporal heterogeneity. The current model struggles to simultaneously predict short-term fluctuations and long-term trends or to capture the spillover effects of carbon emissions between regions.

6.2. Future Directions

(1) Integrating multi-source heterogeneous data and external factors

As future work, we can explore a more comprehensive forecasting framework by integrating multi-source and heterogeneous data. In addition to historical emissions data, future research is expected to incorporate a wider array of external variables. These include macroeconomic indicators (e.g., GDP, industrial value-added), energy and market data (e.g., price fluctuations in coal, oil, natural gas and carbon from the emissions trading system), as well as other drivers such as meteorological data and environmental policy texts. This will lead to more profoundly uncovering the underlying mechanisms of carbon emission dynamics, thereby improving the model’s predictive accuracy and logical consistency.

(2) Optimizing hyperparameter tuning algorithms

The hyperparameter optimization is often computationally intensive, which limits the model’s deployability in scenarios requiring high-frequency, real-time forecasting. More study on the intelligent optimization methods in forecasting models is worthy in the future, such as Bayesian optimization or reinforcement learning, to replace traditional grid search strategies. Dynamic hyperparameter optimization may be helpful to enhance the model’s applicability in real-time prediction contexts.

(3) Enhancing model interpretability and uncertainty quantification

To increase model transparency, future research will explore the use of techniques such as SHapley Additive exPlanations (SHAP) or Local Interpretable Model-agnostic Explanations (LIME). By analyzing the marginal contribution of each feature to the predicted values, one can provide policymakers with more insightful information. Furthermore, research may extend to interval and probabilistic forecasting. Quantifying the uncertainty of prediction results will provide a more robust assessment and sound decision-making.

7. Conclusions and Policy Implications

7.1. Conclusions

Accurate carbon emission forecast is not only essential for addressing the challenges of climate governance but also serves as a theoretical foundation for promoting the green transformation of socio-economic systems. Time-series forecasting remains one of the most challenging tasks in the prediction domain due to the superimposed characteristics of trend, seasonality, and randomness in the data. Constructing a specialized forecasting framework for specific scenarios not only requires overcoming the theoretical challenges of integrating multiple methods but also provides precise support for practical decision-making, thereby holding both significant theoretical innovation value and practical guidance.

The proposed hybrid forecasting model, STL-wLSTM-SVR, follows the framework of “selecting an appropriate baseline model–matching with a time series decomposition method–optimizing parameters in baseline models”. It fully integrates the strengths of STL decomposition (for accurate extraction of multi-scale features in time series), LSTM network (for capturing long- and short-term dependencies), SVR model (for improving nonlinear fitting accuracy), the WOA (for efficient global parameter optimization) and the grid search method (for ensuring reliability in parameter selection). While these are established techniques, their ingenious integration is empirically validated by the model’s exceptional performance. It achieved a high-precision forecast for China’s total daily carbon emissions (MAPE of 0.28%) and demonstrated remarkable adaptability across five sectors—from navigating the high volatility of ground transport (MAPE of 0.36%) to successfully handling the dramatic post-pandemic structural break in aviation (MAPE of 0.72%). These results not only verify the effectiveness of the hybrid framework in complex forecasting scenarios but also provide a valuable methodological reference for similar prediction tasks, such as sector-specific pollutant emissions and regional energy consumption.

7.2. Policy Implications

In this study, we proposed a high-precision short-term carbon emission forecasting model. The model’s accurate forecasting ability, especially in capturing the daily total carbon emissions and sector-specific emission dynamics, provides valuable insights for policy-making, industrial operations, and the development of carbon markets.

From the viewpoint of government governance, high-precision short-term forecasting models enable environment governance to shift from post-event evaluation to proactive early warning. Based on forecast data, governments can establish a dynamic warning system to implement targeted measures in advance—such as temporary traffic control and staggered industrial production—to address potential emission peaks. This achieves “peak shaving and valley filling” at a lower cost. Moreover, sector-specific forecast data help identify major short-term emission sources, providing a scientific basis for crafting differentiated and precise policies such as optimizing grid dispatch and promoting green transportation, thereby enhancing the effectiveness of environmental governance.

At the industrial operations level, accurate short-term emission forecasting facilitates low-carbon operations and cost optimization by enabling optimized production schedules that lower the systemic carbon footprint. For those enterprises engaging in carbon trading markets, this model may serve as a strategic tool for carbon asset management. Companies can develop flexible allowance trading strategies based on emission predictions, transforming passive compliance costs into proactive opportunities for economic value creation.

For the sustainable development of carbon trading markets, precise carbon emission forecasts act as a leading indicator for market demand. By reducing information asymmetry, these forecasts help stabilize market expectations and curb excessive price volatility. In the long term, a market consensus built on reliable data will promote the refinement of the carbon price discovery mechanism, allowing carbon prices to more accurately reflect marginal abatement costs. This creates a solid data foundation for developing carbon financial derivatives, thereby fostering the maturity and growth of China’s carbon finance markets.