Seasonal and Multi-Year Wind Speed Forecasting Using BP-PSO Neural Networks Across Coastal Regions in China
Abstract
1. Introduction
2. Materials and Methods
2.1. Previous Works
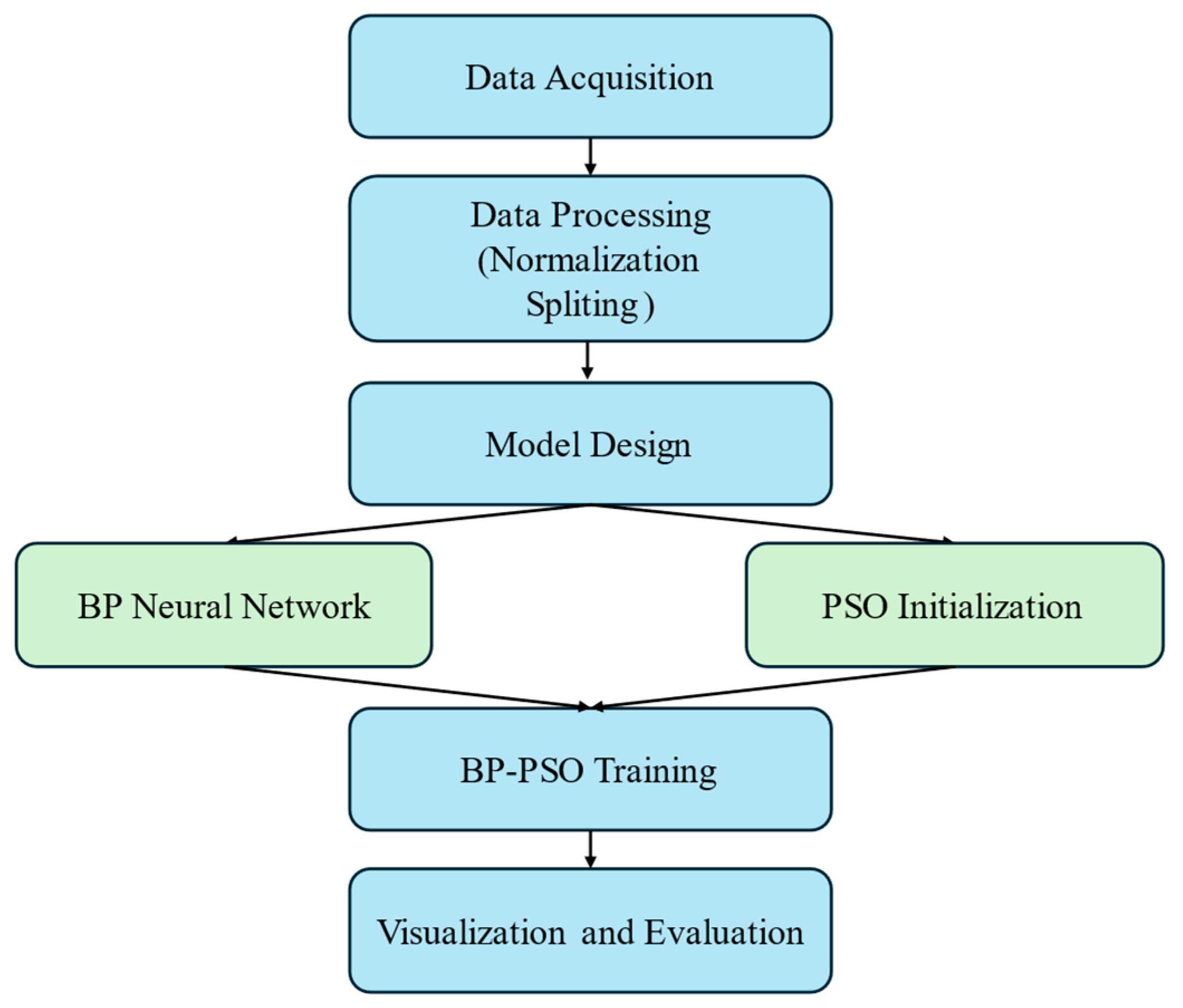
2.2. Overall Framework
2.3. Backpropagation Neural Network and Particle Swarm Optimization Algorithm
2.4. Walk-Forward Cross-Validation
2.5. Baseline Models
- (1)
- Persistence model
- (2)
- ARIMA model
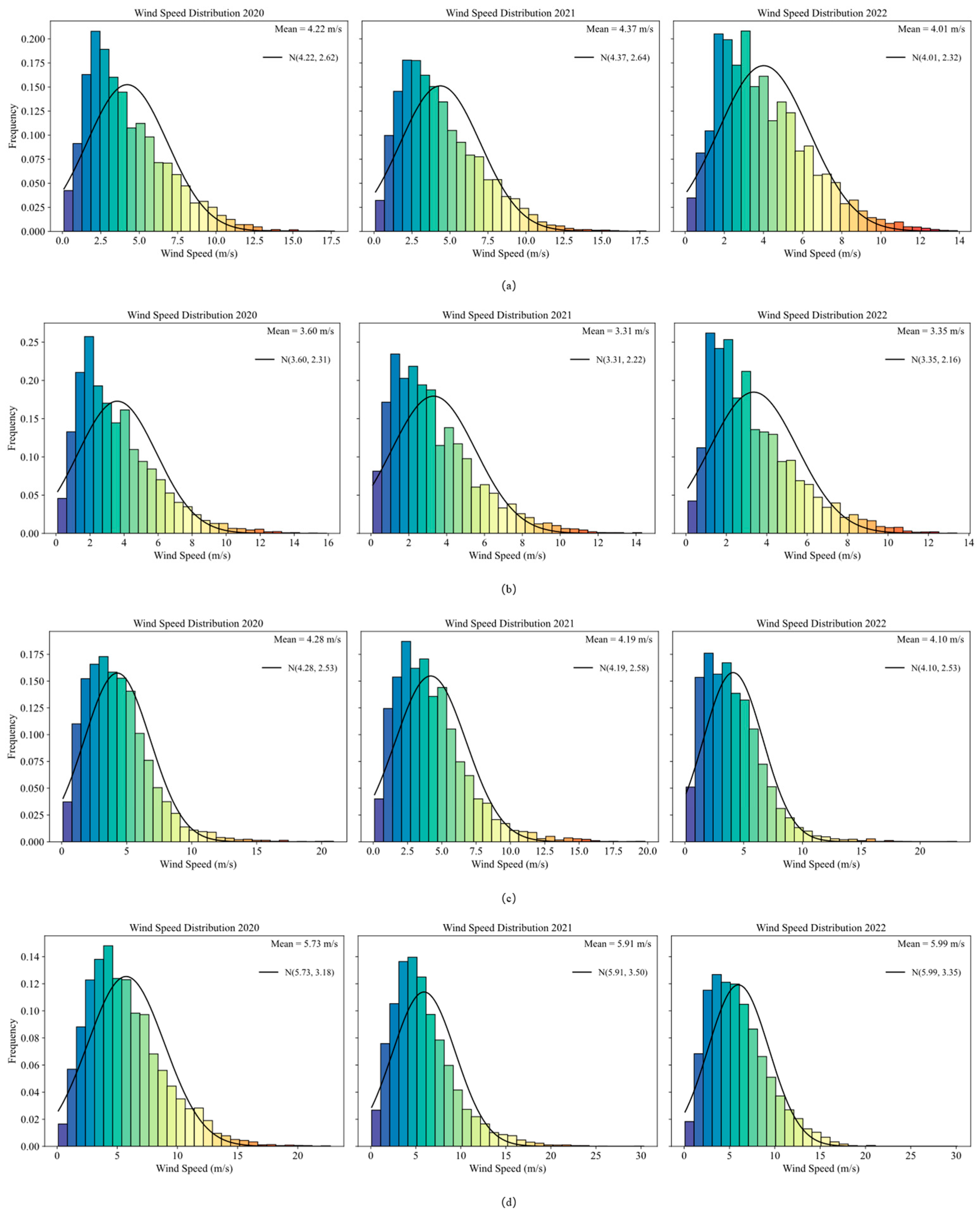
2.6. Data and Site Selection
3. Example
3.1. Dataset Division and Seasonal Configuration
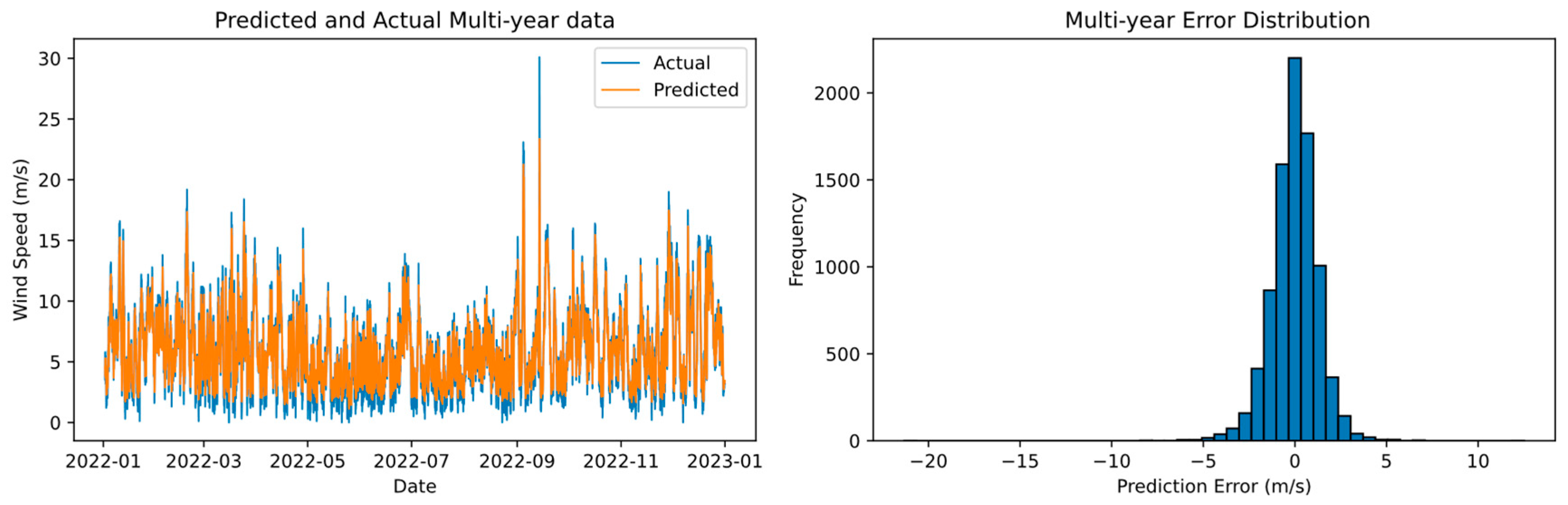
3.2. Multi-Year Forecast Model Performance
3.2.1. Multi-Year Forecast Outcome in LHT
3.2.2. Multi-Year Forecast Outcome in XCS
3.2.3. Multi-Year Forecast Outcome in ZFD
3.2.4. Multi-Year Forecast Outcome in SSN
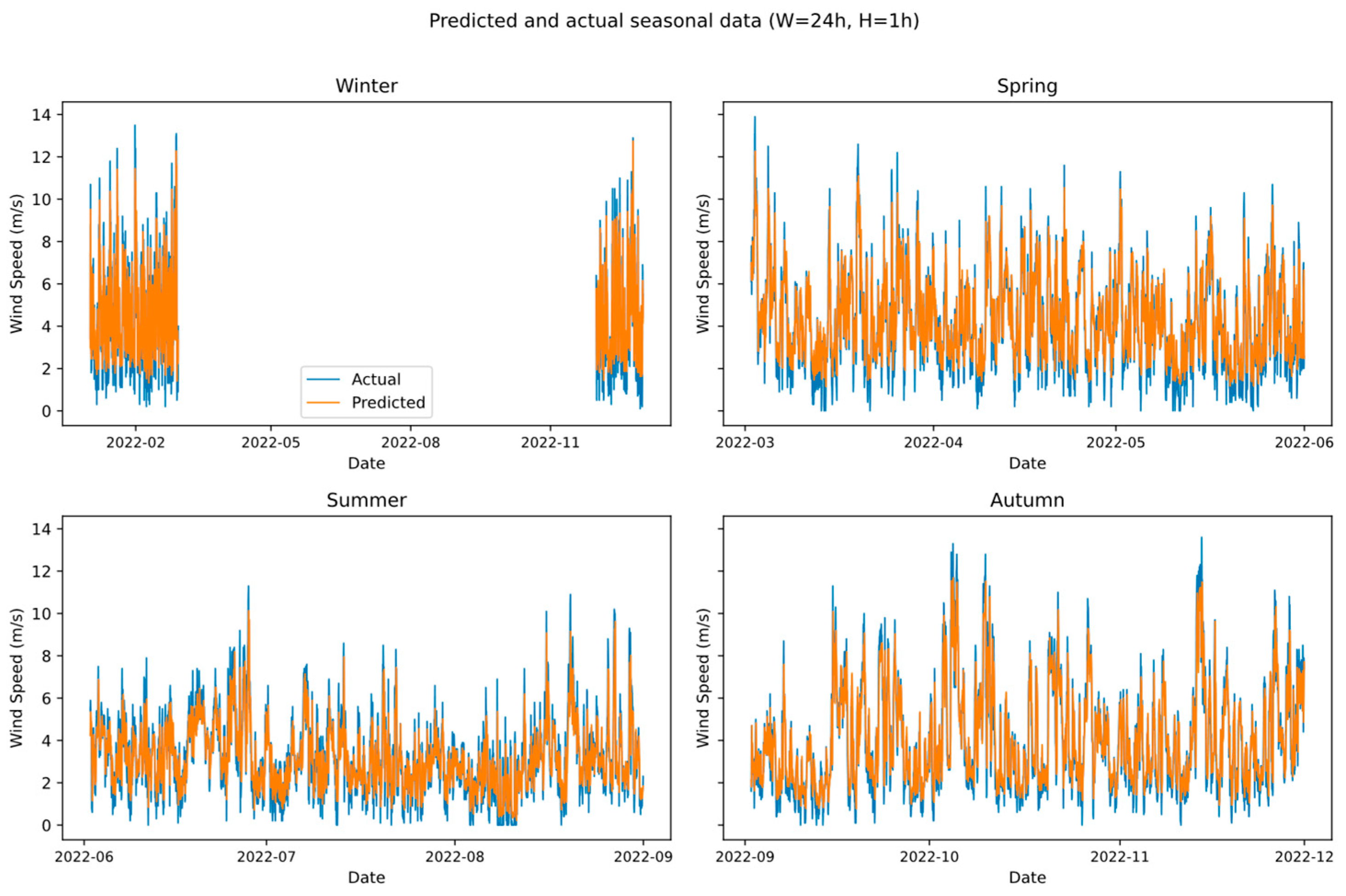
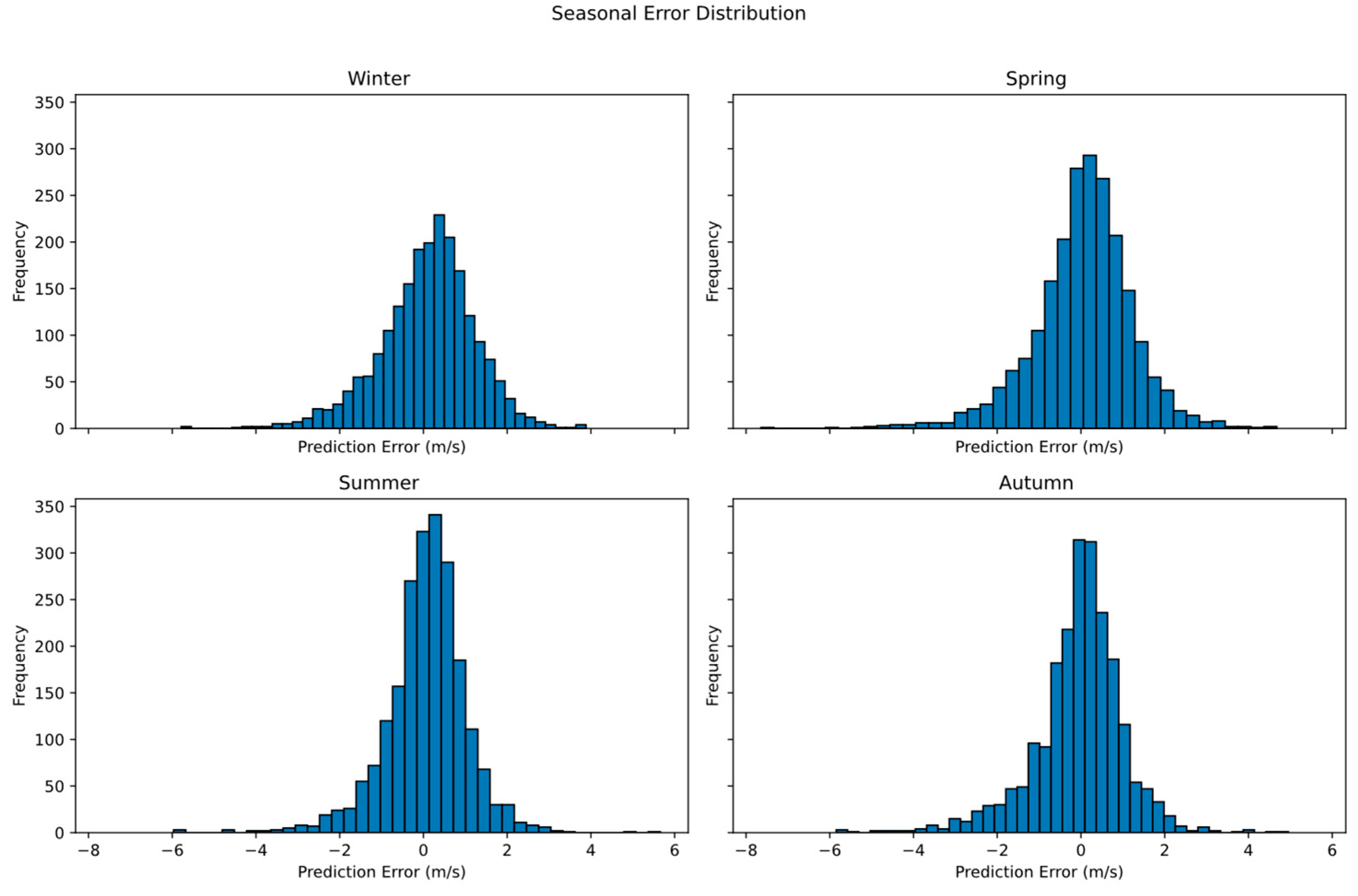
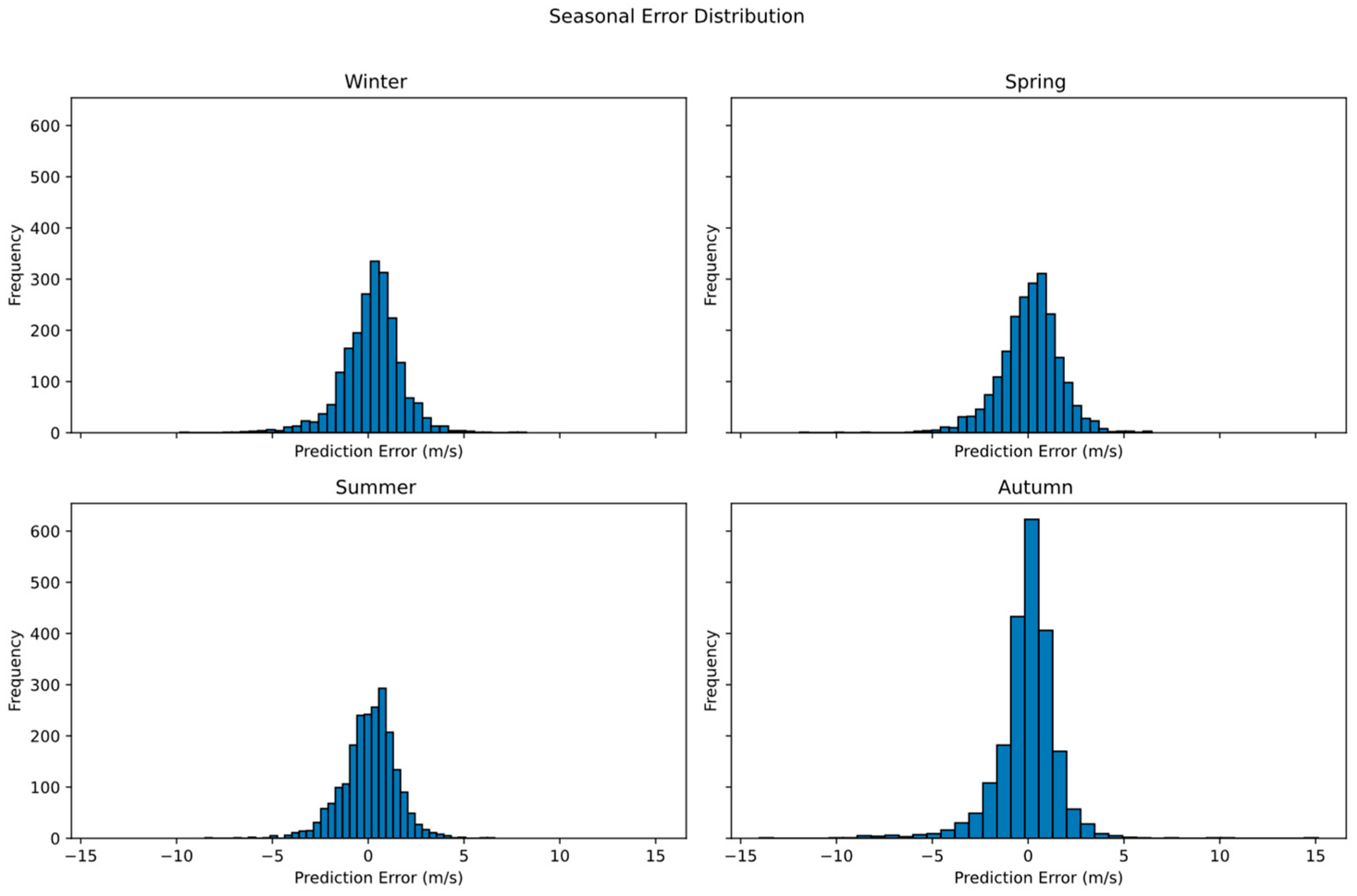
3.3. Seasonal Model Performance
3.3.1. Seasonal Forecast Outcome in LHT
3.3.2. Seasonal Forecast Outcome in XCS
3.3.3. Seasonal Forecast Outcome in ZFD
3.3.4. SSN
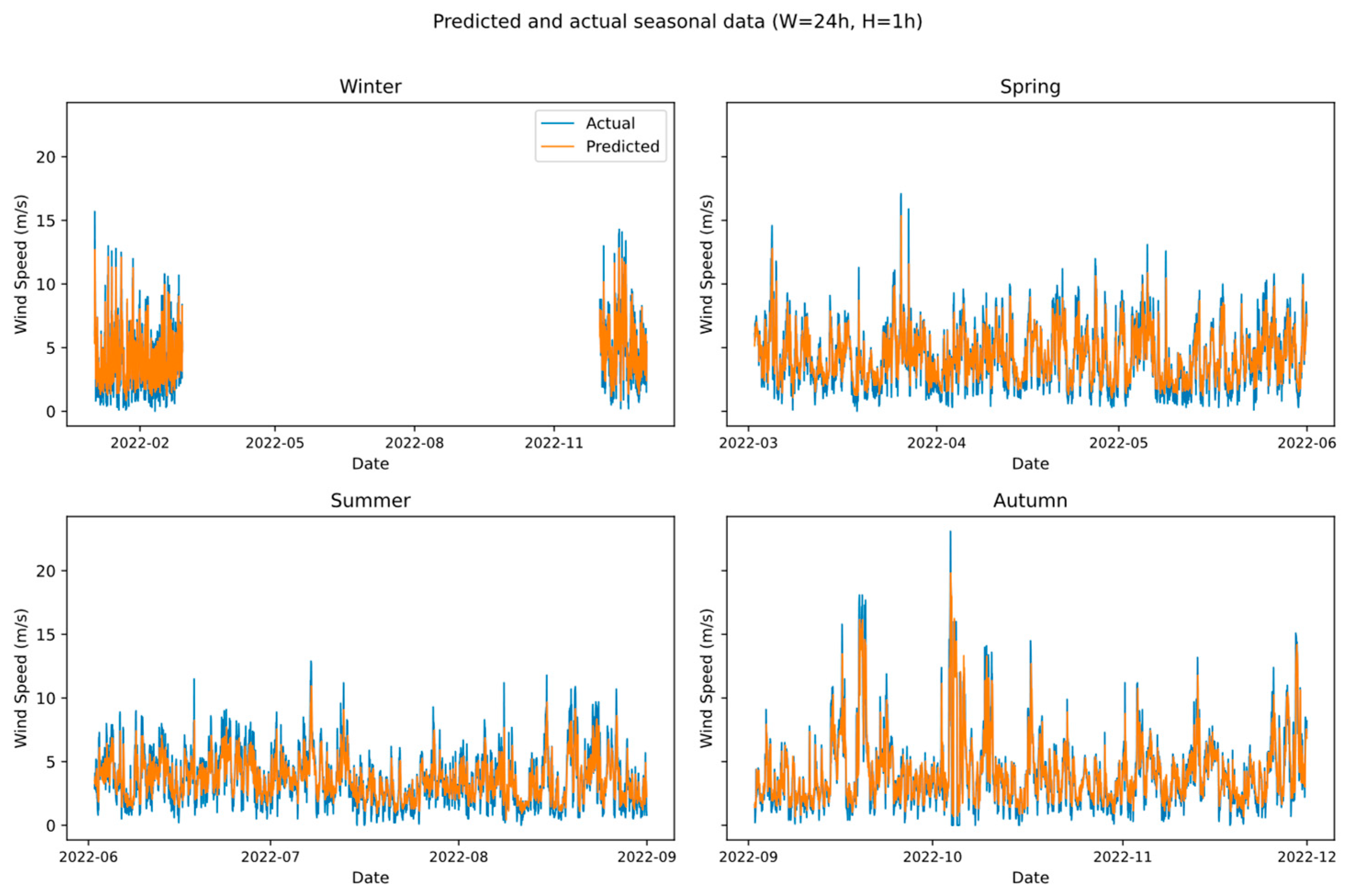
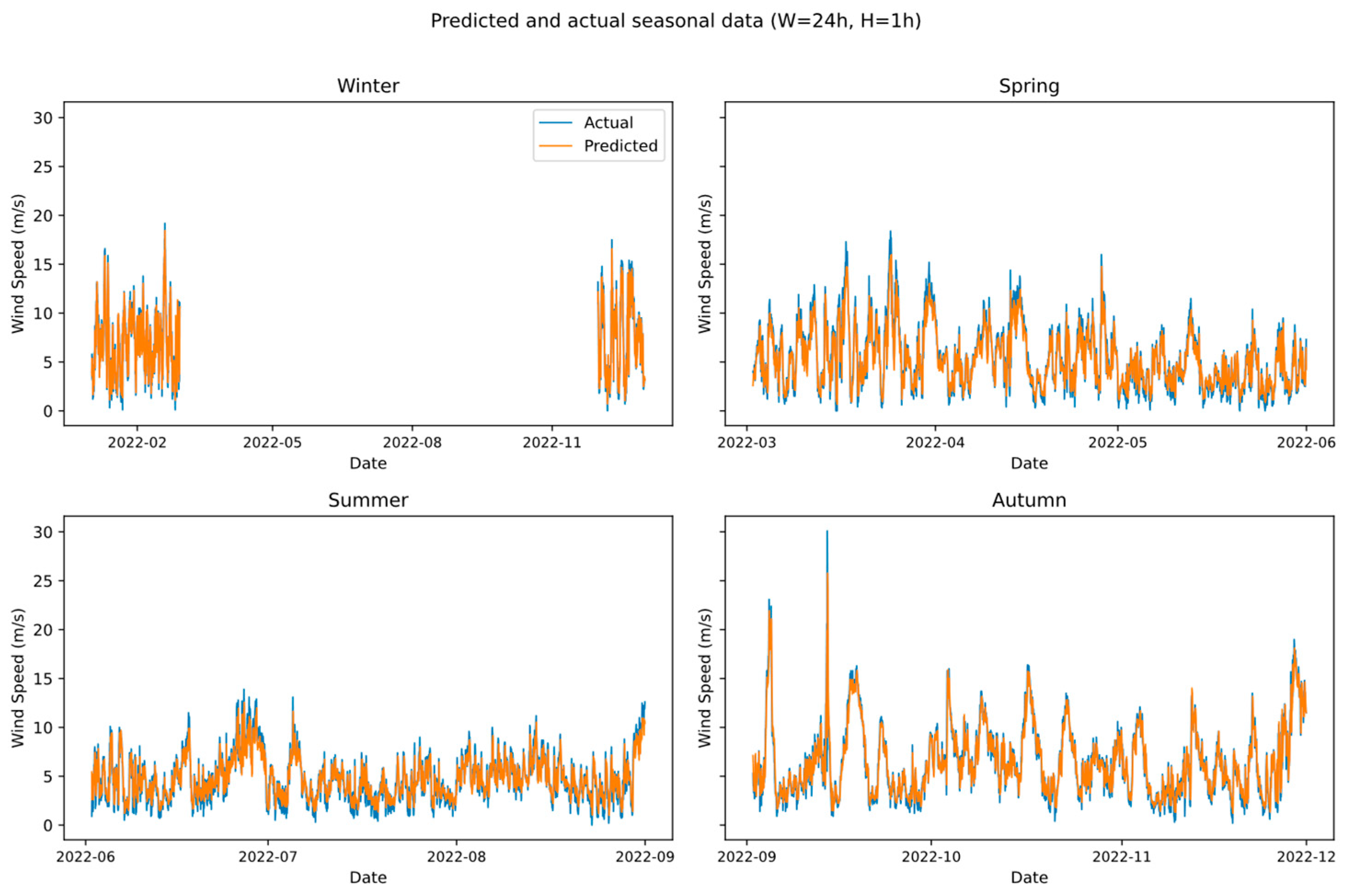
3.4. Forecast Time Series and Prediction Interval
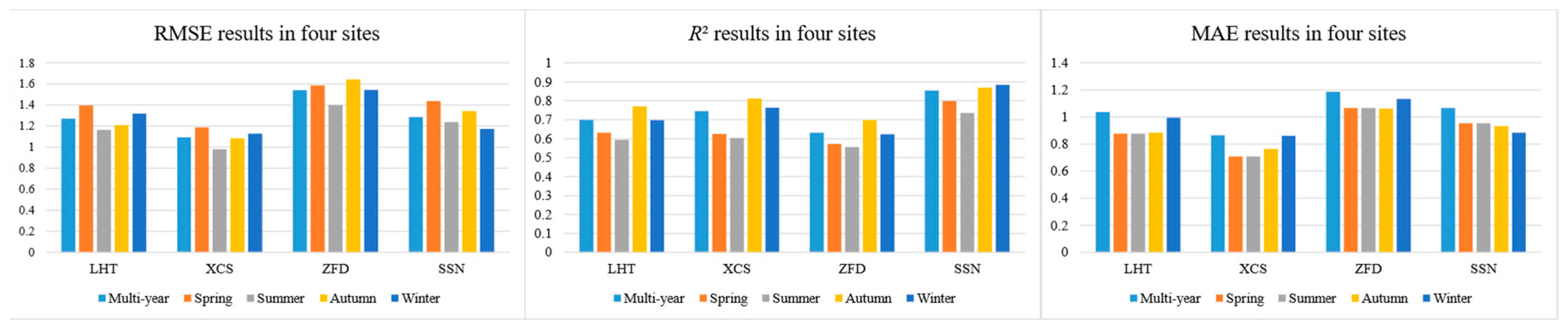
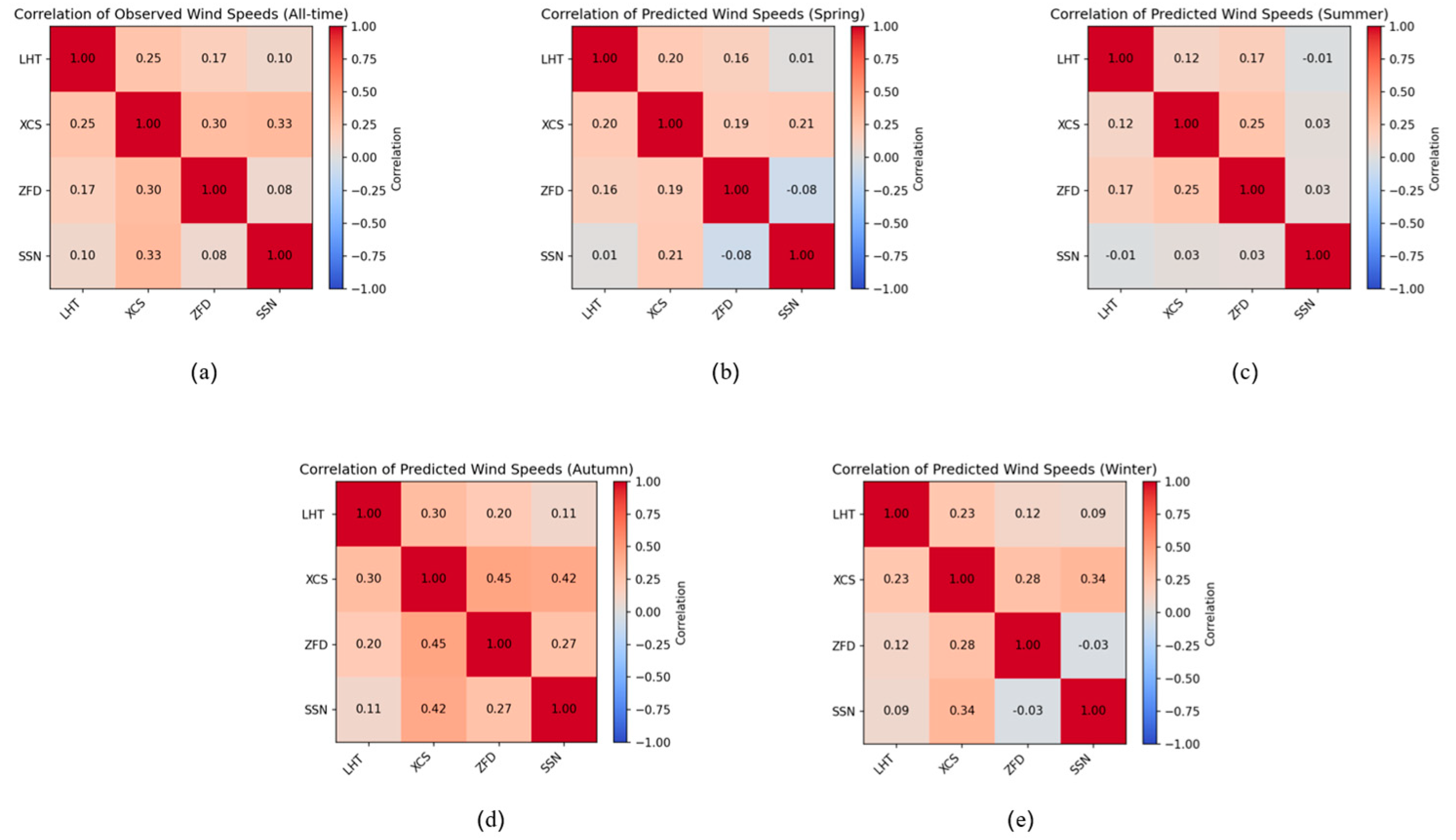
3.5. Results Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BP | Back propagation |
| PSO | Particle swarm optimization |
| LHT | Lao Hu Tan |
| XCS | Xiao Chang Shan |
| ZFD | Zhi Fu Dao |
| SSN | Shen Shan |
| RMSE | Root Mean Square Error |
| NRMSE | Standard deviation |
| MAE | Mean absolute error |
| NRMSE | Normalized Root Mean Square Error |
| RMSE_CI | Root Mean Square Error Credit Interval |
References
- Desalegn, B.; Gebeyehu, D.; Tamrat, B.; Tadiwose, T.; Lata, A. Onshore versus offshore wind power trends and recent study practices in modeling of wind turbines’ life-cycle impact assessments. Clean. Eng. Technol. 2023, 17, 100691. [Google Scholar] [CrossRef]
- Li, J.; Wang, G.; Li, Z.; Yang, S.; Chong, W.T.; Xiang, X. A review on development of offshore wind energy conversion system. Int. J. Energy Res. 2020, 44, 9283–9297. [Google Scholar] [CrossRef]
- Global Wind Energy Council. Global Wind Report 2023; GWEC: Brussels, Belgium, 2023. [Google Scholar]
- Ahmed, S.D.; Al-Ismail, F.S.M.; Shafiullah, M.; Al-Sulaiman, F.A.; El-Amin, I.M. Grid integration challenges of wind energy: A review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- REN21. Renewables 2023 Global Status Report Collection; Report Citation: REN21; REN21: Paris, France, 2023. [Google Scholar]
- Wang, X.; Shne, X.; Ai, X.; Li, S. Short-term wind speed forecasting based on a hybrid model of ICEEMDAN, MFE, LSTM and informer. PLoS ONE 2023, 18, e0289161. [Google Scholar]
- Yousuf, M.U.; Al-Bahadly, I.; Avci, E. Short-term wind speed forecasting based on hybrid MODWT-ARIMA-Markov model. IEEE Access 2021, 9, 79695–79711. [Google Scholar] [CrossRef]
- Clifton, A.; Smith, A.; Fields, M. Wind Plant Preconstruction Energy Estimates. Current Practice and Opportunities; National Renewable Energy Lab (NREL): Golden, CO, USA, 2016. [Google Scholar]
- Dhiman, H.S.; Deb, D. A review of wind speed and wind power forecasting techniques. arXiv 2020, arXiv:2009.02279. [Google Scholar] [CrossRef]
- Han, Y.; Mi, L.; Shen, L.; Cai, C.; Liu, Y.; Li, K.; Xu, G. A short-term wind speed prediction method utilizing novel hybrid deep learning algorithms to correct numerical weather forecasting. Appl. Energy 2022, 312, 118777. [Google Scholar] [CrossRef]
- Meenal, R.; Michael, P.A.; Pamela, D.; Rajasekaran, E. Weather prediction using random forest machine learning model. Indones. J. Electr. Eng. Comput. Sci. 2021, 22, 1208–1215. [Google Scholar] [CrossRef]
- Ren, C.; An, N.; Wang, J.; Li, L.; Hu, B.; Shang, D. Optimal parameters selection for BP neural network based on particle swarm optimization: A case study of wind speed forecasting. Knowl.-Based Syst. 2014, 56, 226–239. [Google Scholar] [CrossRef]
- Acikgoz, H.; Korkmaz, D. Short-term offshore wind speed forecasting approach based on multi-stage decomposition and deep residual network with self-attention. Eng. Appl. Artif. Intell. 2025, 146, 110313. [Google Scholar] [CrossRef]
- Li, Q.; Wang, G.; Wu, X.; Gao, Z.; Dan, B. Arctic short-term wind speed forecasting based on CNN-LSTM model with CEEMDAN. Energy 2024, 299, 131448. [Google Scholar] [CrossRef]
- Zhong, X.; Du, F.; Chen, L.; Wang, Z.; Li, H. Investigating transformer-based models for spatial downscaling and correcting biases of near-surface temperature and wind-speed forecasts. Q. J. R. Meteorol. Soc. 2024, 150, 275–289. [Google Scholar] [CrossRef]
- Wang, Z.; Ying, Y.; Kou, L.; Ke, W.; Wan, J.; Yu, Z.; Liu, H.; Zhang, F. Ultra-short-term offshore wind power prediction based on PCA-SSA-VMD and BiLSTM. Sensors 2024, 24, 444. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.Y.; Deng, E.; Ni, Y.-Q.; Chan, P.-W.; Yang, W.-C.; Tan, Y.-K. Acceleration and Reynolds effects of crosswind flow fields in gorge terrains. Phys. Fluids 2023, 35, 085143. [Google Scholar] [CrossRef]
- Zhao, Y. Research and application on BP neural network algorithm. In International Industrial Informatics and Computer Engineering Conference; Atlantis Press: Dordrecht, The Netherlands, 2015; pp. 1444–1447. [Google Scholar]
- Qu, Z.; Mao, W.; Zhang, K.; Zhang, W.; Li, Z. Multi-step wind speed forecasting based on a hybrid decomposition technique and an improved back-propagation neural network. Renew. Energy 2019, 133, 919–929. [Google Scholar] [CrossRef]
- Viet, D.T.; Phuong, V.V.; Duong, M.Q.; Tran, Q.T. Models for short-term wind power forecasting based on improved artificial neural network using particle swarm optimization and genetic algorithms. Energies 2020, 13, 2873. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, B.; Zhao, Y.; Pan, G. Wind speed prediction of IPSO-BP neural network based on lorenz disturbance. IEEE Access 2018, 6, 53168–53179. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, B.; Liu, C.; Wang, W. Improved BP neural network algorithm to wind power forecast. J. Eng. 2017, 2017, 940–943. [Google Scholar] [CrossRef]
- Bagherpoor, T.; Kazemi Sormoli, S. Forecasting wind speed in Zabol city: A comparative study of CNN, LSTM, and CNN-LSTM models. Agric. Environ. Soc. 2024, 4, 95–107. [Google Scholar]
- Tsai, W.C.; Hong, C.M.; Tu, C.S.; Lin, W.M.; Chen, C.H. A review of modern wind power generation forecasting technologies. Sustainability 2023, 15, 10757. [Google Scholar] [CrossRef]
- Hanifi, S.; Lotfian, S.; Zare-Behtash, H.; Cammarano, A. Offshore wind power forecasting—A new hyperparameter optimisation algorithm for deep learning models. Energies 2022, 15, 6919. [Google Scholar] [CrossRef]
- Arrieta-Prieto, M.; Schell, K.R. Spatially transferable machine learning wind power prediction models: V− logit random forests. Renew. Energy 2024, 223, 120066. [Google Scholar] [CrossRef]
- Hadjoudj, Y.; Pandit, R. A review on data-centric decision tools for offshore wind operation and maintenance activities: Challenges and opportunities. Energy Sci. Eng. 2023, 11, 1501–1515. [Google Scholar] [CrossRef]
- Yang, H.; Tang, J.; Shao, W.; Yin, J.; Liu, B. Wind power data cleaning using RANSAC-based polynomial and linear regression with adaptive threshold. Sci. Rep. 2025, 15, 5105. [Google Scholar] [CrossRef]
- Halder, R.K.; Uddin, M.N.; Uddin, M.A.; Aryal, S.; Khraisat, A. Enhancing K-nearest neighbor algorithm: A comprehensive review and performance analysis of modifications. J. Big Data 2024, 11, 113. [Google Scholar] [CrossRef]
- Caterini, A.L.; Chang, D.E. Deep Neural Networks in a Mathematical Framework; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Foqaha, M.A.M. Email spam classification using hybrid approach of RBF neural network and particle swarm optimization. Int. J. Netw. Secur. Its Appl. 2016, 8, 17–28. [Google Scholar]









| Key Parameters | Value |
|---|---|
| number of neural network layers | 2 |
| number of neurons in the first layer | 150 |
| number of neurons in the second layer | 50 |
| learning rate | 0.000032 |
| batch size | 32 |
| dropout ratio | 0.1–0.3 |
| Key Parameters | Value |
|---|---|
| 0.5 | |
| 1.8 | |
| 2.0 |
| Longitude (°E) | Latitude (°N) | |
|---|---|---|
| LHT | 121.7 | 38.9 |
| XCS | 122.7 | 39.2 |
| ZFD | 121.4 | 37.6 |
| SSN | 122.8 | 30.8 |
| Training Datasets | Index | LHT | XCS | ZFD | SSN |
|---|---|---|---|---|---|
| Multi-year | RMSE | 1.270 | 1.091 | 1.541 | 1.285 |
| R2 | 0.700 | 0.746 | 0.631 | 0.854 | |
| MAE | 0.932 | 0.792 | 1.101 | 0.942 | |
| NRMSE | 0.320 | 0.327 | 0.377 | 0.215 | |
| Skill vs. Persistence | 0.045 | 0.044 | 0.058 | 0.035 | |
| Skill vs. Arima | 0.532 | 0.524 | 0.441 | 0.626 | |
| RMSE_CI | 1.219–1.312 | 1.051–1.130 | 1.462–1.621 | 1.213–1.367 | |
| Spring | RMSE | 1.395 | 1.186 | 1.585 | 1.438 |
| R2 | 0.632 | 0.625 | 0.573 | 0.798 | |
| MAE | 1.036 | 0.865 | 1.186 | 1.066 | |
| NRMSE | 0.330 | 0.358 | 0.373 | 0.262 | |
| Skill vs. Persistence | 0.054 | 0.052 | 0.063 | −0.002 | |
| Skill vs. Arima | 0.401 | 0.395 | 0.358 | 0.553 | |
| RMSE_CI | 1.303–1.363 | 1.095–1.262 | 1.485–1.678 | 1.339–1.537 | |
| Summer | RMSE | 1.164 | 0.981 | 1.399 | 1.237 |
| R2 | 0.594 | 0.604 | 0.555 | 0.735 | |
| MAE | 0.877 | 0.708 | 1.067 | 0.952 | |
| NRMSE | 0.360 | 0.378 | 0.382 | 0.259 | |
| Skill vs. Persistence | 0.063 | 0.054 | 0.068 | 0.029 | |
| Skill vs. Arima | 0.363 | 0.377 | 0.334 | 0.502 | |
| RMSE_CI | 1.093–1.240 | 0.899–1.066 | 1.299–1.499 | 1.165–1.291 | |
| Autumn | RMSE | 1.207 | 1.083 | 1.641 | 1.343 |
| R2 | 0.771 | 0.812 | 0.697 | 0.869 | |
| MAE | 0.883 | 0.763 | 1.062 | 0.932 | |
| NRMSE | 0.300 | 0.311 | 0.402 | 0.205 | |
| Skill vs. Persistence | 0.022 | 0.027 | 0.026 | 0.044 | |
| Skill vs. Arima | 0.588 | 0.577 | 0.458 | 0.646 | |
| RMSE_CI | 1.115–1.293 | 0.995–1.176 | 1.420–1.877 | 1.128–1.580 | |
| Winter | RMSE | 1.318 | 1.128 | 1.543 | 1.172 |
| R2 | 0.697 | 0.764 | 0.624 | 0.884 | |
| MAE | 0.994 | 0.861 | 1.134 | 0.883 | |
| NRMSE | 0.299 | 0.283 | 0.354 | 0.165 | |
| Skill vs. Persistence | 0.018 | 0.021 | 0.055 | 0.017 | |
| Skill vs. Arima | 0.588 | 0.515 | 0.393 | 0.662 | |
| RMSE_CI | 1.229–1.387 | 1.062–1.186 | 1.431–1.647 | 1.116–1.248 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, S.; Jin, J.; Dai, S. Seasonal and Multi-Year Wind Speed Forecasting Using BP-PSO Neural Networks Across Coastal Regions in China. Sustainability 2025, 17, 10127. https://doi.org/10.3390/su172210127
Jiang S, Jin J, Dai S. Seasonal and Multi-Year Wind Speed Forecasting Using BP-PSO Neural Networks Across Coastal Regions in China. Sustainability. 2025; 17(22):10127. https://doi.org/10.3390/su172210127
Chicago/Turabian StyleJiang, Shujie, Jiayi Jin, and Shu Dai. 2025. "Seasonal and Multi-Year Wind Speed Forecasting Using BP-PSO Neural Networks Across Coastal Regions in China" Sustainability 17, no. 22: 10127. https://doi.org/10.3390/su172210127
APA StyleJiang, S., Jin, J., & Dai, S. (2025). Seasonal and Multi-Year Wind Speed Forecasting Using BP-PSO Neural Networks Across Coastal Regions in China. Sustainability, 17(22), 10127. https://doi.org/10.3390/su172210127






