Addressing the Collective Action Dilemma in Resident-Led Urban Regeneration: Designing and Verifying a Multi-Dimensional Policy Lever System Through Evolutionary Game Theory
Abstract
1. Introduction
- Resource-allocation levers (the area-expansion coefficient (w) and the expansion benefit-sharing coefficient (v)), which regulate value creation and distribution structures;
- Cost-sharing levers (the expansion-purchase coefficient (p) and the original-area reconstruction payment coefficient (q)), which refine the allocation of contribution burdens;
- Behavioral-intervention levers (the cost-burden perception coefficient (e) and the accident-risk perception coefficient (d)), which quantify and model principles from behavioral economics (e.g., loss aversion and risk perception) to capture and correct residents’ cognitive biases.
- Under a bounded-rationality setting involving the government–resident–contractor triad, how do multi-dimensional policy levers jointly determine the system’s evolutionary trajectories and stable equilibria?
- For resource allocation (w,v), cost sharing (p,q), and behavioral intervention (e,d), what critical thresholds and nonlinear effects emerge, and how do their interactions reshape the basins of attraction and the probabilities of convergence across equilibria?
- Confronting the common practical bottleneck (E3)—characterized by proactive governments and contractors but indifferent residents—what phased policy portfolios can effectively steer the system toward the ideal three-party cooperative equilibrium?
2. Literature Review
2.1. Fragmentation of Policy Instruments for Resident-Led Urban Regeneration and the Absence of an Integrative Framework
2.2. The Pivotal Role of Behavioral Economics in Decision-Making for Resident-Led Urban Regeneration
2.3. Applications of the Evolutionary-Game Approach and Limitations in Integrating Behavioral Factors
2.4. Innovations of This Study
3. Building and Analysis of Evolutionary Game Model
3.1. Assumptions and Key Variables
3.2. Establishing and Solving the Evolutionary Game Model
+ (1 − y)·z·(-Cg1-s·Cg7) + (1 − y)·(1 − z)·(-Cg1-s·Cg7)
+ y·(1 − z)·(Bg1 + N·w·H·(p·(1 + u·wl)-m)-Cg1-N·wo·Cg3-Rg1-Rg2)
+ (1 − y)·z·(-Cg1-s·Cg7) + (1 − y)·(1 − z)·(-Cg1-s·Cg7))-(y·z·(Bg2-Cg4) + y·(1 − z)·(Bg2-Cg4)
+ (1 − y)·z·(Bg4-Cg4-N·H·r-s·Cg6) + (1 − y)·(1 − z)·(Bg4-Cg4-N·H·r-s·Cg6)))
+ x·(1 − z)·(Br1-e·Cr2-Cr5-Cr7 + Rg1 + Rg2) + (1 − x)·(1 − z)·(Br2-e·Cr3-Cr5-Cr7)
+ x·(1 − z)·(Br3-e·Cr4-Cr6-d·s·Cr8) + (1 − x)·(1 − z)·(Br3-Cr5-d·s·Cr8)
-Cr5-Cr7 + Rg1) + (1 − x)·z·(N·H·j-e·q·N·H·m-Cr5-Cr7) + x·(1 − z)·(N·H·(w + u·wl + w·u·wl)
-e·(p·N·w·H·(1 + u·wl) + H·m·N)-Cr5-Cr7 + Rg1 + Rg2) + (1 − x)·(1 − z)·(N·H·j-e·N·H·m-Cr5-Cr7))
-(x·z·(N·H·i-e·N·H·r-Cr6-d·s·Cr8) + (1 − x)·z·(N·H·i-Cr5-d·s·Cr8)
+ x·(1 − z)·(N·H·i-e·N·H·r-Cr6-d·s·Cr8) + (1 − x)·(1 − z)·(N·H·i-Cr5-d·s·Cr8)))
+ x·(1 − y)·(Bv7-Cv4-Cv6-s·Cv8) + (1 − x)·(1 − y)·(Bv7-Cv4-Cv6-s·Cv8)
+ (1 − x)·(1 − y)·(Bv7-Cv4-Cv7-s·Cv9)
+ (1 − x)·y·((1-q)·N·H·m + Bv6-N·H·f-Cv6) + x·(1 − y)·(N·H·r-N·H·g-Cv6-s·Cv8)
+ (1 − x)·(1 − y)·(N·H·r-N·H·g-Cv6-s·Cv8))-(x·y·(N·(1 + w)·H·m-N·(1 + w)·H·f-Cv7)
+ (1 − x)·y·(N·H·m-N·H·f-Cv7) + x·(1 − y)·(N·H·r-N·H·g
-Cv7-s·Cv9) + (1 − x)·(1 − y)·(N·H·r-N·H·g-Cv7-s·Cv9)))
3.3. Analysis of Points of Equilibrium Under Evolutionarily Stable Strategy
- Initiation phase: Systemic Stalemate (stable at E8(0,0,0))
- Growth phase: Resident Participation Bottleneck (stable at E3(1,0,1))
- Maturation phase: Realization of Collaborative Governance (stable at E1(1,1,1))
4. Simulation Results and Analysis
4.1. Principles for Parameter Value Assignment and Calibration Strategy
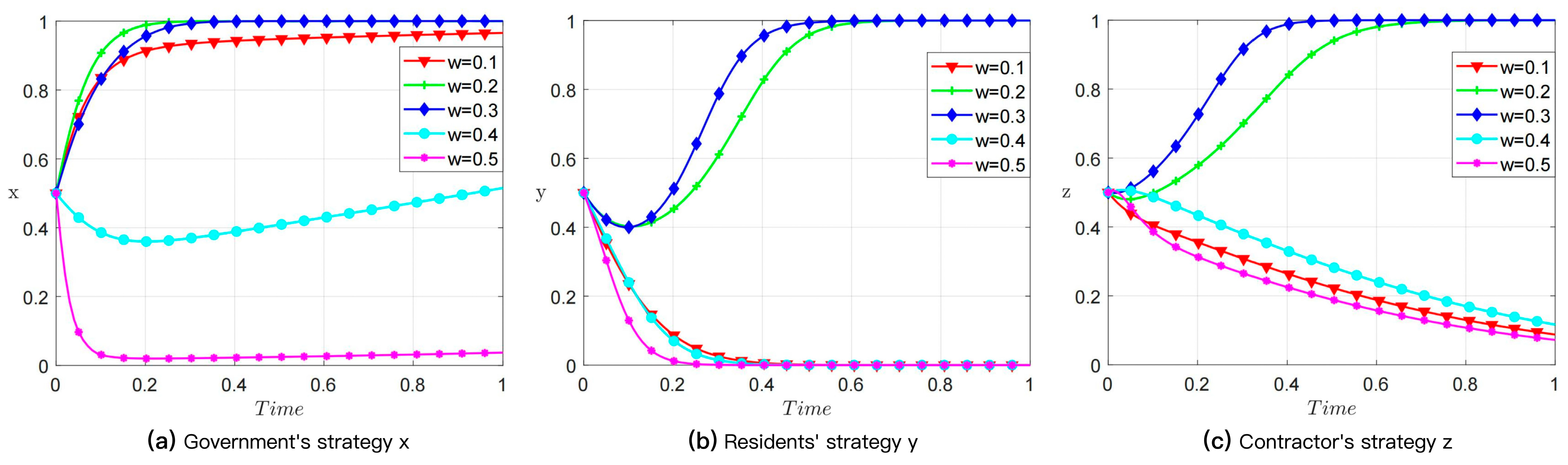
4.2. Area-Expansion Coefficient (w)
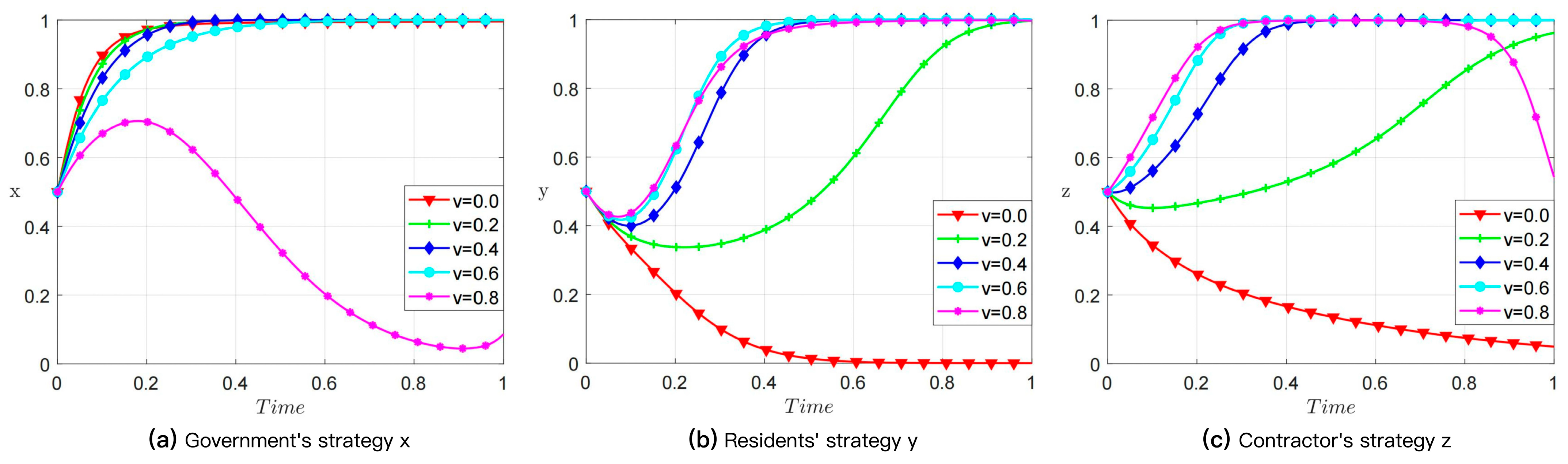
4.3. Expansion Benefit-Sharing Coefficient (v)
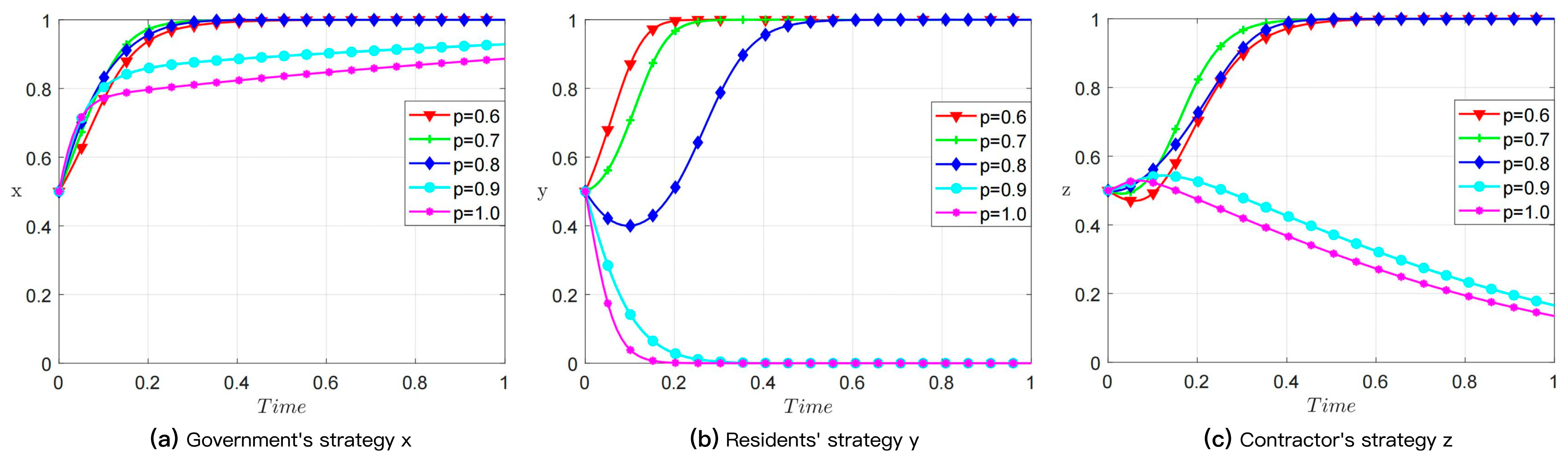
4.4. Expansion-Purchase Coefficient (p)
4.5. Original-Area Reconstruction Payment Coefficient (q)
4.6. Cost-Burden Perception Coefficient (e)
4.7. Accident-Risk Perception Coefficient (d)
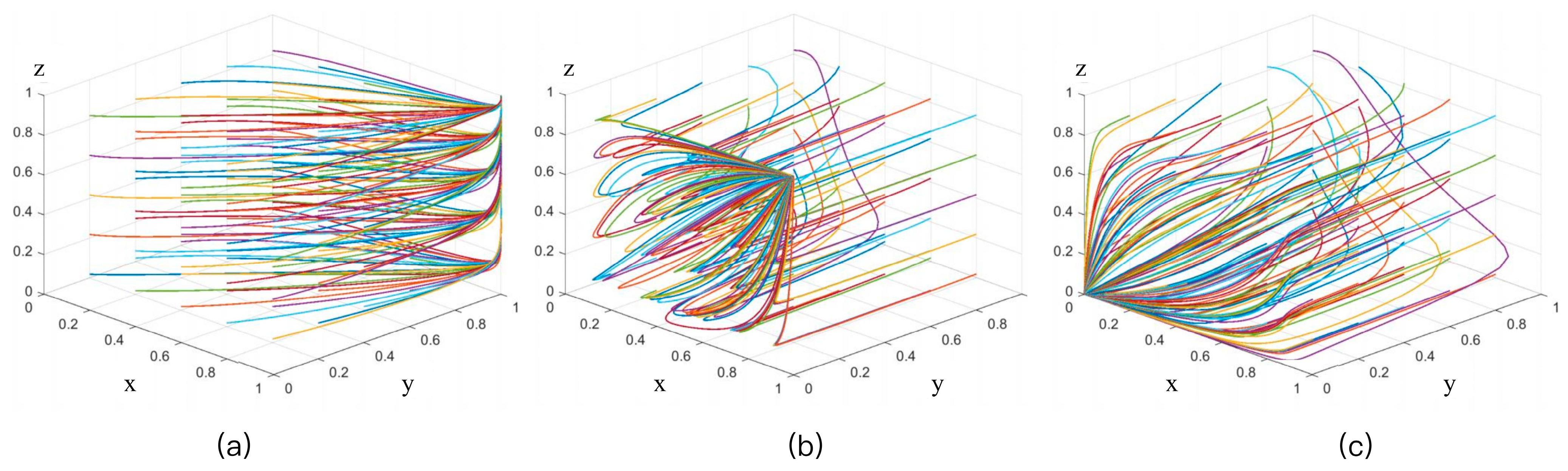
4.8. Sensitivity and Robustness Analysis (w,p,e)
5. Discussion
5.1. Mechanisms of Key Parameters and Policy Implications
5.2. Systemic Coordination of the Parameter System and Pathways to Resolving the E3 Dilemma
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Haase, A.; Rink, D.; Grossmann, K.; Bernt, M.; Mykhnenko, V. Conceptualizing urban shrinkage. Environ. Plan. A Econ. Space 2014, 46, 1519–1534. [Google Scholar] [CrossRef]
- Haase, D.; Haase, A.; Rink, D. Conceptualizing the nexus between urban shrinkage and ecosystem services. Landsc. Urban Plan. 2014, 132, 159–169. [Google Scholar] [CrossRef]
- Lee, D.; Feiertag, P.; Unger, L. Co-production, co-creation or co-design of public space? A systematic review. Cities 2024, 154, 105372. [Google Scholar] [CrossRef]
- Hoffman, J. Toward civic co-production: Using worldbuilding to go beyond participation in urban planning and enact more equitable cities. Front. Sustain. Cities 2022, 4, 907541. [Google Scholar] [CrossRef]
- Bovaird, T. Beyond engagement and participation: User and community coproduction of public services. Public Adm. Rev. 2007, 67, 846–860. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Zhu, D. Co-creation of community micro-renewals: Model analysis and case studies in Shanghai, China. Habitat Int. 2023, 142, 102951. [Google Scholar]
- Zhong, X.; Leung, H.H. Exploring participatory microregeneration as sustainable renewal of built heritage community: Two case studies in Shanghai. Sustainability 2019, 11, 1617. [Google Scholar] [CrossRef]
- Bao, L.; Sun, Y.; Wang, H.; Liu, Z. Study on a Paradigm of Micro-Regeneration of Urban Community—Taking Three Cases of House Upgrading in Xiaoxihu Traditional Block, Nanjing. In International Seminar on Urban Form; Springer Nature: Cham, Switzerland, 2022; pp. 685–700. [Google Scholar]
- Zhao, N.; Liu, Y.; Wang, J. Network governance and the evolving urban regeneration policymaking in China: A case study of insurgent practices in enninglu redevelopment project. Sustainability 2021, 13, 2280. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, J. Collective Action of Autonomous Regeneration in Historic Areas from the Perspective of Selective Incentives: Based on the Empirical Study of “Xiaoxihu” in Nanjing. City Plan. Rev. 2023, 47, 38–48. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, Y. Urban Renewal: Reconstruction or Self-Renewal?: A Case Study of Xiamen Lakeside Transformation. Urban Dev. Stud. 2021, 28, 1–6. [Google Scholar]
- Wang, R.; Wu, H.; Chiles, R.; Yang, Y. Sustainability outcomes and policy implications: Evaluating China’s “old urban neighborhood renewal” experiment. PLoS ONE 2024, 19, e0301380. [Google Scholar] [CrossRef]
- Liang, Y.; Qian, Q.K.; Li, B.; An, Y.; Shi, L.A. critical assessment on China’s old neighborhood renovation: Barriers analysis, solutions and future research prospects. Energy Build. 2025, 332, 115407. [Google Scholar] [CrossRef]
- Li, D.; Xiong, Q.; Huang, G.; Du, B.; Feng, H. How to share benefits of old community renewal project in China? An improved Shapley Value approach. Habitat Int. 2022, 126, 102611. [Google Scholar] [CrossRef]
- The Communist Party of China Central Committee and the State Council. Opinions on Continuously Promoting Urban Renewal Actions. Available online: https://www.gov.cn/zhengce/202505/content_7023880.htm (accessed on 1 October 2025).
- General Office of the Ministry of Natural Resources. Natural Resources Ministry Policy on Supporting Old Neighborhood Renewal. Available online: https://www.gov.cn/zhengce/zhengceku/202406/content_6957452.htm (accessed on 1 October 2025).
- Implementation Opinions of the General Office of Zhejiang Provincial People’s Government on Comprehensive Promotion of Urban Old Residential Community Renovation. Available online: https://www.zj.gov.cn/art/2020/12/7/art_1229620632_2403176.html (accessed on 1 October 2025).
- Wang, Y.; Wu, F.; Zhang, F. Participatory micro-regeneration: Governing urban redevelopment in Qinghe, Beijing. Urban Geogr. 2025, 46, 21–42. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Wang, Y.; Chen, J.; Wu, H. How to Improve Collaboration in Sustainable Urban Community Renewal? An Evolutionary Game Model. Land 2025, 14, 1863. [Google Scholar] [CrossRef]
- Lu, W.; Qiu, B.; Liu, D.; Yu, X.; Chen, J. Collective action dilemmas and solutions in self-led renewal of old communities: A complex-system perspective—The case of Zhigong Xincun. Urban Dev. Stud. 2025, 32, 1–7. (In Chinese) [Google Scholar]
- Wang, X.; Zhao, Y.; Zhang, J. Self-led renewal practice and mechanisms in Zhigong Xincun. City Plan. 2025, 49, 67–73. [Google Scholar]
- Liu, X.; Zhao, Y.; Wang, C. Decision indicators for urban old community renewal: A multi-stakeholder approach in Guangze, China. J. Asian Archit. Build. Eng. 2025, 1–19. [Google Scholar] [CrossRef]
- Haiyirete, X.; Liu, X.; Wang, J. Evolutionary Game Study of Resident Financing Behavior in the Construction and Renewal of Infrastructure from a Sustainable Perspective. J. Urban Plan. Dev. 2025, 151, 04025053. [Google Scholar] [CrossRef]
- Huang, R.; Liu, G.; Li, K.; Liu, Z.; Fu, X.; Wen, J. Evolution of residents’ cooperative behavior in neighborhood renewal: An agent-based computational approach. Comput. Environ. Urban Syst. 2023, 105, 102022. [Google Scholar] [CrossRef]
- He, S.; Wu, F. Property-led redevelopment in post-reform China: A case study of Xintiandi redevelopment project in Shanghai. J. Urban Aff. 2005, 27, 1–23. [Google Scholar]
- Gao, Y.; Liu, J.; Zhang, J.; Xie, H. Modeling the Evolutionary Mechanism of Multi-Stakeholder Decision-Making in the Green Renovation of Existing Residential Buildings in China. Buildings 2025, 15, 2758. [Google Scholar] [CrossRef]
- Wu, F. Planning centrality, market instruments: Governing Chinese urban transformation under state entrepreneurialism. Urban Stud. 2018, 55, 1383–1399. [Google Scholar] [CrossRef]
- Cejudo, G.M.; Michel, C.L. Instruments for policy integration: How policy mixes work together. Sage Open 2021, 11, 21582440211032161. [Google Scholar] [CrossRef]
- Wang, L.; Ren, P.; Shan, Y.; Zhang, G. Subsidy Ceilings and Sequential Synergy: Steering Sustainable Outcomes Through Dynamic Thresholds in China’s Urban Renewal Tripartite Game. Sustainability 2025, 17, 8713. [Google Scholar] [CrossRef]
- Zhu, Y.; Song, J.; Bai, Y. China’s Urban Regeneration Evolution from 1949 to 2022: From the Perspective of Governance Mode. Land 2024, 13, 1806. [Google Scholar] [CrossRef]
- Banerjee, S.; Savani, M.; Shreedhar, G. Public support for ‘soft’ versus ‘hard’ public policies: Review of the evidence. J. Behav. Public Adm. 2021, 4. [Google Scholar] [CrossRef]
- Banerjee, S.; John, P. Behavioral public policy: Past, present, & future. Policy Soc. 2025, puaf012. [Google Scholar] [CrossRef]
- D’Alpaos, C.; Bragolusi, P. The willingness to pay for seismic retrofitted buildings: A discrete choice experiment. Int. J. Disaster Risk Reduct. 2022, 71, 102814. [Google Scholar] [CrossRef]
- Bao, H.X. Between carrots and sticks, from intentions to actions: Behavioural interventions for housing decisions. Hous. Theory Soc. 2024, 41, 292–317. [Google Scholar] [CrossRef]
- Parker, G.; Wargent, M.; Salter, K.; Yuille, A. Neighbourhood planning in England: A decade of institutional learning. Prog. Plan. 2023, 174, 100749. [Google Scholar] [CrossRef]
- Salter, K.; Parker, G.; Wargent, M. Localism and the will to housing: Neighbourhood development plans and their role in local housing site delivery in England. Plan. Pract. Res. 2023, 38, 253–273. [Google Scholar]
- Gallent, N. Re-connecting ‘people and planning’: Parish plans and the English localism agenda. Town Plan. Rev. 2013, 84, 371–396. [Google Scholar] [CrossRef]
- Roberts, P. The evolution, definition and purpose of urban regeneration. In Urban Regeneration: A Handbook; SAGE Publications: London, UK, 2000; Volume 1, pp. 9–36. [Google Scholar]
- Pugalis, L.; Bentley, G. (Re) appraising place-based economic development strategies. Local Econ. 2014, 29, 273–282. [Google Scholar]
- Raco, M.; Ward, C.; Brill, F.; Sanderson, D.; Freire-Trigo, S.; Ferm, J.; Hamiduddin, I.; Livingstone, N. Towards a virtual statecraft: Housing targets and the governance of urban housing markets. Prog. Plan. 2022, 166, 100655. [Google Scholar] [CrossRef]
- dos Santos Figueiredo, Y.D.; Prim, M.A.; Dandolini, G.A. Urban regeneration in the light of social innovation: A systematic integrative literature review. Land Use Policy 2022, 113, 105873. [Google Scholar] [CrossRef]
- Gallent, N.; Hamiduddin, I.; Madeddu, M. Localism, down-scaling and the strategic dilemmas confronting planning in England. Town Plan. Rev. 2013, 84, 563–582. [Google Scholar] [CrossRef]
- Ansell, C.; Gash, A. Collaborative governance in theory and practice. J. Public Adm. Res. Theory 2008, 18, 543–571. [Google Scholar] [CrossRef]
- Bianchi, C.; Nasi, G.; Rivenbark, W.C. Implementing collaborative governance: Models, experiences, and challenges. Public Manag. Rev. 2021, 23, 1581–1589. [Google Scholar] [CrossRef]
- Howlett, M.; Rayner, J. Design principles for policy mixes: Cohesion and coherence in ‘new governance arrangements’. Policy Soc. 2007, 26, 1–18. [Google Scholar] [CrossRef]
- Kai-Ineman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 363–391. [Google Scholar] [CrossRef]
- Barberis, N.C. Thirty years of prospect theory in economics: A review and assessment. J. Econ. Perspect. 2013, 27, 173–196. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Abdellaoui, M.; Bleichrodt, H.; Paraschiv, C. Loss aversion under prospect theory: A parameter-free measurement. Manag. Sci. 2007, 53, 1659–1674. [Google Scholar] [CrossRef]
- Prelec, D. The probability weighting function. Econometrica 1998, 66, 497–527. [Google Scholar] [CrossRef]
- Rogers, R.W. A protection motivation theory of fear appeals and attitude change1. J. Psychol. 1975, 91, 93–114. [Google Scholar] [CrossRef]
- Wakker, P.; Tversky, A. An axiomatization of cumulative prospect theory. J. Risk Uncertain. 1993, 7, 147–175. [Google Scholar] [CrossRef]
- Slovic, P. Perception of risk. In The Perception of Risk; Routledge: Oxfordshire, UK, 2016; pp. 220–231. [Google Scholar]
- Brown, V.J. Risk perception: It’s personal. Environ. Health Perspect. 2014, 122, A276–A279. [Google Scholar] [CrossRef] [PubMed]
- Maddux, J.E.; Rogers, R.W. Protection motivation and self-efficacy: A revised theory of fear appeals and attitude change. J. Exp. Soc. Psychol. 1983, 19, 469–479. [Google Scholar] [CrossRef]
- Perc, M.; Gómez-Gardenes, J.; Szolnoki, A.; Floría, L.M.; Moreno, Y. Evolutionary dynamics of group interactions on structured populations: A review. J. R. Soc. Interface 2013, 10, 20120997. [Google Scholar] [CrossRef]
- Chen, Z.; Ma, C.; Lin, C. Revealing the Impact of Investment Benefits on Marketing Decision in Public Infrastructures Based on Game Theory: Case Study of Large-Scale Exhibition Infrastructures in China. Buildings 2024, 14, 715. [Google Scholar] [CrossRef]
- Liu, L.; Wang, S.; Chen, X.; Perc, M. Evolutionary dynamics in the public goods games with switching between punishment and exclusion. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 103105. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Long, Z.; Jia, K.; Zhang, X.; Liang, X. Tactics to Balance Benefits among Stakeholders in Government-Led Urban Renewal: Case Study in Guangzhou, China. J. Urban Plan. Dev. 2024, 150, 05024034. [Google Scholar] [CrossRef]
- Zhu, X.X.; Mu, Q.R.; Liang, W.Z. An innovative strategic choice for stakeholders in the Chinese traditional commercial street renewal using evolutionary game theory. J. Innov. Knowl. 2022, 7, 100225. [Google Scholar] [CrossRef]
- Zhang, J.; Gu, X. Multi-stakeholder perspectives on urban regeneration: A spatial gradient analysis of heat and pollution effects. Int. J. Biometeorol. 2025, 69, 1325–1345. [Google Scholar] [CrossRef]
- Su, C.; Xu, Z.; Wang, X.; Li, B. Research on the Co-Evolution Mechanism of Electricity Market Entities Enabled by Shared Energy Storage: A Tripartite Game Perspective Incorporating Dynamic Incentives/Penalties and Stochastic Disturbances. Systems 2025, 13, 817. [Google Scholar] [CrossRef]
- Kim, J.; Yook, S.H.; Kim, Y. Reciprocity in spatial evolutionary public goods game on double-layered network. Sci. Rep. 2016, 6, 31299. [Google Scholar] [CrossRef]
- Sasaki, T.; Okada, I.; Uchida, S.; Chen, X. Commitment to cooperation and peer punishment: Its evolution. Games 2015, 6, 574–587. [Google Scholar] [CrossRef]
- Ogbo, N.B.; Elragig, A.; Han, T.A. Evolution of coordination in pairwise and multi-player interactions via prior commitments. Adapt. Behav. 2022, 30, 257–277. [Google Scholar] [CrossRef]
- Barrett, S. Coordination vs. voluntarism and enforcement in sustaining international environmental cooperation. Proc. Natl. Acad. Sci. USA 2016, 113, 14515–14522. [Google Scholar] [CrossRef] [PubMed]
- Han, T.A.; Lenaerts, T.; Santos, F.C.; Pereira, L.M. Voluntary safety commitments provide an escape from over-regulation in AI development. Technol. Soc. 2022, 68, 101843. [Google Scholar] [CrossRef]
- Han, T.A. Institutional incentives for the evolution of committed cooperation: Ensuring participation is as important as enhancing compliance. J. R. Soc. Interface 2022, 19, 20220036. [Google Scholar] [CrossRef] [PubMed]
- Alalawi, Z.; Bova, P.; Cimpeanu, T.; Di Stefano, A.; Duong, M.H.; Domingos, E.F.; Han, T.A.; Krellner, M.; Ogbo, N.B.; Powers, S.T.; et al. Trust AI regulation? Discerning users are vital to build trust and effective AI regulation. arXiv 2024, arXiv:2403.09510. [Google Scholar] [CrossRef]
- Encarnação, S.; Santos, F.P.; Santos, F.C.; Blass, V.; Pacheco, J.M.; Portugali, J. Paradigm shifts and the interplay between state, business and civil sectors. R. Soc. Open Sci. 2016, 3, 160753. [Google Scholar] [CrossRef]
- Alalawi, Z.; Zeng, Y. Toward understanding the interplay between public and private healthcare providers and patients: An agent-based simulation approach. EAI Endorsed Trans. Ind. Networks Intell. Syst. 2020, 7, e04. [Google Scholar] [CrossRef]
- Bova, P.; Di Stefano, A. Both eyes open: Vigilant incentives help auditors improve ai safety. J. Phys. Complex. 2024, 5, 025009. [Google Scholar] [CrossRef]
- Liu, J.; Yu, J.; Yin, Y.; Wei, Q. An evolutionary game approach for private sectors’ behavioral strategies in China’s green energy public–private partnership projects. Energy Rep. 2021, 7, 696–715. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Smith, J.M. Evolution and the Theory of Games. In Did Darwin Get It Right? Essays on Games, Sex and Evolution; Springer: Boston, MA, USA, 1982; pp. 202–215. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Lindell, M.K.; Whitney, D.J. Correlates of household seismic hazard adjustment adoption. Risk Anal. 2000, 20, 13–26. [Google Scholar] [CrossRef]
- United Nations General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development (A/RES/70/1). 2015. Available online: https://sdgs.un.org/2030agenda (accessed on 1 September 2025).
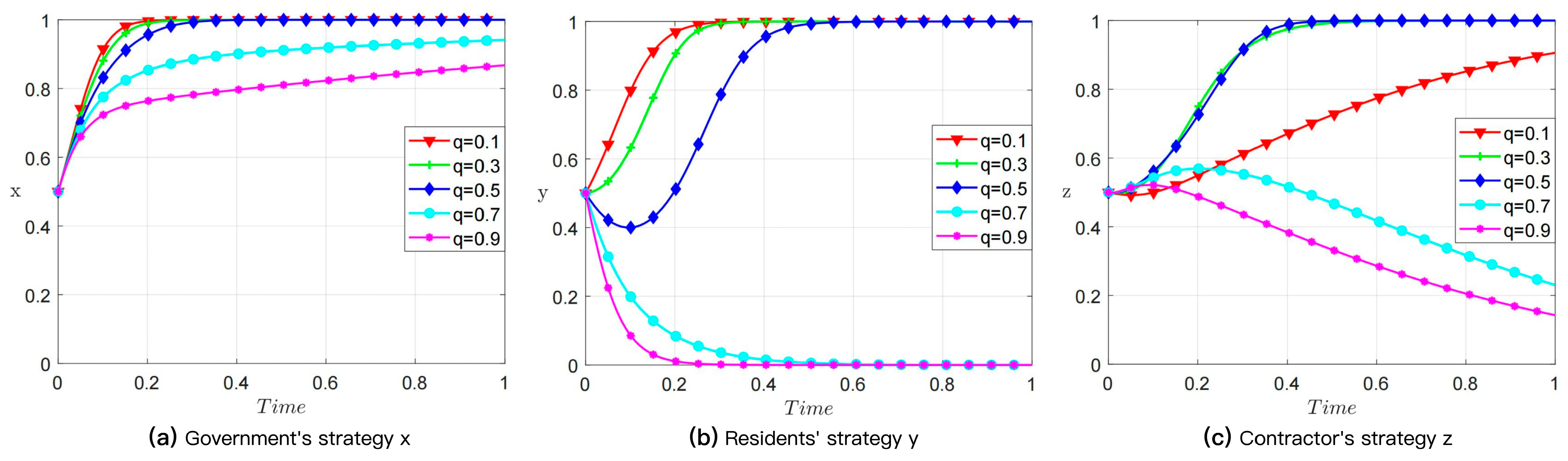
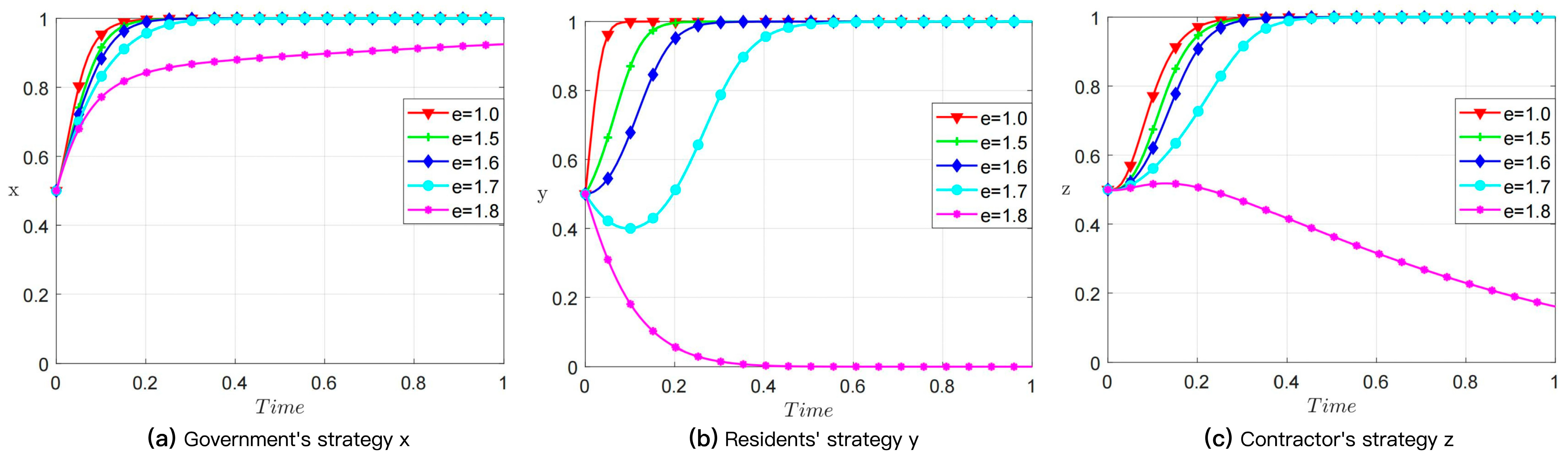
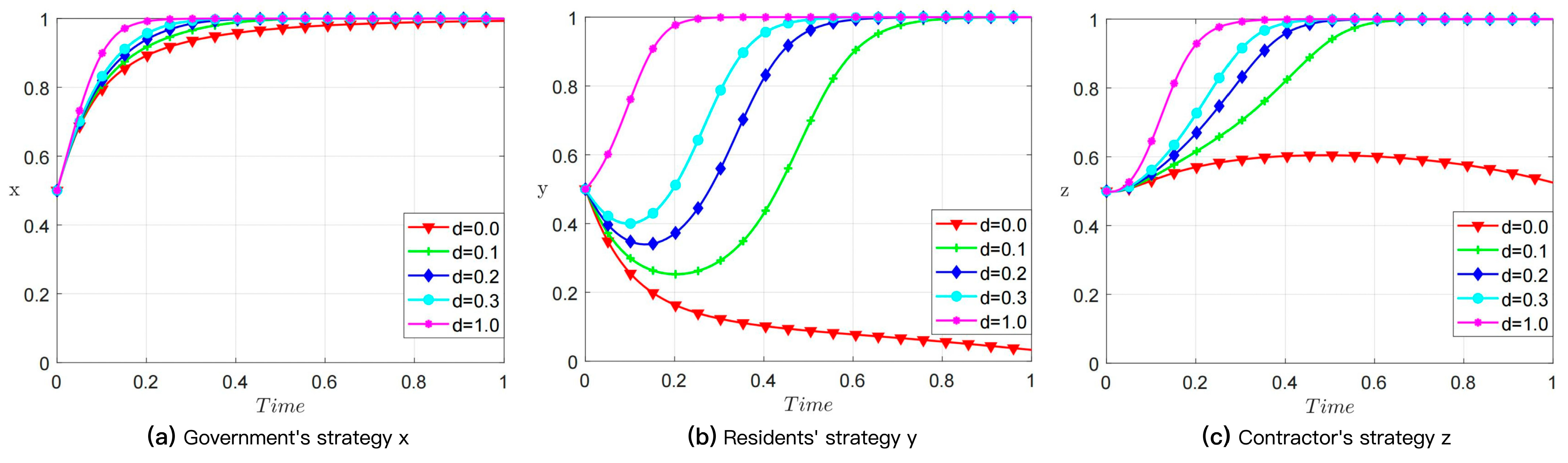
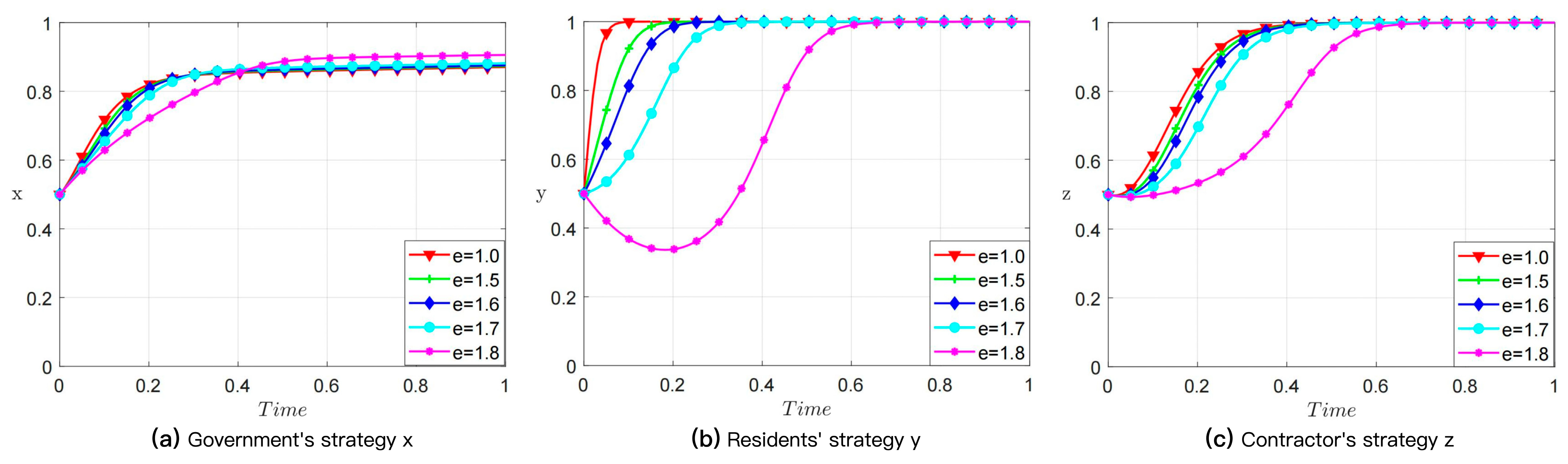
| Resident | In-Situ Demolition-and-Reconstruction (y) | Repair-and-Beautification (1 − y) | |||
|---|---|---|---|---|---|
| Contractor | Proactive Engagement (z) | Passive Response (1 − z) | Proactive Engagement (z) | Passive Response (1 − z) | |
| Government | Proactive Guidance (x) | E1:(1,1,1) | E2:(1,1,0) | E3:(1,0,1) | E4:(1,0,0) |
| Laissez-Faire (1 − x) | E5:(0,1,1) | E6:(0,1,0) | E7:(0,0,1) | E8:(0,0,0) | |
| Parameter | Meaning | Remarks |
|---|---|---|
| H | Pre-renewal unit housing price in the aging community (10,000 CNY/m2). | H > 0 |
| N | Average Original Building Area per Household of Old Residential Communities (m2). | N > 0 |
| w | Area-expansion coefficient: ratio of added floor area to original area granted by the government under strategy profile (1,1,*), including in-unit area, garages, and other public spaces. | w ≥ 0 |
| v | Expansion benefit-sharing coefficient: proportion of economic benefits from the expanded area shared by the government with the contractor under strategy profile (1,1,1). | 0 ≤ v≤1 |
| p | Expansion-purchase coefficient: proportion of the market price residents are required to pay for the expanded area under strategy profile (1,1,*). | p ≥ 0 |
| q | Original-area reconstruction payment coefficient: discount ratio on the contractor’s quoted price for reconstructing the original area under strategy profile (*,1,1). | 0 ≤ q≤1 |
| e | Cost-burden perception coefficient of residents (e.g., when e = 1.8, the perceived financial pressure is 1.8 times the actual cost). | e > 0 |
| d | Accident-risk perception coefficient of residents regarding the aging community. | d > 0 |
| s | Objective probability of accidents occurring in the old housing under strategy profile (*,0,*). | 0 ≤ s ≤ 1 |
| k | Property value appreciation coefficient for the new, expanded housing under strategy profile (1,1,*). | k = u·wl |
| u | Intensity factor influencing the property value appreciation for the new, expanded housing. | |
| l | Rate factor influencing the property value appreciation for the new, expanded housing. | |
| j | Property value appreciation coefficient for the new housing without area expansion under strategy profile (0,1,*). | j ≥ 0 |
| i | Property value appreciation coefficient for the old housing after repair-and-beautification under strategy profile (*,0,*). | i ≥ 0 |
| m | Ratio of the contractor’s unit construction quotation for demolition-and-reconstruction to the original housing price under strategy profile (*,1,*). | m ≥ 0 |
| r | Ratio of the contractor’s unit quotation for repair-and-beautification to the original housing price under strategy profile (*,0,*). | r ≥ 0 |
| f | Ratio of the contractor’s unit construction cost for demolition-and-reconstruction to the original housing price under strategy profile (*,1,*). | f ≥ 0 |
| g | Ratio of the contractor’s unit cost for repair-and-beautification to the original housing price under strategy profile (*,0,*). | g ≥ 0 |
| o | Cost impact coefficient for the government’s infrastructure upgrade. | |
| Bg1 | Government’s integrated benefits (e.g., social reputation) under demolition-and-reconstruction strategy profile (1,1,*). | Bg1 > 0 |
| Bg2 | Government’s negative social reputation under demolition-and-reconstruction strategy profile (0,1,*). | Bg2 < 0 |
| Bg3 | Government’s economic benefits (e.g., taxes) from expansion development under strategy profile (1,1,*). | Bg3 = N·w·p·H·(1 + k) − Bv4·w·N |
| Bg4 | Government’s integrated benefits (e.g., social reputation) under repair-and-beautification strategy profile (0,0,*). | Bg4 > 0 |
| Cg1 | Base implementation cost of the government’s Proactive Guidance policy under strategy profile (1,*,*). | |
| Cg2 | Infrastructure upgrade cost incurred by the government for granting the area expansion under strategy profile (1,1,*). | Cg2 = N·wo·Cg3 |
| Cg3 | Unit base cost for the government’s infrastructure upgrade. | |
| Cg4 | Policy execution cost under the government’s Laissez-faire strategy under strategy profile (0,*,*). | |
| Cg5 | Government’s payment to the contractor for repair-and-beautification under strategy profile (0,0,*). | Cg5 = Bv7 |
| Cg6 | Government’s accident handling cost and reputational loss when accidents occur after repair-and-beautification under strategy profile (0,0,*). | |
| Cg7 | Government’s accident handling cost and reputational loss when accidents occur after repair-and-beautification under strategy profile (1,0,*). | |
| Rg1 | Base subsidy from the government to residents under strategy profile (1,1,*). | |
| Rg2 | Additional subsidy from the government to residents under strategy profile (1,1,0). | |
| Rg3 | Subsidy (share of expansion development benefits) from the government to the contractor under strategy profile (1,1,1). | Rg3 = v·Bg3 |
| Br1 | Residents’ property appreciation benefits under demolition-and-reconstruction strategy profile (1,1,*). | Br1 = N·(1 + w)·H·(1 + k)-N·H |
| Br2 | Residents’ property appreciation benefits under demolition-and-reconstruction strategy profile (0,1,*). | Br2 = N·H·j |
| Br3 | Residents’ property appreciation benefits under repair-and-beautification strategy profile (*,0,*). | Br3 = N·H·i |
| Cr1 | Residents’ contribution payment under demolition-and-reconstruction strategy profile (1,1,1). | Cr1 = p·N·w·H·(1 + k) + q·Bv4·N |
| Cr2 | Residents’ contribution payment under demolition-and-reconstruction strategy profile (1,1,0). | Cr2 = p·N·w·H·(1 + k) + Bv4·N |
| Cr3 | Residents’ contribution payment under demolition-and-reconstruction strategy profile (0,1,*). | Cr3 = Bv3 |
| Cr4 | Residents’ contribution payment under repair-and-beautification strategy profile (1,0,*). | Cr4 = Bv7 |
| Cr5 | Base implementation cost for residents’ demolition-and-reconstruction behavior under strategy profile (*,1,*). | |
| Cr6 | Base implementation cost for residents’ repair-and-beautification behavior under strategy profile (*,0,*). | |
| Cr7 | Temporary off-site living cost for residents during the demolition-and-reconstruction period under strategy profile (*,1,*). | |
| Cr8 | Loss to residents from accidents occurring after repair-and-beautification under strategy profile (*,0,*). | |
| Bv1 | Contractor’s construction quotation for the new project under Proactive Engagement and strategy profile (1,1,1). | Bv1 = Bv4·w·N + q·Bv4·N |
| Bv2 | Contractor’s construction quotation for the new project under Passive Response and strategy profile (1,1,0). | Bv2 = N·(1 + w)·Bv4 |
| Bv3 | Contractor’s construction quotation for the new project under strategy profile (0,1,*). | Bv3 = N·Bv4 |
| Bv4 | Contractor’s unit area quotation for demolition-and-reconstruction (10,000 CNY/㎡) under strategy profile (*,1,*). | Bv4 = H·m |
| Bv5 | Contractor’s additional reputational benefit under strategy profile (1,1,1). | Bv5 > Bv6 |
| Bv6 | Contractor’s additional reputational benefit under strategy profile (0,1,1). | |
| Bv7 | Contractor’s quotation for repair-and-beautification under strategy profile (*,0,*). | Bv7 = N·Bv8 |
| Bv8 | Contractor’s unit area quotation for repair-and-beautification (10,000 CNY/㎡) under strategy profile (*,0,*). | Bv8 = H·r |
| Cv1 | Contractor’s construction cost for demolition-and-reconstruction under strategy profile (1,1,*). | Cv1 = N·(1 + w)·Cv3 |
| Cv2 | Contractor’s construction cost for demolition-and-reconstruction under strategy profile (0,1,*). | Cv2 = N·Cv3 |
| Cv3 | Contractor’s unit area construction cost for demolition-and-reconstruction (10,000 CNY/m2) under strategy profile (*,1,*). | Cv3 = H·f |
| Cv4 | Contractor’s construction cost for repair-and-beautification under strategy profile (*,0,*). | Cv4 = N·Cv5 |
| Cv5 | Contractor’s unit area cost for repair-and-beautification (10,000 CNY/㎡) under strategy profile (*,0,*). | Cv5 = H·g |
| Cv6 | Base implementation cost for the contractor’s Proactive Engagement under strategy profile (*,*,1). | |
| Cv7 | Base implementation cost for the contractor’s Passive Response under strategy profile (*,*,0). | |
| Cv8 | Reputational loss to the contractor when accidents occur after repair-and-beautification and under Proactive Engagement strategy profile (*,0,1). | |
| Cv9 | Reputational loss to the contractor when accidents occur after repair-and-beautification and under Passive Response strategy profile (*,0,0). |
| Resident | In-Situ Demolition-and-Reconstruction (y) | Repair-and-Beautification (1 − y) | |||
|---|---|---|---|---|---|
| Contractor | Proactive Engagement (z) | Passive Response (1 − z) | Proactive Engagement (z) | Passive Response (1 − z) | |
| Government | Proactive Guidance (x) | Bg1 + Bg3-Cg1-Cg2-Rg1-Rg3 | Bg1 + Bg3-Cg1-Cg2-Rg1-Rg2 | -Cg1-s·Cg7 | -Cg1-s·Cg7 |
| Br1-e·Cr1-Cr5-Cr7 + Rg1 | Br1-e·Cr2-Cr5-Cr7 + Rg1 + Rg2 | Br3-e·Cr4-Cr6-d·s·Cr8 | Br3-e·Cr4-Cr6-d·s·Cr8 | ||
| Bv1 + Bv5-Cv1-Cv6 + Rg3 | Bv2-Cv1-Cv7 | Bv7-Cv4-Cv6-s·Cv8 | Bv7-Cv4-Cv7-s·Cv9 | ||
| Laissez- Faire (1 − x) | Bg2-Cg4 | Bg2-Cg4 | Bg4-Cg4-Cg5-s·Cg6 | Bg4-Cg4-Cg5-s·Cg6 | |
| Br2-e·q·Cr3-Cr5-Cr7 | Br2-e·Cr3-Cr5-Cr7 | Br3-Cr5-d·s·Cr8 | Br3-Cr5-d·s·Cr8 | ||
| (1-q)·Bv3 + Bv6-Cv2-Cv6 | Bv3-Cv2-Cv7 | Bv7-Cv4-Cv6-s·Cv8 | Bv7-Cv4-Cv7-s·Cv9 | ||
| ESS | λ1 | λ2 | λ3 |
|---|---|---|---|
| E1 (1,1,1) | Bg2-Bg1 + Cg1-Cg4 + Rg1 + Cg3·N·wo + H·N·w·(m-p·(k + 1)) − H·N·v·w·(m-p·(k + 1)) | Cr5-Cr6 + Cr7-Rg1 + e·(H·N·m·q + H·N·p·w·(k + 1)) + H·N·i-H·N·(k + w+k·w) − Cr8·d·s-H·N·e·r | Cv6-Bv5-Cv7 + H·N·m·(w + 1) − H·N·m·q-H·N·m·w + H·N·v·w·(m-p·(k + 1)) |
| E2 (1,1,0) | Cg3·N·wo + H·N·(m-p·(k + 1))·w-Bg1 + Bg2 + Cg1-Cg4 + Rg1 + Rg2 | Cr5-Cr6 + Cr7-Rg1-Rg2 + e·(H·N·m + H·N·p·w·(k + 1)) + H·N·i-H·N·(k + w+k·w)-Cr8·d·s-H·N·e·r | Bv5-Cv6 + Cv7-H·N·m·(w + 1) + H·N·m·q + H·N·m·w-H·N·v·w·(m-p·(k + 1)) |
| E3 (1,0,1) | Bg4 + Cg1-Cg4-Cg6·s + Cg7·s-H·N·r | Cr6-Cr5-Cr7 + Rg1-e·(H·N·m·q + H·N·p·w·(k + 1))-H·N·i + H·N·(k + w+k·w) + Cr8·d·s + H·N·e·r | Cv6-Cv7 + Cv8·s-Cv9·s |
| E4 (1,0,0) | Bg4 + Cg1-Cg4-Cg6·s + Cg7·s-H·N·r | Cr6-Cr5-Cr7 + Rg1 + Rg2-e·(H·N·m + H·N·p·w·(k + 1))-H·N·i + H·N·(k + w+k·w) + Cr8·d·s + H·N·e·r | Cv7-Cv6-Cv8·s + Cv9·s |
| E5 (0,1,1) | Bg1-Bg2-Cg1 + Cg4-Rg1-Cg3·N·wo-H·N·w·(m-p·(k + 1)) + H·N·v·w·(m-p·(k + 1)) | Cr7 + H·N·i-H·N·j-Cr8·d·s + H·N·e·m·q | Cv6-Bv6-Cv7 + H·N·m + H·N·m·(q-1) |
| E6 (0,1,0) | Bg1-Cg3·N·wo-H·N·(m-p·(k + 1))·w-Bg2-Cg1 + Cg4-Rg1-Rg2 | Cr7 + H·N·i-H·N·j-Cr8·d·s + H·N·e·m·q | Bv6-Cv6 + Cv7-H·N·m-H·N·m·(q-1) |
| E7 (0,0,1) | Cg4-Cg1-Bg4 + Cg6·s-Cg7·s + H·N·r | H·N·j-H·N·i-Cr7 + Cr8·d·s-H·N·e·m·q | Cv6-Cv7 + Cv8·s-Cv9·s |
| E8 (0,0,0) | Cg4-Cg1-Bg4 + Cg6·s-Cg7·s + H·N·r | H·N·j-H·N·i-Cr7 + Cr8·d·s-H·N·e·m·q | Cv7-Cv6-Cv8·s + Cv9·s |
| Parameter | H | N | w | v | p | q | e | l | u | j | i | m | r |
| Value | 3.43 | 77 | 0.3 | 0.4 | 0.8 | 0.5 | 1.7 | 0.3 | 0.72 | 0.3 | 0.08 | 0.2 | 0.015 |
| Parameter | f | g | s | d | o | Bg1 | Bg2 | Bg4 | Cg1 | Cg3 | Cg4 | Cg6 | Cg7 |
| Value | 0.16 | 0.01 | 0.1 | 0.3 | 3 | 20 | −15 | 2 | 2 | 26 | 0.5 | 10 | 6 |
| Parameter | Rg1 | Rg2 | Cr5 | Cr6 | Cr7 | Cr8 | Bv5 | Bv6 | Cv6 | Cv7 | Cv8 | Cv9 | |
| Value | 2 | 10 | 5 | 0.5 | 15 | 200 | 20 | 4 | 2 | 0.4 | 10 | 4 |
| Policy Lever Dimension | Core Parameter | Concrete Policy Instruments |
|---|---|---|
| Resource-Allocation Levers | w | • Granting FAR (Floor Area Ratio) bonuses • Transfer of Development Rights (TDR) |
| v | • Public-private partnership (PPP) agreements • Land concession agreements with profit-sharing clauses | |
| Cost-Sharing Levers | p | • Direct housing price subsidies for the expanded area • Capping the purchase price of new floor area below market rate |
| q | • Mandating or incentivizing contractors to offer “cost-price” or discounted reconstruction packages • Government-negotiated bulk discount rates for residents | |
| Behavioral-Intervention Levers | e | • Financial Innovation: Establishing a dedicated “Renewal Loan” product (e.g., featuring a 20% down-payment and a 3% annual interest rate) to convert large one-time payments into manageable installments • Mental Accounting: Framing the investment as a “home value appreciation fund” rather than a pure cost |
| d | Risk Communication: • VR Hazard Visualization: Using virtual reality to simulate fire, earthquake, or structural failure scenarios in aging buildings • Mandatory Safety Drills: Organizing community-wide emergency evacuation exercises • Transparent Risk Reporting: Publicly sharing official structural safety assessment reports |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Bian, A.; Wu, Z. Addressing the Collective Action Dilemma in Resident-Led Urban Regeneration: Designing and Verifying a Multi-Dimensional Policy Lever System Through Evolutionary Game Theory. Sustainability 2025, 17, 10065. https://doi.org/10.3390/su172210065
Chen Z, Bian A, Wu Z. Addressing the Collective Action Dilemma in Resident-Led Urban Regeneration: Designing and Verifying a Multi-Dimensional Policy Lever System Through Evolutionary Game Theory. Sustainability. 2025; 17(22):10065. https://doi.org/10.3390/su172210065
Chicago/Turabian StyleChen, Zhibiao, Ana Bian, and Zhongping Wu. 2025. "Addressing the Collective Action Dilemma in Resident-Led Urban Regeneration: Designing and Verifying a Multi-Dimensional Policy Lever System Through Evolutionary Game Theory" Sustainability 17, no. 22: 10065. https://doi.org/10.3390/su172210065
APA StyleChen, Z., Bian, A., & Wu, Z. (2025). Addressing the Collective Action Dilemma in Resident-Led Urban Regeneration: Designing and Verifying a Multi-Dimensional Policy Lever System Through Evolutionary Game Theory. Sustainability, 17(22), 10065. https://doi.org/10.3390/su172210065






