Multi-Objective Sustainable Operational Optimization of Fluid Catalytic Cracking

Abstract

Fluid Catalytic Cracking (FCC) constitutes a critical process in petroleum refining, facing increasing pressure to align with sustainable development goals by improving energy efficiency and reducing environmental impact. This study tackles a multi-objective optimization challenge in FCC operations, seeking to simultaneously maximize the gasoline production and minimize the coke yield—the latter being directly linked to $\mathrm{C}{\mathrm{O}}_2$ emissions in FCC. A data-driven optimization model leveraging a dual Long Short-Term Memory architecture is developed to capture complex relationships between operating variables and product yields. To efficiently solve the model, an Improved Multi-Objective Whale Optimization Algorithm (IMOWOA) is proposed, integrating problem-specific adaptive multi-neighborhood search and dynamic restart mechanisms. Extensive experimental evaluations demonstrate that IMOWOA achieves superior convergence characteristics and comprehensive performance compared to established multi-objective algorithms. Relative to the yields before optimization, the proposed methodology increases the gasoline yield by 0.32% on average, coupled with an average reduction of 0.11% in the coke yield. For the studied FCC unit with an annual processing capacity of 2.6 million tons, the coke reduction corresponds to an annual $\mathrm{C}{\mathrm{O}}_2$ emission reduction of approximately 10,277 tons, delivering benefits to sustainable FCC operations.

1. Introduction

The growing global energy challenges and environmental degradation have elevated sustainability to a crucial concern in industrial development [1,2]. Industries worldwide are required to improve energy efficiency and reduce carbon emissions through enhanced operational practices [3,4,5]. The petroleum refining industries, as significant contributors to energy consumption and greenhouse gas emissions, are under increasing pressure to shift toward more environmentally friendly and energy-efficient operational paradigms [6,7,8]. This shift is not only an environmental necessity in response to environmental change, but also a strategic move to comply with economic sustainability policies, such as China’s Carbon Peaking and Carbon Neutrality Goals [9].

Fluid Catalytic Cracking (FCC) is a central unit in modern petroleum refineries [10,11]. It converts heavy petroleum fractions into high-value products, primarily gasoline, which is an important transportation fuel [12]. The economic performance of a refinery, therefore, is highly dependent on FCC, often incentivizing the maximization of the gasoline yield [13]. However, coke is inevitably produced during the FCC gasoline production, which is an undesirable carbonaceous byproduct depositing on the catalyst surface. To restore the activity of the catalyst, the coke-laden catalyst is combusted with air [14]. This process represents a major energy loss and emits substantial amounts of $\mathrm{C}{\mathrm{O}}_2$ within the FCC unit, directly contributing to the refinery’s carbon footprint.

Within this context, coke formation represents not merely an operational concern but a critical sustainability metric. The combustion of coke in the regenerator constitutes a major source of greenhouse gas emissions while simultaneously reflecting inefficient carbon utilization. Consequently, suppressing coke yield is essential for advancing FCC sustainability, directly mitigating environmental impact through lower $\mathrm{C}{\mathrm{O}}_2$ emissions and reducing waste through improved carbon utilization (i.e., preventing valuable carbon from being lost as coke). Operational optimization, which systematically adjusts key operating variables to obtain desired product yields, therefore emerges as a crucial approach for improving FCC sustainability. However, the strong nonlinearity and inherent complexity of FCC pose significant challenges to its operational optimization.

Over the past decades, extensive research has been conducted on FCC operational optimization. Early efforts were predominantly dedicated to single-objective optimization [15,16,17]. John et al. [18] developed a six-lump kinetic model and utilized gPROMS to optimize the catalyst and oil gas mass flow rates, leading to increased propylene yield. Chen et al. [19] applied a random forest algorithm to identify key operating variables affecting gasoline octane number, and established a mapping between these variables and octane number using a Long Short-Term Memory (LSTM) neural network, thereby constructing an optimization model to minimize octane number loss. Chen et al. [20] employed a random weight neural network to develop an optimization model for fossil fuel yields and introduced a fast adaptive differential evolution algorithm to address associated constraints under uncertainty. Li et al. [21] designed a bilevel robust optimization framework that optimizes the feed selection and reaction temperature of an industrial FCC unit to maximize profit under uncertainty of feed properties. Recent years have witnessed growing interest in multi-objective optimization, which more closely aligns with the practical need to simultaneously satisfy multiple performance indicators [22,23]. Jarullah et al.  [24] developed a multi-objective optimization model grounded in first principles and solved it using gPROMS. In a separate approach, Liu et al.  [25] constructed a multi-objective optimization model by nonlinear multiple regression to simultaneously minimize RON loss and operational risk in FCC gasoline processing. José et al. [26] compared the effectiveness of particle swarm optimization and genetic algorithm in solving the multi-objective optimization problem of the product yield distribution. Despite these advances, most studies have emphasized economic objectives, often overlooking sustainability considerations.

Research on multi-objective sustainable operational optimization for FCC remains relatively limited. Wan et al. [27] developed an optimization framework combining a lumped kinetic model and the SPEA-2 algorithm to reduce pollutant gas emissions while balancing the production of light olefins and other chemicals. Liu et al. [28] established a simulation model for the fractionation and absorption-stabilization units of FCC using Aspen Plus and optimized both gasoline yield and energy consumption with the NSGA-II algorithm. However, these studies rely heavily on the availability of accurate mechanism optimization models, posing significant challenges in practical applications. The mechanism models require detailed knowledge of reaction kinetics, catalyst behavior, and complex multiphase flow dynamics information that is often difficult to acquire in industrial-scale FCC units [29,30]. In addition, minimizing coke yield is a crucial objective in FCC sustainable optimization due to its direct contribution to energy losses and $\mathrm{C}{\mathrm{O}}_2$ emissions. Existing optimization approaches predominantly optimize a certain product yield by adjusting operating variables at a given time point. Yet, FCC product yields are influenced by the cumulative effect of the variables over a preceding period. The current multi-objective optimization models and algorithms do not fully take into account this characteristic, thereby constraining the effectiveness and applicability of proposed optimization strategies in practical FCC operation.

This paper investigates an FCC Multi-Objective Sustainable Operational Optimization (FCC-MOSOO) problem, targeting the dual objectives of maintaining gasoline production while suppressing coke formation. The proposed approach facilitates a reduction in environmental impact while maintaining economic profitability, thereby supporting the greener and more sustainable refining operations. The main contributions of this paper are as follows:

(1) A data-driven modeling approach based on a Dual-LSTM architecture is introduced to capture the complex relationship between operating variables and product yields in the FCC-MOSOO problem, overcoming the computational efficiency limitations of traditional mechanism models.

(2) The time lag and cumulative effects in FCC processes are considered in the optimization by adjusting variable trajectories over a future time window, advancing beyond traditional static setpoint optimization to achieve more realistic and effective operational strategies.

(3) An Improved Multi-Objective Whale Optimization Algorithm (IMOWOA) tailored to the FCC-MOSOO problem is developed, enhanced with Adaptive Multi-Neighborhood Search (AMNS) and Dynamic Restart (DR) mechanisms. The algorithm provides actionable Pareto-optimal solutions, enabling effective trade-off analysis between economic and environmental objectives.

2. Problem Formulation

2.1. Problem Description

FCC is a highly integrated chemical process that primarily consists of a reactor and a regenerator operating in a continuous cycle. In the reactor, the heavy oil gas feedstock contacts the hot powdered catalyst, cracking into valuable lighter products such as gasoline, liquefied petroleum gas, and dry gas. During this process, coke deposits on the catalyst surface, leading to its deactivation. The spent catalyst is subsequently transferred to the regenerator, where the deposit is burned off, thereby restoring catalytic activity and providing the necessary heat required for the endothermic cracking reactions in the reactor. The regenerated catalyst is then recirculated back to the reactor, completing the cycle.

A central challenge in FCC is balancing economic performance and environmental impact. Operating conditions that favor high gasoline production (e.g., higher reaction temperature) often promote higher coke formation, which increases energy consumption and $\mathrm{C}{\mathrm{O}}_2$ emissions, leading to a conflict between profit and sustainability. Further complicating the challenge is the time lag in FCC. As illustrated in Figure 1, the product yield at time $t+\tau$ depends on the cumulative effects of operating variables over a preceding period from $t-q+1$ to $t+n$. From an optimization perspective, this period is divided into two segments by the current optimization time t: a historical window from $t-q+1$ to t and a future window from $t+1$ to $t+n$, where q and n are the lengths of the historical and future windows. In the historical window, non-adjustable observed variables that define the FCC operating state are captured. The future window includes the controlled variables that serve as decision variables in optimization. Mathematically, the observed and controlled variables are denoted as ${\mathit{O}}_t$ and ${\mathit{X}}_t$, expressed as Equations (1) and (2). Given a fixed operating state defined by ${\mathit{O}}_t$, the FCC-MOSOO problem seeks to identify optimal controlled variables ${\mathit{X}}_t$ that simultaneously maximize gasoline yield and minimize coke yield.

$${\mathit{O}}_t=\left[\begin{array}{cccc}{o}_{1,t-q+1}& o_{1,t-q+2}& \dots & o_{1,t}\\ o_{2,t-q+1}& o_{2,t-q+2}& \dots & o_{2,t}\\ ⋮& ⋮& \ddots & ⋮\\ o_{p,t-q+1}& o_{p,t-q+2}& \dots & o_{p,t}\end{array}\right]$$

(1)

$${\mathit{X}}_t=\left[\begin{array}{cccc}{x}_{1,t+1}& x_{1,t+2}& \dots & x_{1,t+n}\\ x_{2,t+1}& x_{2,t+2}& \dots & x_{2,t+n}\\ ⋮& ⋮& \ddots & ⋮\\ x_{m,t+1}& x_{m,t+2}& \dots & x_{m,t+n}\end{array}\right]$$

(2)

where p and m are the dimensions of the observed and controlled variables, $o_{ij}$ is the observed variable i sampled at time j, and $x_{ij}$ is the controlled variable i adjusted at time j.

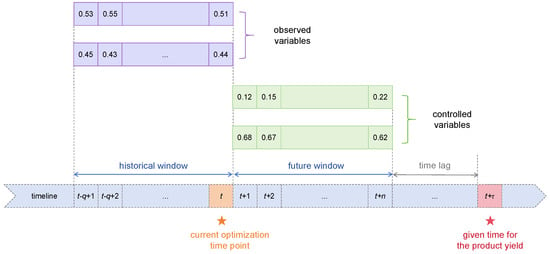
Figure 1. Time lag in the FCC process.

2.2. Optimization Model

Calculating gasoline and coke yields is essential for the FCC-MOSOO problem. Since mechanism methods are often computationally expensive and challenging to calibrate accurately for industrial processes, a data-driven approach based on a Dual-LSTM architecture is employed to calculate the product yields. LSTM is suitable for this application due to its capability to process sequential data and learn long-term dependencies, enabling it to effectively capture the complex temporal relationship between operating variables and the product yield [31,32,33].

The Dual-LSTM architecture employs two parallel LSTM branches to extract final hidden states ${\mathit{h}}_t^{\mathrm{obs}}$ and ${\mathit{h}}_t^{\mathrm{ctrl}}$ from ${\mathit{O}}_t$ and ${\mathit{X}}_t$, respectively. Each branch consists of a multi-layer stacked LSTM. The resulting states are concatenated into a combined feature ${\mathit{h}}_t^{\mathrm{concat}}=\left[{\mathit{h}}_t^{\mathrm{obs}}\right|{\mathit{h}}^{\mathrm{ctrl}}t]$, which is then passed through a dense layer to calculate the product yield ${\widehat{y}}_{t+\tau }$ (i.e., gasoline yield or coke yield) at time $t+\tau$. The complete computational procedure is formalized in Equation (3). The training process utilized historical data collected from an industrial FCC unit at a collaborative refinery. Data acquisition spanned from 8 March 2025 to 14 May 2025, with a sampling interval of 3 min. The raw dataset underwent comprehensive preprocessing, which involved removal of null values, outlier elimination using the 3-$\sigma$ rule, noise reduction via a Butterworth filter, and final normalization through min–max scaling. This procedure finally yielded a refined dataset containing 15,791 valid samples.

$${\widehat{y}}_{t+\tau }=f_{\mathrm{Dual}-\mathrm{LSTM}}({\mathit{O}}_t,{\mathit{X}}_t)$$

(3)

Building upon the Dual-LSTM architecture, the optimization objectives of the FCC-MOSOO problem are formulated as Equations (4) and (5). Based on the reaction mechanism and empirical knowledge of FCC, the selected observed variables and controlled variables are listed in Table 1.

$$\begin{array}{cc}\hfill & \min -{\widehat{y}}_{t+\tau }^{\mathrm{gasoline}}=-f_{\mathrm{Dual}-\mathrm{LSTM}}^{\mathrm{gasoline}}({\mathit{O}}_t,{\mathit{X}}_t)\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \min {\widehat{y}}_{t+\tau }^{\mathrm{coke}}=f_{\mathrm{Dual}-\mathrm{LSTM}}^{\mathrm{coke}}({\mathit{O}}_t,{\mathit{X}}_t)\hfill \end{array}$$

(5)

Table 1. The observed variables and controlled variables of the FCC-MOSOO problem.

Variable No.	Observed Variable	Controlled Variable
1	Regenerated catalyst temperature	Reaction temperature
2	Spent catalyst temperature	Reaction pressure
3	Oil gas temperature	Regenerator pressure
4	Gasoline yield	Lifting steam flow rate
5	Coke yield	Liquid feedstock temperature

According to production requirements, the operational optimization problem is required to meet the following constraints:

$$\begin{array}{cc}\hfill & l{b}_i\le x_{ij}\le u{b}_i\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & |x_{ij}-x_{i,j-1}|\le {\Delta }_i\hfill \end{array}$$

(7)

Constraints (6) ensure that the values of the controlled variables remain within their allowable range at all times, where $l{b}_i$ and $u{b}_i$ are the lower and upper bounds of the controlled variable i.

Constraints (7) restrict that the step size of any adjustment must not exceed the allowable limit, where ${\Delta }_i$ is the maximum adjustment limit of the controlled variable i.

3. Proposed Algorithm

Considering the inherent complexity and strong nonlinearity of the FCC process, swarm intelligence optimization algorithms are particularly suitable for addressing such challenges [34]. Among these, the Whale Optimization Algorithm (WOA) [35] has attracted widespread attention due to its simple parameter adjustment and excellent global search ability. It has been successfully applied in various domains such as traffic scheduling [36], price forecasting [37], and shop scheduling [38]. Based on WOA, the proposed IMOWOA is designed in this section to solve the FCC-MOSOO problem.

3.1. IMOWOA Framework

The basic WOA is inspired by the bubble-net foraging behavior of humpback whales, which comprises three core search operators: spiral updating, shrink encircling, and prey searching, as detailed in the following descriptions. Building upon the WOA search operators, IMOWOA further incorporates AMNS and DR mechanisms that are specifically designed for the FCC-MOSOO problem to improve search performance. The overall framework of IMOWOA is illustrated in Figure 2, with comprehensive details provided in the subsequent subsections.

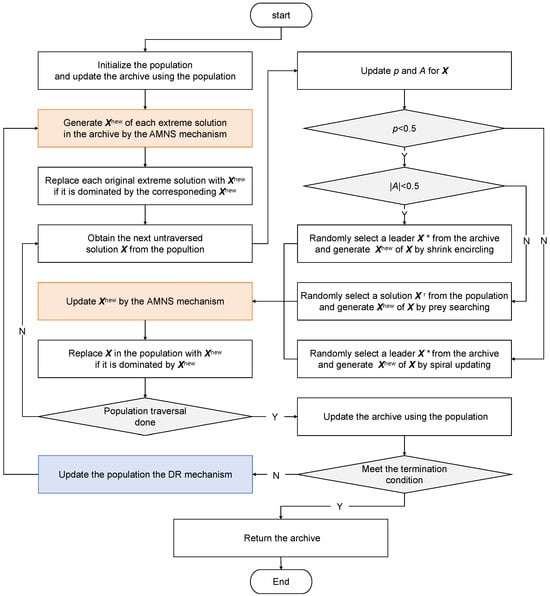
Figure 2. Framework of IMOWOA.

Spiral updating: spiral updating emulates the distinctive spiral-shaped movement of whales to approach the target prey, represented by the following formulation:

$${\mathit{X}}^{\mathrm{new}}=|{\mathit{X}}^{\ast }-\mathit{X}|·e^{bl}·\cos \left(2\pi l\right)+{\mathit{X}}^{\ast }$$

(8)

Shrink encircling: shrink encircling replicates whales encircling the target prey, represented by the following formulation:

$${\mathit{X}}^{\mathrm{new}}={\mathit{X}}^{\ast }-A·|2·\mathrm{rand}\left(\right)·{\mathit{X}}^{\ast }-\mathit{X}|$$

(9)

Prey searching: this operator is responsible for exploring new prey, represented by the following formulation:

$${\mathit{X}}^{\mathrm{new}}={\mathit{X}}^r-A·|2·\mathrm{rand}\left(\right)·{\mathit{X}}^r-\mathit{X}|$$

(10)

where $\mathit{X}$ is a solution in the population, ${\mathit{X}}^{\mathrm{new}}$ is the new solution generated from $\mathit{X}$, ${\mathit{X}}^{\ast }$ is the current best solution, ${\mathit{X}}^r$ is a randomly selected solution, b is a constant used to define the shape of the logarithmic spiral and is recommended to be set as 1, l is a random number between [−1, 1], $A=2a·\mathrm{rand}\left(\right)-a$ is a control number, rand() represents a function that returns a random number in the range of [0, 1], and a linearly decreases from 2 to 0.

3.2. Population Initialization

The population is initialized as a set of whale individuals, each representing a candidate solution. In the context of FCC-MOSOO, the controlled variable matrix ${\mathit{X}}_t$ is adopted as the solution encoding scheme. To ensure the feasibility of the initial solutions, a constrained random walk strategy is utilized for population initialization. Specifically, each element $x_{ij}$ in ${\mathit{X}}_t$ is generated by uniform sampling within dynamic bounds $[l{b}_{ij}^{\ast },u{b}_{ij}^{\ast }]$. These bounds are determined based on the value of the preceding element $x_{i,j-1}$, thereby introducing temporal dependency into the initial population. The formulations of the dynamic bounds are provided as follows:

$$\begin{array}{cc}\hfill & l{b}_{ij}^{\ast }=\max \{l{b}_i,x_{i,j-1}-{\Delta }_i\}\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & u{b}_{ij}^{\ast }=\min \{u{b}_i,x_{i,j-1}+{\Delta }_i\}\hfill \end{array}$$

(12)

3.3. Adaptive Multi-Neighborhood Search Mechanism

To enhance local search capability, the AMNS mechanism is introduced, which incorporates an adaptive execution strategy and three local search operators. The adaptive execution strategy activates the local search using a probability $p^{\mathrm{ls}}$, defined in Equation (13). As optimization progresses, this strategy gradually shifts the focus from global exploration to local refinement, enhancing the quality of the final solutions.

$$p^{\mathrm{ls}}={\displaystyle \frac{1}{2}}·\left[1+\sin \left({\displaystyle \frac{g·\pi }{2·G_{\max }}}\right)\right]$$

(13)

where g is the current iteration count and $G_{\max }$ is the maximum number of iterations.

The three local search operators are specifically designed to align with the structural characteristics of the solutions to the FCC-MOSOO problem. Each operator acts either at the element level or the row level of the solution matrix, offering complementary search behaviors to enhance diversity and adaptability during the optimization process. When the local search is activated, one operator is randomly selected and applied to the target solution. The description of each operator is elaborated as follows:

Element-level polynomial search: this operator leverages modified polynomial mutation to generate a new solution. Governed by an adaptive distribution index, it applies controlled perturbations to a randomly selected element. The perturbation magnitude decreases progressively with iterations, enabling fine-grained exploitation of the solution neighborhood while preserving solution stability. The operation on the randomly selected element is formulated as Equations (14)–(16).

$$x_{ij}^{\mathrm{new}}=x_{ij}+{\delta }_p·(u{b}_{ij}^{\ast }-l{b}_{ij}^{\ast })$$

(14)

$${\delta }_p=\left\{\begin{array}{cc}2·u^{{\displaystyle \frac{1}{\eta +1}}}-1\hfill & u\le 0.5\hfill \\ 1-{\left[2·(1-u)\right]}^{{\displaystyle \frac{1}{\eta +1}}}\hfill & u>0.5\hfill \end{array}\right.$$

(15)

$$\eta =20·{\displaystyle \frac{g}{G_{\max }}}$$

(16)

where $x_{ij}$ is a randomly selected element; $x_{ij}^{\mathrm{new}}$ is the new allele element; ${\delta }_p$ is the perturbation magnitude; u is a random number in [0, 1]; $\eta$ is the adaptive distribution index.

Row-level Gaussian random walk search: this operator implements the Gaussian random walk on a randomly selected row. Each walk step follows a Gaussian distribution with the previous element as its mean and a decaying variance. This process generates smooth modifications along the row, avoiding disruptive jumps. The operation on each element in the randomly selected row is formulated as Equations (17) and (18).

$$\begin{array}{cc}\hfill & x_{ij}^{\mathrm{new}}=\mathrm{Gaussian}(x_{i,j-1}^{\mathrm{new}},{\sigma }^2)\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & \sigma =0.1·\left(1-{\displaystyle \frac{g}{G_{\max }}}\right)\hfill \end{array}$$

(18)

where $\mathrm{Gaussian}(x_{i,j-1}^{\mathrm{new}},{\sigma }^2)$ return a Gaussian random number with mean $x_{i,j-1}^{\mathrm{new}}$ and variance ${\sigma }^2$.

Row-level Cauchy search: this operator utilizes the long-tailed Cauchy distribution to perturb a row randomly selected from the original solution. The long tail facilitates both occasional large-magnitude perturbations and frequent small-step adjustments, making the operator effective in escaping shallow local optima and exploring broader regions surrounding the original solution. The operation on each element in the randomly selected row is formulated as Equations (19) and (20).

$$\begin{array}{cc}\hfill & x_{ij}^{\mathrm{new}}=x_{ij}+\mathrm{Cauchy}(0,1)·{\delta }_c\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & {\delta }_c=0.1·e^{-{\displaystyle \frac{g}{G_{\max }}}}\hfill \end{array}$$

(20)

where ${\delta }_c$ is perturbation magnitude, and $\mathrm{Cauchy}(0,1)$ returns a random number following the standard Cauchy distribution.

The pseudocode of the AMNS mechanism is shown in Algorithm 1.

Algorithm 1 AMNS mechanism

Require: the solution $\mathit{X}$,

the current iteration count g,

the maximum number of iterations $G_{\max }$

1:  Update $p^{\mathrm{ls}}$ by Equation (13) 2:   ${\mathit{X}}^{\mathrm{new}}\leftarrow \mathit{X}$ 3:  if rand() < $p^{\mathrm{ls}}$ then 4:     $p\leftarrow$ rand() 5:     if p < 1/3 then 6:         Generate ${\mathit{X}}^{\mathrm{new}}$ by performing element-level polynomial serach on $\mathit{X}$ 7:     else if p < 2/3 then 8:         Generate ${\mathit{X}}^{\mathrm{new}}$ by performing row-level Gaussian random walk search on $\mathit{X}$ 9:     else 10:         Generate ${\mathit{X}}^{\mathrm{new}}$ by performing row-level Cauchy search on $\mathit{X}$ 11:     end if 12:  end if 13:  return  ${\mathit{X}}^{\mathrm{new}}$

3.4. Dynamic Restart Mechanism

The DR mechanism is embedded in the IMOWOA to inject diversity when search stagnation is detected. This disrupts entrenched solution clusters and facilitates the exploration of undiscovered regions in the objective space. To detect stagnation, the improvement in both objectives is monitored across iterations. For each iteration, stagnation is detected if either objective shows no improvement for $g_{\mathrm{th}}$ consecutive iterations, where $g_{\mathrm{th}}$ is the stagnation threshold decreasing according to Equation (21).

$$g_{\mathrm{th}}={\displaystyle \frac{G_{\max }}{e·g+1}}+2$$

(21)

The DR mechanism includes two operators: the complete random walk and the partial random walk. The complete random walk is identical to the random walk in the population initialization. The partial random walk selects a pivot column randomly and then performs an independent random walk for each row starting from the pivot column element. These two designed operators correspond to wide restarts and narrow restarts, respectively.

Upon detecting stagnation, 10% solutions in the population are randomly selected. For each selected solution, one of the restart operators is applied according to an increased probability $p^{\mathrm{rt}}=g/G_{\max }$: the partial random walk is applied if a random number is less than $p^{\mathrm{rt}}$; otherwise, the complete random walk is applied. This selection method ensures the early dominance of the complete random walk (wide restarts), which facilitates radical exploration to escape deep local optima. Meanwhile, late-stage preference for the partial random walk (narrow restarts) injects diversity without disrupting near-converged solutions.

The pseudocode of the dynamic mechanism is shown in Algorithm 2.

Algorithm 2 DR mechanism

Require: the population $pop$,

the current iteration count g,

the maximum number of iterations $G_{\max }$,

the stagnation iteration count for objective 1 $c_1$,

the stagnation iteration count for objective 2 $c_2$,

1: Update the $g_{\mathrm{th}}$ by Equation (21) 2:  if $c1<g_{\mathrm{th}}$ or $c2<g_{\mathrm{th}}$ then 3:     $p^{\mathrm{rt}}\leftarrow g/G_{\max }$ 4:     Randomly select 10% solutions from $pop$ 5:     for each solution $\mathit{X}$ in the selected solutions do 6:         if rand()< $p^{\mathrm{rt}}$ then 7:            Randomly select a column from $\mathit{X}$ 8:            Generate ${\mathit{X}}^{\mathrm{new}}$ by performing the partial random walk on $\mathit{X}$ 9:            starting from the selected column 10:         else 11:            Generate ${\mathit{X}}^{\mathrm{new}}$ by performing the complete random walk on $\mathit{X}$ 12:         end if 13:         Replace $\mathit{X}$ in the population with ${\mathit{X}}^{\mathrm{new}}$ 14:     end for 15:  end if 16:  return the updated $pop$

3.5. Archive Maintenance

The proposed IMOWOA utilizes an external archive to retain elite non-dominated solutions identified throughout the optimization process. This archive is dynamically updated according to Pareto dominance relations and crowding distance to ensure both convergence and diversity. The update process operates as follows: (1) a new solution is incorporated only if it is not dominated by any solution currently in the archive; (2) existing solutions that are dominated by the new solution are immediately removed; and (3) when the archive reaches its capacity limit, solutions with larger crowding distances are prioritized for retention to maintain a well-distributed and diverse solution set.

4. Experiment Results

Extensive experiments were conducted to evaluate the performance of the proposed IMOWOA in solving the FCC-MOSOO problem. All programs of the experiments were implemented with Python 3.11.9 and executed on a laptop manufactured by Lenovo in Beijing, China, with 16 GB RAM and a 2.3 GHz Intel Core i7-12700H under a Windows 11 (64) system.

4.1. Evaluation Metric and Test Instance

In the experiments, generational distance (GD), inverted generational distance (IGD), and hypervolume (HV) were employed as evaluation metrics. These metrics provide insights into the convergence and overall quality of the non-dominated solution set obtained by the algorithm.

GD is primarily a performance indicator of the convergence ability, as formulated in Equation (22). A smaller GD value signifies a better performance.

$$GD={\displaystyle \frac{1}{\left|U\right|}}\sqrt{\sum _{u\in U}\underset{p\in P\ast }{min}\left(d_{p,u}\right)}$$

(22)

where U is the non-dominated solution set, $P^{\ast }$ is the true Pareto front, and $d_{p,u}$ is the Euclidean distance between solutions p and u in the objective space.

IGD is a comprehensive performance indicator that evaluates convergence and diversity, as formulated in Equation (23). A solution set with a smaller IGD value is preferable.

$$IGD={\displaystyle \frac{1}{|P^{\ast }|}}\sqrt{\sum _{p\in P^{\ast }}\underset{u\in U}{min}\left(d_{p,u}\right)}$$

(23)

HV is calculated as the volume in the objective space dominated by the non-dominated solution set and bounded by a predefined reference point, as formulated in Equation (24). A larger HV value indicates a better performance.

$$HV=\mathrm{volume}\left(\bigcup _{u\in U}{c}_u\right)$$

(24)

where $c_u$ is the hypercube defined by the solution u and the reference point in the objective space.

Since the true Pareto front is a priori unknown, a reference set was constructed for each test instance to calculate GD and IGD. This reference set consists of non-dominated solutions from the combined results of all compared algorithms in the following subsections. For HV, the reference point was defined per instance using the maximum value of each objective.

Test instances were generated from historical operating data of the FCC unit to ensure that the evaluation was grounded in real-world processes. Specifically, fifteen distinct time points were randomly selected from the data. For each time point t, a corresponding test instance was constructed using the observed variables ${\mathit{O}}_t$. Each case represents a unique and realistic initial state from which the optimization algorithm is tasked to find the optimal operating conditions.

4.2. Performance Comparison

To verify the effectiveness of the IMOWOA, comprehensive comparisons were conducted with both classical and emerging multi-objective algorithms, including NSGA-II [39], SPEA-2 [40], and MOGWO [41]. For a fair comparison, all algorithms were configured with a population size of 50 and a maximum iteration of 100. The crossover and mutation probabilities in NSGA-II and SPEA-2 were set to 0.8 and 0.2, respectively, based on parameter tuning by the Taguchi experimental design method.

Each algorithm was independently run 20 times to ensure statistical reliability. Table 2 presents the means and standard deviations of each metric for all algorithms, with the best values highlighted in bold. The last column provides Welch’s t-test results between IMOWOA and each compared algorithm. The symbols “+” and “=” denote IMOWOA is statistically superior and similar to the compared algorithm.

Table 2. Means, standard deviations, and Welch’s t-test results of GD, IGD, and HV for NSGA-II, SPEA-2, MOGWO, and IMOWOA on all test instances.

Test Instance	NSGA-II (Mean/Std)	SPEA-2 (Mean/Std)	MOGWO (Mean/Std)	IMOWOA (Mean/Std)
	GD IGD HV	GD IGD HV	GD IGD HV	GD IGD HV
1	$5.74\times {10}^{-3}/8.00\times {10}^{-4}$ $1.50\times {10}^{-2}/1.57\times {10}^{-3}$ $1.23\times {10}^{-3}/5.81\times {10}^{-5}$	$5.85\times {10}^{-3}/1.30\times {10}^{-3}$ $1.50\times {10}^{-2}/1.40\times {10}^{-3}$ $1.23\times {10}^{-3}/5.26\times {10}^{-5}$	$6.61\times {10}^{-3}/2.26\times {10}^{-3}$ $1.52\times {10}^{-2}/1.70\times {10}^{-3}$ $1.22\times {10}^{-3}/8.25\times {10}^{-5}$	$\mathbf{1}.\mathbf{83}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{9}.\mathbf{62}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{3}.\mathbf{83}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{10}\times {\mathbf{10}}^{-\mathbf{3}}$ (+,+,+) $\mathbf{1}.\mathbf{81}\times {\mathbf{10}}^{-}\mathbf{3}/\mathbf{1}.\mathbf{31}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+)
2	$7.81\times {10}^{-3}/1.54\times {10}^{-3}$ $1.72\times {10}^{-2}/1.62\times {10}^{-3}$ $1.11\times {10}^{-3}/5.28\times {10}^{-5}$	$7.66\times {10}^{-3}/2.07\times {10}^{-3}$ $1.71\times {10}^{-2}/1.66\times {10}^{-3}$ $1.12\times {10}^{-3}/5.88\times {10}^{-5}$	$7.50\times {10}^{-3}/3.28\times {10}^{-3}$ $1.67\times {10}^{-2}/2.71\times {10}^{-3}$ $1.10\times {10}^{-3}/9.72\times {10}^{-5}$	$\mathbf{2}.\mathbf{44}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{1}.\mathbf{23}\times {\mathbf{10}}^{-\mathbf{3}}$ (+,+,+) $\mathbf{4}.\mathbf{51}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{24}\times {\mathbf{10}}^{-\mathbf{3}}$ (+,+,+) $\mathbf{1}.\mathbf{67}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{1}.\mathbf{20}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+)
3	$5.78\times {10}^{-3}/4.89\times {10}^{-4}$ $1.11\times {10}^{-2}/1.79\times {10}^{-3}$ $3.78\times {10}^{-4}/3.37\times {10}^{-5}$	$6.17\times {10}^{-3}/6.40\times {10}^{-4}$ $1.14\times {10}^{-2}/1.01\times {10}^{-3}$ $3.57\times {10}^{-4}/3.89\times {10}^{-5}$	$7.64\times {10}^{-3}/6.92\times {10}^{-4}$ $1.36\times {10}^{-2}/1.29\times {10}^{-3}$ $2.95\times {10}^{-4}/3.16\times {10}^{-5}$	$\mathbf{7}.\mathbf{03}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{6}.\mathbf{20}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{45}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{19}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{8}.\mathbf{17}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{11}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
4	$6.87\times {10}^{-3}/5.68\times {10}^{-4}$ $1.45\times {10}^{-2}/1.43\times {10}^{-3}$ $3.01\times {10}^{-4}/3.35\times {10}^{-5}$	$6.81\times {10}^{-3}/5.50\times {10}^{-4}$ $1.48\times {10}^{-2}/9.11\times {10}^{-4}$ $3.01\times {10}^{-4}/2.62\times {10}^{-5}$	$7.61\times {10}^{-3}/7.15\times {10}^{-4}$ $1.56\times {10}^{-2}/1.23\times {10}^{-3}$ $2.61\times {10}^{-4}/2.85\times {10}^{-5}$	$\mathbf{5}.\mathbf{32}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{13}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{68}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{87}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{7}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{09}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
5	$6.32\times {10}^{-3}/5.02\times {10}^{-4}$ $1.39\times {10}^{-2}/1.58\times {10}^{-3}$ $3.78\times {10}^{-4}/3.28\times {10}^{-5}$	$6.26\times {10}^{-3}/6.39\times {10}^{-4}$ $1.36\times {10}^{-2}/1.08\times {10}^{-3}$ $3.79\times {10}^{-4}/3.76\times {10}^{-5}$	$7.71\times {10}^{-3}/8.53\times {10}^{-4}$ $1.57\times {10}^{-2}/1.03\times {10}^{-3}$ $3.13\times {10}^{-4}/3.18\times {10}^{-5}$	$\mathbf{5}.\mathbf{26}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{82}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{2}.\mathbf{63}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{8}.\mathbf{03}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{8}.\mathbf{65}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{38}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
6	$6.96\times {10}^{-3}/5.39\times {10}^{-4}$ $1.37\times {10}^{-2}/1.48\times {10}^{-3}$ $1.88\times {10}^{-4}/2.58\times {10}^{-5}$	$7.06\times {10}^{-3}/5.20\times {10}^{-4}$ $1.34\times {10}^{-2}/1.24\times {10}^{-3}$ $1.90\times {10}^{-4}/2.26\times {10}^{-5}$	$7.90\times {10}^{-3}/5.39\times {10}^{-4}$ $1.50\times {10}^{-2}/1.13\times {10}^{-3}$ $1.51\times {10}^{-4}/2.17\times {10}^{-5}$	$\mathbf{6}.\mathbf{59}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{4}.\mathbf{81}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{8}.\mathbf{86}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{1}.\mathbf{46}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{6}.\mathbf{55}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{1}.\mathbf{47}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
7	$7.11\times {10}^{-3}/4.62\times {10}^{-4}$ $1.62\times {10}^{-2}/1.16\times {10}^{-3}$ $2.05\times {10}^{-4}/2.18\times {10}^{-5}$	$7.02\times {10}^{-3}/4.98\times {10}^{-4}$ $1.53\times {10}^{-2}/1.46\times {10}^{-3}$ $2.16\times {10}^{-4}/2.34\times {10}^{-5}$	$7.94\times {10}^{-3}/6.21\times {10}^{-4}$ $1.73\times {10}^{-2}/1.16\times {10}^{-3}$ $1.70\times {10}^{-4}/2.27\times {10}^{-5}$	$\mathbf{6}.\mathbf{59}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{4}.\mathbf{40}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{2}.\mathbf{02}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{6}.\mathbf{50}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{6}.\mathbf{95}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{04}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
8	$6.55\times {10}^{-3}/5.57\times {10}^{-4}$ $1.35\times {10}^{-2}/1.30\times {10}^{-3}$ $7.65\times {10}^{-4}/4.20\times {10}^{-5}$	$6.57\times {10}^{-3}/4.18\times {10}^{-4}$ $1.34\times {10}^{-2}/1.25\times {10}^{-3}$ $7.69\times {10}^{-4}/4.10\times {10}^{-5}$	$7.79\times {10}^{-3}/7.17\times {10}^{-4}$ $1.47\times {10}^{-2}/7.01\times {10}^{-4}$ $6.97\times {10}^{-4}/2.49\times {10}^{-5}$	$\mathbf{4}.\mathbf{63}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{64}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{54}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{4}.\mathbf{87}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{44}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{3}.\mathbf{20}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
9	$5.77\times {10}^{-3}/5.93\times {10}^{-4}$ $1.34\times {10}^{-2}/1.45\times {10}^{-3}$ $5.35\times {10}^{-4}/4.37\times {10}^{-5}$	$5.73\times {10}^{-3}/7.33\times {10}^{-4}$ $1.34\times {10}^{-2}/1.09\times {10}^{-3}$ $5.40\times {10}^{-4}/4.41\times {10}^{-5}$	$7.05\times {10}^{-3}/7.04\times {10}^{-4}$ $1.52\times {10}^{-2}/1.04\times {10}^{-3}$ $4.58\times {10}^{-4}/3.19\times {10}^{-5}$	$\mathbf{6}.\mathbf{55}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{28}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{3}.\mathbf{01}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{7}.\mathbf{88}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{04}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{85}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
10	$6.08\times {10}^{-3}/6.07\times {10}^{-4}$ $1.26\times {10}^{-2}/1.05\times {10}^{-3}$ $1.56\times {10}^{-4}/2.52\times {10}^{-5}$	$6.13\times {10}^{-3}/5.35\times {10}^{-4}$ $1.25\times {10}^{-2}/9.36\times {10}^{-4}$ $1.58\times {10}^{-4}/2.06\times {10}^{-5}$	$6.90\times {10}^{-3}/4.92\times {10}^{-4}$ $1.37\times {10}^{-2}/8.90\times {10}^{-4}$ $1.19\times {10}^{-4}/1.87\times {10}^{-5}$	$\mathbf{6}.\mathbf{08}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{11}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{44}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{5}.\mathbf{39}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{79}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
11	$6.60\times {10}^{-3}/6.82\times {10}^{-4}$ $1.41\times {10}^{-2}/1.28\times {10}^{-3}$ $8.41\times {10}^{-4}/4.54\times {10}^{-5}$	$6.42\times {10}^{-3}/9.44\times {10}^{-4}$ $1.36\times {10}^{-2}/1.56\times {10}^{-3}$ $8.63\times {10}^{-4}/6.68\times {10}^{-5}$	$7.88\times {10}^{-3}/1.58\times {10}^{-3}$ $1.61\times {10}^{-2}/1.58\times {10}^{-3}$ $7.74\times {10}^{-4}/5.81\times {10}^{-5}$	$\mathbf{6}.\mathbf{33}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{88}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{2}.\mathbf{82}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{8}.\mathbf{92}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{45}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{92}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
12	$5.97\times {10}^{-3}/8.94\times {10}^{-4}$ $1.34\times {10}^{-2}/1.18\times {10}^{-3}$ $3.29\times {10}^{-4}/3.69\times {10}^{-5}$	$5.62\times {10}^{-3}/5.73\times {10}^{-4}$ $1.21\times {10}^{-2}/1.38\times {10}^{-3}$ $3.50\times {10}^{-4}/3.43\times {10}^{-5}$	$6.83\times {10}^{-3}/8.03\times {10}^{-4}$ $1.44\times {10}^{-2}/1.37\times {10}^{-3}$ $2.70\times {10}^{-4}/3.22\times {10}^{-5}$	$\mathbf{8}.\mathbf{45}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{62}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{2}.\mathbf{24}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{65}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{7}.\mathbf{41}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{58}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
13	$5.81\times {10}^{-3}/6.54\times {10}^{-4}$ $1.20\times {10}^{-2}/1.46\times {10}^{-3}$ $3.07\times {10}^{-4}/4.06\times {10}^{-5}$	$5.70\times {10}^{-3}/5.23\times {10}^{-4}$ $1.20\times {10}^{-2}/1.22\times {10}^{-3}$ $3.16\times {10}^{-4}/2.38\times {10}^{-5}$	$7.09\times {10}^{-3}/8.31\times {10}^{-4}$ $1.39\times {10}^{-2}/1.31\times {10}^{-3}$ $2.40\times {10}^{-4}/2.65\times {10}^{-5}$	$\mathbf{4}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{12}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{51}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{21}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{7}.\mathbf{30}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{79}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
14	$6.13\times {10}^{-3}/5.97\times {10}^{-4}$ $1.38\times {10}^{-2}/1.23\times {10}^{-3}$ $1.52\times {10}^{-4}/2.87\times {10}^{-5}$	$6.22\times {10}^{-3}/9.34\times {10}^{-4}$ $1.29\times {10}^{-2}/1.04\times {10}^{-3}$ $1.70\times {10}^{-4}/3.08\times {10}^{-5}$	$7.00\times {10}^{-3}/4.76\times {10}^{-4}$ $1.46\times {10}^{-2}/9.68\times {10}^{-4}$ $1.11\times {10}^{-4}/2.02\times {10}^{-5}$	$\mathbf{7}.\mathbf{20}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{38}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{14}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{3}.\mathbf{95}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{5}.\mathbf{24}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{72}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
15	$5.95\times {10}^{-3}/5.97\times {10}^{-4}$ $1.26\times {10}^{-2}/1.25\times {10}^{-3}$ $2.83\times {10}^{-4}/2.63\times {10}^{-5}$	$5.90\times {10}^{-3}/5.90\times {10}^{-4}$ $1.21\times {10}^{-2}/9.10\times {10}^{-4}$ $2.91\times {10}^{-4}/2.92\times {10}^{-5}$	$7.00\times {10}^{-3}/5.69\times {10}^{-4}$ $1.36\times {10}^{-2}/8.37\times {10}^{-4}$ $2.33\times {10}^{-4}/2.03\times {10}^{-5}$	$\mathbf{5}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{52}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{92}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{86}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{6}.\mathbf{99}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{97}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)

Notes: Best values are highlighted in bold. “+” and “=” denote that IMOWOA is statistically superior and similar to the compared algorithm, respectively.

As illustrated in Table 2, the proposed IMOWOA obtained the best results of each metric on all test instances, demonstrating its strong convergence capability and well-balanced comprehensive performance in FCC-MOSSO. Among the remaining compared algorithms, NSGA-II and SPEA-2 performed comparably, yet both surpassed MOGWO. For a more intuitive comparison, Figure 3 visualizes the final non-dominated solution sets obtained from 20 runs on four representative test instances (2, 6, 10, and 14). As depicted, MOGWO converged to narrow regions, indicating limited exploration capability and a tendency toward premature convergence. NSGA-II exhibited better distribution uniformity than SPEA-2, though with slightly inferior exploration capability. In contrast, the proposed IMOWOA achieved significantly broader coverage in the objective space. Its solution sets not only spanned a larger area but also dominated most of the solutions derived by the other algorithms.

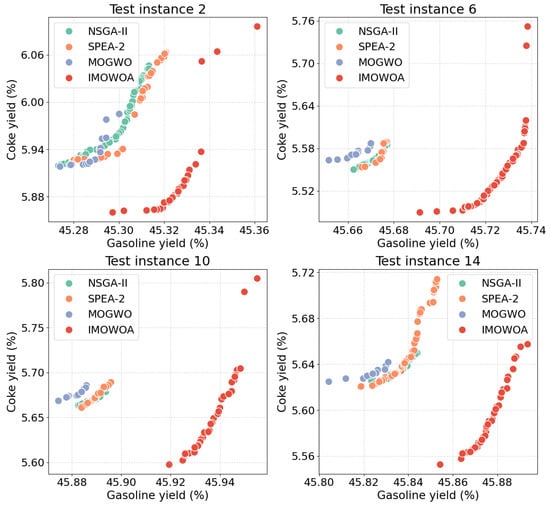
Figure 3. Non-dominated solutions of NSGA-II, SPEA-2, MOGWO, and IMOWOA on test instances 2, 6, 10, and 14. (IMOWOA exhibits wider Pareto front coverage, indicating superior exploration ability).

Overall, the thorough results suggest that IMOWOA exhibits superior search capabilities in the FCC-MOSOO problem, outperforming all compared algorithms in terms of both convergence behavior and comprehensive performance.

4.3. Ablation Study

To evaluate the effectiveness of AMNS and DR mechanisms, an ablation study was carried out comparing IMOWOA against three variants: the basic multi-objective WOA without either mechanism (MOWOA), MOWOA with only DR(MOWOA-D), and MOWOA with only AMNS (MOWOA-A).

The comparison results of GD, IGD, and HV for the above algorithms are summarized in Table 3. For a more detailed analysis, Figure 4 plots the metrics of 20 independent runs of each algorithm on test instances 3, 8, and 13 (each gray dot represents a metric) along with the box plots reflecting statistical distributions. In terms of GD, IMOWOA and MOWOA-A performed similarly, and the best results were produced between them, indicating the contribution of the AMNS mechanism to convergence. Although MOWOA-D performed worse than IMOWOA and MOWOA-A, it still surpassed MOWOA. As illustrated in Figure 4, GD of MOWOA-D exhibited a wider distribution, attributed to the influence of the DR mechanism. In contrast, both IMOWOA and MOWOA-A demonstrated more concentrated and better distributions.

Table 3. Means, standard deviations, and Welch’s t-test results of GD, IGD, and HV for MOWOA, IMOWOA-D, IMOWOA-A, and IMOWOA on all test instances.

Test Instance	MOWOA (Mean/Std)	MOWOA-D (Mean/Std)	MOWOA-A (Mean/Std)	IMOWOA (Mean/Std)
	GD IGD HV	GD IGD HV	GD IGD HV	GD IGD HV
1	$3.24\times {10}^{-3}/1.87\times {10}^{-3}$ $8.98\times {10}^{-3}/2.95\times {10}^{-3}$ $1.56\times {10}^{-3}/1.81\times {10}^{-4}$	$2.87\times {10}^{-3}/9.39\times {10}^{-4}$ $5.87\times {10}^{-3}/2.15\times {10}^{-3}$ $1.66\times {10}^{-3}/1.18\times {10}^{-4}$	$\mathbf{1}.\mathbf{78}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{9}.\mathbf{80}\times {\mathbf{10}}^{-\mathbf{4}}$ $7.24\times {10}^{-3}/1.60\times {10}^{-3}$ $1.75\times {10}^{-3}/1.28\times {10}^{-4}$	$1.83\times {10}^{-3}/9.62\times {10}^{-4}$ (+,+,=) $\mathbf{3}.\mathbf{83}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{10}\times {\mathbf{10}}^{-\mathbf{3}}$ (+,+,+) $\mathbf{1}.\mathbf{81}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{1}.\mathbf{31}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=)
2	$4.97\times {10}^{-3}/4.75\times {10}^{-3}$ $1.23\times {10}^{-2}/5.33\times {10}^{-3}$ $1.33\times {10}^{-3}/2.41\times {10}^{-4}$	$3.01\times {10}^{-3}/1.26\times {10}^{-3}$ $6.42\times {10}^{-3}/2.57\times {10}^{-3}$ $1.57\times {10}^{-3}/1.38\times {10}^{-4}$	$\mathbf{1}.\mathbf{77}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{8}.\mathbf{29}\times {\mathbf{10}}^{-\mathbf{4}}$ $6.77\times {10}^{-3}/1.86\times {10}^{-3}$ $1.62\times {10}^{-3}/1.07\times {10}^{-4}$	$2.44\times {10}^{-3}/1.23\times {10}^{-3}$ (+,=,=) $\mathbf{4}.\mathbf{51}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{24}\times {\mathbf{10}}^{-\mathbf{3}}$ (+,+,+) $\mathbf{1}.\mathbf{67}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{1}.\mathbf{20}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=)
3	$2.24\times {10}^{-3}/1.09\times {10}^{-3}$ $4.74\times {10}^{-3}/2.06\times {10}^{-3}$ $6.31\times {10}^{-4}/8.05\times {10}^{-5}$	$2.16\times {10}^{-3}/1.21\times {10}^{-3}$ $3.09\times {10}^{-3}/1.45\times {10}^{-3}$ $7.08\times {10}^{-4}/5.73\times {10}^{-5}$	$\mathbf{6}.\mathbf{28}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{04}\times {\mathbf{10}}^{-\mathbf{4}}$ $3.43\times {10}^{-3}/1.25\times {10}^{-3}$ $7.56\times {10}^{-4}/3.43\times {10}^{-5}$	$7.03\times {10}^{-4}/6.20\times {10}^{-4}$ (+,+,=) $\mathbf{1}.\mathbf{45}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{19}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{8}.\mathbf{17}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{11}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
4	$2.01\times {10}^{-3}/6.99\times {10}^{-4}$ $5.49\times {10}^{-3}/1.57\times {10}^{-3}$ $6.16\times {10}^{-4}/6.32\times {10}^{-5}$	$1.87\times {10}^{-3}/1.07\times {10}^{-3}$ $3.62\times {10}^{-3}/1.08\times {10}^{-3}$ $6.93\times {10}^{-4}/4.66\times {10}^{-5}$	$6.28\times {10}^{-4}/2.62\times {10}^{-4}$ $3.67\times {10}^{-3}/1.03\times {10}^{-3}$ $7.27\times {10}^{-4}/3.03\times {10}^{-5}$	$\mathbf{5}.\mathbf{32}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{13}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=) $\mathbf{1}.\mathbf{68}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{87}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{7}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{09}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
5	$2.25\times {10}^{-3}/7.31\times {10}^{-4}$ $6.76\times {10}^{-3}/1.63\times {10}^{-3}$ $6.63\times {10}^{-4}/5.60\times {10}^{-5}$	$1.72\times {10}^{-3}/8.36\times {10}^{-4}$ $4.07\times {10}^{-3}/1.45\times {10}^{-3}$ $7.62\times {10}^{-4}/6.23\times {10}^{-5}$	$6.04\times {10}^{-4}/2.98\times {10}^{-4}$ $4.83\times {10}^{-3}/1.43\times {10}^{-3}$ $8.08\times {10}^{-4}/3.74\times {10}^{-5}$	$\mathbf{5}.\mathbf{26}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{82}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=) $\mathbf{2}.\mathbf{63}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{8}.\mathbf{03}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{8}.\mathbf{65}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{38}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
6	$1.93\times {10}^{-3}/6.74\times {10}^{-4}$ $4.45\times {10}^{-3}/1.54\times {10}^{-3}$ $4.88\times {10}^{-4}/4.92\times {10}^{-5}$	$1.80\times {10}^{-3}/1.07\times {10}^{-3}$ $3.13\times {10}^{-3}/1.33\times {10}^{-3}$ $5.59\times {10}^{-4}/4.90\times {10}^{-5}$	$\mathbf{4}.\mathbf{46}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{47}\times {\mathbf{10}}^{-\mathbf{4}}$ $2.03\times {10}^{-3}/8.28\times {10}^{-4}$ $6.06\times {10}^{-4}/2.83\times {10}^{-5}$	$6.59\times {10}^{-4}/4.81\times {10}^{-4}$ (+,+,=) $\mathbf{8}.\mathbf{86}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{1}.\mathbf{46}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{6}.\mathbf{55}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{1}.\mathbf{47}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
7	$1.95\times {10}^{-3}/1.08\times {10}^{-3}$ $5.78\times {10}^{-3}/2.24\times {10}^{-3}$ $5.34\times {10}^{-4}/7.85\times {10}^{-5}$	$2.00\times {10}^{-3}/9.47\times {10}^{-4}$ $4.07\times {10}^{-3}/1.31\times {10}^{-3}$ $5.95\times {10}^{-4}/5.36\times {10}^{-5}$	$\mathbf{5}.\mathbf{05}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{04}\times {\mathbf{10}}^{-\mathbf{4}}$ $3.42\times {10}^{-3}/8.75\times {10}^{-4}$ $6.50\times {10}^{-4}/3.48\times {10}^{-5}$	$6.59\times {10}^{-4/4.40}\times {10}^{-4}$ (+,+,=) $\mathbf{2}.\mathbf{02}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{6}.\mathbf{50}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{6}.\mathbf{95}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{04}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
8	$2.08\times {10}^{-3}/7.38\times {10}^{-4}$ $4.81\times {10}^{-3}/1.47\times {10}^{-3}$ $1.19\times {10}^{-3}/8.42\times {10}^{-5}$	$1.94\times {10}^{-3}/7.47\times {10}^{-4}$ $3.56\times {10}^{-3}/1.42\times {10}^{-3}$ $1.24\times {10}^{-3}/7.32\times {10}^{-5}$	$5.50\times {10}^{-4}/2.57\times {10}^{-4}$ $3.87\times {10}^{-3}/1.74\times {10}^{-3}$ $1.37\times {10}^{-3}/3.21\times {10}^{-5}$	$\mathbf{4}.\mathbf{63}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{64}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=) $\mathbf{1}.\mathbf{54}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{4}.\mathbf{87}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{44}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{3}.\mathbf{20}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
9	$1.98\times {10}^{-3}/7.52\times {10}^{-4}$ $6.30\times {10}^{-3}/1.91\times {10}^{-3}$ $8.51\times {10}^{-4}/7.98\times {10}^{-5}$	$1.82\times {10}^{-3}/6.27\times {10}^{-4}$ $3.74\times {10}^{-3}/7.39\times {10}^{-4}$ $9.20\times {10}^{-4}/4.10\times {10}^{-5}$	$6.70\times {10}^{-4}/3.25\times {10}^{-4}$ $5.33\times {10}^{-3}/1.48\times {10}^{-3}$ $9.80\times {10}^{-4}/3.34\times {10}^{-5}$	$\mathbf{6}.\mathbf{55}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{28}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=) $\mathbf{3}.\mathbf{01}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{7}.\mathbf{88}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{04}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{85}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
10	$2.00\times {10}^{-3}/6.70\times {10}^{-4}$ $5.10\times {10}^{-3}/1.20\times {10}^{-3}$ $3.89\times {10}^{-4}/4.51\times {10}^{-5}$	$1.95\times {10}^{-3}/6.70\times {10}^{-4}$ $3.64\times {10}^{-3}/8.90\times {10}^{-4}$ $4.41\times {10}^{-4}/4.44\times {10}^{-5}$	$8.65\times {10}^{-4}/2.58\times {10}^{-4}$ $4.27\times {10}^{-3}/1.15\times {10}^{-3}$ $4.75\times {10}^{-4}/2.60\times {10}^{-5}$	$\mathbf{6}.\mathbf{08}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{11}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{44}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{5}.\mathbf{39}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{79}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
11	$2.68\times {10}^{-3}/1.17\times {10}^{-3}$ $7.40\times {10}^{-3}/2.07\times {10}^{-3}$ $1.19\times {10}^{-3}/1.06\times {10}^{-4}$	$2.04\times {10}^{-3}/1.06\times {10}^{-3}$ $4.83\times {10}^{-3}/1.70\times {10}^{-3}$ $1.29\times {10}^{-3}/9.87\times {10}^{-5}$	$6.62\times {10}^{-4}/3.03\times {10}^{-4}$ $5.03\times {10}^{-3}/1.05\times {10}^{-3}$ $1.39\times {10}^{-3}/3.71\times {10}^{-5}$	$\mathbf{6}.\mathbf{33}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{88}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=) $\mathbf{2}.\mathbf{82}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{8}.\mathbf{92}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{1}.\mathbf{45}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{2}.\mathbf{92}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
12	$1.83\times {10}^{-3}/7.61\times {10}^{-4}$ $4.66\times {10}^{-3}/1.73\times {10}^{-3}$ $5.99\times {10}^{-4}/5.42\times {10}^{-5}$	$2.46\times {10}^{-3}/9.87\times {10}^{-4}$ $3.67\times {10}^{-3}/1.51\times {10}^{-3}$ $6.35\times {10}^{-4}/5.83\times {10}^{-5}$	$\mathbf{7}.\mathbf{61}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{24}\times {\mathbf{10}}^{-\mathbf{4}}$ $4.00\times {10}^{-3}/9.15\times {10}^{-4}$ $6.79\times {10}^{-4}/3.67\times {10}^{-5}$	$8.45\times {10}^{-4}/3.62\times {10}^{-4}$ (+,+,=) $\mathbf{2}.\mathbf{24}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{65}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{7}.\mathbf{41}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{58}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
13	$2.17\times {10}^{-3}/8.44\times {10}^{-4}$ $4.57\times {10}^{-3}/1.68\times {10}^{-3}$ $5.52\times {10}^{-4}/6.19\times {10}^{-5}$	$1.98\times {10}^{-3}/8.95\times {10}^{-4}$ $2.92\times {10}^{-3}/1.03\times {10}^{-3}$ $6.27\times {10}^{-4}/5.14\times {10}^{-5}$	$6.46\times {10}^{-4}/3.84\times {10}^{-4}$ $3.52\times {10}^{-3}/1.38\times {10}^{-3}$ $6.63\times {10}^{-4}/3.09\times {10}^{-5}$	$\mathbf{4}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{12}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=) $\mathbf{1}.\mathbf{51}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{21}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{7}.\mathbf{30}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{79}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
14	$1.85\times {10}^{-3}/1.11\times {10}^{-3}$ $4.45\times {10}^{-3}/2.22\times {10}^{-3}$ $3.89\times {10}^{-4}/6.91\times {10}^{-5}$	$2.77\times {10}^{-3}/2.02\times {10}^{-3}$ $2.83\times {10}^{-3}/7.88\times {10}^{-4}$ $4.39\times {10}^{-4}/3.73\times {10}^{-5}$	$\mathbf{5}.\mathbf{68}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{63}\times {\mathbf{10}}^{-\mathbf{4}}$ $1.95\times {10}^{-3}/6.96\times {10}^{-4}$ $4.84\times {10}^{-4}/2.28\times {10}^{-5}$	$7.20\times {10}^{-4}/3.38\times {10}^{-4}$ (+,+,=) $\mathbf{1}.\mathbf{14}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{3}.\mathbf{95}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{5}.\mathbf{24}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{72}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)
15	$2.10\times {10}^{-3}/9.01\times {10}^{-4}$ $5.36\times {10}^{-3}/1.55\times {10}^{-3}$ $5.32\times {10}^{-4}/6.39\times {10}^{-5}$	$1.64\times {10}^{-3}/5.87\times {10}^{-4}$ $3.51\times {10}^{-3}/1.02\times {10}^{-3}$ $5.96\times {10}^{-4}/4.34\times {10}^{-5}$	$6.74\times {10}^{-4}/2.75\times {10}^{-4}$ $3.73\times {10}^{-3}/1.23\times {10}^{-3}$ $6.49\times {10}^{-4}/2.20\times {10}^{-5}$	$\mathbf{5}.\mathbf{91}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{3}.\mathbf{52}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,=) $\mathbf{1}.\mathbf{92}\times {\mathbf{10}}^{-\mathbf{3}}/\mathbf{5}.\mathbf{86}\times {\mathbf{10}}^{-\mathbf{4}}$ (+,+,+) $\mathbf{6}.\mathbf{99}\times {\mathbf{10}}^{-\mathbf{4}}/\mathbf{2}.\mathbf{97}\times {\mathbf{10}}^{-\mathbf{5}}$ (+,+,+)

Note: Best values are highlighted in bold. “+” denote that IMOWOA is statistically superior to the compared algorithm.

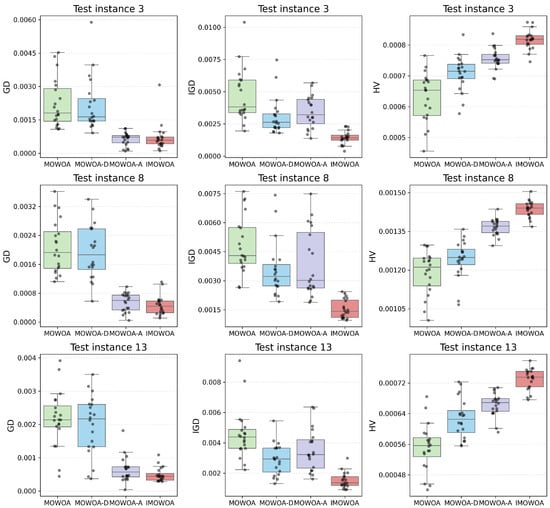
Figure 4. GD, IGD, and HV along with box plots of 20 independent runs of MOWOA, IMOWOA-D, IMOWOA-A, and IMOWOA on test instances 3, 8, and 13. (IMOWOA achieves the best mean values and the most concentrated distribution across all metrics, demonstrating enhanced search capability and stability).

IMOWOA achieved optimal IGD and HV values in all test instances, indicating better comprehensive performance. Both MOWOA-A and MOWOA-D consistently exceeded the performance of MOWOA. Statistically, IMOWOA significantly outperformed all other algorithms in IGD on each test instance. Regarding HV, it surpassed MOWOA-A in 14 instances and dominated MOWOA-D and MOWOA in all instances. Figure 4 further reveals a trade-off between MOWOA-D and MOWOA-A: the former achieved lower IGD values, whereas the latter excelled in HV. IMOWOA, however, displayed the most concentrated distribution in both metrics, reflecting greater robustness and stability.

Based on the above analysis, both proposed mechanisms effectively enhance the search capability of the algorithm. AMNS plays a dominant role in improving convergence and also contributes to the comprehensive performance. Meanwhile, the DR mechanism injects diversity into the search process, further boosting the comprehensive performance.

4.4. Result Evaluation

This subsection presents a comparative analysis between the optimized results and the original actual product yields on each test instance to evaluate the practical industrial value of the proposed optimization method. Since the proposed IMOWOA generates a Pareto non-dominated solution set, the Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) was employed to select the most suitable operational solution from the available alternatives for each instance. TOPSIS is a multi-criteria decision-making method that ranks alternatives based on their relative distance from the ideal and negative-ideal solutions. In this implementation, gasoline yield was defined as a benefit criterion to be maximized, while coke yield was treated as a cost criterion to be minimized. Both criteria were assigned equal weights to enable the selection of an optimal compromise solution.

The comparison results of gasoline and coke yields of the selected optimized solution with their respective original yields on each test instance are summarized in Figure 5. It is clear that the optimized operational solution consistently enhanced gasoline yield while simultaneously reducing coke yield. Specifically, the gasoline yield showed an average increase of 0.32%, while the coke yield exhibited an average reduction of 0.11%. Taking the studied FCC unit as a representative case, a further sustainability impact analysis was conducted. With an annual processing capacity of 2.6 million tons and a coke-to-$\mathrm{C}{\mathrm{O}}_2$ conversion rate of approximately 98%, the unit can achieve an annual $\mathrm{C}{\mathrm{O}}_2$ emission reduction of about 10,277 tons through the coke yield reduction.

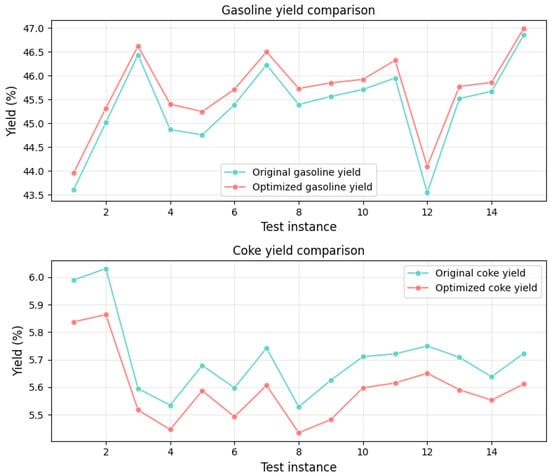
Figure 5. Comparison results of gasoline and coke yields of the selected optimized solution with their respective original yields on 15 test instances. (Optimized gasoline and coke yields show improvement and reduction, respectively, confirming the effectiveness of the proposed approach).

The demonstrated reduction in carbon emissions, along with the simultaneous improvement in gasoline production, validates the effectiveness of the Dual-LSTM modeling approach and the proposed IMOWOA. The proposed approach also exhibits good industrial implementation feasibility, as the data-driven model provides rapid predictions suitable for dynamic optimization, while the optimized operational adjustments can be integrated into existing refinery Distributed Control Systems. These characteristics highlight the significant potential of the proposed approach in supporting refinery sustainability goals while maintaining economic viability.

5. Conclusions

This paper has addressed an FCC-MOSOO problem, targeting the enhancement of gasoline production and the suppression of coke formation to achieve concurrent economic and environmental benefits. A data-driven multi-objective optimization model founded on a Dual-LSTM architecture is established to accurately capture variable-yield relationships with high computational efficiency, thus avoiding the high computational cost and limited applicability of mechanism models. The model optimizes the gasoline and coke yields through adjusting the trajectory of controlled variables over a future window, effectively handling the significant time lag characteristics of the FCC process.

To efficiently solve this model, an IMOWOA enhanced with AMNS and DR mechanisms is designed. Empirical evaluations confirm the superiority of IMOWOA, which outperforms established algorithms, including NSGA-II, SPEA-2, and MOGWO in convergence efficiency and comprehensive performance. Furthermore, the ablation validates the critical role of the proposed AMNS and DR, as IMOWOA consistently exceeds the performance of its variants without these mechanisms. Compared with the yields before optimization, the proposed approach can increase the gasoline yield by an average of 0.32% and reduce the coke yield by an average of 0.11%, demonstrating its capability to improve both economic and environmental performance in FCC operations.

This work provides a practical and intelligent decision-support tool for FCC operators seeking to align with sustainable development goals. Future research will focus on extending the proposed method to incorporate additional sustainability indicators, such as energy consumption, and testing its applicability under wider operational scenarios.