Multicriteria Optimization of Nanocellulose-Reinforced Polyvinyl Alcohol and Pyrrolidone Hydrogels

Abstract

Developing new materials for human cartilage replacement is a hot research topic. These materials have multiple properties of interest, so selecting a new material (hydrogel) is a multi-attribute decision-making problem. A case study illustrates the application of a structured approach and tools to solve this problem type. Ten hydrogels, most of which are new formulations, were evaluated based on three attributes. The weights assigned to the attributes were identified using three methods from the literature, in addition to those previously assigned by an expert. Since the hydrogel properties showed some variability, Monte Carlo simulations were carried out using triangular distribution. Ten thousand decision matrices were built and 10,000 rankings were generated by each of the ten multicriteria decision-making methods employed in this study. Ranking similarity was evaluated through the PS index, whose values ensure consistency and reliability of the results achieved. Rank acceptability and pairwise indexes were used to identify the most promising hydrogels. Two hydrogels were identified as the most promising for further study, for any of the four sets of weights used. Both are annealed nanocellulose-reinforced polyvinyl alcohol and pyrrolidone hydrogels. The robustness of this result is supported on the values of acceptability and pairwise indexes.

1. Introduction

The genesis and theoretical foundations of the three-pillar conception (dimensions) of sustainability were recently reviewed and discussed [1]. Although some controversy (viewpoints) on their relevance or hierarchy exists, the social, economic, and environmental dimensions are, nowadays, widely accepted [1,2,3], and their relevance for society is not ignored in any knowledge areas. From classical engineering areas like mechanics, electrical, chemical, and materials to emerging areas like biomedical and bioinformatics, the number and diversity of studies addressing sustainability issues by applying scientific knowledge, technical methods, and management principles are huge [4,5,6,7,8,9]. In fact, engineering has been crucial for sustainable development in all its dimensions, namely in addressing basic human needs, in addition to its relevant role in the sustainable design and development of products, processes, and technologies that profoundly impact (non)industrial systems and governance [10,11,12,13,14].

The development of biomedical products, namely polyvinyl alcohol (PVA) and pyrrolidone (PVP) hydrogels for articular cartilage damaged replacement, is just one of the multiple examples of biomedical engineering research lines which fits directly to the social dimension of sustainability, namely to basic human needs or expectations like health and well-being [15,16]. Notice that “Good health and Well-being” is a sustainable development goal [17], which is an ambitious and hard-to-achieve goal, as many countries have a rising life expectancy and the pace of population ageing is much faster than in the past [18,19]. According to [20], pain is one of the most common medical complaints among older adults. Pain impacts people’s health and well-being directly, and it is known that chronic pain becomes more common as people grow older [21].

Developing new materials like hydrogels for cartilage replacement is a hot research topic [22]. Contrary to the conventional practice where the anatomic joint area is totally removed and replaced by a mechanical device like hip prosthesis, the use of hydrogels is a very promising approach to replace damaged articular cartilage, which occurs due to trauma, wear and tear, or inflammatory processes, causing pain and difficulty in limb mobility. Hydrogels are two-phase materials, very rich in water, which can mimic the properties of cartilage and are much easier to produce than mechanical devices. They are very versatile materials because their structure can be adapted, and various growth factors can be introduced to stimulate the proliferation of cells responsible for cartilage formation (chondrocytes), enabling the implant integration in the surrounding living tissue [23]. In addition, they can be used as a drug delivery system that carries anti-inflammatory and/or analgesic drugs, allowing fast patient recovery after surgery and lower general costs associated with healthcare. However, the mechanical properties of these materials (hydrogels) are a concern, namely the mechanical strength, if they are to be used as a replacement material for hyaline cartilage [24]. Other concerns are permeability, surface roughness, and pore size properties as they can influence biocompatibility [24,25]. These studies and [16] confirm that designing, developing, and/or selecting a hydrogel among a set of available alternatives is a multi-attribute problem. AI and ML have emerged as powerful tools in hydrogel development, enabling data-driven design and optimization [16,26]. However, to the best of our knowledge, no study explores nanocellulose-reinforced polyvinyl alcohol and pyrrolidone hydrogels from a multicriteria optimization decision-making perspective. Therefore, the major objective of this paper is to employ a structured approach and various optimization methods that support the required science-based framework for identifying a hydrogel with the most favourable values for selected properties, among the ten hydrogels tested, including new hydrogels.

The remainder of the paper is organized as follows: The next section includes the tested materials, assessed properties, experimental strategy, and data analysis methods used. Then, the results and their discussion are presented. The last section includes the conclusion.

2. Materials and Methods

The hydrogel market is experiencing significant growth, driven by increasing demand across distinct industries like medicine and agriculture. In fact, various hydrogels and their features have been studied and tested in a wide range of applications [27]. In biomedical applications, as an example, they have received significant attention due to their physicochemical and biological properties [26,28], which can be tailored to match the soft living tissue, improving the biocompatibility and functionality of the implanted material [29]. Concerning the mechanical properties of hydrogels, various strategies have been applied with the aim of increasing them [24,25], namely the use of reinforcing particles and fibres [30,31]. PVA is another material that has received the most attention due to its versatility in production, making it possible to adjust its mechanical properties. With this purpose, various methods and mixtures have been studied [32]. For example, the PVA hydrogels produced by the freeze–thaw method are more porous and have a higher water content than those produced by the dry casting technique [33]; applying a subsequent annealing treatment to the PVA obtained by dry casting will result in a dramatic increase in the mechanical strength and a loss of water content in the hydrogel [34]; the addition of PVP to PVA increases mechanical performance due to hydrogen bonding between the hydroxyl groups of PVA and the carbonyl group of PVP and, at the same time, increase the water content [35]. The PVP is also important in terms of lubrication, reducing the coefficient of friction and, indirectly, the wear of both the hydrogel and the natural cartilage surface. Nanocellulose has also been investigated as a reinforcing material for PVA hydrogels [36,37].

Although polyvinyl alcohol (PVA) hydrogels have been extensively investigated for articular cartilage restoration due to their excellent biocompatibility and low friction, they still exhibit insufficient mechanical strength and fatigue resistance compared with native cartilage tissue. Conventional PVA hydrogels typically show compressive moduli between 0.3 and 0.8 MPa and tensile strengths below 1 MPa, far below those of native cartilage (4–20 MPa compressive; 5–25 MPa tensile) [38]. The blending of PVA with polyvinylpyrrolidone (PVP) improves elasticity, swelling stability, and viscoelastic behaviour, yet the resulting PVA/PVP hydrogels still present limited stiffness and wear resistance [15,39,40]. To overcome these deficiencies, the incorporation of nanocellulose nanoparticles (NFCs) has proven highly effective in enhancing the mechanical integrity, energy dissipation, and load-bearing capability of PVA-based systems. The strong hydrogen bonding between the hydroxyl groups of PVA and NFC establishes a reinforcing network that increases tensile and compressive moduli by up to 2–3 times while also improving toughness and lubrication under dynamic loading [41]. Therefore, the proposed PVA/PVP/NFC hydrogel offers an attractive alternative in terms of mechanical robustness and structural mimicry to native cartilage.

Here, various PVA/PVP hydrogels with nanocellulose nanoparticles are evaluated, with the aim of identifying a hydrogel for articular cartilage replacement with the most favourable values for some relevant properties, namely the tangent compressive modulus, friction coefficient, and water content. Articular cartilages are subjected to compressive loads during the patient’s daily activities, so the hydrogel must withstand the compressive loads applied; therefore, the tangent compressive modulus is a relevant attribute, and their values must be as close as possible to the natural cartilage tissue value to avoid differences in deformability that could lead to difficulties in integrating the hydrogel into the surrounding natural cartilage. Concerning the friction coefficient, its value needs to be low for minimizing the shear stress on the sliding surfaces, preventing damage and, consequently, the wear of the implanted hydrogel and the surface of the antagonizing natural cartilage. A low friction coefficient is also important because lower shear loads facilitate hydrogel integration into the surrounding living tissue. Because cartilage is an avascular tissue, the hydrogel water content is also a relevant property, since water is a diffusion route for nutrients to the surrounding tissue or drugs that can be previously incorporated in a hydrogel and delivered in the implanted region for controlling, as an example, the post-surgery inflammatory processes. The presence of water also leads to a more pronounced viscoelasticity of the hydrogel, which is important for shock absorption. In addition, a higher water content increases lubricity and, consequently, could reduce the friction coefficient.

2.1. Hydrogels, Components, and Properties

Ten PVA/PVP hydrogels without and with NFCs were produced, according to the proportions shown in

Table 1. Hydrogel and component proportions.

Hydrogel	Component (%)			Annealing
	PVA	PVP	NFCs
$h_1$	15	0	0	-
$h_2$	15	4.5	0	-
$h_3$	15	4.5	0.4	-
$h_4$	15	4.5	0.8	-
$h_5$	15	4.5	1.1	-
$h_6$	15	0	0	Yes
$h_7$	15	4.5	0	Yes
$h_8$	15	4.5	0.4	Yes
$h_9$	15	4.5	0.8	Yes
$h_{10}$	15	4.5	1.1	Yes

, where $h_6$, $h_7$, $h_8$, $h_9$, and $h_{10}$ are hydrogels that were submitted to thermal treatment (annealing). The experimental procedure to produce PVA/PVP hydrogels without and with nanocellulose nanoparticles (NFCs), according to the proportions shown in Table 1, was the following:

-

Prepare aqueous solution (40 g);

-

Heat solution to 90 °C for 24 h;

-

Pour solution into Petri dishes;

-

Dry solution for 7 days at 37 °C to form films;

-

Anneal selected films at 140 °C for 1 h;

-

Put the films in distilled water to hydrate (and become hydrogels).

The hydrogels were evaluated based on three properties (attributes), namely, the water content ($WC$), tangent compressive modulus ($TCM$), and friction coefficient ($FC$).

The $WC$ is calculated with (1), and it is a larger-the-better-type attribute (the higher the $WC$ value is, the better it will be).

$$WC={\displaystyle \frac{\mathrm{Ww}-\mathrm{Wd}}{\mathrm{Ww}}}$$

(1)

where Ww represents the wet weight and Wd represents the dried weight. The $TCM$ was calculated according to (2), for a strain of 15% and $∆\mathsf{\epsilon }$ = 1%, and it is a larger-the-better-type attribute.

$$TCM={\displaystyle \frac{{\mathsf{\sigma }}_{\mathsf{\epsilon }+∆\mathsf{\epsilon }}-{\mathsf{\sigma }}_{\mathsf{\epsilon }-∆\mathsf{\epsilon }}}{2∆\mathsf{\epsilon }}}$$

(2)

The $FC$ is a smaller-the-better-type attribute (the lower the $FC$ value is, the better it will be), and their values were obtained from tribological tests using a tribometer (TRB3, Anton Paar) with a pin-on-plate configuration and reciprocating linear movement at room temperature in synovial fluid. The $FC$, $WC$, and $TCM$ values obtained from laboratory experiments are shown in

Table 2. Experimental values.

Hydrogel	WC			TCM (15%)			FC
	Min	Mean	Max	Min	Mean	Max	Min	Mean	Max
$h_1$	49.22	50.23	51.32	1.76	1.96	2.17	0.076	0.079	0.086
$h_2$	63.53	64.95	65.97	1.54	1.65	1.79	0.040	0.048	0.054
$h_3$	65.07	65.66	66.29	1.06	1.21	1.41	0.034	0.043	0.057
$h_4$	66.46	67.22	68.66	1.03	1.30	1.58	0.035	0.039	0.045
$h_5$	71.76	72.26	72.86	0.99	1.11	1.22	0.044	0.050	0.057
$h_6$	29.80	30.71	32.27	1.42	1.89	2.64	0.080	0.085	0.093
$h_7$	42.42	44.86	46.44	2.03	2.40	2.73	0.083	0.093	0.103
$h_8$	43.19	46.97	50.20	1.61	2.65	4.12	0.023	0.029	0.037
$h_9$	43.14	44.53	49.38	1.75	2.84	4.50	0.022	0.029	0.039
$h_{10}$	53.07	55.16	57.43	0.91	1.40	2.51	0.020	0.027	0.032

.

2.2. Multi-Attribute Optimization

Researchers and practitioners (including managers, engineers, politicians, …) often face difficulties when solving problems that require consideration of various properties (characteristics or attributes) related to technical, economic, social, and/or environmental requirements, and the objective is to select an alternative from a set of feasible options. These alternatives are products, equipment, marketing and operations management strategies, financial investments, or governance politics, just to name a few examples. The decision-making process is really challenging in most problems because of the following:

-

The number of attributes may be large and/or the selection of preference attributes may not be consensual. In addition, some of these attributes may have a qualitative nature that may not be easy to measure or transform into a quantitative and quantifiable attribute.

-

Two or more attributes may be correlated, either linearly or nonlinearly, which can hinder and/or complicate data analysis and compromise the reliability of the conclusions if such correlations are not identified and accounted for in advance.

-

The scale and units of measurement of the attribute can be very different, which requires standardization of their values. It is known that standardizing data significantly impacts the identification of the best compromise alternative, i.e., it introduces bias into the conclusions in multi-attribute optimization problems.

-

The amount of data available to find the best compromise alternative (solution) for a problem with multiple attributes may be limited by the technical, economic, and human resources available.

-

The greater the number of attributes in a problem, the more difficult it will be to find a balanced solution that significantly improves all attributes.

-

Assigning priorities and/or preferences (usually referred to as weights) to the attributes is not an easy and/or consensual task, namely because it requires properly supported technical knowledge and may involve subjective considerations.

-

The number and variety of methods and approaches to solve multi-attribute problems are very large, and one cannot expect that those who need to solve such problems have the required statistical background and access to the literature to select the most appropriate method(s) and approach(es).

This means that solving a multi-attribute problem, such as selecting a hydrogel, should not be based on empirical or expert sensitivity. Multi-attribute decision-making (MADM) methods are useful for this purpose. The efficiency of various MADM methods has been proven, so those who want to solve a multi-attribute problem, i.e., those who need to identify a compromise solution from a set of available solutions, cannot ignore them.

Review papers on MADM methods have been published [41,42,43,44,45], and many papers compare the performance of those methods (see [46,47] as examples). The wide range of MADM method applications, from water resources planning and management [41] to finance [48], has also been reported in the literature where multi-attribute decision-aiding tools have also played a relevant role.

2.3. Experimental Strategy and Approach

There exist numerous MADM methods and approaches for tackling the difficulties encountered in real-life decision-making problems [49,50,51,52,53]. Here, the experimental approach for solving multi-attribute problems was structured as follows:

(a)

Phase 1—Generate data: Monte Carlo simulations were conducted to supplement the data obtained from physical experiments.

(b)

Phase 2—Assign priorities (weights) to attributes: In addition to the expert’s opinion, weights to each attribute were identified by using methods selected from the literature.

(c)

Phase 3—Solution rankings: Hydrogel rankings were obtained by applying various multi-attribute decision-making methods to the data generated in phase 1.

(d)

Phase 4—Results analysis and validation: Acceptability and pairwise indexes were used to identify the most promising hydrogels. Rankings from various optimization methods were also evaluated using similarity indexes.

2.3.1. Generate Data

In (non)industrial settings, human and technical resources required to perform experimental studies are, in general, either limited in quantity and quality, so running the desired or appropriate number of experiments is not easy, if at all possible. Moreover, even when those experiments are well planned and managed, known and unknown variables (called noise factors) will introduce variability in the experimental results [54]. Variability is always a concern in experimental studies. When measurement systems are not the source of that variability [55], the way to better understand the impact of variability in experimental results, namely when running physical experiments, limited by time, human, technical resources, and/or economic constraints, is to obtain more data through computer experiments. Monte Carlo simulation is a valuable tool for gaining insight into problems (systems, processes, products, …) and helping decision-makers to make more informed decisions when solving problems [56,57,58].

Producing PVA/PVP hydrogels with or without nanocellulose requires many hours (>70 h) of work, so the number of physical experiments carried out in the case study presented here was small due to time and resource constraints. For this reason, additional data was generated through Monte Carlo simulation to build the decision matrix (D—a matrix of size m × n, whose elements are the performance measures of ith alternative on jth attribute) and to help identify a hydrogel with the most favourable $WC$, $TCM$, and $FC$ values.

$$\begin{array}{cc}D=\begin{array}{c}\begin{array}{c}\\ A_1\end{array}\\ \begin{array}{c}{A}_2\\ \begin{array}{c}⋮\\ A_m\end{array}\end{array}\end{array}& \begin{array}{c}\begin{array}{cc}{C}_1& \begin{array}{cc}{C}_2& \begin{array}{cc}\dots & C_n\end{array}\end{array}\end{array}\\ \left[\begin{array}{ccc}\begin{array}{c}{x}_{11}\\ x_{21}\\ \begin{array}{c}\begin{array}{c}⋮\\ ⋮\end{array}\\ x_{m1}\end{array}\end{array}& \begin{array}{c}{x}_{12}\\ x_{22}\\ \begin{array}{c}\begin{array}{c}⋮\\ ⋮\end{array}\\ x_{m2}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\dots \\ \dots \\ \begin{array}{c}\begin{array}{c}⋮\\ ⋮\end{array}\\ \dots \end{array}\end{array}& \begin{array}{c}{x}_{1n}\\ x_{21}\\ \begin{array}{c}\begin{array}{c}⋮\\ ⋮\end{array}\\ x_{mn}\end{array}\end{array}\end{array}\end{array}\right]\end{array}\end{array}$$

(3)

where $A_i$ ($i=1,\dots ,m)$ represent the alternatives (hydrogels), $C_j$ ($j=1,\dots ,n)$ represent the criteria or attributes, and $x_{ij}$ is the performance measure of the ith alternative on the jth attribute.

Note that the data for $TCM$ and $FC$ were generated from triangular distributions with different minimum, peak (mean), and maximum values for each hydrogel tested (see Table 2), as variability was evident in the measured values of these attributes ($TCM$ and $FC$) for each hydrogel produced in the laboratory. As variability in the $WC$ values was minimal, they were kept constant in the simulations.

The triangular distribution is typically used as a subjective description of a population/variable when there is only limited sample data due to the aforementioned constraints [59]. In this case study then, a thousand (10,000) data values were generated for each attribute of each tested hydrogel. According to [58,59,60,61], this amount of data is usually more than sufficient to provide robust results.

2.3.2. Assigning Weights to Attributes

This is a subjective task and a crucial input for finding the most balanced solution(s) in MADM problems. Imprecise and/or unreliable information from the decision-maker, i.e., weight values without the required accuracy or put forward without the required confidence must be avoided. Thus, in the case study presented here, the attribute weights are established based on expert knowledge and three structurally different analytical methods: CRITIC, Best–Worst, and Entropy methods. Applications of these methods were reported by various authors; nevertheless, it is important to be aware that any subjective or objective method for determining weights to attributes has its advantages and flaws. The reader is referred to [62] for details and an overview of various methods.

The Criteria Importance Through Inter-criteria Correlation (CRITIC) method does not require subjective information from experts or decision-makers. It calculates the weights for each attribute based on contrast intensity (variability or standard deviation) and conflict (correlation) among attributes. In practice, the greater the contrast intensity of an attribute and the lower its correlation with other attributes, the higher the priority or weight assigned to it. This indicates that the attribute has strong discriminative power and conveys information that is independent from that of the other attributes.

The CRITIC method is applied to a decision matrix as follows:

Step 1—Decision Matrix Normalization: Since the attribute’s values may have different units and magnitudes, it is necessary to normalize the decision matrix (3). For normalization purposes, each $x_{ij}$ is transformed into an $n_{ij}$ value depending on attribute type. For a larger-the-better-type attribute,

$$n_{ij}={\displaystyle \frac{x_{ij}-\min \left(x_j\right)}{\max \left(x_j\right)-\min \left(x_j\right)}}$$

(4)

and for a smaller-the-better-type attribute,

$$n_{ij}={\displaystyle \frac{\max \left(x_j\right)-x_{ij}}{\max \left(x_j\right)-\min \left(x_j\right)}}$$

(5)

where $\min \left(x_j\right)$ is the minimum value of $C_j$ across all alternatives, and $\max \left(x_j\right)$ is the maximum value of $C_j$ across all alternatives. The normalized decision matrix (N) is of size m × n, and it represents the normalized performance of the ith alternative on the jth attribute. The normalized performances ($n_{ij})$ are dimensionless and range between zero and one ($n_{ij}\in \left[\mathrm{0,1}\right])$.

Step 2—Standard deviation calculation: The standard deviation (${\sigma }_j$) for $C_j$ across all alternatives is

$${\sigma }_j=\sqrt{{\displaystyle \frac{1}{m-1}}{\sum }_{i=1}^m{\left(n_{ij}-{\overline{n}}_j\right)}^2}$$

(6)

where ${\overline{n}}_j$ is the mean value of $C_j$ across all alternatives. A higher ${\sigma }_j$ means the attribute better differentiates between alternatives.

Step 3—Correlation matrix computation: Calculate the Pearson correlation coefficient (${\rho }_{jk}$) between each pair of attributes, j and $k$, with $j,k=(1,\dots ,n)$. This measures how similar the attributes are.

$${\rho }_{jk}={\displaystyle \frac{{\sum }_{i=1}^m\left(n_{ij}-{\overline{n}}_j\right)\left(n_{ik}-{\overline{n}}_k\right)}{\sqrt{{\sum }_{i=1}^m{\left(n_{ij}-{\overline{n}}_j\right)}^2}\sqrt{{\sum }_{i=1}^m{\left(n_{ik}-{\overline{n}}_k\right)}^2}}}={\displaystyle \frac{Cov\left(j,k\right)}{{\sigma }_j{\sigma }_k}}$$

(7)

where $Cov\left(j,k\right)$ is the covariance between attribute j and $k$.

Step 4—Calculate the information content: The information content of $C_j$ is

$${Ic}_j={\sigma }_j{\sum }_{k=1}^n\left(1-{\rho }_{jk}\right)$$

(8)

The higher the information content value is, the more important the attribute will be.

Step 5—Attribute weight calculation: The weight of $C_j$ is

$$w_j={\displaystyle \frac{{Ic}_j}{{\sum }_{j=1}^n{Ic}_j}}$$

(9)

and the sum of $w_j$ equals 1.

The Best–Worst Method (BWM) determines the relative importance (weights) of a set of attributes through a structured pairwise comparison process between the most and the least important attribute, according to decision-maker preferences. Its implementation procedure is as follows:

Step 1—Determine the Best and Worst Attributes and their Preference Values

The most important (desirable and influential) attribute and the least relevant (uninfluential and worst) attribute from the set of attributes are selected by the decision-maker (expert). Then, they must assign a preference value to the best attribute compared to each of the other attributes using a predefined scale (e.g., a 1 to 9 scale, where 1 indicates equal importance, and 9 indicates the extreme importance of the best attribute compared to the other attributes). The resulting vector of pairwise comparisons is $V_{BO}={(v}_{B1},\dots ,v_{Bn})$, where $v_{Bj}$ represents the preference of the best attribute ($B$) over all the other attributes.

Step 2—Determine the Preference of All Other Attributes over the Worst Attribute

A preference value is assigned to each one of the attributes compared to the worst attribute by the decision-maker (expert), using the same predefined scale, and represents the resulting vector of pairwise comparisons as $V_{OW}=$ ($v_{1W},\dots ,v_{nW})$, where $v_{jW}$ represents the preference value of each one of the attributes over the worst attribute ($W$).

Step 3—Determine the Optimal Weights ($w_1^{*}$, $w_2^{*}$, …, $w_n^{*}$) for Attributes

To achieve this goal, the maximum absolute difference between $\left|{\displaystyle \frac{w_B}{w_j}}-v_{Bj}\right|$ and $\left|{\displaystyle \frac{w_j}{w_W}}-v_{jW}\right|$ will be minimized for all attributes. For this purpose, the following optimization problem must be solved:

$$\begin{gathered} \mathrm{Minimize}\xi \\ \mathrm{Subject}\mathrm{to} \end{gathered}$$

$$\left|{\displaystyle \frac{w_B}{w_j}}-v_{Bj}\right|\le \mathsf{\xi },\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}j$$

$$\left|{\displaystyle \frac{w_j}{w_W}}-v_{jW}\right|\le \mathsf{\xi },\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}j$$

$${\sum }_{j=1}^n{w}_j=1\mathrm{a}\mathrm{n}\mathrm{d}{w}_j\ge 0\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{l}j.$$

where ξ is the consistency ratio, $w_j$ is the weight of the jth attribute, $w_B$ is the weight of the best attribute, $w_W$ is the weight of the worst attribute, $v_{Bj}$ is the preference of the best attribute over the other attributes, and $v_{jW}$ is the preference of the jth attribute over the worst attribute [47].

Step 4—Check the Consistency Ratio

A consistency ratio indicates how (in)consistent a decision-maker (expert) is. The consistency index (ξ) indicates the consistency level of the pairwise comparisons (set of judgments contained in vectors $V_{BO}$ and $V_{OW}$). The preferences are consistent if $v_{Bj}\times v_{jW}=v_{BW}$ for all j. To check for the consistency, the global input-based consistency ratio for all attributes (${CR}^I)$ is formulated as follows [63]:

$${CR}^I=\mathrm{m}\mathrm{a}\mathrm{x}\left({CR}_j^I\right)$$

(10)

where ${CR}_j^I$ represents the local consistency level associated with attribute $C_j$.

$${CR}_j^I=\left\{\begin{array}{c}{\displaystyle \frac{\left|v_{Bj}\times v_{jW}-v_{BW}\right|}{v_{BW}\times v_{BW}-v_{BW}}},v_{BW}>1\\ \\ {0,v}_{BW}>1\end{array}\right.$$

(11)

If ${CR}^I$ is not greater than a specific threshold that depends on the size of the problem (m) and on the magnitude of $v_{BW}$, then the pairwise comparisons provided by the decision-maker are reliable enough. A ${CR}^I$ value closer to zero indicates higher consistency, otherwise, his/her preference information needs to be revised [64,65].

The Entropy method (EM) assesses the variability for each attribute and assigns weights to attributes considering the value of the diversity factor (${d\mathrm{v}}_j)$. Thus, the higher the entropy value is, the higher the weight assigned to the jth attribute will be. The implementation procedure is as follows:

Step 1—Decision Matrix Normalization: Transform each $x_{ij}$ value into an $n_{ij}$ value. For a larger-the-better-type attribute,

$$n_{ij}={\displaystyle \frac{x_{ij}-\min \left(x_j\right)}{\max \left(x_j\right)-\min \left(x_j\right)}}$$

(12)

and for a smaller-the-better-type attribute,

$$n_{ij}={\displaystyle \frac{\max \left(x_j\right)-x_{ij}}{\max \left(x_j\right)-\min \left(x_j\right)}}$$

(13)

Step 2—Entropy calculation: The entropy of $C_j$ is

$$E_j=-k{\sum }_{i=1}^m{n}_{ij}ln\left(y_{ij}\right)$$

(14)

where $k={\displaystyle \frac{1}{\ln \left(m\right)}}$ is a normalization factor and $y_{ij}={\displaystyle \frac{n_{ij}}{{\sum }_{i=1}^m{n}_{ij}}}$.

Step 3—Determine the optimal weights of the attributes: The weights are calculated as

$$w_j={\displaystyle \frac{{d\mathrm{v}}_j}{{\sum }_{j=1}^n{d\mathrm{v}}_j}}$$

(15)

with ${d\mathrm{v}}_j=1-E_j$.

2.3.3. Select the Best Compromise Solution

There are many MADM methods, and they do not necessarily produce the same ranking for the problem solutions. Therefore, using more than one method is common practice. Extensive studies on those methods and their variants (changes in the performance measure normalization, as an example) have been undertaken over the past decades and their usefulness has been proved. Nevertheless, despite the large number of proposals reported in the literature, reaching a consensus on the most suitable method or approach for a given scenario is difficult [44,45,52].

Ten MADM methods, namely the popular TOPSIS (four different versions), PROMETHEE II, Utility, MOORA, Desirability, WSM, and WASPAS, were selected to analyze data obtained by Monte Carlo simulation for 10 hydrogels and 3 attributes. In this study, 10,000 values were generated for each attribute, so 10,000 decision matrices were built. Method choice was dictated by their popularity, adequacy, and proven effectiveness in many different domains. Notice that 4 sets of weights were tested in the case study presented here, which means that each method analyzed 4 sets of 10,000 decision matrices.

The Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE) has been modified (“adjusted” or improved) by some authors [29]. In this paper, the PROMETHEE II was employed using a V-shape preference function with indifference and preference thresholds. Its implementation procedure is as follows:

Step 1—Calculate the Aggregate Preference Index (after building the decision matrix)

For every pair of alternatives $\left(A_i,A_k\right)$ with $i,k=(1,\dots ,m)$, and for each attribute, compute the aggregated preference index of $A_i$ over $A_{k_i}$,

$$\pi \left(A_i,A_k\right)={\sum }_{j=1}^n{w}_j{P}_j\left(A_i,A_k\right)$$

(16)

where $P_j\left(A_{i,}{A}_k\right)$ represents the preference of the ith alternative with regard to the kth alternative for attribute j, with $P_j\left(A_{i,}{A}_k\right)=P_j\left(\right|x_{ij}-x_{kj}\left|\right)$. Notice that $P_j$ used here is a V-shaped linear preference function, where q represents the indifference threshold and p represents the preference threshold for a larger-the-better-type attribute. For the smaller-the-better-type attribute, p represents the indifference threshold and q represents the preference threshold.

Step 2—Compute the leaving and entering outranking flows

For each alternative $A_i$, compute the following:

• the Leaving Flow (or positive outranking flow)

  $${\varphi }^{+}\left(A_i\right)={\displaystyle \frac{1}{m-1}}{\sum }_{\begin{array}{c}i=1\\ i\ne k\end{array}}^m\pi \left(A_i,A_k\right)$$

  (17)
• the Entering Flow (or negative outranking flow)

  $${\varphi }^{-}\left(A_i\right)={\displaystyle \frac{1}{m-1}}{\sum }_{\begin{array}{c}i=1\\ i\ne k\end{array}}^m\pi \left(A_k,A_i\right)$$

  (18)

Step 3—Calculate the net outranking flow

For each alternative, the net outranking flow is

$$\varphi \left(A_i\right)={\varphi }^{+}\left(A_i\right)-{\varphi }^{-}\left(A_i\right)$$

(19)

The higher the net flow is, the better the alternative will be.

The Weighted Aggregated Sum Product Assessment (WASPAS) method combines two classic methods: the Weighted Sum Model (WSM) and Weighted Product Model (WPM). Its implementation procedure is as follows:

Step 1—Normalize the decision matrix

For larger-the-better-type attributes,

$$n_{ij}={\displaystyle \frac{x_{ij}}{\max \left(x_j\right)}}$$

(20)

For lower-the-better-type attributes,

$$n_{ij}={\displaystyle \frac{\min \left(x_j\right)}{x_{ij}}}$$

(21)

Step 2—Calculate the weighted additive relative importance of the ith alternative:

$$Q_i^1={\sum }_{j=1}^n{n}_{ij}{w}_j$$

(22)

Step 3—Calculate the weighted multiplicative relative importance of the ith alternative:

$$Q_i^2={\prod }_{j=1}^n{n}_{ij}^{w_j}$$

(23)

Step 4—Calculate the combined index ($Q_i^{12}$)

$$Q_i^{12}={\alpha Q}_i^1+(1-\alpha )Q_i^2$$

(24)

where $0\le \alpha \le 1$. The value of α was set to 0.5, as is usually performed. Notice that WASPAS becomes a weighted product method when $\alpha =0$ and a weighted sum method when $\alpha =1$.

Step 5—Sort the alternatives: The alternatives are sorted based on the $Q_i^{12}$ index. The higher this value is, the better it will be.

The weighted sum method is very popular among researchers and practitioners. Thus, the classic version of this method is also employed here. The objective function used, the ${WSM}_i$ index, is as follows:

$${WSM}_i={\sum }_{j=1}^n{w}_j{n}_{ij}$$

(25)

where

$$n_{ij}={\displaystyle \frac{x_{ij}-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}}$$

(26)

for larger-the-better-type attributes, and

$$n_{ij}={\displaystyle \frac{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-x_{ij}}{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}}$$

(27)

for smaller-the-better-type attributes. Note that $n_{ij}$ in ${WSM}_i$ is different from that used in WASPAS, and the higher the ${WSM}_i$ value is, the better it will be.

The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method is one of the most popular methods among researchers and practitioners for multi-attribute optimization, and it has been applied in various scientific fields. It works by converting multiple attributes into a single attribute and then determining the best alternative based on its closeness to the ideal solution. Its implementation procedure is as follows:

Step 1—Normalize the Decision Matrix

Each value in the decision matrix is normalized as

$$n_{ij}={\displaystyle \frac{x_{ij}}{\sqrt{\sum _{i=1}^m{x}_{ij}^2}}}$$

(28)

Step 2—Determine the Weighted Normalized Matrix

Each value in the normalized matrix is multiplied by the respective weight as shown in (29).

$$t_{ij}=n_{ij}{w}_j$$

(29)

Step 3—Identify the Ideal and Negative-Ideal Solutions

The best values for each attribute (ideal solution, Is⁺) and the worst values for each attribute (negative-ideal solution, Is⁻) are determined as

$${Is}^{+}=\left\{\underset{i}{\max }\left(t_{ij}\right)withjϵJ^{+};\underset{i}{\min }\left(t_{ij}\right)withjϵJ^{-}\right\}$$

(30)

and

$${Is}^{-}=\left\{\underset{i}{\min }\left(t_{ij}\right)withjϵJ^{+};\underset{i}{\max }\left(t_{ij}\right)withjϵJ^{-}\right\}$$

(31)

where $J^{+}$ represents the larger-the-better-type attributes and $J^{-}$ represents the smaller-the-better-type attributes.

Step 4—Calculate the Separation Measures

Compute the distance of each alternative from both the ideal and negative-ideal solutions using Euclidean distance as follows:

$$S_i^{+}=\sqrt{{\sum }_{j=1}^n{\left(t_{ij}-{Is}_j^{+}\right)}^2}$$

(32)

and

$$S_i^{-}=\sqrt{{\sum }_{j=1}^n{\left(t_{ij}-{Is}_j^{-}\right)}^2}$$

(33)

where $S_i^{+}$ is the distance from the ideal solution and $S_i^{-}$ is the distance from the negative-ideal solution.

Step 5—Determine the Relative Closeness to the Ideal Solution

The alternative ranking is determined using the closeness coefficient,

$${Rc}_i={\displaystyle \frac{S_i^{-}}{S_i^{+}+S_i^{-}}}$$

(34)

where ${Rc}_i$ represents the relative closeness of the ith alternative to the ideal alternative (that one whose attribute values are as close as possible to the ideal values).

Step 6—Rank the Alternatives

The best alternative is that with a higher ${Rc}_i$ value.

Three additional variants of the TOPSIS method were also tested in the case study presented in this paper. In the first variant of the TOPSIS method, called ${\mathrm{T}\mathrm{O}\mathrm{P}\mathrm{S}\mathrm{I}\mathrm{S}}_N$, the decision matrix is normalized as follows:

$$n_{ij}={\displaystyle \frac{x_{ij}}{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}}$$

(35)

and all the remaining steps of the TOPSIS implementation procedure are kept unchanged. The second variant of the TOPSIS method, called ${\mathrm{T}\mathrm{O}\mathrm{P}\mathrm{S}\mathrm{I}\mathrm{S}}_{L_{\infty }}$, presents an infinite norm instead of a Euclidean distance to calculate the Separation Measures (see step 4 of the TOPSIS implementation procedure). Thus,

$$S_i^{+}=\underset{j}{\max }\left|t_{ij}-{Is}_j^{+}\right|$$

(36)

and

$$S_i^{-}=\underset{j}{\max }\left|t_{ij}-{Is}_j^{-}\right|$$

(37)

The third variant of the TOPSIS method (${\mathrm{T}\mathrm{O}\mathrm{P}\mathrm{S}\mathrm{I}\mathrm{S}}_{{NL}_{\infty }}$) is a combination of ${\mathrm{T}\mathrm{O}\mathrm{P}\mathrm{S}\mathrm{I}\mathrm{S}}_N$ and ${\mathrm{T}\mathrm{O}\mathrm{P}\mathrm{S}\mathrm{I}\mathrm{S}}_{L_{\infty }}$.

The so-called Utility method is another popular option to support the decision-making in multi-attribute optimization problems. In the Utility method, each $x_{ij}$ (performance measures of the ith alternative on the jth attribute) is transformed into a preference score $P_{ij}$ using a logarithmic scale:

$$P_{ij}=A_j\log \left({\displaystyle \frac{x_{ij}}{x_j^{\prime }}}\right)$$

(38)

where $x_j^{\prime }$ is the minimum acceptable value for the jth attribute and $A_j$ is a scaling factor.

$$A_j={\displaystyle \frac{9}{\log (x_j^{*}/x_j^{\prime })}}$$

(39)

where $x_j^{*}$ is the best possible performance measure for the jth attribute and $A_j$is calculated such that the best possible performance value for the jth attribute yields a maximum preference score of 9 ($\underset{i}{\max }{P}_{ij}=9)$. Thus, if weights are assigned to attributes, the overall utility for each alternative, with $\sum _{j=1}^n{w}_j=1$, is calculated as

$$U_i={\sum }_{j=1}^n{w}_j{P}_{ij}$$

(40)

and the higher the weighted overall utility ($U_i$) value is, the better the alternative will be.

The global desirability function proposed by [66], called the Desirability method, have been widely used for solving multi-objective problems developed under the Response Surface Methodology framework in various science fields. In this method, individual desirability functions normalize the performance measures and are aggregated into a geometric mean. The individual desirabilities and the global desirability function take values between 0 and 1, where 1 is the most favourable value.

For smaller-the-better-type attributes, whose performance measure is desired to be smaller than an upper bound $\left(x_{ij}<\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)\right)$, the individual desirability is defined as

$$d_{ij}=\left\{\begin{array}{c}0,x_{ij}<\min \left(x_j\right)\\ \\ {\left({\displaystyle \frac{x_{ij}-\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)}{{\mathrm{m}\mathrm{i}\mathrm{n}(x}_j)-\mathrm{m}\mathrm{a}\mathrm{x}(x_j)}}\right)}^s,{\mathrm{m}\mathrm{i}\mathrm{n}(x}_j)\le x_{ij}<\max (x_j)\\ \\ 0,x_{ij}\ge \max \left(x_j\right)\\ \end{array}\right.$$

(41)

where s is a user-specified parameter $\left(s>0\right)$.

For larger-the-better-type attributes, whose performance measure is desired to be larger than a lower bound $\left(x_{ij}>\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)\right)$, the individual desirability function is defined as

$$d_{ij}=\left\{\begin{array}{c}0,x_{ij}<{\mathrm{m}\mathrm{i}\mathrm{n}(x}_j)\\ \\ {\left({\displaystyle \frac{x_{ij}-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}{\mathrm{m}\mathrm{a}\mathrm{x}\left(x_j\right)-\mathrm{m}\mathrm{i}\mathrm{n}\left(x_j\right)}}\right)}^s,{\mathrm{m}\mathrm{i}\mathrm{n}(x}_j)\le x_{ij}<{\mathrm{m}\mathrm{a}\mathrm{x}(x}_j)\\ \\ 0,x_{ij}\ge {\mathrm{m}\mathrm{a}\mathrm{x}(x}_j)\\ \end{array}\right.$$

(42)

The values assigned to s allow changing the shape of $d_{ij}$. A large value for s implies that the $d_{ij}$ value is very small unless the response comes very close to its desired value. This means that the higher the s values are, the greater the importance of the attribute values being closer to the respective target will be. A small value for s means that the $d_{ij}$ value will be large even when the attribute is distant from its desired value. The global desirability function is defined as the geometric mean of the individual desirabilities,

$$D_i={\left(\left(d_{i1}{)}^{w_1}\right(d_{i2}{)}^{w_2}...(d_{in}{)}^{w_n}\right)}^{{\displaystyle \frac{1}{\sum w_n}}}$$

(43)

where $w_j$ $(j=1,...,n)$ are user-specified parameters that allow assigning priorities (weights) to the individual desirability functions. The objective is to maximize $D_i$. When $D_i=1$, all the attribute values are the best ones $\left(d_{ij}=1,\mathrm{for}\mathrm{any}i,j\right)$. When $D_i=0$, at least the value of one attribute is equal to its worst value $\left(d_{ij}=0,\mathrm{for}\mathrm{any}i,j\right)$. It is for this reason that the geometric mean prevails over the arithmetic mean, such as is shown in [67,68]. For a review on other desirability-based methods, the reader is referred to [69].

Multi-objective optimization on the basis of the ratio analyses (MOORA) method has also been successfully applied to solve various types of multi-attribute problems in (non)manufacturing environments. Examples include selecting a road design, a facility location, an industrial robot, a flexible manufacturing system, a prototyping process, and welding process parameters [70,71].

In the MOORA method the first implementation step is to normalize the performance measures. According to [72], it is recommended to use the square root of the sum of squares of performance measures, which is defined as

$$n_{ij}={\displaystyle \frac{x_{ij}}{\sqrt{\sum _{i=1}^m{x}_{ij}}}}$$

(44)

The $n_{ij}$ are then aggregated depending on the attribute type. In the case of larger-the-better-type attributes, the $n_{ij}$ are added; for smaller-the-better-type attributes, the $n_{ij}$ are subtracted. The aggregate function of the $n_{ij}$ is defined as

$$M_i={\sum }_{j=1}^g{n}_{ij}-{\sum }_{j=g+1}^n{n}_{ij}$$

(45)

where g is the number of larger-the-better-type attributes and n is the total number of attributes. The number of attributes to be minimized is $(n-g)$. If some attribute is more important than the others, which is usual in practice, preference parameters or weights must be assigned to them. In this case, the aggregate function is defined as

$$M_i={\sum }_{j=1}^g{\omega }_j{n}_{ij}-{\sum }_{j=g+1}^n{\omega }_j{n}_{ij}$$

(46)

and the higher the M_i value is, the better the alternative will be.

2.3.4. Ranking Similarity, Ranking Acceptability, and Pairwise Winning

Ten MADM methods were employed to analyze data generated by Monte Carlo simulation. Ten thousand decision matrices were built and 10,000 rankings were generated by each of the 10 methods employed in the case study presented here. Therefore, evaluating ranking similarity (correlation) is necessary to determine how similar obtained rankings are and obtain valuable insights into method efficacy and applicability in real-world contexts. Evaluating ranking similarity is a relevant practice and a helpful input for those who need to select a solution for multi-attribute problems. When rankings align, it makes the decision about the most favourable solution easier to explain and defend to stakeholders and obtain valuable insights into method efficacy and applicability in real-world contexts. However, some methods may favour certain alternatives due to their computational structure. Ranking similarity helps reveal such biases, but other tools must be used to aid in identifying the most promising solution(s) for multi-attribute decision-making problems. For this purpose, ranking acceptability and pairwise winning indexes are helpful and used to identify the most promising hydrogel(s).

Spearman’s rank and Kendall’s rank are two popular ranking similarity indexes widely applied in various domains beyond MADM when dealing with ranked data [73,74,75,76,77]. They provide a comparative assessment of multi-attribute decision-making methods by indicating the relative closeness of a method with other methods in terms of ranking outcome similarity. However, criticisms are reported in the literature [73,77,78]. A major criticism on Spearman’s rank and Kendal’s rank is related with the impact of exchanges at the top-ranking positions into the index values comparatively to exchanges at the bottom-ranking positions. The rankings are determined to help in choosing the best or more promising alternatives (solutions), which are in the top positions of the ranking. Thus, exchanges at the top positions should be more impactful on the similarity than at the bottom of the ranking. As an example, a shift from first to second position in the ranking is more undesirable and impactful on the similarity than a swap between third and fourth positions. According to [77], the $PS$ ranking similarity index overtakes this drawback so it will be a useful tool for testing, comparing, and benchmarking multi-attribute decision-making methods in terms of ranking outcome similarity, thus contributing to better-informed and reliable decision-making on the solution selection for multi-attribute problems.

$PS$ is an asymmetric measure whose value for ranking comparison is determined by the positions in a ranking assumed as the reference ranking in the calculations [78]. The reference ranking is defined here as

$$R_{R_i}={\sum }_{r=1}^{10}r{b}_i^r$$

(47)

where $r$ represents the position in the ranking of the ith alternative (hydrogel). The $PS$ index (48) was developed to be sensitive to the position where the exchanges occur in the ranking, easy to interpret, and its values are limited to a specific interval (takes values from zero to one) [77].

$$PS=1-{\sum }_{i=1}^m{2}^{-p_i}{\displaystyle \frac{\left|p_i-q_i\right|}{\max \left(\left|p_i-1\right|,\left|p_i-m\right|\right)}}$$

(48)

where $p_i$ represents the place of the ith alternative in the reference ranking, $q_i$ represents the place of the ith alternative in another selected ranking, and $m$ represents the length of the ranking.

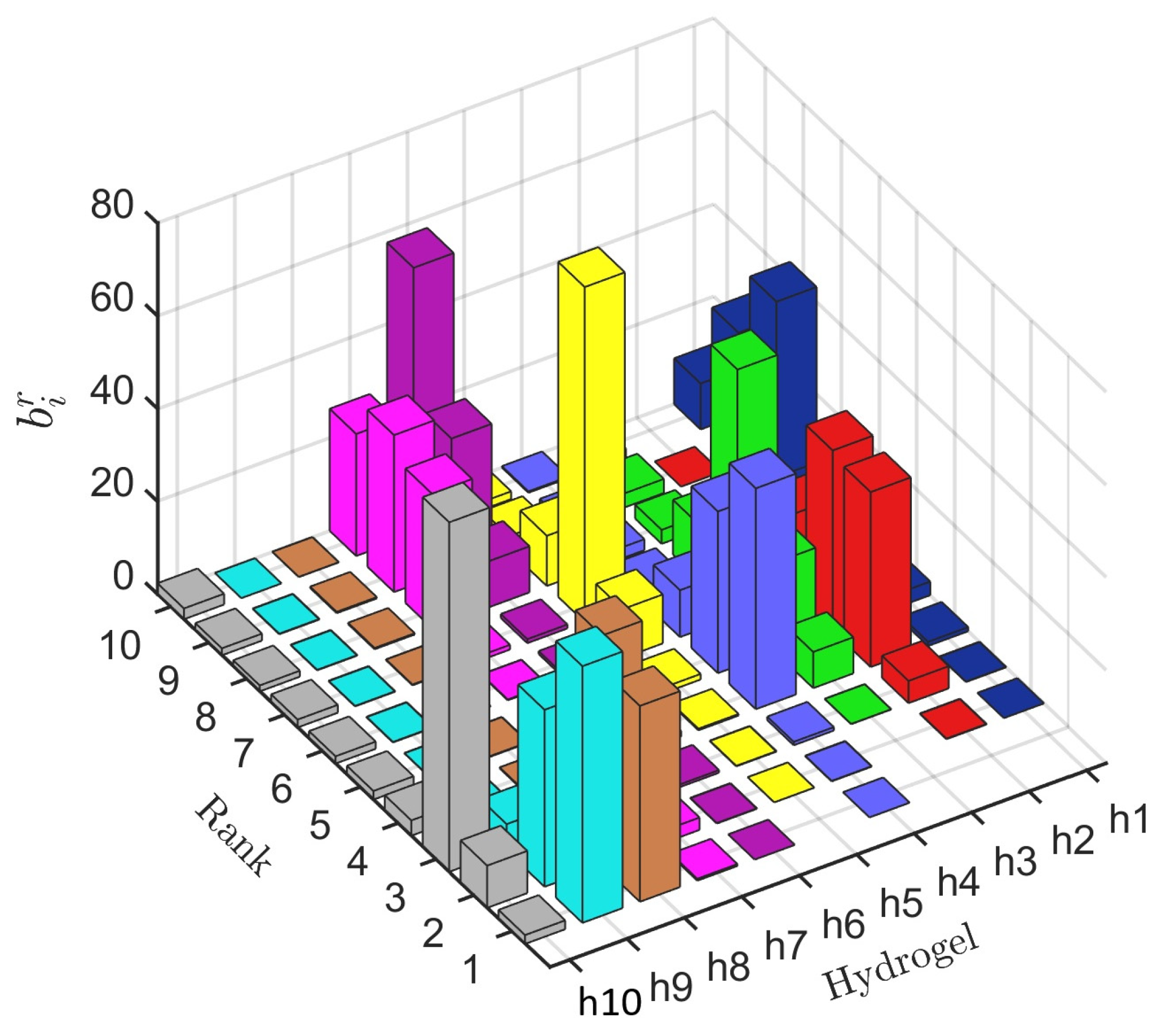
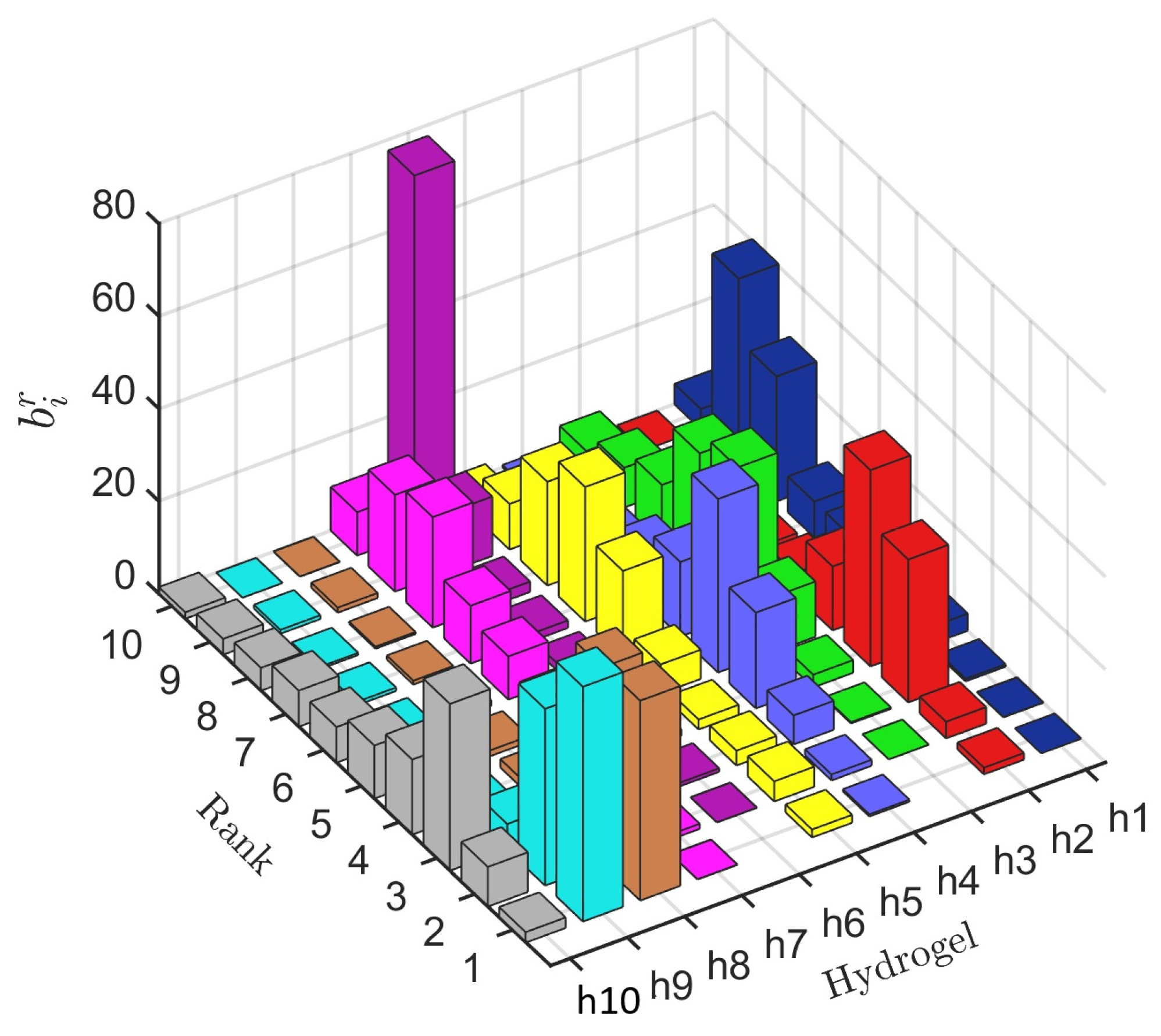
A rank acceptability index, the $b_i^r$ index, which yields the probability that the ith alternative will receive the rth position in the ranking, was obtained based on the rankings yielded by the ten methods (100,000 rankings). High acceptability index values for the best ranks, the first, second, and third, as an example, suggest that alternatives in those rankings are the most promising candidates (are promising solutions) for solving the MADM problem. The first rank acceptability index ($b_i^1)$ determines the probability that the ith alternative is the most preferred, and its value must be equal to or as close as possible to 100%, whereas for inefficient alternatives, the first rank acceptability index is close to or equal to zero. This index is estimated as follows [67]:

$$b_i^r=B_{ir}/K$$

(49)

where K is the number of alternative rankings (Monte Carlo iterations) and $B_{ir}$ is the number of times the ith alternative obtained the rth position in the ranking. Notice that, for the ith hydrogel, ${\sum }_{r=1}^m{b}_i^r=1$. The $b_i^r$ values are characterized by a certain precision and an assumed confidence interval, depending on the number of iterations [60]. The expected precision of $b_i^r$ values can be calculated as

$$\epsilon =z_{\alpha }/\sqrt{4K}$$

(50)

where $z_{\alpha }$ denotes the standard score for a confidence level (1 − $\alpha$) [60,79]. In Monte Carlo simulations, the required number of iterations is inversely proportional to the square of the desired accuracy but does not significantly depend on the dimensionality of the problem. The number of iterations is typically 10⁴–10⁶, which gives a precision of 0.01–0.001 for 95% confidence, respectively [51,60,79,80].

The $b_i^r$ index is useful for screening the alternatives, i.e., eliminating the least promising alternatives. A pairwise winning index, the $c_{ik}$ index, is also calculated. The $c_{ik}$ yields the probability that the ith alternative will achieve a higher ranking than the kth alternative, and unlike the $b_i^r$, the pairwise winning index between one pair of alternatives is independent of the other alternatives. This means that $c_{ik}$ can be used to form a final ranking among the alternatives, eliminating alternatives that are dominated by other alternatives. Alternatives are ranked so that each alternative precedes all the remaining alternatives for which $c_{ik}\ge 50\%$ or another bigger threshold value [51]. The pairwise winning index is estimated as

$$c_{ik}=(C_{ik}/K)$$

(51)

where $C_{ik}$ represents the number of times that the ith alternative precedes the kth alternative in K rankings.

3. Results and Discussion

The rank acceptability index was used for identifying the best alternatives from the set of available alternatives. High acceptability values for the best ranks identify candidates for the most preferred solution. The option here focused on the first three (out of ten) best ranks ($b_i^1,b_i^2,{\mathrm{a}\mathrm{n}\mathrm{d}b}_i^3$). Hydrogels with a high acceptability index value for the worst ranks were discarded. The pairwise similarity index was used for ordering the hydrogels (the higher this index value is, the better the hydrogel properties will be). Recall that 10,000 decision matrices were analyzed by ten MADM methods, which means that $b_i^r$ values were obtained from 100,000 rankings, which gives sufficient robustness for the results [79,80].

Figure 1 displays the $b_i^r$ values for the weights obtained using the BWM, which has a consistency ratio equal to 0.07. This method produced results that are very close to those assigned by the expert in science materials (see

Table 3. Attribute weights.

Methods	Weights
	WC	TCM	FC
Expert	0.10	0.40	0.50
BWM	0.06	0.34	0.60
Entropy	0.24	0.45	0.31
CRITIC	0.32	0.42	0.26

). The CRITIC method yielded weights to the attributes that are far from those assigned by the expert in science materials and from those yielded by the BWM (see Table 3). For the WC attribute, the weight yielded by the CRITIC method is 300% larger than that assigned by the expert, and for the FC attribute, the weight yielded by the CRITIC method is 200% lower than that assigned by the expert. The weight values yielded by the Entropy method are between those yielded by the BWM and CRITIC method, so only the results achieved with the weights yielded by these later methods are presented and discussed below.

Regarding the BWM results, Figure 1 shows that only three hydrogels ($h_{10}$, $h_9$, and $h_8$) have high values in at least one of the first three ranks ($b_i^1,b_i^2,b_i^3$). All the remaining hydrogels can be classified as inefficient alternatives.

Table 4. $b_i^r$ values for BWM’s weights.

Rank	${\mathit{h}}_1$	${\mathit{h}}_2$	${\mathit{h}}_3$	${\mathit{h}}_4$	${\mathit{h}}_5$	${\mathit{h}}_6$	${\mathit{h}}_7$	${\mathit{h}}_8$	${\mathit{h}}_9$	${\mathit{h}}_{10}$
1	0.00	0.00	0.00	0.02	0.00	0.01	0.41	42.27	55.38	1.91
2	0.01	0.12	0.00	0.10	0.03	0.11	2.67	49.66	38.19	9.11
3	0.09	4.80	0.06	0.75	0.12	0.57	5.72	6.76	5.73	75.41
4	0.89	37.75	7.81	47.65	0.34	1.21	0.67	0.22	0.17	3.30
5	2.94	38.94	19.31	34.88	1.20	0.48	0.16	0.15	0.08	1.87
6	5.93	17.57	53.15	10.11	10.57	0.64	0.17	0.19	0.11	1.56
7	8.50	0.76	11.82	2.81	72.26	0.86	1.02	0.16	0.10	1.71
8	43.12	0.05	3.01	2.37	10.83	9.95	29.00	0.27	0.10	1.29
9	28.63	0.00	3.04	1.02	2.97	28.57	33.86	0.28	0.13	1.51
10	9.91	0	1.81	0.29	1.67	57.61	26.32	0.05	0.02	2.33
Mean	8.15	4.72	5.99	4.79	7.07	9.32	8.35	1.71	1.54	3.38
Median	8	5	6	5	7	10	9	2	1	3

displays the $b_i^r$ values and the mean and median values for all the hydrogels. The highest $b_i^r$ value for the first rank was obtained for $h_9$. The $h_8$ has high $b_i^r$ values for the first and second ranks, whereas $h_{10}$ has a high $b_i^r$ value for the third rank. It is also important to note that, as shown in Table 4, the median value of $h_9$ is equal to 1, for $h_8$ it is equal to 2, and for $h_{10}$ it is equal to 3. Note that the median values are equal to the rank of the highest $b_i^r$ value. The pairwise winning index values, shown in

Table 5. $c_{ik}$ values for BWM’s weights.

Hydrogels	${\mathit{h}}_1$	${\mathit{h}}_2$	${\mathit{h}}_3$	${\mathit{h}}_4$	${\mathit{h}}_5$	${\mathit{h}}_6$	${\mathit{h}}_7$	${\mathit{h}}_8$	${\mathit{h}}_9$	${\mathit{h}}_{10}$
$h_8$	99.1	98.8	99.4	99.3	99.2	99.5	98.2	0.0	43.4	92.2
$h_9$	99.6	99.4	99.8	99.7	99.7	99.8	97.9	56.6	0.0	94.1
$h_{10}$	94.0	87.9	95.6	91.2	94.4	95.9	90.3	7.8	5.9	0.0

, confirm that $h_9$ and $h_8$ are more promising than $h_{10}$. In fact, $c_{\mathrm{8,10}}$ and $c_{\mathrm{9,10}}$ are both greater than 90%, which means that hydrogel $h_{10}$ can be discarded as a possible solution to the problem. The choice between $h_9$ and $h_8$ can depend on attributes not considered in this study. Nevertheless, according to the presented results, $c_{\mathrm{9,8}}=56.6\%>c_{\mathrm{8,9}}=43.4\%$ so $h_9$ is considered the most promising hydrogel.

The CRITIC method produced attribute weights that contrasted with those assigned by the expert in science materials and yielded by the BWM (see Table 3). However, the results of $b_i^r$ and $c_{ik}$ values shown in Figure 2 and

Table 6. $b_i^r$ values for CRITIC’s weights.

Rank	${\mathit{h}}_1$	${\mathit{h}}_2$	${\mathit{h}}_3$	${\mathit{h}}_4$	${\mathit{h}}_5$	${\mathit{h}}_6$	${\mathit{h}}_7$	${\mathit{h}}_8$	${\mathit{h}}_9$	${\mathit{h}}_{10}$
1	0.00	1.45	0.00	0.46	1.72	0.00	0.06	43.24	50.80	2.27
2	0.06	3.61	0.02	1.30	4.36	0.05	1.11	42.67	38.24	8.59
3	0.54	30.91	0.27	6.27	3.21	0.77	9.13	7.28	5.54	36.08
4	3.71	42.45	2.76	20.73	2.17	1.42	7.37	1.83	1.31	16.25
5	8.38	13.83	11.96	37.53	6.30	1.88	6.21	1.26	1.14	11.50
6	7.74	4.63	32.01	16.13	18.73	1.55	9.35	1.26	0.89	7.72
7	7.75	2.32	27.27	9.96	29.10	1.63	12.53	0.87	0.76	7.82
8	27.03	0.69	12.67	5.15	22.45	2.23	23.90	0.44	0.47	4.96
9	40.37	0.09	8.60	1.95	9.86	12.84	20.94	1.10	0.83	3.42
10	4.41	0.01	4.44	0.52	2.10	77.63	9.41	0.06	0.02	1.41
Mean	7.83	3.91	6.78	5.23	6.66	9.48	7.08	1.92	1.77	4.36
Median	8	4	7	5	7	10	8	2	1	4

and

Table 7. $c_{ik}$ values for CRITIC’s weights.

Hydrogels	${\mathit{h}}_1$	${\mathit{h}}_2$	${\mathit{h}}_3$	${\mathit{h}}_4$	${\mathit{h}}_5$	${\mathit{h}}_6$	${\mathit{h}}_7$	${\mathit{h}}_8$	${\mathit{h}}_9$	${\mathit{h}}_{10}$
$h_8$	98.5	92.8	96.4	94.3	93.2	99.9	97.3	0.000	46.4	89.7
$h_9$	98.8	94.1	96.8	95.1	95.1	99.96	97.3	53.6	0.0	92.4
$h_{10}$	89.6	53.0	80.6	68.4	79.5	96.4	79.3	10.3	7.6	0.0

are similar to those achieved from the BWM, which is an indication of results robustness, i.e., the decision-maker should select one hydrogel among $h_{10}$, $h_9$, and $h_8$. The best solution could be $h_9$ given that $c_{\mathrm{9,10}}$ and $c_{\mathrm{8,10}}$ values are higher than 85%, and $c_{\mathrm{9,8}}=53.6\%>c_{\mathrm{8,9}}=46.4\%$, with $b_9^1=50.8\%>b_8^1=43.2\%$. The results achieved with the weights defined by the Entropy method and the expert are omitted. However, they are similar to those found using CRITIC and BWM weights. The $b_i^r$ and $c_{ik}$ values obtained from the Entropy method were $b_9^1=53.6\%,b_8^1=43.7\%$, $c_{\mathrm{9,8}}=54.8\%,$and $c_{\mathrm{8,9}}=45.2\%$. The results obtained from the weights assigned by the expert are $b_9^1=54.9\%,b_8^1=43.4\%$, $c_{\mathrm{9,8}}=55.9\%,$and $c_{\mathrm{8,9}}=44.1\%$.

The robustness and reliability of these results are supported by the results achieved with the methods ranking and the $PS$ index.

Table 8. From BWM’s weights.

Rank	Promet	Ut	TOPSIS	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{{\mathit{L}}_{\mathit{\infty }}}$	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{\mathit{N}}$	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{{\mathit{N}\mathit{L}}_{\mathit{\infty }}}$	Moora	Desirab	WSM	WASPAS	Reference Rank
1	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$
2	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$
3	$h_7$	$h_{10}$	$h_{10}$	$h_{10}$	$h_{10}$	$h_{10}$	$h_{10}$	$h_{10}$	$h_{10}$	$h_{10}$	$h_{10}$
4	$h_2$	$h_4$	$h_4$	$h_4$	$h_4$	$h_2$	$h_4$	$h_2$	$h_4$	$h_4$	$h_2$
5	$h_1$	$h_2$	$h_2$	$h_2$	$h_2$	$h_4$	$h_2$	$h_4$	$h_2$	$h_2$	$h_4$
6	$h_4$	$h_3$	$h_3$	$h_3$	$h_3$	$h_3$	$h_3$	$h_3$	$h_3$	$h_3$	$h_3$
7	$h_{10}$	$h_5$	$h_5$	$h_5$	$h_5$	$h_5$	$h_5$	$h_1$	$h_5$	$h_5$	$h_5$
8	$h_5$	$h_1$	$h_1$	$h_7$	$h_1$	$h_7$	$h_1$	$h_5$	$h_1$	$h_7$	$h_1$
9	$h_6$	$h_7$	$h_7$	$h_1$	$h_7$	$h_1$	$h_7$	$h_6$	$h_7$	$h_1$	$h_7$
10	$h_3$	$h_6$	$h_6$	$h_6$	$h_6$	$h_6$	$h_6$	$h_7$	$h_6$	$h_6$	$h_6$

Note: Promet stands for PROMETHEE II, Ut stands for Utility, and Desirab stands for Desirability.

and

Table 9. From CRITIC’s weights.

Rank	Promet	Ut	TOPSIS	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{{\mathit{L}}_{\mathit{\infty }}}$	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{\mathit{N}}$	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{{\mathit{N}\mathit{L}}_{\mathit{\infty }}}$	Moora	Desirab	WSM	WASPAS	Reference Rank
1	$h_5$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$	$h_9$
2	$h_2$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$	$h_8$
3	$h_9$	$h_{10}$	$h_{10}$	$h_{10}$	$h_2$	$h_7$	$h_{10}$	$h_2$	$h_2$	$h_{10}$	$h_2$
4	$h_4$	$h_2$	$h_2$	$h_7$	$h_{10}$	$h_2$	$h_2$	$h_{10}$	$h_{10}$	$h_2$	$h_{10}$
5	$h_8$	$h_4$	$h_4$	$h_2$	$h_4$	$h_{10}$	$h_4$	$h_1$	$h_4$	$h_4$	$h_4$
6	$h_3$	$h_3$	$h_3$	$h_1$	$h_5$	$h_5$	$h_3$	$h_4$	$h_5$	$h_3$	$h_5$
7	$h_7$	$h_7$	$h_7$	$h_4$	$h_3$	$h_4$	$h_5$	$h_3$	$h_3$	$h_5$	$h_3$
8	$h_{10}$	$h_5$	$h_5$	$h_6$	$h_7$	h1	$h_1$	$h_5$	$h_7$	$h_7$	$h_7$
9	$h_1$	$h_1$	$h_1$	$h_5$	$h_1$	$h_3$	$h_7$	$h_6$	$h_1$	$h_1$	$h_1$
10	$h_6$	$h_6$	$h_6$	$h_3$	$h_6$	$h_6$	$h_6$	$h_7$	$h_6$	$h_6$	$h_6$

show the results obtained from the mean of 10,000 rankings per method, and one can state that all methods, except PROMETHEE II, suggest $h_9$ and $h_8$ as the most promising hydrogels, with the weights yielded by the CRITIC method.

Table 10. $PS$ values and attribute weights.

Weighting Method	Promet	Ut	TOPSIS	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{{\mathit{L}}_{\mathit{\infty }}}$	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{\mathit{N}}$	${\mathbf{T}\mathbf{O}\mathbf{P}\mathbf{S}\mathbf{I}\mathbf{S}}_{{\mathit{N}\mathit{L}}_{\mathit{\infty }}}$	Moora	Desirab	WSM	WASPAS
CRITIC	0.712	0.964	0.964	0.925	1.000	0.954	0.966	0.985	1.000	0.967
BWM	0.905	0.983	0.983	0.983	0.983	0.999	0.983	0.998	0.983	0.983

shows the $PS$ index values that result from the comparison of method rankings, presented in Table 8 and Table 9, with the reference ranking in each table. All $PS$ index values are higher than 95%, except for the PROMETHEE II method and ${\mathrm{T}\mathrm{O}\mathrm{P}\mathrm{S}\mathrm{I}\mathrm{S}}_{L_{\infty }}$ with CRITIC’s weights, and PROMETHEE II with BWM’s weights. Nevertheless, $PS$ values for ${\mathrm{T}\mathrm{O}\mathrm{P}\mathrm{S}\mathrm{I}\mathrm{S}}_{L_{\infty }}$ with CRITIC’s weights and BWM’s weights are higher than 90%. These results mean that, in this case study, except for the PROMETHEE II method, the results yielded by the other methods are consistent and reliable across four attribute weight scenarios. These statements are also validated by Spearman’s and Kendal’s rank values, though there are small differences for some optimization methods. These differences are lower than 2% for eight methods and, as is shown in [78], Spearman and Kendall index results are more consistent between themselves than $PS$ and each one of them.

It is important to note that the present work was designed to explore the use of multicriteria decision-making approaches as a rational and systematic tool for hydrogel selection, rather than to provide an exhaustive physicochemical characterization of the studied PVA/PVP/NFCs hydrogels. Consequently, structural, morphological, and thermal analyses were not included here. These aspects will be comprehensively addressed in a forthcoming study dedicated to elucidating the influence of nanocellulose incorporation on the structural organization and morphology of the hydrogels. The present paper, therefore, emphasizes the methodological framework and the decision-making strategy applied to hydrogel optimization. Nevertheless, the mechanical and tribological evaluation confirmed that the top-ranked hydrogels ($h_{10}$, $h_9$, and $h_8$) exhibited compressive modulus and friction coefficient values comparable to those of native porcine cartilage, which showed 2.47 ± 0.57 MPa and 0.04 ± 0.01, respectively. Although the hydrogels presented slightly lower water content (≈70%) than cartilage (74 ± 4%), their structural integrity and durability remained satisfactory. These results validate the multicriteria decision-making approach and highlight $h_9$ as a promising candidate for cartilage-mimicking applications.

4. Conclusions

Hydrogels are widely researched materials due to their potential for applications in various fields like biomedical, environmental protection, and industrial process operation and control. However, they still face many challenges in practical applications. The number and variety of attributes, including mechanical, biological, and chemical attributes, required for the hydrogels depend on their application, but the design and development of these materials is always a challenging multi-attribute optimization problem. To rely on intuitive decisions is not an appropriate approach to solve these problem types, though this is still a current practice among those who do not know or are still reluctant toward the usefulness of multi-attribute decision-making methods.

Ten MADM methods complemented with decision-aiding tools are illustrated in a real case study where new hydrogels for cartilage replacement are tested. To minimize the imprecision and uncertainty in weighting the hydrogel attributes, two objective and one subjective method that require preference information from the decision-maker (expert) were employed for this purpose, in addition to the science materials expert’s preferences. Results were obtained from a large amount of data generated by Monte Carlo simulation based on parameter values obtained from experimental results. Ten thousand decision matrices were built and 10,000 rankings were generated by each of the ten multicriteria decision-making methods, which enables identifying two promising PVA/PVP annealed hydrogels with nanocellulose nanoparticles. Except for PROMETHEE II, all the other methods (nine methods) identified $h_8$ and $h_9$ as the most promising hydrogels. The consistency and reliability of decisions are supported by ranking similarity, acceptability, and pairwise similarity indexes and are valid for each of the four sets of weights tested. Therefore, this paper is another contribution to face the pressing challenges and new requirements raised by sustainable development, where the development of biomedical products or materials with multiple attributes, including hydrogels, is included. For this purpose, researchers and practitioners can adopt the structured approach illustrated here to support the required science-based framework in the multiple-attribute decision-making process. The work presented here is not limited to ranking and selecting hydrogels. Two new hydrogels ($h_8$ and $h_9$) were identified as promising for further study as a result of the incorporation of nanocellulose nanoparticles in PVA/PVP-annealed hydrogels, resulting in a well-balanced combination of hydration, mechanical stability, and tribological performance. The comprehensive structural, morphological, and thermal analyses of these PVA/PVP-annealed hydrogels with nanocellulose nanoparticles, which are currently under development for future publication, will be addressed in detail, namely, the relationships between composition, structure, and properties.