A Sustainable Approach to Vehicle LNG Tank Design Using MOPSO and 3D Modeling

Abstract

Transportation constitutes a major source of global greenhouse gas emissions. As a low-carbon fuel alternative, the design efficiency and performance of Liquefied Natural Gas (LNG) storage tanks for vehicles are critically important. However, traditional design methods have a low degree of automation and lack standardized assessment, which can easily lead to repetitive design modifications, causing resource waste and restricting the process of green development. Based on the Multi-Objective Particle Swarm Optimization (MOPSO) algorithm and three-dimensional modeling technology, this study proposes an intelligent design and automated modeling method for vehicle LNG storage tanks oriented towards sustainable design. The results demonstrate that this method completes both tank parameter design and model generation within 30 min. Compared to traditional designs, the proposed method achieves an 8.992% reduction in heat dissipation, a 26.015% reduction in inner vessel compressive deformation, with a trade-off of a 14.452% increase in total weight. This design approach significantly enhances material utilization efficiency and environmental benefits by optimizing resource allocation and performance balance, providing effective technical support for strengthening the sustainability of LNG storage tank design.

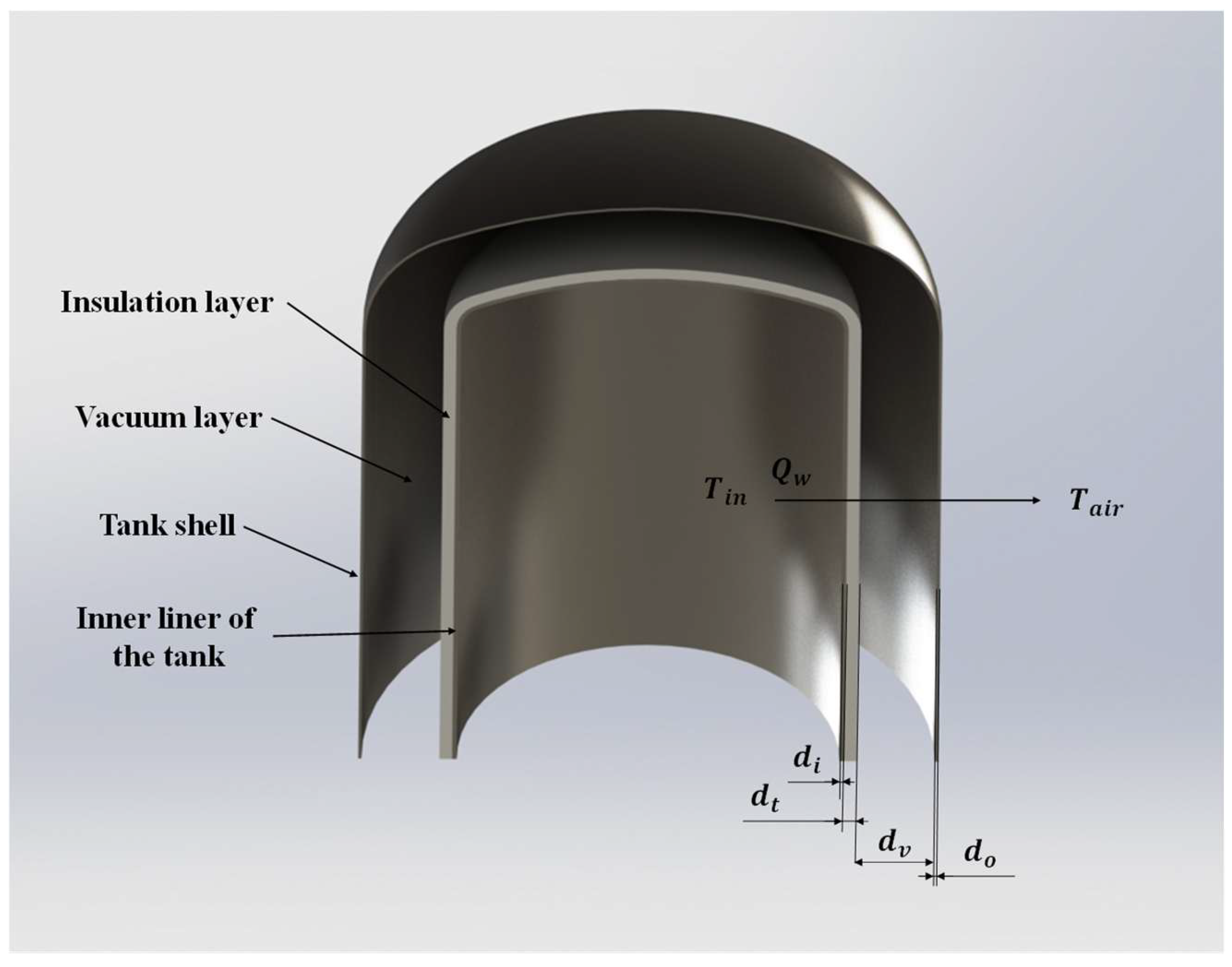
1. Introduction

The transportation sector is a major contributor to global greenhouse gas (GHG) emissions [1]. Currently, it accounts for approximately 24% of total global GHG emissions annually, with heavy-duty vehicles responsible for about 22% of the sector’s emissions [2]. Consequently, effectively reducing emissions from heavy-duty vehicles has become a key strategy in addressing global climate change. When considering well-to-wheel emissions, heavy-duty trucks powered by natural gas can achieve a net reduction in GHG emissions of approximately 28% compared to traditional diesel alternatives [3], despite the potential for methane slippage. Therefore, LNG vehicles are regarded as a lower-carbon alternative [4]. By the end of 2012, the global fleet of LNG vehicles reached over 12 million and were widely used in public transportation, mining, logistics, and other sectors [5]. LNG vehicles need to be equipped with in-vehicle LNG storage tanks, whose main function is to store LNG and continuously supply fuel to the LNG engine during vehicle operation with the increasing adoption of LNG vehicles, the demand for high-performance onboard LNG storage tanks is growing. However, traditional manual design methods reveal several limitations when addressing the complex design requirements of these tanks. Typically, vehicle-mounted LNG storage tanks require pressurization and cooling of gaseous natural gas into liquid form for storage [6], necessitating excellent thermal insulation to minimize heat absorption and subsequent LNG evaporation [7]. Consequently, the thermodynamic performance of these tanks, the structural integrity of the inner vessel, and overall lightweight design constitute critical design considerations. The traditional design process mainly relies on the personal experience of designers, resulting in the stability and expected performance of the design results being difficult to guarantee effectively. Furthermore, conventional design methodologies typically follow a linear, sequential workflow that necessitates engineers alternating between disparate software tools—such as product modeling, cost assessment, and finite element analysis (FEA) simulation—for each design iteration. The modification of the scheme is time-consuming, and the overall design efficiency is low, making it difficult to cope with the complex structural design and requirements of vehicle LNG storage tanks. Within this context, optimization algorithms and computer-aided design (CAD) technologies demonstrate significant advantages in optimization, modeling, analysis, and verification [8]. This is prompting researchers to actively explore the use of digital technologies to revolutionize product design methodologies and workflows, aiming to enhance design efficiency while effectively reducing design costs.

Extensive research has been conducted on the design and accurate prediction of LNG storage tank performance. Wang et al. [9] developed a thermodynamic non-equilibrium model based on a resistor–capacitor (RC) network. Compared to conventional thermodynamic equilibrium models, their approach demonstrated significantly higher accuracy in predicting key parameters, including the inner vessel wall temperature, heat transfer rates, and the complex phase change processes occurring within the tank. Investigating structural integrity, Ruslan et al. [10] analyzed the influence of different support types on the displacement of the inner vessel bottom under pressure loads. Their findings identified column-type support structures as exhibiting optimal performance in minimizing displacement. To address the critical issue of LNG composition, change over time, Chen et al. [11] established an aging model capable of predicting LNG behavior within the tank, thereby providing valuable support for tank design considerations aimed at managing boil-off gas. Focusing on operational optimization, Sharafian et al. [12] formulated models correlating heat transfer rates with holding time. These models serve as essential tools for determining key design parameters such as optimal tank dimensions and initial LNG filling temperatures. To address the computational complexity of physical models and reduce prediction time, Jeong et al. [13] proposed a differential estimation-based artificial neural network (ANN) for predicting the thermodynamic performance of LNG storage tanks. Their results indicated that this ANN approach achieved the lowest average error in predicting both temperature distributions and tank pressure transients. Similarly, Salarkia et al. [14] employed ANN models for LNG tank performance prediction. However, a recognized limitation of such data-driven models, as noted by Jeong et al., is their often-insufficient generalizability, making direct transfer and application to LNG tanks of different configurations challenging. Advancing tank structural design methodologies, Dong et al. [15] employed third-order Bézier curves to mathematically define the contour of the primary barrier in LNG tanks. Treating the curve parameters as design variables, they optimized the contour to minimize permanent deformation under operational loads. Compared to traditional manual design processes, their algorithmically optimized contour resulted in a 7.97% increase in longitudinal stress while achieving a remarkable 94.81% reduction in permanent deformation. This optimization framework presents a novel approach for designing tank membrane contours, applicable not only to LNG but also to storage tanks for other environmentally sensitive liquefied gases. Complementing this, Luo et al. [16] investigated the coupled effects of insulation system properties and internal liquid level height on the mechanical behavior of both the inner vessel and the outer tank in full-containment LNG storage tanks.

Compared to traditional manual parameter design, multi-objective optimization (MOO) algorithms demonstrate significant advantages in product parameter optimization due to their inherent capability to effectively trade-off conflicting design objectives. A wide array of nature-inspired metaheuristic algorithms—such as Genetic Algorithms (GA) [17,18], Particle Swarm Optimization (PSO) [19], and the Bees Algorithm [20]—have been successfully applied to diverse engineering optimization problems. It includes optimization issues such as residential space layout planning [21], concrete formula [22], wellbore trajectory design [23], heat pump blade geometry [24], Stirling engine configuration [25], and permanent magnet motor optimization [26]. Akopov et al. [27] proposes a hybrid MORCGA-MOPSO-II algorithm that utilizes clustering techniques to approximate Pareto fronts, and applies it to optimize an agent-based goods exchange model. Mohammad et al. [28] utilized the particle swarm optimization algorithm to optimize the control strategy of the locomotive controller. In the automatic mode and manual mode, the distribution improved the vehicle performance by 5.19% and 0.534%, respectively. Linh et al. [29] proposes a hybrid PSO-GWO framework to address distribution network reconfiguration with the integration of renewable energy and electric vehicles. In the specific field of LNG storage tank design, MOO technology has also achieved numerous results. Ye et al. [30] applied a multi-objective PSO algorithm to optimize the geometric shape of an LNG tank, simultaneously considering economic cost, energy efficiency, and cold energy waste. Caprace et al. [31] conducted a MOO study on LNG vessel hull structures, balancing production costs against structural response to achieve a Pareto-optimal balance and significantly reduce the design cycle duration. Shao et al. [32] developed an optimization model for the LNG regasification process, aiming for the co-optimization of economic performance and environmental impact. Niu et al. [33] utilized ANSYS Fluent to construct a heat transfer model for a Type B LNG tank and implemented MOO to achieve a synergistic balance between thermal insulation performance and safety criteria. While three-dimensional (3D) modeling is a crucial step in the design process, its efficient generation remains a challenge impacting overall design efficiency. Researchers have explored several computational approaches to address this challenge, including: software customization via secondary development of platforms like UG [34]; parametric optimization through Python-controlled ABAQUS simulations coupled with genetic algorithms [35], or implementation of integrated intelligent design frameworks [36].

The mainstream methods for LNG storage tank design usually rely on simulation software or neural network models to predict the tank performance under specific parameter sets, and then apply the MOO algorithm to select the optimal parameters. This model represents an advancement in manual design, but a key gap still exists: these methods typically require extensive manual iterations among parameter adjustment, performance evaluation, and CAD model regeneration. The reliance on manual labor has led to disadvantages such as low design efficiency, long design cycles, and high workloads for designers. Furthermore, although the MOO algorithm is adopted, many versions do not consider that during the design process, users may need a large number of design schemes to choose from, and there are no specific enhanced functions to improve the quality, extensiveness and convergence of the Pareto front of the complex and limited design space of LNG storage tanks. Therefore, in addition to meeting the design performance specifications, there is an urgent need to enhance the automation level and optimization efficiency of the design methods. The key challenge lies in developing an integrated approach that can not only effectively obtain high-quality design parameter solutions but also automatically convert these solutions into ready-made engineering models, thereby significantly enhancing the overall design throughput.

This paper presents an intelligent and highly automated design method for automotive LNG storage tanks, which integrates the enhanced MOPSO algorithm with modeling software through an application programming interface (API). In product design, people often expect to obtain more complete and extensive design scheme materials so as to better and more meticulously select the desired parameter design schemes. This places high demands on the training speed of the optimization algorithm and the number of training samples. The MOPSO algorithm will be much faster than other optimization algorithms in optimizing large populations. Unlike the application of the standard MOO algorithm, we adopted a variant of MOPSO that includes a dynamic inertia factor strategy. This strategy is crucial for balancing global exploration and local development during the search process, guiding the group towards more diverse and high-quality Pareto frontiers. The superiority of the obtained solution was quantitatively verified using the hypervolume index. The optimized parameter set generated by the enhanced MOPSO algorithm is automatically converted into the corresponding 3D CAD model through the programming control of the modeling software API. This seamless data transfer eliminates the manual steps of model reconstruction and geometry import/export. The framework operates based on the initial input requirements defined by the user. It systematically explores the design space, adjusts key parameters under engineering constraints, and directly outputs a set of Pareto optimal design solutions. Each solution represents a unique trade-off among competing targets and their associated 3D models. Experimental verification shows that this integrated method improves the design quality and efficiency. With the support of dynamic MOPSO, the MOPSO cycle has been reduced to approximately 25 min per design iteration. The subsequent automatic 3D model generation only takes about 3 min, which represents a substantial reduction compared to the traditional manual design workflow. Therefore, this method establishes an effective computational tool that can quickly determine the high-quality design parameters of automotive LNG storage tanks and their corresponding detailed 3D models. By obtaining the verified best design solution within a limited time frame, this approach is expected to enhance the degree of automation, fundamentally shorten the design cycle, reduce development costs, and directly improve the competitiveness of the product in the market.

2. Parameter Model of Vehicle LNG Storage Tank

This section introduces the parametric design methodology for vehicular LNG storage tanks. The parametric design model is first established, incorporating both the optimization framework and its associated constraint conditions. Subsequently, optimization models corresponding to distinct objective functions are analysis. Following this, constraint models governing design parameters are derived. Finally, a comprehensive integration strategy synthesizes these individual models into a unified computational framework, provides a theoretical basis and calculation method for the subsequent optimal design of vehicle LNG storage tanks.

2.1. Parameter Design Model of Vehicle LNG Storage Tank

The structural design of LNG storage tanks for vehicular applications comprises five principal components: the outer shell, inner vessel, insulation system, valve assemblies, and support structure. The outer shell serves as a protective enclosure for the entire tank assembly, while the inner vessel functions as the primary containment system for cryogenic LNG, maintaining structural integrity under internal pressure and preventing fluid leakage. The insulation system—typically incorporating multilayer insulation (MLI) materials within a high-vacuum annulus—preserves the requisite cryogenic environment by minimizing heat ingress. Valve assemblies facilitate LNG transfer operations including filling, venting, and dispensing, whereas the support structure provides mechanical anchoring to the vehicle chassis. This study focuses specifically on the structural configuration and parametric optimization of the inner vessel, insulation system, and outer shell, with particular emphasis on critical design parameter selection. The architecture of a vehicular LNG storage tank is illustrated in Figure 1.

Within the design optimization framework, three key performance objectives are prioritized: minimizing total tank mass, reducing compressive strain in the inner vessel, and limiting heat ingress. Mass reduction directly decreases vehicular payload, thereby enhancing dynamic performance and operational efficiency. Controlling compressive strain ensures structural deformations under LNG pressurization remain within safety-certified limits, safeguarding operational integrity. Suppressing heat ingress optimizes thermal insulation performance, consequently reducing boil-off gas (BOG) generation and preserving LNG inventory. The parametric optimization model seeks to identify the globally optimal design configuration that satisfies all structural, regulatory, and manufacturing constraints while simultaneously minimizing these competing objectives. This methodology facilitates the determination of performance-optimized design parameters for vehicular LNG storage tanks.

2.2. Vehicle LNG Storage Tank Heat Transfer Model

The heat transfer process within a vehicle LNG storage tank can be characterized by three distinct stages: heat transfer through the tank inner vessel, heat transfer through the insulation material and vacuum layer, and heat transfer through the outer tank shell. Within the insulation system of vehicle LNG storage tanks, heat conduction and exchange primarily occur through the insulation material layer and the adjacent vacuum layer. During the dissipation of heat from automotive LNG storage tanks, the contribution of thermal radiation is typically significantly smaller than that of the other two heat transfer modes [37]. Consequently, heat transfer via thermal radiation is neglected in the tank’s heat transfer model.

As illustrated in Figure 2, the key parameters influencing the heat dissipation characteristics of automotive LNG storage tanks are the vacuum layer thickness (d_v), the outer tank shell thickness (d_o), and the tank inner vessel thickness (d_i). Here, T_in represents the temperature of the LNG inside the tank, and T_air denotes the temperature of the surrounding ambient air during heat dissipation. Initially, the thermal energy (Q_w) conducts from the tank’s inner wall through the liner, insulation material, and vacuum layer. It then transfers through the outer shell into the ambient air. Finally, the outer shell exchanges heat with the ambient air. The overall heat dissipation thus encompasses the heat transfer processes occurring within the inner vessel, insulation material, vacuum layer, and shell.

According to Fourier’s law of heat conduction [38], the heat dissipation from a vehicle LNG storage tank is calculated as follows:

$$Q_w={\displaystyle \frac{{\mathrm{T}}_{\mathrm{air}}-{\mathrm{T}}_{\mathrm{in}}}{R_{total}}}$$

(1)

where Q_w is the Heat dissipation per unit time from the storage tank, R_total is the total thermal resistance, T_in denotes the temperature of the LNG within the tank, and T_air represents the ambient air temperature.

The total thermal resistance R_total is calculated as the sum of the thermal resistance of the inner vessel, the thermal resistance of the outer shell (tank wall), and the thermal resistance of the combined thermal insulation material and vacuum layer. This relationship is expressed as follows:

$$R_i={\displaystyle \frac{d_i}{{\mathrm{k}}_{\mathrm{i}}{A}_i}}$$

(2)

$$R_t={\displaystyle \frac{d_t}{{\mathrm{k}}_{\mathrm{t}}{A}_t}}$$

(3)

$$R_v={\displaystyle \frac{d_v}{{\mathrm{k}}_{\mathrm{v}}{A}_v}}$$

(4)

$$R_o={\displaystyle \frac{d_o}{{\mathrm{k}}_{\mathrm{o}}{A}_o}}$$

(5)

$$R_{total}=R_i+R_t+R_v+R_o$$

(6)

where R_i, R_t, R_v, and R_o represent the thermal resistances of the tank inner vessel, insulation material, vacuum layer, and outer shell, respectively; d_i, d_t, d_v, and d_o denote the thicknesses of the tank inner vessel, insulation material, vacuum layer, and outer shell, respectively; k_i, k_t, k_v, and k_o are the coefficient of thermal conductivity of the tank inner vessel, insulation material, vacuum layer, and outer shell, respectively; A_i, A_t, A_v, and A_o correspond to the heat exchange areas for the inner vessel, insulation material, vacuum layer, and outer shell, respectively.

2.3. Vehicle LNG Tank Inner Vessel Compression Model

During vehicle operation, LNG maintained at cryogenic temperatures of −162 °C is stored within a tank inner vessel subject to a maximum working pressure of 1.6 MPa. To ensure thermal insulation performance, the inner vessel of the storage tank is encased in fiberglass wool blanket, while a vacuum layer is established between the liner and the outer shell. This configuration minimizes external heat transfer to the interior, maintaining a cryogenic storage environment within the tank. Throughout all operational phases, the tank inner vessel experiences sustained pressure loading from internal LNG pressurization. Consequently, analysis, dimensional control, and systematic optimization of the tank inner vessel’s compression deformation behavior constitute essential engineering imperatives, to prevent potential failure modes, and ultimately guarantee the operational safety and reliability of the containment system during vehicular service.

The computational modeling of compression deformation in vehicle LNG storage tank inner vessels encompasses two primary methodologies: empirical calculation models and finite element simulation approaches. This investigation adopts an empirical formulation framework, specifically utilizing the Lamé analytical solution for thick-walled pressure vessels. The Lamé formula provides a classical solution for analyzing axisymmetric stress and deformation in cylindrical and spherical structures subjected to mechanical loading. To render the complex geometry of an actual tank inner vessel analytically tractable, simplifications are implemented. The localized stiffness contributions and boundary constraints at the hemispherical end domes are neglected. Furthermore, the inner vessel is idealized as an infinitely long cylinder with uniform wall thickness, subjected to axisymmetric annular pressure loading along its entire length. This fundamental simplification permits the application of plane strain assumptions while preserving the dominant deformation mechanics of the cylindrical body. Figure 3 schematically represents this idealized loading configuration, wherein P denotes the magnitude of the uniformly distributed pressure acting on the inner vessel surface, a signifies the inner wall radius, and b represents the outer wall radius, thereby defining the critical geometric parameters governing the stress–deformation relationship.

Based on the Lamé solution [39], the radial stress σ_r and hoop stress σ_θ in the tank inner vessel are given by:

$${\sigma }_r=\mathrm{P}{\displaystyle \frac{a^2\left(b^2-r^2\right)}{r^2\left(b^2-a^2\right)}}$$

(7)

$${\sigma }_{\theta }=\mathrm{P}{\displaystyle \frac{a^2\left(r^2+b^2\right)}{r^2\left(b^2-a^2\right)}}$$

(8)

The radial displacement (u_a, u_b) at the compressed surface of the tank inner vessel can be determined using the Lamé solution:

$$u_b={\displaystyle \frac{\mathrm{P}a}{\mathrm{E}}}{\displaystyle \frac{\left(1+\mathrm{v}\right)b^2+\left(1-\mathrm{v}\right)a^2}{b^2-a^2}}$$

(9)

where P represents the uniformly distributed pressure load acting on the tank inner vessel, b denotes the outer radius of the inner vessel, a signifies the inner radius of the liner, E is Young’s modulus of the inner vessel material, and v corresponds to Poisson’s ratio of the inner vessel material.

2.4. Vehicle LNG Tank Weight Model

The total mass of a vehicle LNG storage tank constitutes the sum of its constituent components. The core functional elements include the tank inner vessel, outer shell, and thermal insulation layer, collectively responsible for maintaining both thermal insulation performance and structural integrity. Furthermore, to ensure operational safety and functionality, auxiliary components such as valve assemblies, piping systems, and pressure relief devices are incorporated. The mass of these auxiliary components is relatively minor and denoted as m_e. Consequently, the total tank mass comprises the inner vessel mass, outer shell mass, insulation material mass, and additional component mass, which can be expressed as follows.

$$m={\rho }_i{V}_i+{\rho }_o{V}_o+{\rho }_t{V}_t+m_e$$

(10)

where ρ_i denotes the density of the inner vessel material, ρ_o represents the density of the outer shell material, ρ_t corresponds to the density of the insulation layer material, V_i is the volume of the inner vessel, V_o signifies the volume of the outer shell, V_t indicates the volume of the insulation material, and m_e represents the mass of auxiliary components.

2.5. Constraints of Parameter Model of Vehicle LNG Storage Tank

Design specifications for vehicular LNG storage tanks explicitly define wall thickness parameters for both the tank inner vessel and outer shell [40]. Regulatory requirements stipulate that the inner vessel’s nominal working pressure must range between 1.0 MPa and 1.6 MPa, while the outer shell must withstand allowable external stresses no less than 0.2 MPa. The design pressure (P_d) for determining liner wall thickness is defined as twice the nominal working pressure. Additionally, the manufactured wall thickness of the inner vessel shall constitute no less than the minimum value derived from Equation (11).

$$d_{i\_\min }={\displaystyle \frac{a}{2}}\times \left(\sqrt{{\displaystyle \frac{0.4{\mathrm{P}}_{\mathrm{d}}+\sigma }{\sigma -1.3{\mathrm{P}}_{\mathrm{d}}}}}-1\right)$$

(11)

where d_{i_min} denotes the minimum wall thickness of the tank inner vessel, a represents the inner diameter of the tank inner vessel, and σ corresponds to the wall stress. The stress parameter σ is taken as the yield strength of the base material to prevent plastic deformation under design conditions.

For the tank outer shell, wall thickness verification follows the expression:

$$P_1={\displaystyle \frac{2.6{\mathrm{E}}_0{(d_o/D_0)}^{2.5}}{\left(L/D_0\right)-0.45{\left(d_o/D_0\right)}^{0.5}}}$$

(12)

where P₁ denotes the maximum allowable external stress on the outer shell, E₀ represents the elastic modulus of the outer shell material, d₀ corresponds to the nominal wall thickness of the outer shell, and L designates the total axial length of the LNG tank structure. For vehicle LNG storage tank, the stored fluid temperature is maintained at −162 °C with an operating pressure of 1.2 MPa. The thermal insulation system consists of a 20 mm-thick fiberglass wool blanket, while the vacuum layer maintains an absolute pressure of 10 Pa (0.01 bar). Both the inner vessel and outer shell are fabricated from 304 stainless steel. Key design constraints of the LNG store tank are summarized in

Table 1. Design constraints for Vehicle LNG storage tanks.

Capacity (L)	Tank Inner Vessel Radius Constraint (mm)	Tank Inner Vessel Thickness Constraint (mm)	Outer Shell Thickness (mm)	Thickness of Insulation Layer (m)
150–200	[150, 225]	[di_min, 13]	d0	[0.05–0.15]
200–350	[225, 275]
350–500	[275, 375]

, where the minimum tank inner vessel thickness (d_i), tank outer shell thickness (d_o), and inner vessel height are derived from Equations (11) and (12), and volumetric capacity relationships, respectively, with inner vessel height calculated based on the liner radius and design volume.

3. Overall Framework of Intelligent Design Method

The design of vehicle LNG storage tanks is a complex and comprehensive process involving MOO. In the traditional design process, designers must comprehensively consider product performance metrics and establish solid models using three-dimensional modeling software, and preview and evaluate the final solution. However, traditional methods exhibit significant limitations for vehicle LNG tank design. The results are highly dependent on the designer’s personal experience, making the expected outcome difficult to reliably achieve. Additionally, designers typically need to repeatedly alternate between software for modeling and simulation; any modification necessitates model reconstruction and simulation iteration, leading to low overall design efficiency. In this study, an intelligent design method employing a PSO algorithm combined with three-dimensional automatic modeling technology replaces the traditional approach for designing vehicle LNG storage tanks.

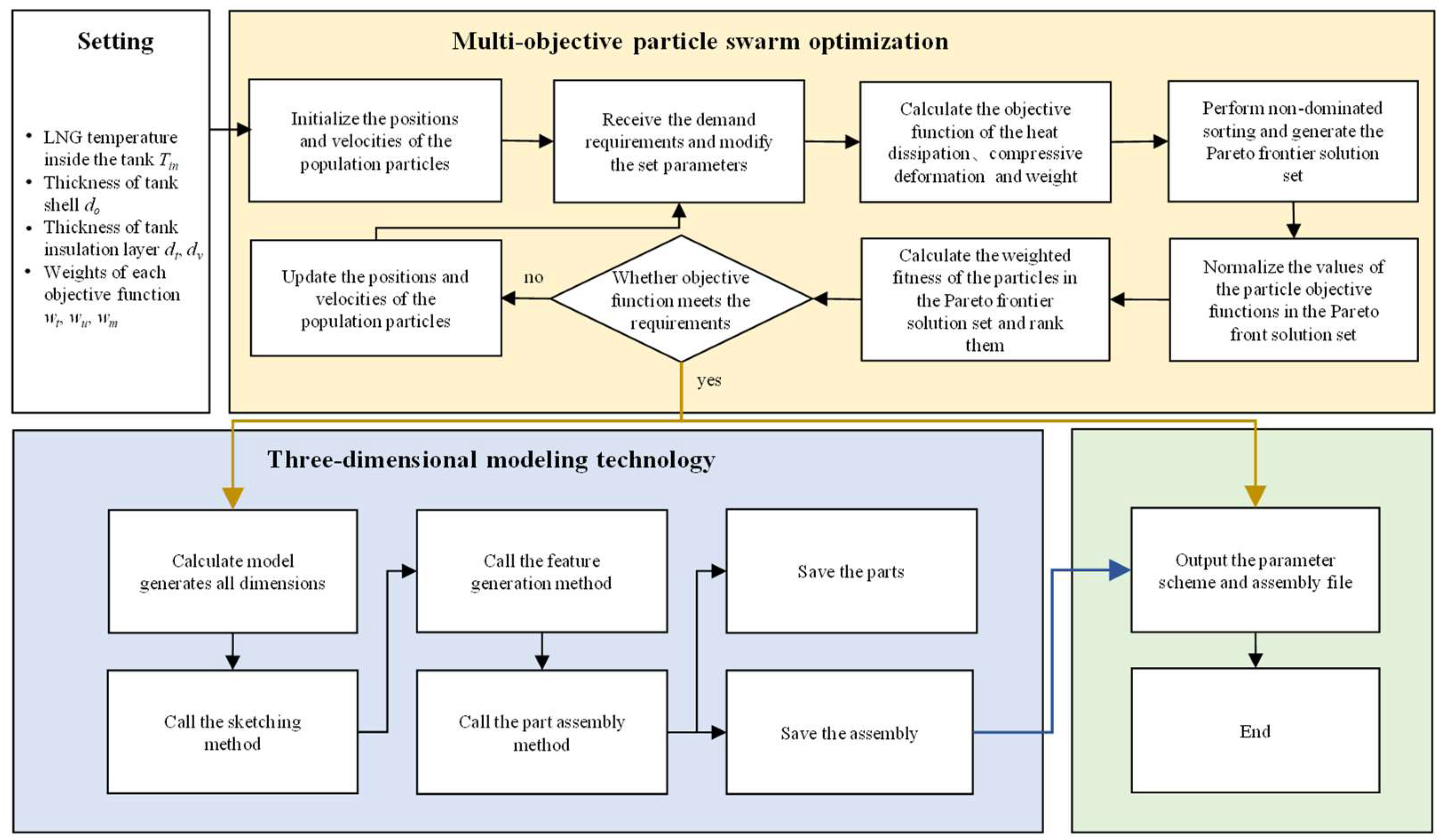
The design process of this intelligent method is shown in Figure 4. After receiving input parameters such as volume requirements, the PSO algorithm optimizes and trains the main design parameters of the storage tank and performs non-dominated sorting to obtain the Pareto front edge solution. Then, determine whether the generated design parameter scheme converges. If it does not meet the convergence standard, conduct iterative training again. When the design scheme meets the convergence conditions, the corresponding weights are set for different objective functions for weighted calculation to rank the user-provided schemes for selection. After selecting the design scheme with specific parameters, the design parameters are automatically generated into the corresponding storage tank model through 3D automatic modeling technology, including the drawing of parts and the assembly of parts. Finally, output and save the final determined design parameters of the gas storage tank and the preview image of the assembly model to complete the design process of the vehicle’s LNG storage tank.

3.1. Multi-Objective Particle Swarm Optimization Algorithm

In the design process of LNG storage tanks for vehicles, designers must simultaneously optimize multiple objectives: the tank’s insulation performance, the compression deformation of its inner vessel, and the overall tank weight. These objective functions exhibit distinct and often competing dependencies. Specifically, the thickness of the tank’s insulation layer critically determines both its heat dissipation performance and the dimensions of the surrounding structural shell. While increased insulation thickness enhances thermal performance, it consequently necessitates a larger shell design, leading to a rapid escalation in the total tank weight. Consequently, the objective functions in vehicle LNG storage tank design involve complex and often competing relationships. It is typically infeasible for a single optimal solution to simultaneously satisfy the ideal values for all objectives due to these inherent trade-offs. Therefore, a MOO approach is essential to identify a set of non-inferior solutions, known as the Pareto frontier. Solutions comprising this frontier represent the optimal compromise state achievable among the competing objectives under the given design constraints [41]. The parameter design scheme optimization for vehicle LNG storage tanks in this article is as follows. Among them, f₁ (x), f₂ (x), and f₃ (x) are the objective functions, and x is the set of decision variables. Among them, f₁ (x) is Equation (1) in Section 2.2, characterizing the heat dissipation performance of the parameter design scheme; f₂ (x) is Equation (9) in Section 2.3, characterizing the safety performance of the parameter design scheme; f₃ (x) is Equation (10) in Section 2.4, characterizing the weight performance of the parameter design scheme. x₁, x₂, x₃ and x₄ respectively represent the inner tank radius, insulation layer thickness, inner tank thickness and outer shell thickness in the design parameters of the storage tank.

$$Z=F(x)=(\min f_1(x),\min f_2(x),\min f_3(x))$$

(13)

$$x_{\min }\le x_i\le x_{\max }(i=1,2,3,4)$$

(14)

Compared to alternative optimization algorithms, the PSO algorithm exhibits distinct advantages, including a simple algorithmic structure and rapid convergence properties [42]. Inspired by collective biological behaviors observed in natural systems—such as bird flocks and fish schools [43] PSO emulates social dynamics to navigate solution spaces. As depicted in Figure 5, the optimization procedure commences with the initialization phase, where position and velocity vectors of particles are initialized; the position dictates a candidate solution (i.e., design parameters), while the velocity dictates the direction and magnitude of parametric updates. Subsequently, an iterative optimization loop ensues: (1) the fitness value of every particle is computed; (2) these evaluations collectively generate a set of non-inferior solutions (Pareto-optimal candidates); (3) each particle’s position and velocity are updated based on its historical best performance (individual best) and the swarm’s global best performance (global best); (4) the non-inferior solution set is archived externally, with dominance relationships resolved through non-dominated sorting and diversity preserved via a crowding distance mechanism; (5) the identified optimal particles subsequently influence the direction and velocity of particles in the next iteration. This cyclic process—encompassing fitness evaluation, solution ranking, particle updates, and elitist preservation, repeats until predefined convergence criteria (e.g., maximum iterations or solution stability thresholds) are satisfied.

The directional trajectory of particles is determined by the velocity update equation:

$$V^{\mathrm{k}+1}=\omega V^k+c_1{r}_1\left(P_{id}^k-X^k\right)+c_2{r}_2\left(P_{gd}^k-X^k\right)$$

(15)

where V denotes the particle velocity and ω represents the inertia factor, signifying the influence of the particle’s historical velocity on its current state, thereby regulating global and local search capabilities [44]. c₁ and c₂ are learning coefficients, k indicates the current iteration, r₁ and r₂ are random numbers, $P_{id}^k$, $P_{gd}^k$ correspond to the positions of the individual optimum and global optimum particles for the kth particle. X denotes the current particle position. During each iteration, the particle fitness is evaluated, with the best fitness value designated as the personal best. Particles update their positions as follows:

$$X^{k+1}=X^k+V^k$$

(16)

The Pareto front solution set undergoes revision based on fitness evaluations, with particles archived and prioritized via the crowding mechanism. Subsequently, particle velocities and positions are updated according to predetermined parameters. The objective function values of the new particle generation are then evaluated, followed by non-dominated sorting. This iterative cycle—comprising solution updating, velocity or position updates, function evaluation, and dominance ranking—continues until predefined convergence criteria are satisfied, such as maximum iterations or solution stability thresholds. Upon obtaining a comprehensive set of Pareto-optimal solutions, the design parameters corresponding to each particle may be utilized as final design candidates.

3.2. Particle Swarm Optimization Adaptive Adjustment of Inertia Factor

In the PSO algorithm, a common issue arises when particles become trapped in local optima, making it difficult for them to escape and leading to an increase in both the number of iterations and the population size required for convergence. To enhance the algorithm’s accuracy, dynamically adjusting the inertia weight proves to be an effective strategy. A larger inertia weight facilitates a broader global search, enabling particles to explore more diverse regions of the search space. Conversely, a smaller inertia weight allows for finer local search, improving the algorithm’s accuracy and convergence capability. However, an excessively small inertia weight may decelerate the convergence speed. Therefore, a well-designed dynamic inertia weight adjustment mechanism can significantly enhance the algorithm’s performance by increasing search diversity, preventing premature convergence to local optima, and achieving better convergence accuracy. In this study, we adopt a dynamic adjustment strategy where the inertia weight decreases linearly with the number of iterations. In the early stages of the algorithm, a larger inertia weight enables particles to move at higher velocities, thereby strengthening their global exploration capability. As the iterations progress, the inertia weight is gradually reduced, causing the particle velocities to decrease. This allows for a more meticulous search of the local region, ultimately improving the convergence accuracy. To further refine the inertia weight adjustment, we introduce a sine-based dynamic adjustment strategy. The specific formula for updating the inertia weight is

$$w=w_{\min }+\left(w_{\max }-w_{\min }\right)\times 0.5\times \left(1+\sin \left({\displaystyle \frac{k\pi }{{\max }_{iteration}}}\right)\right)$$

(17)

where w_min denotes the minimum inertia weight, w_max represents the maximum inertia weight, k is the current iteration number, and max_iteration signifies the predefined maximum number of iterations.

In this section, we focus on a 450 L LNG storage tank designed for vehicles. Utilizing the MOPSO algorithm, we optimize three key design parameters of the storage tank: the radius of the tank inner vessel, the thickness of the tank inner vessel, and the thickness of the insulation layer. Through iterative processes, the optimal solution is obtained. The hypervolume (HV) indicator, which quantifies the extent to which the objective space is covered by the approximation set, is frequently employed to evaluate the quality of the Pareto frontier solution set. In this research, HV is adopted to assess the Pareto frontier solution sets generated by different optimization strategies.

Table 2. The average objective function value of the Pareto frontier solution of the strategy optimization algorithm for fixed inertia factor and dynamically adjusted inertia factor.

	Heat Dissipation Capacity (w)	Compression Deformation (mm)	Weight (kg)	Hypervolume
Dynamically adjust the inertia factor	12.162	0.156	379.347	0.252 ± 0.013
Fixed inertia factor	12.324	0.154	382.439	0.191 ± 0.033

presents the objective function values of the Pareto boundary solution under the fixed inertia weight strategy and the dynamic inertia weight adjustment strategy, as well as the HV distribution values of the last ten trainings. The results demonstrate that the dynamic inertia weight adjustment strategy yields a higher HV value. This indicates that the corresponding Pareto optimal solutions of the dynamic inertia weight adjustment strategy-based optimization algorithm exhibit a broader distribution in terms of objective function values. The solutions are more widely dispersed across the objective space, reflecting superior solution set quality and distributional characteristics. After the Wilcoxon rank sum test, the hypervolume value of the optimization algorithm with variable inertia factor was significantly higher than that of the optimization algorithm with fixed inertia factor (U = 0, n₁ = n₂ = 5, p < 0.05, one-sided test).

3.3. Global Optimal Sample Screening

Upon obtaining the Pareto frontier solutions, a subsequent step involves sorting and selecting the design schemes that satisfy the specified requirements. This process is facilitated by optimizing the weighted calculation of the objective function values. In this context, the weights are adjusted in accordance with the input requirements. It is important to note that the thickness of the insulation layer plays a crucial role in determining both the heat dissipation performance and the weight of the product. Additionally, the diameter of the tank, as well as the thickness and radius of the tank, significantly influences the compression deformation of the tank. To effectively represent the excellence of each particle in terms of different objective function values, it becomes essential to normalize the fitness of the particles prior to performing the weighted calculation. The specific process for fitness normalization is outlined as follows.

$$z_{nor}={\displaystyle \frac{z-z_{\min }}{z_{\max }-z_{\min }+1e^{-10}}}$$

(18)

where z is the fitness before normalization, z_nor represents the normalized fitness, z_min is the minimum fitness within the Pareto frontier solution, z_max is the maximum fitness within the Pareto frontier solution. To prevent the situation where the minimum value is normalized to 0, increase the bias coefficient by 1 × 10⁻¹⁰. Fitness normalization can characterize the superiority or inferiority of the objective function at different scales during the optimization process, providing a standard reference for subsequent fitness evaluation.

Subsequent to the normalization of fitness values, the weight coefficients are adjusted in accordance with the specified input requirements.

$$Z={\omega }_t{z}_{u,cold}+{\omega }_u{z}_u+{\omega }_m{z}_m$$

(19)

where ${\omega }_t$, ${\omega }_u$ and ${\omega }_m$ represent the heat dissipation weight, compression deformation weight, and weight of the mass, respectively. z_t, z_u, and z_m specifically denote the normalized values of heat dissipation, compressive deformation, and weight associated with each particle, respectively.

In the design process of vehicle LNG storage tanks, it is necessary to reasonably set their weight coefficients to achieve the coordination and unity of structural performance and actual engineering requirements. First of all, the storage tank must have sufficient structural strength to ensure its safe and reliable operation under all working conditions. This is the primary prerequisite and fundamental guarantee for the design. Secondly, the insulation performance of the storage tank should be emphasized to reduce the heat exchange between the internal low-temperature medium and the external environment, thereby minimizing evaporation losses and enhancing the overall energy efficiency of the storage tank. Finally, the weight of the storage tank is optimized and controlled to achieve the goal of lightweight design.

The weighted evaluation and ranking of optimized design parameter schemes can significantly assist users in swiftly identifying the most suitable parameter configurations [45]. The optimization objective of the optimization function in this article is to reduce the values of each objective function. By taking negative values of the weights, the evaluation function is maximized while achieving the optimization goal. In order to facilitate the observation of the optimization of different objective functions of the automotive LNG storage tank products, all the weight coefficients are set to the same; that is, the optimization algorithm will optimize the three optimization objectives equally. Therefore, a weighted parameter is set to ${\omega }_t=-0.333$, ${\omega }_u=-0.333$ and ${\omega }_m=-0.333$, to identify the global optimal samples of the products.

For the weighted calculation ranking in the Pareto frontier solution, in this paper, the weights of the three objective functions are set to be the same. Therefore, the design parameter scheme with a higher ranking will be selected as the parameter scheme that is the best for the combination of the three objective functions, rather than the solution on the edge. Usually, solutions on the edge tend to have one objective function receive a high score while performing poorly on other objective functions. Therefore, a strategy where the weights of the three objective functions are the same will result in solutions in the middle region of the leading edge having a high evaluation. In actual design and production, users can adjust the weights of different goals at any time to achieve different emphases. 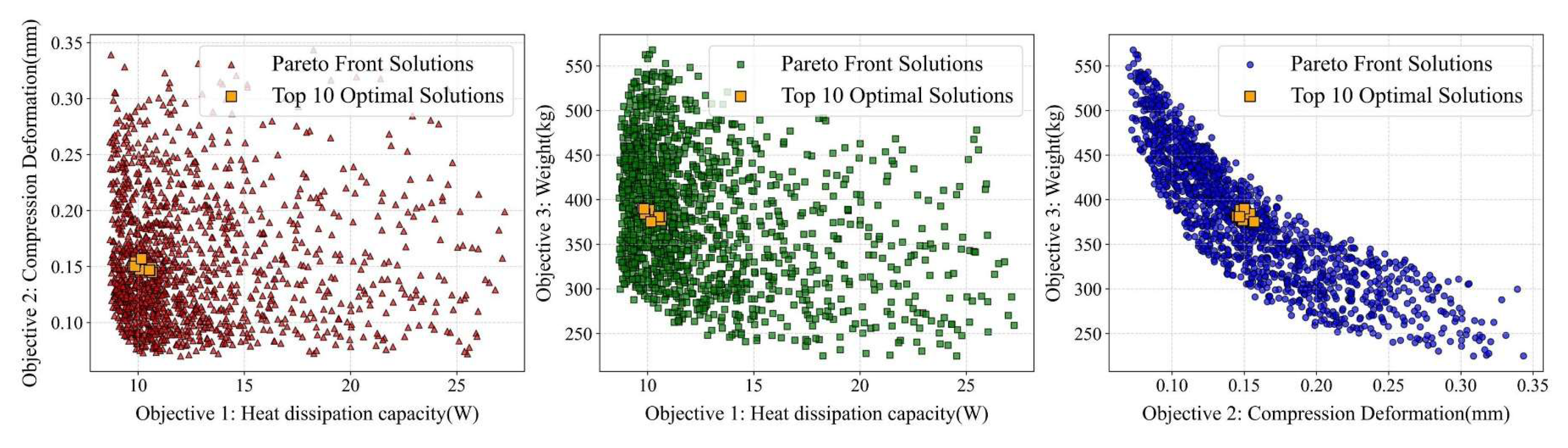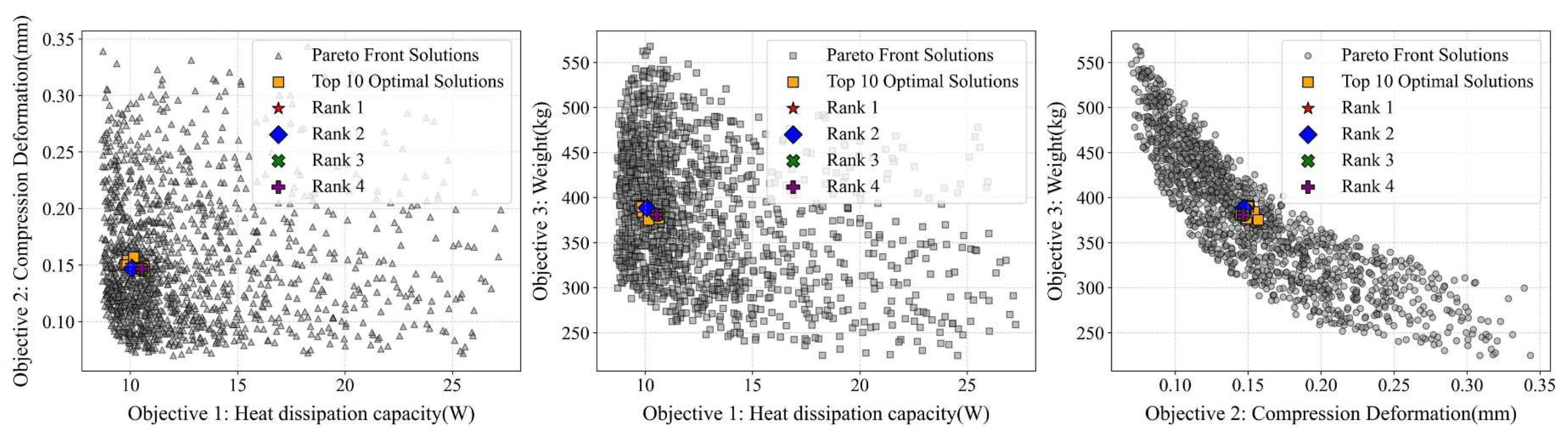Figure 6 presents the distribution of Pareto boundary solutions. According to the weight calculation results, the top 10 Pareto boundary solutions are represented by orange squares. This visualization result provides a valuable reference for evaluating and comparing the optimized design schemes. Among them, the parameter schemes represented by orange represent the design schemes with a higher evaluation level. Figure 7 shows the distribution of the top four design schemes with weighted ranking scores in the Pareto front solution set. The table displays the specific design parameters and objective function values within the top four design parameter schemes.

Table 3. Corresponding objective function values in Pareto front solutions.

Case	Heat Dissipation Capacity (W)	Compression Deformation (mm)	Weight (kg)
Rank1	10.043	0.150	386.042
Rank2	10.080	0.147	388.607
Rank3	10.536	0.147	380.930
Rank4	10.553	0.147	380.888

shows the objective function values corresponding to the top four parameter schemes in the Pareto frontier solution.

3.4. Calculation Strategy of Optimization Function of Vehicle LNG Storage Tank Parameter Model

The optimization function calculation based on the parameter model of the vehicle LNG storage tank primarily considers three key factors: the heat dissipation of the storage tank at a specific temperature, the compression deformation of the storage tank inner vessel at a particular working pressure, and the total weight of the storage tank. In this study, the multi-objective example group optimization algorithm is applied to address the optimization problem of these three objective functions in a simultaneous manner. The following assumptions are made during the iterative solution process:

(1)

When calculating the box’s heat dissipation, the influence of the tank’s valve structure on heat dissipation is neglected.

(2)

When calculating the heat dissipation of storage tanks, thermal radiation and heat transfer are disregarded.

(3)

When calculating the compression deformation of the tank body, the rigidity factors at the top and bottom of the tank body are ignored, and the tank body is treated as an infinite cylinder under the action of a uniformly distributed load.

The experiments utilize a computer equipped with an Intel 12600KF CPU (10 cores, 16 threads, 3.70 GHz) and 32 GB of memory (Fab 42 Wafer Fabrication Plant, Pheonix, AZ, USA).

The PSO model is implemented using the Python 3.12 programming language. Additionally, extension libraries are utilized to optimize the design parameters and adjust the optimization function. After iteration, the average fitness of the Pareto frontier solution is assessed. A larger number of iterations and population size can ensure that the iterative evaluation reaches stability before the iteration is completed and that there are sufficient parameter scheme samples in the Pareto frontier solution for designers to refer to. The maximum number of iterations k is set to 3000, and the number of particles is set to 3000. Moreover, the learning coefficients are defined as c₁ = 0.7 and c₂ = 0.7. After training, the Pareto solution set typically contains around 1000 samples to choose from and presents a continuous asymptotic pattern distribution in the graph. The learning rate is combined with the maximum number of iterations to ensure sufficient convergence accuracy and better solution quality.

3.5. Automatic Model Generation

In the intelligent design system, automated modeling is accomplished through the three-dimensional modeling technology. This intelligent design approach enhances efficiency and accuracy by leveraging MOO algorithms to generate optimal design schemes. Subsequently, via three-dimensional modeling technology and programming, the system enables automated three-dimensional model generation by inputting design parameters. The steps for automatically generating the model are shown in Figure 8.

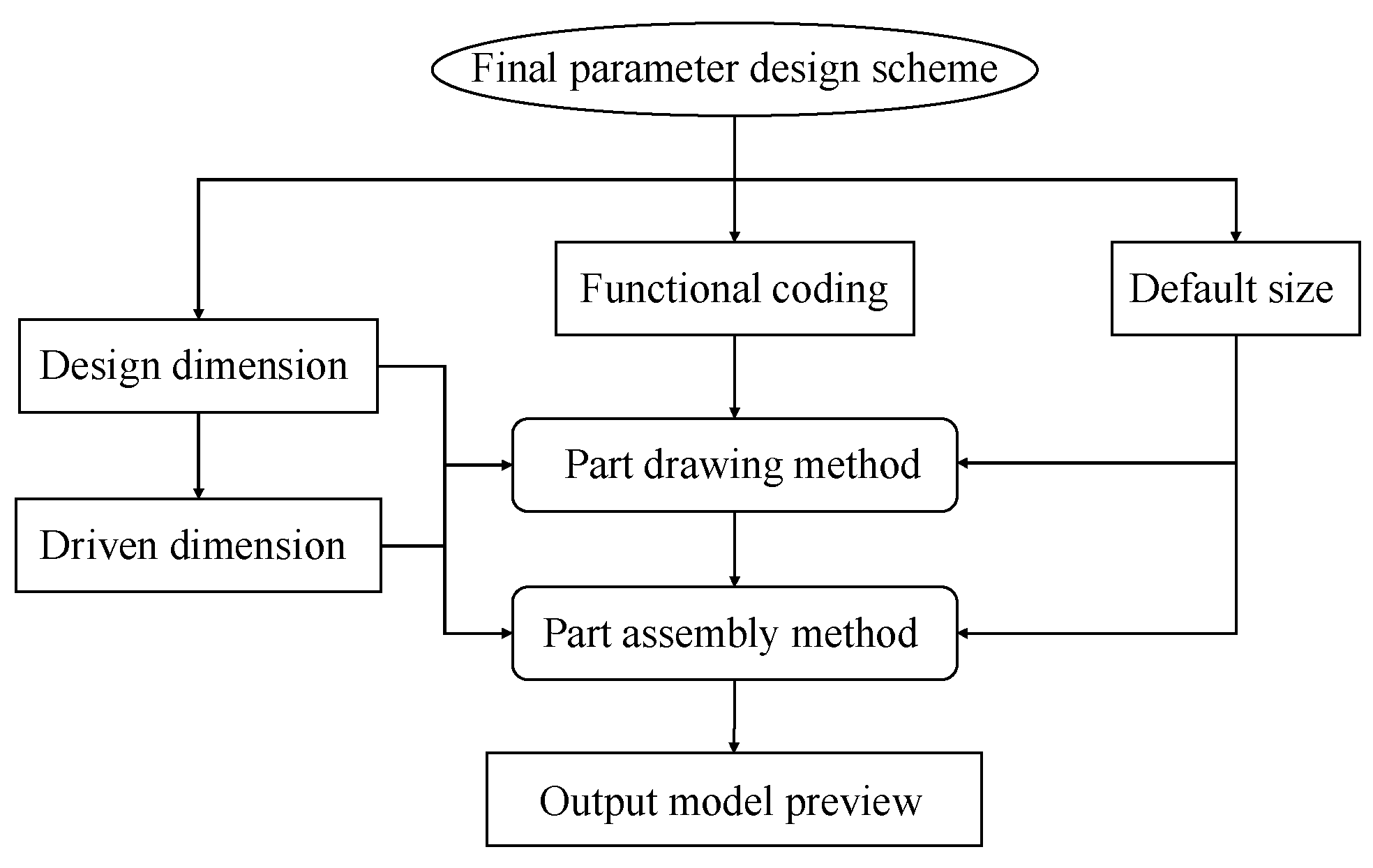
The three-dimensional modeling software API facilitates automation tasks and software extensions through programming. By invoking API methods, the program automates the creation of three-dimensional models for vehicle-mounted LNG storage tank products based on specific parameter schemes. Parametric analysis plays a crucial role in model generation by improving model management, reducing program complexity, and minimizing runtime. The system defines part feature sizes using driving and driven dimensions, collects all necessary feature sizes for assembly model generation, and transmits them to the system to construct a complete assembly model.

During automated modeling, the system transmits activity size and functional coding parameters to the modeling program. Upon receiving the parameter scheme, the system processes the activity size and functional codes to calculate driving dimensions and derive all design dimensions. Based on the functional coding, the system invokes distinct automated modeling methods for different parts to generate structural models. Finally, these parts are assembled into a complete model, and visual results are output, thereby efficiently completing the entire design process. In the specific data transmission process, we use c# to write the secondary development program of the 3D drawing software and through. The implementation of the NET file package enables the invocation of c# programs through Python, achieving the secondary development of software drawing.

4. Results and Discussion

The intelligent design system, which integrates a MOPSO algorithm and Three-dimensional automatic modeling technology, can replace designers in completing the parameter design and model generation of vehicle LNG storage tank. It thereby enhances the efficiency of tank design and strengthens the control over design outcomes. In this section, vehicle LNG tanks with capacities of 150 L, 250 L, 350 L, and 450 L are designed. By comparing with the performance of traditional LNG storage tanks for vehicles, the optimization effect of the intelligent design method on storage tank design time and the optimization results of different objective functions were analyzed, thereby demonstrating the feasibility and advantages of the intelligent design method.

4.1. Multi-Objective Optimization and Result Analysis

Based on the three-objective function model of heat dissipation, structural deformation, and total mass established in Section 2, this study utilizes the intelligent design system to optimize the parameters of four LNG tanks with target capacities of 150 L, 250 L, 350 L, and 450 L under predetermined settings. The optimal parameter design schemes for storage tanks of varying capacities are meticulously detailed in

Table 4. The intelligent design method is used to design the optimal design parameters and objective function values of vehicle LNG storage tanks.

Capacity (L)	Inner Vessel Radius (m)	Thickness of Insulation Layer (m)	Inner Vessel Thickness (mm)	Heat Dissipation Capacity (W)	Compression Deformation (mm)	Weight (kg)
150	0.221	0.106	5.142	6.612	0.110	133.772
250	0.260	0.118	7.185	7.935	0.109	236.252
350	0.295	0.123	7.521	9.082	0.134	308.963
450	0.309	0.123	7.343	10.529	0.151	375.244

. The distribution of the corresponding Pareto frontier solutions is depicted in Figure 9a–d, which reveal the trade-off relationship between different performance objectives. To evaluate the optimization effect of the intelligent design system, this study selects the design parameters of vehicle LNG storage tanks with the same capacity, which were designed using the traditional method, as a comparison. Their performance indices are calculated based on the same objective function model, and the calculated results are presented in

Table 5. Design parameters and objective function values of traditional vehicle LNG storage tanks.

Capacity (L)	Inner Vessel Radius (m)	Thickness of Insulation Layer (m)	Inner Vessel Thickness (mm)	Heat Dissipation Capacity (W)	Compression Deformation (mm)	Weight (kg)
150	0.258	0.100	4.000	6.563	0.193	106.529
250	0.258	0.100	6.000	9.046	0.129	204.186
350	0.258	0.100	8.000	10.101	0.096	332.630
450	0.412	0.100	8.000	11.582	0.246	313.918

. Figure 10 shows the differences in various objective functions between the automatically designed storage tank and the manually designed one.

When juxtaposed with traditional tank design examples, the LNG storage tanks optimized by the intelligent design system—encompassing capacities of 150 L, 250 L, 350 L, and 450 L—demonstrate a notable reduction in heat dissipation, averaging a decrease of 8.992%. Similarly, the compression deformation of the tank inner vessel exhibits a significant average reduction of 26.015%. These reductions underscore the intelligent optimization’s capacity to enhance the thermal insulation performance of storage tanks and to augment their structural strength, thereby addressing critical aspects of tank functionality and longevity. Regarding the total weight of the storage tanks, the intelligent design scheme reveals a pattern of fluctuation. Specifically, the 150 L, 250 L, and 450 L tanks experience weight increases of 27.243 kg, 32.006 kg, and 61.326 kg, respectively. Conversely, the 350 L storage tank evidences a weight reduction of 23.667 kg. When consolidating these findings, the average total weight across all optimized tanks shows an increase of 14.45%. This outcome illustrates that while the optimization process prioritizes the enhancement of thermal and mechanical performance, it concurrently results in a discernible increase in the total mass of the tanks. The increase in the mass of the storage tank will lead to an increase in the overall vehicle mass, thereby having an adverse impact on the vehicle’s load-bearing capacity and economy. The unit energy consumption during driving will increase, which may weaken some of the cost advantages of LNG as a clean energy source. Such a trade-off is an inherent aspect of MOO, where improvements in certain performance metrics may lead to compromises in others. In terms of computational efficiency, the intelligent design system demonstrates remarkable performance. The system accomplishes the optimal design of the four aforementioned storage tanks in 1272.6 s, 1557.4 s, 1353.7 s, and 1427.9 s, respectively. By reducing the parameter design period to under 28.35 min, the intelligent design system significantly enhances the efficiency of product design.

It should be emphasized that in this study, the objective function weight combinations of ω_t = −0.333, ω_u = −0.333, and ω_m = −0.333 not only enhances the storage tank’s thermal insulation and compression resistance capabilities but also plays a crucial role in ensuring the stable storage and transportation of LNG. By effectively reducing the vaporization rate of LNG and mitigating the risk of pressure increases within the tank caused by vaporization, the overall safety of the storage tank is significantly improved. However, this design approach also leads to an increase in the total weight of the storage tank at certain capacities, which reflects the inherent trade-off between performance and weight in MOO.

In general, compared to traditional design methods, the optimal parameter design scheme for vehicle LNG storage tanks generated by the intelligent design system demonstrates markedly better performance in thermal insulation and structural strength. Although there is a certain trade-off in terms of lightweight design, its comprehensive performance more effectively meets the practical operational requirements of vehicle LNG storage tanks. This provides a scientific and reliable reference for the practical engineering design and application of vehicle LNG storage tanks, offering significant guidance for their development and optimization.

4.2. Analysis of Automatic Modeling System

As previously mentioned, the intelligent design system employs a MOPSO algorithm to optimize the key parameters of vehicle LNG storage tanks. It ultimately outputs a set of Pareto optimal design parameter solutions that effectively represent the relationship between different performance objectives. Once the designer specifies the objective function weights according to particular project requirements, the system automatically transfers the precise design parameters of the final implementation plan to the downstream model generation module. The core of this module is parameterized three-dimensional automatic modeling technology. After receiving the optimal parameter set from the upstream process, the module drives the three-dimensional automatic modeling technology to automatically construct a complete three-dimensional assembly model of vehicle LNG storage tanks.

Figure 11a vividly illustrates the three-dimensional model structures of four LNG storage tanks with varying capacities, which are automatically generated by the intelligent design system. These models encompass all the key components essential for achieving the core functions and ensuring the safe operation of the storage tanks. Specifically, the models incorporate valve pipelines, protective rings, bases, outer shells, and inner container structures. The valve pipelines serve the critical function of facilitating LNG supply and pressure adjustment within the storage tank. Protective rings are strategically placed around the external valve pipelines to provide robust protection against deformation and damage that may result from collisions or other mechanical impacts. The outer shell and inner container structures work in tandem to store and insulate the LNG, ensuring its stability and safety during both storage and transportation. By leveraging three-dimensional automatic modeling technology instead of traditional manual drawing methods for the tank structure, the generation times for the four tank models are remarkably efficient at 125.5 s, 134.0 s, 143.7 s, and 124.2 s, respectively. This results in an average model generation time of just 131.85 s. This significant reduction in time highlights the efficiency and effectiveness of the automated model generation process.

When compared to the conventional and often tedious process of manually creating and modifying models within a CAD environment by designers, the intelligent design system adopts Three-dimensional automatic modeling technology to achieve fully automatic model construction. For the four types of tanks mentioned above, the automatic generation times for the three-dimensional models are a mere 125.5 s, 134.0 s, 143.7 s, and 124.2 s, respectively. The average time consumption is as low as 131.85 s. This automated process not only drastically reduces the time required for model generation but also effectively minimizes potential errors that are commonly associated with manual modeling. Consequently, it ensures a high degree of consistency between the generated model and the optimization scheme. Figure 11b–e clearly indicates the distribution position of the system’s optimal design parameter scheme on the Pareto frontier under given weight configurations.

Designing vehicle LNG storage tanks using traditional methods presents a significant challenge. Conventional approaches demand that designers invest considerable time in balancing conflicting design objectives. They require manual parameter setting, performance calculation checking, model building, and model modification. Particularly during the scheme adjustment phase, any change in design variables necessitates the reconstruction and re-simulation of the parameter model. This laborious process struggles to keep pace with the rapidly growing demand for vehicle LNG storage tank designs. In contrast, the intelligent design system empowers designers to swiftly generate product design schemes. By setting weight coefficients, designers can select optimal schemes tailored to diverse requirements and realize the automatic generation of LNG tank models through Three-dimensional automatic modeling technology. This significantly alleviates the designer’s workload and enhances design efficiency.

5. Conclusions

This study proposes an innovative intelligent design methodology that harnesses a MOPSO algorithm to refine product design parameters. Subsequently, it employs the three-dimensional automatic modeling technology to automatically generate design schemes. Tests were conducted on LNG storage tanks of various capacities, achieving automated design and model generation for vehicle LNG storage tanks. The key findings and contributions of this research are detailed as follows:

• This research delves into the distribution performance of Pareto optimal solutions for MOPSO algorithms with both fixed and dynamic inertia weight strategies. By integrating a sinusoidal dynamic inertia weight strategy, the algorithm demonstrates superior performance in reducing heat dissipation and weighted average values compared to the conventional fixed inertia weight strategy. Specifically, the evaluation parameter for HV is enhanced by 31.937%, underscoring the effectiveness of the dynamic inertia weight approach in achieving better optimization outcomes.
• By substituting manual design processes with a PSO algorithm, this study achieves the completion of parameter design for vehicle LNG storage tanks within a 25 min timeframe. The results reveal that this method places a greater emphasis on optimizing the heat dissipation and compression deformation objective functions. Statistical analysis indicates that, on average, the heat dissipation of the tank is reduced by 8.992%, compression deformation by 26.015%, and total tank weight is increased by 14.452%, all based on the optimal design parameters of the vehicle LNG tank model. These improvements highlight the method’s potential in enhancing the thermal and structural performance of LNG storage tanks.
• Through the three-dimensional automatic modeling technology, this study has successfully implemented an automated system for reading parameter scheme details and generating corresponding models. Utilizing this approach, the automatic model generation times for 150 L, 250 L, 350 L, and 450 L LNG tank models are 125.5 s, 134.0 s, 143.7 s, and 124.2 s, respectively. This signifies a significant reduction in model generation time, enhancing the overall design efficiency and accuracy.

In response to the issue of increased design weight of storage tanks, in the future, lightweight and high-strength materials such as carbon fiber composites or aluminum alloys can be used to effectively reduce weight while maintaining structural integrity and thermal performance. Based on parametric design, the wall thickness of the storage tank is finely adjusted. Or in the existing optimization framework, weight can be regarded as a more important objective function to achieve a trade-off among heat dissipation, deformation and mass.

In conclusion, traditional product design methods have long been limited by low efficiency and excessive reliance on designers’ experience and professional knowledge, making it difficult to meet the current demands of green and low-carbon transformation. To address the above issues, this study proposes an intelligent design method that integrates the MOPSO algorithm with 3D automatic modeling technology, promoting the evolution of the product design process towards high efficiency, accuracy and resource conservation. In the design case of vehicle-mounted LNG storage tanks, this method can complete parameter design and model generation within 28.35 min, significantly reducing the consumption of human and time resources and improving design accuracy and efficiency. This method not only helps optimize the performance and material utilization efficiency of energy equipment, but also provides an expandable framework and implementation path for the parametric design of other products under a sustainable orientation. This work lays a foundation for automating mechanical product design, particularly for systems that rely on empirical formulas to calculate and must balance multiple, often competing, design objectives. The methodologies developed here have the potential to significantly streamline the design process, thereby contributing to more sustainable manufacturing practices and accelerating the green transformation of the industry.